Курсовая работа: Современная научно-техническая документация на статистические методы анализа результатов измерений
«Современная НТД на статистические методы анализа прямых,
косвенных, совместных, однократных и многократных измерений»
План
1. Обеспечение единства измерений
2. Характеристики погрешности измерений
3. Методы обработки результатов прямых однократных измерений
4. Метод обработки результатов прямых измерений с многократным наблюдением
5. Методы обработки результатов косвенных измерений.
6. Обработка данных косвенных измерений выборочным методом
Список использованной литературы
1. Обеспечение единства измерений
Метрология – отрасль физики, изучающая единицы измерения, устанавливающая эталоны и разрабатывающая методы и средства точных измерений, а также способы достижения требуемой точности.
Практическая метрология занимается изучением вопросов практического применения в различных сферах деятельности разработок теоретической метрологии с обязательным применением положений законодательной метрологии. Таким образом, сущность практической метрологии сводится к измерению любой заданной величины любого объекта измерения и получение результата измерения с максимально возможной точностью.
Следовательно, непосредственной целью измерения (по определению МИ 1317 – 2004) является определение истинных значений постоянной или изменяющейся измеряемой величины. Результат измерений является реализацией случайной величины, равной сумме истинного значения измеряемой величины и погрешности измерения. В качестве измеряемых величин принимают параметры модели объекта измерений.
С целью исключения разночтений различных методик проведения измерений, самодеятельности в обработке результатов измерений, и их статистического анализа создана законодательная база, устраняющая все вышеперечисленные недостатки и на государственном уровне создавшая систему обеспечения единства измерений.
По данному разделу работы можно указать следующую НТД:
РМГ 29 – 99 Государственная система обеспечения единства измерений. Метрология. Основные термины и определения.
ГОСТ Р 8. 563 – 96 Государственная система обеспечения единства измерений. Методика выполнения измерений.
ГОСТ 8. 009 – 84 Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерения.
МИ 1317 – 2004 Рекомендация. Результаты и характеристики погрешностей измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров.
РД 50 – 453 – 84 Государственная система обеспечения единства измерений. Характеристики погрешностей средств измерений в реальных условиях эксплуатации. Методы расчета.
Несмотря на то, что ряд НТД носит рекомендательный характер, положения, изложенные в них, являются обязательными для исполнения и распространяются на нормативные, методические и технические документы, техническую литературу, в которой указывают требования к измерениям или описывают измерения, проводимые в научных исследованиях и др.
Для удобства работы с числовыми значениями результатов измерений и погрешностей измерений, МИ 1317 – 2004 рекомендует наименьшие разряды числовых значений результатов измерений принимать такими же, как и наименьшие разряды числовых значений среднего квадратического отклонения абсолютной погрешности измерений или числовых значений границ, в которых находится абсолютная погрешность измерений (или статистических оценок этих характеристик погрешности).
В качестве функции плотности распределения вероятностей погрешности измерения принимают закон, близкий к нормальному усеченному, если имеются основания предполагать, что реальная функция распределения−функция симметричная, одномодальная, отличная от нуля на конечном интервале значений аргумента, и другая информация о плотности распределения отсутствует.
В качестве функции плотности распределения вероятностей составляющих погрешности измерений, для которых известны только пределы допускаемых значений, т.е. границы интервала, в которых находится соответствующая составляющая погрешности измерений с вероятностью 1, при расчетах характеристик погрешности измерений принимают закон равномерной плотности, если отсутствует информация об ином виде распределения.
2. Характеристики погрешности измерений
Рекомендация МИ 1317 – 2004 устанавливает следующие группы характеристик погрешности измерений:
1. Задаваемые в качестве требуемых или допускаемых – нормы характеристик погрешности измерений (нормы погрешности измерений).
2. Приписываемые любому результату измерений из совокупности результатов измерений, выполняемых по одной и той же аттестованной МВИ– приписанные погрешности измерений.
3. Отражающие близость отдельного, экспериментально полученного результата измерений к истинному значению измеряемой величины – статистические оценки характеристик погрешности измерений (статистические оценки погрешности измерений).
Нормы погрешности измерений, а также приписанные характеристики – представляют собой вероятные характеристики (характеристики генеральной совокупности) случайной величины – погрешности измерений. Эти нормы применяют преимущественно при массовых технических измерениях, выполняемых, например, при технологической подготовке производства, в процессе разработки, испытаний и эксплуатации продукции и т.п.
При измерениях, которые выполняются при проведении научно – исследовательских и метрологических работ (определение физических констант; свойств и состава стандартных образцов и т.п.) преимущественно применяют статистические оценки погрешности измерений. Они представляют собой статистические (выборочные) характеристики случайной величины – погрешности измерения.
В тоже время Рекомендация устанавливает следующие альтернативные вероятностные и статистические характеристики погрешности измерений:
1. среднее квадратическое отклонение погрешности измерений;
2. границы, в пределах которых погрешность измерений находится с заданной вероятностью;
3. характеристики случайной и систематической составляющих погрешности измерений.
Характеристики погрешности измерений и их статистическая оценка приведены в таблице 1.
Таблица 1.
| Характеристики погрешности измерений | Статистические оценки (по2.1.3) |
| Среднее квадратическое отклонение погрешности измерений |
Оценка |
| Границы, в которых погрешность измерений находится с заданной вероятностью |
Оценка нижней |
| Характеристики случайной составляющей погрешности измерений: Среднее квадратическое отклонение нормализованная автокорреляционная функция Характеристики нормализованной автокорреляционной функции (например, интервал корреляции) |
Оценка Оценка функции Оценка характеристики |
| Характеристики неисключенной систематической составляющей погрешности измерений: среднее квадратическое отклонение неисключенной систематической составляющей границы, в которых неисключенная систематическая составляющая находится с заданной вероятностью |
Оценка Оценка нижней |
В таблице 1 приведены обозначения для характеристик абсолютной погрешности измерений. Для обозначения характеристик относительной погрешности букву ∆ заменяют на д.
Рекомендуемое значение вероятности (доверительной вероятности) Р = 0,95 .
В особых случаях, например при измерениях, которые нельзя повторить, допускается указывать доверительные границы или расширенную неопределенность для уровня доверия Р и более высоких вероятностей.
Статистические оценки характеристик погрешности измерений представляют одной или при необходимости несколькими характеристиками и указывают их в единицах измерения (абсолютные) или процентах (долях) от результата измерения (относительные).
3. Методы обработки результатов прямых однократных измерений
В практической деятельности большинство проводимых измерений являются прямыми и однократными, в обычных условиях их точность вполне приемлема.
Прямые однократные измерения – процесс, при котором искомое значение величины находят непосредственно из опытных данных, причем сам процесс измерения выполняется только один раз.
За результат однократного измерения А принимается значение величины, полученное при измерении.
Выполнение однократных измерений обосновывают следующими факторами:
− производственной необходимостью (невозможность повторения измерения, экономическая целесообразность и т. д.);
− возможностью пренебрежения случайными погрешностями;
− случайные погрешности существенны, но доверительная граница погрешности результата измерения не превышает допускаемой погрешности измерения.
Метрологический анализ однократного измерения выявляет одно в нем следующие особенности:
1. Из множества возможных значений отсчета получается и используется только одно.
2. Представление о законе распределения вероятностей отсчета и его среднем квадратическом отклонении формируется на основе информации и опыта ранее проведенных аналогичных измерений.
При использовании этой информации уточняется:
− физическая сущность изучаемого явления;
− уточняется его модель;
− определяются факторы, влияющие на точность измерения, и меры, направленные на уменьшение влияния этих факторов (экранирование, компенсация электрических и магнитных полей и др.);
− значения поправок;
− выбор решения в пользу той или иной методики измерения;
− выбирается средство измерения, изучаются его метрологические характеристики и опыт проведения подобных измерений, проводимых ранее.
Итогом этой предварительной работы должна стать твердая уверенность в том, что точность однократного измерения достаточна для решения поставленной задачи.
Если это условие выполняется, то производится процесс измерения с целью получения одного значения отсчета.
Но поскольку отсчет (по основному постулату метрологи) является случайным числом, а одно единственное значение отсчета xi и получения одного единственного значения показаний Xi средства измерения, имеющего туже размерность, что и измеряемая величина, это приводит к выводу – необходимо определить погрешность, которая допущена при измерении, и провести оценивание этой погрешности.
Существует две методики оценивания погрешностей и неопределенности результата измерений, которые представлены в НТД Р 50. 038 – 2004 «Измерения прямые однократные» и подразделяются на два типа: тип А и тип В согласно требованиям РМГ 43 – 2001 (Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений»).
Оценивание погрешности и неопределенности результата измерения по методике типа А соответствует методике выражения неопределенности измерений, принятых в основополагающих документах (НД) по метрологии, применяемых в странах – участниках Соглашения.
При оценивании погрешности и неопределенности результата измерения по методике типа В, принятой «Руководством», учитывается, что составляющими погрешности результата измерения являются погрешности СИ (средство измерения), метода измерения, оператора, а также погрешности, обусловленные изменением условий измерения. Погрешность результата однократного измерения чаще всего представлена НСП (неисключенная систематическая погрешность) и случайными погрешностями.
Характеристики НСП в этом случае могут быть представлены границами ±и и доверительными границами ±и(Р), а характеристикой случайных погрешностей могут быть – СКО S и доверительные границы ±е(Р).
Погрешности СИ определяют на основании их метрологических характеристик, которые указываются в нормативных и технических документах; погрешности метода измерения и оператора должны быть определены при разработке и аттестации конкретной МВИ.
Оценивание случайной погрешности и стандартной неопределенности, оцениваемой по типу А, результата измерения
Доверительные границы случайной погрешности и стандартную неопределенность результата измерения вычисляют в следующем порядке.
Если случайные
погрешности представлены несколькими СКО Si![]() , то СКО результата однократного
измерения S(A) вычисляют по формуле:
, то СКО результата однократного
измерения S(A) вычисляют по формуле:

1. Учитывая то, что погрешности представлены несколькими СКО, тогда стандартную неопределенность результата однократного измерения UA вычисляют по формуле:
![]()

Где m - число составляющих случайных погрешностей;
UiA = Si.
Доверительную границу случайной погрешности измерения е(P) вычисляют по формуле
![]()
где ZP/2 – P/2 точка нормированной функции Лапласа, отвечающая вероятности P .При доверительной вероятности P = 0,95 Z095/2 принимают равным 2, при P=0,99 Z0,99/2=2,6 .
Если случайные погрешности представлены доверительными границами еi(P), соответствующими одной и той же вероятности, доверительную границу случайной погрешности результата однократного измерения вычисляют по формуле:

1.4. Если случайные погрешности представлены доверительными границами, соответствующими разным вероятностям, сначала определяют СКО измерения по формуле:

А затем вычисляют доверительные границы случайной погрешности результата измерения по формуле
![]()
Оценивание неисключенной систематической погрешности и стандартной неопределенности, оцениваемой по типу В, результата измерения.
При условии, когда неисключенная систематическая погрешность (НСП) выражена границами этой погрешности и если среди составляющих погрешности результата измерения в наличии одна НСП, то стандартную неопределенность UB, обусловленную неисключенной систематической погрешностью, заданной своими границами ± И оценивают по формуле:
![]()
Доверительные границы НСП результата измерения вычисляют следующим образом:
1.5. Доверительную
границу НСП результата измерения (без учета знака) при наличии нескольких НСП,
заданных своими границами ![]() , доверительную границу НСП
результата измерения (без учета знака) вычисляют по формуле
, доверительную границу НСП
результата измерения (без учета знака) вычисляют по формуле
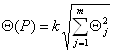
где k – поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих
При доверительной вероятности Р =0,95 поправочный коэффициент k принимают равным 1,1.
При доверительной вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если число суммируемых составляющих m
Если число составляющих равно четырем (m = 4), то поправочный коэффициент k ≈ 1,4; при m = 3 k ≈ 1,3; при m = 2 k ≈ 1,2.
Суммарную стандартную неопределенность Uc,B (при условии, указанном выше в п. 1.1) вычисляют по формуле

1. 6. При наличии нескольких НСП, заданных доверительными границами рассчитанными по формуле п.1,1. доверительную границу НСП результата однократного измерения вычисляют по формуле

Суммарную стандартную неопределенность с учетом условий, указанных выше, вычисляют по формуле

где ![]() − доверительная
граница j − й НСП, соответствующая
доверительной вероятности Рi;
− доверительная
граница j − й НСП, соответствующая
доверительной вероятности Рi;
k и ki − коэффициенты, соответствующие доверительной вероятности Р и Рi
Оценивание погрешности и расширенной неопределенности результата измерения.
1. 7. Если погрешности метода измерения и оператора пренебрежимо малы по сравнению с погрешностью используемых СИ (не превышает 15% погрешности СИ), то за погрешность результата измерения принимают погрешность используемых СИ.
1.8. Если ![]() то НСП или стандартной
неопределенностью, оцениваемой по типу В, пренебрегают и принимают в качестве
погрешности или неопределенности результата измерения доверительные границы
случайной погрешности или расширенную неопределенность для уровня доверия Р,
вычисляемую по формуле
то НСП или стандартной
неопределенностью, оцениваемой по типу В, пренебрегают и принимают в качестве
погрешности или неопределенности результата измерения доверительные границы
случайной погрешности или расширенную неопределенность для уровня доверия Р,
вычисляемую по формуле ![]()
Если ![]() то случайными
погрешностями или стандартной неопределенностью, оцениваемой по типу А,
пренебрегают и принимают в качестве погрешности или неопределенности результата
измерения границы НСП или расширенную неопределенность для уровня доверия Р,
вычисляемую по формуле
то случайными
погрешностями или стандартной неопределенностью, оцениваемой по типу А,
пренебрегают и принимают в качестве погрешности или неопределенности результата
измерения границы НСП или расширенную неопределенность для уровня доверия Р,
вычисляемую по формуле ![]()
1.9. Если ![]() то доверительную
границу погрешности результата измерений ∆Р вычисляют по формуле
то доверительную
границу погрешности результата измерений ∆Р вычисляют по формуле
![]()
где К – коэффициент , значение которого для доверительной вероятности 0,95 равно 0,76; для доверительной вероятности 0,99 значение коэффициента К равно 0,83.
Расширенную неопределенность для уровня доверия Р вычисляют по формуле
![]()
где к0 коэффициент охвата (коэффициент, используемый как множитель суммарной неопределенности для получения расширенной неопределенности). Значения коэффициента охвата для доверительной вероятности Р = 0,95 считают равным 2, для доверительной вероятности Р = 0,99 − равным 3.
1.10. Форма представления результатов однократных измерений должна соответствовать МИ1317.
1.11. При симметричной доверительной погрешности результата однократного измерения представляют в форме A;± ∆(P); P или A± ∆(P), или A; U(P).
4. Метод обработки результатов прямых измерений с многократным наблюдением
Метод обработки результатов прямых измерений с многократным наблюдениями заключается в следующем. В основе любого измерения лежат прямые измерения, в ходе которых находят некоторое числовое значение физической величины. С математической точки зрения прямое измерение можно выразить уравнением, которое имеет вид:
y = cx
где y – значение исследуемой величины;
с – цена деления шкалы прибора в единицах измеряемой величины;
x – отсчет по индикаторному устройству в делениях шкалы.
Каждая измерительная операция (отсчет, замер) называется наблюдением.
Теоретически, для достижения более точных значений погрешностей измерений, необходимо провести бесконечное число наблюдений, что нереально. На практике ограничиваются конечным числом наблюдений (от единицы до нескольких десятков или сотен). Полученный при этом ряд значений физической величины x1 , x2, x3…xi называют выборкой, а
R = xmax – xmin − размахом выборки.
Методы обработки результатов прямых измерений с многократными
После проведения измерений и получения результатов этих измерений необходимо:
Устранить из выборки очевидные промахи, т. е. вид грубой погрешности, зависящий от оператора и связанный с неправильным обращением со средством измерения: неверными отсчетами показаний приборов, описками при записи результатов, невнимательностью экспериментатора и т. п.
Промахи обнаруживают нестатистическими методами; и результаты наблюдений, содержащие промахи, как заведомо неправильные исключают из рассмотрения.
Исключить из результатов наблюдений систематические погрешности, являющиеся составляющими погрешности измерения и остающимися постоянной или закономерно меняющимися при повторных измерениях.
Упорядочить выборку в порядке возрастания ее элементов x↑I
![]()
Провести проверку выборки на наличие грубых погрешностей и ее связанность по размаху выборки
![]() при i=1……………n-1
при i=1……………n-1
и проверить, содержит ли крайний элемент грубую погрешность.
Грубые погрешности крайних элементов из рассмотрения исключить.
Если выборка не является связной – эксперимент необходимо повторить.
Результат измерения и оценка его среднего квадратического отклонения.
После исключения грубых погрешностей из результатов измерений вычисляется среднеарифметическое исправленных результатов наблюдений. Эта величина принимается за результат измерения.
![]()
где n – число исправленных наблюдений.
Если во всех результатах наблюдений содержится постоянная систематическая погрешность, допускается ее исключать, но после вычисления среднего арифметического исправленных результатов измерений.
Вычисляется оценка среднего квадратического отклонения результатов измерения по формуле

Эта величина позволяет проверить, не являются ли некоторые сомнительные результаты наблюдений ошибочными.
Если окажется, что
сомнительные значения отличаются от вычисленной величины ![]() больше, чем на три, то
их следует исключить.
больше, чем на три, то
их следует исключить.
Вычисляется и оценивается
среднее квадратическое отклонение ![]() результата измерения по формуле
результата измерения по формуле

где ![]() − оценка среднего квадратического
отклонения результатов измерения.
− оценка среднего квадратического
отклонения результатов измерения.
Определение доверительных границ случайной погрешности результата измерения.
Доверительные границы случайной погрешности результата измерения в соответствии с требованиями ГОСТ 8. 207 – 76 устанавливают для результатов наблюдений, принадлежащих нормальному распределению.
Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.
Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости q от 10 о 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.
Для определения доверительных границ погрешности результата измерения доверительную вероятность Р принимают равной 0,95.
В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности Р = 0,95, допускается указывать границы для доверительной вероятности Р = 0,99.
При числе результатов
наблюдений ![]() для проверки принадлежности их к
нормальному распределению используется один из критериев
для проверки принадлежности их к
нормальному распределению используется один из критериев![]() К. Пирсона или щ2 Мизеса
– Смирнова.
К. Пирсона или щ2 Мизеса
– Смирнова.
При числе результатов наблюдений 50 > n >16 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий.
При числе результатов наблюдений n < 50 нормальность их распределения проверяют при помощи составного критерия.
Критерий 1. Вычисляют отношение
![]()
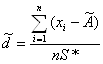
где ![]() − смещенная
оценка среднего квадратического отклонения, вычисленного по формуле
− смещенная
оценка среднего квадратического отклонения, вычисленного по формуле

Результаты наблюдений группы можно считать распределенными нормально, если
![]()
где квантели
распределения, которые берутся из таблицы 1 (ГОСТ 8. 207 – 76 , приложение 1)
по n, ![]() и
и ![]()
q1 − заранее выбранный уровень значимости критерия.
Критерий 2. Можно
считать, что результаты наблюдений принадлежат нормальному распределению, если
не более m разностей ![]() превзошли значение
превзошли значение
![]()
где S − оценка среднего квадратического отклонения, вычисляемая по формуле

где ![]() − верхняя квантиль
распределения нормированной функции Лапласа, отвечающая вероятности
− верхняя квантиль
распределения нормированной функции Лапласа, отвечающая вероятности ![]() .
.
Значения Р определяются из таблицы 2 (ГОСТ 8. 207 – 76 приложение 1) и числу результатов наблюдений n.
При разных принимаемых уровнях значимости q для критериев 1 и 2, то уровень значимости составного критерия равен сумме частных уровней значимости.
В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.
При числе результатов наблюдений n ≤ 15 принадлежность их к нормальному распределению не проверяют.
Доверительные границы е (без учета знака) случайной погрешности результата измерения находят по формуле
![]()
где t − коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа наблюдений n находят по таблице справочного приложения 2 ГОСТ 8. 207 – 76.
Определение доверительных границ неисключенной систематической погрешности результата измерения.
Неисключенная систематическая погрешность результата образуется из составляющих, в качестве корторых могут быть неисключенные систематические погрешности: метода измерения; средства измерения; вызванные другими источниками.
В качестве границ составляющих неисключенной систематической погрешности принимают пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежительно малы.
При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерения каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределение принимают за равномерное.
Границы неисключенной систематической погрешности И результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле

где Иi − граница i – й неисключенной систематической погрешности;
k − коэффициент, определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности Р = 0,95.
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.
Определение границ погрешности результата измерения.
В случае ![]() , то неисключенными
систематическими погрешностями по сравнению со случайными пренебрегают и
принимают, что граница погрешности результата ∆=е. Если
, то неисключенными
систематическими погрешностями по сравнению со случайными пренебрегают и
принимают, что граница погрешности результата ∆=е. Если ![]() , то случайной
погрешностью по сравнению с систематическими пренебрегают и принимают, что
граница погрешности результата ∆=И.
, то случайной
погрешностью по сравнению с систематическими пренебрегают и принимают, что
граница погрешности результата ∆=И.
В случае, если неравенства, указанные в п. 2.7.1. не выполняются, границу погрешности результата измерения находят путем построения композиции распределения случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины в соответствии с
Если доверительные границы случайных погрешностей найдены в соответствии с п. 2.4. допускается границы погрешности результата измерения ∆ (без учета знака) вычислять по формуле
![]()
где К − коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
SУ − оценка суммарного среднего квадратического отклонения результата измерения.
Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле

Коэффициент К вычисляют по эмпирической формуле
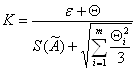
Форма записи результатов измерений.
Оформление результатов измерений производится в соответствии с МИ 1317 – 2001.
При симметричной доверительной погрешности результаты измерений представляют в форме
![]()
где ![]() − результат
измерения.
− результат
измерения.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности ∆ .
При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме
![]()
5. Методы обработки результатов косвенных измерений
Косвенные измерения − это измерения, результат которых определяют на основании прямых измерений величины, связанной с измеряемой величиной известной зависимостью (известными математическими формулами).
Уравнение косвенных измерений имеет вид
y=f(x1, x2, …xn)
где y − искомая величина, являющаяся функцией величин x1, x2 … xn , полученных методом прямых измерений.
На практике для определения искомой величины зачастую необходимо иметь результаты нескольких независимых наблюдений величин x, y, z, которые образуют функцию f = f(x, y, z).
Функция f предполагается дифференцируемой по всем переменным, а также предполагается, что на интервалах, куда попадают значения x, y, z функции f не имеет нулей частных производных.
Обозначение функции fi = f(xi, yi, zi)
Существуют два метода обработки результатов косвенных измерений:
− метод переноса погрешностей;
− выборочный метод.
Обработка результатов измерений методом переноса погрешностей.
Этот метод используется в случае, когда каждая из величин x, y, z, представляющих собой аргументы функций, измеряется независимо от остальных в своей серии опытов, и эти величины организуют выборку (или они близки друг к другу). Число опытов в сериях не обязательно должно быть одинаково, но обязательным условием остается неизменность условий для прямого измерения величин в своей серии, неизменность условий для f во всех сериях и взаимная независимость всех опытов.
Обработка полученных данных измерений каждого опыта производится по алгоритму прямых измерений с многократным наблюдением.
Рассчитать значение
функции ![]() = f(
= f(![]() ,
,![]() ,
, ![]() )
)
Вычислить частные производные от функций
![]() ,
, ![]() ,
, ![]()
Или, для легко логарифмируемой функции f, от ее логарифма
![]()
Вычислить полную погрешность функции
![]()
(формула переноса погрешностей) или по эквивалентной формуле для легко логарифмируемой функции
![]()
Результаты измерений представляются в форме
![]() P %, n
P %, n
6. Обработка данных косвенных измерений выборочным методом
Этот метод применяется в том случае, если совместно измеренные значения аргумента функции xi, yi, zi не образуют выборок, но можно создать выборку значений функции {f}.
По каждому набору совместно измеренных значений аргументов рассчитать значения функции fi = f(xi, yi, zi).
Провести обработку
полученной выборки {fi} согласно
алгоритму обработки данных прямых измерений, находя среднее значение ![]() и случайную
погрешность ∆f функции.
и случайную
погрешность ∆f функции.
Произвести вывод выражений для частных производных от функции
![]()
или для легко логарифмируемой функции f − от ее логарифма
![]()
По каждому набору совместно измеренных значений аргументов и погрешности СИ рассчитать погрешность СИ функции
![]()
Предполагается, что погрешности СИ измеряемых величин могут быть разными в разных опытах или, если функция имеет удобный для логарифмирования вид, по эквивалентной формуле
![]()
где fi − соответствующее данному набору аргументов значение функции.
Вычислить среднюю погрешность СИ функции
![]()
Если погрешности СИ аргументов одинаковы во всех опытах или при нахождении максимальных по всей серии опытов значений погрешностей СИ Иx = maxИxi, Иy = maxИyi, Иz = maxИzi, для определения погрешности СИ величины f можно использовать выражение
![]()
где ![]() ,
, ![]() ,
, ![]() .
.
Вычислить полную
погрешность функции ![]()
Результаты измерений представляются в форме
![]()
![]() P %, n
P %, n
Методы обработки результатов совместных измерений.
Совместными называют производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. Уравнение совместных измерений имеет вид
yi = f (x1i, x2i, …, xni ; a, b, c, ...), i = 1, 2, ..., n,
где yi, x1i, x2i, ..., xni – значения величин, измеренных одновременно (прямо или косвенно) в i-й измерительной операции; а, b, с, ... – неизвестные искомые величины. Если число уравнений превышает число неизвестных, то эти уравнения в отличие от обычной системы уравнений называют условными. Для решения полученной системы используют метод наименьших квадратов.
Задача нахождения наилучшей аппроксимилирующей кривой в общем случае является достаточно сложной и наиболее просто решается, если функциональная зависимость имеет вид прямой линии y = ax + b. Поэтому на практике, если это возможно, сложные функциональные зависимости сводят к линейным зависимостям. При этом задача нахождения регрессионной кривой сводится к решению следующих задач:
− линеаризация нелинейных зависимостей, которая производится путем соответствующей замены переменных с целью получения новой функции,
− нахождение наилучших значений коэффициентов a и b в линейной зависимости y = ax + b или коэффициента a в линейной зависимости
y = ax согласно методу наименьших квадратов (МНК),
− нахождение случайных погрешностей и погрешностей СИ этих коэффициентов,
− нахождение по найденным значениям коэффициентов a и b физических констант, содержащихся в этих коэффициентах. Последняя задача решается стандартным приемом метода переноса погрешностей при косвенных измерениях.
Метод обработки результатов измерений по методу наименьших квадратов (МНК) для уравнения y = ax + b
Все данные результатов замеров свести в таблицу и произвести обработку этих данных по МНК для уравнения y = ax + b.
Вычислить средние значения x и y
![]() ,
, ![]()
Определить средние значения … …
 ,
, ![]()
Рассчитать дисперсии и СКО
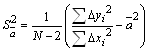 ,
, ![]() ,
, ![]() ,
,![]()
Определить случайные погрешности a и b. Для расчета необходимо брать коэффициент Стьюдента tp,n – 1 , в отличие от прямых измерений, где использовался tp,n :
![]() ,
, ![]()
Вычислить погрешность СИ коэффициента b (погрешность СИ коэффициента a равна нулю)
![]()
Определить полные погрешности a и b
![]() и
и ![]()
Результаты измерений представляются в форме
![]() , P
, P
Метод обработки результатов измерений по методу наименьших квадратов (МНК) для уравнения y = ax.
Все данные результатов замеров свести в таблицу и провести обработку этих данных по МНК для уравнения y = ax
Вычислить среднее значение a
![]()
Вычислить дисперсию и СКО
 ,
, ![]()
Вычислить случайную погрешность коэффициента a
![]()
Вычислить погрешность СИ коэффициента a
![]()
Вычислить полную погрешность коэффициента a
![]()
Результат измерения представляется по форме
![]() , Р
, Р
Список использованной литературы
1. ГОСТ Р 8. 563 – 96 Государственная система обеспечения единства измерений. Методика выполнения измерений.
2. МИ 1317 – 2001 Государственная система обеспечения единств измерений. При
Результаты и характеристика погрешностей измерений.
3. РМГ 43 – 2001 Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений».
4. Р 50. 2. 038 – 2004 Государственная система обеспечения единства измерений. Измерения прямые однократные. Оценивание погрешности и неопределенности результата измерения.
5 МИ 1552 – 86 Методика выполнения прямых однократных измерений.
6. ГОСТ 8. 207 – 76 Государственная система обеспечения единства измерений.
Прямые измерения с многократными наблюдениями, методы обработки результатов наблюдений.
7. ГОСТ ИСО 5479 – 2002 Государственная система обеспечения единства измерений. Проверка отклонения распределения вероятностей от нормального распределения.
8. МИ 199 – 70 Государственная система обеспечения единства измерений. Методика установления вида математической модели распределения погрешностей.
9. МИ 2083 – 90 СИ Измерения косвенные. Определение результатов измерений и оценивание их погрешностей.
10. ГОСТ Р ИСО 5725 – 4 – 2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений.
11. А.Г.Сергеев, В.Г.Крохин. Метрология: Учеб. пособие для студентов вузов. М.: Логос, 2001. 408 с.
12. И.Ф.Шишкин. Теоретическая метрология. М.: Издательство стандартов, 1991.472 с.
13. И.Ф.Шишкин, В.Н.Яншин. Прикладная метрология. М.: РИЦ "Татьянин день", 1993. 150 с.
14. Артемьев Б.Г., Лукашов Ю.Е. Справочное пособие для специалистов метрологических служб. – М.: ИПК Издательство стандартов, 2004.
15. И.Ф.Шишкин. Основы метрологии, стандартизации и контроля качества. М.: Стандарты, 1988.
| Метрология и метрологическое обеспечение | |
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Пензенская государственная технологическая академия Система дистанционного обучения МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И ... Интервальная характеристика случайной погрешности результата измерений, то есть границы, в пределах которых случайная погрешность измерений находится с заданной вероятностью ... Для измерительного прибора нормированы характеристики основной погрешности по ГОСТ 8.009-84: предел допускаемых значений систематической составляющей погрешности ѭс, предел ... |
Раздел: Промышленность, производство Тип: учебное пособие |
| Метрология и ее разделы | |
|
Пензенская Государственная Технологическая Академия структурное подразделение среднего профессионального образования Химико-Технологический Техникум ... û единство измерений - состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерений не выходят за установленные границы с заданной ... 1. Для точных измерений величин в метрологии разработаны приемы использования принципов и средств измерений, применение которых позволяет исключить из результатов измерений ряд ... |
Раздел: Рефераты по коммуникации и связи Тип: учебное пособие |
| Разработка программы факультативного курса по теории вероятностей в ... | |
|
... ПЦК преподавателей естественно-математических дисциплин Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса Рассмотрев ряд примеров случайных величин (число выпавших очков при бросании игровых костей, число голосов, набранных кандидатами, результат измерения формулируется определение ... Таким образом, мы можем вычислить вероятности возможных исходов, не проводя экспериментов, только если очевидно, что все исходы случайного эксперимента равновероятны. |
Раздел: Рефераты по педагогике Тип: курсовая работа |
| ... quot;Основы теории вероятностей и математической статистики" в ... | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Вятский государственный ... Гипотеза исследования заключается в том, что систематическое и целенаправленное изучение теории вероятностей и математической статистики в классах оборонно-спортивного профиля ... - вычислять математическое ожидание и дисперсию дискретной случайной величины; |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Обработка результатов измерений | |
|
Введение В практической жизни человек всюду имеет дело с измерениями. На каждом шагу встречаются измерения таких величин, как длина, объем, вес, время ... Единство измерений - такое состояние измерений, при котором их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью. В массе же измерений различных значений физической величины, осуществляемых одним или многими приборами того же типоразмера, эти систематические погрешности приходится относить к ... |
Раздел: Рефераты по математике Тип: курсовая работа |