Курсовая работа: Составление структурной схемы для установившегося режима
Министерство общего и профессионального образования РФ
Вятский государственный технический университет
Кафедра «Электропривод и автоматизация промышленных установок»
КУРСОВАЯ РАБОТА
по дисциплине
«Теория автоматического управления»
Содержание
1. Составление математического описания системы
1.1 Схема (рис.1) и исходные данные
1.2 Уравнения во временной области и их операторные преобразования. Нахождение передаточных функций для всех элементов системы
1.3 Составить полную и линеаризированную структурные схемы
1.4 Определение численных значений коэффициентов связи и постоянных времени неизменяемой части системы
2. Составление структурной схемы для установившегося режима
2.1 Составление структурной схемы для установившегося режима
2.2 Определение необходимого коэффициента передачи
2.3.Определение значения переменных (Uзад, U2, U3, Ud,Uтг, U1) для режима с заданной частотой nзад
2.4 Определение статических отклонений n частоты вращения вала привода от заданного значения nзад
3. Исследование динамики системы
3.1 Построение аппроксимированной ЛАЧХ системы в разомкнутом состоянии и проверка устойчивости
3.2 Построение желаемой ЛАЧХ системы в разомкнутом состоянии
3.3 Нахождение ЛАЧХ последовательного корректирующего устройства, определение передаточной функции корректирующего устройства
3.4 Расчёт кривой переходного процесса на ЭВМ
Литература
1. Составление математического описания системы
1.1 Схема (рис.1) и исходные данные
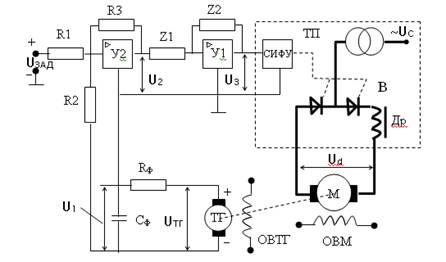
Рисунок 1 - Принципиальная схема.
На рис.1 приведена принципиальная схема замкнутой системы электропривода, состоящего из:
– двигателя постоянного тока независимого возбуждения М;
– тиристорного преобразователя ТП с системой импульсно-фазового управления СИФУ, управляемыми вентилями В и дросселем Др;
– операционного усилителя У1, ре3ализующего устройство коррекции (УК), обеспечивая необходимый из условий статики коэффициент усиления замкнутого контура системы и заданные динамические свойства замкнутой системы;
– сумматора на операционном усилителе У2;
– тахогенератора ТГ с R-C фильтром.
Данные для построения статичес к ой характеристи к и тири сторного преобразователя приведены в таблице 1, емкость конденсатора Cф= 2 0 мкФ , сопротивление R ф=1 кОм фильтра и сопротивления R1=R2=R3=1 0 êÎì. Паспортные данные э л ектродвигателя М: номин ал ьное напряжение Uн, но м ина л ьная скорост ь nн, номи н альный ток Iн, моме н т инерции J системы электропривода ; з аданна я скорость nзад; данные сил овой цепи ТП-Д - сопротивл ение Rя и индуктивность Lяц якорной цепи, а также коэффицие н т передачи тахогенератора Ктг, приведены в таблице 2.
Табли ц а 1. Статическая характеристика ТП.
| Ud, В | 0 | 15 | 50 | 100 | 160 |
2 00 |
220 | 240 | 250 | 255 | 260 |
| Uз, В | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
5 0 |
Таблица 2. Исходные данные
| Вариант | Данные электродвигателя | Силовая цепь | ТГ | ||||||
| Uн , В | Iн, А | nн , 1/с | Рн, кВт | J, кг×м2 | nзад , 1/с | Rяц, Ом | Lяц, мГн | Kтг, В×с | |
| 25 | 220 | 32,6 | 104,7 | 6 | 0,14 | 42 | 0,76 | 20,2 | 0,286 |
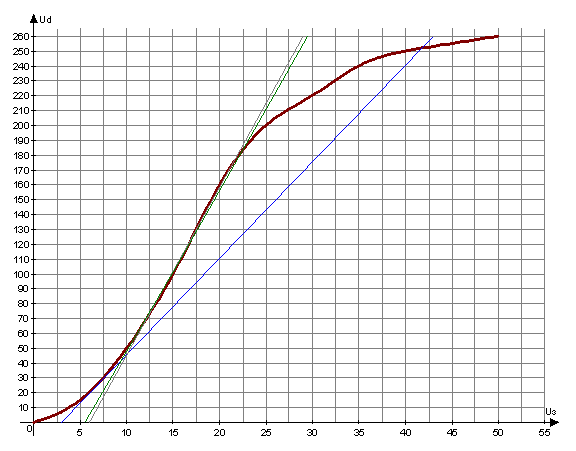
Рисунок 2 - Статическая характеристика ТП.
1.2 Уравнения во временной области и их операторные
преобразования. Нахождение передаточных функций для всех
элементов системы
Математическое описание системы приводится на основе составления системы дифференциальных уравнений для элементов системы при общепринятых допущениях:
- Электродвигатель постоянного тока независимого возбуждения с рабочей машиной, при допущениях постоянного магнитного потока двигателя, скомпенсированной реакции якоря двигателя, абсолютно жёстких механических соединениях и постоянном моменте инерции J привода, описывается системой уравнений, состоящей из дифференциальных уравнений баланса напряжений якорной цепи и движения привода, а также соотношений между э.д.с. Е и частотой вращения n, электромагнитным моментом М и током I якорной цепи:
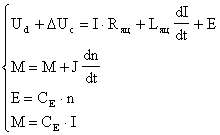 (1)
(1)
где Се - коэффициент, учитывающий магнитный поток и конструктивное исполнение электродвигателя;
в операторной форме система будет выглядеть:
 (1’)
(1’)
При
определении передаточной функции электродвигателя за выходную переменную
следует принимать частоту, вращения вала n, за входное задающее воздействие -
напряжение Ud, в качестве возмущающего воздействия - отклонение напряжении сети
DUc.
Следует учесть, что динамические свойства электродвигателя характеризуются
двумя постоянными времени: электромагнитной ![]() и электромеханической
и электромеханической ![]() . Коэффициент
передачи двигателя относительно Ud определяется соотношением Кд=1/Се
. Коэффициент
передачи двигателя относительно Ud определяется соотношением Кд=1/Се
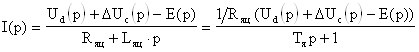 (2)
(2)
На основании системы (1’) можно изобразить структурную схему механической части системы:
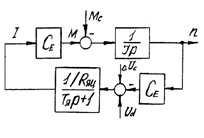
Рисунок 3 – Исходная схема
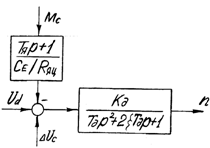
Рисунок 4 – Преобразованная схема
На рисунке 4 изображена преобразованная схема, где двигатель представлен колебательным звеном, поскольку коэффициент демпфирования 0<x<1.
- Тиристорный преобразователь ТП с СИФУ описывается неоднородным дифференциальным уравнением первого порядка.
![]() ,(3)
,(3)
где Тп - постоянная времени (Тп=0,05 с);
Kп - ко эффициент, определяемый статической характеристикой ТП;
В операторной области уравнение (3) будет выглядеть:
![]() , (4)
, (4)
откуда
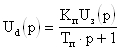 (5)
(5)
Тогда передаточная функция тиристорного преобразователя:
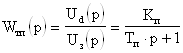 (6)
(6)
На основании этого линеаризованная структурная схема будет выглядеть:
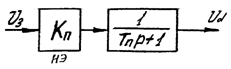
Рисунок 5 – Линеаризованная схема
- Операционные усилители звена коррекции и сумматора У1, У2 описываются передаточной функцией:
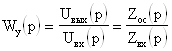 ,(7)
,(7)
где Zoc(p) и Zвх(p) - операторные сопротивления цепей о братной связи и входной данного операционного усилителя.
При этом операторное сопротивление активной цепи равно R, емкостной - 1/Cp, индуктивной - Lp. Если на в х од операционного усилителя (У2) прикладывается несколько различных воздействий U1, U2, с входными сопротивлениями Z1 и Z2 , то операционный усилитель описывается
![]() ,(8)
,(8)
где
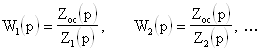 ,(9)
,(9)
т.е. при Zос= Z1= Z2 операционный усилитель может служить сумматором.
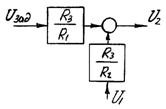
Рисунок 6 – операционный усилитель
- Тахогенератор можно представить в виде линейного безынерционного усилительного звена с передаточным коэффициентом Kтг;
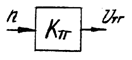
Рисунок 7 – Тахогенератор
Значение выходного напряжение тахогенератора Uтг будет определяться соотношением:
![]() (10)
(10)
- Фильтр на выходе тахогенератора можно рассматривать как отдельное звено с входным напряжением Uтг и выходным U1.
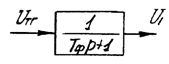
Рисунок 8 – Фильтр на выходе тахогенератора
Такое допущение основывается на том, что внутреннее сопротивление тахогенератора можно считать пренебрежимо малым, а нагрузочное сопротивление R2 на порядок больше внутреннего сопротивления фильтра. Полярность Uтг подбирается такой, чтобы в установившемся режиме сигнал обратной связи на входе У2 был обратным по знаку сигналу Uзад. Постоянная времени фильтра определяется произведением CфRф.
Выходное напряжение фильтра U1 определяется в соответствии со следующими выражениями:
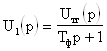 (11)
(11)
![]() (12)
(12)
![]()
1.3 Составить полную и линеаризированную структурные схемы
В целом рассматриваемая система электропривода представляет собой одноконтурную замкнутую САУ с последовательным корректирующим устройством.
Прямой канал полной структурной схемы САУ включает в себя последовательное соединение звеньев сумматора У2 с входными воздействиями - задающим Uзад и обратной связи U1, и выходным воздействием U2; коррекции У1 с входом U2 и выходом U3; тиристорного преобразователя, состоящего из инерционного звена 1-го порядка с коэффициентом усиления равным единице и безынерционного нелинейного звена с графическим изображением статической характеристики преобразователя, входным воздействием преобразователя служит Uз, а выходным - Ud ; электродвигателя с указанными выше воздействиями Ud, n, DUc, Mc.
Канал обратной связи состоит из усилительного звена тахогенератора ТГ с коэффициентам передачи Kтг, входным воздействием n и выходным Uтг и фильтра в виде инерционного звена 1-го порядка.
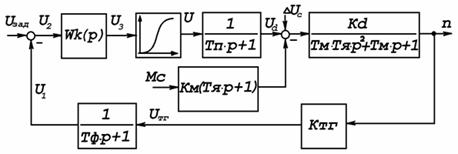
Рисунок 9 - Полная структурная схема САУ
Линеаризованная структурная схема САУ получается, если полные переменные Х (Uзад, U2, U3, Ud, DUc, I, M, Mc, n, Uтг, U1) представи т ь в виде сумм ы ХA+DX, гд е ХA - зна че ния переменных в р абочей точке А статических характеристик з венье в . После с о кращ ения ста ти ческих составляющих в пр а вой и л евой части уравнени й зве нье в, линеаризованны е структурные сх е мы звеньев отразят з а висимость между приращениями выходных и входны х переменных (DUзад, DU2, …, DU1). Форма записи передаточных функций линейных звеньев при этом не изменяется, а статические характеристики нелинейных безынерционных звеньев будут представлены в виде коэффициентов динамической линеаризации в рабочей точке.
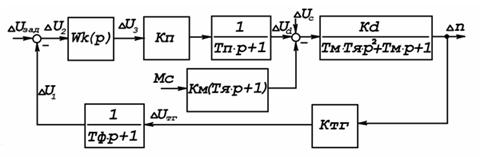
Рисунок 10 - Линеаризованная структурная схема САУ
1.4 Определение численных значений коэффициентов связи и
постоянных времени неизменяемой части системы
Найдём сопротивление якоря двигателя.
![]() (13)
(13)
![]()
Электромагнитная постоянная времени якорной цепи:
![]() (14)
(14)
![]()
Конструктивный коэффициент электродвигателя Сe рассчитывается по уравнению баланса напряжений якоря двигателя в установившемся номинальном режиме.
![]() (15)
(15)
Тогда
![]() (16)
(16)
![]()
Найдём коэффициент передачи двигателя:
![]() .(17)
.(17)
![]()
И электромеханическую постоянную времени двигателя:
![]() (18)
(18)
![]()
Сравнивая передаточные функции электродвигателя по задающему воздействию и колебательного звена можно определить коэффициент затухания:
![]() (19)
(19)
![]()
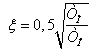 (20)
(20)
![]()
Как видно, коэффициент демпфирования 0<x<1 - тогда можно двигатель представить колебательным звеном, что и было сделано выше. Собственная частота колебаний двигателя:
![]() (21)
(21)
![]()
Из графической зависимости Ud(U3) по данным
таблицы 1, построенном в одинаковом масштабе по обеим осям, определяется
коэффициент Kп динамической линеаризации статической характеристики
тиристорного преобразователя. ![]() Или графически Kп равен тангенсу
угла наклона касательной, проведенной к статической характеристике в рабочей
точке А. Рабочая точка А определяется значением выпрямленного напряжения Ud|A,
в режиме идеального холостого хода электродвигателя. Значение Kп определяется в
трех рабочих точках:
Или графически Kп равен тангенсу
угла наклона касательной, проведенной к статической характеристике в рабочей
точке А. Рабочая точка А определяется значением выпрямленного напряжения Ud|A,
в режиме идеального холостого хода электродвигателя. Значение Kп определяется в
трех рабочих точках:
- Kпмин при минимальном значении Ud в заданном диапазоне регулирования D=10, т.е. Udмин= Uн/D, Udмин=22(В); Kпмин =22/4 =6
- Kпмакс - в точке с максимальным наклоном статической характеристики:
Kпмакс = 60/5=12
- Kпзад при заданном значении выпрямленного напряжения UdЗАД=СЕ×nЗАД=1,98×42=83,2(В) Kпзад=83,2/8=10 используется для построения ЛАЧХ САУ в заданном рабочем режиме.
![]() (22)
(22)
2. Анализ установившегося режима системы
2.1 Составление структурной схемы для установившегося режима
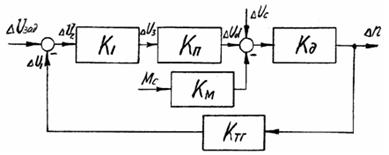
Рисунок 11 - Структурная схема для установившегося режима
Структурная схема дня установившегося режима составляется на основе уравнений элементов САУ в статике или на основе линеаризованной структурной схемы САУ формальным путём приравнивания оператора p к нулю. Следует обратить внимание, что последним способом установившийся режим работы двигателя может быть описан лишь на основе полной передаточной функции двигателя по отношению к Ud и Мс с выходом по частоте вращения, т.е. с учетом внутренней обратной связи двигателя.
2.2 Определение необходимого коэффициента передачи
По полученной структурной схеме в установившемся режиме можно определить статическое отклонение частоты вращения вала Dn при приложении Мc= Mн в разомкнутой системе без обратной связи (без тахогенератора и фильтра) - DnpMc, и в замкнутой САУ - DnзMc. Нетрудно убедиться, что соблюдается равенство
![]() (23)
(23)
где
Kp=K1×Kп×Kд×Kтг (24)
коэффициент передачи замкнутого контура САУ в разомкнутом состоянии.
Отклонение DnpMc рассчитывается непосредственно из структурной схемы в установившемся режиме, при этом согласно (1)
Мс=Мн=СeIн. (25)
Мс=1,98×32,6 = 64,55 (Н×м)
![]() (26)
(26)
Учитывая, что относительное падение частоты вращения в статике при приложении Мс имеет максимальную величину при минимальной частоте вращения в пределах заданного диапазона регулирования D, и, исходя из требований п.п. 2 задания, имеем
![]() (27)
(27)
![]()
Тогда необходимый коэффициент передачи Kpмин может быть найден из уравнения (23), а требуемый из условий статики коэффициент K1 операционного усилителя У1 из уравнения (24), учитывая, что Kpмин в качестве сомножителя имеет коэффициент передачи тиристорного преобразователя равный Kпмин.
![]() (28)
(28)
![]()
![]() (29)
(29)
![]()
![]() (30)
(30)
![]()
![]()
2.3 Определение значения переменных ( Uзад, U2, U3, Ud,Uтг, U1)
для режима с заданной частотой nзад
![]() (31)
(31)
![]()
U3=14(В) - по статической характеристике при Udзад=83,16(В)
![]() (32)
(32)
![]()
![]() (33)
(33)
![]()
![]() (34)
(34)
![]()
2.4 Определение статических отклонений Dn частоты вращения
вала привода от заданного значения nзад
Статическое отклонение частоты вращения Dn вала при приложении Мс=Мн в разомкнутой системе без обратной связи:
![]() (35)
(35)
![]()
В замкнутой САУ:
![]() (36)
(36)
![]() (37)
(37)
![]()
Статическое отклонение частоты вращения Dn вала при ступенчатом воздействии возмущения DUc=0,1Udзад в разомкнутом состоянии системы:
![]() (38)
(38)
![]()
в замкнутой САУ:
![]() (39)
(39)
Из полученных
значений видно, что точность поддержания частоты вращения вала в замкнутой САУ
выше, чем в разомкнутой, т.к. статическое отклонение в замкнутой САУ
уменьшается на коэффициент ![]() , появляющийся при наличии
обратной связи.
, появляющийся при наличии
обратной связи.
3. Исследование динамики системы
3.1 Построение аппроксимированной ЛАЧХ системы в
разомкнутом состоянии и проверка устойчивости
Некорректированная САУ в разомкнутом, состоянии состоит из последовательно соединенных звеньев:
- усилительного - усилителя У1 с коэффициентом передачи K1, найденным из условия статики во второй части задания;
- инерционного - тиристорного преобразователя с коэффициентом передачи Kп и частотой сопряжения wп= 1/Тп;
- колебательного - электродвигателя с коэффициентом передачи
Кд и собственной частотой колебаний ![]() ;
;
- усилительного - тахогенератора с коэффициентом передачи Kп;
- инерционного - фильтра с единичным коэффициентом передачи и частотой сопряжения wф=1/Тф.
Коэффициенты передачи всех звеньев (в том числе и желаемый K1) могут быть объединены в соответствии с (7) в один коэффициентов Kp. Следует учитывать, что наихудшие условия с точки зрения устойчивости при заданных параметрах динамических звеньев будут при максимальном значении Kp в требуемом диапазоне регулирования, т.е. при Kp= Kpмакс.
Процесс построения аппроксимированной ЛАЧХ некорректированной САУ в разомкнутом состоянии можно ускорить, если воспользоваться следующей методикой:
- определить значения ординаты Lp(0) = lg Kpмакс и абсцисс частот сопряжения и колебаний lg wп, lg wд, lg wф;
- на низких частотах графика Lнкp(w) отложить ординату, равную Lp(0), и провести ÷åðåç эту ординату прямую с нулевым наклоном ( параллельно оси абсцисс) до ближайшей меньшей собственной частоты одного из звеньев;
- по мере увеличения частоты изменять наклон ЛАЧХ на -1 лог/дек в абсциссах, соответствующих частотам, сопряжения инерционных звеньев и на -2 лог/дек в абсциссах, соответствующих собственной частоте колебательного звена.
Таким образом, для построения ЛАЧХ необходимы следующие значения:
![]() 1,67
1,67
![]()
![]() 1,57
1,57
![]()
Устойчивость замкнутой САУ может быть определена с помощью критерия Найквиста, который в случае рассматриваемой устойчивой САУ в разомкнутом состоянии и анализа ее частотных характеристик в логарифмическом масштабе сводится к условию, чтобы
![]() (40)
(40)
где частота среза wс системы определяется значением частоты точки пересечения ЛАЧХ САУ в разомкнутом состоянии и оси абсцисс (Lp(wс) = 0). Показатели качества переходного процесса в замкнутой САУ тем лучше, чем больше запас устойчивости по фазе Dj (Dj = 180°-|jp(wс)|) и по амплитуде DL (DL равно абсолютному значению Lp при частоте, где |jp| =180°). В частности, это иллюстрируется рисунком 12, где представлены зависимости перерегулирования s в замкнутой САУ по задающему воздействию от Dj и DL.
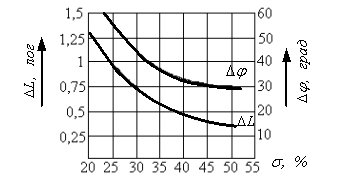
Рисунок. 12. Кривые запасов устойчивости по модулю DL и по фазе Dj от перерегулирования s.
В работе рассматривается минимально-фазовая система, т.е. система в разомкнутом состоянии состоит из звеньев, имеющих однозначную зависимость между АЧХ и ФЧХ. Для такой системы анализ устойчивости можно провести по аппроксимированной ЛАЧХ системы в разомкнутом состоянии без построения ФЧХ. Значение j(wi) при любой выбранной частоте wi для минимально-фазовой системы может быть приближенно определено по усредненному наклону ЛАЧХ в этой частоте и равно
![]() (41)
(41)
где
![]()
![]() (42)
(42)
Усредненный наклон nср(wi) определяется путем нахождения координаты Lв(wi), отстоящей на одну декаду в сторону высоких частот, т.е. Lв(wi) = Lв(10wi), и координаты Lн(wi), отстоящей на одну декаду в сторону низких частот, т.е. Lн(wi) = L(0,1wi).
На рисунке 13 приведена наиболее типичная для заданных вариантов ЛАЧХ Lнкp(w) некорректированной САУ в разомкнутом состоянии, построенная по данной методике. Параметры системы таковы, что некорректированная САУ либо неустойчива, либо имеет малый запас устойчивости, не удовлетворяющий требованиям обеспечения заданного качества регулирования. Для примера, на рисунке 13, определяя значение ФЧХ в частоте wнкс среза некорректированной САУ, имеем Lнкв(wнкс) = - 4 лог, Lнкн(wнкс) = 1,67 лог и
![]() ,(43)
,(43)
т.е. некорректированная САУ неустойчива, т.к.
![]() .(44)
.(44)
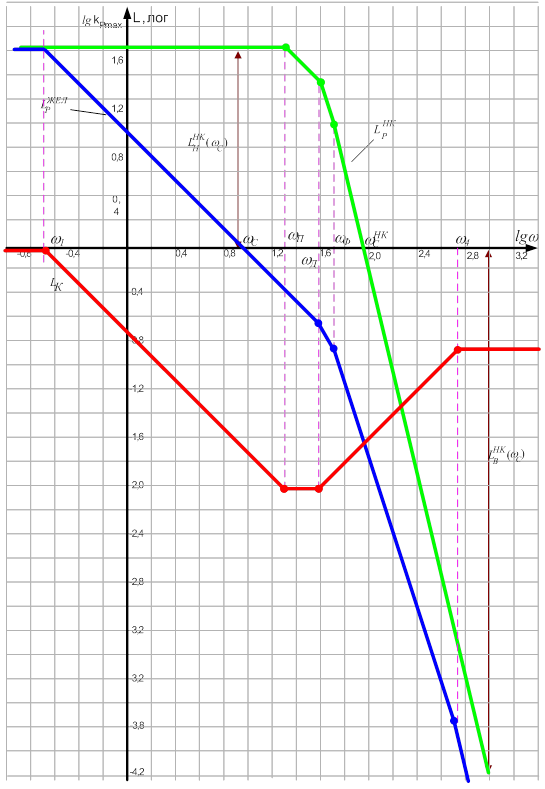
Рисунок 13 – ЛАЧХ
3.2 Построение желаемой ЛАЧХ системы в разомкнутом состоянии
При построении желаемой ЛАЧХ системы в
разомкнутом состоянии требованию обеспечения перерегулирования s по задающему воздействию
не более 30% необходим (согласно рисунку 12) запас по фазе Dj³45° и по амплитуде DL³0,75 лог. Это
соответствует фазе ![]() в частоте среза wc скорректированной САУ
в частоте среза wc скорректированной САУ ![]() или согласно (41)
и (42)
или согласно (41)
и (42)
![]() лог(45)
лог(45)
Следует иметь в виду, что требование минимального времени регулирования выполняется при максимально возможной величине частоты wс скорректированной системы, а требование максимального ослабления возмущений выполняется при минимальном уменьшении координат Lр в области низких частот (до wс).
Частота сопряжения участков желаемой ЛАЧХ ![]() с различными
наклонами следует выбирать с таким расчетом, чтобы передаточная функция
корректирующего устройства была бы реализована наиболее просто. Последнее
достигается, если частоты сопряжения участков желаемой ЛАЧХ выбирать равными
частотам звеньев исходной некорректированной системы. Тогда примем частоты
сопряжения участков с наклонами -1 лог/дек и -2 лог/дек равной wд, участков с наклонами
-2 лог/дек и -3 лог/дек равной wф, и частоту сопряжения w4 участков с наклонами -3
лог/дек и -4 лог/дек достаточно высокой, чтобы она не влияла на запасы
устойчивости DL и Dj. Для такой конфигурации
с различными
наклонами следует выбирать с таким расчетом, чтобы передаточная функция
корректирующего устройства была бы реализована наиболее просто. Последнее
достигается, если частоты сопряжения участков желаемой ЛАЧХ выбирать равными
частотам звеньев исходной некорректированной системы. Тогда примем частоты
сопряжения участков с наклонами -1 лог/дек и -2 лог/дек равной wд, участков с наклонами
-2 лог/дек и -3 лог/дек равной wф, и частоту сопряжения w4 участков с наклонами -3
лог/дек и -4 лог/дек достаточно высокой, чтобы она не влияла на запасы
устойчивости DL и Dj. Для такой конфигурации ![]() DL определяется
координатой при абсциссе, лежащей на середине отрезка между lg wд и lg wф, т.е. должно соблюдаться
неравенство
DL определяется
координатой при абсциссе, лежащей на середине отрезка между lg wд и lg wф, т.е. должно соблюдаться
неравенство
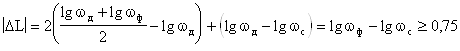 лог(46)
лог(46)
или
![]() (47)
(47)
Аналогично определим Lн(wс) = 1 лог (поскольку
наклон ![]() до
частоты wс
равен -1 лог/дек, а lg Kpмакс>1),
до
частоты wс
равен -1 лог/дек, а lg Kpмакс>1),
![]() Лога согласно (45)
Лога согласно (45)
![]() лог,(48)
лог,(48)
откуда
![]() (49)
(49)
Частота wс среза желаемой ЛАЧХ принимается равной наименьшему из значений, рассчитанных по (47) и (49). Например, для рис.3 имеем:
по (47)![]()
по (49)![]()
Выбираем ![]() .
.
По приведенной выше методике может быть
определена частота среза и построена желаемая ЛАЧХ ![]() и иной конфигурации. Таким образом,
желаемая ЛАЧХ строится по следующим значениям:
и иной конфигурации. Таким образом,
желаемая ЛАЧХ строится по следующим значениям:
![]() ;
; ![]() ;
; ![]() ;
;![]() (рисунок 13).
(рисунок 13).
3.3 Нахождение ЛАЧХ последовательного корректирующего
устройства, определение передаточной функции корректирующего
устройства
Динамическая составляющая ЛАЧХ ![]() корректирующего
устройства (коэффициент передачи K1 учтен в Кpмакс) получается путем вычитания
зависимости
корректирующего
устройства (коэффициент передачи K1 учтен в Кpмакс) получается путем вычитания
зависимости ![]() из
из
![]() , т.е.
, т.е.
![]() .(50)
.(50)
Полная ЛАЧХ корректирующего устройства
![]() .(51)
.(51)
В качестве схемотехнической к реализации корректирующего устройства может быть рекомендован операционной усилитель, включенный по схеме:
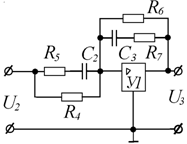
Рисунок 14 - Принципиальная схема корректирующего устройства
Используя методику, изложенную к первой части задания, нетрудно получить выражение передаточной функции в виде:
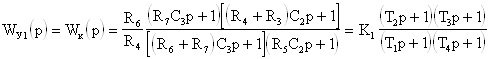 (52)
(52)
Постоянные времени числителя передаточной функции
соответствуют частотам сопряжения аппроксимированной ЛАЧХ ![]() с положительным
переходом, т.е. с наклона -1 на 0 или с 0 на +1 , а знаменатель - частотам
сопряжения участков
с положительным
переходом, т.е. с наклона -1 на 0 или с 0 на +1 , а знаменатель - частотам
сопряжения участков ![]() с отрицательным переходом, т.е. с
0 на -1 или с +1 на 0, если следовать по
с отрицательным переходом, т.е. с
0 на -1 или с +1 на 0, если следовать по ![]() в сторону возрастания частот.
в сторону возрастания частот.
![]()
![]()
![]()
![]()
Из выражения передаточной функции можно составить систему из 5 -и уравнений:
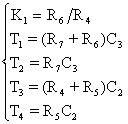 (53)
(53)
Для решения этой системы необходимо задаться одним из параметров С2=1мкФ, тогда:
![]() , (54)
, (54)
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
![]() (58)
(58)
3.4 Расчёт кривой переходного процесса на ЭВМ
Расчет кривой переходного процесса Dn(t) по возмущающему воздействию может быть проведен моделированием на ЭВМ. Результатом моделирования получается график Dn(t) показывающего изменение параметра (оборотов двигателя) от Dnзад при воздействии возмущения DUc. Моделирование производится на ЭВМ в пакете PDS по следующей структурной схеме:

Рисунок 16 – Структурная схема САУ
Таблица 3 – Значения элементов САУ
| Т1=5,6 ,с | Т2=0,05 ,с | Т3=0,027 ,с |
| Т4=0,01 ,с | К1=26,36 | Се=1,98 |
| КПзад=10 | Тф=0,02 ,с | Тя=0,026 ,с |
| Тп=0,05 ,с | J=0,14 | Rя=0,38 ,Ом |
1/Rя=2,63
Т2Т3р2+Т2р+Т3р+1=0,00135р2+0,077р+1
Т1Т4р2+(Т1+Т4)р+1=0,056р2+5,61р+1
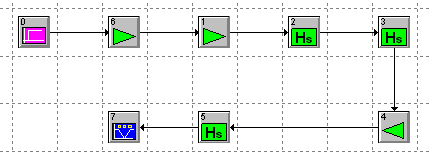
Рисунок 17 - Схема разомкнутой нескорректированной системы
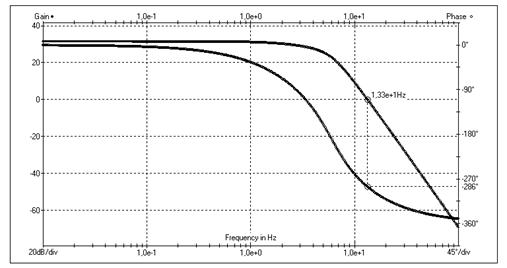
Рисунок 18 - ЛАЧХ разомкнутой нескорректированной системы
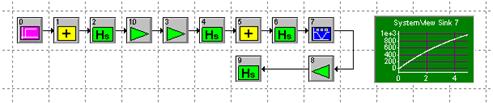
Рисунок 19 – Схема разомкнутой скорректированной системы
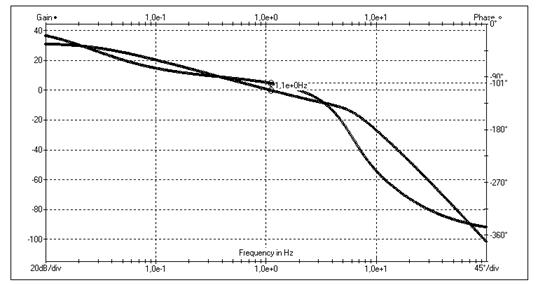
Рисунок 20 - ЛАЧХ разомкнутой скорректированной системы
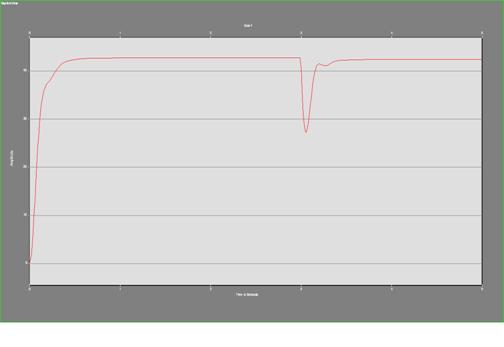
Рисунок 21 – Переходный процесс
Таблица 4 - Сравнение показателей регулирования
| Моделирование на ЭВМ | ||
| по задающему | по возмущающему | |
| Dx | 3,427 | 0,001 |
| tp | 0,53 | 0,68 |
| s | - | 38900 |
| Dxu | ||
| M | 0 | 2 |
Литература
1. Теория автоматического управления, под общей редакцией Нетушила А.В., ч. I, М., “Высшая школа”, 1976.
2. Куропаткин П.В. Теория автоматического управления, М., ”Высшая школа”, 1973.
3. В.В. Солодовников, В.И. Плотников, А.В. Яковлев. Основы теории и элементы систем автоматического регулирования. М., “Машиностроение”,1985.
4. А.П. Протасов. Теория управления. Задания и методические указания к курсовой работе. Для специальности 180400-“Электропривод и автоматизация промышленных установок”, Киров, изд. ВятГТУ, 1996, с.30.