Учебное пособие: Статика рідин та газів

11. СТАТИКА РІДИН ТА ГАЗІВ.

В цій лекції розглядаються основні питання гідро та аеро-статики, тобто умови і закономірності рівноваги рідин і газів під дією прикладених до них сил і, крім того, умови рівноваги твердих тіл, що знаходяться в рідині чи газі.

1. ТИСК В РІДИНАХ І ГАЗАХ. ЗАКОН ПАСКАЛЯ.

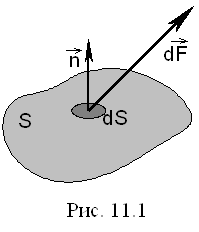
Введемо спочатку поняття тиску. Розглянемо деяку поверхню S, на яку діє розподілена сила. Виділимо на цій поверхні нескінченно малий майданчик dS (рис. 11.1). Нехай  – це сила, що діє на майданчик dS.

Відношення сили  до площі dS називають напругою:

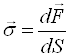                                                      (11.1)

Орієнтацію майданчика dS задають з допомогою вектора нормалі до нього. Якщо S – це поверхня якогось тіла, то домовились проводити нормаль назовні від поверхні тіла. На рис. 11.1 показано одиничний вектор  цієї нормалі.

Напругу  можна розкласти на дві складові: вздовж нормалі  і перпендикулярно до неї, тобто в площині, дотичній до майданчика dS. Першу складову називають нормальною, а другу – тангенціальною напругами, що діють на майданчику dS:

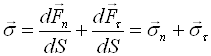                                   (11.2)

Якщо напрям  і  співпадають, то цю напругу називають натягом T, в протилежному випадку – тиском P.

Тиском Р називається фізична величина, що дорівнює модулю нормальної складової сили, яка діє на одиницю площі поверхні тіла:

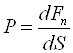                                              (11.3)

Напруга в цьому випадку дорівнює:

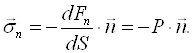
Зауважимо, що тиск – величина скалярна.

Особливістю рідин та газів є їх текучість, зумовлена малими силами тертя під час відносного руху шарів, що дотикаються, та відсутністю тертя спокою. Рідинам і газам не властива пружність форми, вони мають лише об’ємну пружність. В стані рівноваги напруга в рідинах і газах завжди нормальна до майданчика, на який вона діє. Дотичні (тангенціальні) напруги із-за текучості в рідинах та газах під час рівноваги не виникають.

З цієї точки зору рідини та гази можна означити як середовища, в яких при рівновазі дотичні напруги існувати не можуть.

З даного означення випливає, що в стані рівноваги нормальна напруга в рідині чи газі (тиск) не залежить від орієнтації майданчика, на який вона діє. Це твердження називають законом Паскаля. Іншим чином його можна сформулювати так:

Тиск, що діє на рідину чи газ, передається в усіх напрямках без зміни.

Закон Паскаля пояснює роботу гідравлічного пресу (рис. 11.2).

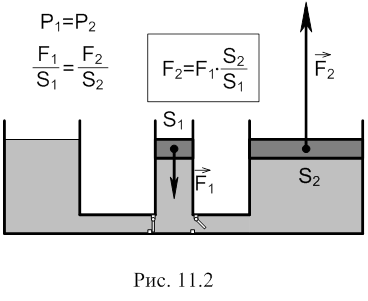
В газах нормальна напруга завжди направлена всередину газу, тобто – це тиск. В рідинах , як правило, теж тиск, хоч інколи можна реалізувати випадки, коли  буде натягом (від’ємний тиск).

2. ОСНОВНЕ РІВНЯННЯ ГІДРОСТАТИКИ. БАРОМЕТРИЧНА ФОРМУЛА.

Сили, що діють в рідині, ділять звичайно на сили масові (об’ємні) і сили поверхневі.

Масова сила пропорційна масі , а отже, і об’єму  елемента рідини, на який вона діє. Цю силу можна записати як , де  називають об’ємною густиною масових сил. Прикладом масових сил є сила тяжіння:     де  – густина рідини.

Поверхневі сили – це сили, що діють на поверхню даного об’єму рідини завдяки дії нормальних та дотичних напруг з боку оточуючої рідини.

Розглянемо рідину, що перебуває у рівновазі. В цьому випадку дотичних напруг немає. Виділимо в рідині нескінченно малий елемент об’єму  у вигляді циліндра з площею основи  і довжиною , розташованого вздовж вісі X (рис. 11.3):

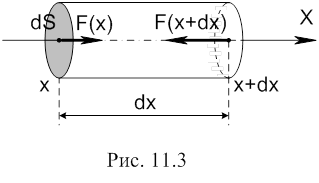
Тиск в т. x дорівнює , в т. :  . Сили тиску на основи циліндра відповідно дорівнюють:

Проекція рівнодійної сил тиску на вісь X:

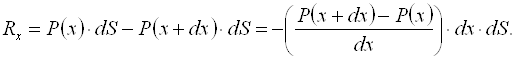
Вираз в дужках є не що інше, як похідна від Р по x; але, оскільки P залежить також і від y та z, то це частинна похідна:

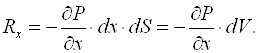                          (11.4)

Таким чином, проекція рівнодійної сил тиску на вісь X пропорційна елементу об’єму і її можна подати у виді:

.

 – це проекція на вісь X сили, яка діє на одиницю об’єму рідини.

Аналогічно для двох інших осей Y та Z:

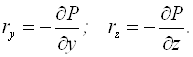
Вектор 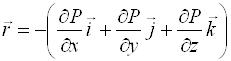                     (11.5)

Вираз в дужках є градієнт скаляра Р:

                                          (11.6)

Об’ємна густина рівнодійної сил тиску, що діють на елементи об’єму рідини, дорівнює градієнту тиску, взятому з протилежним знаком.

В стані рівноваги сила  повинна зрівноважуватись масовою силою :      . Це дає рівняння

,                                              (11.7)

яке називають основним рівнянням гідростатики. В координатній формі воно має вид системи (11.8):

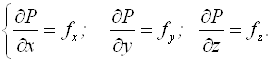                           (11.8)

Якщо масових сил немає, тобто , то з виразу (11.8) матимемо:

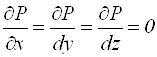      або    .

При рівновазі у відсутності масових сил тиск Р один і той же по всьому об’єму рідини.

Це ще одне формулювання закону Паскаля (Блез Паскаль,
1623 – 1662).

Зокрема, якщо масові сили відсутні, рідина може перебувати в рівновазі тільки тоді, коли зовнішній тиск на її поверхню один і той же в усіх точках цієї поверхні. Інакше виникне рух рідини. У відсутності масових сил однаковий тиск на поверхню рідини приводить до появи такого ж тиску в усіх точках всередині рідини.

Якщо рідина знаходиться в полі тяжіння, то ; направимо вісь Z вертикально вгору, тоді:

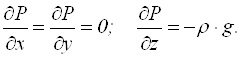                                 (11.9)

Тиск залишається сталим в кожній площині . Горизонтальні площини – це площини однакового тиску. Вільна поверхня рідини горизонтальна тому, що вона перебуває під сталим тиском атмосфери.

Якщо рідина не стискується, то  і (11.9) інтегрується:

,                                            (11.10)

де  – тиск на висоті  тобто атмосферний тиск, якщо початок розташувати на вільній поверхні рідини.

Рівняння (11.10) охоплює практично всю шкільну гідростатику.  (інакше ) – це гідростатичний тиск, викликаний вагою рідини, який залежить від глибини занурення в рідину.

Застосуємо основне рівняння гідростатики до земної атмосфери. Одержимо (див. (11.9)):

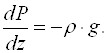                                             (11.11)

В останньому виразі замість частинної похідної записана звичайна, оскільки Р не залежить від x та y. Для земної атмосфери наближено можна використати рівняння Клапейрона-Менделєєва:

,

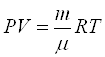звідки: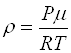 .                                     (11.12)

Підставимо (11.12) в (11.11) і проінтегруємо в припущенні, що :

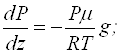
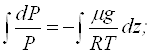
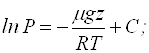
при , отже стала інтегрування .

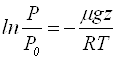, або:

                                            (11.13)

(11.13) називають барометричною формулою.

Аналогічно:                        (11.14)

У виразах (11.13) і (11.14)  і  - це тиск і густина повітря на поверхні Землі.

3. ЗАКОН АРХІМЕДА. ПЛАВАННЯ ТІЛ.

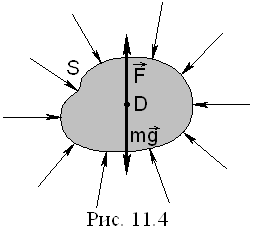Уявно виділимо в рідині довільний об’єм, обмежений замкненою поверхнею S (рис. 11.4). Якщо рідина перебуває в рівновазі, то рівнодійна всіх зовнішніх сил, що діють на виділений об’єм рідини, і її момент повинен дорівнювати нулю. На виділений об’єм діють сила тяжіння  і сили тиску, рівнодійна  яких повинна дорівнювати за модулем  і бути прикладеною в центрі мас  виділеного об’єму рідини. Видалимо тепер рідину з вказаного об’єму і вмістимо туди будь-яке тверде тіло. Якщо це тіло перебуває в рівновазі, то стан оточуючої рідини не зазнає ніяких змін.

Таким чином, якщо тіло, занурене в рідину, перебуває в стані рівноваги, то з боку рідини воно зазнає дії виштовхувальної сили гідростатичного тиску. Ця сила чисельно дорівнює силі тяжіння, що діє на рідину, яка має об’єм зануреної частини тіла.

Виштовхувальна сила направлена вгору і прикладена до центра мас  рідини, яку витіснило тіло. Точку  називають центром тиску або центром плавучості тіла. Вищенаведене твердження і називають законом Архімеда, а виштовхувальну силу називають архімедовою силою:

                                            (11.15)

Використовуючи поняття ваги, архімедову силу можна означити, як силу, що дорівнює вазі рідини, яку витіснило тіло.

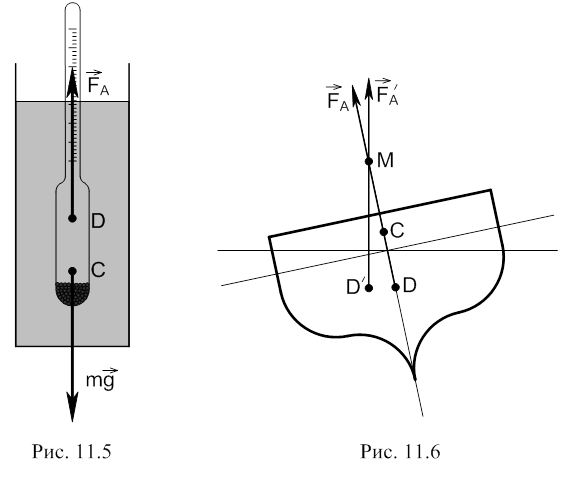
Для рівноваги необхідно, щоб вага тіла дорівнювала вазі витісненої ним рідини, а центр плавучості  лежав на одній вертикалі з центром мас С самого тіла. Для тіла, яке занурене в рідину повністю, рівновага буде стійкою, якщо центр мас тіла С лежатиме нижче його центра плавучості , і нестійкою в протилежному випадку. Якщо тіло занурене в рідину частково, то рівновага буде стійкою в двох випадках: по-перше, якщо центр мас С буде розташований нижче центра плавучості, і, по-друге, якщо центр мас С буде розташований нижче метацентра. Метацентром називають точку М тіла, в якій перетинаються лінії дії виштовхувальних сил в стані рівноваги і при відхилення тіла від положення рівноваги на малий кут (див. рис. 11.6).