Доклад: Экспериментальное наблюдение волн магнитного поля и исследование их распространения в металлах

ЭКСПЕРИМЕНТАЛЬНОЕ НАБЛЮДЕНИЕ ВОЛН МАГНИТНОГО ПОЛЯ И ИССЛЕДОВАНИЕ ИХ РАСПРОСТРАНЕНИЯ В МЕТАЛЛАХ

В.В. Сидоренков

МГТУ им. Н.Э. Баумана

В настоящее время установлено [1], что реальная структура электромагнитного (ЭМ) поля представляет собой необычное с общепринятых позиций вихревое векторное поле, состоящее из двух функционально связанных между собой электродинамических полей: вихревог ЭМ поля с компонентами электрической и магнитной напряженностей и поля ЭМ векторного потенциала с электрической и магнитной компонентами. Указанное поле описывается системой базовых исходных фундаментальных соотношений в виде дифференциальных уравнений:

(a) , (b) , (1)

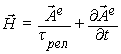которые непосредственно получаются из традиционных [2] уравнений Максвелла для ЭМ поля. Здесь - постоянная времени релаксации заряда в среде за счет электропроводности. Проведенный анализ показал [1], что с концептуальной точки зрения электродинамическое поле, описываемое системой (1) физически логично называть реальное электромагнитное поле.

Основным фундаментальным своством соотношений (1) является возможность вывода на их основе не только системы уравнений Максвелла с и компонентами, но и структурно аналогичных максвелловской трех других систем электродинамических уравнений: поля ЭМ векторного потенциала с и компонентами, электрического поля с и компонентами и, наконец, магнитное поле с и компонентами. В частности, система электродинамических уравнений для магнитного поля будет иметь следующий вид:

(a) , (b) , (2)

Поскольку при изучении взаимодействия электродинамического поля с материальной средой, в сущности, все сводится к стремлению описать энергетику явлений электромагнетизма, то однозначным подтверждением реальности структуры магнитного поля в виде двух компонент и служит следующее из уравнений (2) соотношение энергетического баланса для потока энергии, обуславливающей явление намагничивания материальной среды:

div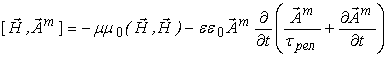. (3)

Данное соотношение баланса описывает энергетику условий реализации обычной магнитной поляризации среды (первое слагаемое правой части (3)) посредством переноса извне в данную точку потока вектора соответствующей энергии. Однако это соотношение устанавливает также и наличие динамической поляризации вещества (в частности, проводящих сред) за счет действия переменной во времени магнитной компоненты поля векторного потенциала . Важно отметить, что явления динамической магнитной поляризации уже имеет прямое экспериментальное воплощение: это эффект динамического намагничивания в ферритах и магнитоупорядоченных металлах [3].

Форма представленных систем уравнений системы (2) говорит о существовании волновых решений для компонент и магнитного поля. В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений системы, и после чего подставить в него другое роторное уравнение. В качестве иллюстрации получим волновое уравнение, например, относительно :

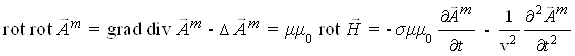Здесь, согласно (2d), , - оператор Лапласа, а - фазовая скорость волны в отсутствие поглощения. Как показал анализ [1], компоненты и волн магнитного поля в диэлектрической среде ведут себя специфично: , то есть имеют взаимный сдвиг по фазе на π/2. Кроме того, в зависимости от частоты их амплитуды связаны между собой весьма необычно: . Конечно, математически данный результат тривиально очевиден, поскольку, согласно (1), компоненты магнитного поля связаны посредством производной по времени. Однако концептуально с физической точки зрения это неожиданно и требует всестороннего анализа.

Справедливости ради следует сказать, что впервые о возможности реального существования чисто магнитной поперечной волны с двумя компонентами и , сдвинутыми при распространении по фазе на π/2, официально в виде приоритета на открытие заявил Докторович еще в 1980 году, и этот факт он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других, ссылаясь на заявленный приоритет и свою статью по этой теме, везде публикуемую многие годы (например, [4]). Печально, но только Время - высший судья, и именно оно расставит всех и все по своим местам! Однако будем надеяться, что независимое подтверждение этого научного достижения Докторовича будет для него серьезной поддержкой в общении с оппонентами.

Анализ уравнений системы (2) показывает [1], что для проводящей среды в асимптотике металлов (), как и должно быть [2], их волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на π/4.

Наряду с теоретическим анализом, были проведены эксперименты по изучению необходимых условий возбуждения и возможность распространения электродинамических полей в металлах, отвечающие на два физически важных вопроса: волны каких полей можно реально возбудить в металлах и каковы частотные ограничения дисперсионного соотношения для проводящей среды в асимптотике металлов при длинах волн l ® ¥?

Возбуждение электродинамических полей в металле (пластинки меди и алюминия) производилось на низких частотах n = 50 - 50.103 Гц и было возможным только с помощью магнитной антенны, так как импеданс ближней зоны излучения лишь у магнитного диполя сопоставим с импедансом металлической среды. Прием прошедшего через металл излучения был возможным также лишь магнитной антенной, что однозначно говорит о наличии в принимаемом сигнале составляющей только магнитного поля и об отсутствии на выходе других составляющих электродинамического поля, названного в [1] реальное электромагнитное поля .

Для определения закона частотной дисперсии волнового числа магнитной волны в металле его действительная часть измерялась по сдвигу фазы колебаний волны при ее прохождении в плоском слое толщиной l : , а мнимая часть - по затуханию амплитуды волны. Так как в теории металлов хорошим приближением является равенство [2], то следует ожидать, что указанные измерения посредством этих двух способов должны давать одинаковые результаты.

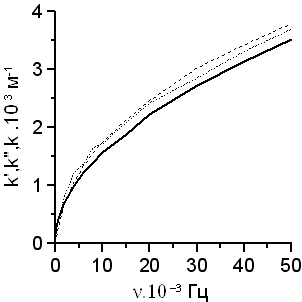
На рис. графически представлены результаты измерений по фазе (мелкие штрихи) и по затуханию (штрихи крупнее) для медной пластинки толщиной l = 1,9 мм. Видно, что измеренные указанными способами частотные зависимости значений и практически совпадают (различия менее 5 %) и соответствуют формуле волнового числа для плоской ЭМ волны в проводящей среде в асимптотике металлов [2] при (сплошная линия). Все это позволяет утверждать, что известная технология индукционного нагрева металлов с помощью магнитного индуктора – это использование в реальной практике физического процесса возбуждения в проводящей среде магнитных поперечных волн. Здесь вполне уместно и пошутить: если Вам повезло и Вы сделали открытие, то загляните в книгу, там об этом уже все написано!

Однако с понижением частоты значения мнимой части волнового числа сильно отклоняются от его действительной части : в медной пластинке на частотах 2.103 Гц и алюминия ( l = 1,4 мм) при 3.103 Гц. В области этих частот при их уменьшении, график переходит от обычного к линейной зависимости по и окончательно . Соответственно, определяемая из частотная зависимость скорости распространения волны в металле сначала ведет себя обычно , но при понижении частоты переходит к const и затем окончательно . Абсолютный минимум значений скорости для пластинки меди был ~ 14 м/с, а алюминия ~ 22 м/с. Отклонение характера частотных зависимостей и от обычных определяется толщиной проводящего слоя: в толстых пластинках это изменение наступает на меньших частотах, а в тонких – на более высоких частотах. Поскольку на фиксированной частоте величина является константой данного материала и не может зависеть от толщины слоя, то наблюдаемое отклонение закона дисперсии от , справедливого для поперечных плоских волн, физически обусловлено регистрацией структуры поля ближней зоны возбуждаемого излучателем (согласно измерениям, дипольного). Именно это и отражается в измерениях с понижением частоты при приеме сигнала прошедшего через пластинку излучения.