Дипломная работа: Экспериментальные исследования процесса тепломассообмена и химических реакций углерода с газами
1. Экспериментальные исследования процесса тепломассообмена и химических реакций углерода с газами.
Для получения наиболее простого экспериментального решения и проведения строгого анализа процесса горения и газификации углерода необходимо изучать процесс горения на телах определенной геометрической формы. Существуют различные методы исследования: метод канала, засыпки, метод сферической частицы и т.д.
При использовании метода канала затруднительна
точная оценка так называемого «внутреннего» горения углерода, которое
наблюдается в различных температурных условиях и которое при высоких
температурах потребует особого внимания. Поэтому исследование было проведено на
сферической частице. Частицы правильной геометрической формы в виде шара
вытачивались на токарном станке из блоков графитизированного углерода марки
ЭГ-14 (d= 0,015 м) плотностью ![]() =1,73
=1,73![]() Мг/м3 или
изготавливались на заводе из графитизированного углерода марки ВТМ-4 (d =
0,0125 м). Для такого графита характерны произвольная ориентация кристаллитов и
отсутствие четкой границы между зернами, где не наступает полной графитизации
углерода даже при нагревании до 3900 К. Рентгенографические данные для
выбранного нами графита показали, что исходный размер кристаллитов по оси С равен
15,4 им, а по оси а — 95,8 нм. Материал имеет значительное количество
пор. Пористость достигает иногда 25%, при этом основную массу составляют поры
размером 0.5-5*10 –6 м.
Мг/м3 или
изготавливались на заводе из графитизированного углерода марки ВТМ-4 (d =
0,0125 м). Для такого графита характерны произвольная ориентация кристаллитов и
отсутствие четкой границы между зернами, где не наступает полной графитизации
углерода даже при нагревании до 3900 К. Рентгенографические данные для
выбранного нами графита показали, что исходный размер кристаллитов по оси С равен
15,4 им, а по оси а — 95,8 нм. Материал имеет значительное количество
пор. Пористость достигает иногда 25%, при этом основную массу составляют поры
размером 0.5-5*10 –6 м.
Наиболее сложной и ответственной частью работы было получение очень высоких температур в широком диапазоне. Был использован метод высокочастотного нагрева, который, как нам представляется, достаточно хорошо себя оправдал, о чем свидетельствуют работы. В настоящее время этот метод получил распространение.
Благодаря тому что углерод, как и уголь, является проводником, хотя и с высоким удельным сопротивлением, он может быть очень легко нагрет в высокочастотном электромагнитном поле. Отрицательный температурный коэффициент и возможность варьирования параметров высокочастотного генератора и индуктора в широких пределах принципиально не ограничивают достижимого верхнего температурного предела. Главными параметрами, которые определяют количество теплоты, выделяющейся на 1*10-4 м2 поверхности, глубину прогрева объекта и распределение тока по поверхности, являются мощность генератора, его частота, геометрические размеры индуктора, куда помещается нагреваемый объект, и электрические свойства нагреваемого объекта. Геометрические параметры индуктора - соотношение между размером индуктора и объекта, соотношение между диаметром индуктора и его высотой -определяют в значительной мере КПД системы.
Градиент температуры в объеме сферической частицы
при ВЧ -нагреве неизбежен, как и при любом другом методе нагрева. Он
определяется прежде всего характером реакции - ее эндотермикой или экзотермикой
и теплообменом с окружающей средой. Качественных различий в характер
распределения температур метод ВЧ -нагрева внести не может, так как источник
теплоты (токи Фуко) находится в узком поверхностном слое. Глубина проникновения
токов Фуко σ = 5030 ![]() мала, в
нашем случае составляла 2 • 10-3 -3*10 –3 м, здесь ρ-
удельное сопротивление; μ-магнитная проницаемостъ; f — частота тока. Поток
теплоты, как и при нагреве потоком горячего газа, был направлен внутрь тела.
мала, в
нашем случае составляла 2 • 10-3 -3*10 –3 м, здесь ρ-
удельное сопротивление; μ-магнитная проницаемостъ; f — частота тока. Поток
теплоты, как и при нагреве потоком горячего газа, был направлен внутрь тела.
Экспериментально на примере реакции С + 02 для 1800 К показано, что метод нагрева не вносит особенностей протекание реакции.
Индукционный метод нагрева предъявляет определенные требования к системе регистрации изменения массы. Для обеспечения высокой точности наблюдения за процессом образец, нагреваемый в индукторе высокочастотного генератора, не должен смещаться по высоте индуктора при изменении его массы. Вследствие существующей неоднородности распределения напряженности электромагнитного поля по высоте индуктора смещение образца будет приводить к изменению температурного уровня нагрева и электродинамической силы, действующей на образец в индукторе. В соответствии с этими требованиями экспериментальная установка была снабжена прецизионной автоматической весовой системой. Были приняты меры к автоматической стабилизации температуры и к созданию условий нагрева образца с минимально возможным градиентом температуры на его поверхности (см. ниже). Мощность рабочего генератора составляла 5*104 Вт
Установка (рис.1.1) состоит из следующих узлов: 1. экспериментальной камеры высокого давления с нагревательным элементом и реакционной трубкой;
2. камеры высокого давления с весовым механизмом;
3. высокочастотного генератора;
4. системы измерения, регулирования и стабилизации температуры;
5. системы приготовления и подачи газовой смеси в реакционную трубку;
6. пультов управления, регулирования и регистрации температуры тела, давления, расхода газа и измерения массы испытуемого материала.
Экспериментальная камера и камера весового устройства устанавливались на общем стенде одна над другой. Камера с весовым устройством может перемещаться вертикально по двум направляющим стежкам при помощи подъемного механизма . Последний состоит из электродвигателя, редуктора, группы шестерен и червяка, жестко скрепленного в вертикальном положении с весовой камерой. Вертикальное перемещение весовой камеры предусмотрено для смены образцов испытуемого материала и ввода их в экспериментальную камеру.
Обе камеры соединяются трубопроводом нижнего фланца весовой камеры, внутри которого проходит подвеска весового механизма; на нем крепится образец исследуемого материала. Соединение герметизируется уплотнением плунжерного типа, находящимся в верхнем фланце экспериментальной камеры.
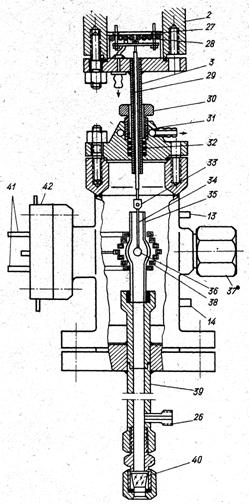
Рис. 1.1. Схема экспериментальной установки (а) и реакционной камеры (б) 1 -экспериментальная камера, 2- весовая камера, 3 –соединительный трубопровод, 4 - подъемный; механизм, 5-к высокочастотному генератору, 6- электрический пирометр к пульту управления весов, 9 - блок генератора высокой частоты (ГВЧ);. Ю - регулятор температуры "Редмет-201"; 11 - блок конденсаторов контура индуктора; 12 -водяное охлаждение; 13 — сброс газа из камеры; 14 - ввод газа в камеру; 15 - кран сброса газа; 16 - редукторы; 17 - осушка газа; 18 - очистка газа от О2; 19-- игольчатые краны регулировки рас- • хода газа; 20 - фильтр; 21 - сверхзвуковое сопло; 22 - дифманометр ДТ-150 с измерительной диафрагмой; 23 - образцовый манометр; 24 - смеситель; 25 - система приготовления и подачи газовой смеси; 26 - ввод газа в реакционную трубку; 27 - отражательный экран; 28 - змеевик водяного охлаждения; 29 - кварцевый участок подвески; 30 - гайка плунжерного уплотнения; 31 - верхний фланец экспериментальной камеры с водяным охлаждением; 32 - плунжерное уплотнение; 33 -устройство для подвешивания образца; 34 - графитовый участок подвески; 35 - кварцевая реакционная трубка; 36 -углеродная частица; 37-смотровое окно; 38 -индуктор; 39 - металлический участок реакционной трубки; 40 - оптическое стекло; 41 -вводы индуктора; 42 -фланец для вводов индуктора с водяным охлаждением.
Экспериментальная камера высокого давления представляет собой цилиндр из нержавеющей стали с приваренными к нему фланцами. Внутренний диаметр камеры 0,130 м, высота 0,400 м. Верхний съемный фланец снабжен водяным охлаждением для уменьшения подвода теплоты к весовому механизму.
В центральной части камеры помещена реакционная кварцевая трубка, соединенная нижним концом с металлической трубкой нижнего фланца камеры. Осесимметрично кварцевой трубке расположен индуктор высокочастотного генератора, вводы которого для подачи высокочастотного напряжения проходят через специальный фланец, расположенный на боковой стенке камеры. Вводы индуктора тщательно герметизированы и электроизолированы.
В кварцевую трубку симметрично относительно индуктора помещается испытуемый образец на графитовой подвеске, прикрепленной к подвеске весового механизма.
1.2.НАГРЕВАТЕЛЬНЫЙ ЭЛЕМЕНТ
Нагревательный элемент – индуктор питается от лампового высокочастотного генератора, смонтированного на базе промышленного генератора типа ИО.60.011. Для увеличения его мощности в схему включены параллельно две генераторные лампы типа Г-452. Мощность в рабочем контуре генератора составляет 50 *103 Вт. Контур индуктора соединен с рабочим контуром генератора по двухконтурной схеме со средней нулевой точкой индуктора и обратной связью по сетке генераторных ламп .
Особого внимания требует нагревательный элемент - высокочастотный индуктор. От правильного выбора его конфигурации и размеров, а также рабочей частоты генератора для заданных формы и размеров нагреваемого тела в значительной степени зависит КПД нагреваемого устройства. Это, в свою очередь, определяет максимально достижимую температуру при данной мощности генератора и характер ее распределения по поверхности и глубине нагреваемого тела.
Распределение выделяемой теплоты в теле и соответственно температуры зависят от распределения индуцируемых токов по поверхности и глубине нагреваемого тела, а также от его теплопроводности и условий теплообмена на границе тела. Известно, что для сферического тела, нагреваемого в цилиндрическом индукторе, распределение настила потока обеспечивает максимальное тепловыделение соответственно температуру на экваторе.
Экспериментальные результаты сублимации углерода были получены на цилиндрическом индукторе с раздвинутым витком. Индуктор был изготовлен из медной трубки прямоугольного сечения размером 6 х 4*10-3 м Высота индуктора 0,042 м, диаметр 0,018 м; расстояние между раздвинутыми витками 0,014 м.
Опыты по взаимодействию углерода с СО2 при повышенных давлениях были проведены с бочкообразным семи витковым индуктором из медной трубки прямоугольного сечения 6-10 -3х4-10 -3 м с толщиной стенки 5 • 10-3 м с крайними витками d = 1,5 • 10 -2 м и средним витком d = 3,5-10 -2 м.
Максимально допустимая частота, необходимая для получения достаточно высокого КПД индукционного нагрева тела сферической формы, оценивалась по формуле
fдоп >4*108 ρ/r2,
где r — радиус нагреваемого тела; ρ — его удельное сопротивление. Для сферического образца из поликристаллического графита диаметром d= 1,25 • 10 -2 м и ρ = 1,0 • 10 -5 Ом • м fдоп > 1 МГц. В качестве рабочей была выбрана часта 1,8 МГц ближайшая разрешенная по радиопомехам.
Применение выбранного индуктора при указанных параметрах высокочастотного генератора (мощность 5,0 *104 Вт и частота 1,8 МГц) позволило при нагреве сферической углеродной частицы диаметром 1,5*10 -2 — 1,25*10 -2 м достигать температуры 3500 К. Этот предел лимитировался больше прочностными свойствами графита, чем параметрами нагревательной системы.
1.3 ВЕСОВОЕ УСТРОЙСТВО
В качестве весового устройства использовались регистрирующие автоматические весы РАВ-10.Они состоят из следующих основных частей: камеры высокого давления с весовым механизмом, электронной следящей схемы автоматического уравновешивания коромысла и пульта управления с самописцем для регистрации изменения массы.
Коромысло весов двуплечее с двумя подвесками. Левая подвеска служит для подвешивания образца и имеет гиревую планку с компенсационными гирями для расширения диапазона регистрируемого изменения массы, правая также имеет гиревую планку с гирями, предназначенными для тарировки весов перед началом работы. Наложение гирь производится с помощью специальных гиревых механизмов.
Автоматический принцип работы весов с непрерывной компенсацией изменения массы осуществляется путем преобразования отклонения коромысла в электрический сигнал. Это преобразование осуществляется с помощью высокочастотного датчика угла отклонения, представляющего собой алюминиевую пластину (рис. 1.2.), жестко закрепленную на коромыле весов и расположенную между двумя катушками, каждая из которых включена в контур высокочастотного генератора (ГВЧ) синусоидальных колебаний. Перемещению пластины соответствует изменение добротности контуров генератора, приводящее к изменению напряжения на его выходе, которое в результате выпрямления и усиления преобразуется в сигнал постоянного тока. Этот сигнал одновременно поступает на потенциометр, шкала которого соответствующим образом проградуирована в единицах массы,и на компенсационные катушки магнитоэлектрического преобразователя, внутри которых могут свободно перемещаться постоянные магниты, жестко связанные с коромыслом весов. Отклвнение коромысла весов регистрируется на диаграмме автоматического потенциометра ЭГШ-09-М2Д
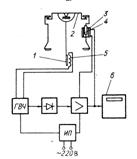
Рис. 1.2. Схема регистрирующих весов с системой автоматического уравновешивания коромысла.
1-датчик угла отклонения, 2-коромысло весов,
3-катушка магнитного преобразователя,
4-постоянные магниты, 5-катушк индуктивности контуров генератора высокой частоты, 6-поценциометр.
Весы снабжены также системой тарировки, которая производится дискретно по 2 *10-5 кг в пределах до 2 *10-4 кг с помощью механизма наложения гирь, управляемого вручную с пульта управления посредством специального кнопочного устройства.
На пульт управления весов вынесены самописец, блоки радиоэлектронной схемы, за исключением генератора высокой частоты, прикрепленного непосредственно к весовой камере, блоки исполнительных реле системы управления, устройства регулировки и настройки. Панель управления содержит переключатель диапазонов чувствительности, переключатель режима с тремя положениям (автоматического арретирования и дискретной компенсации изменения массы в диапазоне до 5*10-4 кг, принудительного арретирования нажатием специальной кнопки, принудительного сброса наложенных гирь), системы автоматической компенсации, кнопки принудительного арретирования и тарировки цифровой ламповый указатель скомпенсированного изменения массы.
Для обеспечения работы весов при высокой температуре образца применена подвеска из термостойкого материала с малым коэффициентом теплового расширения.
1.4. Экспериментальные исследования процесса горения и газификации угольной частицы.
Рассмотрим основные результаты экспериментальных исследований процесса горения и газификации угольной частицы;
Первые опыты по исследованию горения угольной частицы в потоке воздуха методом непрерывного взвешивания были проведены советским ученым В. И. Блиновым и американским исследователем Г.К. Хоттелем и сотрудниками.
Г. К. Хоттель и сотрудники проводили опыты с угольным шаром диаметром 2,5 см, подвешенным к чувствительным весам. Скорость горения замеряли при условии небольшого изменения диаметра частиц при различных температурах, 'концентрациях кислорода и расходах дутья. Анализ опытов был сделан с учётом скорости химической реакции.
В опытах В. И. Блинова было исследовано горение сферических частиц диаметром 5 мм при различном содержании кислорода (от 21% и выше) и разнььх скоростях потока (от 1,9 до 27,4 см/сек), при температурах 700-800°. Скорости горения частиц измеряли с помощью чувствительных весов оптическим отсчетом. Температуру поверхности частицы измеряли посредством оптического пирометра. В момент воспламенения наблюдалось возникновение голубого пламени СО, которое в дальнейшем принимало характер ореола вокруг частицы, что указывало на содержание СО в продуктах сгорания.
Анализ опытов В. И. Блиновым также был сделан с учетом скорости химической реакции. В дальнейшей работе В. И. Блинов и С. Э. Хайкина исследовали горение угольной частицы при изменении давления воздуха в пределах от 1 до 7 ата, причем было выявлено, что скорость горения зависит только от весовой скорости потока воздуха, т. е. от произведения %. В исследовании В.И.Блинова, Е. С. Головиной и С. Э. Хайкиной изучался процесс горения угольной частицы при низких температурах.
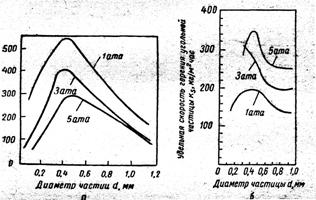
На рис. 1.4 показан график, иллюстрирующий результаты опытов. Из него видно, что удельная скорость горения сначала с увеличением диаметра частицы возрастает, а затем уменьшается. Максимум кривой объясняется переходом реакции ( по мере увеличения размера частицы) из внутреннего кинетического во внешний кинетический режим и наконец в диффузионный режим.
Теоретический анализ влияния летучих на скорость вьгорания частицы в связи с изменением давления, сделанный Б. В. Канторовичем, В. В. Есиным и Н. Н. Шигаевьш, показывает, что в связи с совместным горением летучих и коксовой частицы торможение скорости ее горения проявляется только на известном участке, величина которого зависит от ряда факторов: выхода летучих, температуры, скорости потока и др.
В. В. Есиным и Н. Н. Шигаевьш при участии автора сделан эксперимент, из которого выяснено влияние летучих на скорость выгорания измельченных топлив. Опыпы проводились с торфяной пылью с различным выходом летучих (от 13 до 64%). Пыль сжигали в бомбе при изменении давления от 2,68 до 15 ата. Время выгорания определяли .по индикаторной диаграмме с помощью пьезокварцевого датчика и осциллографа. Экспериментальные кривые зависимости времени τ горения частиц от давления p, соответствуют теоретической зависимости.
Представляют интерес экспериментальные исследования процесса горения отдельной угольной частицы, движущейся в потоке газа. Такого рода опыты проводили Н. И. Сыромятников и 3.И.Леонтьева. После воспламенения частицы наблюдалось замедление скорости ее движения. Это явление объясняется неравномерным выгоранием частицы, причем наибольшее выгорание получается со стороны, обращенной к потоку воздуха. При этом образующиеся продукты сгорания движутся навстречу кислороду, диффундирующему к поверхности частицы, и создают обратный (так называемый стефановский) поток, в результате чего получается сила реакции, величина которой определяется из известной теоремы: импульс силы равен изменению количества движения. Эта сила может быть равна нулю только при двух обстоятельствах: симметричном выгорании частицы и образовании .только одного окисла ОС2.
В последнем случае скорость результирующего потока равна нулю, поскольку изменение числа молекул при образовании двуокиси углерода равно нулю.
При симметричном выгорании частицы, что можно предполагать например в случае движения мелких пылинок в потоке воздуха, реактивная сила также отсутствует, поскольку в этом случае результирующая скорость газифицируемых молекул равна нулю или пренебрежимо мала по сравнению со скоростью самой частицы.
3. И. Леонтьевой были сфотографированы падающие горящие угольные частицы во встречном потоке воздуха. Движение горящей угольной частицы в силу изменения ее массы и выделения газообразных продуктов реакции уже не определяется обычным уравнением движения. В этом случае следует применять уравнение движущегося тела переменной массы, выведенное русским ученым И.В. Мещерским. В. М. Третьяковым проводились исследования процесса воспламенения угольной пыли из подмосковного, тощего угля и антрацита, а также из кокса подмосковного и тощего угля из частиц размером от 75 до 105 μ. Скорость воздуха в камере при нормальных условиях составляла 86 см/сек, температура стенок камеры— от 500 до 1100°. Время пребывания частиц определялось по скорости газа в камере при данной отрегулированной температуре стенок.
2. Теоретические исследования кинетики химических реакций и массообмена пористых углеродных частиц с газами с учетом эндотермической реакции и стефановского течения.
2.1. Кинетика параллельных и последовательных реакций углеродной частицы с газами.
Тепломассообмен (ТМО) твердого или жидкого тела с газами протекает взаимосвязанно с химическими реакциями и фазовыми превращениями (испарение, конденсация), которые являются источниками (стоками) энергии и новых масс газов (продуктов реакции). Появление или исчезновение газовых масс на поверхности твердого тела является причиной появления стефановского течения, направленного в первом случае от поверхности тела, а во втором к поверхности, дополнительно учавствующего в переносе тепла и газообразных компонент [1 - 4]. В целом ряде случаев необходимо учитывать пористую структуру твердого тела и, следовательно, внутреннюю диффузию и кинетику химических реакций на поверхностях пор. Так же необходимо учитывать, что при определенных условиях возможно протекание гомогенных химических реакций в пространстве около частицы. Наилучшим примером является реагирование углерода (графит, электродный уголь, коксы различных топлив) с газами. Известно [1, 5], что на поверхности углерода протекают параллельно экзотермические химические реакции
С+О2 =СО2+![]() (І),
2С+О2=2СО+
(І),
2С+О2=2СО+![]() (ІІ),
(ІІ),
а так же последовательная эндотермическая химическая реакция
С+СО2=2СО-![]() (ІІІ),
(ІІІ),
где ![]() ,
, ![]() ,
, ![]() - тепловые эффекты
химических реакций (І), (ІІ), (ІІІ), Дж/моль.
- тепловые эффекты
химических реакций (І), (ІІ), (ІІІ), Дж/моль.
В газовой фазе возможно протекание экзотермической гомогенной химической реакции
2СО+О2=2СО+![]() (ІV),
(ІV),
где ![]() - тепловой эффект
химической реакции (ІV), Дж/моль.
- тепловой эффект
химической реакции (ІV), Дж/моль.
Если
скорость гомогенной реакции (ІV) меньше скорости массопереноса (критерий
Дамкелера (Damkohier) или критерий Семенова) ![]() <
0.4, то ее влиянием на тепломассообмен твердого тела можно пренебречь [1]
<
0.4, то ее влиянием на тепломассообмен твердого тела можно пренебречь [1]
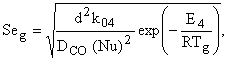
где d –
диаметр углеродной частицы, м; ![]() -
предэкспоненциальный множитель, 1/с;
-
предэкспоненциальный множитель, 1/с; ![]() -
энергия активации реакции (ІV), Дж/моль;
-
энергия активации реакции (ІV), Дж/моль; ![]() -
температура газовой смеси, К;
-
температура газовой смеси, К; ![]() -
коэффициент диффузии окиси углерода, м2/с; Nu – критерий Нуссельта.
Малое значение критерия Семенова определяется экспериментальными условиями,
когда частица дополнительно разогревается током высокой частоты или в
результате поглощения лазерного излучения и обдувается холодным газом [5-7].
Так в [5] частица электродного угля d=1.2 – 1.5 см, нагреваемая током высокой
частоты, обдувалась воздухом комнатной температуры (Тg=293 К) со
скоростью V=0.6 м/с. В [6-7] приведены экспериментальные и теоретические
результаты временных зависимостей температуры и диаметра углеродной частицы,
горение которой в воздухе комнатной температуры поддерживается лазерным
излучением.
-
коэффициент диффузии окиси углерода, м2/с; Nu – критерий Нуссельта.
Малое значение критерия Семенова определяется экспериментальными условиями,
когда частица дополнительно разогревается током высокой частоты или в
результате поглощения лазерного излучения и обдувается холодным газом [5-7].
Так в [5] частица электродного угля d=1.2 – 1.5 см, нагреваемая током высокой
частоты, обдувалась воздухом комнатной температуры (Тg=293 К) со
скоростью V=0.6 м/с. В [6-7] приведены экспериментальные и теоретические
результаты временных зависимостей температуры и диаметра углеродной частицы,
горение которой в воздухе комнатной температуры поддерживается лазерным
излучением.
Проведенный анализ тепломассообмена и кинетики химических реакций (І), (ІІ), (ІІІ) углеродной частицы с газами показал на необходимость учета стефановского течения и позволил получить аналитические выражения качественно верно описывающие влияние условий и свойств на газовый состав продуктов реакции, скорость химического превращения углерода, плотности тепловых и массовых потоков на поверхности частицы [3]. Однако, пренебрежение внутренним реагированием привело к несовпадению экспериментальных и расчетных результатов по скорости химического превращения углеродной частицы при различных ее температурах и диаметрах.
Задачей настоящей работы является выявление роли внутреннего реагирования и стефановского течения в процессах ТМО и химических реакций пористой углеродной частицы с газами с учетом вынужденной и естественной конвекции в зависимости от температуры и диаметра частицы.
Скорость химического превращения углерода в газообразные компоненты определяется скоростью химической реакции на внешней поверхности частицы и внутри частицы на поверхностях пор
![]() ,
,
где ![]() - соответственно,
суммарная скорость химического превращения, скорость химического превращения
на поверхности углеродной частицы и внутри, на поверхностях пор, кг/(м2
с).
- соответственно,
суммарная скорость химического превращения, скорость химического превращения
на поверхности углеродной частицы и внутри, на поверхностях пор, кг/(м2
с).
Скорость химического превращения углерода на поверхности частицы определяется кинетикой реакций (I), (II) и (III)
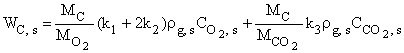 , (2.1)
, (2.1)
![]()
![]() ,
,
![]() ,
,
где ![]() – молярные массы углерода,
кислорода, углекислого газа, кг/моль;
– молярные массы углерода,
кислорода, углекислого газа, кг/моль; ![]() –
относительные массовые концентрации O2 и CO2 на
поверхности частицы;
–
относительные массовые концентрации O2 и CO2 на
поверхности частицы; ![]() ,
, ![]() ,
, ![]() – константы скоростей
химических реакций (I), (II), (III), м/с;
– константы скоростей
химических реакций (I), (II), (III), м/с; ![]() ,
,
![]() ,
, ![]() - предэкспоненциальные
множители, м/с; E1, E2, Е3 – энергии активации
(I), (II) и (III) реакций, Дж/моль; R – универсальная газовая постоянная,
Дж/(моль×К); Т – температура частицы, К;
- предэкспоненциальные
множители, м/с; E1, E2, Е3 – энергии активации
(I), (II) и (III) реакций, Дж/моль; R – универсальная газовая постоянная,
Дж/(моль×К); Т – температура частицы, К; ![]() ,
, ![]() - плотность газа при
температуре частицы и при Т0=273.15 К, кг/м3.
- плотность газа при
температуре частицы и при Т0=273.15 К, кг/м3.
Энергии активации и предэкспоненциальные множители реакций (I), (II) и (III) связаны между собой [1]:
![]() ;
; ![]() ,
,
где ![]() =1 для реакции (I), 2- для
реакции (II) и 3- для реакции (III).
=1 для реакции (I), 2- для
реакции (II) и 3- для реакции (III).
Выражение для скорости химического превращения углерода в результате химических реакций на поверхностях пор внутри объёма частицы получается из решения задачи внутренней диффузии и может быть представлено в виде
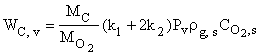 ,
, ![]() ,
(2)
,
(2)
![]() , (3)
, (3)
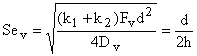 ,
, 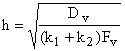 , (4)
, (4)
где ![]() -эффективная константа
внутреннего реагирования, м/с; Sev - критерий Семенова, определяющий
соотношение констант скоростей химических превращений на поверхностях пор и
диффузии [8, 9] или отношение радиуса частицы к глубине реакционной зоны, Dv
– коэффициент внутренней диффузии кислорода в порах, м2/с;
-эффективная константа
внутреннего реагирования, м/с; Sev - критерий Семенова, определяющий
соотношение констант скоростей химических превращений на поверхностях пор и
диффузии [8, 9] или отношение радиуса частицы к глубине реакционной зоны, Dv
– коэффициент внутренней диффузии кислорода в порах, м2/с; ![]() - глубина реакционной зоны
внутреннего реагирования, м,
- глубина реакционной зоны
внутреннего реагирования, м, ![]() –
удельная поверхность пор, м-1.
–
удельная поверхность пор, м-1.
Коэффициент внутренней диффузии выражается через порозность частицы [1, 5]
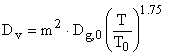 , (5)
, (5)
где ![]() - коэффициент диффузии
кислорода в воздухе при температуре
- коэффициент диффузии
кислорода в воздухе при температуре ![]() , м2/с;
, м2/с;
![]() - порозность частицы.
- порозность частицы.
Суммарная скорость химического превращения углеродной частицы и плотность химического тепловыделения
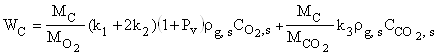 , (6)
, (6)
![]()
![]() , (7)
, (7)
где Q1,
Q2 – тепловые эффекты химических реакций (I) и (II), рассчитанные на
единицу массы кислорода, Дж/кг; Q3 – тепловой эффект реакции (III),
рассчитанный на единицу массы углекислого газа, Дж/кг; ![]() - суммарная плотность
химического тепловыделения, на поверхности и внутри частицы, соответственно,
Вт/м2.
- суммарная плотность
химического тепловыделения, на поверхности и внутри частицы, соответственно,
Вт/м2.
2.2. Взаимовлияние кинетики химических реакций и массообмена пористых углеродных частиц с газами.
Влияние
относительной скорости движения частицы на кинетику химических реакций и
тепломассообмен учитывается радиусом приведенной пленки ![]() , на поверхности которой
задаются параметры невозмущенного потока [1, 2]. Для случая отсутствия
вынужденной и естественной конвекций (частица неподвижна относительно газа,
Nu=2) радиус приведенной пленки
, на поверхности которой
задаются параметры невозмущенного потока [1, 2]. Для случая отсутствия
вынужденной и естественной конвекций (частица неподвижна относительно газа,
Nu=2) радиус приведенной пленки ![]() равен
бесконечности. Радиус приведенной пленки уменьшается с увеличением
интенсивности естественной и вынужденной конвекций, приближаясь к радиусу
частицы
равен
бесконечности. Радиус приведенной пленки уменьшается с увеличением
интенсивности естественной и вынужденной конвекций, приближаясь к радиусу
частицы ![]() . Зависимость
. Зависимость ![]() от критерия Нуссельта
имеет вид:
от критерия Нуссельта
имеет вид:
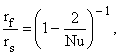 (8)
(8)
![]() ,
(9)
,
(9)
![]() , [5, 10]
, [5, 10]
![]() ,
, 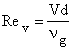 ,
, ![]() ,
, ![]() ,
,
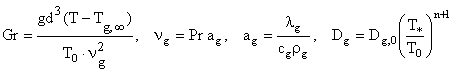 ,
,
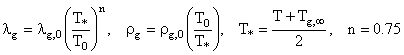 ,
,
где ![]()
![]() – критерии Рейнольдса,
определяющие суммарную, вынужденную и естественную конвекции; Gr, Pr –
критерии Грасгофа и Прандтля; V - относительная скорость частицы, м/с;
– критерии Рейнольдса,
определяющие суммарную, вынужденную и естественную конвекции; Gr, Pr –
критерии Грасгофа и Прандтля; V - относительная скорость частицы, м/с; ![]() g –
кинематическая вязкость газа, м2/с; g – ускорение свободного
падения, м/с2; аg – температуропроводность газовой смеси,
м2/с;
g –
кинематическая вязкость газа, м2/с; g – ускорение свободного
падения, м/с2; аg – температуропроводность газовой смеси,
м2/с; ![]() - коэффициент
теплопроводности газовой смеси, Вт/(м К);
- коэффициент
теплопроводности газовой смеси, Вт/(м К); ![]() -
коэффициент теплопроводности газовой смеси при
-
коэффициент теплопроводности газовой смеси при ![]() ,
Вт/(м К);
,
Вт/(м К); ![]() - коэффициент массообмена,
м/с;
- коэффициент массообмена,
м/с; ![]() - удельная теплоемкость
газовой смеси, Дж/(кг К);
- удельная теплоемкость
газовой смеси, Дж/(кг К); ![]() -
температура газовой смеси на бесконечном удалении от поверхности частицы, К;
-
температура газовой смеси на бесконечном удалении от поверхности частицы, К; ![]() - коэффициент диффузии
кислорода в газовой смеси, м2/с;
- коэффициент диффузии
кислорода в газовой смеси, м2/с; ![]() -
коэффициент теплообмена, Вт/м2 К.
-
коэффициент теплообмена, Вт/м2 К.
Зависимости относительных массовых концентраций кислорода (![]() ), диоксида углерода (
), диоксида углерода (![]() ), оксида углерода (
), оксида углерода (![]() ) и азота (
) и азота (![]() ), а так же скорость
стефановского течения (
), а так же скорость
стефановского течения (![]() ), для
), для ![]() , находятся из решений
уравнений, в которых левые части представляют потоки масс газообразных
компонент через произвольную поверхность радиуса r, а правые – скорости
образования или исчезновения масс этих компонент в результате химических
реакций
, находятся из решений
уравнений, в которых левые части представляют потоки масс газообразных
компонент через произвольную поверхность радиуса r, а правые – скорости
образования или исчезновения масс этих компонент в результате химических
реакций
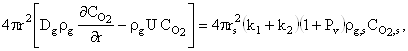
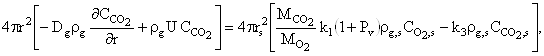
(10)
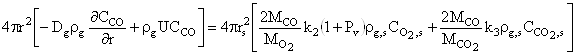 ,
,
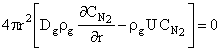 ,
,
где ![]() – молярная масса угарного
газа, кг/моль;
– молярная масса угарного
газа, кг/моль; ![]() - текущая скорость стефановского течения, м/с.
- текущая скорость стефановского течения, м/с.
Предполагая,
что коэффициенты диффузии компонент газовой смеси равны ![]() и, применяя условие,
и, применяя условие, ![]() , из (10) получим уравнение
неразрывности
, из (10) получим уравнение
неразрывности
![]() ,
(11)
,
(11)
где Wc
определяется формулой (6), ![]() - скорость стефановского течения на поверхности частицы,
м/с.
- скорость стефановского течения на поверхности частицы,
м/с.
Для решения (10) зададим граничные условия
![]()
и введем безразмерные координаты
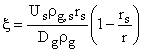 ,
,
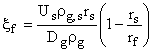 .
(12)
.
(12)
Учитывая (8) и (9), получим, что безразмерная скорость стефановского течения на поверхности частицы
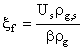 ,
,
где ![]() - относительные массовые концентрации; j-1 для О2,
2 - СО2, 3 - СО, 4 - N2;
- относительные массовые концентрации; j-1 для О2,
2 - СО2, 3 - СО, 4 - N2; ![]() ―
относительные массовые концентрации компонент газовой смеси на поверхности
частицы и приведенной пленки.
―
относительные массовые концентрации компонент газовой смеси на поверхности
частицы и приведенной пленки.
Решение (10) и (11) представим в виде
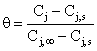
![]() или
или ![]() (13)
(13)
Скорость
химического превращения углерода в газообразные компоненты может оказывать
влияние на интенсивность теплообмена поверхности частицы с газом. Для
определения плотности теплового потока, характеризующего теплообмен частицы с
газом, воспользуемся предположением о квазистационарности поля температуры
газовой фазы и частицы. В этом случае (![]() )
тепловой поток через произвольную поверхность радиуса
)
тепловой поток через произвольную поверхность радиуса ![]() является постоянным и
равен произведению плотности теплового потока на поверхность частицы.
является постоянным и
равен произведению плотности теплового потока на поверхность частицы.
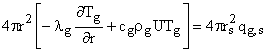 .
.
С учетом уравнения неразрывности (11) представим в виде
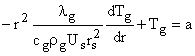 .
.
Задавая граничные условия
![]() ,
, ![]() и безразмерные координаты
в виде (12), решение представим в аналогичном (13) виде
и безразмерные координаты
в виде (12), решение представим в аналогичном (13) виде
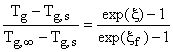 ,
, ![]() .
.
При ![]() выражение для
выражение для ![]() получим в виде
получим в виде
![]() .
.
Так как ![]() , то, представляя
, то, представляя ![]() , из последнего выражения
получим возможность выразить
, из последнего выражения
получим возможность выразить ![]() в виде
суммы плотностей тепловых потоков за счет теплообмена и стефановского течения
в виде
суммы плотностей тепловых потоков за счет теплообмена и стефановского течения
![]()
или
![]() .
.
Получено, что
плотность теплового потока ![]() в
основном определяется теплообменом, а стефановкое течение оказывает не
значительное влияние, таким образом, плотностью теплового потока за счет
стефановского течения можно пренебречь.
в
основном определяется теплообменом, а стефановкое течение оказывает не
значительное влияние, таким образом, плотностью теплового потока за счет
стефановского течения можно пренебречь.
Подставив
(13) в левые части уравнений (10) и, полагая ![]() получим
систему уравнений, которая совместно с (11) позволяет найти
получим
систему уравнений, которая совместно с (11) позволяет найти ![]() и
и ![]()
![]() ,
,
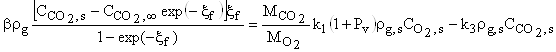 ,
,
(14)
 ,
,
![]() .
.
Обозначив
![]() , из (14) выразим
поверхностные концентрации компонент через
, из (14) выразим
поверхностные концентрации компонент через ![]()
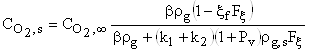 , (15)
, (15)
 , (16)
, (16)
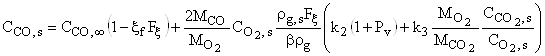 , (17)
, (17)
![]() . (18)
. (18)
Подставляя (15) и (16) в первое и второе уравнения системы (10) при r=rs, получим трансцендентное уравнение для определения безразмерной скорости стефановского течения на поверхности частицы
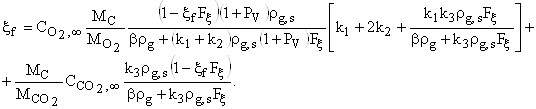 (19)
(19)
Численные
расчеты показывают, что ![]() <<1.
С учетом линейного приближения
<<1.
С учетом линейного приближения ![]() и,
полагая, что
и,
полагая, что ![]() , из (19) получим, что
безразмерная скорость стефановского течения и, следовательно, скорость
химического превращения углеродной частицы имеют следующий вид:
, из (19) получим, что
безразмерная скорость стефановского течения и, следовательно, скорость
химического превращения углеродной частицы имеют следующий вид:
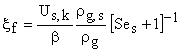 , (20)
, (20)
![]() ,
,
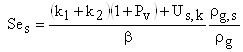 , (21)
, (21)
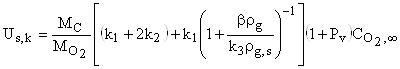 , (22)
, (22)
где ![]() - скорость стефановского
течения при протекании химической реакции в кинетической области,
- скорость стефановского
течения при протекании химической реакции в кинетической области, ![]() - число Семенова,
диффузионно-кинетическое соотношение.
- число Семенова,
диффузионно-кинетическое соотношение.
Подставляя
(20) в (15) при ![]() =1, получим связь
=1, получим связь
![]() с
с ![]() в явном виде
в явном виде
![]() . (23)
. (23)
В
предположении, что ![]() , аналогичным
образом из (16), (17), (18) находим поверхностные концентрации
, аналогичным
образом из (16), (17), (18) находим поверхностные концентрации ![]() и
и ![]()
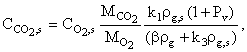 (24)
(24)
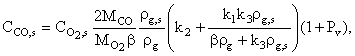 (25)
(25)
![]() (26)
(26)
Используя
формулы (23) и (24), проведем анализ влияния температуры на ![]() и, следовательно, на
и, следовательно, на ![]() и
и ![]() .
.
При
невысоких температурах и диаметрах частицы, для которых (![]() ,
,  ,
, 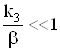 ), то есть реализуется
кинетическая область протекания химических реакций.
), то есть реализуется
кинетическая область протекания химических реакций.
Учитывая,
что при этих условиях (3) приймет вид 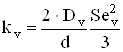 , при этом
, при этом ![]() .
.
Подставляя (23) и (24) в (6), получим, что для кинетической области
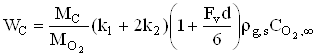 , (27)
, (27)
![]() ,
, 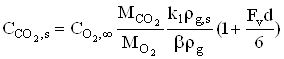 ,
,
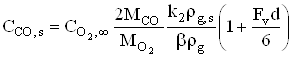 ,
,
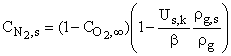 ,
,
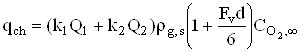 . (28)
. (28)
Т.е.
при протекании реакции в кинетической области ![]() и
и
![]() определяются внутренним
реагированием и увеличиваются с ростом температуры по аррениусовской
зависимости и не зависят от относительной скорости движения частицы. При этом
химической реакцией (III) можно пренебречь. Это подтверждается
экспериментальными данными [5].
определяются внутренним
реагированием и увеличиваются с ростом температуры по аррениусовской
зависимости и не зависят от относительной скорости движения частицы. При этом
химической реакцией (III) можно пренебречь. Это подтверждается
экспериментальными данными [5].
В
области промежуточных температур и диаметров (![]() ,
,
 ,
, 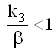 ) повышение температуры
приводит к подключению процессов массопереноса и эндотермической реакции (III),
что сдвигает кинетику химических реакций в переходную область. Для этой области
можно записать
) повышение температуры
приводит к подключению процессов массопереноса и эндотермической реакции (III),
что сдвигает кинетику химических реакций в переходную область. Для этой области
можно записать
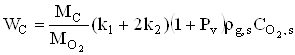 ,
,
![]() .
.
В этой
области температур, в результате действия эндотермической реакции (III), в
определенном диапазоне размеров частицы, с ростом температуры происходит
понижение ![]() .
.
Дальнейшее повышение температуры и диаметра частицы может привести к смещению кинетики химических реакций в диффузионную область, в которой выполняются условия
![]() ,
, ![]() .
.
Используя
условие![]() , из (22) получим
, из (22) получим
![]() , (29)
, (29)
При протекании реакций в диффузионной области, из (23)-(26) с учетом (21), получим выражения для поверхностных концентраций
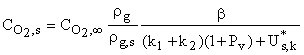 , (30)
, (30)
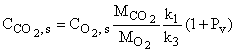 , (31)
, (31)
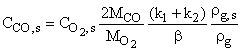 , (32)
, (32)
![]() , (33)
, (33)
где
 , (34)
, (34)
Подставляя (30) и (31) в (7) получим, что при протекании химических реакций в диффузионной области плотность химического тепловыделения
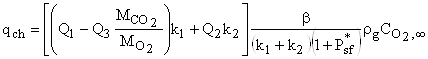 .
.
Учитывая, что тепловые эффекты реакций (I) – (III) связаны между собой
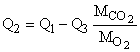 ,
,
получим, что плотность химического тепловыделения в диффузионной области определяется тепловым эффектом реакции (II)
![]() . (35)
. (35)
Скорости
химического превращения углеродной частицы ![]() и
и
![]() при протекании химических
реакций в диффузионном режиме, получаются в результате подстановки (30), (31) в
(1) и (2)
при протекании химических
реакций в диффузионном режиме, получаются в результате подстановки (30), (31) в
(1) и (2)
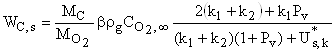 ,
,
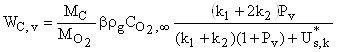 .
.
С учетом (29) и (34) получим, что суммарная скорость химического превращения углерода при высокой температуре определяется скоростью химической реакции 2С+О2=2СО (ІІ), протекающей в диффузионной области
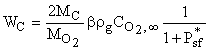 . (36)
. (36)
3. Аналіз влияния температури и диаметра частицы на кинетику химических реакций и тепломассообмен углеродной частицы с газами.
3.1. Влияние температуры при заданном диаметре частицы.
Расчеты скоростей
химических реакций (![]() ,
, ![]() ,
, ![]() ), плотностей химического
тепловыделения (
), плотностей химического
тепловыделения (![]() ,
, ![]() ,
, ![]() ) и относительных массовых
концентраций газообразных компонент на поверхности углеродной частицы (
) и относительных массовых
концентраций газообразных компонент на поверхности углеродной частицы (![]() ,
, ![]() ,
, ![]() ) проводились по формулам
) проводились по формулам
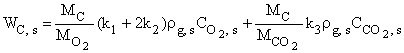 ,
,
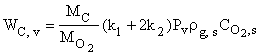 ,
, ![]() ,
,
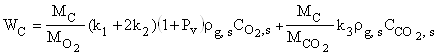 ,
,
![]()
![]() ,
,
![]()
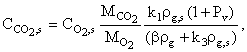
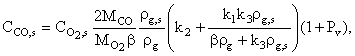
![]()
при следующих
параметрах: ![]() =1,234·107,
=1,234·107,
![]() =6,859·106,
=6,859·106,
![]() =3,989·106
Дж/кг О2;
=3,989·106
Дж/кг О2; ![]() = 2,188·105,
= 2,188·105,
![]() = 4,721·105,
= 4,721·105,
![]() = 2,228·105
м/с;
= 2,228·105
м/с; ![]() = 1,67·105,
= 1,67·105,
![]() = 1,837·105,
= 1,837·105,
![]() = 3,674·105
Дж/моль;
= 3,674·105
Дж/моль; ![]() =8,31 Дж/(моль·К);
=8,31 Дж/(моль·К); ![]() = 2·105 м-1;
постоянные величины:
= 2·105 м-1;
постоянные величины: ![]() = 0,178·10-4
м2/с;
= 0,178·10-4
м2/с; ![]() =1,293кг/м3;
=1,293кг/м3;
![]() =0,0244Вт·м/К
определены для
=0,0244Вт·м/К
определены для ![]() =273,15 К, m=0.2
и соответствуют графиту марки ЭГ-14.
=273,15 К, m=0.2
и соответствуют графиту марки ЭГ-14.
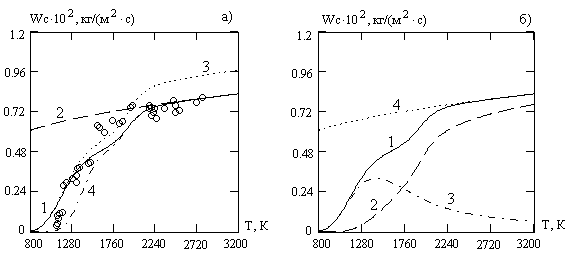
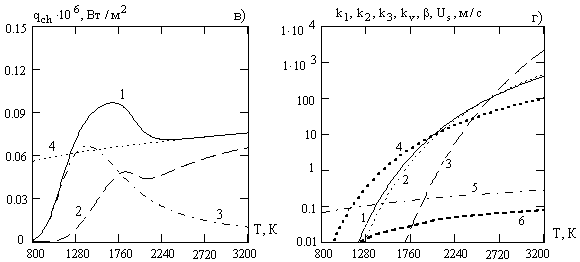
Рис.1. Температурные зависимости скоростей химических реакций пористой углеродной частицы в воздухе, плотностей химического тепловыделения, констант скоростей химических реакций, коэффициента массообмена, эффективной константы внутреннего реагирования и скорости стефановского течения
а) 1 - ![]() , 2 - расчет по формуле
(36), 3 - WC без учета стефановского течения, 4 -
, 2 - расчет по формуле
(36), 3 - WC без учета стефановского течения, 4 -![]() без учета внутреннего
реагирования, °°°°° - эксперимент Головиной [5],
без учета внутреннего
реагирования, °°°°° - эксперимент Головиной [5],
б) 1 - ![]() , 2 -
, 2 - ![]() , 3 -
, 3 - ![]() , 4 – расчет по формуле
(36),
, 4 – расчет по формуле
(36),
в) 1 - ![]() , 2 -
, 2 - ![]() , 3 -
, 3 - ![]() , 4 - протекание реакции
2С+О2=2СО в диффузионном режиме(расчет по формуле (35).
, 4 - протекание реакции
2С+О2=2СО в диффузионном режиме(расчет по формуле (35).
г) 1-![]() , 2-
, 2-![]() , 3-
, 3-![]() , 4-
, 4-![]() , 5-
, 5-![]() , 6-
, 6-![]() . (d = 1.5∙10-2
м, V=0,6 м/с,
. (d = 1.5∙10-2
м, V=0,6 м/с, ![]() =293К).
=293К).
3.2. Влияние диаметра частицы на скорости химического превращения и тепломассообмен.
На рис. 2 (а-в)
представлены кривые ![]() и
и ![]() при различных температурах
частицы (Т=1000, 1500, 2000 К). С повышением температуры качественный ход этих
зависимостей изменяется. При низких температурах на кривой
при различных температурах
частицы (Т=1000, 1500, 2000 К). С повышением температуры качественный ход этих
зависимостей изменяется. При низких температурах на кривой ![]() имеется максимум, такой
ход зависимости подтверждается экспериментальными данными [11]. Концентрация
имеется максимум, такой
ход зависимости подтверждается экспериментальными данными [11]. Концентрация ![]() монотонно уменьшается, а
монотонно уменьшается, а ![]() и
и ![]() - увеличиваются, при чем
концентрация
- увеличиваются, при чем
концентрация ![]() растет в большей степени.
Максимум на кривой
растет в большей степени.
Максимум на кривой ![]() определяется
конкуренцией процессов внутрипористого реагирования и процессов, протекающих
на внешней поверхности частицы при фактически малом участии в процессе внешней
поверхности. Увеличение температуры от 1100 К до 1500 К приводит к смещению
максимума на зависимости
определяется
конкуренцией процессов внутрипористого реагирования и процессов, протекающих
на внешней поверхности частицы при фактически малом участии в процессе внешней
поверхности. Увеличение температуры от 1100 К до 1500 К приводит к смещению
максимума на зависимости ![]() в
область малых диаметров и повышению роли реакции на внешней поверхности частицы
(рис. 1 в).
в
область малых диаметров и повышению роли реакции на внешней поверхности частицы
(рис. 1 в).
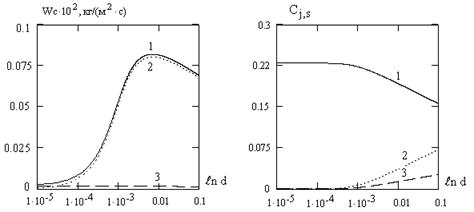
а) Т = 1000 К
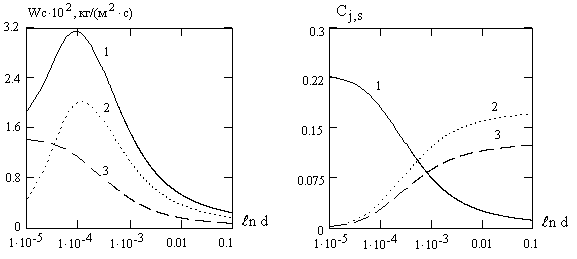
б) Т=1500 К
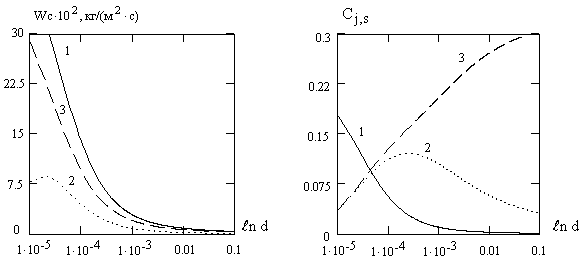
в) Т=2000К
Рис2. Зависимости скорости химического превращения
углерода от размера частицы ( 1- ![]() , 2 -
, 2 - ![]() , 3-
, 3- ![]() ) и концентраций газообразных
компонент на поверхности от размера частицы ( 1 -
) и концентраций газообразных
компонент на поверхности от размера частицы ( 1 - ![]() ,
2 -
,
2 - ![]() , 3 -
, 3 -![]() ).
).
Дальнейшее
повышение температуры до 2000 К приводит к смещению реакции на внешнюю
поверхность. При больших диметрах преимущественным продуктом реакции становится
СО. На кривой ![]() появляется
максимум, определяемый конкуренцией процессов появления СО2 в
реакции (І) и исчезновение в реакции (ІІІ).
появляется
максимум, определяемый конкуренцией процессов появления СО2 в
реакции (І) и исчезновение в реакции (ІІІ).
ЛИТЕРАТУРА
1. Основы практической теории горения / Под ред. В.В. Померанцева. ― Л.: Энергоатомиздат, 1986. – 312 с.
2. Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. ― М.: Наука, 1987. ― 502 с.
3. Калинчак В. В. Влияние стефановского течения и конвекции на кинетику химических реакций тепломассообмена углеродных частиц с газами // Инженерно-физический журнал. ― 2001. ― Т. 74, № 2. – С. 51 – 56.
4. Калинчак В.В., Орловская С.Г., Калинчак А.И., Дубинский А.В. Высоко- и низкотемпературный тепломассообмен углеродной частицы с воздухом при учете стефановского течения и теплопотерь излучением // Теплофизика высоких температур. - 1996. - Т.34, № 1. - С. 83 - 91.
5. Головина Е.С. Высокотемпературное горение и газификация углерода, - М.,1986. – 176 с.
6.Букатый В.И., Суторихин И.А. Высокотемпературное горение углеродных частиц в поле лазерного излучения // Физика горения и взрыва. – 1988. – Т.24, №3.-С.9-11.
7. Калинчак В.В., Орловская С.Г., Мандель А.В. Устойчивые и критические режимы тепло- и массообмена частицы, находящейся в поле лазерного излучения // Физика горения и взрыва.-1999.-Т.35, №6.-С.1-6.
8. Калинчак В. В., Орловская С. Г., Гулеватая О. Н. Высокотемпературный тепломассообмен нагреваемой лазерным излучением углеродной частицы с учетом стефановского течения на ее поверхности // Физика аэродисперсных систем. – 2001. – Т. 38. ― С. 158 – 169.
9. Калинчак В.В., Садковский В.И., Харлампиева Н.А. Влияние внутренней диффузии на критические условия и характеристики высоко- и низкотемпературных состояний углеродной частицы // Теплофизика высоких температур. -1997. - Т.35, №1.- С.73-79.
10. Нигматулин Р. И. Динамика многофазных сред. Часть первая. ― М.: Наука, 1987. – 464 с.
11. Канторович Б.В. Введение в теорию горения и газификации твердого топлива. - М.: Гос-ное н.-т. изд-во лит-ры по черной и цветной металлургии, 1960.- 356с.