Контрольная работа: Электромагнитные поля и волны

Задача №1

Дано: вектор напряжённости электрического поля в воздухе изменяется по закону –

где Е₀=5мВ/м;  10 м^-1 ; 40 м^-1; f =*10⁶ рад/с задано согласно варианта.

Решение.

Для нахождения вектора напряжённости магнитного поля воспользуемся вторым уравнением Максвелла в дифференциальной форме [1],[2]:

  (1)

В воздухе векторы напряжённости магнитного поля и магнитной индукции связаны материальным уравнением [1], [2] перепишем (1) в виде:

 (2)

Вектор напряжённости электрического поля является гармонической функцией времени поэтому можно записать:

 (3)

 Комплексная амплитуда вектора напряжённости электрического поля:

  (4)

Учитывая, что комплексная амплитуда вектора напряжённости электрического поля имеет лишь одну составляющую  , то раскроем определитель ротора комплексного вектора (4) по первой строке:

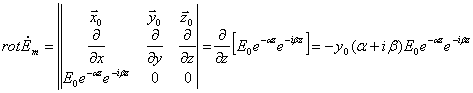 (5)

 Представим комплексный вектор (5) в показательной форме:

  (6)

Выразим из (3) комплексную амплитуду вектора напряжённости магнитного поля:

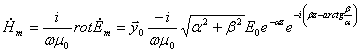  (7)

Представим (7) в показательной форме:

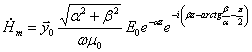   (8)

 Определим мгновенное значение вектора напряжённости магнитного поля по формуле:

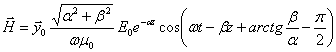 (9)

Следовательно, амплитуда напряжённости магнитного поля в начале координат будет равна:

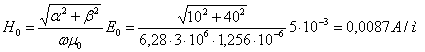  (10)

где ₀ = 1,256*10^-6 Гн/м магнитная постоянная

 Начальную фазу определим по формуле:

  (11)

Окончательно (9) примет вид:

По определению вектор Пойтинга находится как векторное произведение векторов электрического и магнитного полей [1], [2]:

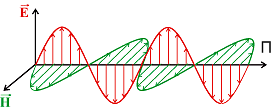
Рис.1 К определению вектора Пойтинга.

 (12)

Учитывая, что векторное произведение ортов , получим (12) в виде:

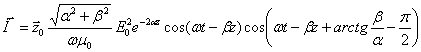 (13)

Тогда согласно (13) амплитуда вектора Пойтинга в начале координат будет равна:

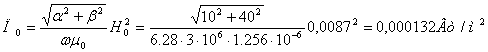  (14)

Среднее за период значение вектора Пойтинга находится по формуле:

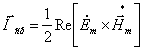  (15)

Таким образом,  вычислим среднее значение вектора Пойтинга:

   (16)

Задача№2

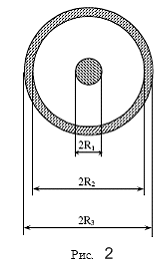
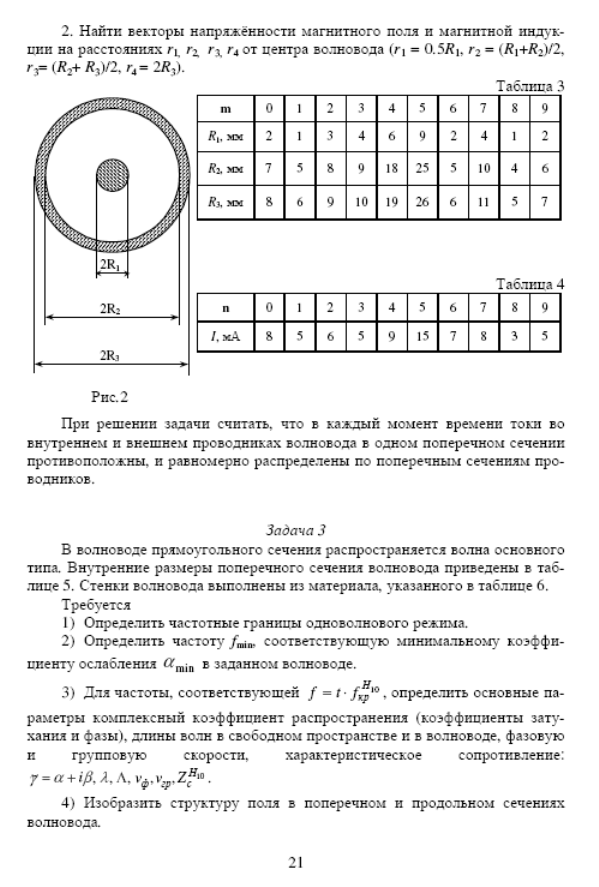
Дано: R₁=2 мм; R₂=7 мм; R₃=8 мм; I = 5мА.

Решение.

Введём цилиндрическую систему координат, с осью аппликат, направленной вдоль оси волновода.

Напряжённость магнитного поля имеет отличную от нуля азимутальную компоненту, модуль которой зависит лишь от расстояния до оси волновода т.е:

 (17)

Воспользуемся первым уравнением Максвелла в интегральной форме [1],[2]:

 (18)

Интеграл в левой части (18) может быть найден для произвольного кругового контура по формуле, выражающую зависимость напряжённости магнитного поля от расстояния от центра волновода:

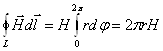  (19)

 Плотность тока  в диапазоне   0 <r R₁ внутреннем проводнике равна:

  (20)

 Для определения напряжённости магнитного поля введём контур L1, радиус которого лежит в указанном диапазоне расстояний , тогда контур охватывает ток:

  (21)

 Приравняем (19) и (21) и выразим магнитную напряжённость и индукцию и получим для r₁=0,5R₁ :

  (22)

где для меди, относительная магнитная проницаемость

Запишем (22) в векторной форме: 

 (23)

  В диапазоне расстояний R1< r < R2  контур L2 охватывает полный ток внутреннего проводника (I2 = I). Напряжённость и индукцию магнитного поля на расстоянии r₂ = (R1+R2)/2=4,5мм определим аналогично (22):

   (24)

Или в векторной форме:

 (25)

Внутри внешнего проводника  R2< r < R3 плотность тока определяется как:

   (26)

Контур L3  охватывает ток , равный сумме полного тока во внутреннем проводнике и части тока во внешнем проводнике, взятом с противоположным знаком:

I3 I - I*  (27)

Часть тока находится по формуле:

 (28)

Подставим (28) в (27) и приведём к общему знаменателю:

 (29)

Приравняем (19) и (29) получим:

   (30)

Из (30) выразим напряжённость и индукцию и запишем сразу в векторной форме для r₃ = (R3+R2)/2=7,5мм  :

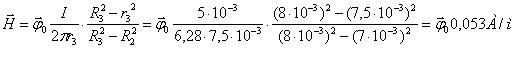
В диапазоне расстояний  контур L4 охватывает ток:

I4 I -I 0.  (31)

Итак, H=B=0, - магнитное поле вне волновода отсутствует.

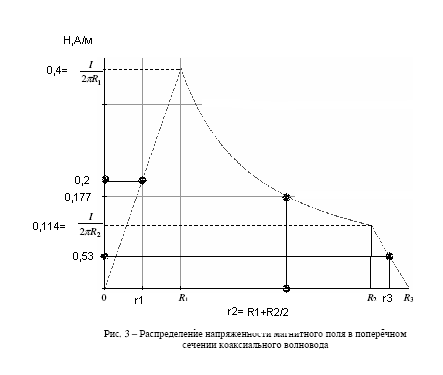
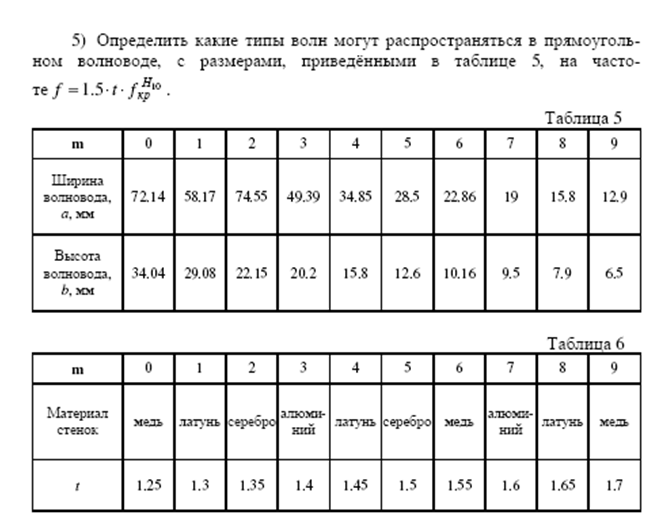
Задача№3

Дано:  Размеры волновода медь t=1,25.

Решение.

1.  Волной первого высшего типа в прямоугольном волноводе является волна Н²⁰ , поэтому условия одноволнового режима имеют вид:

они являются частотными границами.

Здесь с=3*10⁸ м/с – скорость света.

2.  Поверхностное сопротивление и характеристическое сопротивление заполнения определяются из выражений:

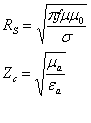 (32)

Коэффициент ослабления в волноводе находится по формуле:

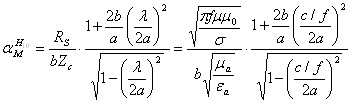   (33)

 где 59,5*10⁶ См/м  - удельная проводимость меди;

относительная магнитная проницаемость меди;

_а =₀ = 8,85*10^-12*1 = 8,85*10^-12 Кл/(В*м) ^– абсолютная диэлектрическая проницаемость воздуха внутри волновода.

=

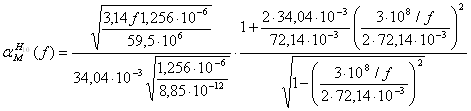для f=2,08ГГц  =0,068 м^-1, для f=4,16ГГц  =0,00184 м^-1, для f=5ГГц  =0,001816 м^-1,

прировняв первую производную по частоте к нулю получим, что =0,001816 м^-1 при f=4,949ГГц

Воспользуемся программой Maple для построения графика.

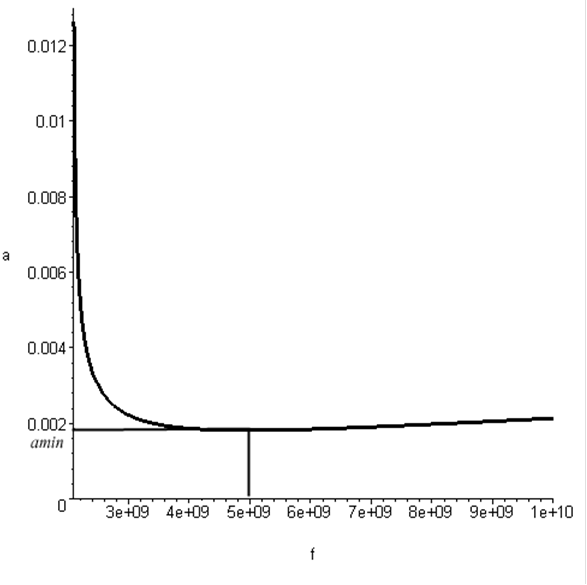
Рис.4.

3.  Определим  параметры основной волны для частоты f = 1,25 =1,25*2.08=2,6ГГц с длиной волны  с/f = 0,115м

Коэффициент ослабления за счёт омических потерь в стенках волновода:

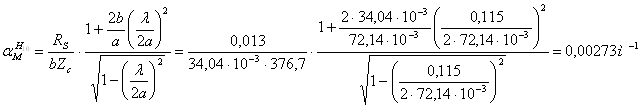(35)

Коэффициент фазы:

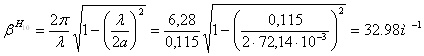 (36)

Длина волны  в волноводе:

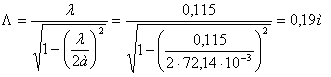  (37)

Фазовая скорость и скорость переноса электромагнитной энергии соответственно:

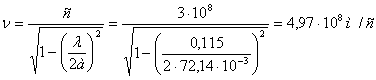  (38)

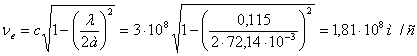 (39)

 Характеристическое сопротивление равно:

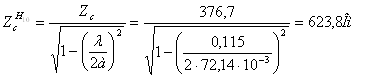 (40)

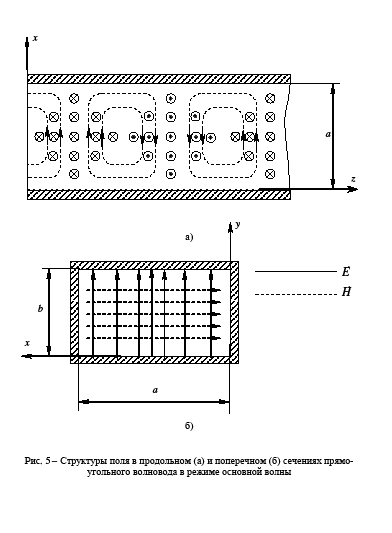
5.Частота волн и их длина равны:

 (41)

 (42)

Проверим условие  _кр для разных мод

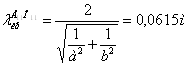
Следовательно, могут распространятся на этой частоте волны только типа 10.

Список используемых источников

1.  Ю.В. Пименов,  В.И. Вольман, А.Д. Муравцов  «Техническая  электродинамика», М: «Радио и связь», 2000 г. – 536 с.

2.   Никольский В.В. Электродинамика и распространение радиоволн. – М: «Наука» 1973г – 607с.