Дипломная работа: Модель синхронного генератора в фазных координатах
МОиН Украины
Национальный технический университет
“Харьковский политехнический институт”
Кафедра электрических станций
Расчётное задание
по курсу: “Математическое моделирование”
на тему: “Модель синхронного генератора в фазных координатах”
Выполнил: ст. гр. Э-51а
Абашкина О.С.
Сербиненко М.С.
Бабенков А.А.
Шаповал О.
Проверил: доц. Пискурёв М.Ф.
Харьков 2005
Общие понятия и определения в математическом моделировании
Модель – некоторый объект, с помощью которого исследуются свойства оригинала и находящегося во взаимозначном соответствии с ним и более доступном для изучения.
Моделирование – исследование свойств объекта методом изучения свойств другого объекта находящегося в определённом соответствии с первым объектом и более удобным для исследования.
Под “моделью” понимают некоторые технические устройства, процесс, схемы замещения, мысленные образы, математические формулы.
Модель должна удовлетворять 3 условиям:
1. достоверно отображать некоторые свойства оригинала подлежащие изучению;
2. должно быть определённое соответствие, т.е. правила позволяющие осуществить переход от свойств модели к оригиналу и наоборот;
3. должна быть наглядной, простой и доступной для изучения.
Виды моделей:
1) Структурная. Показывает структуру объекта и взаимную связь между элементами этого объекта;
2) Модели прямой аналогии. В них процессы совпадают с процессами оригинала.
3) Физические модели. Они имеют одну и ту же физическую природу с оригиналом.
4) Математические модели, которые имеют одинаковое математическое описание с оригиналом. Эти модели бывают аналоговые и цифровые.
Основные допущения при составлении математической модели синхронного генератора
1. Не учитывается магнитное насыщение генератора.
2. В воздушном зазоре машины действуют намагничивающие силы только первой гармоники. Следовательно, ЭДС синхронного генератора – синусоидальный.
3. Не учитываются потери на перемагничивание.
4. Считают, что обмотки статора выполнены симметрично, а ротор генератора симметричен относительно осей d и q.
5. Все демпферные обмотки по оси d заменены одной демпферной обмоткой аналогичной по оси q.
6. При исследовании электромагнитных переходных процессов не учитывают изменение вращения скорости генератора.
Математическая модель синхронного генератора в фазных координатах
При составлении этой модели, в целях упрощения, не будем учитывать демпферные обмотки. Следовательно, уравнение баланса напряжений имеет вид:
Уравнение статора: Уравнение ротора:
( 1 )
где 
, 
, 
, 
- мгновенные
значения напряжений обмоток статора и ротора;
, 
, 
, 
-
потокосцепления, связанные с соответствующими обмотками;
, 
, 
, 
- мгновенные
токи, протекающие в свободных обмотках.
( 2 )
где 
и 
- индуктивности
и взаимоиндуктивности соответствующих обмоток.
Система уравнений 1 после подставления в неё значений из уравнений 2 превращается в систему из 4 дифференциальных уравнений с переменными коэффициентами, т.к. практически все индуктивности и взаимоиндуктивности – переменные величины, т.е. являются функцией времени (вращение ротора генератора) за исключением индуктивной обмотки возбуждения.
const
Эти коэффициенты оказываются непостоянными из-за электрической и магнитной несимметрии ротора генератора. Т. о. система уравнений 1 и 2 позволяет смоделировать процессы в СГ в фазных координатах в режиме ХХ.
Чтобы смоделировать СГ в нагруженном режиме или в режиме КЗ необходимо добавить систему уравнений, позволяющую найти токи в обмотках статора и ротора.
Т. о. систему уравнений 1 дополненную системой уравнений 2 и уравнениями внешней цепи генератора будут представлять собой математическую модель СГ в фазных координатах.
Реализация модели синхронного генератора в фазных координатах
С целью упрощения модели представим её в виде 9 суперблоков. Первый суперблок моделирует переменные коэффициенты в уравнения для определения потокосцепления. Суперблоки 2,3,4,5 моделируют потокосцепление, 6,7,8 - фазное напряжение, 9-й – ток в обмотках возбуждения.
Первый
суперблок в свою очередь состоит из подблоков. Первые три моделируют постоянные
коэффициенты 
, 
, 
, 
; подблоки 4 – 6 моделируют
индуктивности 
, 
, 
; подблоки 7 – 9 моделируют
взаимоиндукцию между фазами 
, 
, 
; подблоки 10 – 12 моделируют
взаимоиндукцию между обмотками возбуждения и фазными обмотками статора.
Порядок выполнения работы
I. Реализация первого суперблока
1. При
реализации модели СГ в первую очередь необходимо смоделировать постоянные
коэффициенты , , , .
Первый подблок имеет следующую реализацию:
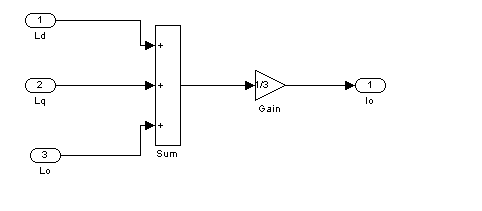
Рис.1
– Первый подблок первого суперблока, моделирующий
Реализация второго подблока:
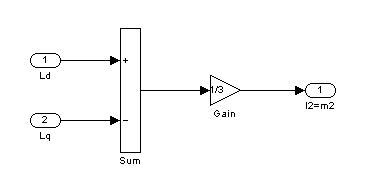
Рис.2
– Второй подблок первого суперблока, моделирующий ,
Реализация третьего подблока:
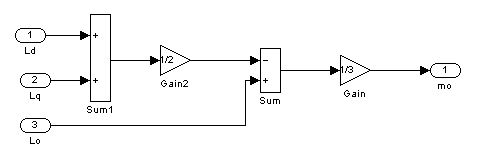
Рис.3
– Третий подблок первого суперблока, моделирующий
Каждый из трёх подблоков представляем в виде субблоков. Для этого:
а) выделяем подблок;
б) с помощью правой кнопки мыши находим операцию “Create subsystem”;
в) образуем субблок;
г) обозначаем входящие и выходящие параметры.
2.
Моделирование индуктивностей , , :
cos
cos
cos
,
где 
= 
;
- переход
времени от секунд к о.е.
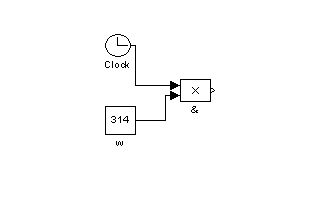
Рис. 4
– Модель
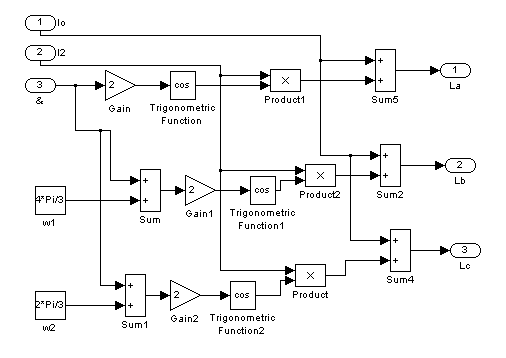
Рис. 5 –
Четвертый подблок первого суперблока, моделирующий , ,
3. Моделирование
взаимоиндуктивностей между фазами , 
cos
cos
cos
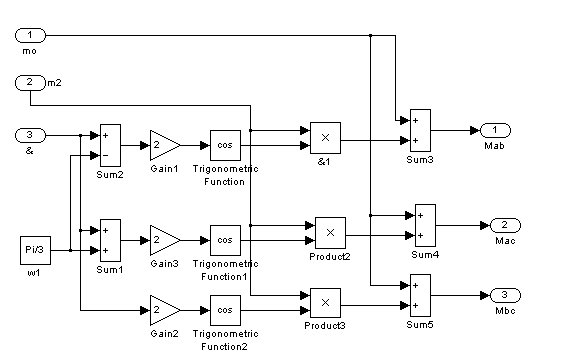
Рис. 6 – Пятый подблок
первого суперблока, моделирующий ,
4. Моделирование
взаимоиндуктивностей между обмоткой возбуждения и фазными обмотками 
, 
.
cos
cos
cos
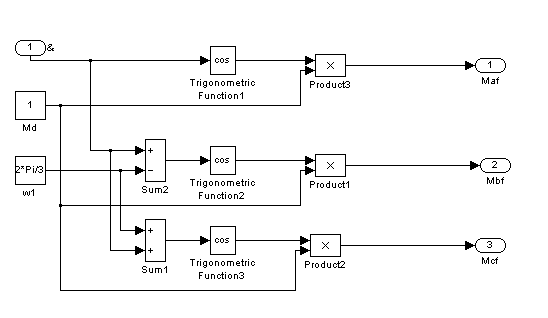
Рис. 7 – Шестой подблок
первого суперблока, моделирующий ,
4. Каждый из подблоков преобразуем в субблок аналогично первым трём подблокам, при этом соединяя одноимённые входы и выходы подблоков.
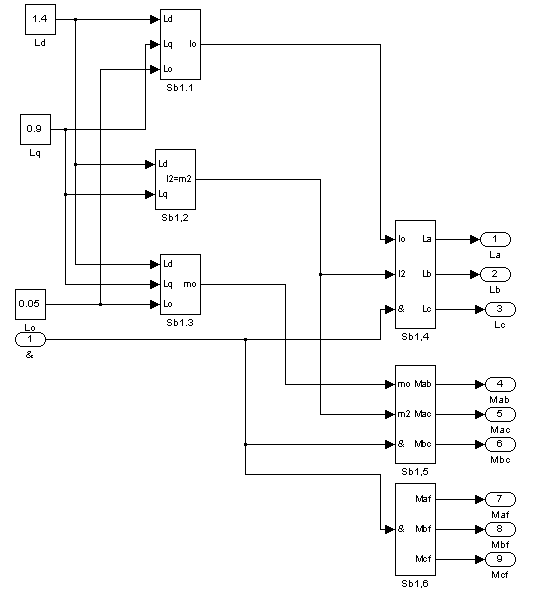
Рис. 8 – Содержимое первого суперблока
6. Образуем первый суперблок (Sb1).
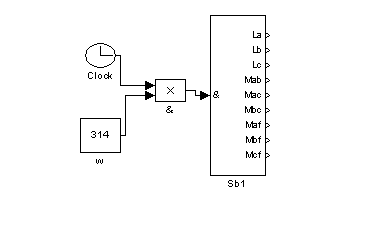
Рис. 9 – Первый суперблок (Sb1)
II. Реализация 2 - 5 суперблоков
Согласно системе уравнений (2) моделируем потокосцепления, связанные с соответствующими обмотками.
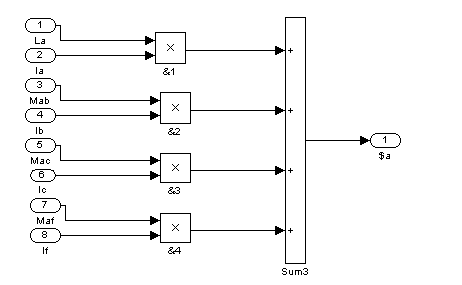
Рис. 10 – Второй суперблок (Sb2)
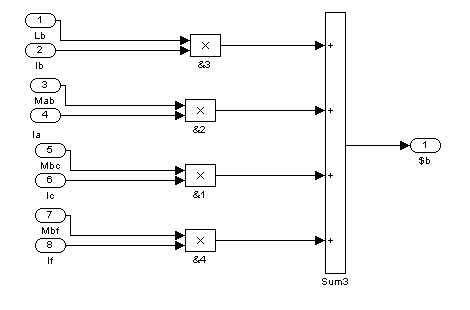
Рис. 11 – Третий суперблок (Sb3)
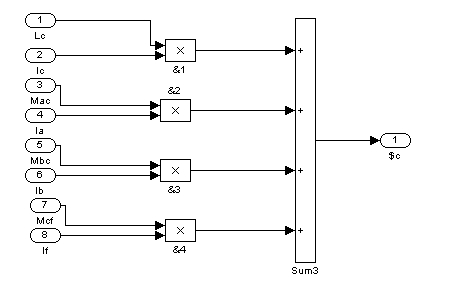
Рис. 12 – Четвертый суперблок (Sb4)
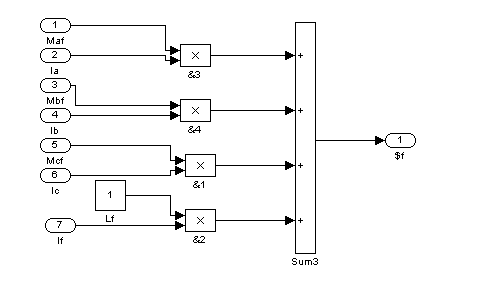
Рис. 13 – Пятый суперблок (Sb5)
Преобразуем суперблоки Sb2 - Sb5 в субблоки.
III. Реализация 6 – 8 суперблоков
Согласно системе уравнений (1) моделируем фазные напряжения в обмотках статора.
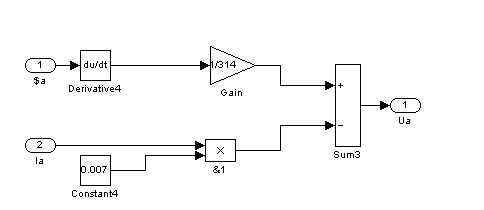
Рис. 14 – Шестой суперблок, моделирующий напряжение фазы А (Sb6)
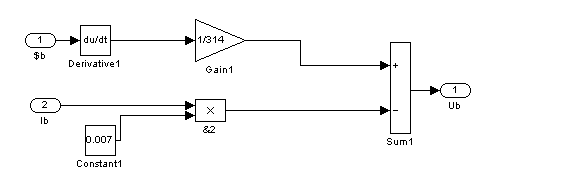
Рис. 15 – Седьмой суперблок, моделирующий напряжение фазы В (Sb7)
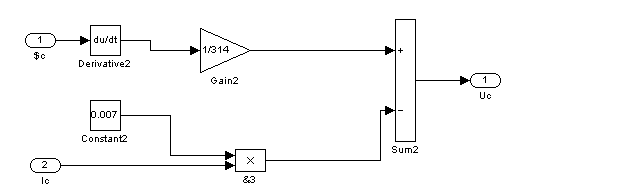
Рис. 16 – Восьмой суперблок, моделирующий напряжение фазы С (Sb8)
IV. Реализация девятого суперблока
Согласно той же системе уравнений (1) моделируем ток в обмотке возбуждения.
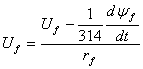
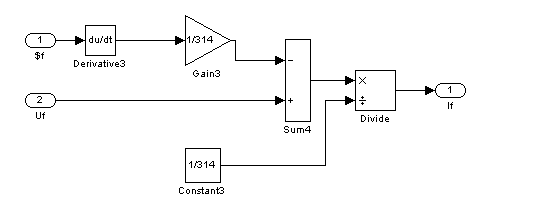
Рис. 17 – Девятый суперблок, моделирующий ток в обмотке возбуждения (Sb9)
Преобразуем каждый из
суперблоков в субблоки и соединяем их одноимённые входы и выходы с предыдущими
блоками. Затем аналогичным образом получим суперсуперблок (SSb), на вход которого подаём и Uf.
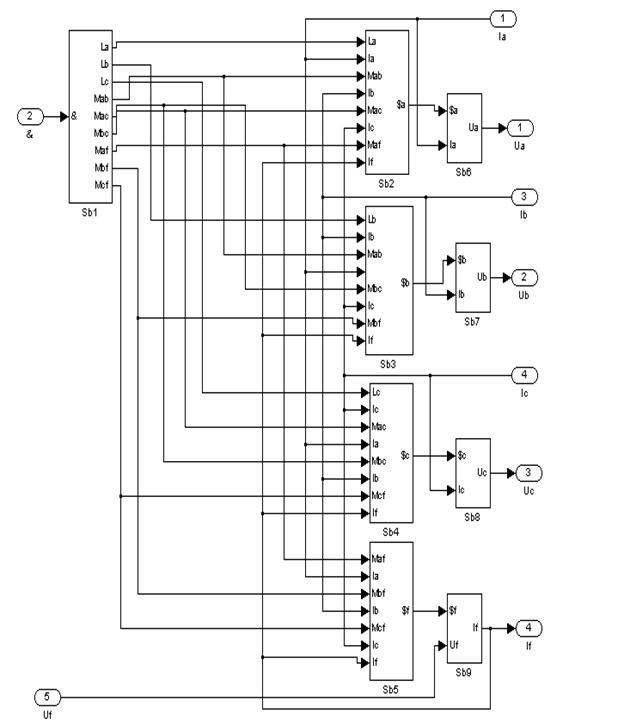
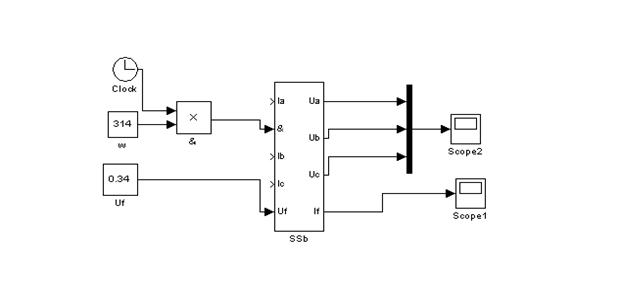
Рис. 18 – Содержимое SSb
Рис. 19 – Суперсуперблок SSb
V. Модель СГ в режиме ХХ
Подключив осциллографы к
соответствующим выходам SSb,
будем наблюдать изменение фазных напряжений и тока в обмотке возбуждения СГ в
режиме ХХ. С помощью 
объединяем фазные напряжения для
просмотра в одной системе координат. Т.к. в данной модели фазные токи равны 0,
то это модель СГ в режиме ХХ.
