Доклад: Взаимодействие тел
Взаимодействие тел.
Опыт показывает, что при сближении тел (или систем тел) характер их поведения меняется. Поскольку эти изменения носят взаимный характер, говорят, что тела взаимодействуют друг с другом. При разведении тел на очень большие расстояния (на бесконечность) все известные на сегодняшний день взаимодействия исчезают.
Галлилей
первым дал правильный ответ на вопрос, какое движение характерно для свободных
(т.е. не взаимодействующих тел). Вопреки существующему тогда мнению, что
свободные тела “стремятся” к состоянию покоя (![]() ), он утверждал, что при отсутствии
взаимодействия тела находятся в состоянии равномерного движения (
), он утверждал, что при отсутствии
взаимодействия тела находятся в состоянии равномерного движения (![]() ), включающего покой как
частный случай.
), включающего покой как
частный случай.
Инерциальные системы отсчета.
В рамках формального математического подхода, реализуемого в кинематике, утверждение Галилея выглядит бессмысленным, поскольку равномерное в одной системе отсчета движение может оказаться ускоренным в другой, которая “ничем не хуже” исходной. Наличие взаимодействия позволяет выделить особый класс систем отсчета, в которых свободные тела движутся без ускорения (в этих системах большинство законов природы имеют наиболее простую форму). Такие системы называются инерциальными.
Все инерциальные системы эквивалентны друг другу, в любой из них законы механики проявляются одинаково. Это свойство было также отмечено Галилеем в сформулированном им принципе относительности: никаким механическим опытом в замкнутой (т.е. не сообщающейся с внешним миром) системе отсчета невозможно установить покоится ли она или равномерно движется. Любая система отсчета, равномерно движущаяся относительно инерциальной тоже является инерциальной.
Между инерциальными и неинерциальными системами отсчета существует принципиальное отличие: находящийся в замкнутой системе наблюдатель способен установить факт движения с ускорением последних, “не выглядывая наружу”(напр. при разгоне самолета пассажиры ощущают, что их “вдавливает” в кресла). В дальнейшем будет показано, что в неинерциальных системах геометрия пространства перестает быть евклидовой.
Законы Ньютона как основа классической механики.
Сформулированные И.Ньютоном три закона движения в принципе позволяют решить основную задачу механики, т.е. по известным начальному положению и скорости тела определить его положение и скорость в произвольный момент времени.
Первый закон Ньютона постулирует существование инерциальных систем отсчета.
Второй закон Ньютона утверждает, что в инерциальных системах ускорение тела пропорционально приложенной силе, физической величине, являющейся количественной мерой взаимодействия. Величину силы, характеризующей взаимодействие тел, можно определить, например, по деформации упругого тела, дополнительно введенного в систему так, что взаимодействие с ним полностью компенсирует исходное. Коэффициент пропорциональности между силой и ускорением называют массой тела:
(1) F=ma
Под действием одинаковых сил тела с большей массой приобретают меньшие ускорения. Массивные тела при взаимодействии в меньшей степени меняют свои скорости, “стремясь сохранить естественное движение по инерции”. Иногда говорят, что масса является мерой инертности тел (рис. 4_1).
К классическим свойствам массы следует отнести 1) ее положительность (тела приобретают ускорения в направлении приложенных сил), 2) аддитивность (масса тела равна сумме масс его частей), 3) независимость массы от характера движения (напр. от скорости).
Третий закон утверждает, что взаимодействия оба объекта испытывают действия сил, причем эти силы равны по величине и противоположно направлены.
Типы фундаментальных взаимодействий. Попытки классификации взаимодействий привели к идее выделения минимального набора фундаментальных взаимодействий, при помощи которых можно объяснить все наблюдаемые явления. По мере развития естествознания этот набор менялся. В ходе экспериментальных исследований периодически обнаруживались новые явления природы, не укладывающиеся в принятый фундаментальный набор, что приводило к его расширению (например, открытие структуры ядра потребовало введения ядерных сил). Теоретические же осмысление, вцелом стремящееся к единому, максимально экономному описанию наблюдаемого многообразия, неоднократно приволило к “великим объединениям” внешне совершенно несхожих явлений природы (ньютон понял, что падение яблока и движение планет вокруг Солнца являются результатами проявления гравитационных взаимодействий, Эйнштейн установил единую природу электрических и магнитных взаимодействий, Бутлеров опроверг утверждения о различной природе органических и неорганических веществ).
В настоящее время принят набор из четырех типов фундаментальных взаимодействий: гравитационные, электромагнитные, сильное и слабые ядерные. Все остальные, известные на сегодняшний день, могут быть сведены к суперпозиции перечисленных.
Гравитационные взаимодействия обусловлены наличием у тел массы и являются самыми слабыми из фундаментального набора. Они доминируют на расстояниях космических масштабов (в мега-мире).
Электромагнитные взаимодействия обусловлены специфическим свойством ряда элементарных частиц, называемым электрическим зарядом. Играют доминирующую роль в макро мире и микромире вплоть на расстояниях, превосходящих характерные размеры атомных ядер.
Ядерные взаимодействия играют доминирующую роль в ядерных процессах и проявляются лишь на расстояниях, сравнимых с размером ядра, где классическое описание заведомо неприменимо.
В настоящее время стали весьма популярны рассуждения о биополе, при помощи которого “объясняется” ряд не очень надежно установленных на эксперименте явлений природы, связанных с биологическими объектами. Серьезное отношение к понятию биополя зависит от того, какой конкретный смысл. Вкладывается в этот термин. Если понятие биополя используется для описания взаимодействий с участием биологических объектов, сводящихся к четырем фундаментальным, такой подход не вызывает принципиальных возражений, хотя введение нового понятия для описания “старых” явлений противоречит общепринятой в естествознании тенденции к минимизации теоретического описания. Если же под биополем понимается новый тип фундаментальных взаимодействий, проявляющийся на макроскопическом уровне (возможности существования которого априорно, очевидно, отрицать бессмысленно), то для столь далеко идущих выводов необходимы очень серьезные теоретические и экспериментальные обоснования, сделанные на языке и методами современного естествознания, которые до настоящего времени представлены не были.
Законы Ньютона и основная задача механики.
Для решения основной задачи механики (определение положения тела в произвольный момент времени по известным начальному положению и скорости) достаточно найти ускорение тела как функцию времени a(t). Эту задачу решают законы Ньютона (1) при условии известных сил. В общем случае силы могут зависеть от времени, положения и скорости тела:
(2) F=F(r,v,t) ,
т.е. для нахождения ускорения тела необходимо знать его положение и скорость. Описанная ситуация в математике носит название дифференциального уравнения второго порядка:
(3)
![]() ,
,
(4)
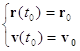
В математике показывается, что задача (3-4) при наличии двух начальных условий (положение и скорость в начальный момент времени) всегда имеет решение и притом единственное. Т.о. основная задача механики в принципе всегда имеет решение, однако найти его часто бывает весьма трудно.
Детерминизм Лапласа. Немецкий математик Лаплас применил аналогичную теорему о существовании и единственности решения задачи типа (3-4) для системы из конечного числа уравнений для описания движения всех взаимодействующих друг с другом частиц реального мира и пришел к выводу о принципиальной возможности расчета положения всех тел в любой момент времени. Очевидно, что это означало возможность однозначного предсказанная будущего (хотя бы в принципе) и полную детерменированность (предопределенность) нашего мира. Сделанное утверждение, носящее скорее философский, а не естественно научный характер, получило название детерминизма Лапласа. При желании из него можно было сделать весьма далеко идущие философские и социальные выводы о невозможности влиять на предопределенный ход событий. Ошибочность этого учения состояла в том, что атомы или элементарные частицы (“материальные точки”, из которых составлены реальные тела) на самом деле не подчиняются классическому закону движения (3), верному лишь для макроскопических объектов (т.е. обладающих достаточно большими массами и размерами). Правильное с точки зрения сегодняшней физики описание движения во времени микроскопических объектов, какими являются составляющие макроскопические тела атомы и молекулы, дается уравнениями квантовой механики,, позволяющими определить только вероятность нахождения частицы в заданной точке, но принципиально не дающего возможности расчета траекторий движения для последующих моментов времени.
Список литературы