Курсовая работа: Характеристика и применение риск (САРМ, АРТ)
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО – ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Финансово-кредитный факультет
Кафедра "Финансового менеджмента"
КУРСОВАЯ РАБОТА
По дисциплине: "Теория инвестиций"
На тему: "Характеристика и применение моделей оценки финансовых активов (САРМ, АРТ)"
Руководитель Грибов Е.В.
Выполнила: Шкалябина И.Ф.
№ личного дела 06ДФД50311
№ группы ДО 52 Ю
Владимир
2009г.
Содержание
Введение
1. Модель оценки стоимости активов (CAPM)
1.1 Линия рынка капитала
1.2 Рыночный и нерыночный риски. Эффект диверсификации
1.3 Бета
1.4 Линия рынка актива SML
1.5 Вопросы, возникающие при построении SML
1.6 CML и SML
1.7 Альфа
2. Модификации CAPM
2.1 САРМ для случая, когда ставки по займам и депозитам не равны
2.2 САРМ с нулевой бетой
2.3 Версия САРМ для облигаций
3. Теоретические и практические аспекты использования моделиарбитражного ценообразования (АРТ)
3.1 Общий вид модели арбитражного ценообразования
3.2 Выбор факторов, влияющих на доходность
3.3 Расчет элементов ставки дисконтирования
Заключение
Практическая часть
Список литературы
Введение
Инвесторы сталкиваются с проблемой оценки стоимости активов. Она зависит главным образом от их риска и доходности.
На рынке выдерживается закономерность: чем выше потенциальный риск, тем выше должна быть и ожидаемая доходность. У каждого инвестора формируются свои прогнозы относительно отмеченных параметров. В то же время рынок постоянно движется в направлении определенной равновесной оценки риска и доходности активов. Возможные расхождения в оценках, в первую очередь, связаны с ассиметричностью информации, которой обладают разные инвесторы.
В условиях хорошо развитого рынка новая информация находит быстрое отражение в курсовой стоимости активов. Поэтому для таких условий можно разработать модель, которая бы удовлетворительно описывала взаимосвязь между риском и ожидаемой доходностью активов. Такая модель разработана в середине 60-х гг. У. Шарпом и Дж. Линтерном и получила название модели оценки стоимости активов (capital asset pricing model - САРМ ).
Как известно, стоимость актива определяется путем дисконтирования будущих доходов, которые он принесет, под процентную ставку, соответствующую его риску. Модель оценки стоимости активов не дает непосредственного ответа на вопрос, какой должна быть цена актива. Однако она получила такое название, потому что позволяет определить ставку дисконтирования, используемую для расчета стоимости финансового инструмента.
Расчет ставки дисконта – один из основных этапов доходного подхода к оценке компании, т.к. ее величина значительно влияет на конечный результат, получаемый в рамках доходного подхода (и конечной стоимости компании в целом). Следовательно, важность ее наиболее правомерного расчета очевидна.
Тем не менее, существует ряд проблем информационного и методологического характера, с которыми приходится сталкиваться при расчетах ставки дисконтирования. Такое положение вещей во многом связано с тем, что наиболее часто используемые методы построения ставки дисконтирования разработаны зарубежными специалистами для использования в развитых странах с эффективно функционирующими финансовыми рынками. Одним из таких методов является метод, основанный на использовании теории арбитражного ценообразования. Метод арбитражного ценообразования нельзя назвать распространенным методом расчета ставки дисконтирования, но, тем не менее, он имеет ряд преимуществ.
Актуальность темы данной курсовой работы связана с рациональным применением моделей оценки финансовых активов (САРМ и АРТ) российского финансового рынка, объективно требующего нахождения оригинальных подходов к вложению и оценке в ценные бумаги (финансовые активы).
Объектом исследования будут являться модели оценки финансовых активов САРМ и АРТ.
Предмет исследования - применение моделей оценки финансовых активов САРМ и АРТ.
Целью исследования является характеристика и применение моделей оценки финансовых активов САРМ и АРТ в условиях Российского инвестиционного рынка.
Цель позволила сформулировать задачи, которые решались в работе:
1. Понятие "инвестиционный портфель": принципы и этапы его формирования;
2. Риск и доходность портфеля;
3. Оптимизация инвестиционного портфеля (кривые безразличия инвестора и эффективное множество);
4. Модель оценки стоимости финансовых активов (САРМ);
5. Модель арбитражного ценообразования (АРТ);
6. Практическое применение моделей финансовых активов.
Структура работы состоит: введение, 3 главы, заключения, списка использованной литературы, практической части.
1. Модель оценки стоимости активов (CAPM)
1.1 Линия рынка капитала
Каждый инвестор ставит перед собой две задачи – максимизировать доход и минимизировать риск. В связи с противоречивостью этих задач процесс обоснования инвестиционных решений носит оптимизационный характер. Средством такой оптимизации выступают разнообразные модели оценки стоимости финансовых инструментов инвестирования, в основе которых лежит выявление оптимальной шкалы соотношений уровня доходности и риска таких финансовых инструментов, удовлетворяющих любого инвестора.
Модель оценки стоимости финансовых активов была предложена рядом американских ученых - У. Шарпом, Дж.Линтерном, Дж. Трейноном и Я. Мосстным. Эта модель основана на следующих предположениях:
1. Инвесторы производят оценку финансовых активов исходя из двух факторов – ожидаемого уровня их доходности и уровня риска, определяемого колеблемостью доходности.
2. Инвесторы ведут себя рационально: при выборе из двух финансовых активов они при прочих равных условиях изберут тот, по которому ожидаемый уровень доходности выше; соответственно, при выборе из двух финансовых активов они изберут тот, по которому уровень риска ниже.
1. Существует единая безрисковая ставка процента, по которой инвестор может как инвестировать свой капитал, так и формировать свои инвестиционные ресурсы. Эта ставка одинакова для всех инвесторов.
2. Налоги и трансакционные издержки, связанные с финансовым инвестированием, несущественны и в процессе расчетов во внимание не принимаются.
3. Период вложения капитала в финансовые инструменты инвестирования одинаков для всех инвесторов.
4. Фондовый рынок характеризуется как эффективный – необходимая информация свободно и быстро предоставляется всем инвесторам.
5. Инвесторы одинаково оценивают ожидаемый уровень доходности и риска каждой из ценных бумаг.
Модель оценки стоимости финансовых активов исходит из того, что каждая ценная бумага является частью общей совокупности ценных бумаг, обращающихся на фондовом рынке, т.е. частью так называемого "рыночного портфеля". Рыночный портфель включает в себя все ценные бумаги фондового рынка, в котором доля каждой конкретной ценной бумаги равна отношению ее рыночной стоимости к суммарной рыночной стоимости всех ценных бумаг, обращающихся на рынке.
При равновесном сотсоянии спроса и предложения на фондовом рынке стоимость рыночного портфеля отражает среднее соотношение уровня его доходности и риска (определяемого среднеквадратическим отклонением этой доходности).
В САРМ зависимость между риском и ожидаемой доходностью графически можно описать с помощью линии рынка капитала (Capital Market Line - CML), которая представлена на рис. 1.
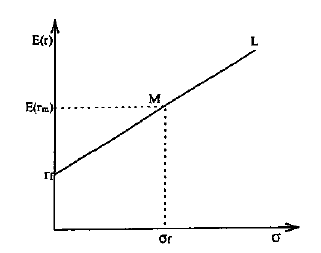
Рис. 1. Линия рынка капитала
М - это рыночный портфель, rf - актив без риска; rf L - линия рынка капитала; m - риск рыночного портфеля; Е(rm) - ожидаемая доходность рыночного портфеля. Все возможные оптимальные (эффективные) портфели, т. е. портфели, которые включают в себя рыночный портфель М, расположены на линии rfL.
Она проходит через две точки - rf и М. Таким образом, линия рынка капитала является касательной к эффективной границе. Все другие портфели, в которые не входит рыночный портфель, располагаются ниже линии rf L. CML поднимается вверх слева направо и говорит о том, что если портфель имеет более высокий риск, то он должен предлагать инвестору и более высокую ожидаемую доходность, и если вкладчик желает получить более высокую ожидаемую доходность, он должен согласиться на более высокий риск.
Наклон СML следует рассматривать как вознаграждение (в единицах ожидаемой доходности) за каждую дополнительную единицу риска, которую берет на себя вкладчик. Когда вкладчик приобретает актив без риска, он обеспечивает себе доходность на уровне ставки без риска rf. Если он стремится получить более высокую ожидаемую доходность, то должен согласиться и на некоторый риск. Ставка без риска является вознаграждением за время, т. е. деньги во времени имеют ценность.
Дополнительная доходность, получаемая инвестором сверх ставки без риска, есть вознаграждение за риск. Таким образом, вознаграждение лица, инвестировавшего свои средства в рыночный портфель, складывается из ставки rf, которая является вознаграждением за время, и премии за риск в размере Е(rf) - rf. Другими словами, на финансовом рынке его участники уторговывают между собой цену времени и цену риска. CML представляет собой прямую линию. Уравнение прямой можно представить следующим образом:
y = a + bx
где: а - значение ординаты в точке пересечения ее линией СML, оно соответствует ставке без риска rf,
b - угол наклона СML.
Угол наклона определяется как отношение изменения значения функции к изменению аргумента. В нашем случае (см. рис. 1) угол наклона равен:
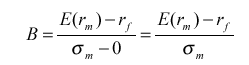
Поскольку ожидаемая доходность (у) есть функция риска (х), то в уже принятых терминах доходности и риска уравнение CML примет вид:
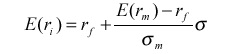
где: σ- риск i-го портфеля, для которого определяется уровень ожидаемой доходности,
Е(ri) - ожидаемая доходность i-го портфеля.
Данное уравнение можно записать следующим образом:
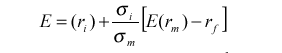
Таким образом, ожидаемая доходность портфеля равна ставке без риска плюс произведение отношения риска портфеля к риску рыночного портфеля и разности между ожидаемой доходностью рыночного портфеля и ставкой без риска.
Пример. rf = 10%, Е(rm) = 25%, si = 30%, sm = 15%. Определить ожидаемую доходность портфеля. Она равна:
![]()
CML говорит о соотношении риска и ожидаемой доходности только для широко диверсифицированных портфелей, т. е. портфелей, включающих рыночный портфель, но не отвечает на вопрос, какой ожидаемой доходностью должны обладать менее диверсифицированные портфели или отдельные активы.
1.2 Рыночный и нерыночный риски. Эффект диверсификации
Риск, с которым связано владение активом, можно разделить на две части. Первая составляющая - это рыночный риск. Его также именуют системным или недиверсифицируемым, или неспецифическим. Он связан с состоянием конъюнктуры рынка, общезначимыми событиями, например, войной, революцией. Его нельзя исключить, потому что это риск всей системы. Вторая часть - нерыночный, специфический или диверсифицируемый риск.
Он связан с индивидуальными чертами конкретного актива, а не с состоянием рынка в целом. Например, владелец какой-либо акции подвергается риску потерь в связи с забастовкой на предприятии, выпустившем данную бумагу, некомпетентностью его руководства и т. п. Данный риск является диверсифицируемым, поскольку его можно свести практически к нулю с помощью диверсификации портфеля.
Как показали исследования западных ученых, портфель, состоящий из хорошо подобранных 10-20 активов, способен фактически полностью исключить нерыночный риск (см. рис. 2).
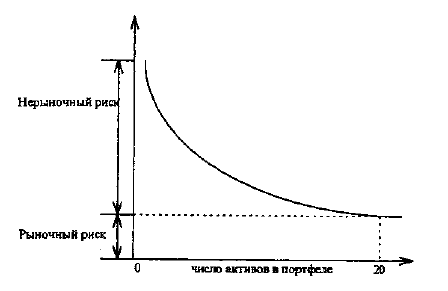
Рис. 2. Эффект диверсификации
Широко диверсифицированный портфель заключает в себе практически только рыночный риск. Слабо диверсифицированный портфель обладает как рыночным, так и нерыночным рисками. Таким образом, инвестор может снизить свой риск только до уровня рыночного, если сформирует широко диверсифицированный портфель.
Приобретая актив, вкладчик рассчитывает получить компенсацию за риск, на который он идет. Однако риск состоит из двух частей. Каким образом рынок оценивает компоненты риска с точки зрения ожидаемой доходности? Как было сказано выше, инвестор способен практически полностью исключить специфический риск за счет формирования широко диверсифицированного портфеля. В рамках модели САРМ предполагается, что вкладчик может свободно покупать и продавать активы без дополнительных издержек.
Поэтому формирование более диверсифицированного портфеля не ведет к увеличению его расходов. Таким образом, без затрат вкладчик может легко исключить специфический риск. Поэтому в теории предполагается, что нерыночный риск не подлежит вознаграждению, поскольку он легко устраняется диверсификацией. В связи с этим, если инвестор не диверсифицирует должным образом свой портфель, он идет на ненужный риск с точки зрения той выгоды, которую он приносит обществу.
Приобретая, например, акцию, инвестор финансирует производство и таким образом приносит обществу пользу. Покупка акции связана с нерыночным риском, который является неустранимым. Поэтому инвестор должен получать вознаграждение адекватное только данному риску. В противном случае он не приобретет эту бумагу, и экономика не получит необходимые финансовые ресурсы. Однако общество (рынок) не будет вознаграждать его за специфический риск, поскольку он легко устраняется диверсификацией. С точки зрения финансирования потребностей экономики, данный риск не имеет смысла. Таким образом, вознаграждению подлежит только системный риск.
Поэтому стоимость активов должна оцениваться относительно величины именно этого риска. Весь риск актива (портфеля) измеряется такими показателями как дисперсия и стандартное отклонение. Для оценки рыночного риска служит другая величина, которую называют бета.
1.3 Бета
Для измерения рыночного риска актива (портфеля) используется величина бета. Она показывает зависимость между доходностью актива (портфеля) и доходностью рынка. Доходность рынка - это доходность рыночного портфеля.
Поскольку невозможно сформировать портфель, в который бы входили все финансовые активы, то в качестве него принимается какой-либо индекс с широкой базой. Поэтому доходность рынка - это доходность портфеля, представленного выбранным индексом. Бета рассчитывается по формуле:
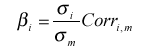 (*)
(*)
или
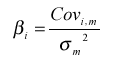
где: βi - бета i-го актива(портфеля);
Covi, m - ковариация доходности i-го актива (портфеля) с доходностью рыночного портфеля;
Соrri, m - корреляция доходности i-го актива (портфеля) с доходностью рыночного портфеля.
Поскольку величина бета определяется по отношению к рыночному портфелю, то бета самого рыночного портфеля равна единице, так как ковариация доходности рыночного портфеля с самим собой есть его дисперсия, отсюда
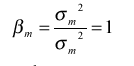
где: βm - бета рыночного портфеля.
Бета актива (портфеля) без риска равна нулю, потому что нулю равна ковариация доходности актива (портфеля) без риска с доходностью рыночного портфеля. Величина σ актива (портфеля) говорит о том, насколько его риск больше или меньше риска рыночного портфеля. Активы с бетой больше единицы более рискованны, а с бетой меньше единицы - менее рискованны чем рыночной портфель. Относительно величины бета активы делят на агрессивные и защитные.
Бета агрессивных активов больше единицы, а защитных - меньше единицы. Если бета актива равна единице, то его риск равен риску рыночного портфеля. Бета может быть как положительной, так и отрицательной величиной. Положительное значение беты говорит о том, что доходности актива (портфеля) и рынка при изменении конъюнктуры меняются в одном направлении. Отрицательная бета показывает, что доходности актива (портфеля) и рынка меняются в противоположных направлениях.
Подавляющая часть активов имеет положительную бету. Бета актива (портфеля) показывает, в какой степени доходность актива (и соответственно его цена) будет реагировать на действие рыночных сил. Зная бету конкретного актива (портфеля), можно оценить, насколько должна измениться его ожидаемая доходность при изменении ожидаемой доходности рынка. Например, бета бумаги равна +2. Это значит, что при увеличении ожидаемой доходности рыночного портфеля на 1% доходность бумаги возрастет на 2%, и наоборот, при уменьшении доходности рыночного портфеля на 1% доходность бумаги снизится на 2%. Поскольку бета бумаги больше единицы, то она рискованнее рыночного портфеля.
Активы с отрицательной бетой являются ценными инструментами для диверсификации портфеля, поскольку в этом случае можно построить портфель с "нулевой бетой", который не будет нести риска. Здесь, однако, следует помнить, что такой портфель не аналогичен активу без риска, так как при нулевом значении беты он не содержит только системного риска. В то же время данный портфель сохранит риск нерыночный.
Зная величину беты для каждого из активов, вкладчик может легко сформировать портфель требуемого уровня риска и доходности.
Бета портфеля - это средневзвешенное значение величин бета активов, входящих в портфель, где весами выступают их удельные веса в портфеле. Она рассчитывается по формуле:
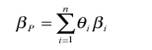
где: ßP - бета портфеля;
ßi - бета i-го актива;
Qi - уд. вес i-го актива.
Пример.
Инвестор формирует портфель из трех активов:
А, В и С. QA = 0,8; QB = 0,95; QC = 1,3; βA = 0,5; βB = 0,2; βC = 0,3.
Бета портфеля равна:
0,5*0,8 + 0,2*0,95 + 0,3*1,3 = 0,98.
Бета каждого актива рассчитывается на основе доходности актива и рынка за предыдущие периоды времени. Информацию о значениях беты можно получить от аналитических компаний, которые занимаются анализом финансового рынка, а также из периодической печати.
1.4 Линия рынка актива SML
CML показывает соотношение риска и доходности для эффективных портфелей, но ничего не говорит о том, как будут оцениваться неэффективные портфели или отдельные активы. На этот вопрос отвечает линия рынка актива (Security Market Line - SML). SML является главным итогом САРМ . Она говорит о том, что в состоянии равновесия ожидаемая доходность актива равна ставке без риска плюс вознаграждение за рыночный риск, который измеряется величиной бета. SML изображена на рис. 3.
Она представляет собой прямую линию, проходящую через две точки, координаты которых равны (0; rf) и (1; E(rm)). Таким образом, зная ставку без риска и ожидаемую доходность рыночного портфеля, можно построить SML. В состоянии равновесия рынка ожидаемая доходность каждого актива и портфеля, независимо от того, эффективный он или нет, должна располагаться на SML.
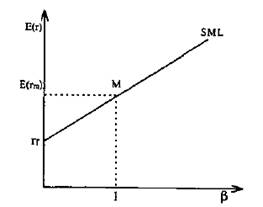
Рис. 3. Линия рынка актива
Следует еще раз подчеркнуть, что если на CML находятся только эффективные портфели, то на SML располагаются как широко диверсифицированные, так и неэффективные портфели и отдельные активы. Ожидаемую доходность актива (портфеля) определяют с помощью уравнения SML.
![]() (**)
(**)
Пример. rf = 15%, E(rm) = 25%, βi = 1,5. Определить E(ri).
![]()
Наклон SML определяется отношением инвесторов к риску в различных условиях рыночной конъюнктуры. Если у вкладчиков оптимистичные прогнозы на будущее, то наклон SML будет менее крутой, так как в условиях хорошей конъюнктуры инвесторы согласны на более высокие риски (поскольку они менее вероятны на их взгляд) при меньших значениях ожидаемой доходности (см. рис. 4 SML).
Напротив, в преддверии неблагоприятной конъюнктуры SML примет более крутой наклон, так как в этом случае инвесторы в качестве компенсации потребуют более высокую ожидаемую доходность на приобретаемые активы для тех же значений риска (см. рис. 4 SML2). Если у инвесторов меняются ожидания относительно ставки без риска, это приведет к сдвигам SML. При увеличении rf SML сдвинется вверх, при понижении - вниз, как показано на рис. 5.
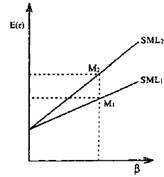
Рис. 4. Наклон SML в зависимости от ожиданий будущей конъюнктуры
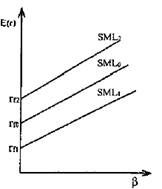
Рис. 5. Наклон SML при изменении ставки без риска
1.5 Вопросы, возникающие при построении SML
На практике возникает ряд проблем, затрудняющих четкий ответ на вопрос, по каким данным следует строить SML. Как уже отмечалось, САРМ является моделью одного временного периода. Поэтому в теории ставка без риска принимается равной ставке по краткосрочным ценным бумагам. Однако вкладчики строят инвестиционные стратегии, ориентируясь и на долгосрочную перспективу.
Если в качестве ставки без риска принять ставку по долгосрочным ценным бумагам, то, как правило, SML примет более пологий наклон (см. рис. 6 SML2), чем в случае краткосрочных бумаг (см. рис. 6 SML1).
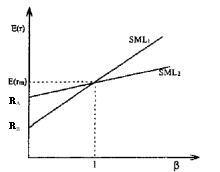
Рис. 6. Наклон SML в зависимости от ставки без риска по краткосрочным и долгосрочным бумагам
На практике отмеченная проблема возникнет в том случае, когда ставки без риска по долгосрочным и краткосрочным облигациям отличаются в существенной степени и для активов (портфелей) с высокой или низкой бетой, поскольку для активов (портфелей) с бетой близкой к единице разница в доходности для двух случаев не будут большой. Возникает вопрос и относительно точности прогнозирования ожидаемой доходности рынка.
1.6 CML и SML
Чтобы лучше понять CML и SML, сравним их характеристики. В состоянии рыночного равновесия на CML располагаются только эффективные портфели. Другие портфели и отдельные активы находятся под СML. CML учитывает весь риск актива (портфеля), единицей риска выступает стандартное отклонение. В состоянии равновесия на SML расположены все портфели, как эффективные, так и неэффективные и отдельные активы. SML учитывает только системный риск портфеля (актива). Единицей риска является величина бета.
В состоянии равновесия неэффективные портфели и отдельные активы располагаются ниже СML, но лежат на SML, так как рынок оценивает только системный риск данных портфелей (активов)
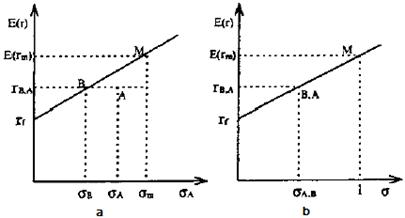
Рис. 7 a - CML, b- SML
На рис. 7a представлен эффективный портфель В, который располагается на CML. Риск портфеля равен σB, а ожидаемая доходность - rB.
На этом же рисунке представлена бумага А. Она имеет такую же ожидаемую доходность, что и портфель В, однако ее риск (σA) больше риска портфеля В. Так как бумага А - это отдельный актив, то она лежит ниже линии CML. Бета портфеля В и бета бумаги А равны, поэтому и портфель В и бумага А располагаются на SML в одной точке (см. рис. 7b). Так получается потому, что рынок оценивает портфели (активы) не с точки зрения их общего риска, который измеряется стандартным отклонением, а только на основе рыночного риска, измеряемого бетой. В результате актив А оценивается рынком точно также как и портфель В, хотя общий риск актива А больше, чем риск портфеля В. CML и SML можно сравнить еще следующим образом. Подставим из формулы (*) значение σ в формулу SML (**). В результате получим уравнение SML несколько в ином виде:
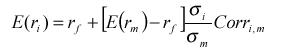
Формулу для CML также можно записать аналогичным образом:
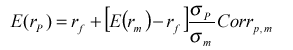
Однако в случае СML коэффициент корреляции равен +1, что говорит о полной корреляции эффективных портфелей с рынком. Неэффективные портфели и отдельные активы не имеют полной корреляции с рынком, что и нашло отражение в уравнении SML.
САРМ ничего не говорит о взаимосвязи ожидаемой доходности отдельного актива и его полного риска, измеряемого стандартным отклонением. SML устанавливает зависимость только между ожидаемой доходностью актива и его систематическим риском.
1.7 Альфа
Согласно САРМ цена актива будет изменяться до тех пор, пока он не окажется на SML. На практике можно обнаружить активы, которые неверно оценены рынком относительно уровня его равновесной ожидаемой доходности.
Если эта оценка не соответствует реальному инвестиционному качеству актива, то в следующий момент рынок изменит свое мнение в направлении более объективной оценки. В результате мнение рынка будет стремиться к некоторому равновесному (т. е. верному) уровню оценки. В реальной практике периодически происходит изменение конъюнктуры рынка, что вызывает и изменение оценок в отношении ожидаемой равновесной доходности.
Поэтому если учитывать протяженный период времени, то будет пересматриваться и сам уровень равновесной ожидаемой доходности. Однако в САРМ мы рассматриваем только один временной период, поэтому и можем говорить о равновесной доходности, которая в конечном итоге должна возникнуть на рынке для данного актива. Возможные отклонения от равновесного уровня могут наблюдаться в силу каких-либо частных причин в течение коротких промежутков времени.
Однако в следующие моменты должно возникнуть движение доходности актива к точке равновесного уровня. Если актив переоценен рынком, уровень его доходности ниже чем активов с аналогичной характеристикой риска, если недооценен, то выше. Показатель, который говорит о величине переоценки или недооценки актива рынком, называется альфой.
Альфа представляет собой разность между действительной ожидаемой доходностью актива и равновесной ожидаемой доходностью, т. е. доходностью, которую требует рынок для данного уровня риска. Альфа определяется по формуле:
![]()
где: αi - альфа i-го актива;
ri - действительная ожидаемая доходность i-го актива;
E(ri) - равновесная ожидаемая доходность.
Доходность актива в этом случае можно записать как
![]()
Откуда:
![]()
На рис. 8 представлены два актива, которые неверно оценены рынком по отношению к уровню их риска. Актив А недооценен, В - переоценен.
Согласно SML доходность А в условиях равновесия должна составлять 12,5%, фактическая оценка - 13%, т. е. актив предлагает 0,5% дополнительной доходности, поэтому его альфа равна +0,5. Противоположная ситуация представлена для актива В. Его равновесная ожидаемая доходность согласно SML составляет 17,5%, фактически он предлагает 13%, т. е. его альфа равна -4,5. Таким образом, актив недооценен рынком, если его альфа положительна, и переоценен, если отрицательна.
Для равновесной ожидаемой доходности альфа равна нулю. Инвесторы, желающие получить более высокие доходы, должны стремиться приобретать активы с положительной альфой. Через некоторое время рынок заметит недооценку, и их цена повысится. Одновременно инвесторам следует продавать активы с отрицательной альфой, так как в последующем их цена понизиться.
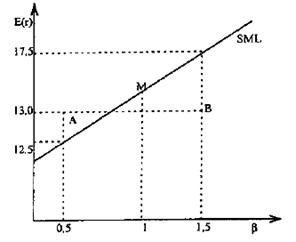
Рис. 8. Альфа активов
Доходность портфеля - это средневзвешенная величина доходностей входящих в него активов, поэтому альфа портфеля также является средневзвешенной величиной и определяется по формуле:
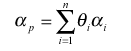
где: αP - альфа портфеля;
Qi - уд. вес i-го актива в портфеле;
αi - альфа i-го актива.
Пример.
Портфель состоит из трех бумаг - А, В и С QA = 2; QB = 1,5; QC = -1;
αA = 0,5; αB = 0,2 и αC = 0,3. Альфа такого портфеля равна:
0,5*2 + 0,2*1,5 + 0,3*(-1) = 1.
2. Модификации CAPM
2.1 САРМ для случая, когда ставки по займам и депозитам не равны
Начальная версия САРМ предполагает, что ставки по займам и депозитам одинаковы. В реальной жизни они отличаются. Напомним, что в таких условиях эффективная граница не является линейной, а представляет собой несколько отрезков, как показано на рис. 9. Любой рискованный портфель, расположенный на сегменте M1M2 рассматривается в качестве рыночного.
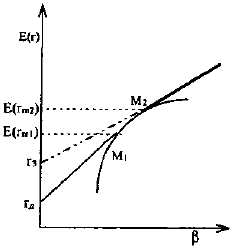
Рис. 9. CAPM при различии в ставках по кредитам и депозитам
Для данного варианта возникают две формулы САРМ и SML, которые рассчитываются относительно двух рыночных портфелей в точках M1 и M2.
для случая, когда E(ri) < Е(rm 1) - (кредитный портфель), и
![]()
![]()
для случая, когда E(ri) > Е(rm 2) - (заемный портфель),
где: βim 1 - бета, рассчитанная относительно портфеля M1
βim 2 - бета, рассчитанная относительно портфеля M2.
2.2 САРМ с нулевой бетой
Вторая модификация САРМ возникает для случая, когда имеется актив, который содержит только нерыночный риск. Рыночный риск у него отсутствует, и поэтому его бета равна нулю. Для такой ситуации можно построить SML, которая будет проходить через рыночный портфель и рискованный актив с нулевой бетой. Уравнение САРМ в этом случае принимает вид
![]()
где: r0 - рискованный актив с нулевой бетой.
В качестве актива с нулевой бетой можно, например, рассматривать облигацию крупной компании. Если инвестор будет держать ее до погашения, то гарантирует себе определенный уровень процента, который не зависит уже от последующих колебаний цены этой бумаги. Единственный риск, которому подвергается вкладчик, это риск банкротства эмитента, поскольку в этом случае предприятие может и не осуществить причитающиеся ему платежи по облигациям.
2.3 Версия САРМ для облигаций
Модель САРМ можно построить для облигаций. Она имеет следующий вид:
![]() (***)
(***)
где: E(ri) - ожидаемая доходность i-й облигации;
Е(rm) - ожидаемая доходность рыночного портфеля облигаций;
βi - коэффициент бета i-й облигации. Он равен отношению дюрации облигации i (Di) к дюрации рыночного портфеля облигаций (Dm).
Формула (***) говорит: если доходность рыночного портфеля облигаций вырастет на 1%, то доходность i-й облигации возрастет на величину β . На рис. 10 представлена линия рынка облигаций. Как следует из формулы, в данной версии САРМ доходность облигации является линейной функцией дюрации облигации.
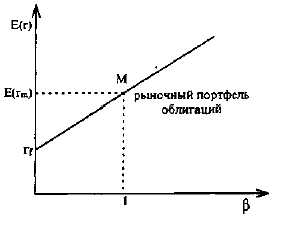
Рис. 10. Линия рынка облигаций
При использовании данной модели следует помнить, что она завышает доходность долгосрочных облигаций при повышении ставок. Так, для облигации с дюрацией 10 лет формула дает результат, который в 10 раз больше, чем для облигации с дюрацией 1 год. На практике данная разница не столь велика.
3. Теоретические и практические аспекты использования модели арбитражного ценообразования (АРТ)
3.1 Общий вид модели арбитражного ценообразования
Теория арбитражного ценообразования (АРТ) была предложена профессором Йельского университета С. Россом в 1976 г. и является альтернативной САРМ моделью общего равновесия на финансовом рынке. Главным предположением теории является то, что каждый инвестор стремится использовать возможность увеличения доходности своего портфеля без увеличения риска. Механизмом, способствующим реализации данной возможности, является арбитражный портфель.
Арбитраж (arbitrage) — это получение безрисковой прибыли путем использования разных цен на одинаковую продукцию или ценные бумаги. Арбитраж, являющийся широко распространенной инвестиционной тактикой, обычно состоит из продажи ценной бумаги по относительно высокой цене и одновременной покупки такой же ценной бумаги (или ее функционального эквивалента) по относительно низкой цене. Арбитражная деятельность является важной составляющей современных эффективных рынков ценных бумаг. Поскольку арбитражные доходы являются безрисковыми по определению, то все инвесторы стремятся получать такие доходы при каждой возможности.
Определить, подходит ли ценная бумага или портфель для арбитражных операций, можно различными способами. Одним из них является анализ общих факторов, которые влияют на курс ценных бумаг. Факторная модель подразумевает, что ценные бумаги или портфели с одинаковыми чувствительностями к факторам ведут себя одинаково, за исключением внефакторного риска. Поэтому ценные бумаги или портфели с одинаковыми чувствительностями к факторам должны иметь одинаковые ожидаемые доходности, в противном случае имелись бы "почти арбитражные" возможности. Но как только такие возможности появляются, деятельность инвесторов приводит к их исчезновению.
Теория арбитражного ценообразования утверждает, что ожидаемая доходность отдельной ценной бумаги зависит от множества разнообразных факторов, а не от одного интегрированного рыночного фактора, отражаемого классической Моделью САРМ. В качестве таких факторов он рассматривает все виды систематичсеких рисков раздельно, предлагая компенсировать каждый из факторов риска в процессе оценки стоимости финансового актива (ценной бумаги). При наличии n таких независимых
Модель теории арбитражного ценообразования имеет следующий вид:
Дфа = Дб/р + β1(Дрп1 – Дб/р) + + β2(Дрп2 – Дб/р) +…++ βn(Дрпn – Дб/р),
β1… βn- коэффициент "бета", измеряющий чувствительность рассматриваемого финансового актива к фактору 1…n;
Дрп1…Дрпn – уровень ожидаемой доходности рыночного портфеля, компенсирующий данный вид риска (фактора);
n – общее количество рассматриваемых факторов, систематически влияющих на уровень доходности отдельных финансовых активов и рыночного портфеля в целом.
Арбитражная теория ценообразования позволяет существенно сократить число ограничительных предложений, принятых при построении классической модели оценки стоимости финансовых активов, что усиливает возможность ее практического использования.
Модель АРТ обычно сравнивают с моделью САРМ. С теоретической точки зрения модель АРТ обладает неоспоримыми преимуществами:
- Модель АРТ расщепляет факторы риска на составляющие, приближая их к условиям, в которых действует конкретный бизнес;
- АРТ использует относительно более слабые упрощающие анализ предположения по сравнению с моделью оценки капитальных активов САРМ.
Однако у модели АРТ есть и свои недостатки, а именно:
- АРТ умалчивает о конкретных систематических факторах, влияющих на риск и доходность;
- АРТ требует тщательной подготовки информации и подробного анализа деятельности предприятия-конкурентов, занимаемой рыночной ниши и макроэкономических условий.
3.2 Выбор факторов, влияющих на доходность
Как уже было отмечено, существенным недостатком теории арбитражного ценообразования является неопределенность факторов, влияющих на доходность. Однако, экономисты, использующие АРТ в своих исследованиях, сами определяют круг показателей, которые, по их мнению, тесно связаны с доходностью того или иного актива.
Набор факторов, используемых в анализе очень широк. Среди них такие показатели, как темп прироста промышленного производства, величина инфляции, разница между долгосрочными и краткосрочными ставками, разница между надежными и ненадежными облигациями, темп роста валового национального продукта, процентная ставка, динамика изменения цен на нефть, темп роста расходов на оборону и др.
Все эти факторы имеют некоторые общие характеристики. Во-первых, они отражают показатели общей экономической активности (промышленное производство, общие продажи и ВНП). Во-вторых, они отражают инфляцию. В-третьих, они содержат разновидности фактора процентной ставки (либо разность, либо саму ставку).
Действие модели арбитражного ценообразования в условиях российского фондового рынка исследовалось в работах Е.А. Дорофеева и М.В. Алексеенковой.
Е.А. Дорофеев, рассматривая вопрос об эффективности российского фондового рынка, при проверке APT в качестве факторов использовал объем ВВП, индекс цен, разницу между ставкой рефинансирования и кредитования у крупнейших банков, валютный курс, котировки рынка ГКО-ОФЗ. Для акций, торгуемых в РТС, проверялась регрессионная зависимость курсовой стоимости акций от перечисленных факторов.
3.3 Расчет элементов ставки дисконтирования
Практические возможности использования модели арбитражного ценообразования для расчета ставки дисконта в российских условиях ограничены по нескольким причинам. Во-первых, это недостаток информации. АРТ требует изучения статистических данных по предприятию и конкурентам, а также динамики экономических показателей. С этой точки зрения использовать ее можно только для компаний, акции которых торгуются на фондовом рынке.
Во-вторых, это отсутствие специальных методик расчета отдельных элементов в рамках модели арбитражного ценообразования, вынуждающее использовать проверенные способы расчета ставки дисконтирования для получения более обоснованных и надежных результатов.
И, в-третьих, сложность расчетов. Учитывая первые два момента, сложность расчетов может сделать использование АРТ попросту нецелесообразным исходя из соотношения затрат труда и качества полученных результатов.
Разобраться в целесообразности использования АРТ на практике поможет ответ на вопрос о способах расчета премий за риск (k1…kn) и чувствительностей (b1…bn) по каждому фактору в российских условиях.
В соответствии с теорией арбитражного ценообразования премия за риск, связанный с каждым отдельным фактором, представляет собой разницу между доходностью среднего актива с единичной чувствительностью к данному фактору и нулевой ко всем остальным (рыночной ставкой доходности) и безрисковой нормой доходности:
kj = rmj – rf,
где rmj – рыночная ставка доходности за риск по фактору j;
rf – безрисковая норма доходности.
На практике не существует активов, чувствительных лишь к одному фактору. Поэтому приходится выделять из средней доходности всего рынка премии за риск, связанные с тем или иным фактором. Среднерыночная доходность российского фондового рынка определяется на основе фондовых индексов.
Одним из вариантов выделения премий за риск является ранжирование факторов по степени влияния на доходность и последующее разделение премии за риск всего рынка на факторные составляющие в соответствии с рангом. В любом случае вопрос расчета премий за риск по различным факторам требует серьезного изучения.
Бета-коэффициенты (b1,…,bn) рассчитываются на основе сопоставления динамики показателей эффективности деятельности компании (объемы продаж, выручка, чистая прибыль, сумма выплаченных дивидендов по акциям и др.), стоимости акций компании на фондовом рынке и аналогичных показателей по экономике или фондовому рынку в целом.
Процедура расчета бета-коэффициентов представляет собой статистическое исследование, исходными данными для которого являются экономические показатели деятельности компании и экономики в целом.
Заключение
Мы рассмотрели модель САРМ . Одним из основополагающих моментов в ней выступает актив без риска. Им обычно служит государственная ценная бумага.
В то же время уровень доходности периодически колеблется и по данным активам. Таким образом, получается, что и они подвержены рыночному риску. В рамках же САРМ государственная ценная бумага не содержит рыночного риска. САРМ не противоречит такому положению вещей. Рассматривая бумагу без риска, необходимо не забывать, что САРМ - это модель одного временного периода.
Поэтому, если инвестор приобретает бумагу без риска по некоторой цене и держит ее до погашения, то он обеспечивает себе фиксированный процент доходности, соответствующий уплаченной цене. Последующие изменения конъюнктуры уже не влияют на доходность операции. Рыночный риск по данной бумаге возникает для инвестора только в том случае, если он решает продать ее до момента погашения. В заключение следует сказать о результатах проверки САРМ на практике.
Они показали, что эмпирическая SML или, как ее еще называют, эмпирическая линия рынка является линейной и более пологой по сравнению с теоретической SML и проходит через рыночный портфель.
Ряд исследователей подвергают САРМ сомнению. Одна из критик представлена Р. Роллом.
Она состоит в том, что теоретически рыночный портфель САРМ должен включать в себя все существующие активы пропорционально их удельному весу на рынке, в том числе зарубежные активы, недвижимость, предметы искусства, человеческий капитал. Поэтому невозможно создать такой портфель на практике и, в первую очередь, с точки зрения определения веса активов в портфеле и оценки их доходности.
Сложно оценить результаты проверки САРМ, поскольку нет определенности в отношении того, является ли выбранный для экспериментов портфель рыночным (эффективным) или нет. В целом, проверки САРМ скорее говорят о том, представляют портфели (индексы), используемые в тестах, эффективные портфели или нет, чем подтверждают или опровергают саму модель САРМ.
Теория арбитражного ценообразования, основные положения которой были также рассмотрены в данной работе, с теоретической точки зрения обладает преимуществами по сравнению с другими моделями. Неопределенность факторов, влияющих на доходность, снижает эффективность использования модели арбитражного ценообразования для расчета ставок дисконта. Поэтому требуется разработка методик определения факторных составляющих ставки дисконтирования, поскольку их отсутствие в совокупности с ограниченностью информации значительно снижают адекватность результатов расчета ставок дисконта в российских условиях.
Несмотря на преимущества модели арбитражного ценообразования, ее использование в российской оценочной практике на сегодняшний день нецелесообразно, поскольку другие более простые модели дают более обоснованные результаты.
Практическая часть
Задача 1
Рассматривается возможность приобретения еврооблигаций МФ РФ на 09.04.2003. Имеются следующие данные. Дата выпуска – 26.06.1997. Дата погашения – 26.06.2007. Купонная ставка – 10%. Число выплат – 2 раза в год. Средняя курсовая цена – 99,70. Требуемая норма доходности (рыночная ставка) – 12 % годовых.
Определите дюрацию этого обязательства. Как изменится цена облигации, если рыночная ставка :а)возрастет на 1,5%; б) упадет на 0,5 %.
Решение
1. Принимаем, что цена погашения равна номиналу: F=N.
Принимаем номинал облигации за 1 ед. N=1.
Срок облигации n=10 лет.
Всего выплат m*n=2*10=20.
Всего оставшихся выплат: 8.
2. Определим дюрацию еврооблигации:
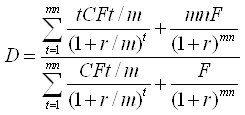 ;
;
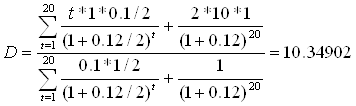 .
.
3. Определим рыночную цену облигации:
![]() ;
;
![]() или 71,44 %.
или 71,44 %.
4. Определим рыночную цену облигации при росте ставки на 1,5 %, или до 13,5% (r=0,135):
![]() ;
;
![]() или 66,46%.
или 66,46%.
5. Определим рыночную цену облигации при падении ставки на 0,5% или до 11,5% (r=0,115):
![]() или 73,22 %
или 73,22 %
Изменение рыночной цены облигации
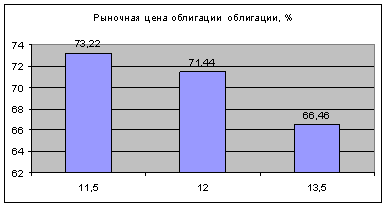
Из рисунка отчетливо видно, что при росте рыночной ставки на 1,5 % рыночная цена облигации падает на 4,98 %, а при уменьшении рыночной ставки на 0,5% -цена облигации увеличивается на 1,78%.
Задача 2
Акции предприятия "Н" продаются по 45.00. Ожидаемый дивиденд равен 3,00. Инвестор считает, что стоимость акции в следующем году вырастет на 11,11 %.
Определите ожидаемую доходность инвестиции. Как измениться доходность при прочих неизменных условиях, если инвестор намеривается продать акцию через два года, а ее стоимость снизится на 15 % от предыдущего уровня?
Решение
1. Определим доходность инвестиции:
![]()
2. Воспользуемся формулой доходности инвестиции для определения ожидаемой доходности инвестиции:
![]()
![]()
Доходность увеличится на (18,52-6,66) = 11,86%.
3. Воспользуемся формулой доходности инвестиции для определения доходности инвестиции, если инвестор намеревается продать акцию через два года, а ее стоимость при этом снизится на 15 % от предыдущего уровня.
![]()
![]()
Доходность уменьшится на (11,86-(-14))% =- 25,86%.
Задача 3
Имеются следующие данные о значении фондового индекса и стоимости акции А.
| Период | Индекс, J | Стоимость акции А |
| 645,5 | 41,63 | |
| 1 | 654,17 | 38,88 |
| 2 | 669,12 | 41,63 |
| 3 | 670,63 | 40 |
| 4 | 639,95 | 35,75 |
| 5 | 651,99 | 39,75 |
| 6 | 687,31 | 42 |
| 7 | 705,27 | 41,88 |
| 8 | 757,02 | 44,63 |
| 9 | 740,74 | 40,5 |
| 10 | 786,16 | 42,75 |
| 11 | 790,82 | 42,63 |
| 12 | 757,12 | 43,5 |
Определите бета коэффициент акции. Построить график линии SML для акции А.
Решение
1. Для простоты дальнейших вычислений, используя следующие формулы, заполним таблицу:
· Определим доходность индекса в различных периодах:
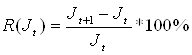 .
.
· Определим доходность акций в различных периодах:
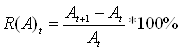 .
.
| Период | Индекс, J | Стоимость акции А | Доходность индекса, R(Jt), % | Доходность акции R(A)t, % | R(Jt)*R(A)t | 2 [R(Jt)] |
| 645,5 | 41,63 | |||||
| 1 | 654,17 | 38,88 | 1,34 | -6,61 | -8,87 | 1,80 |
| 2 | 669,12 | 41,63 | 2,29 | 7,07 | 16,16 | 5,22 |
| 3 | 670,63 | 40 | 0,23 | -3,92 | -0,88 | 0,05 |
| 4 | 639,95 | 35,75 | -4,57 | -10,63 | 48,61 | 20,93 |
| 5 | 651,99 | 39,75 | 1,88 | 11,19 | 21,05 | 3,54 |
| 6 | 687,31 | 42 | 5,42 | 5,66 | 30,66 | 29,35 |
| 7 | 705,27 | 41,88 | 2,61 | -0,29 | -0,75 | 6,83 |
| 8 | 757,02 | 44,63 | 7,34 | 6,57 | 48,18 | 53,84 |
| 9 | 740,74 | 40,5 | -2,15 | -9,25 | 19,90 | 4,62 |
| 10 | 786,16 | 42,75 | 6,13 | 5,56 | 34,07 | 37,60 |
| 11 | 790,82 | 42,63 | 0,59 | -0,28 | -0,17 | 0,35 |
| 12 | 757,12 | 43,5 | -4,26 | 2,04 | -8,70 | 18,16 |
| СУММА | 16,84 | 7,12 | 199,27 | 182,30 |
2. Определим бета-коэффициент акции:
 ;
;
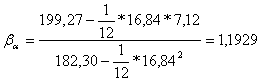
3. Определяем параметр ![]() представляющий
нерыночное составляющее доходности актива А:
представляющий
нерыночное составляющее доходности актива А:
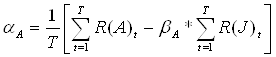
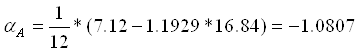
4. Подставляем найденные значения в линейную регрессионную модель CAMP:
![]()
![]()
![]()
При подстановке получаем следующие значения:
| R(At) | R(Jt) |
| 0,52 | 1,34 |
| 1,65 | 2,29 |
| -0,81 | 0,23 |
| -6,54 | -4,57 |
| 1,16 | 1,88 |
| 5,38 | 5,42 |
| 2,04 | 2,61 |
| 7,67 | 7,34 |
| -3,65 | -2,15 |
| 6,23 | 6,13 |
| -0,37 | 0,59 |
| -6,16 | -4,26 |
5. Строим график линии SML для акции А.
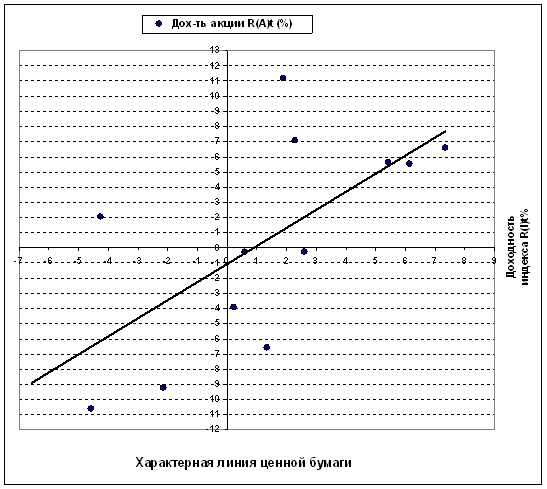
Задача 4
Текущая цена акции В составляет 65,00 (S). Стоимость трехмесячного опциона "колл" с ценой исполнения 60,00 (X) равна 6,20. Стандартное отклонение по акции В равно 0,18 (s). Безрисковая ставка составляет 10 % (r).
Определите справедливую стоимость опциона. Выгодно ли осуществлять покупку опциона?
Решение
1. Стоимость опциона "колл" определяется по модели оценки опциона Блэка – Шоулза:
![]() , е = 2,718
, е = 2,718
Найдем d1:
![]()
T=3/12=0.25
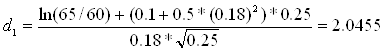
Найдем d2:
![]()
![]()
2.Из таблицы нормального распределения получаем:
N(2.0455) = 0.9798
N(1.9555) = 0.9744
3.Определим справедливую (внутреннюю) стоимость опциона:
![]()
Так как справедливая стоимость опциона равна 6,65 и она больше стоимости фактической, которая равна 6,20, то покупка опциона является выгодной. Такой опцион следует купить, так как он недооценен и в будущем, можно ожидать роста его стоимости.
Задача 5
Брокеры К, Н, М (условие задачи 23) не хотят сложа руки наблюдать, как арбитражер за счет их получает безрисковые доходы. У них возникает следующая идея: К продает только инструмент Д по цене 15,00 за штуку, а Н продает только инструмент А по цене 20,00. Брокер М остается на прежних позициях.
Удастся ли, действуя, таким образом, устранить арбитражные возможности? Обоснуйте свой ответ.
|
Инструмент Брокер |
Д | А | Цена за портфель |
| К | |||
| Н | |||
| М | 5 | 7 | 185,00 |
Решение
Арбитраж - операции на одном и том же рынке от любой необычной разницы в котировках цен на финансовые активы с различными сроками поставки.
Арбитражёр может купить портфель акций у брокера М за 185,00. Таким образом у него окажется 5 акций Д и 7 акций А. Арбитражёр может продать 5 акций Д брокеру К по цене 15,00 и получить за это 75,00. Акции А арбитражёр может продать брокеру Н по цене 20,00 за штуку. Таким образом, продав все акции арбитражер получит сумму = 5*15+20*7=140+75=215, его прибыль составит 215-185 =30,00.
Таким образом, мы видим, что арбитраж возможен.
Список литературы
1. Алексеенкова М.В. Факторы отраслевого анализа для российской переходной экономики - М.: ГУ-ВШЭ, 2005.
2. Бригхем Ю., Гапенски Л. Финансовый менеджмент. - СПб., 1997.
3. Бронштейн Е.М. Пособие по финансовой математике Уфа: Изд.УГАТУ, 1999.
4. Ван Хорн Дж.К. Основы управления финансами. - М.: Финансы и статистика, 1997. - 800 с.
5. Галиц Л. Финансовая инженерия: инструменты и способы управления финансовым риском. - М.:ТВП, 1998. - 576 с.
6. Дорофеев Е.А. Влияние колебаний экономических факторов на динамику российского фондового рынка. - М.: РПЭИ, 2000.
7. Синадский В. Расчет ставки дисконтирования // "Финансовый директор", 2003, № 4.
8. Устименко В.А. О возможностях использования модели арбитражного ценообразования для расчета ставки дисконтирования в российских условиях // "Вопросы оценки", № 3, октябрь 2003.
9. Шарп У.Ф., Александер Г.Дж., Бейли Д.В. Инвестиции - М.: ИНФРА-М, 2001.
10. Шеннон П.Пратт Анализ и оценка закрытых компаний, Издание 2 - М., Институт Экономического Развития Всемирного Банка, 1999.
11. Бланк И. А. Основы инвестиционного менеджмента. В 2 томах- 2-е изд., перераб..- К.: Эльга, Ника-Центр, 2004.
12. Лукасевич И.Я. Анализ финансовых операций. Методы, модели, техника вычислений.- М.:Финансы; ЮНИТИ, 1998;
13. Шарп У., Александер Г., Бейли Дж. Инвестиции. – М. Инфра-М, 2003; С.185-214
14. Фабоцци Ф.Дж. "Управление инвестициями.- М.:Инфра-М, 2000
15. Кох И.А. Аналитические модели рынка ценных бумаг. – Казань:КФЭИ – 2001. – С.48-68.
16. Капитаненко В.В. Инвестиции и хеджирование. – Москва: - 2001. –С. 157-168.
17. Рукин А. Портфельные инвестиции. Финансово – математические методы./ Рынок ценных бумаг, 2000, №18,с. 45-47.
18. Константинов А. Портфельное инвестирование на российском рынке акций./ Финансист, 2000, №8, с. 28-31.
19. Рынок ценных бумаг/ под ред. Галанова В.А., Басова А.И. – М:. Финансы и статистика. – 2002. – С 352.
20. Волкова В. Выбор акций для портфельного инвестирования./ Финансовый бизнес. – 2000. - № 2.- с. 47-48