Статья: Как обнаружить "черную дыру"
Как обнаружить «черную дыру»
В.Н. Леонович
Черная дыра – область пространства, в которой гравитационное притяжение настолько сильно, что ни вещество, ни излучение не могут эту область покинуть. Для находящихся там тел вторая космическая скорость (скорость убегания) должна была бы превышать скорость света, что невозможно, поскольку ни вещество, ни излучение не могут двигаться быстрее света. Поэтому из черной дыры ничто не может вылететь. Границу области, за которую не выходит свет, называют «горизонтом событий», или просто «горизонтом» черной дыры.
Чтобы поле
тяготения смогло «запереть» излучение, создающая это поле, масса (M) должна
сжаться в объем с радиусом, меньшим «гравитационного радиуса» rg = 2GM/![]() ,
гравитационная постоянная G = 6,672×
,
гравитационная постоянная G = 6,672×![]()
![]()
![]()
![]() и скорость света c = 299792458
м/с. Значение гравитационного радиуса чрезвычайно мало по сравнению с привычным
размером физических тел. Например, для Солнца с массой около 2 ×
и скорость света c = 299792458
м/с. Значение гравитационного радиуса чрезвычайно мало по сравнению с привычным
размером физических тел. Например, для Солнца с массой около 2 ×![]() кг и радиусом
около 700 тыс. км значение rg ≈ 3 км. А для Земли (M = 6 ×
кг и радиусом
около 700 тыс. км значение rg ≈ 3 км. А для Земли (M = 6 × ![]() кг) значение
rg ≈ 1 см, для звезды в десять солнечных масс — 30 км, а для объекта в два
миллиарда солнечных масс — 40 астрономических единиц, то есть размер Солнечной системы.
кг) значение
rg ≈ 1 см, для звезды в десять солнечных масс — 30 км, а для объекта в два
миллиарда солнечных масс — 40 астрономических единиц, то есть размер Солнечной системы.
Теория звездной эволюции указывает, что за 12 млрд. лет существования нашей Галактики, содержащей порядка 100 млрд. звезд, в результате коллапса наиболее массивных из них должно было образоваться несколько десятков миллионов черных дыр.
В настоящее время в зоне видимости наблюдается около 200 объектов – кандидатов в черные дыры, но нет пока ни одного объекта, в отношение которого можно утверждать, что это черная дыра.
Черная дыра как физический объект обладает очень многими интересными и необычными свойствами, но подавляющее большинство этих свойств проявляются в непосредственной близости или даже за горизонтом событий. Для удаленного наблюдателя они недоступны и в качестве признаков обнаружения не представляют интереса.
Ищут черные дыры по косвенным признакам, т.е. по искажению нормальных характеристик ближайших объектов, например, среди двойных звезд, одна из которых – черная дыра. Есть и другие признаки, нет смысла их перечислять. Все они основаны на проявлении именно необычных свойств черных дыр, и представляют значительные трудность для обнаружения. Исследователи так увлеклись экзотическими свойствами черных дыр, что упустили из виду самый доступный вид исследования – фотонное излучение.
Исходя из теории «черных дыр», самым вероятным местом нахождения дыр является центр Галактики. Рассмотрим этот вариант. Проанализируем оптические эффекты, которые должен обнаружить в этом случае земной наблюдатель.
Черная дыра не излучает. Лучи света от звезд расположенных за черной дырой не могут достичь Земли по прямой линии, т.к. все излучение телесного угла, определяемого диаметром "горизонта событий", поглощается черной дырой. Но черная дыра искривляет смежное пространство определенным образом, так что оно действует как идеальная и универсальная линза, фокусное расстояние которой зависит от расстояния отклоняемого луча от центра линзы. Фокусное расстояние, тем меньшее, чем ближе луч к центру черной дыры. Фокус универсальной линзы всегда направлен в сторону наблюдателя, а количество наблюдателей и их размещение на оси наблюдения может быть произвольным. Так что для каждой точки пространства такую линзу можно рассматривать как набранную из тонких цилиндров, каждый из которых имеет свое фокусное расстояние. Для любой точки, определяемой положением наблюдателя, всегда найдется условная тонкая линза, обеспечивающая фокусировку лучей загороженной звезды именно в точке наблюдателя. В результате все геометрически экранированные звезды предстанут для наблюдателя в форме кольцевых псевдообъектов, рис. 1, диаметры которых определяются массой черной дыры (чем больше масса, тем больше радиус) и расстояниями от «черной
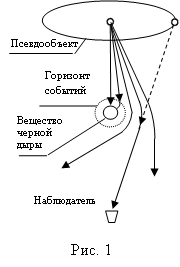 |
дыры» до наблюдателя и от «черной дыры» до наблюдаемой звезды.
Суммарная яркость псевдообъекта может превзойти яркость самой звезды. А если учесть, что каждая звезда, загороженная «черной дырой», формирует псевдообъект, то суммарная яркость всех колец, которые для наблюдателя практически сольются в одно кольцо, должна превысить суммарную яркость экранированных звезд. Самое большое кольцо сформируется самой ближней загороженной звездой. Если экранированная звезда несколько смещена от оси наблюдения, то яркость кольца становится неоднородной, а при выходе звезды из тени, кольцо вырождается в два точечных псевдообъекта. Один наблюдается, как реальная звезда, смещенная от черной дыры, а другой, как звезда внутри кольца, и оба псевдообъекта при малых отклонениях имеют почти одинаковую яркость (внутри кольца яркость меньше). Звезды, наблюдаемые в значительном отдалении от черной дыры, практически не изменят своего положения на небе, но должны быть представлены земному наблюдателю также двумя объектами, первый из которых будет собственно видимой звездой, а второй будет псевдозвездой внутри кольца псевдообъекта. Псевдозвезда в этом случае будет значительно менее яркой по сравнению с реальной звездой, т.к. действующее расстояние до нее складывается из двух прямолинейных участков: наблюдатель-«черная дыра»-реальный объект. Но таких объектов так много (все видимые звезды), что суммарная яркость кольца черной дыры должна быть сравнимой с самыми яркими звездами или превосходить их. Точечные псевдозвезды заполнят зону от самого большого кольца до радиуса горизонта событий. Эффект кажущегося смещения звезд вблизи «черной дыры» сформирует вокруг кольца псевдообъекта область относительно "разреженных" звезд.
Таким образом, окончательно получаем, что на месте черной дыры должен наблюдаться яркий псевдообъект с темной областью в середине, и затемненной вокруг него. Характерные размеры псевдообъекта, формируемого черной дырой, для земного наблюдателя всегда меньше размеров исходного объекта, послужившего материалом при коллапсе в черную дыру, т.е. очень малы для черных дыр, возникших из звезд средней величины. Темную область в центре псевдообъекта заметить трудно, да и не нужно. Дело в том, что спектр излучения псевдообъекта должен быть интегральным, т.е. с суммарным набором стандартных линий всех звезд – это одна из самых важных характеристик для поиска.
Из выше изложенного следует, что черные дыры нужно искать не как темные провалы в звездном небе, а наоборот, среди самых ярких объектов, очень похожих на звезды. Необходимым атрибутом поиска должен быть анализатор спектра.
Изложенная здесь информация позволяет включиться в поиск черных дыр астрономам-любителям. Для решивших начать поиск черных дыр, необходимо сообщить следующее. Черную дыру в центре Галактики, казалось бы, трудно не обнаружить; по теории она должна быть очень большой, более миллиона масс Солнца. Но ее пока не обнаружили. Кроме того, следует обратить внимание на то, что строгое решение Карла Шварцшильда, положенное в основу теории «черных дыр», найдено для упрощенных и, как следствие, приблизительных уравнений Эйнштейна. Строгие уравнения гравитации, опубликованные Эйнштейном, до сих пор не имеют решения и не проверены. Несколько существующих частных решений, найденных для упрощенных уравнений, справедливы только для очень малых значений кривизны пространства, что соответствует малой концентрации вещества. Но кривизна в области дыр не то что мала, а стремится к бесконечности. Применение упомянутых частных решений уравнений гравитации для построения теории черных дыр аналогично применению уравнений ламинарных течений для анализа турбулентности.
Таким образом, теория черных дыр может оказаться всего лишь экзотическим и эфемерным продуктом тренировки ума азартных энтузиастов, не желающих (или не умеющих) видеть физику за абстрактными построениями математики.
Однако случается, что люди находят не то, что ищут. В такой ситуации остается только переадресовать им совет Великого Комбинатора: «Пилите, Шура, пилите».
Нижний Новгород, 2009г.
Список литературы
1) Паули В. Теория относительности. — 2-е изд. — М.: Наука, 1983.
2) Новиков И.Д. Черные дыры и Вселенная. М., Молодая гвардия, 1985.
3) Чандрасекар С. Математическая теория черных дыр. М., Мир, 1986.
4) Черепащук А.М. Поиски черных дыр. – Успехи физических наук, 2003, т.173, № 4.