Курсовая работа: Моделирование SH-волны
Кафедра общей и прикладной геофизики
Курсовая работа
по сейсморазведке
на тему:
Моделирование SH-волны
Выполнили: студенты группы 3151
Кузнецова А.О., Колбенко А.В., Климов Ю.С.
Проверил: доц. Сердобольский Л.А.
Дубна, 2005
Содержание
Введение
I. Теоретическая часть
1. Описание волн и создаваемых ими на границе напряжений
2. Граничные условия и спектральные коэффициенты рассеивания
3. Волны рассеивания при падении SH-волны на кровлю низкоскоростной среды
4. Волны рассеивания при падении SH-волны на кровлю высокоскоростной среды
II. Расчётная часть
1. Падение SH-волны на кровлю низкоскоростной среды
2. Падение SH-волны на кровлю высокоскоростной среды
Список литературы
Введение
Сейсморазведка является одним из важнейших видов геофизической разведки земных недр. Она включает в себя комплекс методов исследований геологического строения земной коры, основанных на изучении особенностей распространения в ней искусственно возбуждённых упругих волн. Вызванные взрывом или другим способом упругие волны, распространяясь во всех направлениях от источника колебания, проникают в толщу земной коры на большие глубины. В процессе распространения в земной коре упругие волны претерпевают процессы отражения и преломления. Это приводит к тому, что часть сейсмической энергии возвращается к поверхности Земли, где вызывает дополнительные сравнительно слабые колебания. Эти колебания регистрируются специальной аппаратурой. Полученные записи подвергаются глубокой обработке. Анализируя и интерпретируя полученные после обработки результаты, квалифицированный специалист-геофизик может определить глубину залегания, форму и свойства тех слоёв, на поверхности которых произошло отражение или преломление упругих волн.
Упругие волны делятся на объёмные и поверхностные. Традиционно в сейсморазведке наибольшее применение нашли объёмные волны: продольные (P-волны) и поперечные (S-волны). Скорости Vp всегда больше, чем Vs.
В данной курсовой работе рассматривается распространение SH-волны в различных геологических условиях среды.
I. Теоретическая часть
Пусть верхняя среда имеет скорость поперечной волны ![]() , плотность
, плотность ![]() и модуль сдвига
и модуль сдвига ![]() , а нижняя среда характеризуется
параметрами
, а нижняя среда характеризуется
параметрами ![]() . Напомним, что
. Напомним, что ![]() , и для сокращения письма
опустим индекс поперечной волны (S) и будем обозначать
, и для сокращения письма
опустим индекс поперечной волны (S) и будем обозначать ![]() , не забывая, конечно, о
том, что в этом разделе речь идет о поперечной горизонтально-поляризованной
волне, падающей на плоскую, горизонтальную, разрывно-резкую границу раздела.
, не забывая, конечно, о
том, что в этом разделе речь идет о поперечной горизонтально-поляризованной
волне, падающей на плоскую, горизонтальную, разрывно-резкую границу раздела.
1. Описание волн и создаваемых ими на границе напряжений
Пусть первичная плоская SH-волна
падает на границу (z = 0) под углом α и имеет
фронт, параллельный оси Oy. Она описывается вектором
смещения ![]() , также ориентированным
вдоль Оу, но не зависящим от у:
, также ориентированным
вдоль Оу, но не зависящим от у:
![]() .
.
Как отмечалось, SH-волна в выбранных
условиях порождает на границе только монотипные (также SH)
вторичные волны. Отраженная SH-волна ![]() распространяется вверх, в
противоположном по отношению к первичной волне направлении. Поэтому в ее
волновом аргументе переменная z отрицательна:
распространяется вверх, в
противоположном по отношению к первичной волне направлении. Поэтому в ее
волновом аргументе переменная z отрицательна:
![]()
Проходящая SH-волна распространяется
в том же направлении, что и падающая волна (вниз), но во второй нижней среде со
скоростью ![]() и под углом
и под углом ![]() :
:
![]() .
.
Закон Снеллиуса для SH-волн имеет вид:
![]()
Горизонтальное вдоль Оу смещение SH-волн создает на границе лишь касательное напряжение:
![]()
в соответствии с законом Гука, где ![]() - сдвиговая деформация в
плоскости zOy:
- сдвиговая деформация в
плоскости zOy:
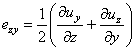 .
.
Но SH-волна несет смещение,
ориентированное вдоль Оу, и для нее ![]() .Кроме
того, фронты всех волн параллельны той же оси Оу, и поэтому
.Кроме
того, фронты всех волн параллельны той же оси Оу, и поэтому ![]() .
.
Следовательно, для касательного напряжения можно записать:
![]()
Напряжение, создаваемое на границе падающей волной, описывается так:
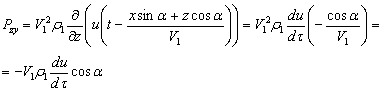
Отраженная волна создает на границе касательное напряжение:
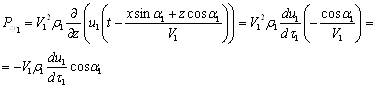
Наконец, проходящая волна создает напряжение:

Поскольку ![]() , для
унификации обозначений будем всегда использовать угол
, для
унификации обозначений будем всегда использовать угол ![]() .
.
2. Граничные условия и спектральные коэффициенты рассеивания
Из общих трех граничных условий для компонент векторов
смещения и стольких же граничных условий для компонент напряжений в условиях
рассматриваемой в данном разделе задачи актуальны лишь два граничных условия: равенство
суммарных у-компонент смещений (кинематическое) и равенство суммарных
касательных ![]() напряжений (динамическое).
напряжений (динамическое).
На границе, при z = 0, сумма
смещений падающей ![]() и отраженной
и отраженной ![]() волн должна быть равна
смещению
волн должна быть равна
смещению ![]() проходящей волны:
проходящей волны:
![]()
При подстановке z=0 волновые аргументы всех трех волн равны:
![]()
то есть ![]() , так
как t и x -
общие время и координата точки границы, а множители при х равны в соответствии
с законом Снеллиуса. Поэтому первое граничное условие дает уравнение:
, так
как t и x -
общие время и координата точки границы, а множители при х равны в соответствии
с законом Снеллиуса. Поэтому первое граничное условие дает уравнение:
![]()
или в спектрах:
![]() .
.
Обратим внимание на отсутствие в первом уравнении углов падения, отражения и прохождения. Это значит, что уравнение должно быть справедливом при любом угле падения 0 ≤ α ≤ π⁄2.
Динамическое граничное условие требует, чтобы на границе, при z=0, сумма напряжений, создаваемых падающей и отраженной волнами, равнялось напряжению, создаваемому проходящей волной:
![]() .
.
Используя определения касательных напряжений, получим, подставляя z = 0, второе уравнение:
![]() ,
,
или в спектральной форме после сокращения на jω:
![]() .
.
Вместе уравнения для смещений и напряжений создают систему из двух уравнений, в которые входят спектры трех волн - отраженной, проходящей и, породившей их, первичной (падающей):

Очевидно, эта система позволяет определить лишь отношения спектров вторичных волн к спектру первичной волны. Так вводятся спектральные коэффициенты рассеяния:
спектральный коэффициент отражения ![]() ,
,
спектральный коэффициент прохождения ![]() .
.
Как в любой линейной системе, чья спектральная
характеристика определена отношением спектра сигнала на выходе к спектру
входного сигнала, и в данном случае спектры “выходных сигналов” - отраженной
волны (“выход 1”) и проходящей волны (“выход 2”) соотносятся со спектром
“входного сигнала" - падающей волны. Поделив уравнения на ![]() и введя А и В, запишем:
и введя А и В, запишем:
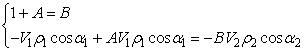
Решая любым способом эту простую систему уравнений, получим определения спектральных коэффициентов рассеивания:
![]() .
.
Обратим внимание на очень удобную особенность - при любом
угле падения коэффициент прохождения В на единицу больше коэффициента отражения
А. Произведение скорости на плотность в сейсморазведке называют волновым
сопротивлением (или акустической жесткостью): ![]() Используя
определение спектральных коэффициентов рассеивания, можно записать для спектров
вторичных волн:
Используя
определение спектральных коэффициентов рассеивания, можно записать для спектров
вторичных волн:
![]() .
.
Так как В = 1 + А, то при любом угле падения спектры волн связаны соотношением:
![]() .
.
В том же соотношении находятся и сами сигналы - первичная и вторичные волны:
![]() .
.
Видно, что всегда проходящая волна представляет собой сумму волн падающей и отраженной. Заметим, что для SH-волн так и должно быть для соблюдения неизменной сплошности всей среды и неразрывности контакта пород на границе.
При нормальном (по перпендикуляру к границе) падении ![]() и коэффициента рассеивания
равны:
и коэффициента рассеивания
равны:
![]() .
.
Очевидно, что условием возникновения отраженной волны служит
неравенство волновых сопротивлений, контактирующих на границе сред ![]() вне зависимости от того,
чем это неравенство вызывается - различием скоростей или различием плотностей. Отражающей
является граница с различными волновыми сопротивлениями. Могут быть “скоростные"
границы, на которых изменяются скорости, могут существовать “плотностные” границы,
на которых меняются плотности, и границы обоих типов являются отражающими. Наоборот,
граница, на которой
вне зависимости от того,
чем это неравенство вызывается - различием скоростей или различием плотностей. Отражающей
является граница с различными волновыми сопротивлениями. Могут быть “скоростные"
границы, на которых изменяются скорости, могут существовать “плотностные” границы,
на которых меняются плотности, и границы обоих типов являются отражающими. Наоборот,
граница, на которой ![]() и
и ![]() , но
, но ![]() , не является отражающей.
, не является отражающей.
В большинстве случаев скорости и плотности пород изменяются согласованно - более плотные породы являются и более всокоскоростными и наоборот. Исключения из этого правила довольно редки. Наиболее яркий пример - граница между залегающими над соляным куполом известняками и каменной солью. Скорость волны в известняках может быть меньше скорости в соли, тогда как плотность соли меньше плотности известняка.
В зависимости от знака неравенства ![]() выделяют случаи
выделяют случаи ![]() тогда верхняя среда имеет
большее волновое сопротивление, чем нижнее, и обратный случай, когда нижняя
среда характеризуется большим волновым сопротивлением:
тогда верхняя среда имеет
большее волновое сопротивление, чем нижнее, и обратный случай, когда нижняя
среда характеризуется большим волновым сопротивлением: ![]() . В геологическом разрезе
из-за статического давление вышележащих пород волновое сопротивление обычно
растете с увеличением глубины залегания. Уменьшению его на границе обычно
соответствуют границы перерыва в осадконакоплении (границы разрыва).
. В геологическом разрезе
из-за статического давление вышележащих пород волновое сопротивление обычно
растете с увеличением глубины залегания. Уменьшению его на границе обычно
соответствуют границы перерыва в осадконакоплении (границы разрыва).
Проведем последовательный анализ поведения коэффициентов рассеивания А и В вторичных волн при изменении угле падения первичной SH-волны: 0≤ α ≤ π⁄2. Угол α = 0 соответствует нормальному падению волны, угол α = π⁄2 является теоретически возможным пределом изменения угла падения, при котором волна скользит вдоль границы.
3. Волны рассеивания при падении SH-волны на кровлю низкоскоростной среды
Верхняя среда более плотная и имеет большую скорость распространения волны, чем нижняя:
![]() .
.
Из закона Снеллиуса следует, что в том же соотношении
находятся углы падения и отражения ![]() и угол
прохождения
и угол
прохождения ![]() :
:
![]() .
.
Поэтому при изменении угла падения от 0 до теоретически возможного
предела ![]() угол прохождения этого
предела не достигает: всегда
угол прохождения этого
предела не достигает: всегда ![]() <
<![]() .
.
Поэтому коэффициенты рассеивания при любых углах падения являются действительными числами - просто амплитудными множителями, лишь уменьшающими (при А, В < 1) или увеличивающими (при В > 1) амплитуду вторичной волны по сравнению с амплитудой первичной, падающей волны.
Возможно еще одно воздействие коэффициента отражения А на отраженную волну. Если А > 0, то отраженная волна имеет тот же знак (направление) смещения, что и первичная волна. Если же А < 0, то первичная и отраженная волны имеют разные направления смещения (рис.8). Пусть, например, падающая волна имеет направление первого смещения в сторону у > 0.
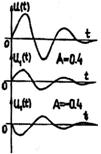
Рис.8
Тогда при А < 0 первое смещение отраженной волны
направлено в сторону у < 0. В физике такое явление называют отражением с
потерей полуволны, в сейсморазведке - изменением полярности первого вступления
волны. При нормальном падении ![]() и при
и при ![]() :
:
![]() .
.
Например, при ![]() км/с,
км/с, ![]() г/cм
г/cм![]() ,
, ![]() км/с,
км/с, ![]() г/см
г/см![]() коэффициенты рассеивания
имеют значения: A = 0,25, В = 1,25. При нормальном
падении отраженная волна имеет амплитуду, в четыре раза меньшую амплитуды
первичной волны, а проходящая волна превосходит ее по амплитуде на 25%. Подстановка
теоретически возможного предела изменения угла падения
коэффициенты рассеивания
имеют значения: A = 0,25, В = 1,25. При нормальном
падении отраженная волна имеет амплитуду, в четыре раза меньшую амплитуды
первичной волны, а проходящая волна превосходит ее по амплитуде на 25%. Подстановка
теоретически возможного предела изменения угла падения ![]() дает
дает ![]() и А = - 1, а В = 0. Отраженная
волна имеет ту же амплитуду, что и волна падающая, но инвертирована (обращена) по
знаку смещения в сравнении с ней. Проходящая волна отсутствует, что вполне
естественно. Обратим внимание на то, что при изменении угла падения от 0 до
и А = - 1, а В = 0. Отраженная
волна имеет ту же амплитуду, что и волна падающая, но инвертирована (обращена) по
знаку смещения в сравнении с ней. Проходящая волна отсутствует, что вполне
естественно. Обратим внимание на то, что при изменении угла падения от 0 до ![]() коэффициент отражения
меняет знак - при α = 0 A > 0, а при α =
коэффициент отражения
меняет знак - при α = 0 A > 0, а при α = ![]() А<0. Значит, при
некотором угле падения
А<0. Значит, при
некотором угле падения ![]() коэффициент
отражения равен 0 и отраженная волна отсутствует (!). Так как В = 1 + А, то при
α =
коэффициент
отражения равен 0 и отраженная волна отсутствует (!). Так как В = 1 + А, то при
α = ![]() В = 1 и проходящая волна
имеет в точности ту же амплитуду, что и первичная волна. Найдем этот угол
В = 1 и проходящая волна
имеет в точности ту же амплитуду, что и первичная волна. Найдем этот угол ![]() из условия А = 0:
из условия А = 0:
![]() .
.
По закону Снеллиуса
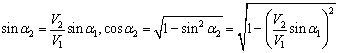 .
.
Поэтому условие А = 0 принимает вид:
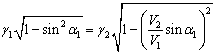 .
.
Отсюда, после преобразований найдем ![]() по его синусу:
по его синусу:
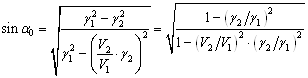 .
.
При уменьшении различия физических свойств плотности пород
сближаются более быстро, чем скорости. При ![]() :
:
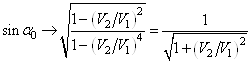 .
.
В пределе, когда и ![]() . Следовательно, в
рассматриваемом случае угол падения
. Следовательно, в
рассматриваемом случае угол падения ![]() , при
котором А = 0, находится в диапазоне углов падения, больших
, при
котором А = 0, находится в диапазоне углов падения, больших ![]() , удаляясь от этой величины
в сторону больших углов по мере увеличения различий физических свойств
контактирующих сред (контрастности границы).
, удаляясь от этой величины
в сторону больших углов по мере увеличения различий физических свойств
контактирующих сред (контрастности границы).
Для выбранных ранее в качестве примера параметров сред sin ![]()
![]() 0,84 и
0,84 и ![]()
![]()
![]() . Значит, в диапазоне углов
падения от 0° до 57° коэффициент отражения А положителен, коэффициент
прохождения В >1. При
. Значит, в диапазоне углов
падения от 0° до 57° коэффициент отражения А положителен, коэффициент
прохождения В >1. При ![]()
![]()
![]() А
= 0, В = 1, а при α >
А
= 0, В = 1, а при α > ![]() А <
0, В < 1. При углах, меньших
А <
0, В < 1. При углах, меньших ![]() ,
отраженный сигнал имеет тот же знак смещения, что и первичная волна, при угле
падения, равном
,
отраженный сигнал имеет тот же знак смещения, что и первичная волна, при угле
падения, равном ![]() , отраженная
волна отсутствует, а при углах, больших
, отраженная
волна отсутствует, а при углах, больших ![]() ,
она подобна первичной волне с инвертированным знаком смещения.
,
она подобна первичной волне с инвертированным знаком смещения.
Для выбранных параметров разреза на рис.9 приведен единый
график А (α) и В (α) = 1 + А (α), снабженный двумя шкалами оси
ординат со смещенными на единицу нулями. В нижней части рисунка изображены
схематические импульсоиды падающей волны u (t) и вторичных волн - отраженной ![]() и
проходящей
и
проходящей ![]() для различных углов
падения.
для различных углов
падения.
Как видно из рисунка, при малых углах падения изменения спектральных коэффициентов А и В незначительны. Соответственно, малы и изменения амплитуды вторичных волн. Это является благоприятным фактором для сейсмической разведки.
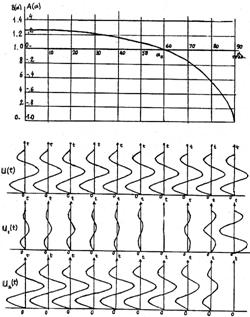
Рис.9
С приближением угла падения к ![]() спад
кривой ускоряется, отраженная волна затухает до нуля при
спад
кривой ускоряется, отраженная волна затухает до нуля при ![]() , а амплитуда проходящей
волны стремится к амплитуде волны падающей.
, а амплитуда проходящей
волны стремится к амплитуде волны падающей.
При углах, больших ![]() ,
происходит стремительное падение кривой к пределам: А (α → 90°) →
-1; B (α → 90°) → 0. Отраженная волна,
поменяв знак смещения на обратный при
,
происходит стремительное падение кривой к пределам: А (α → 90°) →
-1; B (α → 90°) → 0. Отраженная волна,
поменяв знак смещения на обратный при ![]() ,
стремится к падающей волне с инвертированным знаком смещения. Проходящая волна
столь же быстро затухает до нуля.
,
стремится к падающей волне с инвертированным знаком смещения. Проходящая волна
столь же быстро затухает до нуля.
4. Волны рассеивания при падении SH-волны на кровлю высокоскоростной среды
Нижняя среда - более плотная и имеет большую скорость распространения волны, чем верхняя:.
![]() и
и ![]() .
.
В соответствии с законом Снеллиуса, угол прохождения всегда
больше угла падения и равному ему угла отражения: ![]() .
При изменении угле падения
.
При изменении угле падения ![]() от нуля
до теоретически возможного предела 90° угол прохождения растет быстрее и
становится равным 90° при
от нуля
до теоретически возможного предела 90° угол прохождения растет быстрее и
становится равным 90° при ![]() . В этом
случае
. В этом
случае
![]() и
и ![]() ,
,
где ![]() - критический
угол падения. При таком падении проходящая волна не уходит в глубь нижней
среды, а скользит вдоль границы со скоростью
- критический
угол падения. При таком падении проходящая волна не уходит в глубь нижней
среды, а скользит вдоль границы со скоростью ![]() .Эта
скользящая волна порождает в верхней низкоскоростной среде вторичную волну,
называемую в сейсморазведке головной или преломленной. На регистрации таких
волн основан второй метод сейсморазведки - метод преломленных волн (МПВ), - первым
и основным, но вторым по времени возникновения, является метод отраженных волн
(МОВ).
.Эта
скользящая волна порождает в верхней низкоскоростной среде вторичную волну,
называемую в сейсморазведке головной или преломленной. На регистрации таких
волн основан второй метод сейсморазведки - метод преломленных волн (МПВ), - первым
и основным, но вторым по времени возникновения, является метод отраженных волн
(МОВ).
При нормальном падении все косинусы равны единице, коэффициент отражения отрицателен, а коэффициент прохождения меньше единицы. Следовательно, в этом случае отраженная волна противоположна падающей по знаку смещений (отражение с потерей полуволны), а проходящая волна имеет меньшую амплитуду, чем волна падающая:
при α = 0 и A < 0 и ![]() B
< 1 и
B
< 1 и ![]() = B · u
(τ) < u (τ).
= B · u
(τ) < u (τ).
При критическом угле падения ![]() угол
прохождения
угол
прохождения ![]() и А = 1, В = 1 + А = 2. Отраженная
волна имеет ту же амплитуду, что и волна падающая, а проходящая волна по
амплитуде вдвое превосходит ее:
и А = 1, В = 1 + А = 2. Отраженная
волна имеет ту же амплитуду, что и волна падающая, а проходящая волна по
амплитуде вдвое превосходит ее:
при ![]() А = 1 и
А = 1 и ![]() В = 2 и
В = 2 и ![]() .
.
Видно, что и при ![]() коэффициент
отражения меняет свой знак: при нормальном падении А < 0, а при
коэффициент
отражения меняет свой знак: при нормальном падении А < 0, а при ![]() А = 1 > 0, и существует
угол
А = 1 > 0, и существует
угол ![]() , при котором А = 0 и
, при котором А = 0 и ![]() , В = 1 и
, В = 1 и ![]() , - отраженной волны нет,
есть только проходящая вторичная волна с амплитудой, равной амплитуде падающей
волны. Синус этого угла определен ранее, но, так как
, - отраженной волны нет,
есть только проходящая вторичная волна с амплитудой, равной амплитуде падающей
волны. Синус этого угла определен ранее, но, так как ![]() , формулу для
, формулу для ![]() удобнее записать, умножив
числитель и знаменатель подкоренного выражения на - 1:
удобнее записать, умножив
числитель и знаменатель подкоренного выражения на - 1:
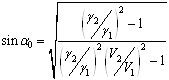 .
.
При дальнейшем увеличении угла падения, когда ![]() , коэффициент отражения А
стремительно возрастает от 0 при
, коэффициент отражения А
стремительно возрастает от 0 при ![]() до 1,
при
до 1,
при![]() одновременно и также
быстро В растет от 1 до 2. Однако, более существенные изменения коэффициентов А
и В и вторичных волн - отраженной и проходящей - происходят, когда угол падения
становится больше критического. Если
одновременно и также
быстро В растет от 1 до 2. Однако, более существенные изменения коэффициентов А
и В и вторичных волн - отраженной и проходящей - происходят, когда угол падения
становится больше критического. Если ![]() (напомним,
(напомним,
![]() ), в соответствии с законом
Снеллиуса:
), в соответствии с законом
Снеллиуса:
![]() и
и ![]()
синус угле прохождения при закритическом падении становится больше единицы (?!). Это не может быть в области действительных тригонометрических функций. Определим косинус угле прохождения по обычной формуле:
![]() , так как
, так как ![]() .
.
Синусу, большему 1, соответствует чисто мнимый косинус.
Встретившись с этой неожиданной трансформацией косинуса, мы,
из осторожности, записали оба возможных знака (±) корня. Установим, какой из
них имеет физический смысл. Для этого вспомним описание проходящей волны (в
волновой аргумент которой и входит ![]() ) и ее
спектра:
) и ее
спектра:

Подставим в последнее определение
![]() :
:

Наличие мнимой единицы в определении косинуса выводит
зависимость от z из функции запаздывания и превращает
ее в амплитудный множитель ![]() . Если
определить
. Если
определить ![]() , то с ростом z (то есть, при удалении от границы и от предполагаемого
источника колебаний) амплитуда гармоники частоты ω неограниченно возрастает:
, то с ростом z (то есть, при удалении от границы и от предполагаемого
источника колебаний) амплитуда гармоники частоты ω неограниченно возрастает:
при z → ∞ ![]() .
.
Физически это абсолютно невозможно, поэтому из двух знаков
мнимого косинуса следует выбрать минус: ![]() .
Тогда амплитуда вторичной волны, определяемая множителем
.
Тогда амплитуда вторичной волны, определяемая множителем ![]() , стремится к нулю при
удалении от границы (z → ∞).
, стремится к нулю при
удалении от границы (z → ∞).
Однако, спектр импульсного сигнала определен на всем
бесконечном интервале частот: - ∞ ≤ ω ≤ ∞ и в
волновом импульсе присутствуют как гармоники с положительными частотами, так и
гармоники с ω < 0. Знак минус в определении ![]() “правильно
действует" только для положительных частот. Для отрицательных частот знак
минус гаснет и амплитуда гармоники частоты ω < 0 неограниченно
возрастает по мере удаления от границы z → ∞. Это - снова нереально.
“правильно
действует" только для положительных частот. Для отрицательных частот знак
минус гаснет и амплитуда гармоники частоты ω < 0 неограниченно
возрастает по мере удаления от границы z → ∞. Это - снова нереально.
Чтобы обеспечить затухание всего спектра волны ![]() как для положительных, так
и для отрицательных частот, определим:
как для положительных, так
и для отрицательных частот, определим:
![]() ,
,
где sgn (ω) - знаковая функция частоты:
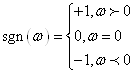 .
.
В таком определении амплитудный множитель ![]() обеспечивает затухание
гармонических составляющих со всеми частотами: если ω > 0, sgn (ω) = + 1 и
обеспечивает затухание
гармонических составляющих со всеми частотами: если ω > 0, sgn (ω) = + 1 и ![]() -
функция, убывающая с ростом z, если же ω < 0, sgn (ω) = - 1 и
-
функция, убывающая с ростом z, если же ω < 0, sgn (ω) = - 1 и ![]() -
так же убывающая по мере удаления от границы функция.
-
так же убывающая по мере удаления от границы функция.
Обратим внимание на то, что с ростом абсолютного значения частоты ω затухание ускоряется - чем выше частота гармоники, тем быстрее она затухает с ростом z.
В функции запаздывания спектра проходящей волны ![]() осталась лишь
пространственная переменная x:
осталась лишь
пространственная переменная x: ![]() . Эта функция соответствует
скольжению плоской волны
. Эта функция соответствует
скольжению плоской волны ![]() вдоль
границы со скоростью
вдоль
границы со скоростью ![]() , меньшей
истинной скорости
, меньшей
истинной скорости ![]() волны в нижней
среде, так как
волны в нижней
среде, так как ![]() . Эта скользящая
с “неправильной" скоростью волна имеет амплитуду, экспоненциально
уменьшающуюся с глубиной, вдоль фронта волны. Эти две особенности закритической
проходящей волны дают основание для ее специального наименования - она
называется неоднородной плоской волной, в соответствии с
характером распределения ее амплитуды по фронту.
. Эта скользящая
с “неправильной" скоростью волна имеет амплитуду, экспоненциально
уменьшающуюся с глубиной, вдоль фронта волны. Эти две особенности закритической
проходящей волны дают основание для ее специального наименования - она
называется неоднородной плоской волной, в соответствии с
характером распределения ее амплитуды по фронту.
Неоднородные плоские волны играют главенствующую роль в
образовании преломленной (головной) волны, которую рассмотрим несколько позже в
отдельном разделе. Здесь подчеркнем одно - все особенности неоднородной волны
выявлены в результате анализа лишь волнового аргумента проходящей волны при
закритическом падении плоской волны на границу раздела. Вид самой волновой
функции ![]() этим анализом не затронут.
Поэтому вернемся к исследованию поведения спектральных коэффициентов
рассеивания и вторичных волн при закритическом падении первичной волны.
этим анализом не затронут.
Поэтому вернемся к исследованию поведения спектральных коэффициентов
рассеивания и вторичных волн при закритическом падении первичной волны.
Итак, установлено, что при
![]()
![]() где
где
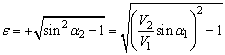 .
.
Коэффициенты рассеивания А и В в этом случае описываются выражениями:
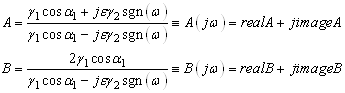
Знаком тождества подчеркнута комплексная зависимость коэффициентов рассеивания от частоты, оправдывающая введенное ранее определение А и В как спектральных коэффициентов рассеивания.
В числителе и знаменателе дроби, определяющей А -
комплексно-сопряженные выражения: ![]() ,
имеющие одинаковый модуль (так как
,
имеющие одинаковый модуль (так как ![]() ) и
противоположные по знаку аргументы. Поэтому модуль спектрального коэффициента
выражения равен 1:
) и
противоположные по знаку аргументы. Поэтому модуль спектрального коэффициента
выражения равен 1:
![]()
и не зависит ни от частоты, ни от угла падения. Фазово-частотный коэффициент отражения как аргумент дроби с комплексно-сопряженными числителем и знаменателем, равен:
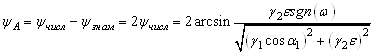 .
.
Действительная realA и мнимая imageA части спектрального коэффициента отражения (СКО) равны:
 ,
,
где
 .
.
Используя формулы косинуса и синуса двойного угла (![]() ), получим выражения для
действительной и мнимой частей СКО в виде:
), получим выражения для
действительной и мнимой частей СКО в виде:
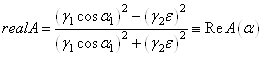 ;
;
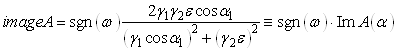 .
.
Действительная часть СКО не зависит от частоты, а
зависимость мнимой части от нее задается множителем в виде знаковой функции
частоты. Обе части СКО являются функциями угла падения. Спектральная характеристика
отражения обладает всеми свойствами устойчивой линейной системы - четными
амплитудно-частотной характеристикой (модулем СКО) и действительной части СКО,
и нечетными фазово-частотной характеристикой (аргументом СКО) и мнимой частью
СКО. При этом, четность обеспечивается отсутствием зависимости ![]() и realA
от частоты, а нечетность
и realA
от частоты, а нечетность ![]() и imageA - множителем в виде знаковой
функции sgn (ω). Таким образом, комплексный
спектральный коэффициент отражения может быть записан в виде:
и imageA - множителем в виде знаковой
функции sgn (ω). Таким образом, комплексный
спектральный коэффициент отражения может быть записан в виде:
![]() .
.
Спектр отраженной волны разделяется на два слагаемых:
![]() .
.
В первом слагаемом присутствует спектр первичной волны с амплитудным множителем (весом) ReA (α), независимым от частоты и меняющимся с увеличением угла падения.
Во втором слагаемом - произведение двух частотно-зависимых
функций - знаковой ![]() и комплексного
спектра первичной волны u (jf) - с амплитудным множителем ImA
(α), также изменяющимся с увеличением угла падения.
и комплексного
спектра первичной волны u (jf) - с амплитудным множителем ImA
(α), также изменяющимся с увеличением угла падения.
Так как преобразование Фурье - линейная операция, сам отраженный сигнал также является взвешенной суммой Фурье-трансформант слагаемых своего спектра:
![]() .
.
Здесь ![]() - результат
обратного Фурье-преобразования знаковой функции частоты sgn
(f), u (t)
- результат
обратного Фурье-преобразования знаковой функции частоты sgn
(f), u (t)
![]() u (jf), а произведение
спектров заменено сверткой Фурье-трансформант сомножителей в соответствии со
спектральной теоремой свертывания функций.
u (jf), а произведение
спектров заменено сверткой Фурье-трансформант сомножителей в соответствии со
спектральной теоремой свертывания функций.
В теории спектров рассматривалась знаковая функция времени sgn (t) и ее спектр:
![]() .
.
Аналогично определяется обратное Фурье-преобразование знаковой функции частоты:
![]() .
.
Здесь появился знак минус как следствие противоположных
знаков ядер прямого (![]() ) и обратного (
) и обратного (![]() ) преобразований Фурье.
) преобразований Фурье.
Тогда отраженный сигнал может быть описан выражением:
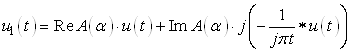 .
.
Сокращая мнимую единицу и раскрывая символьную запись свертки, получим описание отраженного сигнала при углах падения, превышающих критический угол:
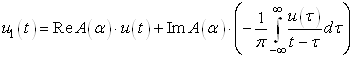 .
.
В скобках записано обратное Гильберт-преобразование функции u (t), описывающей первичную волну:
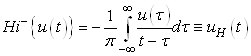 .
.
Таким образом, отраженный сигнал за критическим углом
падения представляется взвешенной суммой падающего сигнала u
(t) и его Гильберт-трансформанты ![]() :
:
![]() .
.
Веса слагаемых - ReA (α) и ImA
(α) - изменяются при увеличении угла падения. Соответственно, изменяется
по форме и суммарный отраженный сигнал ![]() .
.
Проведем анализ зависимости от угла падения α весовых
множителей ReA (α) и ImA (α) и структуры суммарной отраженной волны при
изменении α от критического угла ![]() до
теоретически возможного предела 90°. Как отмечалось, при α =
до
теоретически возможного предела 90°. Как отмечалось, при α = ![]() А (
А (![]() ) = 1 = ReA
(
) = 1 = ReA
(![]() ), ImA
(
), ImA
(![]() ) = 0. Отраженная волна
имеет те ж форму и амплитуду, что и падающая волна:
) = 0. Отраженная волна
имеет те ж форму и амплитуду, что и падающая волна: ![]() =
=
![]() .
.
Как только угол падения превысит критический угол, ReA (α) стремительно уменьшается, а мнимая часть ImA (α) столь же быстро возрастает. Доля первичного
сигнала в суммарной отраженной волне быстро уменьшается, и так же быстро растет
доля Гильберт-трансформанты падающей волны. При некотором угле падения ![]() действительная часть
спадает до 0, а мнимая - возрастает до 1:
действительная часть
спадает до 0, а мнимая - возрастает до 1:
при α = ![]() ReA (
ReA (![]() ) = 0; ImA (
) = 0; ImA (![]() ) = 1.
) = 1.
Отраженный сигнал представлен только Гильберт-трансформантой
первичной волны: ![]() . Угол
. Угол ![]() находится из условия ReA (
находится из условия ReA (![]() ) = 0:
) = 0:
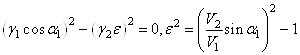 .
.
Синус его равен:
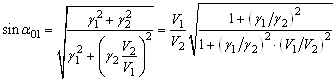
и не намного превышает ![]() ,
то есть
,
то есть ![]() не намного больше
не намного больше ![]() .
.
Дальнейшее увеличение угла падения (α > ![]() ) приводит к перемене знака
действительной части и к соответствующему инвертированию знака смещения
первичной волны в суммарном отраженном сигнале.
) приводит к перемене знака
действительной части и к соответствующему инвертированию знака смещения
первичной волны в суммарном отраженном сигнале.
В пределе, при ![]() : ReA
: ReA![]() ; ImA
; ImA ![]() и
и
![]() .
.
С увеличением угла падения при ![]() доля
падающей волны с инвертированным знаком смещения в суммарной волне растет, а
доля Гильберт-трансформанты уменьшается в пределе, при α = 90°, до 0.
доля
падающей волны с инвертированным знаком смещения в суммарной волне растет, а
доля Гильберт-трансформанты уменьшается в пределе, при α = 90°, до 0.
При этом отраженный сигнал повторяет по форме и амплитуде
колебаний падающую волну с инвертированным знаком смещений. Напомним, что такой
же предел был выявлен и в случае ![]() (см. раздел
8.3), что вполне естественно.
(см. раздел
8.3), что вполне естественно.
Анализ закритических изменений спектрального коэффициента
прохождения В и вызванных ими трансформаций неоднородных плоских волн ![]() фактически не нужен, так
как имеется связь между коэффициентами рассеивания SH-волны:
В = 1 + А, справедливая при любых углах падения.
фактически не нужен, так
как имеется связь между коэффициентами рассеивания SH-волны:
В = 1 + А, справедливая при любых углах падения.
Для комплексных коэффициентов рассеивания А = ReA + jImA; B = ReB + jImB имеем:
ReB + jImB = 1 + ReA + jImA.
Видно, что А и В имеют действительные части, различающиеся на единицу, и равные мнимые части:
ReB = 1 + ReA; ImB = ImA.
Напомним, что связь между А и В получена из первого граничного условия (для упругих смещений):
![]() .
.
В соответствии с ним, при любых соотношениях физических
свойств контактирующих на границе сред и при любом угле падения первичной SH-волны при z = 0 проходящая волна ![]() представляет собой простую
сумму падающей волны u (τ) и отраженной волны
представляет собой простую
сумму падающей волны u (τ) и отраженной волны ![]() .
.
Поэтому все трансформации отраженной волны в закритической зоне входят составной частью в изменения проходящей волны.
Вне зависимости от угла падения в этой волне всегда присутствует “постоянная" составляющая - первичная, падающая на границу волна, по предположению, не меняющаяся с изменением угла падения.
В заключение приведем цифровые оценки особых углов падения ![]() для границы раздела сред
со следующими упругими параметрами:
для границы раздела сред
со следующими упругими параметрами:
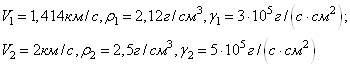 .
.
Это - довольно “сильная” отражающая граница.
Ей может соответствовать, например, граница между обводненной верхней средой (где скорость S-волны резко уменьшена) и “сухим” нижним полупространством.
При нормальном падении (α = 0) SH-волны коэффициенты рассеивания равны:
![]() .
.
Отраженная волна имеет амплитуду, в четыре раза меньшую
амплитуды первичной волны, и инвертирована по знаку смещения. Проходящая волна
ослаблена по амплитуде на четверть в сравнении с падающей волной. Для выбранных
параметров сред определим отношения волновых сопротивлений ![]() ≈1,667 и скоростей
≈1,667 и скоростей ![]() ≈1,414 (
≈1,414 (![]() ≈0,707). Используя
их, найдем особые углы падения первичной волны:
≈0,707). Используя
их, найдем особые углы падения первичной волны:
угол ![]() , при
котором А = 0, В = 1 и
, при
котором А = 0, В = 1 и ![]() = 0,
= 0, ![]()
![]() = arcsin
= arcsin ![]() ≈38°,7;
≈38°,7;
критический угол ![]() , при
котором А = 1, В = 2 и
, при
котором А = 1, В = 2 и
![]()
![]() :
:
![]() .
.
угол ![]() , при
котором ReA = 0, ImA = ImB = ReB = 1 и
, при
котором ReA = 0, ImA = ImB = ReB = 1 и
![]() ,
, ![]() :
:
![]() ≈49°,4.
≈49°,4.
Как видно из этих оценок, зона наибыстрейшего и наибольшего
изменения спектральных коэффициентов рассеивания (СКР) и вторичных волн весьма
узка: ![]() ≈10,7. В интервале
≈10,7. В интервале ![]() коэффициенты А и В
возрастают на единицу: А от 0 до 1, В от 1 до 2. Затем, как только угол падения
превысит критический, коэффициенты становятся комплексными. В интервале
коэффициенты А и В
возрастают на единицу: А от 0 до 1, В от 1 до 2. Затем, как только угол падения
превысит критический, коэффициенты становятся комплексными. В интервале ![]() действительная часть А
спадает от 1 до 0 (ReB от 2 до
1), а мнимая часть А и В возрастает от 0 до 1.
действительная часть А
спадает от 1 до 0 (ReB от 2 до
1), а мнимая часть А и В возрастает от 0 до 1.
Вне зоны (![]() ) коэффициенты
рассеивания ведут себя более спокойно. При изменении
) коэффициенты
рассеивания ведут себя более спокойно. При изменении ![]() от 0 до
от 0 до ![]() отрицательный коэффициент
отражения уменьшается (по модулю) от - 0,25 до 0. В ближней к источнику зоне,
при
отрицательный коэффициент
отражения уменьшается (по модулю) от - 0,25 до 0. В ближней к источнику зоне,
при ![]() , СКР изменяются незначительно.
Соответственно, и вторичные волны в этой зоне изменяются мало.
, СКР изменяются незначительно.
Соответственно, и вторичные волны в этой зоне изменяются мало.
С увеличением различия свойств контактирующих на границе
сред все особые точки (![]() ) смещаются в сторону
меньших углов падения, а интервалы между ними уменьшаются. Наоборот, для границ
раздела сред с близкими упругими константами критический угол большой и углы
) смещаются в сторону
меньших углов падения, а интервалы между ними уменьшаются. Наоборот, для границ
раздела сред с близкими упругими константами критический угол большой и углы ![]() отдалены от него.
отдалены от него.
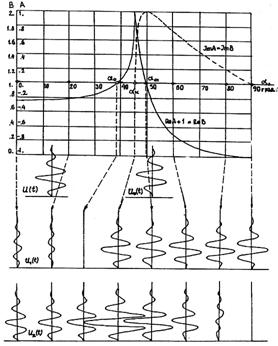
Рис.10
Описание изменений СКР SH-волны
иллюстрирует (рис.10), на котором построены графики ![]() и
импульсоиды первичной волны и ее Гильберт-трансформанты, а также импульсоиды
суммарных вторичных волн
и
импульсоиды первичной волны и ее Гильберт-трансформанты, а также импульсоиды
суммарных вторичных волн ![]() для
различных углов падения. Так как ReB = ReA + 1, график
для
различных углов падения. Так как ReB = ReA + 1, график ![]() снабжен
второй осью ординат для
снабжен
второй осью ординат для ![]() со
смещенной на 1 шкалой. График
со
смещенной на 1 шкалой. График ![]() одновременно
является и графиком
одновременно
является и графиком ![]() .
.
Импульсоиды вторичных волн соответствуют углам падения, отмеченным на шкале оси абсцисс стрелками.
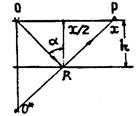
В заключение анализа отметим, что угол падения α
определяет удаление х точки приема Р от точки возбуждения 0 (рис.11). Тангенс
этого угла равен отношению половины удаления х/2 к эхо-глубине границы h: ![]() . Поэтому малые
углы падения соответствуют ближней к источнику зоне, а большие - дальней.
. Поэтому малые
углы падения соответствуют ближней к источнику зоне, а большие - дальней.
![]()
Рис.11
Приведем оценки x/h, соответствующие особым углам для выбранных ранее параметров сред:
при ![]() ≈38°,7
≈38°,7 ![]() ≈1,6;
≈1,6;
при ![]()
![]() ;
;
при ![]() ≈49,4
≈49,4 ![]() ≈2,33.
≈2,33.
Добавим еще оценку границы ближней зоны:
при ![]() ≈12,8
≈12,8 ![]() ≈0,46.
≈0,46.
Таким образом, область наибольшей стабильности отраженной волны не превышает половины эхо-глубины границы. Наибольшие изменения этой волны начинаются на удалениях, в полтора раза превышающих глубину. В промежуточной зоне с ростом х изменения отраженной волны становятся все более существенными и заметными.
II. Расчётная часть
1. Падение SH-волны на кровлю низкоскоростной среды
Зададим три случая параметров среды - укажем их в таблице:
| Среда 1 | Среда 2 | Среда 3 | |||
|
V1, км/с |
1,3 |
V1, км/с |
2,0 |
V1, км/с |
2,5 |
|
ρ1, г/см3 |
2,2 |
ρ1, г/см3 |
3,0 |
ρ1, г/см3 |
3,5 |
|
V2, км/с |
1,2 |
V2, км/с |
1,2 |
V2, км/с |
1,2 |
|
ρ2, г/см3 |
2,1 |
ρ2, г/см3 |
2,1 |
ρ2, г/см3 |
2,1 |
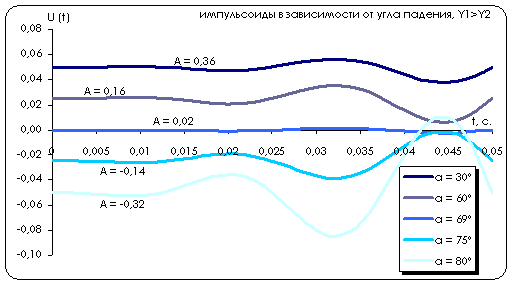
Получим график спектрального коэффициента отражения A в зависимости от угла падения α1. В первом случае критический угол составляет α0 = 55˚, во втором - близок к α0 = 70˚, третий случай - α0 = 75˚.

Анализируя полученные графики, видим, что по мере увеличения различий физических свойств между средами критический угол α0 увеличивается, стремясь к 45˚ для практически однородных сред.
Покажем изменение амплитуды отражённого сигнала, в
зависимости от спектрального коэффициента отражения для Среды 2. В качестве
исходного сигнала возьмём импульс Берлаге, вычисляемый по формуле ![]() . Возьмём случай f0 = 40Гц:
. Возьмём случай f0 = 40Гц:
2. Падение SH-волны на кровлю высокоскоростной среды
Зададим три случая параметров среды - укажем их в таблице:
| Среда 1 | Среда 2 | Среда 3 | |||
|
V1, км/с |
1,2 |
V1, км/с |
1,2 |
V1, км/с |
1,2 |
|
ρ1, г/см3 |
2,1 |
ρ1, г/см3 |
2,1 |
ρ1, г/см3 |
2,1 |
|
V2, км/с |
1,3 |
V2, км/с |
2,0 |
V2, км/с |
2,5 |
|
ρ2, г/см3 |
2,2 |
ρ2, г/см3 |
3,0 |
ρ2, г/см3 |
3,5 |
Получим график спектрального коэффициента отражения A в зависимости от угла падения α1. В первом случае критический угол составляет α0 = 68˚, во втором - близок к α0 = 38˚, третий случай - α0 = 28˚.
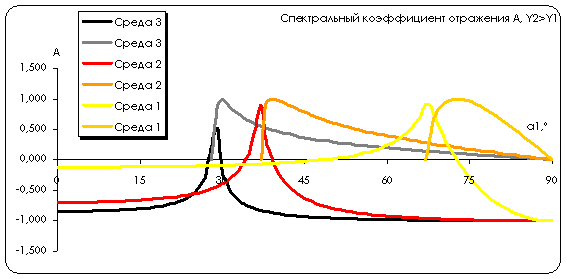
Анализируя полученные графики, видим, что по мере увеличения различий физических свойств между средами критический угол α0 уменьшается.
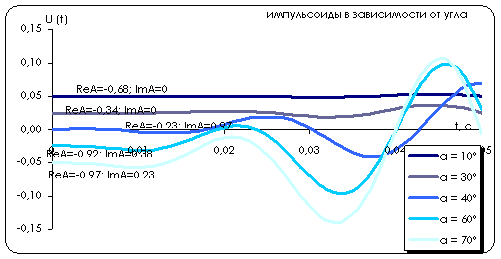
Покажем изменение амплитуды отражённого сигнала, в
зависимости от спектрального коэффициента отражения для Среды 2. В качестве
исходного сигнала возьмём импульс Берлаге, вычисляемого по формуле ![]() . Возьмём случай f0 = 40Гц:
. Возьмём случай f0 = 40Гц:
Список литературы
1. Бондарев В.И., 2000, Основы сейсморазведки. Екатеринбург: Изд-во УГГГА.
2. Сейсморазведка: Справочник геофизика, 1990 / Под ред. В.П. Номоконова. М.: Недра.
3. Гурвич И.И., Боганик Г.Н., 1980, Сейсморазведка. М.: Недра.
| Устройства генерирования и канализации субмиллиметровых волн | |
|
Устройства генерирования и канализации субмиллиметровых волн СОДЕРЖАНИЕ Введение 1. Ламповые и полупроводниковые генераторные приборы ... Под воздействием различных факторов спектральная линия современных генераторов субмиллиметровых волн уширяется, однако ширина этой спектральной линии значительно уже, чем спектр ... Если электромагнитная волна падает под углом 45° на проволочную решетку или диэлектрическую пластину, то ее энергия делится на две части: одна часть проходит прямо, а другая ... |
Раздел: Рефераты по коммуникации и связи Тип: дипломная работа |
| Спиральные антенны | |
|
Введение Современное состояние техники связи радиодиапазона нельзя представить без спиральных антенн. Этот тип антенных систем используется благодаря ... Следовательно, изменение длины волны вызывает только смещение активной области спирали на некоторый угол , а отношение и направленное действие антенны от этого не меняются. Так как на большей части провода спирали амплитуда падающей волны значительно превосходит амплитуду волны отраженной, то в результате интерференции распределение амплитуды тока ... |
Раздел: Рефераты по коммуникации и связи Тип: дипломная работа |
| Методы химического анализа | |
|
Введение в учебную дисциплину Рыночная экономика не может обходиться без широкого использования современных методик по оценке производственной и ... Линейчатый спектр каждого элемента содержит ряд спектральных линий, соответствующих испускаемым лучам, характеризующихся определенной длиной волны ѭ или частотой колебания ѭ. При переходе луча из среды менее оптически плотной в среду более оптически плотную угол падения луча (ѭ) больше угла преломления (ѭ), таким же образом изменяется и скорость ... |
Раздел: Промышленность, производство Тип: учебное пособие |
| Лекции по физике | |
|
Лекция 10 8.5. Линии равной толщины Как ясно уже из заголовка, речь пойдет о пластинах (тонких пленках), толщина которых непостоянна. И, по существу ... Очевидно, что дифракционная решетка может быть использована для разворачивания падающего на нее света в спектр, когда угловое положение максимума зависит от длины волны l. При q=0 ... Длина вектора, проведенного от начала к центру спирали, дает, очевидно, амплитуду падающей волны - скручивание спирали к центру соответствует бесконечно большому радиуса отверстия ... |
Раздел: Рефераты по физике Тип: реферат |
| Организация учебного процесса при изучении темы "Световые волны ... | |
|
Содержание Введение Глава 1. Анализ психолого-педагогической и методической литературы по теме исследования 1.1 Состояние учебного процесса по физике ... При падении луча на границу раздела двух сред угол отражения равен углу падения; падающий и отраженный лучи и перпендикуляр, восстановленный к поверхности в точке падения, лежат в ... Измерение углов падения - ѭ и преломления - ѭ покажет, что отношение их синусов при различных углах падения остается неизменным и равно n2,1. |
Раздел: Рефераты по педагогике Тип: дипломная работа |