Курсовая работа: Interpolation, approximation and differential equations solvers
Problem 1
1.1 Problem definition
1.2 Solution of the problem
1.2.1 Linear interpolation
1.2.2 Method of least squares interpolation
1.2.3 Lagrange interpolating polynomial
1.2.4 Cubic spline interpolation
1.3 Results and discussion
1.3.1 Lagrange polynomial
Problem 2
2.1 Problem definition
2.2 Problem solution
2.2.1 Rectangular method
2.2.2 Trapezoidal rule
2.2.3 Simpson's rule
2.2.4 Gauss-Legendre method and Gauss-Chebyshev method
Problem 3
3.1 Problem definition
3.2 Problem solution
Problem 4
4.1 Problem definition
4.2 Problem solution
References
Problem 1
1.1 Problem definition
For the
following data set, please discuss the possibility of obtaining a reasonable
interpolated value at ![]() ,
, ![]() , and
, and ![]() via at least 4 different
interpolation formulas you are have learned in this semester.
via at least 4 different
interpolation formulas you are have learned in this semester.
![]()
![]()
1.2 Solution of the problem
Interpolation is a method of constructing new data points within the range of a discrete set of known data points.
In engineering and science one often has a number of data points, as obtained by sampling or experimentation, and tries to construct a function which closely fits those data points. This is called curve fitting or regression analysis. Interpolation is a specific case of curve fitting, in which the function must go exactly through the data points.
First we have to plot data points, such plot provides better picture for analysis than data arrays
Following four interpolation methods will be discussed in order to solve the problem:
· Linear interpolation
· Method of least squares interpolation
· Lagrange interpolating polynomial
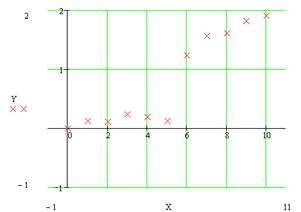
Fig 1. Initial data points
· Cubic spline interpolation
1.2.1 Linear interpolation
One of the
simplest methods is linear interpolation (sometimes known as lerp). Generally,
linear interpolation tales two data points, say ![]() and
and
![]() , and the interpolant is
given by:
, and the interpolant is
given by:
![]() at the point
at the point ![]()
Linear
interpolation is quick and easy, but it is not very precise/ Another
disadvantage is that the interpolant is not differentiable at the point ![]() .
.
1.2.2 Method of least squares interpolation
The method of least squares is an alternative to interpolation for fitting a function to a set of points. Unlike interpolation, it does not require the fitted function to intersect each point. The method of least squares is probably best known for its use in statistical regression, but it is used in many contexts unrelated to statistics.

Fig 2. Plot of the data with linear interpolation superimposed
Generally, if
we have ![]() data points, there is
exactly one polynomial of degree at most
data points, there is
exactly one polynomial of degree at most ![]() going
through all the data points. The interpolation error is proportional to the
distance between the data points to the power n. Furthermore, the interpolant
is a polynomial and thus infinitely differentiable. So, we see that polynomial
interpolation solves all the problems of linear interpolation.
going
through all the data points. The interpolation error is proportional to the
distance between the data points to the power n. Furthermore, the interpolant
is a polynomial and thus infinitely differentiable. So, we see that polynomial
interpolation solves all the problems of linear interpolation.
However, polynomial interpolation also has some disadvantages. Calculating the interpolating polynomial is computationaly expensive compared to linear interpolation. Furthermore, polynomial interpolation may not be so exact after all, especially at the end points. These disadvantages can be avoided by using spline interpolation.
Example of construction of polynomial by least square method
Data is given by the table:
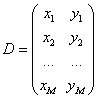
Polynomial is given by the model:
![]()
In order to
find the optimal parameters ![]() the
following substitution is being executed:
the
following substitution is being executed:
![]() ,
, ![]() , …,
, …, ![]()
Then: 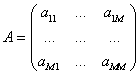
The error function:
![]()
It is
necessary to find parameters ![]() , which
provide minimums to function
, which
provide minimums to function ![]() :
:
![]()
![]()
![]()
![]()
It should be
noted that the matrix ![]() must be
nonsingular matrix.
must be
nonsingular matrix.
For the given
data points matrix ![]() become singular,
and it makes impossible to construct polynomial with
become singular,
and it makes impossible to construct polynomial with ![]() order, where
order, where ![]() - number of data points,
so we will use
- number of data points,
so we will use ![]() polynomial
polynomial
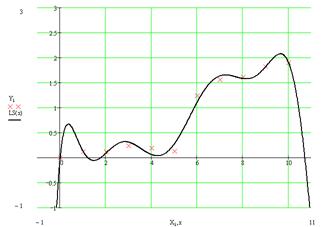
Fig 3. Plot of the data with polynomial interpolation superimposed
Because the polynomial is forced to intercept every point, it weaves up and down.
1.2.3 Lagrange interpolating polynomial
The Lagrange
interpolating polynomial is the polynomial ![]() of
degree
of
degree ![]() that passes through the
that passes through the ![]() points
points ![]() ,
, ![]() , …,
, …, ![]() and is given by:
and is given by:
![]() ,
,
Where

Written explicitly

When constructing interpolating polynomials, there is a tradeoff between having a better fit and having a smooth well-behaved fitting function. The more data points that are used in the interpolation, the higher the degree of the resulting polynomial, and therefore the greater oscillation it will exhibit between the data points. Therefore, a high-degree interpolation may be a poor predictor of the function between points, although the accuracy at the data points will be "perfect."
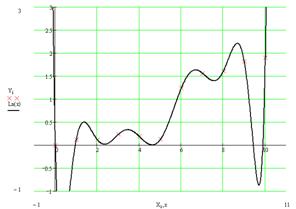
Fig 4. Plot of the data with Lagrange interpolating polynomial interpolation superimposed
One can see, that Lagrange polynomial has a lot of oscillations due to the high order if polynomial.
1.2.4 Cubic spline interpolation
Remember that
linear interpolation uses a linear function for each of intervals ![]() . Spline interpolation uses
low-degree polynomials in each of the intervals, and chooses the polynomial
pieces such that they fit smoothly together. The resulting function is called a
spline. For instance, the natural cubic spline is piecewise cubic and twice
continuously differentiable. Furthermore, its second derivative is zero at the
end points.
. Spline interpolation uses
low-degree polynomials in each of the intervals, and chooses the polynomial
pieces such that they fit smoothly together. The resulting function is called a
spline. For instance, the natural cubic spline is piecewise cubic and twice
continuously differentiable. Furthermore, its second derivative is zero at the
end points.
Like polynomial interpolation, spline interpolation incurs a smaller error than linear interpolation and the interpolant is smoother. However, the interpolant is easier to evaluate than the high-degree polynomials used in polynomial interpolation. It also does not suffer from Runge's phenomenon.

Fig 5. Plot of the data with Lagrange interpolating polynomial interpolation superimposed
It should be noted that cubic spline curve looks like metal ruler fixed in the nodal points, one can see that such interpolation method could not be used for modeling sudden data points jumps.
1.3 Results and discussion
The following
results were obtained by employing described interpolation methods for the
points ![]() ;
; ![]() ;
; ![]() :
:
| Linear interpolation | Least squares interpolation |
Lagrange polynomial |
Cubic spline | Root mean square | |
|
|
0.148 | 0.209 | 0.015 | 0.14 | 0.146 |
|
|
0.678 | 0.664 | 0.612 | 0.641 | 0.649 |
|
|
1.569 | 1.649 | 1.479 | 1.562 | 1.566 |
Table 1. Results of interpolation by different methods in the given points.
In order to determine the best interpolation method for the current case should be constructed the table of deviation between interpolation results and root mean square, if number of interpolations methods increases then value of RMS become closer to the true value.
| Linear interpolation | Least squares interpolation | Lagrange polynomial | Cubic spline | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Average deviation from the RMS |
|
|
|
|
Table 2. Table of Average deviation between average deviation and interpolation results.
One can see that cubic spline interpolation gives the best results among discussed methods, but it should be noted that sometimes cubic spline gives wrong interpolation, especially near the sudden function change. Also good interpolation results are provided by Linear interpolation method, but actually this method gives average values on each segment between values on it boundaries.
Problem 2
2.1 Problem definition
For the above
mentioned data set, if you are asked to give the integration of ![]() between two ends
between two ends ![]() and
and ![]() ? Please discuss the
possibility accuracies of all the numerical integration formulas you have
learned in this semester.
? Please discuss the
possibility accuracies of all the numerical integration formulas you have
learned in this semester.
2.2 Problem solution
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral.
There are
several reasons for carrying out numerical integration. The integrand ![]() may be known only at
certain points, such as obtained by sampling. Some embedded systems and other
computer applications may need numerical integration for this reason.
may be known only at
certain points, such as obtained by sampling. Some embedded systems and other
computer applications may need numerical integration for this reason.
A formula for
the integrand may be known, but it may be difficult or impossible to find an
antiderivative which is an elementary function. An example of such an integrand
is ![]() , the antiderivative of
which cannot be written in elementary form.
, the antiderivative of
which cannot be written in elementary form.
It may be possible to find an antiderivative symbolically, but it may be easier to compute a numerical approximation than to compute the antiderivative. That may be the case if the antiderivative is given as an infinite series or product, or if its evaluation requires a special function which is not available.
The following methods were described in this semester:
· Rectangular method
· Trapezoidal rule
· Simpson's rule
· Gauss-Legendre method
· Gauss-Chebyshev method
2.2.1 Rectangular method
The most
straightforward way to approximate the area under a curve is to divide up the
interval along the x-axis between ![]() and
and ![]() into a number of smaller
intervals, each of the same length. For example, if we divide the interval into
into a number of smaller
intervals, each of the same length. For example, if we divide the interval into
![]() subintervals, then the
width of each one will be given by:
subintervals, then the
width of each one will be given by:
![]()
The approximate area under the curve is then simply the sum of the areas of all the rectangles formed by our subintervals:
![]()
The summary
approximation error for ![]() intervals
with width
intervals
with width ![]() is less than or equal to
is less than or equal to
![]()
Thus it is impossible to calculate maximum of the derivative function, we can estimate integration error like value:
![]()
2.2.2 Trapezoidal rule
Trapezoidal
rule is a way to approximately calculate the definite integral. The trapezium
rule works by approximating the region under the graph of the function ![]() by a trapezium and calculating
its area. It follows that
by a trapezium and calculating
its area. It follows that
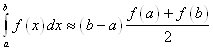
To calculate
this integral more accurately, one first splits the interval of integration ![]() into n smaller
subintervals, and then applies the trapezium rule on each of them. One obtains
the composite trapezium rule:
into n smaller
subintervals, and then applies the trapezium rule on each of them. One obtains
the composite trapezium rule:
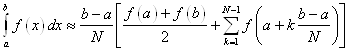
The summary
approximation error for ![]() intervals
with width
intervals
with width ![]() is less than or equal to:
is less than or equal to:
![]()
2.2.3 Simpson's rule
Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:
![]()
If the
interval of integration ![]() is in
some sense "small", then Simpson's rule will provide an adequate
approximation to the exact integral. By small, what we really mean is that the
function being integrated is relatively smooth over the interval
is in
some sense "small", then Simpson's rule will provide an adequate
approximation to the exact integral. By small, what we really mean is that the
function being integrated is relatively smooth over the interval ![]() . For such a function, a
smooth quadratic interpolant like the one used in Simpson's rule will give good
results.
. For such a function, a
smooth quadratic interpolant like the one used in Simpson's rule will give good
results.
However, it is
often the case that the function we are trying to integrate is not smooth over
the interval. Typically, this means that either the function is highly
oscillatory, or it lacks derivatives at certain points. In these cases,
Simpson's rule may give very poor results. One common way of handling this
problem is by breaking up the interval ![]() into
a number of small subintervals. Simpson's rule is then applied to each
subinterval, with the results being summed to produce an approximation for the
integral over the entire interval. This sort of approach is termed the
composite Simpson's rule.
into
a number of small subintervals. Simpson's rule is then applied to each
subinterval, with the results being summed to produce an approximation for the
integral over the entire interval. This sort of approach is termed the
composite Simpson's rule.
Suppose that
the interval ![]() is split up in
is split up in ![]() subintervals, with n an
even number. Then, the composite Simpson's rule is given by
subintervals, with n an
even number. Then, the composite Simpson's rule is given by

The error committed by the composite Simpson's rule is bounded (in absolute value) by
![]()
2.2.4 Gauss-Legendre method and Gauss-Chebyshev method
Since function values are given in fixed points then just two points
Gauss-Legendre method can be applied. If ![]() is
continuous on
is
continuous on ![]() , then
, then
![]()
The Gauss-Legendre rule ![]() G2( f ) has degree of precision
G2( f ) has degree of precision ![]() . If
. If ![]() , then
, then
![]() ,
,
where
![]()
It should be
noted that even in case of two points method we have to calculate values of the
function in related to ![]() ,
, ![]() , this values could be
evaluated by linear interpolation (because it is necessary to avoid
oscillations), so estimation of integration error become very complicated
process, but this error will be less or equal to trapezoidal rule.
, this values could be
evaluated by linear interpolation (because it is necessary to avoid
oscillations), so estimation of integration error become very complicated
process, but this error will be less or equal to trapezoidal rule.
Mechanism of Gauss-Chebyshev method is almost the same like described above, and integration error will be almost the same, so there is no reason to use such methods for the current problem.
Problem 3
3.1 Problem definition
It is well known that the third order Runge-Kutta method is of the following form
![]() ,
, ![]()
![]()
![]()
Suppose that you are asked to derived a new third order Runge-Kutta method in the following from
![]() ,
, ![]()
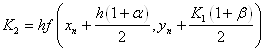
![]()
Find determine
the unknowns ![]() ,
, ![]() ,
, ![]() and
and ![]() so that your scheme is a
third order Runge-Kutta method.
so that your scheme is a
third order Runge-Kutta method.
3.2 Problem solution
Generally Runge-Kutta method looks like:
![]() ,
,
where
coefficients ![]() could be calculated by the
scheme:
could be calculated by the
scheme:
![]()
![]()
![]()
The error function:
![]()
Coefficients ![]() ,
, ![]() ,
, ![]() must be found to satisfy
conditions
must be found to satisfy
conditions ![]() , consequently we can
suppose that for each order of Runge-Kutta scheme those coefficients are
determined uniquely, it means that there are no two different third order
schemes with different coefficients. Now it is necessary to prove statement.
, consequently we can
suppose that for each order of Runge-Kutta scheme those coefficients are
determined uniquely, it means that there are no two different third order
schemes with different coefficients. Now it is necessary to prove statement.
For ![]() ,
, ![]() :
:

![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]()
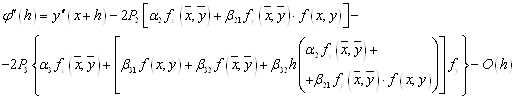
![]()
![]()
![]()
![]() ;
; ![]()

![]() ;
; ![]() ;
; ![]()
Thus we have system of equations:
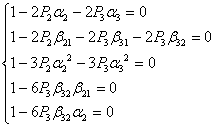
Some of coefficients are already predefined:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
![]()
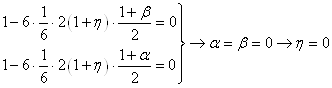
![]()
Obtained results show that Runge-Kutta scheme for every order is unique.
Problem 4
Discuss the
stability problem of solving the ordinary equation ![]() ,
,
![]() via the Euler explicit
scheme
via the Euler explicit
scheme ![]() , say
, say ![]() . If
. If ![]() , how to apply your
stability restriction?
, how to apply your
stability restriction?
4.2 Problem solution
The Euler method is 1st order accurate. Given scheme could be rewritten in form of:
![]()
If ![]() has a magnitude greater
than one then
has a magnitude greater
than one then ![]() will tend to
grow with increasing
will tend to
grow with increasing ![]() and may eventually
dominate over the required solution. Hence the Euler method is stable only if
and may eventually
dominate over the required solution. Hence the Euler method is stable only if ![]() or:
or:
![]()
For the case ![]() mentioned above inequality
looks like:
mentioned above inequality
looks like:
![]()
Last result
shows that integration step mast be less or equal to ![]() .
.
For the case ![]() , for the iteration method
coefficient looks like
, for the iteration method
coefficient looks like
![]()
![]()
As step ![]() is positive value of the
function
is positive value of the
function ![]() must be less then
must be less then ![]() . There are two ways to
define the best value of step
. There are two ways to
define the best value of step ![]() , the
firs one is to define maximum value of function
, the
firs one is to define maximum value of function ![]() on
the integration area, another way is to use different
on
the integration area, another way is to use different ![]() for each value
for each value ![]() , where
, where ![]() . So integration step is
strongly depends on value of
. So integration step is
strongly depends on value of ![]() .
.
References
1. J. C. Butcher, Numerical methods for ordinary differential equations, ISBN 0471967580
2. George E. Forsythe, Michael A. Malcolm, and Cleve B. Moler. Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977. (See Chapter 6.)
3. Ernst Hairer, Syvert Paul Nørsett, and Gerhard Wanner. Solving ordinary differential equations I: Nonstiff problems, second edition. Berlin: Springer Verlag, 1993. ISBN 3-540-56670-8.
4. William H. Press, Brian P. Flannery, Saul A. Teukolsky, William T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1988. (See Sections 16.1 and 16.2.)
5. Kendall E. Atkinson. An Introduction to Numerical Analysis. John Wiley & Sons - 1989
6. F. Cellier, E. Kofman. Continuous System Simulation. Springer Verlag, 2006. ISBN 0-387-26102-8.
7. Gaussian Quadrature Rule of Integration - Notes, PPT, Matlab, Mathematica, Maple, Mathcad at Holistic Numerical Methods Institute
8. Burden, Richard L.; J. Douglas Faires (2000). Numerical Analysis (7th Ed. ed.). Brooks/Cole. ISBN 0-534-38216-9.