Курсовая работа: Выбор схемы балочной клетки
Выбор схемы балочной клетки
Конструкция, состоящая из системы пересекающихся балок, называется балочной клеткой. На балочную клетку укладывают настил в виде металлического листа, железобетонных плит и др. балочная клетка состоит из главных балок, перекрывающих большой пролет, и вспомогательных балок. Главные балки опираются на опоры, а вспомогательные – на главные.
Выбираем тип балочной клетки с поэтажным расположением вспомогательных балок.
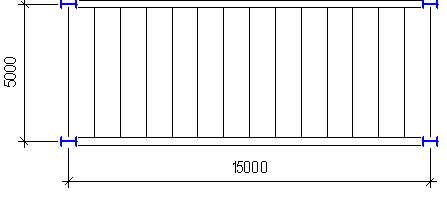
Расчет несущего настила, балок настила и подбор сечения балок настила
Плоский настил из металлического листа располагают на полках балок и обычно приваривают его к ним. Толщина настила назначается чаще всего в зависимости от допустимого прогиба:
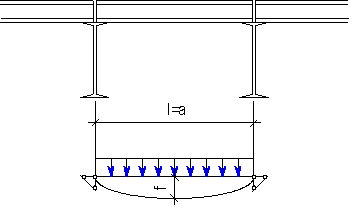
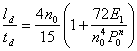 ,
,
где ![]() - относительный прогиб
настила;
- относительный прогиб
настила;
![]() - нормативная полезная равномерно
распределенная нагрузка;
- нормативная полезная равномерно
распределенная нагрузка;
![]() - цилиндрическая жесткость
пластинки, определяют по формуле:
- цилиндрическая жесткость
пластинки, определяют по формуле:
![]() ,
,
где ![]() – коэффициент Пуассона;
– коэффициент Пуассона;
![]() - модуль упругости при цилиндрическом
изгибе пластинки, когда невозможна поперечная деформация.
- модуль упругости при цилиндрическом
изгибе пластинки, когда невозможна поперечная деформация.
![]()
Расчет по жесткости проводим от действия нормативных нагрузок, расчет по прочности на действие расчетных нагрузок.
Задаемся шагом балок настила: 1м и 1,25м.
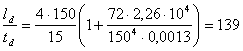
![]()
Принимаем td = 8 мм.
Определяем расход стали от настила 1 м2, толщиной 8 мм – весит 66,6 кг.
Расчет балок настила
Пролет балки настила l = 5 м; нормативная нагрузка![]() ; материал балки - сталь
С235 (ГОСТ 27772-88) с расчетным сопротивлением по пределу текучести
; материал балки - сталь
С235 (ГОСТ 27772-88) с расчетным сопротивлением по пределу текучести ![]() (для толщины листа t = 4…20 мм).
(для толщины листа t = 4…20 мм).
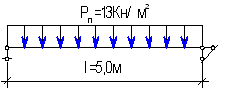
Нормативную погонную нагрузку на балку настила определяем по формуле:
![]() ,
,
где ![]() - вес настила;
- вес настила;
![]() - шаг балок настила.
- шаг балок настила.
![]()
Расчетная нагрузка на балку:
![]() ,
,
где γfр = 1,2; γgf = 1,05– коэффициенты надежности по нагрузке.
![]()
Расчетный изгибающий момент определяется по формуле:
![]()
Из условия прочности для пластической стадии деформаций
![]()
выражаем требуемый момент сопротивления балки Wтр:
![]() ,
,
где γс = 1 – коэффициент условий работы[1];
С1 = 1,12.
![]()
Принимаем двутавр №22: Wx=232см3 ; Jx=2550 см4 ; Вес = 24 кг/м
Проверяем прогиб настила по формуле:
![]() ,
,
где Jx = 2550 см4 – момент инерции сечения.
Предельный прогиб установленный для балок настила:
![]()
![]() -
-
удовлетворяет требованиям СНиП, следовательно жесткость настила обеспечена.
Определяем расход стали для первого варианта:
![]()
Определяем толщину настила при шаге балок настила l = 125 см.
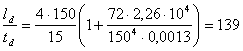
![]()
Принимаем td = 10 мм.
Определяем расход стали от настила 1 м2, толщиной 10 мм – весит 83 кг.
Нормативная погонная нагрузка на балку настила:
![]() ,
,
где ![]() - вес настила;
- вес настила;
Расчетная нагрузка на балку:
![]()
Расчетный изгибающий момент:
![]()
Требуемый момент сопротивления балки Wтр:
![]()
Принимаем двутавр №24: Wx= 289см3 ; Jx=3460 см4 ; Вес = 27,3 кг/м
Проверяем прогиб настила:
![]() -
-
удовлетворяет требованиям СНиП2.01.07-85*, следовательно жесткость настила обеспечена.
Определяем расход стали для второго варианта:
![]()
Исходя из экономических условий, целесообразно принять первый вариант.
Проектирование составной сварной балки (главной балки)
Исходные данные:
![]() ;
;
![]() ;
;
l = 15 м
a = 1,0 м
С245
Определяем нормативную нагрузку:
![]()
Определяем расчетную погонную нагрузку:
![]()
Расчетный изгибающий момент в середине пролета определяем по формуле:
![]()
Поперечную силу на опоре находим по формуле:
![]()
Требуемый момент сопротивления балки Wтр выражаем из условия прочности:
![]()
Расчет производим в упругой стали, так как учет развития ограниченных пластических деформаций для оптимально подобранного сечения малоэффективен.
Определяем высоту балки
По имперической формуле определяем предварительную толщину стенки балки:
![]()
где h – предварительная высота балки; ![]()
Принимаем предварительную высоту балки:
![]()
![]()
Принимаем толщину стенки ![]() .
.
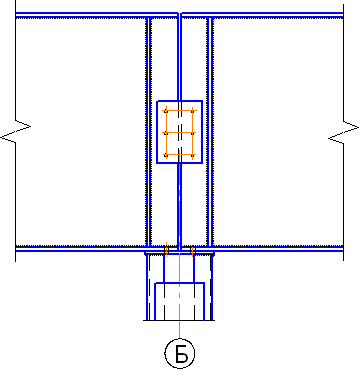
Установим высоту главной балки из условия экономичности, характеризующимся наименьшим расходом металла. Определяем оптимальную высоту балки по формуле:
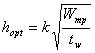 ,
,
где k = 1,15 – конструктивный коэффициент.
![]()
Определяем высоту балки из условий жесткости:
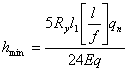
Предельный прогиб установленный СНиП 2.01.07-85* для главных балок:
![]()
![]()
Принимаем высоту стенки балки[2] hef = 125 см.
Определяем минимальную толщину стенки из условия работы ее на срез:
![]() ,
,
где k = 1,2 - коэффициент, принимаемый с учетом работы поясов балки;
hef = 125 см - высота стенки балки;
![]() - расчетное сопротивление стали
срезу;
- расчетное сопротивление стали
срезу;
γс = 1 – коэффициент условий работы.
![]()
Принимаем толщину стенки
балки ![]() .
.
Толщину полки принимаем конструктивно tf = 20 мм, тогда высота главной балки h = 129 см.
Определяем требуемый момент инерции сечения балки по формуле:
![]() ,
,
где Wтр – требуемый момент сопротивления;
h – высота балки.
![]()
Определяем момент инерции стенки по формуле:
![]()
Требуемый момент инерции поясов определяем по формуле:
![]()
Определяем требуемую площадь пояса:
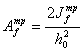 ,
,
где h0 = 127 см – расстояние между осями поясов.
![]()
Находим ширину полки из отношения:
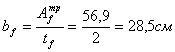
Принимаем сечения пояса[3] из универсальной стали 300х20.
Рекомендуемое отношение свеса пояса к толщине
![]()
![]()
Определяем фактические геометрические характеристики подобранного сечения балки. Статический момент инерции всей балки определяем по формуле:
![]() ,
,
где ![]() - статический момент
инерции полки;
- статический момент
инерции полки;
А – площадь сечения полки;
![]()
расстояние между осями симметрии балки и полки.
![]()
Момент сопротивления сечения определяем по формуле:
![]()
Определяем нормальное напряжение из условия прочности:
![]()
Подобранное сечение балки удовлетворяет проверке прочности и не имеет недонапряженности больше 5%.
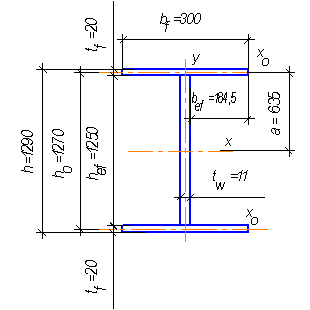
Изменение сечения составной сварной балки
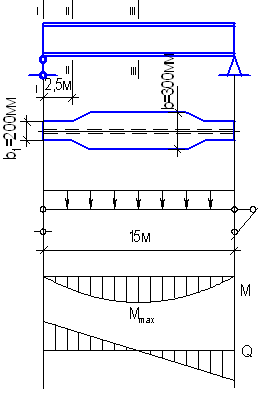
Изменение сечения по длине балки целесообразно применять при длине пролета ≥ 12 м. В сварных конструкциях используют два варианта изменения сечения: за счет изменения ширины пояса или высоты стенки. Наибольший эффект дает изменение сечения на расстоянии 1/6 пролета от опоры:
![]()
Определяем расчетный момент на расстоянии х = 2,5м:
![]()
Определяем перерезывающую силу в сечении на расстоянии х = 2,5м:
![]()
Определяем требуемый момент сопротивления измененного сечения из условия прочности:
![]()
Требуемый момент инерции измененного сечения определяем по формуле:
![]()
Определяем требуемый момент инерции поясов:
![]()
Определяем требуемую площадь сечения одного пояса:
![]()
Находим ширину полки из отношения:
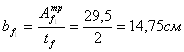
Согласно условию опирания
балки должно выполняться условие ![]() . Так
как полученная ширина полки не удовлетворяет условия, принимаем лист сечением
200х20.
. Так
как полученная ширина полки не удовлетворяет условия, принимаем лист сечением
200х20.
Определяем фактические геометрические характеристики измененного сечения балки.
Момент инерции уменьшенного сечения:
![]()
![]()
Момент сопротивления уменьшенного сечения:
![]()
Проверка прочности балки
Прочность балки проверяется в месте действия максимального момента, максимальной поперечной силы и в месте изменения сечения на совместное действие M и Q (нормальных и касательных напряжений).
Проверка прочности на опоре (сечение I-I)
Значение касательных напряжений τ в сечениях изгибаемых элементов должны удовлетворять условию:
![]() ,
,
где ![]() ;
;
S – статический момент сечения, определяемый по формуле:
![]()
![]()
Прочность балки на опоре обеспечена.
Проверка прочности балки в месте уменьшения сечения (сечениеII-II)
Проверяем прочность стыкового шва (соединяющего два листа) на растяжение:
![]()
Прочность стыкового шва обеспечена.
Проверяем прочность сечения на совместное действие нормальных и касательных напряжений. В соответствии с энергетической теорией прочности, проверку производим по приведенным напряжениям:
![]()
![]()
![]()
![]()
![]()
Прочность балки в сечении II-II обеспечена.
Проверка прочности балки в месте действия максимального момента (сечение III-III)
![]()
Прочность балки в сечении III-III обеспечена.
Жесткость балки также
будет обеспечена, так как ![]() .
.
Проверка местной устойчивости элементов балки
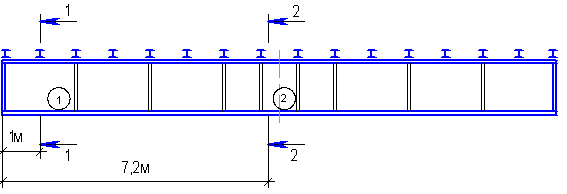
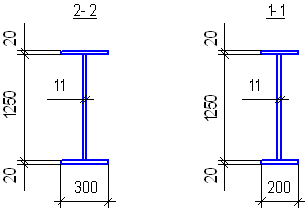
Проверка местной устойчивости сжатого пояса
В изгибаемых элементах
отношение ширины свеса ![]() сжатого пояса к
толщине
сжатого пояса к
толщине ![]() следует принимать не более
значений[4]
следует принимать не более
значений[4]
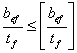

![]()
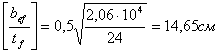
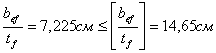
Местная устойчивость балки обеспечена.
Проверка местной устойчивости стенки
Расчет на устойчивость
стенок балок симметричного сечения при наличии местного напряжения ![]() следует выполнять по
формуле
следует выполнять по
формуле
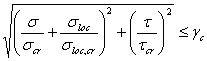 ,
,
где ![]() - определяют согласно
требованиям п.7.2* СНиП II-23-81*;
- определяют согласно
требованиям п.7.2* СНиП II-23-81*;
Определяем фактические напряжения для проверки устойчивости стенки балки в первом отсеке (сечение I-I)
Принимаем сечение I-I расстоянии х = 1м.
![]()
![]()
Фактическое значение нормативных напряжений на уровне верха стенки определяем по формуле:
![]()
Для проверки местной устойчивости принимаем среднее значение касательных напряжений при условии, что они воспринимаются только стенкой:
![]()
Местное напряжение ![]() в стенке под
сосредоточенной нагрузкой следует определять согласно требованиям п.5.13. СНиП II-23-81*:
в стенке под
сосредоточенной нагрузкой следует определять согласно требованиям п.5.13. СНиП II-23-81*:
![]() ,
,
где F – расчетное значение нагрузки, определяем по формуле:
![]()
![]() - условная длина распределения
нагрузки, определяемая в зависимости от условий опирания, определяем по
формуле:
- условная длина распределения
нагрузки, определяемая в зависимости от условий опирания, определяем по
формуле:
![]() ,
,
где ![]() - ширина балки настила,
определяемая по сортаменту для принятого номера двутавра.
- ширина балки настила,
определяемая по сортаменту для принятого номера двутавра.
![]()
Критическое напряжение определяем по формуле:
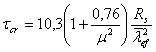 ,
,
где ![]() - условная гибкость
стенки, определяем по формуле:
- условная гибкость
стенки, определяем по формуле:
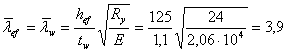
На основании п.7.10. СНиП II-23-81* принимаем расстояние между основными поперечными ребрами не более
![]()
Принимаем а = 200 см.
Ширину ребер жесткости определяем по формуле:
![]()
Толщину ребер принимаем:
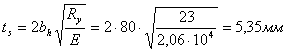
Принимаем толщину ребер ![]() .
.
μ – отношение большей стороны к меньшей
![]()
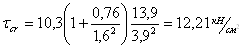
Значения ![]() определяем в зависимости
от отношений
определяем в зависимости
от отношений
![]()
![]()
![]() ,
,
где ![]() - коэффициент, зависящий
от δ и отношения a/hef
- коэффициент, зависящий
от δ и отношения a/hef
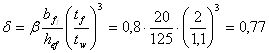 ,
,
![]()
![]() ,
,
где ![]() - табличный коэффициент,
зависящий от δ и отношения a/hef
- табличный коэффициент,
зависящий от δ и отношения a/hef
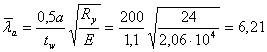
![]()
Проверяем местную устойчивость стенки в первом отсеке:
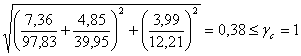
Устойчивость в первом отсеке обеспечена.
Определяем фактические напряжения для проверки устойчивости стенки балки в первом отсеке (сечение II-II)
Принимаем сечение II-II расстоянии х = 7.2м.
![]()
![]()
Определяем фактическое значение нормативных напряжений на уровне верха стенки:
![]()
Определяем среднее значение касательных напряжений:
![]()
Определяем местное напряжение в стенке:
![]()
Определяем критическое напряжение:
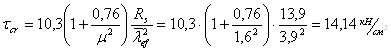 ,
,
![]()
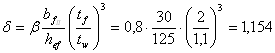
![]()
где ![]()
![]()
где ![]()
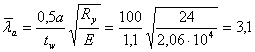
Проверяем местную устойчивость стенки во втором отсеке:
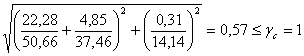
Устойчивость во втором отсеке обеспечена.
Расчет поясных швов
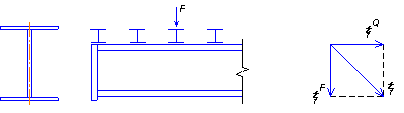
В общем случае поясные швы препятствуют взаимному смещению поясов и стенки, и работают на срез от действия поперечной силы Q, при передаче давления с балок настила на стенку, они дополнительно работают на срез, вызванной силой F.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]()
По табл.38* СНиП II-23-81* определяем минимальный катет
шва, с учетом, что ![]() , для
автоматической сварки электродом Э42
, для
автоматической сварки электродом Э42 ![]() .
.
Коэффициенты ![]() определяем по таблице 34*
СНиП II-23-81*: для автоматической сварки
при
определяем по таблице 34*
СНиП II-23-81*: для автоматической сварки
при ![]() в лодочку принимаем
в лодочку принимаем
![]()
![]()
Определяем расчетное
сопротивление на срез швов по металлу границы сплавления ![]() [5]
и расчетное сопротивление металла швов сварных соединений
[5]
и расчетное сопротивление металла швов сварных соединений ![]() [6].
[6].
![]()
![]()
Определяем, какое из сечений будет наиболее опасным:
![]()
![]() - min
- min
Расчет ведем по металлу границы сплавления.
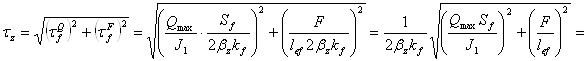
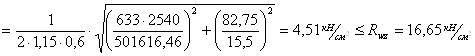
Конструирование и расчет опорной части балки
Так как балка опирается на колонну пристроганной торцевой площадью, то проверка торца балки на смятие не производится. В этом случае делают расчет на смятие. Проверяют опорную часть балки устойчивость из плоскости балки как условного опорного стержня, площадь сечения которого включает опорные ребра и часть стенки балки шириной ∆.
Толщину внутреннего
опорного ребра принимаем конструктивно ![]() .
.
Ширину ребра определяем по формуле:
![]()
Конструктивно принимаем
ширину ребра ![]() , с учетом среза 4 см. Расчетная
ширина ребра по торцу смятия
, с учетом среза 4 см. Расчетная
ширина ребра по торцу смятия ![]() .
.
Общая площадь опорного ребра:
![]()
Расстояние от края балки до ребра, из условия размещения болтов, принимаем конструктивно 12см.
Проверка прочности сварных швов, прикрепляющих опорные ребра к стенке, на срез.
Расчет ведем по металлу шва.
Минимальный катет шва
принимаем ![]() . Для ручной сварки
. Для ручной сварки ![]() ;
; ![]() .
.
Для фланговых швов определяем расчетную длину из условия
![]()
Определяем общую площадь сварных швов:
![]()
Проверяем прочность сварных швов:
![]()
Прочность швов обеспечена.
Проверка устойчивости опорного участка балки
Расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию, выполняем по формуле:
![]()
где As – общая площадь условного опорного стержня, включая опорные ребра и часть стенки балки шириной ∆.
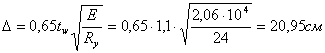
Площадь опорного стержня определяем по формуле:
![]()
Значение продольного коэффициента
φ определяем в зависимости от условной гибкости ![]()
![]()
Расчетную гибкость ![]() определим по формуле:
определим по формуле:
![]() ,
,
где ![]() - радиус инерции,
определяем по формуле:
- радиус инерции,
определяем по формуле:
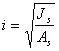 ,
,
Момент инерции сечения ребра ![]() определяем
по формуле:
определяем
по формуле:
![]()
![]()
![]()
Определяем условную гибкость
![]()
Согласно СНиП II-23-81* для ![]() значение φ определяем
по формуле:
значение φ определяем
по формуле:
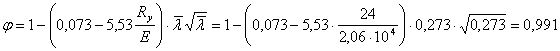
Проверяем опорный участок балки на устойчивость:
![]()
Устойчивость опорного участка балки обеспечена.
Расчет стыка сварной балки на высокопрочных болтах
Стык делаем в середине пролета, где М = 2373,75 кН.м и Q = 0.
Стык осуществляем
высокопрочными болтами ![]() из стали по ГОСТ
4543-71* 40Х "Селект" с наименьшим временным сопротивлением
из стали по ГОСТ
4543-71* 40Х "Селект" с наименьшим временным сопротивлением ![]() [7],
диаметр отверстия
[7],
диаметр отверстия ![]() обработка
соединяемых поверхностей газопламенным способом, способ регулирования натяжения
болтов по углу поворота гайки.
обработка
соединяемых поверхностей газопламенным способом, способ регулирования натяжения
болтов по углу поворота гайки.
Расчетное усилие, которое может быть воспринято каждой поверхностью трения соединяемых элементов, стянутых одним высокопрочным болтом, определяем по формуле:
![]() ,
,
где ![]() - расчетное сопротивление
растяжению высокопрочных болтов;
- расчетное сопротивление
растяжению высокопрочных болтов;
![]() - коэффициент условий работы
соединения, принимаемый по табл.35* СНиП II-23-81*;
- коэффициент условий работы
соединения, принимаемый по табл.35* СНиП II-23-81*;
![]() - площадь сечения болта нетто,
определяемая по табл.62* СНиП II-23-81*;
- площадь сечения болта нетто,
определяемая по табл.62* СНиП II-23-81*;
![]() - коэффициент трения, принимаемый по
табл.36* СНиП II-23-81*;
- коэффициент трения, принимаемый по
табл.36* СНиП II-23-81*;
![]() - коэффициент надежности,
принимаемый по табл.36* СНиП II-23-81*.
- коэффициент надежности,
принимаемый по табл.36* СНиП II-23-81*.
![]()
Проверяем ослабление нижнего растянутого пояса отверстиями под болты d0=22 мм.
![]()
![]()
![]()
![]()
Стык поясов
Каждый пояс балки перекрываем тремя накладками сечениями 300х14 и 2х120х14.
Общая площадь сечения накладок
![]()
Определяем усилие в поясе:
![]()
![]()
Количество болтов для крепления площадок определяем по формуле:
![]() ,
,
где k = 2 – количество поверхностей трения соединяемых элементов.
Принимаем 10 болтов.
Проверяем ослабленное сечение в полках на краю стыка:
![]() ,
,
где Аn – площадь сечения нетто, определяем по формуле:
![]()
![]() ?
?
Af – площадь пояса, определяем по формуле:
![]()
![]()
Прочность ослабленного сечения соединяемых элементов обеспечена.
Расставляем болты с учетом минимальных расстояний.
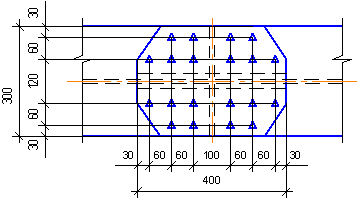
Стык стенки
Стенку перекрываем двумя накладками сечением …..
Определяем момент, действующий на стенку:
![]()
Принимаем расстояние между крайними по высоте рядами болтов:
![]()
Находим коэффициент стыка α:
![]() ,
,
где m = 2 – количество болтов в ряду.
![]()
Принимаем 14 рядов.
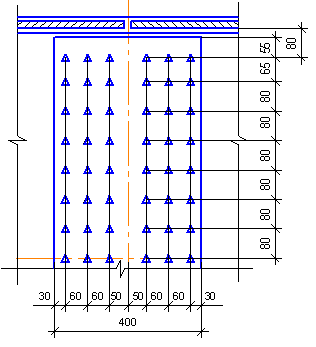
Расставляем болты с учетом минимальных расстояний.
Проверяем стык стенки:
![]()
![]()
![]()
Прочность соединения обеспечена.
Конструирование и расчет стержня сквозной центрально - сжатой колонны
Центрально – сжатые колонны воспринимают продольную силу, приложенную по оси, при этом все поперечные сечения колонны испытывают равномерное сжатие.
Значение продольной силы определяем по формуле:
![]()
![]() ,
,
где ![]() - собственный вес колонны.
- собственный вес колонны.
![]()
Расчет стержня
Расчетную длину стержня находим в соответствии с условиями закрепления концов колонны. Конструктивно сопряжение колонны и балок выполняем по этажной схеме.
Определяем расчетную длину колонны относительно оси Х:
![]() ,
,
где ![]() - коэффициент приведения,
зависящий от способа закрепления;
- коэффициент приведения,
зависящий от способа закрепления;
![]() - геометрическая длина колонны,
определяемая по формуле:
- геометрическая длина колонны,
определяемая по формуле:
![]() ,
,
где a = 60 см – заглубление колонны.
![]()
Требуемую площадь сечения определяем по формуле:
![]()
Задаемся гибкостью ![]() , для которой
, для которой ![]() .
.
![]()
По сортаменту ГОСТ 8240-72 предварительно принимаем колонну из двух швеллеров №27, для которых
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Гибкость по материальной оси х – х:
![]()
Определяем ![]() по формуле 8 СНиП.
по формуле 8 СНиП.
![]()
![]()
Фактическое напряжение составит
![]()
Окончательно принимаем стержень колонны из двух швеллеров №27.
Расчет планок
Ветви раздвигаем на такое расстояние от свободной оси у – у, чтобы соблюдалось условие
![]()
Задаемся гибкостью
ветвей, заключенными между планками ![]() [8].
[8].
Требуемую гибкость относительно свободной оси определим по формуле:
![]()
Необходимый радиус инерции
![]()
Для сечения из двух швеллеров с планками находим приближенный радиус инерции
![]() ,
,
откуда ![]() . Принимаем
. Принимаем ![]() .
.
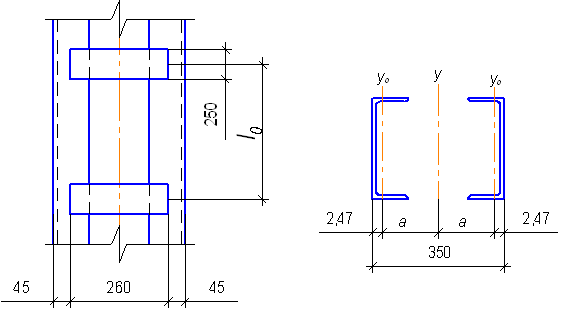
При этом должно удовлетворяться условие
![]()
Проверяем устойчивость
колонны по свободной оси, предварительно вычисляя геометрические характеристики
![]() :
:
Момент инерции сечения:
![]() ,
,
где ![]() .
.
Радиус инерции:
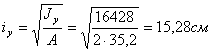
Гибкость:
![]()
Расчетную длину ветви, заключенную между планками определяем по формуле:
![]()
Ширина планки принимается
в пределах ![]() . Принимаем
. Принимаем ![]() .
.
Толщину планки определим по формуле:
![]()
Для вычисления приведенной гибкости относительно свободной оси необходимо проверить погонную жесткость ветви и планки:
![]()
где Js – момент инерции планки, определяем по формуле:
![]() ;
;
![]() - расстояние между центрами планок;
- расстояние между центрами планок;
![]() - момент инерции ветви;
- момент инерции ветви;
![]() - расстояние между ветвями.
- расстояние между ветвями.
![]()
Согласно табл.7 СНиП II-23-81* приведенную гибкость ![]() определяем по формуле:
определяем по формуле:
![]()
Условие гибкости выполняется.
Определяем условную поперченную силу по формуле:
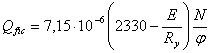
![]() определяем по формуле 8 СНиП.
определяем по формуле 8 СНиП.
![]()
![]()
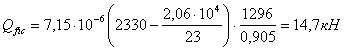
Рассчитываем планки на перерезывающую силу F и момент М1:
![]()
![]()
Крепление планки
выполняем на ручной сварке электродами Э42 (![]() ),
катет шва принимаем
),
катет шва принимаем ![]() , длина шва
, длина шва ![]() .
.
Определяем момент
сопротивления ![]() и площадь
сечения шва
и площадь
сечения шва ![]() (с учетом расчетного
сечения по металлу шва):
(с учетом расчетного
сечения по металлу шва):
![]()
![]()
Проверяем прочность сварного шва от совместного действия перерезывающей силы и момента:
![]()
![]()
![]()
Тогда
![]()
Прочность сварного шва обеспечена.
Расчет и конструирование базы
Определяем размеры опорной плиты из условия смятия бетона под плитой фундамента:
![]()
где ![]() - расчетное сопротивление
бетона при местном сжатии, определяем по формуле
- расчетное сопротивление
бетона при местном сжатии, определяем по формуле
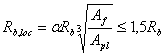
где ![]() - коэффициент увеличения
сопротивления бетона при смятии;
- коэффициент увеличения
сопротивления бетона при смятии;
![]() - расчетное сопротивление бетона
сжатию[9], принимаем для бетона
класса В12,5.
- расчетное сопротивление бетона
сжатию[9], принимаем для бетона
класса В12,5.
Предварительно принимаем
![]()
Тогда требуемая площадь плиты
![]()
Принимаем плиту размером 650х600мм,
![]() ; а верх фундамента
размером 950х900мм,
; а верх фундамента
размером 950х900мм, ![]() .
.
Проверяем напряжение ![]()
![]()
Определяем толщину плиты
Плита работает на изгиб от равномерно распределенной нагрузки, равной:
![]()
Рассмотрим различные участки плиты.
Выделяем в консоли (участок I) плиту шириной 1 см и определяем момент
![]() ,
,
где с = 155мм – вылет консоли.
Проверяем работу II участка, опёртого по трем сторонам.
![]()
![]()
Проверяем работу III участка, опертого по четырем
сторонам. Отношение ![]()
![]() . Момент для полосы шириной
1 см в направлении короткой стороны определяем по формуле:
. Момент для полосы шириной
1 см в направлении короткой стороны определяем по формуле:
![]()
![]()
Для определения толщины
плиты расчетный момент принимаем максимальный ![]() .
.
![]()
Тогда требуемый момент сопротивления сечения плиты составит
![]()
Принимаем расчетное
сопротивление ![]() (для толщины
листа t = 20…40 мм).
(для толщины
листа t = 20…40 мм).
Момент сопротивления сечения при b = 1 см определяем по формуле
![]()
Толщину плиты определяем по формуле:
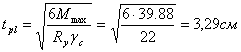
Принимаем толщину плиты в
соответствии с сортаментом ![]() .
.
Определяем высоту листов траверсы:
![]() ,
,
где ![]() - число швов, которые
удобно варить.
- число швов, которые
удобно варить.
Катет шва принимаем
конструктивно ![]() .
.
![]()
Принимаем высоту траверсы
согласно со стандартом на листы ![]() .
.
Анкерные болты назначаем конструктивно диаметром 20 мм, глубина заделки которых должна быть не менее 700 мм.
Список литературы
1. Васильченко В.Т. Справочник конструктора металлических конструкций. Будiвельник, 1980;
2. СНиП II-23-81* «Стальные конструкции»;
3. Горев В.В. и др. Металлические конструкции. Элементы конструкций. Высшая школа, 2001;
4. Муханов К.К. Металлические конструкции. Стройиздат, 1978;
5. Мандриков А.П. и др. Примеры расчета металлических конструкций, 2-е издание. М., Строийздат, 1991;
6. Беленя Е.И. Металлические конструкции. М., Стройиздат, 1995.
[1] Следует принимать по табл.6* СНиП II-23-81*
[2] Согласно с сортаментом на полосовую горячекатаную сталь по ГОСТ 19903-74*
[3] Согласно с сортаментом на универсальную полосовую горячекатаную сталь по ГОСТ 82-70
[4] Согласно п.7.24. СНиП II-23-81*
[5] Принимается согласно табл.3, табл.51 СНиП II-23-81*
[6] Принимается по табл.56 СНиП II-23-81*
[7] Принимаем по таблице 61 СНиП II -23-81*
[8] Принимаем согласно п.5.6. СНиП II-23-81*
[9] Принимается по СНиП 2.03.01-84