Контрольная работа: Анализ электрической цепи синусоидального тока
КУРСОВАЯ РАБОТА
по дисциплине : « Электротехника и электроника »
тема: « Анализ электрической цепи синусоидального тока »
2005
Содержание:
Задание
1. Введение
2. Расчётная часть
2.1 Составление системы уравнений по законам Кирхгофа и представление её в дифференциальной и символической формах
2.2 Расчёт токов в ветвях
2.3 Расчёт потенциалов точек цепи
2.4 Построение временных графиков мгновенных значений тока в одной из ветвей и напряжения между узлами электрической цепи
3. Вывод
Используемая литература
Задание
1) для заданной электрической схемы составить систему уравнений по законам Кирхгофа и записать её в двух формах:
а) в дифференциальной форме;
б) в символической форме;
2) рассчитать токи в ветвях, используя любой целесообразный для заданной схемы метод расчета;
3) рассчитать потенциалы точек схемы и построить векторную диаграмму;
4) записать уравнения для мгновенных значений тока в одной из ветвей и напряжения между узлами электрической цепи. Построить эти функции на одном временном графике.
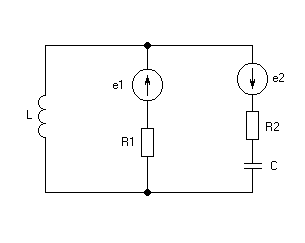
е – источник переменной ЭДС
L – индуктивность
С – конденсатор
![]()
![]() 141В
141В
![]() -90˚
-90˚
![]()
![]()
![]() 84,6В
84,6В
![]() 60˚
60˚
![]() 80 Ом
80 Ом
![]() 60 Ом
60 Ом
![]() 40 мГн
40 мГн
![]() 10 мкФ
10 мкФ
1. Введение
В настоящее время централизованное производство и распределение электрической энергии осуществляется на переменном токе. Переменный ток занял господствующее положение в промышленном приводе и электрическом освещении, в сельском хозяйстве и на транспорте, в технике связи и электротермии, а также в быту.
Переменными называют э.д.с., токи и напряжения изменяющиеся с течением времени. Они могут изменяться только по значению или только по направлению, а также по значению и направлению.
Цепи, в которых действует переменный ток - называют цепями переменного тока.
В электроэнергетике наибольшее применение получил переменный ток, изменяющийся во времени по синусоидальному закону.
Переменные электрические
величины являются функциями времени, их значения в любой момент времени t называют мгновенными и
обозначают строчными буквами. Например, выражение мгновенного значения
синусоидального тока определяется тригонометрической функцией i=I![]() sin(
sin(![]() t+
t+![]()
![]() ), единственной переменной в правой части, которой
является время t. Амплитуда I
), единственной переменной в правой части, которой
является время t. Амплитуда I![]() равна максимальному значению тока. Аргумент синуса (
равна максимальному значению тока. Аргумент синуса (![]() t+
t+![]()
![]() ), измеряемый в радианах, определяет фазный угол
синусоидальной функции тока в любой момент времени t и называется фазой, а величина
), измеряемый в радианах, определяет фазный угол
синусоидальной функции тока в любой момент времени t и называется фазой, а величина ![]()
![]() , равная фазному углу в момент начала отсчёта времени
(t=0), - начальной фазой. Величина
, равная фазному углу в момент начала отсчёта времени
(t=0), - начальной фазой. Величина ![]() определяет число радианов, на которое изменяется фаза
колебаний за секунду, и называется угловой частотой.
определяет число радианов, на которое изменяется фаза
колебаний за секунду, и называется угловой частотой.
Синусоидальные
э.д.с., ток и напряжение являются периодическими функциями времени. Через промежуток
времени Т, называемый периодом, фаза колебаний изменяется на угол 2![]() , и цикл колебаний повторяется снова: i(t)=i(t+T), следовательно, период и угловая частота связаны
соотношением
, и цикл колебаний повторяется снова: i(t)=i(t+T), следовательно, период и угловая частота связаны
соотношением ![]() Т=2
Т=2![]() . Длительность периода принято измерять в секундах.
Величену, обратную периоду, называют частотой и обозначают f. Частота определяется количеством
периодов в секунду: f=1/T и измеряется в герцах (Гц).
Очевидно, что
. Длительность периода принято измерять в секундах.
Величену, обратную периоду, называют частотой и обозначают f. Частота определяется количеством
периодов в секунду: f=1/T и измеряется в герцах (Гц).
Очевидно, что ![]() = 2
= 2![]() /T = 2
/T = 2![]() f.
f.
Всё сказанное относительно тока справедливо также для синусоидально изменяющихся напряжений u(t) и э.д.с. e(t).
При совместном рассмотрении нескольких синусоидальных
электрических величин одной частоты обычно интересуются разностью их фазовых
углов, называемой углом сдвига фаз. Угол сдвига фаз двух синусоидальных функций
определяют как разность их начальных фаз. Если синусоиды имеют одинаковые
начальные фазы, то говорят о совпадении по фазе, если разность фаз равна ![]() , то говорят,
что синусоиды противоположны по фазе. Фазовые соотношения имеют очень важное
значение при анализе электрических цепей переменного тока. Угол сдвига фаз
между током и напряжением участка цепи принято обозначать буквой
, то говорят,
что синусоиды противоположны по фазе. Фазовые соотношения имеют очень важное
значение при анализе электрических цепей переменного тока. Угол сдвига фаз
между током и напряжением участка цепи принято обозначать буквой ![]() и определять вычитанием
начальные фазы тока из начальной фазы напряжения:
и определять вычитанием
начальные фазы тока из начальной фазы напряжения:
![]() =
= ![]()
![]() -
-![]()
![]()
Угол ![]() - величина алгебраическая. Если
- величина алгебраическая. Если ![]()
![]() >
>![]()
![]() , то
, то ![]() >0, при этом
говорят, что напряжение опережает ток по фазе или ток отстаёт по фазе от
напряжения. В случае
>0, при этом
говорят, что напряжение опережает ток по фазе или ток отстаёт по фазе от
напряжения. В случае ![]()
![]() <
<![]()
![]()
![]() <0,
т.е. напряжение отстаёт по фазе от тока или ток опережает напряжение.
<0,
т.е. напряжение отстаёт по фазе от тока или ток опережает напряжение.
В практике применения переменных токов широко пользуются понятием действующего значения электрической величины. Действующим называют среднее квадратичное значение переменной электрической величины за период. Действующий ток обозначают той же буквой, что и соответствующее амплитудное значение, но без индекса m:
I = 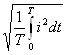 .
.
Тепловое и электромеханическое действия тока пропорциональны квадрату его мгновенного значения, поэтому именно действующий ток I может служить количественной мерой их оценки за период.
Между амплитудой и действующим значением для синусоидальных
величин установлена связь. Если i = I![]() sin
sin ![]() t, то
t, то

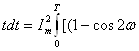
![]() ,
,
следовательно в соответствии с определением I
= I![]() /
/![]() .
.
Для действующих значений синусоидально изменяющихся напряжения, э.д.с. и магнитного потока справедливы аналогичные выражения
U = U![]() /
/![]() ,
E = E
,
E = E![]() /
/![]() , Ф = Ф
, Ф = Ф![]() /
/![]() .
.
Если говорят о значениях переменного напряжения, э.д.с. или тока, то, как правило, подразумевают их действующие значения.
Диапазон напряжений и токов, используемых в электротехнике очень широк. Обычно приборы для измерения переменных токов и напряжений градуируют в действующих значениях.
Во многих случаях основные характеристики электротехнических устройств могут быть получены и описаны с помощью известных из курса физики интегральных понятий (скалярных величин): тока, электродвижущей силы (э.д.с.), напряжения. При таком описании совокупность электротехнических устройств рассматривают как электрическую цепь, состоящую из источников и приёмников электрической энергии, характеризуемых э.д.с. Е.током I, напряжением U. Источники и приёмники электрической энергии, являющиеся основными элементами электрической цепи, соединяют проводами для обеспечения замкнутого пути для электрического тока. Для включения и отключения электротехнических устройств применяют коммутационную аппаратуру (выключатели, рубильники, тумблеры). Кроме этих элементов в электрическую цепь могут включаться электрические приборы для измерения тока, напряжения, мощности.
Для анализа цепей переменного тока как правило пользуются схемами замещения составленными из идеальных элементов: резистивного R, емкостного C, индуктивного L, источника э.д.с. E, источника тока J.
К идеальным резистивным элементам могут быть отнесены реостаты, большинство электронагревательных устройств; резисторы.
К емкостным отнестяся конденсаторы.
Примером индуктивного идеального элемента электрической цепи является индуктивная катушка.
Идеальным источником может служить энергосистема и промышленная сеть переменного тока.
Применение законов Кирхгофа для описания состояния электрических цепей.
Основными законами, используемыми для анализа и расчёта электрических цепей, являются первый и второй законы Кирхгофа.
Первый закон Кирхгофа является следствием закона
сохранения заряда, согласно которому в любом узле заряд одного знака не может
ни накапливаться, ни убывать. Согласно первому закону Кирхгофа алгебраическая
сумма токов ветвей, сходящихся в узле, равна нулю:![]()
При этом токи, направленные от узла, следует брать со знаком плюс, а токи, направленные к узлу,- со знаком минус.
Второй закон Кирхгофа является следствием закона
сохранения энергии, в силу которого изменение потенциала в замкнутом контуре
равно нулю. Изменение потенциала между двумя точками участка цепи
характеризуется разностью потенциалов, которую можно измерить вольтметром. В
электротехнике разность потенциалов между двумя любыми точками цепи принято
называть напряжением. Поэтому согласно второму закону Кирхгофа алгебраическая
сумма напряжений всех участков замкнутого контура равна нулю:![]()
При составлении уравнений по второму закону Кирхгофа слагаемые берут со знаком плюс в случае, когда направление обхода контура совпадает с направлением соответственно напряжения, тока или э.д.с., в противном случае берут со знаком минус.
Рекомендуется следующий порядок составления уравнений по законам Кирхгофа: определяют число ветвей, узлов и независимых контуров, устанавливают число независимых уравнений по первому закону Кирхгофа, остальные уравнения составляют по второму закону Кирхгофа.
Для определения неизвестных токов в ветвях необходимо составить уравнения по первому второму закону Кирхгофа, количество которых должно быть равно количеству неизвестны4х токов. По первому закону Кирхгофа можно составить y-1 независимых уравнений, где y- количество узлов цепи. Использовать все y уравнений невозможно, так как одно из них обязательно будет зависимым.
Количество уравнений, составляемых по второму закону Кирхгофа, должно быть равно количеству независимых контуров. Независимым называют контур, в который входит хотя бы одна новая ветвь.
Если в результате решения этих уравнений получатся отрицательные значения токов, то это означает, что истинные направления токов в ветвях цепи противоположны тем направлениям, для которых составлялись уравнения.
Метод контурных токов.
Сложную электрическую цепь, содержащую несколько активных и
пассивных элементов и имеющую много узлов и контуров, рассчитать с помощью
первого и второго законов Кирхгофа будет довольно трудно, так как будет связано
с решением большого количества уравнений. Вводя понятие о контурных токах, можно
свести уравнения, составленные по законам Кирхгофа, к системе уравнений,
составленных лишь для независимых контуров, т. е. исключить уравнения,
составляемые по первому закону Кирхгофа. Благодаря этому удаётся снизить
порядок системы уравнений. Под контурными токами понимают условные (расчётные)
токи, замыкающиеся в соответствующих контурах. На основе составленных уравнений
выписывается матрица вида ![]() Здесь
Здесь ![]() квадратная матрица коэффициентов
при неизвестных контурных токах;
квадратная матрица коэффициентов
при неизвестных контурных токах; ![]() матрица- столбец неизвестных
контурных токов;
матрица- столбец неизвестных
контурных токов; ![]() матрица- столбец известных
контурных э.д.с. Диагональные элементы матрицы
матрица- столбец известных
контурных э.д.с. Диагональные элементы матрицы ![]() , называемые контурными
сопротивлениями или собственными сопротивлениями контуров, равны сумме
сопротивлений всех элементов, входящих в контур. Остальные элементы матрицы
, называемые контурными
сопротивлениями или собственными сопротивлениями контуров, равны сумме
сопротивлений всех элементов, входящих в контур. Остальные элементы матрицы ![]() равны
сопротивлениям общих ветвей смежных контуров и имеют знак минус. Если
какие-либо контуры не имеют общих ветвей, то соответствующие элементы матрицы
равны нулю. Решением уравнения
равны
сопротивлениям общих ветвей смежных контуров и имеют знак минус. Если
какие-либо контуры не имеют общих ветвей, то соответствующие элементы матрицы
равны нулю. Решением уравнения ![]() будет
будет ![]() , где
, где ![]() - матрица, обратная матрице
коэффициентов
- матрица, обратная матрице
коэффициентов ![]() .
.
Использование принципа суперпозиции для анализа электрических цепей.
Применяя принцип суперпозиции можно найти ток любой ветви или напряжение любого участка электрической цепи как алгебраическую сумму частичных токов или напряжений, вызываемых отдельным действием источников э.д.с. и тока. С помощью принципа суперпозиции (наложения) расчёт сложной цепи с несколькими источниками э.д.с. и тока можно свести к расчёту нескольких цепей с одним источником.
Для определения токов в цепи вначале полагают, что в ней
действует только один источник э.д.с. (например ![]() ). При этом сопротивления всех
элементов считают неизменными. Определяют частичные токи от действия этого
источника. Далее проводят расчёт частичных токов от действия другого источника
э.д.с. и т. д. рассматривая каждый следующий источник в отдельности и находя
частичные токи от их действия. Алгебраическое суммирование частичных токов с
учётом их направлений даёт значения действительных токов ветвей.
). При этом сопротивления всех
элементов считают неизменными. Определяют частичные токи от действия этого
источника. Далее проводят расчёт частичных токов от действия другого источника
э.д.с. и т. д. рассматривая каждый следующий источник в отдельности и находя
частичные токи от их действия. Алгебраическое суммирование частичных токов с
учётом их направлений даёт значения действительных токов ветвей.
Метод расчёта электрических цепей с использованием принципа
суперпозиции является довольно громоздким и поэтому применяется редко. Он
целесообразен тогда, когда электрическое состояние цепи определено для каких
либо источников э.д.с. и токов и требуется проанализировать электрическое
состояние цепи при изменении э.д.с. или тока одного из источников. В этом
случае нет необходимости вновь рассчитывать значения токов и напряжений от
действия всех источников, а достаточно определить лишь частичные токи и
напряжения от действия дополнительной э.д.с. ![]() или дополнительного тока
или дополнительного тока ![]() источника, а
также токи и напряжения от действия нового источника как алгебраическую сумму
прежних и частичных токов и напряжений.
источника, а
также токи и напряжения от действия нового источника как алгебраическую сумму
прежних и частичных токов и напряжений.
Метод междуузлового напряжения.
В реальных электрических цепях очень часто несколько источников и приёмников электрической энергии включаются параллельно. Схема замещения такой цепи, содержащей активные и пассивные ветви, соединённые параллельно, имеет только два узла, например узлы А и В. Для определения токов во всех ветвях достаточно найти напряжение между двумя узлами. Формулу для этого напряжения можно получить, используя принцип суперпозиции.
Частичное напряжение от действия источника тока J можно определить исходя из того, что ток J равен сумме токов всех ветвей. Далее необходимо определить частичные напряжения от действия каждого источника э.д.с. в отдельности. Таким образом, если схема содержит k источников тока и m источников э.д.с., то напряжение между узлами равно алгебраической сумме всех частичных напряжений, т.е.

Произведения ![]() и
и ![]() берут со знаком плюс, когда
направление Е и J противоположны
выбранному условно-положительному направлению междуузлового напряжения и со
знаком минус, когда эти направления совпадают.
берут со знаком плюс, когда
направление Е и J противоположны
выбранному условно-положительному направлению междуузлового напряжения и со
знаком минус, когда эти направления совпадают.
Зная междуузловое напряжение, легко найти токи как в пассивных, так и в активных ветвях.
2. Расчетная часть
2.1 Составление системы уравнений по законам Кирхгофа и представление её в дифференциальной и символической формах
Система уравнений в дифференциальной форме:

Система уравнений в символической форме:
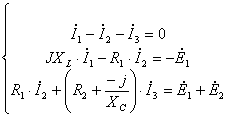
2.2 Расчёт токов в ветвях
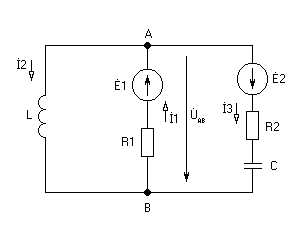
Для расчёта токов в ветвях воспользуемся методом междуузлового напряжения.

![]()
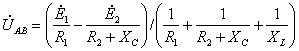
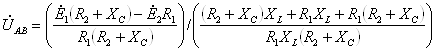
![]()
![]()
![]()

![]()
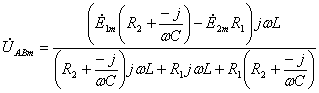
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
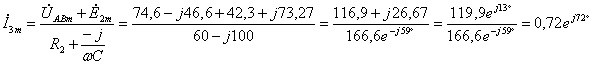
2.3 Расчёт потенциалов точек цепи
Представим данную схему в виде:
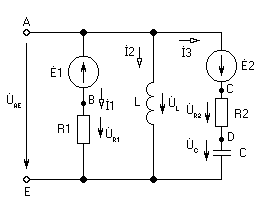
Представим ![]() ,
, ![]() и
и ![]() в комплексном виде:
в комплексном виде:
![]()
![]()
![]()
При построении диаграммы
предположим, что ![]() .Для определения потенциалов
остальных точек цепи обойдём контур цепи в направлении, противоположном
положительному направлению тока или, как принято говорить, против тока. При
таком обходе контура комплексный потенциал каждой последующей точки будет
определяться как сумма комплексного потенциала предыдущей точки и комплексного
напряжения на элементе, включённом между ними.
.Для определения потенциалов
остальных точек цепи обойдём контур цепи в направлении, противоположном
положительному направлению тока или, как принято говорить, против тока. При
таком обходе контура комплексный потенциал каждой последующей точки будет
определяться как сумма комплексного потенциала предыдущей точки и комплексного
напряжения на элементе, включённом между ними.
Для первой ветви можно записать:
![]()
![]()
![]()
![]()
![]()
Для второй ветви:
![]()
![]()
![]()
Для третьей:
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
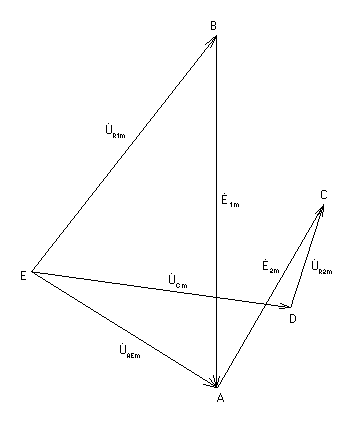
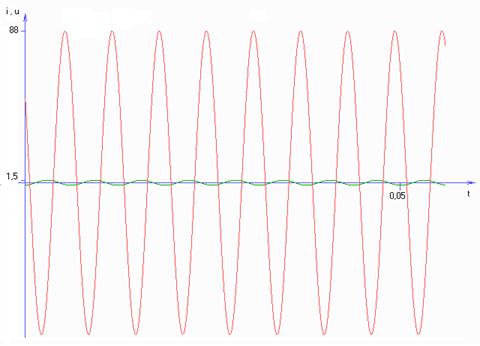
2.4 Построение временных графиков мгновенных значений тока в одной из ветвей и напряжения между узлами электрической цепи
![]()
![]()
Для наглядности приводятся графики указанных функций в двух масштабах по оси t.

3. Вывод
В результате расчётов были получены токи в ветвях электрической цепи с несколькими источниками э.д.с. и с резистивными, емкостным и индуктивным приёмниками. Были определены потенциалы точек электрической цепи и построена топографическая диаграмма, с помощью которой можно найти напряжения между двумя любыми точками цепи. Графически представлены мгновенные значения некоторых величин электрической цепи, что даёт представление о процессах происходящих в ней в определённый момент времени.
Используемая литература
1. Бессонов Л.А. Теоретические основы электротехники.- М.:Высшая школа, 1978.
2. Зевеке Г.В. и др. Основы теории цепей.- М.: Энергия, 1975.
3. Электротехника п.р. проф. Герасимова В.Г. – М.: Высшая школа, 1985.