Контрольная работа: Дисперсія у одномодових телекомунікаційних волокнах
Дисперсія у одномодових телекомунікаційних волокнах
З декількох причин найбільш підхожим оптичним варіантом схеми модуляцiї носійної для оптичних телекомунікацій є кодоiмпульсна модуляція, в якій сигнал (інформація) кодується в формі струму оптичних iмпульсів, які генеруються прямо модулюючим керуючим струмом лазерного діоду (світловипромінюючого діоду) – джерела. Коли оптичний iмпульс запускається в багатомодове волокно, що залежить від початкових умов запуску, звичайно його енергія буде розподілятися в великій кількості можливих мод волокна.
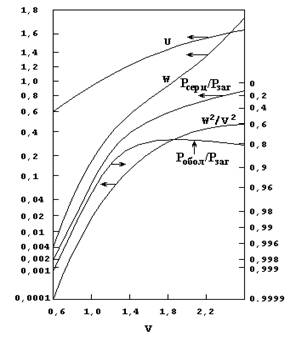
Рисунок 1 – Змінення різних характеристик розповсюдження LP01 моди в волокні зі східчастим ППЗ в залежності від індекса V.
Кожна з цих мод буде поширюватися вздовж довжини волокна з характерною груповою швидкістю, Vr=1/(db/dw). На виході з волокна вони будуть кінець кінцем єднатися, створюючи iмпульс звичайно більшої тривалості, ніж вхідний і, крім того, більшої часової ширини, ніж вхідний iмпульс. Це явище названо внутришньомодовою iмпульсною дисперсією. І, фактично, є головним механізмом, який визначає ширину смуги пропускання багатомодового волокна. Швидка оцінка дисперсії в східчастому багатомодовому волокні може бути одержана шляхом розрахунку часу передачі самої швидкої (тобто нижчої моди) і самої повільної (тобто вищої) мод і обчисленням різниці часу. Час, який затрачується променем відповідаючи специфічній моді, що поширюється вздовж довжини L волокна, є:
![]() . (1)
. (1)
З того, що Q' може змінюватися від 0 до Qс' (=p/2-Qкр), якщо всі можливі спрямовані моди збуджуються з рівною потужністю, різниця часу між самим коротким (Q¢=0) і самим довгим шляхом (Q¢=Qс) буде даватися як:
Dt=tсамий повільний - tсамий швидкий @(n1L/c)D. (2)
В типовому волокні, припускаючи n1»1,46; D=1% на довжині 1 км Dt складе ~48 нс; це означає для нас, що iмпульс нескінченно малої тривалості (часової ширини) збільшиться до ширини 48 нс після проходження дільниці волокна довжиною 1 км. Слід вивести, що швидкість передачі імпульсів крізь цей світловод не може бути більше ніж ~(1/50)´109=20 Мбіт/c для передачі без спотворення на відстань 1 км до прийомного кінця лінії. Це не дуже прийнятна величина з точки зору можливості передачі інформації, яку сподіваються одержати оптичні комунікаційні системи. Якщо, проте, профіль серцевини волокна змусити бути градiєнтним, це приводить до значного зростання ширини смуги пропускання волокна. Найбільш популярна форма профілю була обрана, як градiєнтний профіль, аналітично виражається як:
 , (3)
, (3)
де n1 – осьовий індекс заломлення, а – радіус серцевини, q визначає форму профіля серцевини і D представляє відносну різницю індексів серцевини і оболонки:
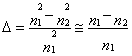 (для слабко направляючих
волокон). (4)
(для слабко направляючих
волокон). (4)
Велика множина профiлів може бути одержана через (3) просто зміною q, наприклад, q=1 відповідало б трикутному профiлю, q=2 – параболічному, тоді як q=¥ зробило б профіль східчастою функцією (див. рисунок 2 а). В разі q=2 – волокна, дисперсія (див. (2)) Dt дається як:
![]() , (5)
, (5)
яка ясно показує, що Dt було б багато менше в цьому випадку, в порівнянні з такими ж n1 та D при q=¥. Для волокна, що має n1=1.46, D@0.01, L=1 км дисперсія Dt була б »48 нс при q=¥, в той час як при q=2 вона склала б 0,24 нс. Фізично, в градiєнтній серцевині волокна, з-за більш низького рівня індексів заломлення, промінь поширюється до кордону серцевина-оболонка від осі волокна і зазнає безупинне заломлення, як показано на рисунку 2б. Таким чином, якщо ми розглянемо оптичні промені двох типових променей, позначених 1 і 2 (див. рисунку 2.б), то промінь 2 буде ефективно поширюватися через області різноманітного показника заломлення порівняно з осьовим променем 1 – це істотно приведе до певного вирівнювання в часі поширення різноманітних променів (мод) і, крім того, дисперсія буде низькою. Ширина смуги передачі (»1/t) багатомодового волокна з градiєнтною серцевиною буде від 300 МГц км до такої великої величини, як 18 ГГц км (в так званих волокнах з оптимальним профілем – що будуть розглянуті пізніше) з середньою величиною майже 500–600 МГц км. Для того, щоб зробити електромагнiтний аналіз поширення в волокнах з градієнтною серцевиною, ми визначимо, що показник заломлення змінюється безупинно з r (r<a) на відміну від волокна зі східчастим показником, де n(r)=n1 для 0<r<a. Може бути використано скалярне хвильове рівняння.
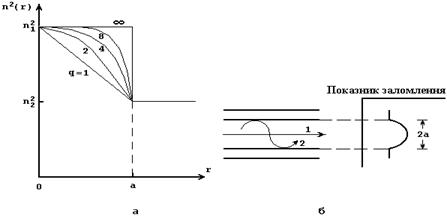
а – класифікація профілів показника заломлення по закону потужності; q визначає форму профілю; а – радіус серцевини; б – шлях променів у волокні з градієнтною серцевиною.
Рисунок 2 – Профіли показників заломлення
Для волокон з градієнтною серцевиною, вважаючи n=n(r), ми можемо переписати для радiальної частини Y шляхом заміни постійного показника заломлення n1 – n(2) у вигляді:
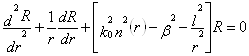 . (6)
. (6)
Проте для (3) не існує загального аналітично точного рішення для профілю з довільною серцевиною, оточеною оболонкою, крім профілів з параболічним (q=2) і вже одержаним східчастим виглядом профілю показника заломлення волокна (q=¥). Деякі приблизні рішення, як, наприклад, метод теорії збурення ВКБ (Вентцеля, Крамера, Брiллюена), варіаційний аналіз кінцевих елементів та інші були розглянуті в літературі по вивченню волокон з градiєнтною серцевиною. Проте, з точки зору найбільшої популярностi, засіб ВКБ рішення (6) опинився найбільш прийнятним5. Вживання методу ВКБ вимагає щоб виконувалася така умова:
(1 / n)×dn / dr<< l-1, (7)
що буквально означає, що показник заломлення – функція, що дуже слабко змінюється у просторі, являючись практично постійною на відстані порядку довжини хвилі. В слабко спрямовуючих багатомодових волокнах з градiєнтною серцевиною (7) в загальному виконуються і можна застосувати результати стандартного методу ВКБ, прямо трансформуючи (6) в одновимірне хвильове рівняння шляхом слідуючої підстановки
![]() . (8)
. (8)
В величинах цієї нової функції f(r), (6) трансформується в
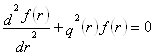 , (9)
, (9)
де ![]() .
.
Використовуючи квантово-механічну аналогію межових енергетичних станів при наближенні ВКБ, можна показати, що для межових мод в волокні треба мати:
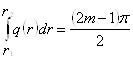 , (10)
, (10)
де m=1, 2… буде представляти номер реальної моди. Межі інтегрування r1 та r2 визначаються умовою q(r)=0 так, що q(r) – реально в межах r1 та r2 що приводить до того, що поле осцилює в межах цієї області, в той час як поза q(r) – має уявне значення, приводячи, таким чином, до експоненціального затухання нескінченно малих полів в цих областях.
Рівняння (10) становить рівняння для власного значення при ВКБ наближення для волокон з градiєнтною серцевиною, і рішення (10) для різноманітних комбiнаций l та m буде визначати відповідні постійні розповсюдження для мод – blm. Проте, поки ми не розглядали окремо моди дуже низьких порядків, щоб одержати загальний вид модової структури в волокнах з градiєнтною серцевиною, можна переписати (10) приблизно як
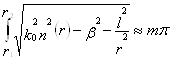 , (11)
, (11)
і взяти (11) для визначення характеристики чи рівняння власного значення для одержання постійної розповсюдження (blm взагалі для волокна з градiєнтною серцевиною поки задовольняється (7). Використовуючи (11), можна також зробити розрахунок числа мод, як показано в:
 , (12)
, (12)
та
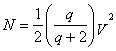 , (13)
, (13)
де M(b') представляє кількість мод, що мають постійні поширення більші, ніж b', та N відповідає загальній кількості можливих спрямованих мод. Для східчастого профіля волокна (q=¥)
![]() , (14)
, (14)
в той час як для волокна з параболічною серцевиною (q=2)
![]() . (15)
. (15)
Таким чином, для даного V загальна кількість спрямованих мод в волокні зі східчастим профiлем вдвічі більше, ніж в еквівалентному (що має з ним однакові (D та а) волокні з параболічним профілем. Звичайно V в багатомодових волокнах ~30, тоді при q=¥ N буде дорівнюватися »450, тоді як при q=2 N@225.
Встановлено, що в оптичних системах передачі з iмпульсно-кодовою модуляцією з-за того, що сигнал передається в формі серій iмпульсів, ці iмпульси розширюються при поширенні в середині волокна в основному з-за межмодової дисперсії і міра дисперсії буде визначати можливу швидкість передачi інформації (даних) через волокно. Реально, дисперсія чи поширення iмпульсу в волокні породжується, як це можна показати, трьома механізмами:
1) міжмодовою,
2) матеріальною,
3) хвильоводною дисперсією (останні дві разом відомі як внутрішньомодова або хроматична дисперсія). Навіть якщо шляхом підбору градiєнтного профіля можна мiнiмiзувати міжмодову дисперсію, кінцева спектральна ширина практично доступних оптичних джерел, як і Фур'є-спектр iмпульсних сигналів призведе до внутрішньомодової дисперсії. Матеріальна дисперсія, що є однією з компонент її, зобов'язана своєю появою залежності показника заломлення, з якого зроблено волокно, від довжини хвилі. З іншого боку, хвилєводна дисперсія виникає із-за явної залежності постійної розповсюдження моди від довжини хвилі і, по суті, залежить від хвилєводного параметру: a/l.
Якщо ми, наприклад, візьмемо поширення iмпульсу гаусовської форми:
 , (16)
, (16)
де Т – половина ширини iмпульсу на рівні інтенсивності 1/e та wс – частота несучої, тоді можливо показати після одержання Фур'є-спектра від f(t), що після поширення через довжину L волокна кожної p-ї моди, розподіл інтенсивності p-ї моди буде даватися як:
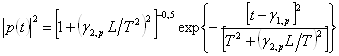 . (17)
. (17)
Тут індекс p для композиційної моди замінює номер двох індексів l і m, звичайно використовуваних для подання довільної моди, g1,p=gbp /dw½w=wc, g2,p=d2bp/dw2½w=wc. Рівняння (17) показує, що, як і вхідний iмпульс, вихідний імпульс має також гаусову форму і половина ширини вихідного iмпульсу, відповідного p-й моді, більше, ніж вхідний iмпульс, стосовно до Т це:
![]() . (18)
. (18)
В дійсності, так як багатомодове волокно підтримує велику кількість мод, повна інтенсивність, що буде визначатися законом другого ступеня в приймачі на виході лінії, буде даватися виразом:
![]() , (19)
, (19)
де Ap – амплітудний коефіцієнт p-ї моди. Важлива деталь, яку треба визначити – те, що час затримки передачі чи групова затримка (tg), зв'язана з кожною модою і, як очікувалося, дається як L dbp/dw і, крім того, міжмодова дисперсія приведе до різниці часу передачі між різноманітними модами. Понад того, спотворення форми iмпульсу в основному визначається другою похідною: d2bp / dw2.
Використовуючи (11) і (12), може бути показано, що
 . (20)
. (20)
Прості дії сводять вираз до:
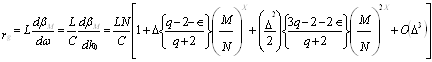 , (21)
, (21)
де 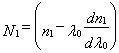 називається груповим
індексом, l0 – довжина хвилі в
свободному просторі і Î відоме як профіль
дисперсійного параметра, що дається формулою:
називається груповим
індексом, l0 – довжина хвилі в
свободному просторі і Î відоме як профіль
дисперсійного параметра, що дається формулою:
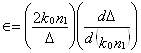 . (22)
. (22)
З (21) явно виходить, що для
q=2+κqopt, (23)
різниця в затримці серед мод щезне в першому порядку D, бо всі моди ефективно витратять однаковий час на переміщення (=LN1/C). На рисунку 3 зображений графік залежності qopt від l, зроблений так, щоб відобразити залежність для різних легуючих матеріалів, широко використованих в виробництві градiєнтних волокон для телекомунікацій. Він явно показує, що для одержання широкої смуги пропускання оптичних комунікацій на безлічі довжин хвиль (для систем з розгалуженням довжин хвиль) треба вибирати потрійну сукупність матеріалів, як, наприклад, P2O5-GeO2-SiO2 для серцевини.
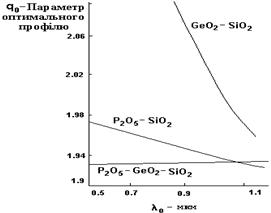
Рисунок 3 – Залежність qопт від довжини хвилі для різних хімічних складів матеріалу серцевини.
Тут необхідно визначити, що на практиці, з-за того, що послідовні імпульси, що випромінюються променями можуть не бути ідентичними по формі і в той же час їх форма з неминучістю не може бути вірно визначена, інженери систем воліють використати визначення площі iмпульса у вигляді основного значення шляхом розрахунку дисперсії вхідного і вихідного імпульсів. По визначенню, середня ширина iмпульсу f(t) довільної форми дається формулою:
 . (24)
. (24)
Цим визначенням s Ольшанський і Кек показали, що
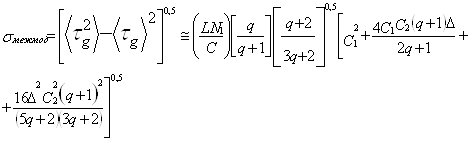 , (25)
, (25)
де
![]() . (26)
. (26)
Мiнiмiзация міжмодових середніх значень ширини iмпульса дозволяє одержати оптимальне значення q в формулі (23) як
![]() . (27)
. (27)
Якщо описувати загальне поширення iмпульсу в багатомодовому волокні як суму середніх тривалостей у відповідності як міжмодової, так і внутрішньомодової дисперсією, тоді
sзагальне=(s2міжмодов+s2внутрішньомодов)0,5, (28)
де:
sвнутрішньомод @ (L/C) (sS/l0)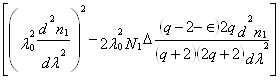 , (29)
, (29)
де ss =[(l-l0)2S(l) dl]0,5 – як середня ширина спектрального розподілення джерела, l0 – значення довжини хвилі. З (25) можна побачити, що за відсутності матеріальної дисперсії (n¹f(l)) та дисперсії із-за прoфiлю (Î=0) будe:
sq=¥ / sopt =10 / D. (30)
Звичайно, для D=1%, середнє поширення iмпульса в східчастому волокні буде майже 14 нс/км, в той час як оптимальний профіль волокна забезпечить (для того ж D) ~ 0,014 нс/км, тобто в 1000 раз менше.
Треба визначити, що відповідно до виробничих допусків навряд чи можна досягти практично оптимального профілю і навіть малі відхилення від оптимального профіля приведут до зростання дисперсії iмпульсу. Наприклад, добре відомо, що найбільш широко використовуваний процес виробництва волокон MCVD – метод (метод модіфікованого хімічного парового осідання) звичайно приводить до характерного провалу в профілі показника заломлення вздовж осі волокна з-за випарування деяких з добавок від найбільш глибоких шарів утворюючої форми на так званій стадії зупинки. Хуллар та інші, показали, що в волокні з параболічним профілем серцевини (волокно з параметрами n1=1,476; n2=1,458; v=30), різниця між часом передачі самої повільної та самої швидкої мод зростає від 0,37 нс/км (за відсутності провалу) до 1,73 нс/км в присутності 10% осьового провалу відносно ширини b/a=0,03, b – половина ширини провалу, а – радіус серцевини.