Дипломная работа: Математическое моделирование роста доходности страховой компании
Министерство образования Российской Федерации
Воронежский государственный университет
Факультет прикладной математике и механики
Кафедра математических методов исследования операций
ДИПЛОМНАЯ РАБОТА
НА ТЕМУ: Математическое моделирование роста доходности страховой компании
Исполнитель:
студентка 5 - го курса д.о. Ачуева А.В.
Воронеж
Содержание
Введение
Глава 1. Математическое моделирование роста доходности страховых компаний.
§1 Общая характеристика основных фактов и понятий при моделировании деятельности страховых компаний
§2 Математические модели роста доходности страховой компании
п.1 Простейшая модель роста доходности страховой компании
п.2 Многомерная модель роста доходности страховой компании
п.3 Многосекторная модель роста доходности страховой компании
п.4 Дискретный аналог простейшей модели роста доходности страховой компании
Глава 2. Математический анализ моделей роста доходности страховой компании
§1 Математический анализ простейшей модели роста доходности
страховой компании
§2 Математический анализ многомерной модели роста доходности страховой компании
§3 Математический анализ многосекторной модели роста
доходности страховой компании
§4 Математический анализ дискретного аналога простейшей модели
роста доходности страховой компании
Глава 3. Моделирование роста доходности на основе совершенствования отношений Страховщика и Страхователя
§1 Основные положения, блок-схема функциональных возможностей и характеристика структур данных Справочника
§2 Процедура выдачи рекомендаций по выбору страховой компании
§3 Инструкция пользователю программой
Заключение
Литература
Введение
Страхование - одна из древнейших категорий общественных отношений и видов деятельности. Зародившись в период разложения первобытно - общественного строя, оно постепенно стало непременным спутником общественного производства. Идея страхования заключается в солидарной замкнутой раскладке ущерба. Сущность страхования состоит в формировании определенного денежного (страхового) фонда и его распределении во времени и пространстве с целью возмещения возможного ущерба (убытков) его участникам при наступлении несчастных случаев, стихийных бедствий и других обстоятельств, приводящих к потере различных видов собственности и активов, предусмотренных договором страхования. Таким образом перераспределительные отношения, присущие страхованию, связаны, с одной стороны, с формированием страхового фонда с помощью заранее зафиксированных страховых платежей, с другой с возмещением ущерба из этого фонда участникам страхования. Специфичность финансовых отношений при страховании состоит в вероятностном характере этих отношений.
Страхование как защита имущественных интересов граждан, организаций и государства является необходимым элементом социально - экономической системы общества. Страхование предоставляет гарантии восстановления нарушенных имущественных интересов в случае непредвиденных природных, техногенных и других явлений, оказывает позитивное влияние на укрепление финансов государства.
Продолжают создаваться крупные страховые компании, способные адаптироваться к динамично меняющейся конъюктуре рынка. Но тем не менее весь объём страховых взносов в нашей стране сопоставим с аналогичными показателями лишь одной западной компании, замыкающей перечень ста крупнейших страховых компаний мира. Финансовые возможности национальных страховых компаний по покрытию крупных убытков остаются низкими. У большинства из них вкладами в уставной капитал являются права на имущество, другие низколиквидные средства, что не лучшим образом влияет на надежность и платёжеспособность страховых компаний.
В настоящее время на территории России страхование осуществляют около 2300 страховых компаний, внесённых в государственный реестр. Как и в других странах, страховое дело в России представлено множеством различных по масштабам и формам организации страховых обществ. По характеру страховых операций все фирмы, функционирующие на страховом рынке, можно разделить на две группы независимо от их организационно-правовой формы.
Первая - универсальные страховщики, которые ориентируются на оказание широкого спектра страховых услуг, осуществляют “все виды деятельности”. У таких компаний наиболее распространено следующее страхование: жизни, от несчастных случаев, медицинское, имущества, грузов, наземного транспорта.
Вторая группа - страховые общества, специализирующиеся на определенном виде страхования ( например, общества медицинского страхования).
Эффективность работы страховых компаний в значительной степени зависит от эффективности работы их организационных служб и от успешности деятельности страховых агентов. Одним из факторов, обеспечивающих выявление путей совершенствования этой деятельности является применение математических методов. В известной литературе по этой проблеме, смотри например [1,4,5,8,10], рассматривают конкретные виды страхования либо проблему автоматизации их собственной деятельности.[3,7,2]
Важнейшей проблемой успешной жизнедеятельности страховых компаний является ее выживание. Проблема выживания многоаспектна. В русле ее решения находятся исследования эффективной тарифной, кредитной, банковской, рекламной, информационной политике и т.д. Некоторые из этих аспектов рассмотрены в литературе и находятся под пристальным вниманием страховых компаний.[9] Однако с нашей точки зрения два направления требуют внимания. Речь идет, во-первых, о совершенствовании работы с физическими лицами, так как именно их средства являются основой поступления надежного денежного потока. Во-вторых, о совершенствовании работы страховых агентов. Это направление требует в настоящее время особого внимания в силу малых средств у физических лиц и появившихся свидетельств неполной заинтересованности отдельных страховых агентов в работе страховых компаний. В связи с этим весьма актуальной является задача выявления таких способов и правил работы страховых агентов, при которых его интересы в большей степени соответствовали интересам фирмы.
В связи со сказанным выше в данной дипломной работе рассматриваются математические модели и методы реализации этих двух направлений. Дипломная работа состоит из 3 глав, приложения, литературы и заключения.
Глава 1. Математическое моделирование роста доходности страховых компаний
§1 Общая характеристика основных фактов и понятий при моделировании деятельности страховых компаний
Рассматривается страховая компания, в которой имеются две группы сотрудников:
· штатные сотрудники (бухгалтера, управленческий персонал и т.д.)
· сотрудники работающие по контракту (страховые агенты)
Затраты по оплате труда штатных сотрудников считаются известными. Общие принципы оплаты труда работников по контракту тоже.
Будем рассматривать всех страховых агентов в объединенной группе, политика выплат администрации относительно каждого из элементов группы одинакова. Эту группу впредь будем называть обобщенным страховым агентом (ОбщСтрахА).
Оплата труда штатных сотрудников осуществляется за счет их собственной деятельности и работы обобщенного страхового агента. Рассмотрим ситуацию, когда деятельность штатных сотрудников оплачивается на основе результатов работы обобщенного страхового агента.
ОбщСтрахА не физическое лицо, а некоторая их совокупность, которая образует динамически стабильную структуру в системе сложившихся экономических отношений внутри страховой компании. Эта группа может рассматриваться в виде относительно независимой ассоциации, поскольку исполняет определенную функцию и в определенных правилах, сформулированных администрацией страховой компании.
Доход страховых агентов складывается из комиссионных вознаграждений за заключенные им договора. Также страховые агенты, как и штатные сотрудники, имеют право на оплачиваемый отпуск, получают премии.
Страховая компания работает на принципе самоокупаемости, осуществляя свои расходы за счет собственных доходов. Основным источником дохода страховых компаний являются страховые взносы ( поступления ). В распоряжении компании имеются следующие виды капиталов: уставной фонд, добавочный капитал, резервный капитал, фонд социальной сферы, фонд накопления, резерв незаработанной премии и другие. Все виды капиталов кроме уставного относятся к оборотному капиталу. Из страховых взносов формируются все необходимые капиталы и фонды, относящиеся к оборотному капиталу. Резервный капитал используется, если расходы на страховое возмещение превышают размер капитала, отведенного на покрытие этих расходов. Он пополняется за счет доходов по инвестициям ( покупка акций, облигаций, вложение средств в банки и т.д.)
Расходы страховой компании включают в себя затраты по заключению договоров страхования, административные расходы (премии страховым агентам, зарплата штатным сотрудникам и другие виды расходов), управленческие расходы (амортизация основных средств, расходы на создание основных фондов, налоги, сборы, затраты на рекламу, затраты на аренду и т.д.).
Все компании предлагают практически одни и те же услуги. Любой страховой продукт, независимо от видов страхования, строится по единой схеме. Каждая страховая услуга включает в себя:
1. технические характеристики - описание рисков и объектов страхования;
2. юридические условия - набор правовых условий, определяющих существо гарантии или ответственности страховщика, оговорки, исключения, особые условия, условия внесения страховой премии и выплаты возмещения;
3. экономические условия - цены, страховые суммы, размер франшиз, индексации и т.д.;
4. дополнительные услуги и сервис, предоставляемые страховщиком;
В процессе заключения договоров страхования страховщик и страхователь определяют и согласовывают необходимые его условия ( все выше перечисленные ). Страховщик при этом стремится, чтобы условия договора обеспечили бы полное и своевременное выполнение им принимаемой на себя ответственности. Страхователь заинтересован в получении полномасштабной страховой защиты при минимизации затрат на нее.
В период смены экономического уклада сложившиеся отношения между страховыми агентами и компанией перестают быть эффективными, так как интересы агента могут выступать в противоречии с интересами страховой компании. Бывают случаи, когда агент заключает заведомо невыгодные договора страхования: страхуют уже разбитую машину, датируя договор задним числом. В связи с этим формируется следующая задача.
Задача: отыскать способы, процедуры оплаты работы страховых агентов, при которых интересы последних и страховых компаний в целом наилучшим образом сочетались бы, и разработать справочник для страхователей и страховщиков, в котором страхователи получили бы полную необходимую им информацию об услугах и правилах страхования, а страховщик всю необходимую справочную информацию о совершенствовании собственной деятельности.
Поставленная выше задача предполагает необходимость решения двух следующих подзадач:
1) задачи сопряжения интересов страховых агентов и страховых компаний;
2) задачи разработки Справочника страховщика и страхователя;
Математическое описание моделей, обеспечивающих решение первой подзадачи приведено в §2 главы 1. Качественный математический анализ разработанных моделей, способы сведения их к оптимизационным задачам стандартного вида и программный комплекс реализации алгоритмов описаны в главе 2. Постановка и решение задачи формирования Справочника приведены в главе 3.
§2 Математические модели роста доходности страховых компаний
Математические модели выживания страховых компаний на основе оптимизации деятельности страховых агентов формулируется как задачи оптимального управления с коэффициентами, характеризующими долю участия агента в суммарном доходе страховой компании. При этом формулируется простейший алгоритм модели, в которой по отношению ко всем страховым агентам проводится единая политика их заинтересованности, и два более сложных аналога (многомерный и многосекторный). В многомерном при описании модели предполагается, что политика администрации компании по отношению к страховым не одинакова и оплата труда страховых агентов производится дифференцировано с учетом их участка работы, оборотный капитал компании складывается как сумма капиталов, заработанных каждым агентом.
В многосекторной аналоге предполагается, что страховая компания является неспециализированной, доходность страховой компании есть сумма частей, принесенных каждым страховым агентом.
п.1 Формулировка простейшей модели роста доходности страховых компаний.
При формулировке этой модели используется идея работы Яновского Л.П. [14], переписывается в условиях новой сферы и модифицируется в следствие новых условий.
Пусть I(t) - доход обобщенного страхового агента, R(t) - доходность страховой компании (объем поступивших страховых платежей), a - весовой коэффициент,0<a<1, взвешивающий суммарный доход страховой компании и обобщенного страхового агента.
Тогда целевой функционал модели, характеризующий суммарный специальным образом рассчитанный доход страховой компании может быть записан в следующем виде:
?
J(t)=ò(aI(t)+(1-a)R(t))e-rt dt ® max
0
Здесь e-rt- функция дисконтирования; r - коэффициент дисконтирования. Заметим, что доходность страховой компании, мы будем рассматривать как функцию от оборотного капитала (K(t)) и фонда оплаты труда штатных сотрудников (L(t)).
R(t)=F(k(t),L(t)) (2.1)
Отметим, что обобщенный страховой агент не входят в число штатных сотрудников, а работает на основе контракта. Его доход I(t)) определяется как доля от величины поступивших за счет его работы страховых платежей. При этом, если представить, что работа обобщенного страхового агента является единственным источником дохода страховой компании, а ставка комиссионного вознаграждения (m) известна, тогда справедливо соотношение.
I(t)=mR(t), 0<m<1
Полученный доход R(t) используется по следующим направлениям:
· формирование дохода обобщенного страхового агента: mR(t)
· развитие жизнедеятельности фирмы
(1-m)R(t)=Wa(t)+L(t)+K’(t)+dK(t)+p(t)K(t)
p(t)³pc, p(t)- прибыль держателей акций
Wa(t) - затраты, связанные с процессом и обслуживанием заключения договоров страхования и средств, выделяемых администрацией обобщенному страховому агенту в форме отпускных и других положенных ему денежных вознаграждений
Wa(t) = gK(t)+CmL(t)
Здесь g - доля капитала, отведенная на покрытие расходов, связанных с процессом и обслуживанием заключения договоров страхования, 0<g<1,Cm - коэффициент, характеризующий премию в форме отпускных за участие в создании и пополнении фонда отпускных средств, 0<Cm<1, K’(t)- чистые инвестиции, d- коэффициент обслуживания процесса вложения оборотного капитала, 0<d<1.
Таким образом, простейшая модель записывается ввиде
? -rt
J(t)=ò(aI(t)+(1-a)R(t))e dt
0
R(t)=F(K(t),L(t))
I(t)=mR(t)
(1-m)R(t)=Wa(t)+L(t)+K’(t)+dK(t)+p(t)K(t)
p(t)³pc, 0<d<1
Wa(t) = gK(t)+CmL(t)
0<g<1, 0<Cm<1, 0<a<1, 0<m<1
L(0)=L0, L0>0, K(0)=K0, K0>0
L0, K0-фиксированы
Модель представляет собой задачу оптимального управления с параметрами управления a,g,m,d,Сm.
n2. Многомерная модель роста доходности страховой компании.
Рассматривается страховая фирма, в которой работают n страховых агентов. Каждый агент работает на своем участке. Участки считаются неэквивалентными. Для того чтобы оценить работу страхового агента, введем коэффициент b, который зависит от следующих факторов:
1.плотность населения участка
2. уровень доходности жителей и т.д.
3. тип района, где расположен участок
4. опыт работы страхового агента
Обозначим коэффициент каждого агента bi,где i=1,n и
Предположим, что капитал фирмы есть сумма капиталов, заработанных каждым агентом.
n
K(t)=åKj(t) (2.2)
j=1
Предположим, что оплата труда организационных работников осуществляется за счет работы страховых агентов и затраты на их содержание распределяются пропорционально между всеми агентами.
Как и в модели рассмотренной выше, нас интересует ситуация, когда интересы, заключающиеся в получении максимума прибыли, агента и компании взаимосвязаны.
В силу аналогичных рассуждений целевой функционал построим в виде:
¥ n
J(t)=ò( åaIj(t) +(1-a)R(t))e-rt dt
0 j=1
здесь Ij(t)- доход j - го агента, "j j=1,n
R(t) можно представить в виде производственной функции.
Т.е.
R(t)=F(K1(t),K2(t),..., Kn(t), L(t)) (2.3)
Здесь Kj(t) - капитал, заработанный j - ым агентом.
Доход страхового агента можно представить как долю от величины поступивших за счет его работы страховых платежей с учетом коэффициента, характеризующего его страховое поле.(Определения, связанные со страхованием смотри в приложении 1) Все необходимые предположения для определения дохода j-го страхового агента сделаны в п.1
Ij(t)=mbjR(t), где 0<m<1, bj>0, "j j=1,n
Аналогично рассуждениям, приведенным в предыдущей модели, R(t) используется по тем же направлениям. Часть дохода страховой компании, идущая на развитие жизнедеятельности фирмы, распределяется следующим образом:
n
(1-m)R(t)=åWaj(t) +L(t)+dK(t)+ K’(t) +p(t) K(t) (2.4)
j=1
Здесь Waj(t) - затраты, связанные с процессом и обслуживанием заключения договоров страхования и средств, выделяемых администрацией j - му страховому агенту в форме отпускных и других положенных ему денежных вознаграждений.
Waj(t) = gKj(t)+CmL(t)/n "j j=1,n (2.5)
Все прочие обозначения смотрите в п.1.
Таким образом модель имеет вид:
Максимизировать
¥ n
J(t)=ò( åaIj(t) +(1-a)R(t))e-rt dt
0 j=1
при условиях
n
(1-m)R(t)=åWaj(t) +L(t)+dK(t)+ K’(t) +p(t) K(t)
j=1
R(t)=F(K1(t),K2(t),..., Kn(t), L(t))
Ij(t)=mbjR(t), где 0<m<1, bj>0, "j j=1,n
Waj(t) = gKj(t)+CmL(t), "j j=1,n
0<g<1,0<Cm<1, 0<d<1
p(t)³pс,0<a<1,
L(0)=L0, L0>0,K(0)=K0,K0>0
п3. Многосекторная модель роста доходности страховой фирмы.
Рассматривается страховая фирма, которая предлагает n видов страхования. Каждый агент занимается только одним видом страхования, таким образом имеем n агентов. Все агенты работают на одном и том же участке.
Предполагается, что доходность фирмы складывается из договоров, заключенных агентами, т.е.
n
R(t)= åRj(t).
j=1
Верно также и соотношение (2.2)
В силу аналогичных рассуждений целевой функционал построим в виде:
¥ n n
J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e-rt dt
0 j=1 j=1
Здесь Ij(t)- доход агента, где j=1,n. Rj(t) - объем заключенных договоров j-ым агентом, в руб.
Rj(t) можно представить в виде производственной функции.
Rj(t)=F(Kj(t), L(t)), "j j=1,n. (2.6).
Из рассуждений приведенных в п.2 доход j - го страхового агента определяется по формуле
Ij(t)=mjRj(t), "j j=1,n.
Рассуждения, связанные с распределением дохода страховой компании аналогичны приведенным выше. ( п.2). Соответственно сохраняются выражения (2.4) и (2.5).
Таким образом многосекторная модель имеет вид
Максимизировать
¥ n n
J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e -rt dt
0 j=1 j=1
при ограничениях
Rj(t)=F(Kj(t), L(t)) "j j=1,n
Ij(t)=m jRj(t) "j,j=1,n
n
(1- m)R(t)= åWaj(t)+L(t)+K’(t)+dK(t)+p(t)K(t)
j=1
Waj(t) = gKj(t)+CmL(t) "j,j=1,n
0<g<1, 0<Cm <1, 0<d<1
0<a<1, 0<m<1, p(t)³pc
L(0)=L0, L0>0, K(0)=K0, K0>0
п.4 Дискретный аналог простейшей модели роста доходности.
Дискретным аналогом простейшей модели является следующая модель, при постановке которой использовалась идея модели Лурье [6,стр.173]
aIT+(1-a)(RT+pcKT) ® max
при ограничениях
It=mRt-1-haD Kt-1 "t t=1,T
Rt=F(Kt,Lt) "t t=1,T
Kt=Kt-1+(1-a)D Kt "t t=1,T
Lt=Lt-1+D Lt "t t=1,T
(1-m)Rt=Wat+Lt+dKt+pcKt "t t=1,T
Wat=g Kt+CmLt "t t=1,T
0<a<1,0<m<1,0<h<1,Kt>0, Lt>0, DKt>0, DLt>0 "t t=1,T
K0, L0,а, d, pc,g, Cm- заданы
Здесь Т- конец рассматриваемого периода, а- доля выплат в общем потоке поступления средств, h - коэффициент штрафа, DKt-величина поступления оборотного капитала в период t, DLt- величина поступления фонда оплаты труда в период t.
Все остальные обозначения смотри в п.1.
Глава 2. Математический анализ моделей роста доходности страховой компании
§1 Математические анализ модели роста доходности страховой компании
Рассмотрим простейший аналог модели, приведенный в §2 главы 1. Приведем ее формулировку:
Максимизировать
?
ò (aI(t) + (1-a) R(t)) e-rt dt
0
при условии
(1-m)R(t)=gK(t)+CmL(t)+L(t)+dK(t)+K’(t)+p(t)K, 0<d<1
p(t)³pc,0<g+d+p<1,0<a<1, 0<m<1
L(0)=L0, L0>0 K(0)= K0, K0>0
K0 - начальный капитал фирмы, L0 - начальное значение фонда оплаты труда. Осуществим некоторые упрощения.
Предположим, что p(t)=pc. (1.1)
Учитывая (2.1) (гл.1) и тот факт, что F(K(t),L(t)) однородна и построив функцию Лагранжа, получим:
W(t)=(1- a+am)Lj(K(t)/L(t))e-rt + l(t)( -(1-m)L(t)j(K(t)/L(t)) + (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t))
В результате исходная модель приводится к виду:
?
ò W(t) dt ®max (1.2)
0
при условиях
L(0)=L0, K(0)=K0 (1.3)
0<g+d+pc<1,0<a<1, 0<m<1,0<Cm<1 (1.4)
Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (1.2)-(1.4)
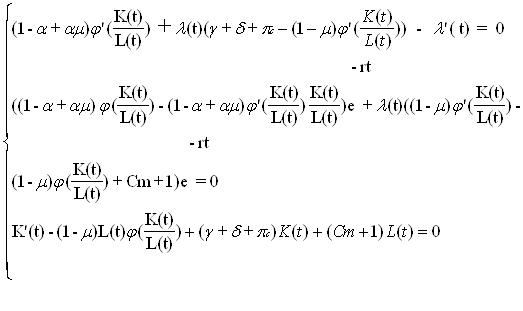
![]() Перепишем последнюю систему в удобном
виде.
Перепишем последнюю систему в удобном
виде.
![]() l¢(t)=(1-a+am)j’(
l¢(t)=(1-a+am)j’(![]() )e-rt+l(t)(g+d+pc-(1-m)j’(
)e-rt+l(t)(g+d+pc-(1-m)j’(![]() )
)
e-rt(1-a+am)(j(![]() )-j’(
)-j’(![]() )
)![]() )+l(t)((1-m)(j’(
)+l(t)((1-m)(j’(![]() )
)![]() -j(
-j(![]() ))+ Cm+1)=0
))+ Cm+1)=0
K’(t)-(1-m)L(t)j( ![]() )+(g+d+pc)K(t)+(Cm+1)L(t)=0 (1.5)
)+(g+d+pc)K(t)+(Cm+1)L(t)=0 (1.5)
Обозначим k(t)=K(t)/L(t) и продифференцируем по t
k’(t)= ![]() (1.6)
(1.6)
Из (1.5) учитывая, что n(t)=(dL/dt)/L(t), получим:
K’(t)/L(t) = k’(t)+ k (t)n(t) (1.7)
ля упрощения выписанных выше выражений введем еще одно обозначение: z(k) = j’(k) k -j(k) (1.8)
Функция j(k) построена на основе F(![]() ,1) и поэтому для нее выполняются
следующие свойства:
,1) и поэтому для нее выполняются
следующие свойства:
a) j¢(k)>0
b) j¢¢(k)<0
c) j’(k) ® ? для k ® 0
d) j’(k) ® 0 для k ® ?
Разделив последнее уравнение из (1.5) на L(t) и учтя обозначения, получим:
l’(t)= (1-a+am)j’(k(t))e-rt+l(t)(g+d+pc-(1-m)j’(k(t))) (1.9)
l(t) =( 1-a+am)z(k(t))e-rt /((1-m)z(k(t))+Cm+ 1) (1.10)
k’(t)=(1-m)j(k(t))-(g+d+pc)k(t)- (Cm+1) (1.11)
Продифференцировав (1.10) по t, получим:
-rt
l¢(t)=![]() 2 -rl(t) (1.12)
2 -rl(t) (1.12)
Учитывая, что
z’(k(t)) =j’’(k(t))k’(t)k(t) (1.13),
получаем, что формула (1.12) примет вид.
-rt
l¢(t)=![]() 2-rl(t) (1.14)
2-rl(t) (1.14)
Подставляя в (1.14) соотношения (1.9) и (1.10), выясним, что темп изменения капиталовооруженности вычисляется по формуле:
k’(t) =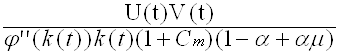 (1.15)
(1.15)
где
U(t) = (1 -m ) z(k(t)) + 1 + Cm
V(t) =(1-a+am)(j¢(k(t))U(t) + z(k(t))(r + d+g+pc-(1-m)j¢(k(t)))
Проведем качественный анализ уравнения ( 1.15 ).
Так как j¢(k) <0 для k >0, знаменатель в ( 1.15 ) отрицателен.(Мы предполагаем, что (1-a+am)(1+Cm)>0).
Далее из условий на функцию j(k) для z(k)=j¢(k)k-j(k) получаем z(k)£0 и z(k)® 0 при k ®0, и z(k) ® - ? при к ® ?. Для малых k
получаем U>0, V>0, так как j¢(k) - большое число, то k’<0. Для больших k получаем U<0, V<0, так как z(k) ® - ?, следовательно k’ <0. Из монотонного убывания U и V, что каждое из рассматриваемых уравнений U=0 и V=0 имеет единственный корень.
Таким образом область разбивается на три участка: kÎ[0,k1),
k Î[ k1, k2),kÎ[ k2,¥)
Из рисунка 1 видно, что
существует одна точка не устойчивого равновесия k1(m) и
две точки 0 и k2(m) устойчивого равновесия. Нетрудно видеть, что k1(m) и
k2(a,m) монотонно возрастающие функции по m. Если начальное значение k0=K0/L0 меньше чем k1(m), тогда k® 0 и фирма гибнет. В противном случае размеры фирмы стабилизируются и
стремятся к k2(m). Следовательно мы можем рассматривать k2(m)
как оптимальный размер фирмы для данных значений параметров управления a,m,g,d,Wr,Cm. Таким образом,
если заданы величины указанных выше параметров, то по величине k(t)=![]() может быть оценено качество начального состояния и
перспективы развития страховой компании.
может быть оценено качество начального состояния и
перспективы развития страховой компании.
Предлагается следующий путь:
Если ![]() <K(0), то необходимы меры по росту капитала или уменьшению L(t).Если есть возможность увеличить капитал, например за счет
кредита, то получаем следующую задачу:
<K(0), то необходимы меры по росту капитала или уменьшению L(t).Если есть возможность увеличить капитал, например за счет
кредита, то получаем следующую задачу:
![]() >K(0)
>K(0)
DK(t)®max
Если нет никакой возможности по увеличению капитала, то уменьшают фонд оплаты труда. В этом случае задача выглядит следующим образом:
![]() >K(0)
>K(0)
L(t)*<L(t)<L(t)**
DL(t)®min
Приведем пример расчетов оптимального размера фирмы.
Рассмотрим влияние изменений параметра управления a на оптимальный размер страховой компании. Данные для расчета были предоставлены компанией Росгосстрах. Предполагается, что d=0.13, g=0.03, m= 0.1, Cm=0.8. Тогда зависимость k1, k2 представлены в таблице 1.
| k/a | 0 | ¼ | 1/2 | ¾ | 1 |
|
k1 |
7.2 | 7.2 | 7.2 | 7.2 | 7.2 |
|
k2 |
3.49 | 3.39 | 3.15 | 3.13 | 2.93 |
Таб.1
Можно исследовать значения k1 и k2 для других значений параметров, полагая m= 0.05, получаем таблицу 2.
| a | 0 | 1/4 | 1/2 | 3/4 | 1 |
|
k1 |
6.8 | 6.8 | 6.8 | 6.8 | 6.8 |
|
k2 |
3.4 | 3.23 | 3.15 | 3.13 | 3 |
Таб.2
Окончательно заметим, что изменение ставки комиссионного вознаграждения m при фиксированном капитале К ведет к уменьшению капиталовооруженности k.
§2 Математический анализ многомерной модели роста доходности страховых компаний
Рассматриваемая модель имеет вид:
Максимизировать
![]() m
m ![]() R(t) + (1-a) R(t)) e-rt dt
R(t) + (1-a) R(t)) e-rt dt
при условии
(1-m)R(t)=![]() +(Cm+1)L(t) + dK(t)+ K’(t)+ p(t)K,
+(Cm+1)L(t) + dK(t)+ K’(t)+ p(t)K,
0<d<1, p(t)³pc, 0<g+d+p<1,0<a<1, 0<m<1
L(0)= L0, L0>0 K(0)= K0,K0>0
K0 - начальный оборотный капитал фирмы, L0 - начальный фонд оплаты труда штатных работников.
Будем рассматривать случай для n=2. Тогда рассматриваемая модель примет вид:
Максимизировать
![]() (am (b1+b2)R(t) + (1-a) R(t)) e -rt dt
(am (b1+b2)R(t) + (1-a) R(t)) e -rt dt
при условии
(1-m)R(t)=g(K1(t)+K2(t))+CmL(t)+L(t)+dK(t)+K’(t)+p(t)K(t),
0<d<1, p(t)³pc, 0<g+d+p<1, 0<a<1, 0<m<1
L(0)=L0, L0>0 K(0)= K0, K0>0
Выпишем функцию Лагранжа, учитывая (2.3) (гл.1) для случая n=2,(1.1) и тот факт, что F(K1(t), K2(t),L(t)) однородна, получим:
W(t)=(1- a+am(b1+b2))L(t)j![]() e-rt+
e-rt+
l(t)(-(1-m)L(t) j![]() + (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t))
+ (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t))
В результате исходная модель примет вид:
![]() W(t) dt ® max (2.1)
W(t) dt ® max (2.1)
при условиях L(0)=L0, K(0)=K0 (2.2)
0<d<1, 0<g+d+pc<1, 0<a<1, 0<m<1 (2.3)
Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (2.1)-(2.3)
(1-a+am(b1+b2))j’k1/l![]() e-rt+l(t)(g+d+pc-(1-m)
e-rt+l(t)(g+d+pc-(1-m)
j’ ![]() )-l’(t)=0
)-l’(t)=0
(1-a+am(b1+b2))j’k2/l![]() )e-rt+l(t)(g+d+pc-(1-m)j’k2/l
)e-rt+l(t)(g+d+pc-(1-m)j’k2/l![]() ) -l’(t)=0
) -l’(t)=0
l(t)=[(1-a+am(b1+b2))(![]() j’k1/l
j’k1/l![]() +
+ ![]() j’k2/l
j’k2/l![]() -j
-j![]() +e-rt]/[(1-m)(
+e-rt]/[(1-m)(![]() j’k1/l
j’k1/l![]() +
+![]()
j’![]()
![]() -j
-j![]() -Cm-1]
-Cm-1]
K’(t)-(1-m)L(t)j ![]() +(g+d+pc)K(t)+(Cm+1)L(t)=0
+(g+d+pc)K(t)+(Cm+1)L(t)=0
Перепишем последнюю систему в удобном виде.
l’(t)=(1-a+am(b1+b2))j’k1/l l![]() )e-rt+
)e-rt+
l(t)(g+d+pc-(1-m)j’k1/l l![]() )
)
l’(t)=(1-a+am(b1+b2))j’k2/l l![]() e-rt+
e-rt+
l(t)(g+d+pc-(1-m)j’k2/l l![]() )
)
l(t)=[(1-a+am(b1+b2))(![]() j’k1/l
j’k1/l![]() +
+ ![]() j’k2/l
j’k2/l![]() -j
-j![]() +e-rt]/[(1-m)(
+e-rt]/[(1-m)(![]() j’k1/l
j’k1/l![]() +
+![]()
j’![]()
![]() -j
-j![]() -Cm-1]
-Cm-1]
K’(t)=(1-m)L(t)j ![]() -(g+d+pc)K(t)-(Cm+1)L(t) (2.4)
-(g+d+pc)K(t)-(Cm+1)L(t) (2.4)
Обозначим
k(t)=K(t)/L(t), k1(t)=K1(t)/L(t), k2(t)=K2(t)/L(t) и n(t)=(dL/dt)/L (2.5)
и проведем аналогичные §1 рассуждения. Тогда справедливо соотношение (1.7).
Для упрощения полученной системы введем еще одно обозначение:
z(k(t)) = j’k1(t)(k1(t),k2(t)) k1(t) +j’k2(t)(k1(t),k2(t)) k2(t)-j(k1(t),k2(t))
Разделив уравнение (2.4) на L(t) и учитывая обозначения, получим:
l’(t)=(1-a+am(b1+b2))j’k1(k1(t), k2(t))e-rt+
l(t)(g+d+pc-(1-m)j’k1(k1(t), k2(t))) (2.6)
l’(t)=(1-a+am(b1+b2))j’k2(k1(t),k2(t))e-rt+
l(t)(g+d+pc-(1-m)j’k2(k1(t), k2(t))) (2.7)
l(t)=[(1-a+am(b1+b2))z(k1(t),k2(t))e-rt]/[(1-m)(z(k1(t),k2(t))+Cm+1] (2.8)
k’(t)=(1-m)j(k1(t),k2(t))-(g+d+pc)k(t)-(Cm+1) (2.9)
Продифференцируем (2.8) по t. Получим:
-rt
l¢(t)=![]() 2 -rl(t) (2.10)
2 -rl(t) (2.10)
Учитывая, что z’(k1(t),k2(t)) =j’’k1k1( k1(t),k2(t))k’1(t)k1(t) +j’’k2k2( k1(t),k2(t))k’2(t)k2(t), получаем, что формула (2.10) примет вид
l¢(t) =e -rt(j’’k1k1( k1(t),k2(t))k’1(t)k1(t) +j’’k2k2( k1(t),k2(t))k’2(t)k2(t))(1- a+am(b1+b2))(Cm+1) / [(1 -m)z(k1(t),k2(t)) + Cm +1] 2 - rl(t) (2.11)
Подставляем в (2.11) соотношения (2.6) и (2.8), (2.7) и (2.8) соответственно, получим, что темп изменения капиталовооруженности вычисляется по формулам:
k’(t)=(1-m)j(k1(t),k2(t))-(g+d+pc)k(t)-(Cm+1)
k’1(t)=![]()
k’2(t)= ![]()
где
U(t)= (1 -m)z(k1(t),k2(t)) + Cm +1
V1(t)= Cm +1+z(k1(t),k2(t))((1 -m) +j’k1( k1(t),k2(t))(1 -m)-(g+d+pc+r))
V2(t)= Cm +1+z(k1(t),k2(t))((1 -m) +j’k2( k1(t),k2(t))(1 -m)-(g+d+pc+r))
Рассмотрим случай, когда оба агента участвуют в формировании капитала фирмы в равных долях. Тогда (при n=1) рассматриваемая модель сводится к сличаю приведенному в §1. Однако, если доли не равны, то приходим к качественно новой задаче.
§3 Математический анализ многосекторной модели роста доходности страховой компании
Напишем ее формулировку.
Максимизировать
¥ n n -rt
J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e dt
0 j=1 j=1
при ограничениях
Rj(t)=F(Kj(t), L(t)) "j j=1,n
Ij(t)=m jRj(t), 0<mj<1,"j,j=1,n
n
(1- m)R(t)= åWaj(t)+L(t)+K’(t)+dK(t)+p(t)K(t)
j=1
Waj(t) = gKj(t)+CmL(t) "j,j=1,n
0<g<1, 0<Cm <1, 0<d<1
0<a<1, p(t)³pc
L(0)=L0, L0>0, K(0)=K0, K0>0
Выпишем модель для случая n=2.
Максимизировать
?
ò (a(m1 R1(t) + m1R2(t)) + (1-a) (R1(t)+R(t)) e -rt dt
0
при условии
(1-m1-m2)R(t)=g( K1(t)+ K2(t))+ CmL(t)+L(t) + dK(t)+K’(t)+p(t)K(t),
0<d<1, p(t)³pc,0<g+d+p<1
L(0)=L0, L0>0 K(0)=K0,K0>0
K0 - начальный капитал фирмы, L0 - начальное количество работников.
Выпишем функцию Лагранжа, учитывая (2.6), (1.1) и тот факт, что F(Kî(t),L(t)) "j,j=1,2 однородна, получим:
W(t)=(am1L(t)j( (![]() )+am2L(t)j( (
)+am2L(t)j( (![]() )+(1- a)L(t)j( (
)+(1- a)L(t)j( (![]() )e-rt + l(t)( -(1-m1-m2)L(t)j((
)e-rt + l(t)( -(1-m1-m2)L(t)j((![]() ) + (g+d+pc)K(t) + (Cm +1)L(t) + K’(t))
) + (g+d+pc)K(t) + (Cm +1)L(t) + K’(t))
В результате исходная модель записывается в виде (2.1)-(2.3)
Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (2.1)-(2.3)
( am1j ‘(![]() ) + (1-a)j’(
) + (1-a)j’(![]() )e-rt+l(t)(g+d+pc-(1-m1-m2)j’(
)e-rt+l(t)(g+d+pc-(1-m1-m2)j’(![]() )-l’(t)=0
)-l’(t)=0
( am2j ‘(![]() ) + (1-a)j’(
) + (1-a)j’(![]() )e-rt+l(t)(g+d+pc-(1-m1-m2)j’(
)e-rt+l(t)(g+d+pc-(1-m1-m2)j’(![]() )-l’(t)=0
)-l’(t)=0
(a ( m1j(![]() ) +m2j(
) +m2j(![]() )-(m1j’(
)-(m1j’(![]() )
)![]() +m2j’ (
+m2j’ (![]() )
)![]() )) + (1-a) (j(
)) + (1-a) (j(![]() )-j’(
)-j’(![]() )
)![]() ))e -rt+l(t)((1-m1-m2)j’(
))e -rt+l(t)((1-m1-m2)j’(![]() )
)![]() -(1-m1-m2)j(
-(1-m1-m2)j(![]() ) + Cm+1)=0
) + Cm+1)=0
K’(t)-(1-m)L(t)j(![]() )+(g+d+pc)K(t)+(Cm+1 )L(t)=0 (3.1)
)+(g+d+pc)K(t)+(Cm+1 )L(t)=0 (3.1)
Перепишем последнюю систему в удобном виде.
l¢(t)=(am1j’(![]() )+(1-a)j’(
)+(1-a)j’(![]() ))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((
))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((![]() ))
))
l¢(t)=(am2j’(![]() )+(1-a)j’(
)+(1-a)j’(![]() ))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((
))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((![]() ))
))
(am1(j(![]() )-j’(
)-j’(![]() )
)![]() )+am2(j(
)+am2(j(![]() )-j’(
)-j’(![]() )
)![]() )+(1-a)(j(
)+(1-a)(j(![]() )-j’(
)-j’(![]() )
)![]() ))e-rt+l(t)((1-m1-m2)(j’(
))e-rt+l(t)((1-m1-m2)(j’(![]() )
)![]() -j(
-j(![]() ))+Cm+1)=0
))+Cm+1)=0
K’(t)-(1-m)L(t)j(![]() )+(g+d+pc)K(t)+(Cm+1 )L(t)=0 (3.2)
)+(g+d+pc)K(t)+(Cm+1 )L(t)=0 (3.2)
Проведя аналогичные рассуждения, что и в §1, введем обозначения аналогичные (1.8) z(kj(t)) = j’(kj(t)) kj(t) -j( kj(t) ) для j=1,2. (3.3)
Разделив (3.2) на L(t) и учитывая обозначения (3.3) и (1.8), получим:
l’(t)=(am1j’(k1(t))+(1-a)j’(k(t)))e-rt+l(t)(g+d+pc-(1-m1-m2)j’(k(t))) (3.4)
l’(t)=(am2j’(k2(t))+(1-a)j’(k(t)))e-rt+l(t)(g+d+pc-(1-m1-m2)j’(k(t))) (3.5)
-rt
l(t)=![]() (3.6)
(3.6)
k’(t) = (1 -m)j(k(t))-(g+d+pc)k(t) - (Cm + 1) (3.7)
После дифференцирования (3.7) по t получим:
l¢(t) = e-rt[(am1z’(k1(t))+am2z’(k2(t))+(1-a) z’(k(t)))(Cm+1+(1-m1-m2)z(k(t))) - (am1z(k1(t))+am2z(k2(t))+(1-a)z(k(t)))(1-m1-m2)z’(k(t))]/ [(1-m1-m2)z(k(t)) + Cm + 1 ]2 - rl(t) (3.8)
Учитывая (1.8) и аналогичные выражения для z(kj(t)) для j=1,2,получаем, что формула (3.8) примет вид:
l¢(t)=e-rt[(am1j’’(k1(t))k’1(t)k1(t)+am2j’’(k2(t))k’2(t)k2(t)+(1-a)j’’(k(t)) k’(t)k(t))(Cm+1+(1-m1-m2)z(k(t)))-(am1z(k1(t))+am2z(k2(t))+(1-a)z(k(t)))(1-m1-m2) j’’(k(t))k’(t)k(t))]/ [(1-m1-m2)z(k(t)) + Cm + 1 ]2 - rl(t) (3.9)
Подставляем в (3.9) соотношения (3.5),(3.7) и (3.6),(3.7), получим, что темп изменения капиталовооруженностей вычисляется по формулам:
k’(t) = (1 -m)j(k(t))-(g+d+pc)k(t) - (Cm + 1)
k’1(t)=[(am1j’(k1(t))+(1-a)j’(k(t)))U(t)+(g+d+pc-(1-m1-m2)j’(k(t)))
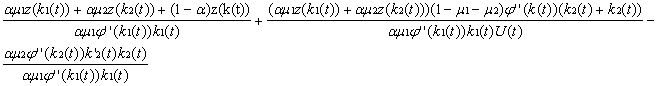 k’2(t)=[(am2j’(k2(t))+(1-a)j’(k(t)))U(t)+(g+d+pc-(1-m1-m2)j’(k(t)))
k’2(t)=[(am2j’(k2(t))+(1-a)j’(k(t)))U(t)+(g+d+pc-(1-m1-m2)j’(k(t)))
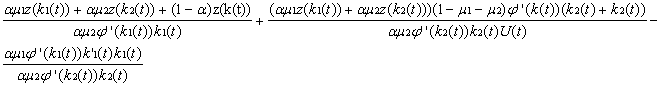
где
U(t) = (1-m1-m2 ) z(k(t)) + 1 + Cm
Если заданы параметры a, m1, m2, Cm,d, g может быть рассчитана капиталовооруженность по каждому виду страхования. Это позволит сделать обоснованные выводы о целесообразности включения нового вида страхования.
§4 Анализ дискретного аналога простейшей модели роста доходности страховой компании
Разработка и качественный анализ задач управления показал их теоретическую значимость для определения путей совершенствования работы страховых фирм и одновременно наличие вычислительных и информационных трудностей в их реализации. Однако, используя логику приведенных выше соотношений, можно сформулировать дискретные аналоги моделей, позволяющие записать задачу в виде привычных достаточно легко реализуемых задач оптимизации и разрешить их имеющимися математическими и программными средствами. Этот путь был реализован для простейшей модели.
Рассматриваемая модель имеет вид:
aIT+(1-a)(RT+pcKT) ® max
при ограничениях
It=mRt-1-haD Kt-1 "t t=1,T
Rt=F(Kt,Lt) "t t=1,T
Kt=Kt-1+(1-a)D Kt "t t=1,T
Lt=Lt-1+D Lt "t t=1,T
(1-m)Rt=Wat+Lt+dKt+pcKt "t t=1,T
Wat=g Kt+CmLt "t t=1,T
0<a<1,0<m<1,0<h<1,Kt>0, Lt>0, DKt>0, DLt>0 "t t=1,T
K0, L0,а, d, pc,g, Cm- заданы
Для реализации этой модели предлагается использовать метод Соболя.
Отличительной чертой данного метода является систематический просмотр многомерных областей: в качестве пробных точек в пространстве параметров (переменных) используются точки равномерно распределенных последовательностей. Для этих целей были применены так называемые ЛПt- последовательности, которые обладают наилучшими характеристиками равномерности. Подробнее этот метод приведен в [11] с обоснованием и доказательством сходимости последовательностей к решению.
Сверхбыстрый алгоритм. В
работе [12] предложен способ расчета ЛПt- последовательностей. Для этого порядок следования точек Qi меняется так, чтобы каждая следующая
точка Qi вычислялась по предыдущей точке Qi-1 с помощью одной операции ![]() , где
, где ![]() означает поразрядное
сложение по модулю два в двоичной системе (операция “ исключающее ИЛИ”).
Приведем таблицу истинности для этой логической операции:
означает поразрядное
сложение по модулю два в двоичной системе (операция “ исключающее ИЛИ”).
Приведем таблицу истинности для этой логической операции:
x |
y |
x |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Приведем характеристики общей схемы алгоритма.
Пусть Г(i)-так называемый код Грея,
соответствующий номеру i. По
определению Г(i)= i ![]() [i/2],
где [z] - целая часть z. Два соседних кода Г(i) и Г(i-1) всегда различаются в одном и только в одном разряде l=l(i), номер которого
можно вычислить по формуле
[i/2],
где [z] - целая часть z. Два соседних кода Г(i) и Г(i-1) всегда различаются в одном и только в одном разряде l=l(i), номер которого
можно вычислить по формуле
l = 1+ log2 [Г(i) ![]() Г(i-1)]
Г(i-1)]
Поэтому, для расчета Qi получаем следующий простой алгоритм:
шаг1. q 0,1 =q 0,n=0
шаг2. q i,j= q i-1,j
![]() Vj(l) j=1,2,...n
(4.1).
Vj(l) j=1,2,...n
(4.1).
де Vj(l)=rj(l)2-l, rj(l)-числители направляющих чисел при 1?j?51, 1? l ?20
Счет оканчивается, когда i ( номер точки ) достигает необходимого количества. Сколько нужно брать точек описано в методе, приведенном ниже.
Приведем краткое описание алгоритма Соболя.
Пусть задана математическая модель, которая зависит от n неизвестных.
Каждой точке А поставим в соответствие набор параметров (а1, а2,...,аn).
аj?аj? аj* j=1,n (4.2)
Ограничения вида (4.2) выделяют в пространстве параметров параллелепипед. В дальнейшем нас будут интересовать только точки принадлежащие параллелепипеду.
Кроме этих ограничений в задачу обычно включают так называемые функциональные ограничения
f(A)< c** (4.3)
c** - некоторое значение, которое необходимо определить для того, чтобы множество G было замкнутым.
Обозначим через G={A| (4.1), (4.3)}.
Так же имеем некоторую функцию цели F(А).
Таким образом исходная задача имеет вид
F(А) ® мах
АÎG
Тогда для нахождения оптимальной точки используется следующий алгоритм.
Шаг1. Выбор точки Qi = (q1i,...,qni), где n- число неизвестных в модели.
Перебор точек осуществляется по алгоритму (4.1).
Шаг2. Пересчет точек.
Так как нас интересуют точки, удовлетворяющие ограничениям (4.2),
то пересчет осуществляется по формулам:
aij= aij + (aij* - aij) qij "j: j=1,n.
В результате получим точку Аi = (a1i,...,ani).
Шаг3. Проверка на удовлетворение множеству G.
Так как точки Аi i=1,N по построению удовлетворяет ограничениям (4.2), то осталось удовлетворяют ли точки ограничениям (4.3). Если нет, то эти точки отбрасываются. Если да, то считают F(А). Переход к шагу1.
Количество точек выбирается самим программистом с учетом следующего факта:
Пусть N - количество точек. При N® ? ЛП - последовательность становится равномерной и F(АN) ® max F(А)
AÎG
Глава3. Моделирование роста доходности на основе совершенствования отношений Страховщика и Страхователя
§1 Основные положения, блок-схема функциональных возможностей и характеристика структур данных Справочника
Наша программа - Справочник страхователя и страховщика содержит информацию о страховых компаниях, имеющихся в г. Воронеже, их координатах (адрес и телефон), правилах страхования, рейтингах крупнейших страховых компаний в России, и кроме того, Вы можете получить ответ на вопрос - “ в какие страховые компании Вы можете обратиться “, если указан вид страхования. Кроме того, предлагаются рекомендации по выбору страхового партнера и рекомендации по пользованию программой.
Программа написана для использования в среде Ms-Windows на языке Delphi 3, средствами которой можно получить всю необходимую информацию. Все имеющиеся сведения содержаться в базах данных, просмотреть которые можно в удобном для пользователя виде. Так как программа позволяет вносить, изменять и удалять данные, не требуя при этом какого - либо изменения текста программы.
Блок - схема функциональных возможностей и запросов справочника приведена на Рис.1.
Работа программы начинается с появления меню, в котором предлагаются функциональные возможности справочника, такие как: просмотр имеющихся в Воронеже страховых компаний, их координаты, виды страхования которые они предлагают, соответствующие правила страхования, запрос о страховых компаниях, в которые может обратиться страховщик, если известен выбранный им вид страхования, так же предлагаются рекомендации по выбору подходящей компании и справочная информация о рейтингах крупнейших в России страховых компаниях. После выбора соответствующего запроса, появляется новое окно, в котором предлагается соответствующая информация. Все необходимая информация хранится в базах данных. Большим достоинством системы является то, что от пользователя не требуется каких - либо особых навыков общения с компьютером. Работа осуществляется в диалоговом режиме с помощью мыши.
Используемые базы:
1) ania.db- база данных, содержащая информацию о страховых компаниях и их координатах;
2) strah.db - база данных, содержащая виды страхования;
3) rey.db - база данных, содержащая рейтинги крупнейших страховых компаний России;
4) svaz.db - база данных, связывающая номера компаний с номерами видов страхования;
Структура используемых баз данных приведена на рис.2.
Основной программный файл - project.res.
Все остальные файлы вспомогательные, описывают работу на соответствующей форме.
Unit1.pas- формирует главное меню программы;
Unit2.pas- осуществляет просмотр страховых компаний;
Unit3.pas- выдает список видов страхования. При обращении к любому виду выдает правила страхования;
Unit4.pas- выдает список видов страхования. При выборе любого вида страхования выдает список компаний, в которые может обратиться Страховщик, и рекомендации по выбору страхового партнера.
Unit5.pas- осуществляет просмотр крупнейших страховых компаний и их рейтингов;
Unit6.pas- файл, соответствующий вспомогательной форме, на которой выдаются правила страхования;
Unit7.pas- файл, соответствующий вспомогательной форме, на которой выдается список компаний, в которые может обратиться страхователь;
Unit8.pas- файл, выдающий справку по пользованию программой;
Unit9.pas- файл, соответствующий вспомогательной форме, на которой выдаются рекомендации по выбору страховщика;
Основные используемые процедуры в программе:
1) procedure. InsertButtonClick - осуществляет добавление записи в базу данных;
2) procedure.DeleteButtonClick - осуществляет удаление записи из базы данных;
3) procedure.PostButtonClick - запоминает запись в базе;
4) procedure.CancelButtonClick - осуществляет отмену выполняемых действий;
5) procedure.ButtonClick - осуществляет выход в главное меню;
6) procedure.Tform3.ButtonClick - позволяет просмотреть правила страхования;
7) procedure. Tform7.ButtonClick - позволяет просмотреть рекомендации по выбору страховщика;
8) procedure. Tform4.ButtonClick - осуществляет процедуру поиска. Результатом поиска является список страховых компаний, в которые может обратиться Страхователь;
§2 Процедура выдачи рекомендаций по выбору страховой компании
После того как Вы определили вид страхования, в котором возможен Ваш интерес, Вы можете поступить следующим образом:
I. Ознакомьтесь с рейтингом страховых организаций России.
В настоящее время некоторые издания (например, “Экономика и жизнь”) публикуют рейтинги страховых организаций. Так и в нашей программе приведены рейтинги крупнейших компаний в России за 98 и 99 г.г. Само по себе включение страховщика в подобный рейтинг еже в какой - то степени говорит о его надежности. Это может быть основанием для предварительного отбора. Нужно также учесть частоту включения Страховщика в рейтинг и динамику места компании в рейтинге. При этом возможны следующие ситуации:
а) стабильное место в рейтинге;
б) отрицательная динамика (компания на протяжении рассматриваемого периода ухудшало свое место в рейтинге);
в) положительная динамика (компания на протяжении
рассматриваемого периода улучшало свое место в рейтинге);
II. Обратите внимание в выбранной Вами компании на:
1) Наличие лицензии Департамента по надзору за страховой деятельностью на право проведения страхования по интересующему Страхователя виду страхования.
2) Срок существования страховой организации (как правило, чем дольше Страховщик активно работает на рынке, тем он надежнее).
3) Личные характеристики первого лица (лиц) страховой компании.
Возможны следующие варианты:
· за руководителем тянется шлейф банкротств и сомнительных финансовых афер;
· руководитель ничем себя не проявил;
· руководитель известная личность в финансовых и промышленных кругах, сотрудничает с органами Государственной власти, известен своими публикациями в прессе;
4) Список клиентов страховой компании (о надежности Страховщика свидетельствует факт, что среди страхователей - юридический лиц - крупные банки, промышленные предприятия, зарубежные фирмы и т.п.).
5) Список учредителей Страховщика. Размер оплаченного уставного капитала (чем больше оплаченный уставной капитал, тем надежнее Страховщик. Хорошо, когда учредителем является крупная и известная организация. Еще лучше, если учредителем является известный и крупный банк с развитой региональной сетью филиалов).
6) Тарифную политику страховщика (Страхователь должен провести предварительный маркетинг цен на страховые услуги (страховые тарифы) по выбранному кругу страховщиков. При этом лучше ориентироваться на средние цены страховых тарифов. Низкий тариф иногда назначается Страховщиком специально чтобы переманить к себе страхователей от других компаний. Но такая операция опасна для страховщика, так как подрывает его финансовую устойчивость. Высокий тариф так же таит в себе опасность для Страхователя - слишком высокие тарифы говорят о том, что у Страховщика слишком мал размер собственных средств и он хочет поправить свое материальное положение за счет Страхователя).
7) Наличие системы перестрахования рисков у Страховщика (все крупные страховщики выстраивают систему надежной перестраховочной защиты).
8) наличие (отсутствие) негативной информации в прессе о Страховщике.
III. Посетите офис Страховщика.
Немаловажно субъективное ощущение Страхователя, возникшее от посещения им офиса Страховщика. При разговоре с представителями Страховщика важно оценить следующие параметры:
1) Открытость Страховщика (в пределах разумного и в пределах, обусловленных законодательством) в представлении данных о себе (показывает ли Страховщик важнейший набор документов:
лицензию на проведение страхования со всеми приложениями, годовой баланс, аудиторское заключение по этому балансу, устав, учредительный договор и т.д.)
2) Вежливость, культура общения, внешний вид представителей Страховщика. Компетентность сотрудников Страховщика.
Также важно отметить, как организован прием посетителей страховщиком:
страховая компания имеет легко доступный сервисный зал для приема посетителей;
посещение офиса возможно только по предварительному разрешению;
страховая компания общается с потенциальными клиентами только через страховых агентов (в этом случае наиболее сложно оценить возможности Страховщика);
Выполнение указанных рекомендаций поможет Вам выбрать профессионального Страховщика.
§3 Инструкция пользователю программой
После запуска программы Вашему вниманию предлагается основное меню, которое содержит всю необходимую информацию. Для того, чтобы получить эту информацию нужно выделить соответствующую строку и щелкнуть по ней левой кнопкой мыши.
Если Вы выбираете просмотр страховых компаний, то Вашему вниманию предлагается форма, на которой расположена база данных, содержащая страховые компании г. Воронежа с их координатами. Просмотр базы данных осуществляется путем перемещения курсора по строкам базы.
Если Вы хотите добавить запись в базу, то нажмите копку “Добавить” и в прямоугольники, расположенные под соответствующем полем базы, внесите необходимую информацию. После внесения записи ее необходимо запомнить. Для этого нажмите кнопку “Запомнить”.
Если Вы хотите удалить запись из базы, то выделите соответствующую запись и нажмите копку “Удалить” и после появления соответствующего запроса подтвердите удаление, т.е. нажмите кнопку “Да”.
Если Вы хотите изменить запись в базе, то выделите соответствующую запись и нажмите копку “Изменить”. Все необходимые изменения вносятся в прямоугольники, расположенные под базой данных. Затем изменения необходимо сохранить.
Если Вы хотите закончить просмотр, то нажмите кнопку “Возврат в главное меню” или кнопку ý, которая располагается в верхнем правом углу формы.
Если Вы выбираете просмотр видов страхования, то Вашему вниманию предлагается форма, на которой расположена база данных, содержащая виды страхования. Для того, чтобы посмотреть необходимые Вам правила страхования нажмите кнопку “Правила”.
Для возврата к предыдущей форме, содержащей виды страхования, нажмите ý.Добавление, удаление и запоминание записи описано выше.
Если Вы выбираете выбор страховщика, то Вашему вниманию предлагается форма, на которой расположена база данных, содержащая виды страхования, предлагаемые всеми страховыми компаниями г. Воронежа. Выберите интересующий Вас вид страхования и нажмите кнопку “Подтвердите выбор”. Появится форма, на которой располагается список страховых компаний, которые предлагают этот вид услуг. Для получения рекомендаций по выбору страхового Партнера нажмите кнопку “Рекомендации”. Вашему вниманию предлагаются советы, которые необходимо учесть при выборе надежной страховой компании. Для возврата к форме, предлагающей выбор страховщика нажмите кнопку “ОК”.
Если Вы выбираете просмотр рейтингов крупнейших в России страховых компаний, то Вашему вниманию предлагается форма. на которой расположена база данных, содержащая наименования страховых компаний с их рейтингами за 98 и 99 г.г.
Если Вы хотите закончить работу, то Вам необходимо вернуться к лавному меню и нажать “Выход”.
Приложение1
Основные факты и определения связанные со страхованием
СТРАХОВАЯ ЗАЩИТА - понятие, имеющее двоякое смысловое значение ( в широком и узком смысле слова ):
1. экономическая категория, отражающая совокупность распределительных и перераспределительных отношений, связанных преодолением или возмещением потерь, наносимого производству и жизненному уровню населения стихийными бедствиями и другими чрезвычайными событиями;
2. совокупность перераспределительных отношений по поводу преодоления и возмещения ущерба, наносимого конкретным объектам общественного производства ( например, страховая защита жизни );
СТРАХОВЩИК - специализированная организация, проводящая страхование.
СТРАХОВАТЕЛЬ - физическое или юридическое лицо, уплачивающее страховые взносы и вступающее в конкретные страховые отношения со страховщиком.
СТРАХОВАЯ ОТВЕТСТВЕННОСТЬ - обязанность страховщика выплатить страховое возмещение или страховую сумму при оговоренных последствиях происшедших страховых случаев.
СТРАХОВАЯ СУММА - определенная договором страхования или установленная законом денежная сумма, исходя из которой устанавливаются размеры страхового взноса и страховой выплаты.
СТРАХОВАЯ ПРЕМИЯ (страховой взнос) - плата за страхование, которую страхователь обязан внести страховщику в соответствии с договором страхования или законом.
СТРАХОВАЯ ВЫПЛАТА - полная или частичная компенсация страховщиком ущерба при страховом случае.
СРАХОВОЙ ТАРИФ - выраженная в деньгах плата с единицы страховой суммы или процентная ставка для формирования страхового фонда.
СТРАХОВОЙ ПОЛИС - документ, выдаваемый страховщиком страхователю в качестве официального подтверждения факта заключения договора страхования, принятие на страхование оговоренных рисков.
СТРАХОВОЙ РИСК - предполагаемое событие, на случай наступления которого проводится страхование. Событие, которое рассматривается в качестве страхового риска, должно обладать признаками вероятности и случайности наступления.
СТРАХОВОЕ ПОЛЕ - максимальное количество объектов, которое можно застраховать на определенной территории.
Заключение
В настоящей работе изучено влияние поведения страховых агентов на рост доходности страховых компаний. Это направление в настоящее время требует особого внимания в силу, во-первых, малых свободных средств у физических лиц и, во-вторых, в силу появившихся свидетельств неполной заинтересованности отдельных страховых агентов в работе страховых компаний.( Бывают случаи, когда агент заключает заведомо невыгодные договора страхования: страхуют уже разбитую машину, датируя договор задним числом.)
В работе предложен путь сопряжения интересов и компании, определен способ выявления зоны банкротства последней и пути выхода из этой зоны. Кроме этого, получены доказательства существования оптимального размера фирмы, которые на прямую зависят от общего дохода страховых агентов. Предложенная простейшая модель положена в основу построения нескольких, важных для решения проблемы приближения условий ее реализации к реальным условиям функционирования страховой компании, математических моделей (многомерная модель роста доходности страховой компании, многосекторная модель роста доходности страховой компании, дискретный аналог простейшей модели роста доходности страховой компании,).
Разработан справочник страхователя и страховщика, позволяющий усовершенствовать работу с физическими лицами, так как именно их средства являются немаловажной частью поступлений надежного денежного потока.
Литература
1. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. - Наука, 1979г.,- 345с.
2. Гамаюмов М.В., Демент С.Е. Партнеры предприятия. - М.: Центр экономики и маркетинга, 1999г., - 240с.
3. Евдокимов А. Оптимизация затрат промышленного предприятия при страховании ракетно-космической техники. - Страховое дело №9, 1998г., 45-50с.
4. Интриллигатор Н. Математические методы оптимизации и экономическая теория. - М.: Прогресс, 1975г. - 320с.
5. Лисковец О.А. Вариационные методы решения неустойчивых задач.- Минск: Наука и Техника, 1981г. - 325с.
6. Лурье А.Л., Нит И.В. Экономико-математическое моделирование социалистического хозяйства. - изд. Московского университета, 1973г. -284с.
7. Медведчиков Д. Страховые премии при организации космического страхования. - Страховое дело №8 1998г., 29-33с.
8. Моисеев Н.Н., Иванников Ю.П., Столерова Е.М. Методы оптимизации. М.: Наука, 1978г. - 310с.
9. Орналюк-Малицкая. Платежеспособность страховых организаций.- 125с.
10. Петров А.А., Поспелов И.Г., Шананин А.А.. Опыт математического моделирования экономики. - М.: Энергоатомиздат, 1996г. -545с.
11. Соболь И.М. Точки равномерно заполняющие равномерный куб. - Знание, 1985г.,- 32с.
12. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. - М.: Наука, 1981 г., - 110с.
13. Шумаков П.В. Delphi 3 и создание приложений баз данных.
14. Яновский Л.П. Динамическая модель выживания крупного предприятия с рентоориентированным менеджментом. - Экономика и мат. методы. Т. 36, №2, 2000г., 75-82с.