Реферат: Измерение функции распределения атомов серебра методом Штерна-Ламмерта

Федеральное агентство по образованию

Волжский политехнический институт (филиал) Государственного образовательного учреждения высшего профессионального образования

"Волгоградский государственный технический университет"

Кафедра (ВТО).

Реферат

На тему: Измерение функции распределения атомов серебра методом Штерна - Ламмерта

Выполнил:

студент группы ВМ-236

Новиков Р.А.

Проверил:

к.т.н., доцент Авилов А.В.

Волжский 2010

Содержание

Введение

1. Физические основы измерений

2. Конструктивные особенности метода

3. Альтернативные способы измерения

Список используемой литературы

Введение

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ – раздел молекулярной физики, изучающий свойства вещества на основе представлений об их молекулярном строении и определенных законах взаимодействия между атомами (молекулами), из которых состоит вещество. Считается, что частицы вещества находятся в непрерывном, беспорядочном движении и это их движение воспринимается как тепло.

До 19 в. весьма популярной основой учения о тепле была теория теплорода или некоторой жидкой субстанции, перетекающей от одного тела к другому. Нагревание тел объяснялось увеличением, а охлаждение – уменьшением содержащегося внутри них теплорода. Понятие об атомах долго казалось ненужным для теории тепла, однако многие ученые уже тогда интуитивно связывали тепло с движением молекул. Так, в частности, думал русский ученый М.В.Ломоносов. Прошло немало времени, прежде чем молекулярно-кинетическая теория окончательно победила в сознании ученых и стала неотъемлемым достоянием физики.

Распределение молекул по скоростям. Для газа, находящегося в замкнутом сосуде, результатом многочисленных столкновений молекул между собой и со стенками сосуда, является достаточно быстрое установление универсального распределения молекул по скоростям, которое было теоретически получено Максвеллом в 1860. На уровне макроскопического описания газа максвелловскому распределению молекул по скоростям соответствует состояние теплового равновесия в газе: давление и температура во всех местах внутри сосуда оказываются одинаковыми.

Молекулы газа даже в равновесии движутся беспорядочно, сталкиваясь между собой и со стенкой сосуда, беспрерывно меняя свою скорость. Это означает, что в каждый момент времени в газе есть молекулы, которые имеют самые различные скорости. Вместе с тем, поскольку давление и температура в газе остаются постоянными, то, как бы не менялась скорость молекул, среднее значение ее квадрата остается постоянным. Это оказывается возможным лишь при наличии неизменного во времени и одинакового во всех частях сосуда распределения молекул по скоростям.

В 1920-х появилась реальная возможность экспериментальной проверки максвелловского закона распределения скоростей молекул. Первый прибор для этих целей, состоявший из двух коаксиальных цилиндров, был сконструирован немецким физиком Штерном. По оси прибора была натянута нагреваемая электрическим током платиновая нить, с поверхности которого испарялись атомы серебра. В условиях созданного внутри прибора вакуума узкий пучок этих атомов, движущихся в радиальном направлении, проходил через продольную щель на поверхности внутреннего цилиндра и оседал в виде узкой вертикальной полоски на поверхности внешнего цилиндра. Если привести весь прибор во вращение, то за время, пока атомы серебра пролетают зазор между цилиндрами, прибор успевает повернуться на некоторый угол и положение следа от пучка на внешнем цилиндре сместится относительно первоначального. Нетрудно установить связь этого смещения с величиной скорости в пучке молекул и угловой скоростью вращения прибора. Исследования профиля следа, который размывается из-за наличия распределения скоростей в пучке, позволило установить качественную картину этого распределения, которое примерно соответствовало максвелловскому.

1. Физические основы измерении

О. Штерн в 1920 г., воспользовавшись методом молекулярных пучков, изобретенным французским физиком Луи Дюнойе (1911 г.) измерил скорость газовых молекул и на опыте подтвердил полученное Д. Максвеллом распределение молекул газа по скоростям. (Результаты опыта Штерна подтвердили правильность оценки средней скорости атомов, которая вытекает из распределения Максвелла. О характере самого распределения этот опыт мог дать лишь весьма приближенные сведения.

Более точно закон распределения был проверен в опытах Ламмерта (1929 г.), в которых молекулярный пучок пропускался через два вращающихся диска с радиальными щелями, смещенными относительно друг друга на некоторый угол. Меняя скорость вращения прибора или угол между щелями, можно выделить из пучка молекулы, обладающими различными значениями скорости. Результаты опытов Ламмерта и других исследований, предпринимавшихся с той же целью, находятся в полном соответствии с теоретическим законом распределения скоростей молекул Максвелла.)

1.1 Приборы и материалы, необходимые для постановки опыта, принципиальная схема установки

Для постановки опыта по измерению средней скорости движения молекул О. Штерн спроектировал специальную установку. Прибор состоял из двух жестко соединенных коаксиальных цилиндров с радиусами R и r (рис. 1-3). Во внутреннем цилиндре по оси была расположена платиновая нить А. Исследуемым газом в опыте служили разреженные пары серебра. Атомы получались при испарении слоя серебра, нанесённого на платиновую нить, нагревавшуюся электрическим током. Воздух в малом цилиндре был откачан, поэтому испарившиеся атомы серебра свободно разлетались от нити во все стороны.

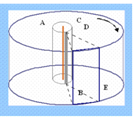
Рисунок1. Схема устройства прибора О. Штерна для измерения средней скорости движении молекул

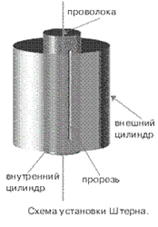
Рисунок 2 Схема устройства прибора О. Штерна для измерения средней скорости движения молекул (Интернет школа Просвещение.RU -http://www.internet-school.ru

Вдоль поверхности внутреннего цилиндра была вырезана узкая щель С. Рядом с щелью располагалась диафрагма, которая позволяла "вырезать" из потока атомов серебра тонкий пучок. Конструкция диафрагмы D обеспечивала одно и то же направление скорости всем атомам серебра, попадавшим далее в камеру большого цилиндра. Другими словами, диафрагма фильтровала атомы, движущиеся только в определенном направлении. В вакуумной камере большого цилиндра обеспечивалась высокая степень разреженности (порядка Па.). Вероятность столкновений атомов серебра с молекулами воздуха была очень мала и, следовательно, была очень невелика вероятность какого-либо отклонения атомов серебра при их равномерном и прямолинейном движении (т.е. рассеяния пучка). На внутренней поверхности внешнего цилиндра помещалась съемная латунная пластинка В. Пластинка имела комнатную температуру. На этой пластинке в области E атомы серебра, охладившись, оседали в виде узкой серебренной полоски. Специальным устройством установка могла приводиться во вращение вокруг собственной оси с частотой 25-45 оборотов в секунду.

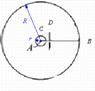
Рисунок 3 Схема установки О.Штерна (вид сверху). При покоящейся установке налет серебра образуется точно против щели C

1.3 Порядок проведения опыта

Опыт проводился в следующей последовательности. По платиновой нити, располагающейся по оси малого цилиндра, пропускался электрический ток. Нить нагревалась практически до температуры плавления серебра Тп = 1234° К, и серебро начинало испаряться. Часть атомов серебра проходило сквозь щель. Отфильтрованные диафрагмой, далее они двигались по радиальным направлениям к внутренней поверхности большого цилиндра прямолинейно и равномерно со скоростью, соответствующей температуре платиновой нити. Стенка большого цилиндра охлаждалась так, чтобы попадающие на нее атомы "прилипали" к ней, образуя налет серебра в форме щели, но немного больших размеров. [1, С. 147] Сначала прибор покоился, и изображение щели на экране (латунной пластинке) приходилось как раз против нее самой (рис. 3). Затем прибор приводился в быстрое вращение вокруг собственной оси с частотой 1500 - 2700 об/мин и, результаты опыта существенно изменялись. Каждый атом по-прежнему двигался прямолинейно, но за время, которое требовалось атому, чтобы, пройдя щель, долететь до латунной пластинки, последняя успевала повернуться на некоторый угол, и атом уже прилипал к ней не точно против щели, а несколько в стороне [ там же] (рис. 4). Смещение полоски серебра при вращении установки позволяло определить величину скорости движения атомов серебра и сравнить ее со значением, полученным теоретическим путем. Способ нахождения скорости атомов серебра был достаточно прост. Атом, двигаясь со скоростью υ, проходил расстояние:

(1.3.1)

где R и r – радиусы внешнего и внутреннего цилиндров, а τ – время прохождения этого расстояния. Любая точка внешнего цилиндра за это время проходила путь:

(1.3.2)

Решая эти уравнения совместно, О. Штерн определил среднюю скорость движения атомов:

(1.3.3)

Измеряя значения ω, R, r и S можно рассчитать среднюю скорость движения атомов серебра при температуре нити – Тн. Меняя температуру накала нити можно найти температурную зависимость скорости теплового движения атомов.

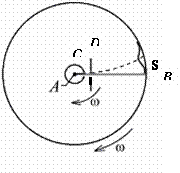
Рисунок 4 При вращении прибора по часовой стрелке налет серебра смещается.

Толщина налета серебра определялась в опыте О.Штерна оптическим методом.

1.4 Объяснение данных опыта с позиции современных научных теорий

Результаты опыта О. Штерна подтвердили справедливость предсказанного Р.Клаузиусом значения скорости движения молекул газа, послужили ярким доказательством верности полученного Д. Максвеллом закона распределения числа молекул по скоростям и явились, в конечном счете, блестящим свидетельством правильности молекулярно-кинетических представлений о строении вещества, а также статистического характера закономерностей, которым подчиняется поведение молекулярных систем.

Изобразим полученный Д. Максвеллом результат графически (рис. 5). По оси абсцисс отложим возможные различные значения скоростей молекул V и интервалов этих скоростей ΔV. По оси ординат отложим ΔN/N·ΔV.

Площадь густо заштрихованной фигуры численно равна доле ΔN/N общего числа молекул N со скоростями между V и V + ΔV. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

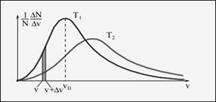
Рисунок 5 Распределение молекул по скоростям (Т2>T1) [2]

Кривые распределения молекул по скоростям имеют следующие особенности:

· они проходят через начало координат,

· асимптотически приближаются к оси абсцисс при бесконечно больших скоростях,

· имеют максимум,

· асимметричны (слева от максимума кривые идут круче, чем справа).

То, что кривая распределения проходит через начало координат, означает, что неподвижных молекул в газе нет. Из того, что кривая при бесконечно больших скоростях асимптотически приближается к оси абсцисс, следует, что слишком большие скорости молекул маловероятны. Значение наиболее вероятной скорости движения молекул соответствует максимуму кривой распределения [3, C. 34]. Вид функции распределения молекул по скорости движения, которую Д. Максвелл определил теоретическим путем, качественно совпал с профилем налета атомов серебра на латунной пластинке в опыте О.Штерна. Опыт О. Штерна (наряду с опытом Ж. Перрена) был первым прямым доказательством справедливости молекулярно-кинетической теории строения вещества. В настоящее время атомно-молекулярное учение подтверждено многочисленными опытами и является общепризнанным.

1.5 Усовершенствованные опыты Штерна

Элдридж (1927 г.) и Ламмерт (1926-1929) ввели селекторы скоростей, работающие на принципе зубчатого колеса (как в опытах Физо со светом). Идея опыта схематически изображена на рис.6. Пучок молекул из печи А коллимировался на щелях и попадал на вращающиеся зубчатые диски D1 и D2.

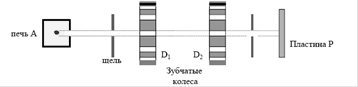
Рисунок 6 Прорези у зубчатых дисков смещены на угол a

Когда зубчатые диски покоятся (не вращаются), то атомы не проходят к регистрирующей пластинке Р (не осаждаются), поскольку щель одного диска попадает на зуб второго. Когда диски вращаются, то проходят атомы определенных скоростей, т.е. только те, которые пролетят расстояние между дисками за время их поворота на угол α.. По количеству атомов, осажденных на пластине Р, можно судить о распределении молекул по проекции скорости вдоль направления пучка. Недостатком этого метода является то, что на пластинку приходят атомы с другими скоростями, когда поворот происходит на большие углы.

Цартман попытался избежать этого эффекта и усовершенствовал опыты (рис. 7). Из печи коллимированный пучок атомов попадал на вращающийся цилиндр с отверстием. При попадании пучка в отверстие молекулы осаждались на внутренней стенке цилиндра. При этом у точки А собирались атомы или молекулы с очень большими скоростями, а к точке В – более медленные молекулы.

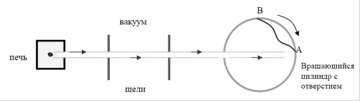
Рисунок 7

Если диаметр цилиндра равен d, то расстояние от точки А на стенку цилиндра, куда осаждаются молекулы равно:

где v – скорость молекул, а ω - угловая скорость вращения цилиндра. По почернению пластины (по числу осажденных молекул) можно судить о распределении молекул по скоростям.

Все эксперименты получили результаты в согласии с Максвелловским распределением молекул по скоростям.

2. Конструктивные особенности метода

Установка состоит из двух коаксиальных (имеющих одну ось симметрии) цилиндров между которыми создавался вакуум. Вдоль оси цилиндров натянута платиновая нить, покрытая серебром. При пропускании через нее электрического тока атомы серебра испарялись. Во внутреннем цилиндре вырезалась щель через, которую атомы серебра проникали на поверхность внешнего цилиндра, оставляя на ней след в виде узкой вертикальной полоски. При приведении цилиндров во вращение с постоянной угловой скоростью w след, оставляемый молекулами серебра смещался и размывался. Действительно, на атомы серебра в неинерциальной системе отсчета, связанной с вращающимися цилиндрами действует сила Кориолиса Fк

Fк = 2·m·[v·w]. (2.1)

Эта сила отклоняет атомы серебра от прямолинейного распространения. Средняя величина смещения атомов Ds равна:

Ds = w·R·Dt = w2·R/<v>. (2.2)

Измерив величину Ds из эксперимента, исходя из формулы (14.28), можно найти среднюю скорость движения молекул.

Ее значение совпадает с теоретическим значением, полученным с помощью формулы Максвелла.

2.1 Коаксиальные цилиндры

Коаксиальные цилиндры - два вертикальных цилиндра, имеющие параллельную общую центральную ось и различный диаметр , один из которых вращается, а второй неподвижен.

Рисунок 8

2.3 Ва́куум

Вакум — среда, содержащая газ при давлениях значительно ниже атмосферного. Вакуум характеризуется соотношением между длиной свободного пробега молекул газа λ и характерным размером процесса d. Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т. д. В зависимости от величины соотношения λ/d различают низкий (λ/d 1), средний (λ/d~1) и высокий (λ/d 1) вакуум.

Также вакуумом называют состояние газа, для которого средняя длина пробега его молекул сравнима с размерами сосуда или больше этих размеров.

2.4 Платиновая нить

Платиновая нить - толщина 0,07 – 0,1 мм является чувствительным элементом датчика, через нее пропускается электрический ток таким образом, чтобы она нагревалась до 150 градусов. Чем больше воздуха проходит через поперечное сечение трубопровода, тем сильнее охлаждается нить. На поддержание температуры требуется увеличение тока. Электронная схема преобразует этот прирост тока в полезный сигнал ДМРВ. Чем холодней воздух, тем сильнее охлаждается платиновая нить. Платиновая нить боится грязи. Поэтому воздухофильтр должен быть чистым и изготовлен из качественной фильтровальной бумаги. Схема датчика обеспечивает кратковременный нагрев нити для выгорания загрязнений - "режим прожига".

2.5 Серебро

Серебро Ag, (лат. Argrentum), химический элемент I группы периодической системы Д.И. Менделеева, атомный номер 47, атомная масса 107,8682. Серебро - металл белого цвета, ковкий, пластичный, хорошо полируется. Плотность 10,5 г/см3 (относится к тяжелым металлам), tпл=960,5 oС, tкип=2212 oС. Природное серебро состоит из двух стабильных изотопов 107Ag (51,35%) и 109Ag (48,65%), известны также 14 радиоактивных изотопов серебра и несколько изомеров.

2.6 Си́ла Кориоли́са

Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения.

Сила Кориолиса равна:

(2.3)

где m — точечная масса, ω — вектор угловой скорости вращающейся системы отсчёта, ύ — вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операция векторного произведения.

Величина называется кориолисовым ускорением.

2.7 Радиальные щели

Радиальные щели, образованные цилиндрическими соосными поверхностями, называют цилиндрическими концентричными щелями, а с не-соосными поверхностями - цилиндрическими эксцентричными щелями. Радиальные щели, образованные поверхностями с небольшой конусностью, называют конусными, а если оси поверхностей непараллельны, то - щелями с перекосом осей. Конусные щели в зависимости от того, сужается или расширяется зазор в направлении утечки, называют конфузорными или диффу-зорными. Радиальные щели наиболее часто используют в качестве передних и задних уплотнений закрытых рабочих колес роторных гидравлических машин. В целях повышения гидравлического сопротивления применяют многощелевые уплотнения. Радиальные щели широко используют также в качестве межступен-ных уплотнений, в устройствах, понижающих давление перед основным уплотнением вала, и в устройствах защиты основного уплотнения от абразивного изнашивания при герметизации жидкостей с твердыми включениями.

Радиальные и торцовые щели применяют в гидравлических и газовых затворах, в разгрузочных и уравновешивающих гидравлических устройствах, опорах скольжения, гидростатических уплотнениях и подшипниках.

2.8 Азот

Азо́т — элемент главной подгруппы пятой группы второго периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 7. Обозначается символом N (лат. Nitrogenium). Простое вещество азот (CAS-номер: 7727-37-9) — достаточно инертный при нормальных условиях двухатомный газ без цвета, вкуса и запаха (формула N2), из которого на три четверти состоит земная атмосфера.

2.9 Максвелловское распределение молекул по скоростям

Для газа, находящегося в замкнутом сосуде, результатом многочисленных столкновений молекул между собой и со стенками сосуда, является достаточно быстрое установление универсального распределения молекул по скоростям, которое было теоретически получено Максвеллом в 1860. На уровне макроскопического описания газа максвелловскому распределению молекул по скоростям соответствует состояние теплового равновесия в газе: давление и температура во всех местах внутри сосуда оказываются одинаковыми.

Максвелловское распределение по скоростям можно вывести несколькими различными способами. Вид его может быть, в частности, установлен на основе простых соображений, основанных на применении так называемого принципа детального равновесия. Нужно однако предварительно отметить, что утверждение типа: "Такое-то число молекул в газе имеет скорость, например, 100 м/с" – не имеет конкретного смысла. Нельзя точно указать скорость какой-либо группы молекул, но можно говорить о среднем числе молекул, скорости которых находятся в некотором малом интервале скоростей dv между значениями v и v + dv. Число (доля) этих молекул – dn(v) = nf(v)dv, где n – число молекул в единице объема. Следует напомнить, что скорость v является вектором, поэтому функция распределения f(v), имеющая смысл функции вероятности, характеризует распределение молекул как по абсолютным значениям (модулям) скоростей, так и по их направлениям. В декартовой системе координат с осями x, y, z это соответствует представлению интервала скоростей в виде dv = dvx * dvy * dvz. Если интересоваться распределением только по модулям скорости, то в сферической системе координат

dn(v) = 4p nn2f(v)dv(2.4)

Для вывода максвелловского распределения рассматриваются две группы молекул, скорости которых лежат в интервалах dv и dvi.В результате столкновений молекул первой и второй групп скорости v и vi сталкивающихся молекул изменяются и переходят в v’ и vi соответственно. Среднее число таких столкновений, называемых прямыми столкновениями, будет пропорционально dndn1 или

Соответствующие им обратные столкновения переводят молекулы из интервалов dv’ и dvi в dv и dv1 . Среднее число обратных столкновений пропорционально

(2.5)

Принцип детального равновесия состоит в том, что в состоянии хаотического движения, соответствующего тепловому равновесию, скорости прямого и обратного процессов должны быть одинаковы. В данном случае это соответствует выполнению условия

(2.6)

Можно показать, что произведения элементов объема в пространстве скоростей для прямых и обратных столкновений равны. Поэтому написанное выше условие переходит в соотношение

(2.7)

Логарифмирование этого соотношения дает

(2.8)

Полученное равенство означает, что натуральные логарифмы функции распределения являются так называемыми аддитивными инвариантами. Они могут быть выражены через линейную комбинацию величин, которые сохраняются в парных столкновениях частиц, а именно массы, импульса и кинетической энергии частиц.

(2.9)

Константы a, и c можно определить через известные макроскопические параметры газа – плотность n, скорость v0 и температуру T. Тогда в покоящемся газе (v0 = 0) максвелловское распределение по скоростям, следующее из (2.9), имеет вид

(2.10)

Используя этот результат, с помощью выражения (2.4) можно определить относительную долю молекул, абсолютные скорости которых лежат в некотором узком интервале значений dv,

(2.11)

Вид распределения dn/ndv, описываемого выражением (2.11), для двух различных температур (T2 > T1) представлен на рис. 9.

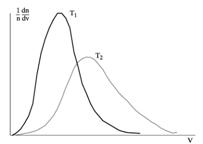
Рисунок 9

Площади под каждой кривой оказываются, очевидно, одинаковыми, что следует из нормировки на заданную плотность частиц n. Из представленного графика видно, что большинство частиц имеет скорости, близкие к некоторому среднему значению, и лишь малое их число обладает весьма высокими или низкими скоростями. С помощью распределения (2.11) могут быть рассчитаны такие характеристики как средняя, среднеквадратичная и наиболее вероятная скорость теплового движения молекул, число столкновений молекул со стенкой и другие важные параметры газа.

3. Альтернативные способы измерения

3.1 Спин

Любое вращающееся тело обладает моментом импульса относительно своего центра масс; это собственный момент тела, или спин. Спиновый момент, или просто, спин атома или атомного ядра является характеристикой, аналогичной моменту импульса вращающегося волчка или гироскопа. Момент импульса твердого тела, вращающегося вокруг оси, определяется как сумма моментов импульсов всех частиц этого тела относительно той же оси; этот момент равен сумме произведений массы частицы на ее скорость и на кратчайшее расстояние частицы до оси вращения. Вектор момента импульса параллелен оси вращения и направлен в сторону перемещения винта с правой резьбой при таком же вращении. Спин атомов и ядер измеряется в единицах h/2p, где h – постоянная Планка, равная 6,6261Ч10–34 ДжЧс. Экспериментально установлено, что в этих единицах (в соответствии с правилами квантовой механики) наблюдаемые проекции всех спинов на заданное направление принимают либо целое, либо полуцелое значение, т.е. либо 1, 2, 3,..., либо 1/2, 3/2, 5/2,.... Максимальное значение проекции совпадает с величиной спина; например, если спин ядра j равен 5/2, то измеренное максимальное значение проекции спина составит 5/2 в единицах h/2p ДжЧс.

3.2 Магнитный дипольный момент

. Магнитный дипольный момент атома или ядра аналогичен характеристике стрелки компаса. Он представляет собой вращающий момент, действующий на атом или ядро в магнитном поле. Дипольный момент – векторная величина. Магнитный момент атома обычно измеряют в единицах магнетона Бора, m0 = еh/4pmc = 9,27Ч10–24 Дж/Тл, где е – заряд электрона, h – постоянная Планка, m – масса электрона и c – скорость света. Магнитные же моменты ядер обычно измеряют в единицах ядерного магнетона mN, который равен магнетону Бора, деленному на отношение масс протона и электрона, а именно mN = 5,051Ч10–27 Дж/Тл.

3.3 Электрический квадрупольный момент

Электрический квадрупольный момент служит мерой отклонения распределения электрического заряда ядра от сферической симметрии. Количественно он определяется как при условии, что проекция спина ядра максимальна вдоль оси z прямоугольной системы координат, начало которой совпадает с центром ядра. В этом выражении Z – заряд ядра, или его атомный номер, z – координата протона в ядре, r – расстояние от протона до центра ядра, а черта над выражением в скобках означает усреднение плотности заряда по всему ядру. Можно показать, что в сферически симметричном случае Q = 0.

3.4 Другие моменты

В принципе могли бы существовать электрические и магнитные мультипольные моменты любого порядка 2n, где n – нуль или положительное целое число. Например, у ядер иода, индия и галлия были измерены магнитные октуполи. Можно показать, однако, что вследствие квантовой природы спина атом или ядро со спином j не может иметь мультипольных моментов более высокого порядка, чем n = 2j. Так, атом с j = l/2 не может иметь мультипольных моментов выше дипольного, а атом с j = 0 – даже дипольного момента. Проводились необычайно чувствительные эксперименты по обнаружению у ядер электрических дипольных моментов, но пока что найти их не удалось.

3.5 Эффект Зеемана

Один из первых и наиболее мощных методов исследования атомных моментов был основан на так называемом эффекте П.Зеемана, т.е. на расщеплении спектральных линий во внешних магнитных полях. Если разрядную трубку, в которой возбуждается атомное излучение, поместить во внешнее магнитное поле, то спектральные линии расщепятся на ряд компонент. Расстояние между линиями компонент определяется энергией взаимодействия атомных моментов с внешними магнитными полями. Поскольку энергия взаимодействия зависит от магнитных моментов атомов, измеренное расщепление дает информацию об их величине. Числом спектральных линий определяются значения спина.

Первоначально при изучении оптических спектров атомов последние возбуждались за счет столкновений с электронами в газоразрядных трубках или за счет поглощения электромагнитного излучения, возникающего в таких трубках. В наши дни атомы часто возбуждают лазерным излучением.

3.6 Метод молекулярных пучков

Особенно простой, показательный и прямой метод измерения атомных магнитных моментов предложили О.Штерн и В.Герлах в 1921. Он основан на измерении отклонения атомов, обладающих магнитным моментом, в неоднородном магнитном поле. В однородном магнитном поле магнитный момент не отклоняется, т.к. на северный и южный полюса атомного магнитика поле действует с одинаковой силой. Поэтому центр масс атома не смещается; атом может лишь прецессировать или вращаться вокруг своего центра масс. Если же магнитное поле неоднородно на расстояниях порядка размеров атома, то из-за различий в напряженности магнитного поля на один из полюсов атомного магнитика поле будет действовать сильнее, чем на другой, и атом отклонится под действием разности этих сил.

В эксперименте материал нагревается в печи и его атомы через щель проходят в вакуумную камеру, где коллимируются в пучок и осаждаются на пластинке. Затем включается неоднородное магнитное поле, направленное поперек пучка, и регистрируется отклонение атомов. Каждому из возможных значений проекции магнитного момента и спина на направление поля должно соответствовать свое отклонение. Соответствующее классической физике непрерывное распределение проекций привело бы к сплошному размытию сигнала на регистрирующей пластинке. Но в квантовой механике допустимы лишь определенные дискретные проекции, и поэтому наблюдаемая картина расщепляется на две или несколько линий, число которых равно 2j + 1, где j – момент импульса атома в указанных выше единицах. По числу компонент 2j + 1 можно определить момент импульса – спин j. Расстояние между линиями позволяет вычислить величину магнитного момента.

Для измерения атомных магнитных моментов были приспособлены также рассматриваемые ниже резонансные методы молекулярных пучков, и они дали наиболее точные результаты. Точно так же для измерения атомных магнитных моментов применяется метод электронного парамагнитного резонанса, подобный методу ЯМР

3.7 Выводы из опытов по определению атомных моментов

Результаты упомянутых выше и других аналогичных экспериментов согласуются со следующими утверждениями относительно спиновых и магнитных моментов атомных структур.

Каждый элемент в атоме имеет соответствующий его движению по беровской орбите орбитальный момент l. Это движение электрона по орбите можно рассматривать как круговой ток, в результате чего возникает магнитный момент, соответствующий такому движению.

Величина магнитного момента, связанного с орбитальным движением, в классической механике была бы пропорциональна величине орбитального момента. Но у электрона есть еще и собственный момент – спин. Со спином также должен быть связан магнитный момент.

В результате магнитный момент частицы оказывается пропорционален полному механическому моменту (сумме орбитального и спинового моментов).

Важно иметь в виду, что моменты – механические и магнитные – векторные величины. В квантовой механике разработаны определенные способы их суммирования и вычисления магнитных моментов атомов.

Список используемой литературы

1. . Розенбергер, Ф. История физики. Часть 1. История физики в древности и в средние века/ Ф. Розенбергер; пер. с нем. под ред. И. Сеченова, вновь проверенный и переработанный В.С. Гохманом – Л.:ОНТИГТТИ – 1934.

2. Открытая физика. В 2 ч. (CD) / Под ред. С.М. Козела. – М.: ООО "Физикон". - 2002 (http://www.physicon.ru/.)

3. Радченко, И. В. Молекулярная физика/ И.В. Радченко - М.:Наука, 1965.

4. Большая советская энциклопедия. Т. 19.- М.: Советская энциклопедия, 1975

5. http://mdito.pspu.ru/nfpk/um17/Shtren.php

6. http://www.physics.spbstu.ru/forstudents/lectures/ivanov/molec2-4.pdf

7. http://www.krugosvet.ru/enc/nauka_i_tehnika/fizika/MOLEKULYARNO-KINETICHESKAYA_TEORIYA.php

8. http://www.krugosvet.ru/enc/nauka_i_tehnika/fizika/MOMENTI_ATOMOV_I_YADER.php

5rik.ru

Материалы для учебы и работы

Реферат: Измерение функции распределения атомов серебра методом Штерна-Ламмерта