Контрольная работа: Теорія споживання
Контрольна робота з теми:
ТЕОРІЯ СПОЖИВАННЯ
Вступ
Математичні моделі й методи, що досліджуються в даній роботі, є необхідними для вивчення споживчого поводження на ринку готової продукції, переваг індивідуального споживача, корисності й класифікації товарів, еластичності й інших властивостей попиту.
1. Математичний вступ: опуклі множини
Множину ![]() називають
опуклою, якщо разом з будь-якими двома своїми точками
називають
опуклою, якщо разом з будь-якими двома своїми точками ![]() ,
, ![]() ,
, ![]() вона містить і всі точки вигляду
вона містить і всі точки вигляду ![]() , де
, де ![]() .
.
Щоб пояснити
геометричний зміст поняття опуклої множини, нагадаємо спосіб задання відрізка ![]() між двома
точками
між двома
точками ![]() ,
, ![]() в
в ![]() -вимірному
просторі. Параметричне рівняння прямої, що проходить через точки
-вимірному
просторі. Параметричне рівняння прямої, що проходить через точки ![]() ,
, ![]() , має вигляд
, має вигляд ![]() , де
, де ![]() –
напрямний вектор прямої. При
–
напрямний вектор прямої. При ![]() , при
, при ![]() . Коли
. Коли ![]() змінюється в межах від 0 до 1,
точка
змінюється в межах від 0 до 1,
точка ![]() пробігає
весь відрізок між точками
пробігає
весь відрізок між точками ![]() і
і ![]()
![]() .
.
З геометричної
точки зору множина ![]() є опуклою лише тоді, коли разом з
будь-якими двома своїми точками ця множина містить і відрізок, який їх поєднує.
є опуклою лише тоді, коли разом з
будь-якими двома своїми точками ця множина містить і відрізок, який їх поєднує.
Для двовимірного
простору прикладом опуклої множини є опуклий багатогранник. У просторі при ![]() опуклими
множинами можуть бути куля, еліпсоїд, еліптичний параболоїд, циліндр і тощо.
опуклими
множинами можуть бути куля, еліпсоїд, еліптичний параболоїд, циліндр і тощо.
Опуклу множину, всі границі якої лінійні, називають опуклою багатогранною множиною (опуклим багатогранником).
Розглянемо властивості опуклих множин:
1. Якщо ![]() – точки
опуклої множини
– точки
опуклої множини ![]() , то точка
, то точка 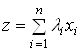 , де
, де ![]() ,
, 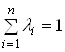 також належить
також належить ![]() , де
, де 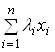 називають
опуклою комбінацією точок
називають
опуклою комбінацією точок ![]() . Це окремий випадок лінійної
комбінації. Дану властивість приймаємо без доказу.
. Це окремий випадок лінійної
комбінації. Дану властивість приймаємо без доказу.
2. Множина
опуклих комбінацій будь-якої заданої кількості комбінацій з ![]() є опуклою множиною.
Доказ цієї властивості не наводимо.
є опуклою множиною.
Доказ цієї властивості не наводимо.
3. Якщо ![]() і
і ![]() – опуклі
множини, а точки
– опуклі
множини, а точки ![]() і
і ![]() такі, що
такі, що ![]() й
й ![]() , то весь відрізок знаходиться в
обох множинах
, то весь відрізок знаходиться в
обох множинах ![]() і
і ![]() , тобто перетинання опуклих множин
є опуклим.
, тобто перетинання опуклих множин
є опуклим.
Розглянемо доказ.
Нехай ![]() , де
, де
![]() і
і ![]() – опуклі
множини. Розглянемо дві довільні точки
– опуклі
множини. Розглянемо дві довільні точки ![]() і
і ![]() множини
множини ![]() . Оскільки
. Оскільки ![]() , то
, то ![]() . З опуклості множини
. З опуклості множини ![]() випливає, що
весь відрізок
випливає, що
весь відрізок ![]() належить
належить ![]() . Так само,
. Так само, ![]() . Але тоді
. Але тоді ![]() . Доказ
завершено.
. Доказ
завершено.
4. Сума двох опуклих множин опукла.
Розглянемо доказ.
Нехай ![]() , де
, де
![]() . Тоді в
. Тоді в ![]() і
і ![]() знайдуться
такі елементи, що
знайдуться
такі елементи, що ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Припустимо тепер
. Припустимо тепер ![]() – довільне число,
– довільне число, ![]() . Тоді
. Тоді
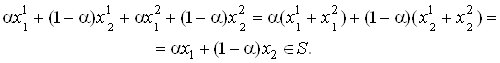
5. Основною
властивістю, яка характеризує опуклі множини, є так звана властивість
віддільності. Для пояснення цієї властивості розглянемо на площині замкнуту
опуклу множину ![]() і точку
і точку ![]() . Тоді знайдеться така пряма
. Тоді знайдеться така пряма ![]() , що множина
, що множина ![]() і точка
і точка ![]() знаходяться по
різні сторони від цієї прямої, тобто для будь-якої точки
знаходяться по
різні сторони від цієї прямої, тобто для будь-якої точки ![]() виконується нерівність
виконується нерівність ![]() , у той час, як
, у той час, як
![]() .
.
2. Відношення переваги
Одним з основних
елементів економічної теорії є споживач або група споживачів (домашнє
господарство, родина). У споживача виникає задача раціонального ведення
господарства (розподілу особистого бюджету). Отже, в даній задачі споживачеві
необхідно з'ясувати, яку кількість кожного наявного товару або послуг він
повинен придбати при заданих цінах ![]() і відомому доході
і відомому доході ![]() . Будемо аналізувати
поводження споживача й у підсумку сформулюємо оптимізаційну математичну модель
поводження споживача на ринку товарів і послуг.
. Будемо аналізувати
поводження споживача й у підсумку сформулюємо оптимізаційну математичну модель
поводження споживача на ринку товарів і послуг.
Під товаром або
послугою розумітимемо деяке благо, що надійшло в продаж у певний час в певному
місці. Припустимо, існує кінцева кількість наявних товарів ![]() , кількість кожного з
них характеризується набором товарів
, кількість кожного з
них характеризується набором товарів ![]() , де
, де ![]() – кількість
– кількість ![]() -го товару (
-го товару (![]() ), придбана
споживачем.
), придбана
споживачем.
Простором товарів
назвемо невід’ємний ортант ![]()
![]() -вимірного простору, кожна точка
-вимірного простору, кожна точка ![]() є певним
набором товарів. Нехай
є певним
набором товарів. Нехай ![]() – множина, на якій визначені
інтереси споживача.
– множина, на якій визначені
інтереси споживача. ![]() –множина всіх уявних наборів
товарів, доступних споживачеві й придатних для нього.
–множина всіх уявних наборів
товарів, доступних споживачеві й придатних для нього.
Будь-які два
вектори ![]() споживач
може порівнювати та обирати з них. Цей вибір залежить від бюджету споживача,
цін на товари і його смаку. Отже, вибір характеризується відношенням переваги,
що записується знаком
споживач
може порівнювати та обирати з них. Цей вибір залежить від бюджету споживача,
цін на товари і його смаку. Отже, вибір характеризується відношенням переваги,
що записується знаком ![]() і читається як «переважніший або
рівноцінний за». Запис
і читається як «переважніший або
рівноцінний за». Запис ![]() , де
, де ![]() й
й ![]() є наборами товарів з
є наборами товарів з ![]() означає, що
споживач віддає перевагу набору
означає, що
споживач віддає перевагу набору ![]() по відношенню до набора
по відношенню до набора ![]() .
. ![]() виконується
тільки, якщо
виконується
тільки, якщо ![]() і відношення
і відношення ![]() не є справедливим.
не є справедливим.
Запис ![]() означає, що
набори товарів
означає, що
набори товарів ![]() й
й ![]() для споживача рівнозначні
(еквівалентні, байдужні).
для споживача рівнозначні
(еквівалентні, байдужні).
Розглянемо аксіоми відношення переваги:
1.
Транзитивність: якщо є три набори ![]() ,
, ![]() й
й ![]() і відомо, що
і відомо, що ![]() , то
, то ![]() .
.
2. Ненасиченість:
якщо ![]() й
й ![]() такі, що
такі, що ![]() і
і ![]() , то
, то ![]() . Ця аксіома
стверджує, що точки насичення споживача не існує, більший набір товарів завжди
є переважнішим за менший.
. Ця аксіома
стверджує, що точки насичення споживача не існує, більший набір товарів завжди
є переважнішим за менший.
3. Опуклість: для
будь-яких ![]() й
й
![]() таких, що
таких, що
![]() і
і ![]() маємо
маємо ![]() або
або ![]() для всіх
для всіх ![]() . Ця вимога
забезпечує строгу опуклість множини комбінацій наборів, не менш переважніших за
даний.
. Ця вимога
забезпечує строгу опуклість множини комбінацій наборів, не менш переважніших за
даний.
3. Функція корисності споживання
Нехай існує
безперервна дійсна функція ![]() , визначена на
, визначена на ![]() , для якої виконуються
співвідношення:
, для якої виконуються
співвідношення:
![]() , тільки якщо
, тільки якщо ![]() ;
;
![]() , тільки якщо
, тільки якщо ![]() .
.
Функцію ![]() називають
функцією корисності або порядковою функцією корисності.
називають
функцією корисності або порядковою функцією корисності.
Дамо геометричну інтерпретацію функції корисності. Для цього розглянемо будь-який промінь у просторі товарів, що проходить через початок координат. Приймемо як корисність будь-якого товару відстань від початку до точки на промені, що належить тій самій множині байдужності, що й розглянутий набір. Як правило, якщо така функція корисності існує, то вона не єдина.
Наприклад, за ![]() можна взяти
будь-яку монотонну чітко зростаючу функцію. Якщо
можна взяти
будь-яку монотонну чітко зростаючу функцію. Якщо ![]() – функція корисності, то
– функція корисності, то ![]() також буде
функцією корисності, де
також буде
функцією корисності, де ![]() – довільна монотонно зростаюча
функція, тобто
– довільна монотонно зростаюча
функція, тобто ![]() .
.
На рис. 1 кожній
точці площини, що відноситься до різних комбінацій наборів товарів ![]() і
і ![]() , відповідають
точки поверхні
, відповідають
точки поверхні ![]() , які відображають рівні
корисності цих товарів.
, які відображають рівні
корисності цих товарів.
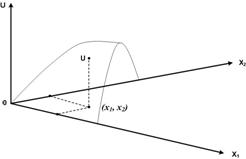
Рисунок 1
Для кожного
товарного набору ![]() можна вказати множину таких
наборів, яка за перевагою еквівалентна даному. Ця множина називається кривою
байдужності, що проходить через
можна вказати множину таких
наборів, яка за перевагою еквівалентна даному. Ця множина називається кривою
байдужності, що проходить через ![]() . Кожній кривій байдужності
можна поставити у відповідність певний рівень корисності, оскільки корисність
будь-яких двох наборів, що знаходяться на одній і тій самій кривій, однакова.
Математичним аналогом кривої байдужності є лінія рівня.
. Кожній кривій байдужності
можна поставити у відповідність певний рівень корисності, оскільки корисність
будь-яких двох наборів, що знаходяться на одній і тій самій кривій, однакова.
Математичним аналогом кривої байдужності є лінія рівня.
Вважатимемо ![]() диференційованою,
тоді аксіома ненасичення вимагає, щоб всі перші часткові похідні функції
корисності, які звуться граничними корисностями, були додатними
диференційованою,
тоді аксіома ненасичення вимагає, щоб всі перші часткові похідні функції
корисності, які звуться граничними корисностями, були додатними
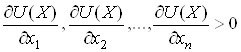 .
.
Відповідно до аксіоми 3
(опуклості множини простору товарів) вимагатимемо, щоб функція ![]() була строго увігнутою
функцією й отже,
була строго увігнутою
функцією й отже, ![]() має бути двічі диференційованою і
мати безперервні другі часткові похідні, тобто матриця Гессе, що складається з
других часткових похідних, повинна бути вiд’ємно визначеною
має бути двічі диференційованою і
мати безперервні другі часткові похідні, тобто матриця Гессе, що складається з
других часткових похідних, повинна бути вiд’ємно визначеною
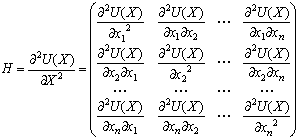 .
.
Зокрема 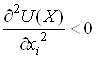 ,
, ![]() означає, що
корисність товару зменшується в міру того, як продукт споживається. Це
допущення одержало назву закону Госена.
означає, що
корисність товару зменшується в міру того, як продукт споживається. Це
допущення одержало назву закону Госена.
З властивості опуклості відношення переваги випливає, що криві байдужності опуклі відносно початку координат.
Найважливішою характеристикою кривої байдужності є її нахил. Абсолютне значення нахилу на різних відрізках кривої виражає норму заміни благ. Тому криву байдужності можна назвати кривою взаємозамінності благ.
Розглянемо рис.
2. На відрізку АВ норма заміни блага 1 благом 2 за визначенням дорівнює ![]() , а на відрізку
CD –
, а на відрізку
CD – ![]() .
Норма заміни одного блага іншим безпосередньо пов'язана з їх граничними
корисностями. Під час руху по кривій байдужності вправо вниз на
.
Норма заміни одного блага іншим безпосередньо пов'язана з їх граничними
корисностями. Під час руху по кривій байдужності вправо вниз на ![]() здобуваємо приблизно
здобуваємо приблизно ![]() одиниць
корисності зі збільшенням споживання блага 1 й одночасно втрачаємо
одиниць
корисності зі збільшенням споживання блага 1 й одночасно втрачаємо ![]() одиниць
корисності зі зменшенням споживання блага 2. Оскільки виграш і втрата взаємно
компенсуються (ми перебуваємо на одній і тій самий кривій байдужності), то при
досить малих
одиниць
корисності зі зменшенням споживання блага 2. Оскільки виграш і втрата взаємно
компенсуються (ми перебуваємо на одній і тій самий кривій байдужності), то при
досить малих ![]() і
і ![]() можна записати
можна записати ![]() .
.
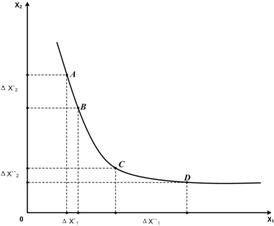
Рисунок 2
Розділивши
отриману рівність на 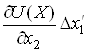 , знайдемо
, знайдемо
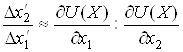 ,
,
тобто нахил кривої
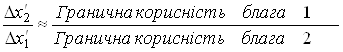 .
.
Переходячи до нескінченно малих приростів, одержимо строгу рівність. Отже, гранична норма заміни двох благ дорівнює зворотному відношенню їх граничних корисностей. Геометрично гранична норма заміни характеризує нахил кривої байдужності в точці.
Гранична норма
заміни на кривих байдужності є спадною функцією, тобто зі зростанням споживання
одного продукту для його заміни потрібно все менша кількість іншого. Як видно з
рис. 1.2, 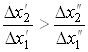 .
.
4. Оптимізаційна математична модель поведінки споживача на ринку товарів і послуг
Задача споживача
полягає у виборі набору товарів і послуг при заданій функції корисності ![]() й бюджетному
обмеженні, що відносить споживача до деякої підмножини простору товарів.
й бюджетному
обмеженні, що відносить споживача до деякої підмножини простору товарів.
Введемо поняття
бюджетної лінії або лінії цін. Така лінія визначається як геометричне місце
точок всіх комбінацій товарів, вартість яких дорівнює певній сумі ![]() . Вона
характеризує реальну купівельну спроможність споживача й співвідношення цін цих
товарів. Наприклад, у випадку двох товарів, при постійних цінах – це пряма
. Вона
характеризує реальну купівельну спроможність споживача й співвідношення цін цих
товарів. Наприклад, у випадку двох товарів, при постійних цінах – це пряма ![]() , де
, де ![]() – ціни, а
– ціни, а
![]() –
доход (рис. 3).
–
доход (рис. 3).
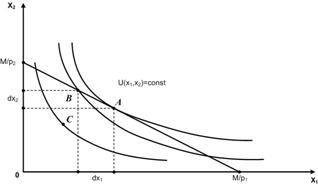
Рисунок 3
Лінії цін характеризуються такими властивостями:
1) мають
від’ємний нахил, який дорівнює зворотному співвідношенню цін двох товарів,
тобто ![]() ;
;
2) при постійних цінах різним рівням доходу відповідають різні паралельні прямі; більшому доходу відповідає більш висока лінія цін.
При даних цінах і
доході споживач прагне забезпечити максимум корисності. Цей максимум
досягається в точці дотику самої верхньої кривої байдужності й лінії цін. Точка
![]() є точкою
рівноваги, тобто у споживача немає будь-яких мотивів для перегляду даного плану
покупок. Інша точка, що знаходиться на лінії цін, наприклад, точка
є точкою
рівноваги, тобто у споживача немає будь-яких мотивів для перегляду даного плану
покупок. Інша точка, що знаходиться на лінії цін, наприклад, точка ![]() , або
нижча за неї, наприклад, точка
, або
нижча за неї, наприклад, точка ![]() , перебуватиме на більш
низькій кривій байдужності, з більш низьким рівнем корисності та не влаштує
споживача.
, перебуватиме на більш
низькій кривій байдужності, з більш низьким рівнем корисності та не влаштує
споживача.
В точці рівноваги
![]() нахил
лінії цін дорівнює нахилу кривої байдужності й забезпечує максимум корисності
від закуповуваних товарів. При цьому виконується рівність відношення цін
відношенню граничних корисностей товарів
нахил
лінії цін дорівнює нахилу кривої байдужності й забезпечує максимум корисності
від закуповуваних товарів. При цьому виконується рівність відношення цін
відношенню граничних корисностей товарів
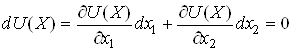 ,
, 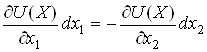 ,
,
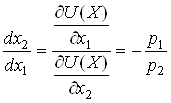 ,
,
де величина ![]() – гранична
норма заміни двох благ.
– гранична
норма заміни двох благ.
Формально модель поведінки споживача на ринку є задачею нелінійного програмування з метою відшукання умовного максимуму
![]() ,
, ![]() (1)
(1)
або в розгорнутому вигляді
![]() ,
,  ,
, ![]() ,
,
де ![]() – вектор цін,
– вектор цін,
![]() – ціна
– ціна ![]() -го товару,
-го товару, ![]() – витрати
на
– витрати
на ![]() -й
товар. Отже, задача споживача полягає у виборі такого набору
-й
товар. Отже, задача споживача полягає у виборі такого набору ![]() з множини
з множини ![]() , який є
«найкращим», тобто для всіх інших наборів
, який є
«найкращим», тобто для всіх інших наборів ![]() справедливе співвідношення
справедливе співвідношення ![]() .
.
Через те, що
цільова функція ![]() безперервна, вона має додатні
перші часткові похідні та вiд’ємно визначену матрицю Гессе, а також припустима
множина
безперервна, вона має додатні
перші часткові похідні та вiд’ємно визначену матрицю Гессе, а також припустима
множина ![]() замкнута
й опукла, то відповідно до теореми Вейєрштраса розв’язок існує і єдиний.
замкнута
й опукла, то відповідно до теореми Вейєрштраса розв’язок існує і єдиний.
Визначимо функцію Лагранжа
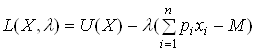 ,
,
де ![]() –множник Лагранжа.
–множник Лагранжа.
Необхідними й достатніми умовами для розв’язання задачі споживання (1.1) є умови Куна-Такера
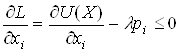 ,
, ![]() ,
,
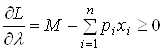 ,(2)
,(2)
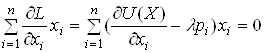 ,
,
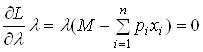 ,
, ![]() ,
, ![]() .
.
Вважають, що споживачі одержують усі види товарів і послуг. Тоді умова (2) матиме такий вигляд:
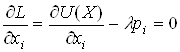 ,
, ![]() ,
, 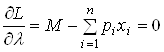 .(3)
.(3)
Ці умови
виконуються тільки в точці ![]() , де
, де ![]() є оптимальним розв’язком (планом)
задачі споживання.
є оптимальним розв’язком (планом)
задачі споживання.
Наприклад, у випадку двох товарів розв’язок має задовольняти системі
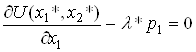 ,
,
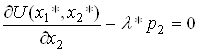 ,
,
![]() .
.
Геометрично розв’язок знаходяться в точці дотику лінії цін і кривої байдужності (див. рис. 3).
Сформулюємо основні висновки, які випливають із розв’язання задачі споживання:
1) у точці
оптимального вибору ![]() ціни пропорційні граничним
корисностям товарів, тобто
ціни пропорційні граничним
корисностям товарів, тобто 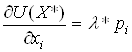 ,
, ![]() або відношення граничних
корисностей товарів дорівнює відношенню цін
або відношення граничних
корисностей товарів дорівнює відношенню цін
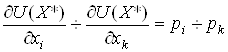 ,
, ![]() ;
;
2) гранична корисність, що доводиться на грошову одиницю, має бути однаковою для всіх товарів, які купують, отже
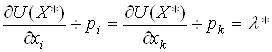 ,
, ![]() ,
,
3) рівні граничні
корисності, що доводяться на грошову одиницю, яку витрачають, дорівнюють ![]() – граничній
корисності грошей. Гранична корисність грошей для споживачів з різним рівнем
доходів різна:
– граничній
корисності грошей. Гранична корисність грошей для споживачів з різним рівнем
доходів різна: ![]() зменшується зі зростанням
зменшується зі зростанням ![]() і
зростає з його зменшенням.
і
зростає з його зменшенням.