Контрольная работа: Cтатистическая надежность регрессионного моделирования
Вариант 4-1
1. Рассчитайте параметры уравнения линейной регрессии
2. Оцените тесноту связи с помощью показателей корреляции и детерминации
3. Определите среднюю ошибку аппроксимации. Сделайте выводы
4. Оцените статистическую надежность регрессионного моделирования с помощью F-критерия Фишера и t-критерия Стьюдента
5. Оцените полученные результаты, оформите выводы
| № набл. | Район | Средний размер назначенных ежемесячных пенсий, тыс.руб., y | Прожиточный минимум в среднем на одного пенсионера в месяц, тыс.руб., x | |
| 1 | Брянская обл. | 240 | 178 | |
| 2 | Владимирская обл. | 226 | 202 | |
| 3 | Ивановская обл. | 221 | 197 | |
| 4 | Калужская обл. | 226 | 201 | |
| 5 | Костромская обл. | 220 | 189 | |
| 6 | г.Моска | 250 | 302 | |
| 7 | Москавская обл. | 237 | 215 | |
| 8 | Орловская обл. | 232 | 166 | |
| 9 | Рязанская обл. | 215 | 199 | |
| 10 | Смоленская обл. | 220 | 180 | |
| 11 | Тверская обл. | 222 | 181 | |
| 12 | Тульская обл. | 231 | 186 | |
| 13 | Ярославская обл. | 229 | 250 | |
|
Fтабл.=4,84(α =0,05) |
=9,29 | =34,75 |
1. Расчет параметров уравнения линейной регрессии по данным таблицы:
Решение:
1. Уравнение линейной регрессии имеет следующий вид:
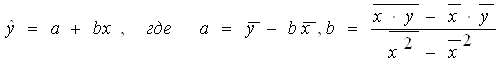
|
№ наблюдения |
х |
y |
X2 |
X·Y |
yx |
y- yx |
Ai |
|
| 1 | 178 | 240 | 31684 | 42720 | 222,51 | 17,49 | 7,29 | |
| 2 | 202 | 226 | 40804 | 45652 | 227,67 | -1,67 | 0,74 | |
| 3 | 197 | 221 | 38809 | 43537 | 226,59 | -5,59 | 2,53 | |
| 4 | 201 | 226 | 40401 | 45426 | 227,45 | -1,45 | 0,64 | |
| 5 | 189 | 220 | 35721 | 41580 | 224,87 | -4,87 | 2,22 | |
| 6 | 302 | 250 | 91204 | 75500 | 249,17 | 0,83 | 0,33 | |
| 7 | 215 | 237 | 46225 | 50955 | 230,46 | 6,54 | 2,76 | |
| 8 | 166 | 232 | 27556 | 38512 | 219,93 | 12,07 | 5,20 | |
| 9 | 199 | 215 | 39601 | 42785 | 227,02 | -12,02 | 5,59 | |
| 10 | 180 | 220 | 32400 | 39600 | 222,94 | -2,94 | 1,34 | |
| 11 | 181 | 222 | 32761 | 40182 | 223,15 | -1,15 | 0,52 | |
| 12 | 186 | 231 | 34596 | 42966 | 224,23 | 6,77 | 2,93 | |
| 13 | 250 | 229 | 62500 | 57250 | 237,99 | -8,99 | 3,93 | |
|
Сумма |
2646 | 2969 | 554262 | 606665 | ||||
|
Ср. значение |
203,54 | 228,38 | 42635,54 | 46666,54 | 2,77 | |||
Найдем b:

Тогда
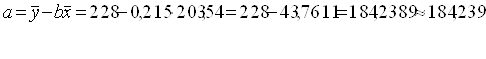
Уравнение линейной регрессии имеет вид:
ŷx =184,239+0,215x
2. а) Рассчитываем коэффициент корреляции:
по формуле:
rxy = b — = 0,21 =0,78
с помощью статистической функции КОРРЕЛ-r =0,78
Связь между переменными x и y прямая, средняя, близкая к сильной, т.е. величина среднемесячной пенсии в значительной мере зависит от прожиточного минимума в среднем на одного пенсионера в месяц
б) Для определения средней ошибки аппроксимации рассчитываем столбцы
yx , y- yx , Ai :
Ai = y- yx * 100, А = 1/n∑ni=1 Ai
Получаем значение средней ошибки аппроксимации
А = 2,77%
Величина ошибки аппроксимации говорит о хорошем качестве модели.
в) Величина коэффициента детерминации получена с помощью функции
ЛИНЕЙН R2 = rxy2 = 0,61,
то есть в 61% случаев изменения среднемесячного прожиточного минимума на одного пенсионера приводят к изменению среднемесячной пенсии. Другими словами – точность подбора регрессии 61 % - средняя.
3. Оценка статистической значимости
а) по критерию Фишера:
1. Выдвигаем нулевую гипотезу о статистической незначимости параметров регрессии и показателя корреляции а = b = rxy =0;
2. Фактическое значение критерия получено из функции ЛИНЕЙН
∑(ỹx-y)²/m r²xy0,61
Fфакт= = (n-2) = (13-2) = 1,56*11 = 17,2;
∑(y-ỹ)² /(n-m-1) 1-r²xy 1-0,61
3. Fтабл =4,84
4. Сравниваем фактическое и табличное значения критерия Fфакт> Fтабл , т.е.нулевую гипотезу отклоняем и делаем вывод о статистической значимости и надежности полученной модели.
б) по критерию Стьюдента:
1. Выдвигаем гипотезу о статистически незначимом отличии показателей от нуля: a = b = r²xy = 0;
2. Табличное значение t – критерия зависит от числа степеней свободы и заданного уровня значимости α. Уровень значимости – это вероятность отвергнуть правильную гипотезу.
![]() rxy √(n-m)
rxy √(n-m)
t=
![]() √(1- r2xy)
√(1- r2xy)
Где n – количество наблюдений; m – количество факторов.
t= 0,78√(13-2)= 2,59=4,18
![]() √(1-0,61)0,62
√(1-0,61)0,62
3. Фактические значения t-критерия рассчитываются отдельно для каждого параметра модели. С этой целью сначала определяются случайные ошибки параметров mа , mb, mrxy .
![]() mа=Sост √∑х2 = 1,65;
mа=Sост √∑х2 = 1,65;
mb= Sост = 0,004
![]() nσх σх√n
nσх σх√n
![]() mrxy= √(1- r2xy) = 0,062
mrxy= √(1- r2xy) = 0,062
n-m-1
![]() где Sост=√(∑ (y- yx ) ) = 5 = 0,5
где Sост=√(∑ (y- yx ) ) = 5 = 0,5
n-m-110
Рассчитываем фактические значения t – критерия:
tфа =a/ mа =111,66
tфb =b/ mb =53,75
tфrxy= rxy/mrxy = 12,58
tфа>tтабл ; tфb>tтабл ; tфrxy >tтабл . Нулевую гипотезу отклоняем , параметры a, b, rxy - не случайно отличаются от нуля и являются статистически значимыми и надежными.