Курсовая работа: Анализ рядов динамики на примере организации "Салон красоты Goddess"
Введение
Ряды динамики – это статистические данные, отображающие развитие во времени изучаемого явления. Их также называют динамическими рядами и временными.
Актуальность их изучения основывается на том, что с помощью рядов динамики изучаются закономерности развития социально – экономических явлений по важнейшим направлениям. Например, таким, как характеристика уровней развития изучаемых явлений во времени, изменение динамики изучаемых явлений посредством системы статистических показателей, выявление и количественная оценка основной тенденции развития, изучение периодических колебаний, экстраполяция, прогнозирование и многим другим.
Данная курсовая работа состоит из двух глав, каждая из которых разбита на параграфы.
В первой главе рассматриваются понятия о статистических рядах динамики (моментные, интервальные ряды динамики), а так же статистические показатели, рассчитанные на их основе: абсолютный прирост, темп роста, темп прироста коэффициент роста и абсолютное значение для 1% прироста.
Вторая глава посвящена статистическому анализу по рядам динамики на примере организации «Салон красоты Goddess», которая с 2007 года осуществляет свою деятельность на территории г. Барнаула, предоставляя клиентам различный спектр парикмахерских и косметических услуг.
Структура данной организации является линейно-штабной, что подразумевает наличие подразделений, помогающих руководителю, но не обладающими правами принятия решений.
Объект: «Салон красоты Goddess»
Предмет: анализ рядов динамики на примере организации «Салон красоты Goddess»
Цель: изучить динамику и провести анализ временных рядов и на основе задачи сформулировать выводы
Задачи:
Определить основные понятия и классификации рядов динамики
Изучить показатели, рассчитываемые на основе рядов динамики
Установить историю деятельности организации и его структуру
Проанализировать деятельность организации и сопоставить данные по бухгалтерскому балансу
Сформулировать выводы
Глава I. Понятие и классификация рядов динамики
1.1 Понятие о статистических рядах динамики
Массовые явления развиваются в пространстве и во времени. Изучение происходящих при этом изменений является одной из важнейших задач статистики.
Процесс развития массового явления во времени принято возникать динамикой, а показатели, характеризующие это развитие – статистическими рядами динамики. Следовательно, ряды динамики – это статистические данные, отображающие развитие во времени изучаемого явления. Их также называют динамическими и временными рядами.
Временные ряды состоят из двух элементов:
периода времени, за который или по состоянию на который приводятся числовые значения;
числовых значений того или иного показателя, называемых уровнями ряда.
В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы, кварталы, месяцы, сутки).
В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения.
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Такие показатели называются цепными.
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели живых объектов, а, также, характеристики природных явлений (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Ряды динамики, как правило, представляют в виде таблицы или графически. При графическом изображении ряда динамики (динамического ряда) на оси абсцисс строится шкала времени, а на оси ординат – шкала уравнений ряда (арифметическая или иногда логарифмическая). Изучение рядов динамики осуществляется в разных направлениях анализа состояния.
Ряды динамики различаются по следующим признакам:
По времени.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 1991 году (таб. 1):
Таблица 1
Списочная численность работников магазина в 1991 году
| Дата | 1.01.1991 | 1.04.1991 | 1.07.1991 | 1.10.1991 | 1.01.1992 |
| Число работ., чел. | 212 | 207 | 215 | 226 | 231 |
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Хотя и в моментном ряду есть интервалы – промежутки между соседними в ряду датами, - величина того или иного конкретного уровня не зависит от продолжительности периода между двумя датами.
Так, основная часть персонала магазина, составляющая списочную численность на 1.01.1991 , продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда может возникнуть повторный счет.
Посредством моментных рядов динамики в торговле изучаются товарные запасы, состояние кадров, количество оборудования и других показателей, отображающих состояние изучаемых явлений на отдельные даты (моменты) времени.
Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Примером интервального ряда могут служить данные о розничном товарообороте магазина в 1987 – 1991 гг. (таб. 2):
Таблица 2
Объем розничного товарооборота магазина в 1987 - 1991 гг.
| Год | 1987 | 1988 | 1989 | 1990 | 1991 |
| Объем розничного товарооборота, тыс. р. | 885.7 | 932.6 | 980.1 | 1028.7 | 1088.4 |
Каждый уровень интервального ряда уже представляет собой сумму уровней за более короткие промежутки времени. При этом единица совокупности, входящая в состав одного уровня, не входит в состав других уровней.
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а суммируя товарооборот за четыре квартала, получают его величину за год и т. д. При прочих равных условиях уровень интервального ряда тем больше, чем больше длина интервал, к которому этот уровень относится.
Свойство суммирования уровней за последовательные интервалы времени позволяет получить ряды динамики более укрупненных периодов.
Посредством интервальных рядов динамики в торговле изучают изменения во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования изучаемого явления за отдельные периоды.
Статистическое отображение изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями отображения результатов развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (года, месяца, квартала и т. д.).
Ряды динамики с нарастающими итогами строятся при определении общего объема товарооборота в розничной торговле. Так, обобщением товарно-денежных отчетов за последние операционные периоды (пятидневки, недели, декады и т. д.).
По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики.
Если ведется анализ во времени одного показателя, имеем изолированный ряд динамики.
Комплексный ряд динамики получается в том случае, когда в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления.
По расстоянию между датами или интервалам времени выделяют полные (равноотстоящие) или неполные (неравноотстоящие) ряды динамики.
Полные ряды динамики имеют место тогда, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Это равноотстоящие ряды динамики. Неполные – когда принцип равных интервалов не соблюдается[1].
По форме представления уровней.
Ряды абсолютных показателей. Характеризуют численность, совокупность и объем изучаемого социально – экономического явления в определенных гранях времени и места. Они всегда имеют наименования с числами, так как имеют какую-либо единицу изменения.
Ряды относительных показателей. Результат сопоставления двух статистических показателей, дающий цифровую меру их соотносителей (динамика, плановое задание, выполнение плана и т.д.).
Ряды средних величин. Обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях и местах времени.
Исходными, первоначальными являются ряды динамики абсолютных величин, ряды динамики относительных и средних величин составляются на основе рядов динамики абсолютных величин и рассматриваются как производные.
При изучении массовых явлений в статистике приходится иметь дело с
Различными видами рядов динамики. Однако с каким бы рядом динамики не приходилось иметь дело, основным требованием, предъявляемым к анализируемому ряду, является сопоставимость его уровней.
Несопоставимость статистических данных во времени (уровней рядов динамики) может быть обусловлена различными причинами:
различная система охвата явления статистическими наблюдениями (например, изменение границ территории, к которой отнесены те или иные показатели);
различная продолжительность интервалов времени, к которым относятся уровни (нельзя в рамках одного динамического ряда приводить данные за год и за 9 месяцев или в одном ряду совмещать данные в нарастающих итогах за ряд лет: в январе следующего года будет резкое снижение уровня по сравнению с декабрем предыдущего года, фиксирующего значения показателя в год);
изменением круга охватываемых предприятий за ряд лет (особенно остро этот вопрос возникает при анализе малого бизнеса, для которого характерна частая смена деятельности);
изменения в методике первичного учета и обобщения цеховой информации или в методике расчета показателей;
различия применяемых в отдельные периоды единиц измерения, цен и т.п.
несовершенство методологии систематического наблюдения[2].
Вопрос об обеспечении сопоставимости может решаться по-разному в зависимости от целей исследования и причин возникновения непоправимости.
Для обеспечения сопоставимости осуществляются дополнительные расчеты; изучаются все изменения, происшедшие за анализируемый период в пределах явлений. Например, данные за прошлые годы при территориальных
изменениях пересчитываются в новых границах. Аналогично поступают при
изменении в методах расчетов показателей, изменении цен и т.д.
Один и тот же ряд динамики для одних цепей является сопоставимым, а для других может быть несопоставимым.
Следовательно, прежде чем анализировать ряды динамики, надо, исходя из цели исследования, убедиться в сопоставимости уровней ряда и, если имеет место несопоставимость, добиться, при возможности сопоставимости дополнительными расчетами.
Одним из приемов обеспечения сопоставимость рядов динамики является так называемо смыкание рядов динамики.
Под смыканием рядов динамики понимают объединение в один ряд (более длинный) двух или несомых рядов, уровни которых исчислены по разной методологии или в разных границах. При этом для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имеешь данные, исчисленные по разной методологии (или в разных границах).
Для переходного периода определяется коэффициент соотношения двух уровней (отыщите уровни по старой методологии или границе и уровни по новой методологии или границе). Разделив этот коэффициент уровни первого ряда (по старой методологии или территории), можно построить ряд динамики сопоставимых уровней (объединяющих уровни рассматриваемых рядов).
1.2 Показатели, рассчитываемые на основе рядов динамики
Уровни временного ряда могут изменяться в самых разных направлениях: они могут возрастать или убывать, повторять ранее достигнутый уровень. Интенсивность их изменения бывает различной. Уровни ряда могут изменяться быстрее или медленнее. Для характеристики развития явления во времени применяются следующие показатели:
Абсолютный прирост (∆у)
Темп роста (Тр)
Коэффициент роста (Кр)
Темп прироста (снижения) (Тпр)
Абсолютное значение на 1% прироста (А)
Абсолютный прирост (абсолютное изменение) уровней ряда рассчитывается как разность двух уровней. Он показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.
В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными:
∆у цепной = уi – yi – 1;
∆базисный = yi – y0
Если каждый последующий уровень ряда динамики сравнивается со своим предыдущим уровнем, то прирост называется цепным.
Если же в качестве базы сравнения выступает за ряд лет один и тот же период, то прирост называется базисным.
Один и тот же по величине абсолютный прирост может означать разную интенсивность изменения (таб. 3):[3]
Таблица 3
| года | Произведено продукции, тыс. шт. | Абсолютные приросты, тыс. шт. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, тыс. шт. | |||
| цепные | базисные | цепные | базисные | цепные | базисные | |||
| 1995 | 20 | - | - | - | 100 | - | - | - |
| 1996 | 25 | 5 | 5 | 125 | 125 | 25 | 25 | 0,2 |
| 1997 | 35 | 10 | 15 | 140 | 175 | 40 | 75 | 0,25 |
| 1998 | 40 | 5 | 20 | 114,3 | 200 | 14,3 | 100 | 0,35 |
| 1999 | 50 | 10 | 30 | 125 | 250 | 25 | 150 | 0,40 |
| Итого | 170 | 30 | - | - | - | - | - | - |
В данном примере в 1996 и 1998 гг. абсолютное изменение объема продукции было одинаковым – 5 тыс. шт., но интенсивность роста объема произведенной продукции в эти годы была различной: в 1996 г. прирост в 5 тыс. ед. по сравнению с предыдущим годом составил 25%, а в 1998 г. по сравнению с предыдущим годом – лишь 14,3%. Аналогично один и тот же прирост в 10 тыс. ед. для 1997 и 1999 гг. означает разную интенсивность роста: в 1997 г. – прирост составил по сравнению с предыдущим годом 40%, а в 1999 г. – 25%.
Темп роста есть отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные:
Тр цепной ![]() ;
;
Tp базисный ![]()
Если база сравнения по периодам меняется, то найденные темпы поста называются цепными. Если же база сравнения по периодам неизменна (у0), то темпы роста называются базисными.
Темпы роста, выраженные в коэффициентах, принято называть коэффициентами роста:
Кp цепной ![]()
Кз базисный ![]()
В анализе используется один из этих показателей: либо темп роста, либо коэффициент роста, ибо экономическое их содержание одно и то же, но по-разному выражено: в % (темп роста) и в разах (коэффициент роста).
Так, по данным таблицы 3 можно сделать вывод, что наибольшая интенсивность роста была достигнута в 1997 г., когда темп роста составил 140%, или в 1,4 раза превысил уровень предыдущего года.
Если цепные темпы роста характеризуют интенсивность изменения уровней от года к году (от месяца к месяцу), то базисные темпы роста фиксируют интенсивность роста (снижения) за весь интервал времени между текущим и базисным уровнями. Так, по данным таблицы 3 базисный темп роста за весь период с 1996 по 1999 г. составил 250% (1995 г. взят за базу сравнения).
Темп прироста есть отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель).
∆Тр цепной = ![]()
∆Тр базисный = ![]()
По данным таблицы 3 темп прироста для 1999 г. составит:
цепной – 25% (![]() ) и базисный – 150% (
) и базисный – 150% (![]() ), т. е. в 1999 г. объем
продукции увеличился по сравнению с 1998 г. на 25%, а в целом за весь
рассматриваемый период прирост составил 150%.
), т. е. в 1999 г. объем
продукции увеличился по сравнению с 1998 г. на 25%, а в целом за весь
рассматриваемый период прирост составил 150%.
Между цепными и базисными показателями изменения уровня ряда существует следующая взаимосвязь:
А) сумма цепных абсолютных приростов равно базисному приросту (см. в таблице 3, где в итоговой строке накопленный прирост за 1996 – 1999 гг. – 30 тыс. шт. – совпадает с базисным абсолютным ростом для 1999 г.);
Б) произведение цепных коэффициентов роста равно базисному.
В) произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентом роста. Так по данным таблице 3 имеем:
1,25 • 1,40 • 1,43 • 1,25 = 2,5, или 250% - базисный темп роста;
200/175 = 1,143, или 114,3% - цепной коэффициент роста для 1998 г.
Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным и наоборот;
Г) Темп прироста связан с темпом роста: ∆Тр – Тр – 100 (см. таблицу 3, где темпы прироста меньше темпов роста на 100). Поэтому при анализе обычно приводится какой-то один инз них: темп роста либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста.
Для этого нужно от темпов прироста перейти к темпам (коэффициентам) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.
Так, например, изменение цен на потребительские товары и услуги за I квартал 2001 г. оказалось в Санкт-Петербурге следующим (таб. 4).
Таблица 4
Изменение цен (в % к предыдущему месяцу)
| Месяц | Январь | Февраль | Март |
| Изменение цен | 3,7 | 1,7 | 1,8 |
В целом за I квартал прирост цен составит:
(1,037 ×1,017×1,018) • 100 = 7,4%.
То есть в марте 2001 года по сравнению с декабрем 2000 года цены выросли на 7,4%.
Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за этот же промежуток времени:
А = ![]() или
или
А = 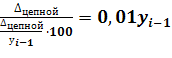 .
.
Иными словами, абсолютное значение 1% прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде (см. таблице 3, последнюю графу). В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина – сотая часть уровня базисного периода.
Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как ∆″ = ∆i - ∆i – 1, то есть по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости. По таблице 3 в нашем примере ускорение имело место лишь в 1997 и в 1999 гг., когда ∆″ = 10 – 5 = 5 тыс. шт.
Если систематически растут цепные темпы роста, то ряд развивается с относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:
∆% = Трi – Трi – 1
Или
∆% = ∆Трi - ∆Npi – 1.
Полученная величина выражается в процентных пунктах (п.п.). По данным таблицы 3, относительное ускорение имело место лишь в 1997 г. – 15 процентных пунктов по сравнению с предыдущим годом.
Относительное ускорение может быть измерено и с помощью коэффициента опережения.
Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:
Копережения = ![]() .
.
В нашем примере коэффициент опережения для 1997 года составил 140/125 = 1,12, что означает, что в 1997 году темп роста был в 1,12 раза больше, чем в 1996 году.
Коэффициент опережения принято рассчитывать в сравнительном анализе нескольких рядов динамики. При параллельном изучении нескольких рядов динамики обычно их приводят к одному основанию путем расчета базисных темпов роста с одинаковой по времени базой сравнения для всех рядов. Это позволяет наглядно видеть, для какого ряда интенсивность изменений уровней наибольшая. Сравнивая далее наибольшие темпы роста с наименьшими, определяют коэффициенты опережения в развитии одного явления по отношению к другому (таб. 5).
Таблица 5
Динамика доходов предприятия за 1-е полугодие 2001 г.
| Месяцы | Прибыль от реализации продукции | Прибыль от продажи прочих активов | Доходы по акциям |
| Декабрь 2000 г. | 205 | 30 | 21 |
|
2001 г.: Январь |
220 | 32 | 27 |
| Февраль | 226 | 40 | 32 |
| Март | 252 | 48 | 38 |
| Апрель | 280 | 60 | 54 |
| Май | 310 | 100 | 66 |
| Июнь | 356 | 120 | 88 |
Во всех рядах заметна тенденция к росту из месяца в месяц отдельных видов доходов. Однако сделать вывод об интенсивности роста отдельных видов доходов только по данным таблицы 5 затруднительно. Для наглядности приведем к одному основанию, приняв для каждого из них за базу сравнения декабрь 2000 г. (таб. 6).
Таблица 6
Динамика доходов предприятия за 1-е полугодие 2001 г.
| Месяцы | Прибыль от реализации продукции | Прибыль от продажи прочих активов | Доходы по акциям |
| Декабрь 2000 г. | 100 | 100 | 100 |
|
2001 г.: Январь |
107,3 | 106,7 | 128,6 |
| Февраль | 110,2 | 133,3 | 152,4 |
| Март | 122,9 | 160,0 | 181,0 |
| Апрель | 136,6 | 200,0 | 257,1 |
| Май | 151,2 | 333,3 | 314,3 |
| Июнь | 173,7 | 400,0 | 419,0 |
Как видим, наиболее интенсивно на предприятии росли доходы по акциям, а также прибыль от продажи прочих активов. Коэффициент опережения их роста за 1-е полугодие по сравнению с ростом прибыли от реализации продукции составили: 2,3 – для прибыли от продажи прочих активов и 2,4 – для доходов по акциям.
При анализе, произведенном на основе вышерассмотренных данных, приводятся средние показатели. То есть:
Средний уровень интервального ряда динамики
![]() , где n – число периодов.
, где n – число периодов.
Средний абсолютный прирост
![]() , где n – число периодов
или
, где n – число периодов
или
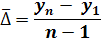
Средний коэффициент роста
![]()
или
![]() =
= ![]()
Средний темп роста
![]() =
= ![]()
Средний темп прироста
![]() - 1)
- 1)![]()
или
![]() - 100
- 100
Средняя величина абсолютного значения на 1 единицу % прироста
![]() =
= ![]()
Глава II. Статистический анализ по рядам динамики на примере предприятия «Салон красоты Goddess
2.1 История деятельности и структура предприятия «Салон красоты Goddess»
«Салон красоты Goddess» осуществляет свою деятельность в течение двух полных лет (с 2007года) на территории города Барнаула.
При открытии салона никаких юридических препятствий быть не может, т.к. на основании ст. 92 п.1 Гражданского кодекса РФ ООО может быть реорганизовано или ликвидировано по единогласному решению его участников, а так же на основании ст. 93 п.1 Гражданского Кодекса РФ.[4] Участник общества вправе продать или иным образом уступить свою долю в уставном капитале. «Салон красоты Goddess» осуществляет различный спектр деятельность в области красоты, здоровья и омоложения:
парикмахерские услуги (женский и мужской зал);
маникюр и педикюр (стандартный уход; наращивание и лечение ногтей);
косметологические услуги (уход за кожей лица; уход за бровями и ресницами; эпиляция);
уход за кожей тела, в том числе массажные услуги;
услуги визажиста
солярий.
Основные данные об организации
| Форма организационно - правовой собственности | Товарищество с ограниченной ответственностью |
| Наименование фирмы | «Салон красоты Goddess» |
| Кол-во пайщиков | Два человека |
| Дата открытия ТОО | Январь, 2007год |
| Собственный капитал | 30 000$ |
Организация была основана в январе 2007года в виде общей собственности как товарищество с ограниченной ответственностью и с собственным капиталом 30 000 $.
Чем обоснован выбор:
-личное доверие участников;
-нет двойного налогообложения подоходным налогом;
-не требует особых усилий и расходов при организации;
-простое распределение прибыли - пропорционально доле пая
-ограниченная ответственность;
-каждый партнёр может и руководить и представлять других партнёров по товариществу;
Собственниками предприятия являются:
Красильникова Юлия -50%
Новикова Валерия - 50%
Собственный капитал поделён на 2 пая, соответственно — 50:50%.
Собственники напрямую участвуют в руководстве деятельностью товарищества.
Организация относится к типу элит-салона. Это подразумевает под собой то, что она рассчитана на состоятельных клиентов. Цены на обслуживание в салоне данного типа достаточно высокие.
Если говорить об организационной структуре предприятия, то следует
отметить, что высшим органом ответственности товарищества с ог-
раниченной ответственностью является общее собрание пайщиков, в компетенцию которого входит:
-внесение изменений в устав;
-увеличение и уменьшение паевого капитала;
-избрание и отзыв членов правления;
-учреждение отчета за хозяйственный год и распределение прибыли;
-раздел пая;
-вынесения решения о прекращении деятельности ТОО.
Для осуществления своей деятельности и внутреннего управления организация использует линейно – штабную структуру. Она включает в себя специализированные подразделения (штабы), которые не обладают правами принятия решений и руководства какими - либо нижестоящими подразделениями, а лишь помогают соответствующему руководителю в выполнении отдельных функций, прежде всего, функций стратегического планирования и анализа.
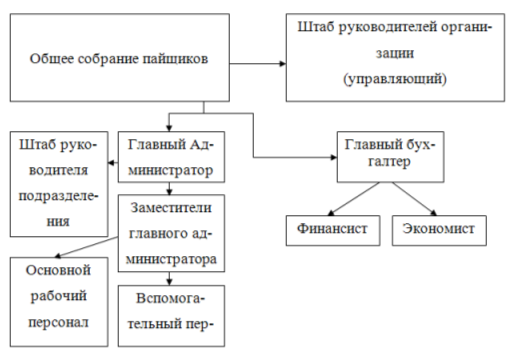
Штаб руководителей организации во главе с управляющим занимается кадрами, организацией работы персонала, отслеживает изменения на локальном рынке, управляет рекламным бюджетом, изменяет стоимость услуг, проводит закупки расходных материалов и аксессуаров, косметики, ведет работу по повышению мастерства персонала, организует работу с контролирующими организациями, заключает договора на техническое обслуживание.
Главный бухгалтер ведет всю финансовую деятельность фирмы при взаимодействии с подчиненными ему финансистом и экономистом (начисления и уплата налогов, распределение прибыли, расчет зарплаты).
Главный администратор при сотрудничестве со штабом руководителя подразделения организует подготовку персонала на рабочих местах. Отвечает за его компетентность, умение обслуживать систему управления соляриями.
Заместители главного администратора отвечают за непосредственную работу с клиентами и грамотную эксплуатацию системы управления.
Анализ деятельности и сопоставление данных бухгалтерского баланса организации «Салон красоты Goddess»
| Год | 2007 (тыс. $) | 2008(тыс. $) | 2009 (тыс. $) |
| Расходы | 25,5 | 19,1 | 11,9 |
| Доходы | 12,9 | 19,2 | 28,1 |
Представим расчетные таблицы показателей рядов динамики от года к году.
Расходы
| Показатели | Года | |||
| 2007 | 2008 | 2009 | ||
| Абсолютный прирост (∆) | с переменной базой | - | ∆1 = 19,1 – 25,5 =-6,4 | ∆2 = 11,9 – 19,1 =-7,2 |
| с постоянной базой | - | ∆1 = 19,1 – 25,5 =-6,4 | ∆2 = 11,9 – 25,5 =-13,6 | |
| Коэффициент роста (Кр) | с переменной базой | - | Кр1 = 19,1/25,5 = 0,75 | Кр2 = 11,9/19,1 = 0,62 |
| с постоянной базой | - | Кр1 = 19,1/25,5 =0,75 | Кр2 = 11,9/25,5 =0,47 | |
| Темп роста (Тр) | с переменной базой | - | Тр1 = 0,75•100%=75% | Тр2 = 0,62•100%=62% |
| с постоянной базой | - | Тр1 = 0,75•100%= 75% | Тр2 = 0,47•100%=47% | |
| Темп прироста (Тпр) | с переменной базой | - | Тпр1=75%-100%=-25% | Тпр2=62%-100%=-38% |
| с постоянной базой | - | Тпр1=75%-100%=-25% | Тпр2=47%-100%=-53% | |
| Абсолютное значение для 1% прироста (А) | с переменной базой | - | А1 = -6,4/-25 =0,26 | А2 = -13,6/-3,8 =0,36 |
| с постоянной базой | - | А1 = 25,5/100 = 0,25 | А2 = А1 = 0,25 |
Средний уровень интервального ряда динамики:
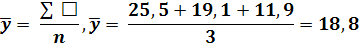
Средний абсолютный прирост:
![]() ,
,
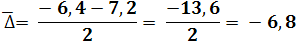
или
![]() ,
,
![]()
Средний коэффициент роста
![]() ,
, ![]() =
= ![]() ≈ 0,681
≈ 0,681
или
![]() =
= ![]() ,
, ![]() =
= 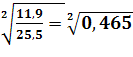 ≈ 0,681
≈ 0,681
Средний темп роста
![]() =
= ![]() ,
, ![]() = 0,681•100% = 68,1%
= 0,681•100% = 68,1%
Средний темп прироста
![]() - 1)
- 1)![]() ,
, ![]() = -31,9%
= -31,9%
или
![]() – 100%,
– 100%, ![]() – 100% = -31,9%
– 100% = -31,9%
Средняя величина абсолютного значения на 1 единицу % прироста
![]() =
= ![]() ,
, ![]() =
= ![]() = 0,213
= 0,213
Проведем анализ представленных данных:
Абсолютный прирост. Изменение цепного абсолютного прироста показало, что в сравнении с предыдущим годом показатель уровня расходов организации в 2008 году снизился на 6,4 единиц, а в 2009 – на 7,2. Базисный абсолютный прирост, заключающийся в разности показателей 2009 и 2007 года, равен снижению на 13,6 единиц. Значение среднего абсолютного прироста составило 6,8 единиц.
Данные показатели характеризуют заметный спад затрат организации, что может быть спровоцировано тем, что в самом начале деятельности организации она нуждалась в закупке вспомогательных рабочих средств, обустройстве рабочих мест, ремонте и проч., а после приобретения большого количества товаров, в которых нуждается персонал, расходы организации сократились.
Коэффициент роста. Цепной коэффициент роста 2009 года превысил уровень предыдущего года в 0,62 раза, в то время как Кр 2008 года – в 0,75 против 2007. Базисный коэффициент роста в 2008 и 2009 году увеличился по равнению с 2007 в 0,75 и 0,47 раза соответственно. Средний коэффициент роста ≈ 0,681
Темп роста. Темпы роста с переменной базой составили в 2008 и 2009 году 75% и 62% соответственно. Базисный темп роста в 2009 году составил 47%. Средний темп роста равен 68,1%.
Данные значения характеризуют интенсивный спад расходов.
Темп прироста. Самым значительный показателем является базисный темп прироста в 2009 году, который составил -53%. Средний темп прироста составляет -31,9%.
Абсолютное значение для 1% прироста. Так как цепные темпы прироста растут (0,26 и 0,36 в 2008 и 2009 году соответственно), мы можем говорить об относительном ускорении в снижении уровня расходов организации. Средняя величина абсолютного значения на 1 единицу % прироста равно 0,213.
Доходы
| Показатели | Года | |||
| 2007 | 2008 | 2009 | ||
| Абсолютный прирост (∆) | с переменной базой | - | ∆1 = 19,1 – 12,9=6,3 | ∆2 = 28,1 – 19,2 =8,9 |
| с постоянной базой | - | ∆1 = 19,1 – 12,9=6,3 | ∆2 = 28,1 – 12,9 = 15,2 | |
| Коэффициент роста (Кр) | с переменной базой | - | Кр1 = 19,2/12,9 = 1,49 | Кр2 = 28,1/19,2 = 1,46 |
| с постоянной базой | - | Кр1 = 19,2/12,9 = 1,49 | Кр2 = 28,1/12,9 = 2,18 | |
| Темп роста (Тр) | с переменной базой | - | Тр1 =1,49•100%= 149% | Тр2 = 1,46•100%= 146% |
| с постоянной базой | - | Тр1 =1,49•100%= 149% | Тр2 = 2,18•100%= 218% | |
| Темп прироста (Тпр) | с переменной базой | - | Тпр1=149-100= 49% | Тпр2=146-100= 46% |
| с постоянной базой | - | Тпр1=149-100= 49% | Тпр2=218-100= 118% | |
| Абсолютное значение для 1% прироста (А) | с переменной базой | - | А1 = 6,3/49 = 0,13 | А2 = 8,9/46 = 0,19 |
| с постоянной базой | - | А1 = 12,9/100 = 0,129 | А2 = А1 = 0,129 |
Средний уровень интервального ряда динамики:
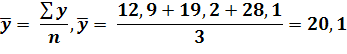
Средний абсолютный прирост:
![]() ,
, ![]()
![]() ,
, ![]()
Средний коэффициент роста
![]() ,
, ![]() =
= ![]() ≈ 1,47
≈ 1,47
![]() =
= ![]() ,
, ![]() =
= 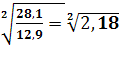 ≈ 1,47
≈ 1,47
Средний темп роста
![]() =
= ![]() ,
, ![]() = 1,47•100% = 147%
= 1,47•100% = 147%
Средний темп прироста
![]() - 1)
- 1)![]() ,
, ![]() = 47%
= 47%
![]() – 100%,
– 100%, ![]() – 100% = 47%
– 100% = 47%
Средняя величина абсолютного значения на 1 единицу % прироста
![]() =
= ![]() ,
, ![]() =
= ![]() = 0,16
= 0,16
Проведем анализ представленных данных:
Абсолютный прирост. Наиболее ярко выраженное значение абсолютного прироста выражается в базисном показателе за 2009 год, которое равняется 15,2. Средний абсолютный прирост составил 7,6 единиц.
Обоснование данных заключается в увеличении прибыли предприятия вследствие привлечения новых клиентов, повышении качества предлагаемых услуг.
Коэффициент роста. Коэффициент роста с переменной базой в 2008 и 2009 годах превысили уровни предыдущего ряда в 1,49 и 1,46 раз соответственно. Максимальное значение приобрел базисный темп роста в 2009 году, который показал, что в сравнении с 2007 уровень доходов повысился на 2,18 раза. Средний коэффициент роста приблизительно равен 1,47 раза.
Темп роста. Темп роста доходов организации, выраженный в переменном показателе, в 2008 и 2009 году равен 149% и 146% соответственно. В отчетном году по сравнению с начальным уровень роста доходов организации составил 218%.
Данные показатели говорят об интенсивном повышении доходов организации.
Темп прироста. Базисный темп прироста в 2008 и 2009 году составил 49% и 118% соответственно. Средний темп прироста равен 147%.
Абсолютное значение для 1% прироста. Цепной показатель в 2008 и 2009 году равен 0,13 и 0,19 соответственно, в то время как средняя величина абсолютного значения на 1 единицу % прироста равна 0,16.
Заключение
Ряды динамики, как статистические данные, отображающие развитие во времени изучаемого явления, можно классифицировать по различным признакам: по времени (моментные, интервальные), по расстоянию между датами или интервалам времени (равноотстоящие, неравноотстоящие), по числу показателей (изолированные и комплексные) и по форме представления уровней (ряды относительных, средних и абсолютных величин).
Важным условием при изучении массовых явлений в статистике, основывающихся на различных рядах динамики, является их сопоставимость.
Для характеристики развития явления во времени на основе анализа рядов динамики могут рассчитываться такие показатели, как абсолютный прирост, темп роста, коэффициент роста, темп прироста и абсолютное значение на 1% прироста.
В данной курсовой работе аналитический анализ по рядам динамики осуществлялся на примере организации «Салон красоты Goddess», которая с 2007 года осуществляет свою деятельность на территории г. Барнаула, как товарищество с ограниченной ответственностью, используя линейно-штабную структуру организации.
Анализ деятельности и сопоставление данных бухгалтерского баланса показали, что в организации наблюдается интенсивный спад расходов и повышение доходов из года в год.
Обоснование данного вывода может заключаться в увеличении прибыли организации вследствие привлечения новых клиентов, успешно размещенной рекламы в средствах массовой информации и на телевидении.
Уменьшение расходов организации вызвано сокращением закупок различных внеоборотных и оборотных активов организации.
Таким образом, ряды динамики, а так же их анализ, являются одним из самых эффективных методов планирования и прогнозирования во всех сферах социальной и экономической жизни предприятий и общества.
[1] Материал из Википедии – свободной интернет – энциклопедии. -ru.wikipedia.org
[2] Обеспечение сопоставимости в рядах динамики. - http://allstats.ru/?p=124
[3] Статистика: Учебник / И. И. Елисеева, И. И. Егорова и др.; Под ред. Проф. И. И. Елисеевой. – М.: ТК ВЕЛБИ, Изд-во Проспект, 2003. – С.115.
[4] Гражданский кодекс Российской Федерации Часть первая: официальное издание. – М.: Юрид. лит., 2004. – С.47.
| Теория экономического анализа | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Красноярский государственный ... В ходе трендового анализа рассчитываются относительные величины динамики (базисные и цепные) - темпы роста. 4) определятся величина изменения результативного показателя за счет второго из факторов: базисную величину результативного показателя, увеличенную на его прирост за счет первого ... |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Статистика | |
|
... статистической информации 7 2. Сводка и группировка материалов статистического наблюдения. 15 3. Абсолютные и относительные статистические величины. Абсолютное значение 1% прироста (А1%) получается в результате сравнения абсолютного прироста и темпа прироста (в%) за один и тот же промежуток времени. или (yn-yn-k): , т.е. равно ... Либо по данным уровней ряда , т.к. сумма цепных абсолютных приростов всегда равна последнему базисному абсолютному приросту (смотри решение тренировочных заданий, дискета №1 PR-2 ... |
Раздел: Рефераты по статистике Тип: реферат |
| Анализ финансово-хозяйственной деятельности предприятия | |
|
оглавление Введение 1 ПРЕДМЕТ, ЗНАЧЕНИЕ И ЗАДАЧИ АНАЛИЗА ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ, СПОСОБЫ ИЗМЕРЕНИЯ ВЛИЯНИЯ ФАКТОРОВ В АНАЛИЗЕ 1.1 Понятие ... Темп прироста прибыли от продаж составил 67,96 %, абсолютный прирост 1964 тыс. руб. Цепные темпы роста (прироста) рассчитываются по отношению к предыдущему периоду. |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Статистическое наблюдение | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Санкт-Петербургский ... Специфическими показателями динамического ряда являются абсолютный прирост (разность между последующим уровнем и предыдущим), темпы роста (цепные и базисные, так как являются ... где DС - абсолютная разность производственных затрат; с1 и с0 - индивидуальные значения себестоимости у единиц изучаемой совокупности в отчетном и базисном периодах соответственно ... |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Применение индексного метода при анализе цен | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Амурский государственный ... Для анализа рядов динамики рассчитываются: абсолютные приросты, темпы роста, темпы прироста, абсолютное значение одного процента. Абсолютный прирост показывает на сколько в абсолютном выражении уровень текущего периода больше (или меньше) базисного (предыдущего). |
Раздел: Рефераты по экономике Тип: курсовая работа |