Лабораторная работа: Векторные линии в векторном поле

Вариант 9

  1. Найти векторные линии в векторном поле

Решение:

Векторные линии  - это линии, в каждой точке которых вектор поля является касательным

Для нахождения векторных линий поля



решим дифференциальное уравнение:


Имеем

                                                                 -9xdx=4ydy


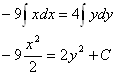     Векторные линии представляют собой семейство эллипсов


  1. Вычислить длину дуги линии ; 

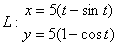Решение:

Найдем производные

 ;

Длина дуги кривой в параметрических координатах равна:

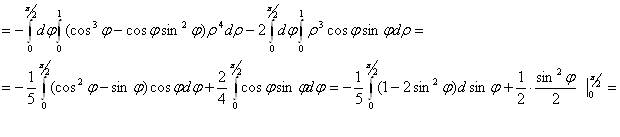
  1. Вычислить поток векторного поля 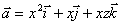 через поверхность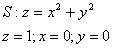

Решение:

По определениюпотока векторного поля П, имеем

, где  - единичный нормальный вектор к поверхности.

Вычислим  . Как известно, если уравнение поверхности , то единичный нормальный вектор

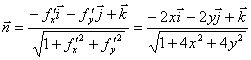
                Тогда поток векторного поля

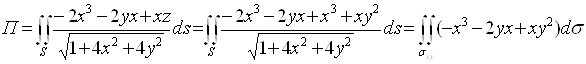
Где часть круга радиуса R=1  в плоскости Оху с центром в начале координат, ограниченная  условиями

                                              

Y
 
                                              

                                                                        Введем полярные координаты ; 

    

1
 
                                                                                                              Получим

0
 

1
 

X
 
                                                                                                             


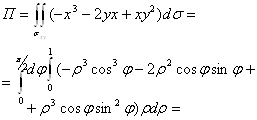
4. Найти  все значения корня

    Решение:

                    Пусть z=1=1+0i

    Arg z=0;  |z|=1


    По формуле корней из комплексного числа, имеем


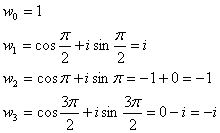                                                                                                                                                                                            где k=0,1,2,3

Получим

Ответ: 4 корня – 1;i;-i;-1

5. Представить в алгебраической форме Ln(-1-i)

                    Решение:


                    Из определения логарифма комплексного числа Lnz=ln|z|+i argz