Дипломная работа: Высшая математика для менеджеров
ПРЕДИСЛОВИЕ
Учебное пособие “Высшая математика для менеджеров” включает такие разделы высшей математики, изучение которых дает математический аппарат, наиболее активно применяемый для решения прикладных экономических и управленческих задач. Это аналитическая геометрия, линейная алгебра и математический анализ.
Знание аналитической геометрии необходимо современному менеджеру, чтобы грамотно толковать экономическую информацию, представляемую в виде различных графиков - это кривые и поверхности безразличия, кривые потребительского бюджета, инвестиционного спроса, кривые Филлипса, Лаффера, Лоренца и т. д.; выводить интерполяционные формулы по методу наименьших квадратов; находить наилучший план производства при заданных ресурсах.
В разделе “Линейная алгебра” основное внимание уделяется матрицам, определителям и системам линейных уравнений, поскольку в экономических исследованиях широко используются различные матричные модели - межотраслевого баланса, в плановых расчетах, при расчетах фонда заработной платы и т.д. Линейные модели, сводящиеся к системам алгебраических линейных уравнений или неравенств, c достаточно высокой точностью соответствуют описываемым ими явлениям; с их помощью решаются многие управленческие задачи.
Математический анализ дает ряд фундаментальных понятий, которыми оперирует экономист, - это функция, предел, производная, интеграл, дифференциальное уравнение. Например, второй замечательный предел применяется при решении задач о росте банковского вклада по закону сложных процентов; использование понятия производной приводит к такой специальной дисциплине, как предельный анализ в экономике и т.д.
В начале каждого параграфа приводятся краткие сведения из теории, носящие справочный характер. Основное внимание уделяется практическому освоению студентами изучаемого материала. Для достижения этой цели приводится большое число упражнений. Их выполнение будет способствовать выработке навыков рационального решения типовых примеров и задач, а также задач экономического и производственного содержания, развивающих навыки применения изученного математического инструментария. Задания для самостоятельных индивидуальных работ предлагаются в книге: Корсакова Л.Г. Математика для экономистов в примерах и задачах: Учеб. пособие/ Калинингр. ун-т. - Калининград, 1994.
В конце пособия приводится список литературы, в который вошли все источники, использованные в той или иной мере при его написании.
Автор выражает глубокую благодарность рецензентам - профессорам Афинского университета экономики и бизнеса Танасу Скурасу и Анике Харламбиду, а также доценту кафедры вычислительной математики Л.В. Зинину, коллегам по математическому факультету за ценные замечания и помощь при подготовке пособия.
I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1. Векторы
Упорядоченную совокупность ( x1, x2, ... , x n
) n вещественных чисел называют n-мерным вектором, а числа xi
( i = ![]() ) - компонентами,
или координатами, вектора.
) - компонентами,
или координатами, вектора.
Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент. Векторы обозначают жирными строчными буквами или буквами с чертой или стрелкой наверху, например, a или `a. Два вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны.
Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1) ¹ ¹ (2, 3, 5, 0, 1).
Произведением вектора x = (x1, x2 , ... ,xn) на действительное число l называется вектор l x = (l x1, l x2, ... , l xn).
Суммой векторов x = (x1, x2, ... ,xn) и y = (y1, y2 , ... ,yn) называется вектор x + y = (x1 + y1, x2 + y2, ... , x n + yn).
N-мерное векторное пространство Rn определяется как множество всех n-мерных векторов, для которых определены операции умножения на действительные числа и сложение.
Экономическая иллюстрация n-мерного векторного пространства: пространство
благ (товаров). Под товаром мы будем понимать некоторое благо
или услугу, поступившие в продажу в определенное время в определенном месте.
Предположим, что существует конечное число наличных товаров n; количества
каждого из них, приобретенные потребителем, характеризуются набором товаров x
= (x1, x2, ..., xn), где через xi
обозначается количество i-го блага, приобретенного потребителем. Будем считать,
что все товары обладают свойством произвольной делимости, так что может быть
куплено любое неотрицательное количество каждого из них. Тогда все возможные
наборы товаров являются векторами пространства товаров C = { x = (x1,
x2, ... , xn) ê xi
³ 0, i = ![]() }.
}.
Система e1, e2, ... , em n-мерных векторов называется линейно зависимой, если найдутся такие числа l1, l2, ... , lm, из которых хотя бы одно отлично от нуля, что выполняется равенство l1 e1 + l2 e2 +... + lm em = 0; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все l1 = l2 = ... = lm = 0. Геометрический смысл линейной зависимости векторов в R3, интерпретируемых как направленные отрезки, поясняют следующие теоремы.
Теорема 1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
Теорема 2. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.
Теорема 3. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.
Тройка некомпланарных векторов a, b, c называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
Тройка e1, e2, e3 некомпланарных векторов в R3 называется базисом, а сами векторы e1, e2, e3 - базисными. Любой вектор a может быть единственным образом разложен по базисным векторам, то есть представлен в виде
а = x1 e1 + x2 e2 + x3 e3, (1.1)
числа x1, x2, x3 в разложении (1.1) называются координатами вектора a в базисе e1, e2, e3 и обозначаются a(x1, x2, x3). Если векторы e1, e2, e3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x1, x2, x3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R3 выбрана правая система декартовых прямоугольных координат {0, i, j, k}.
Векторным произведением вектора а на вектор b называется вектор c, который определяется следующими тремя условиями:
1. Длина вектора c численно равна площади параллелограмма, построенного на векторах a и b, т. е. êc ê = êa ê êb êsin (a^b).
2. Вектор c перпендикулярен к каждому из векторов a и b.
3. Векторы a, b и c, взятые в указанном порядке, образуют правую тройку.
Для векторного произведения c вводится обозначение c = [ab] или c = a´ b.
Если векторы a и b коллинеарны, то sin(a^b) = 0 и [ab] = 0, в частности, [aa] = 0. Векторные произведения ортов: [ij] = k, [jk] = i, [ki] = j.
Если векторы a и b заданы в базисе i, j, k координатами a(a1, a2, a3), b(b1, b2, b3), то
[ab]
= 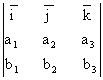 =`i (a2b3 - a3b2)
- `j (a1b3 - a3b1)
+ `k (a1b2 - a2b1).
=`i (a2b3 - a3b2)
- `j (a1b3 - a3b1)
+ `k (a1b2 - a2b1).
Если векторное произведение двух векторов а и b скалярно умножается на третий вектор c, то такое произведение трех векторов называется смешанным произведением и обозначается символом a b c.
Если векторы a, b и c в базисе i, j, k заданы своими координатами a(a1, a2, a3), b(b1, b2, b3), c(c1, c2, c3), то
abc = 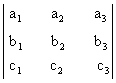 .
.
Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.
Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка a, b, c - левая, то a b c<0 и V = - a b c, следовательно V = êa b cê.
Координаты векторов, встречающиеся в задачах первой главы, предполагаются заданными относительно правого ортонормированного базиса. Единичный вектор, сонаправленный вектору а, обозначается символом ао. Символом r=ОМ обозначается радиус-вектор точки М, символами а, АВ или êа ê, êАВ ê обозначаются модули векторов а и АВ.
Пример 1.1. Зная векторы a и b, на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной к стороне a.
Решение. Обозначим AB=a, AC=b, CD=h, где CD^a, D-основание перпендикуляра, опущенного из точки C на сторону a. По правилу сложения векторов имеем: b + h = AD, h = AD - b. Поскольку AD çça, то AD = l a.
Найдем значение l, используя ортогональность векторов a и h: ah=0 или a(l a-b)=0, откуда l = ab /a2. Следовательно, h = (ab /a2) a - b.
А
B![]()
![]()

![]()

b h a
C D
Рис. 1
Пример 1.2. Найдите угол между векторами a = 2m+4n и b = m-n, где m и n - единичные векторы и угол между m и n равен 120о.
Решение.
Имеем: cos j = ab/ab, ab = (2m+4n) (m-n)
= 2 m2 - 4n2 +2mn = = 2 - 4+2cos120o
= - 2 + 2(-0.5) = -3; a = ![]() ; a2
= (2m+4n) (2m+4n) = = 4 m2 +16mn+16
n2 = 4+16(-0.5)+16=12, значит a =
; a2
= (2m+4n) (2m+4n) = = 4 m2 +16mn+16
n2 = 4+16(-0.5)+16=12, значит a = ![]() .
b =
.
b = ![]() ; b2 =
= (m-n)(m-n) = m2 -2mn+ n2
= 1-2(-0.5)+1 = 3, значит b =
; b2 =
= (m-n)(m-n) = m2 -2mn+ n2
= 1-2(-0.5)+1 = 3, значит b = ![]() . Окончательно
имеем: cos j =
. Окончательно
имеем: cos j =![]() = -1/2, Þ j = 120o.
= -1/2, Þ j = 120o.
Пример 1.3. Зная векторы AB(-3,-2,6) и BC(-2,4,4),вычислите длину высоты AD треугольника ABC.
Решение.
Обозначая площадь треугольника ABC через S, получим: S = 1/2 BC AD. Тогда
AD=2S/BC, BC= ![]() =
=![]() = 6, S = 1/2 çAB ´ACç. AC=AB+BC, значит, вектор AC имеет
координаты AC(-5,2,10). AB´AC =
= 6, S = 1/2 çAB ´ACç. AC=AB+BC, значит, вектор AC имеет
координаты AC(-5,2,10). AB´AC = 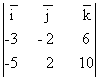 = i
(-20 -12) - j (30 -30) + k (- 6 - 10) = = -16(2`i +`k ). çAB´ACç =
= i
(-20 -12) - j (30 -30) + k (- 6 - 10) = = -16(2`i +`k ). çAB´ACç = ![]() = 16
= 16![]() ; S = 8
; S = 8![]() , откуда
AD =
, откуда
AD = ![]() =
=![]() .
.
Пример 1.4. Даны два вектора a(11,10,2) и b(4,0,3). Найдите единичный вектор c, ортогональный векторам a и b и направленный так, чтобы упорядоченная тройка векторов a, b, c была правой.
Решение. Обозначим координаты вектора c относительно данного правого ортонормированного базиса через x, y, z.
Поскольку c ^ a, c ^ b, то ca = 0, cb = 0. По условию задачи требуется, чтобы c = 1 и a b c >0.
Имеем систему уравнений для нахождения x,y,z: 11x +10y + 2z = 0, 4x+3z=0, x2 + y2 + z2 = 0.
Из первого и второго уравнений системы получим z = -4/3 x, y = -5/6 x.
Подставляя y и z в третье уравнение, будем иметь: x2 = 36/125,
откуда x = ± ![]() .
Используя условие a b c >0, получим неравенство
.
Используя условие a b c >0, получим неравенство
 > 0 или 5(6x-5y-8z) > 0.
> 0 или 5(6x-5y-8z) > 0.
С учетом выражений для z и y перепишем полученное неравенство в виде:
625/6 x > 0, откуда следует, что x>0. Итак, x = ![]() , y = -
, y = -![]() , z =-
, z =-![]() .
.
2. Линии на плоскости
При чтении экономической литературы приходится иметь дело с большим количеством графиков. Укажем некоторые из них.
Кривая безразличия - кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета - кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей - кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса - кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса - кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера - кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и разбираться в свойствах простейших кривых, каковыми являются прямые линии и кривые второго порядка - окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной системой неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0. При этом на функцию F должны быть наложены ограничения так, чтобы, с одной стороны, это уравнение имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло “куска плоскости”. Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, cуть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
10. Общее уравнение прямой:
Ax + By + C = 0. (2.1)
Вектор n(А,В) ортогонален прямой, числа A и B одновременно не равны нулю.
20. Уравнение прямой с угловым коэффициентом:
y - yo = k (x - xo), (2.2)
где k - угловой коэффициент прямой, то есть k = tg a, где a - величина угла, образованного прямой с осью Оx, M (xo, yo ) - некоторая точка, принадлежащая прямой.
Уравнение (2.2) принимает вид y = kx + b, если M (0, b) есть точка пересечения прямой с осью Оy.
30. Уравнение прямой в отрезках:
x/a + y/b = 1, (2.3)
где a и b - величины отрезков, отсекаемых прямой на осях координат.
40. Уравнение прямой, проходящей через две данные точки - A(x1, y1) и B(x2, y2 ):
![]() . (2.4)
. (2.4)
50. Уравнение прямой, проходящей через данную точку A(x1, y1) параллельно данному вектору a(m, n):
![]() . (2.5)
. (2.5)
60. Нормальное уравнение прямой:
rnо - р = 0, (2.6)
где r - радиус-вектор произвольной точки M(x, y) этой прямой, nо - единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; р - расстояние от начала координат до прямой.
Нормальное уравнение прямой в координатной форме имеет вид:
x cos a + y sin a - р = 0,
где a - величина угла, образованного прямой с осью Оx.
Уравнение пучка прямых с центром в точке А(x1, y1) имеет вид:
y-y1 = l(x-x1 ),
где l - параметр пучка. Если пучок задается двумя пересекающимися прямыми A1 x + B1 y + C1= 0, A2 x + B2 y + C2 = 0, то его уравнение имеет вид:
l (A1 x + B1 y + C1) + m (A2 x + B2 y + C2 )=0,
где l и m - параметры пучка, не обращающиеся в 0 одновременно.
Величина угла между прямыми y = kx + b и y = k1 x + b1 задается формулой:
tg j = 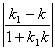 .
.
Равенство 1 + k1 k = 0 есть необходимое и достаточное условие перпендикулярности прямых.
Для того, чтобы два уравнения
A1 x + B1 y + C1= 0, (2.7)
A2 x + B2 y + C2 = 0, (2.8)
задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:
A1/A2 = B1/B2 = C1/C2.
Уравнения (2.7), (2.8) задают две различные параллельные прямые, если A1/A2 = B1/B2 и B1/B2 ¹ C1/C2; прямые пересекаются, если A1/A2 ¹ B1/B2.
Расстояние d от точки Mо(xо, yо) до прямой есть длина перпендикуляра, проведенного из точки Mо к прямой. Если прямая задана нормальным уравнением, то d = êrо nо - р ê, где rо - радиус-вектор точки Mо или, в координатной форме, d = êxо cosa + yо sina - р ê.
Общее уравнение кривой второго порядка имеет вид:
a11x2 + 2a12xy + a22y2 + 2a1x +2a2y +a = 0.
Предполагается, что среди коэффициентов a11, a12, a22 есть отличные от нуля.
Уравнение окружности с центром в точке С(a, b) и радиусом, равным R:
(x - a)2 + (y - b)2 = R2. (2.9)
Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2a.
Каноническое (простейшее) уравнение эллипса:
x2/a2 + y2/a2 = 1. (2.10)
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат. Параметры a и b называются полуосями эллипса.
Пусть a>b, тогда фокусы F1 и F2 находятся на оси
Оx на расстоянии c= ![]() от начала
координат. Отношение c/a = e < 1 называется эксцентриситетом
эллипса. Расстояния от точки M(x, y) эллипса до его фокусов (фокальные
радиусы-векторы) определяются формулами:
от начала
координат. Отношение c/a = e < 1 называется эксцентриситетом
эллипса. Расстояния от точки M(x, y) эллипса до его фокусов (фокальные
радиусы-векторы) определяются формулами:
r1 = a - ex, r2 = a +ex.
Если же a < b, то фокусы находятся на оси Оy, c=![]() , e = c/b, r1 = b + ex, r2 = b
- ex.
, e = c/b, r1 = b + ex, r2 = b
- ex.
Если a = b, то эллипс является окружностью с центром в начале координат радиуса a.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек F1 и F2 (фокусов) равна по абсолютной величине данному числу 2a.
Каноническое уравнение гиперболы:
x2/a2 - y2/b2 = 1. (2.11)
Гипербола, заданная уравнением (2.11), симметрична относительно осей
координат. Она пересекает ось Оx в точках A (a,0) и A (-a,0) - вершинах
гиперболы и не пересекает ось Оy. Параметр a называется вещественной
полуосью, b - мнимой полуосью. Параметр c=![]() есть расстояние от фокуса
до начала координат. Отношение c/a = e >1 называется
эксцентриситетом гиперболы. Прямые y = ± b/a x
называются асимптотами гиперболы. Расстояния от точки M(x,y) гиперболы
до ее фокусов (фокальные радиусы-векторы) определяются формулами:
есть расстояние от фокуса
до начала координат. Отношение c/a = e >1 называется
эксцентриситетом гиперболы. Прямые y = ± b/a x
называются асимптотами гиперболы. Расстояния от точки M(x,y) гиперболы
до ее фокусов (фокальные радиусы-векторы) определяются формулами:
r1 = êex - a ê, r2 = êex + a ê.
Гипербола, у которой a = b, называется равносторонней, ее уравнение x2 - y2 = a 2, а уравнение асимптот y = ± x. Гиперболы x2/a2 - y2/b2 = 1 и y2/b2 - x2/a2 = 1 называются сопряженными.
Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Каноническое уравнение параболы имеет два вида:
1) y2 = 2рx - парабола симметрична относительно оси Оx.
2) x2 = 2рy - парабола симметрична относительно оси Оy.
В обоих случаях р>0 и вершина параболы, то есть точка, лежащая на оси симметрии, находится в начале координат.
Парабола y 2 = 2рx имеет фокус F( р/2,0) и директрису x = - р/2, фокальный радиус-вектор точки M(x,y) на ней r = x+ р/2.
Парабола x2 =2рy имеет фокус F(0, р/2) и директрису y = - р/2; фокальный радиус-вектор точки M(x,y) параболы равен r = y + р/2.
Уравнение F(x, y) = 0 задает линию, разбивающую плоскость на две или несколько частей. В одних из этих частей выполняется неравенство F(x, y)<0, а в других - неравенство F(x, y)>0. Иными словами, линия F(x, y)=0 отделяет часть плоскости, где F(x, y)>0, от части плоскости, где F(x, y)<0.
Прямая Ax+By+C = 0 разбивает плоскость на две полуплоскости. На практике для выяснения того, в какой полуплоскости мы имеем Ax+By+C<0, а в какой Ax+By+C>0, применяют метод контрольных точек. Для этого берут контрольную точку (разумеется, не лежащую на прямой Ax+By+C = 0) и проверяют, какой знак имеет в этой точке выражение Ax+By+C. Тот же знак имеет указанное выражение и во всей полуплоскости, где лежит контрольная точка. Во второй полуплоскости Ax+By+C имеет противоположный знак.
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство x2-4x+y2+6y-12 > 0. Его можно переписать в виде (x-2)2 + (y+3)2 - 25 > 0.
Уравнение (x-2)2 + (y+3)2 - 25 = 0 задает окружность с центром в точке C(2,-3) и радиусом 5. Окружность разбивает плоскость на две части - внутреннюю и внешнюю. Чтобы узнать, в какой из них имеет место данное неравенство, возьмем контрольную точку во внутренней области, например, центр C(2,-3) нашей окружности. Подставляя координаты точки C в левую часть неравенства, получаем отрицательное число -25. Значит, и во всех точках, лежащих внутри окружности, выполняется неравенство x2-4x+y2+6y-12 < 0. Отсюда следует, что данное неравенство имеет место во внешней для окружности области.
Пример 1.5. Составьте уравнения прямых, проходящих через точку A(3,1) и наклоненных к прямой 2x+3y-1 = 0 под углом 45o.
Решение. Будем
искать уравнение прямой в виде y=kx+b. Поскольку прямая проходит через точку A,
то ее координаты удовлетворяют уравнению прямой, т.е. 1=3k+b, Þ b=1-3k. Величина угла между прямыми y= k1 x+b1
и y= kx+b определяется формулой tgj = 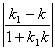 . Так как угловой
коэффициент k1 исходной прямой 2x+3y-1=0 равен - 2/3, а угол j = 45o, то имеем уравнение для определения k:
. Так как угловой
коэффициент k1 исходной прямой 2x+3y-1=0 равен - 2/3, а угол j = 45o, то имеем уравнение для определения k:
(2/3 + k)/(1 - 2/3k) = 1 или (2/3 + k)/(1 - 2/3k) = -1.
Имеем два значения k: k1 = 1/5, k2 = -5. Находя соответствующие значения b по формуле b=1-3k, получим две искомые прямые: x - 5y + 2 = 0 и 5x + y - 16 = 0.
Пример 1.6. При каком значении параметра t прямые, заданные уравнениями 3tx-8y+1 = 0 и (1+t)x-2ty = 0, параллельны ?
Решение. Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 3t/(1+t) = -8/(-2t). Решая полученное уравнение, находим t: t1 = 2, t2 = -2/3.
Пример 1.7. Найти уравнение общей хорды двух окружностей: x2 +y2 =10 и x2+y2-10x-10y+30=0.
Решение. Найдем точки пересечения окружностей, для этого решим систему уравнений:
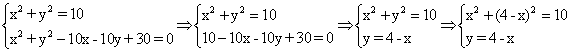
Решая первое уравнение, находим значения x1 = 3, x2 = 1. Из второго уравнения - соответствующие значения y: y1 = 1, y2 = 3. Теперь получим уравнение общей хорды, зная две точки А(3,1) и B(1,3), принадлежащие этой прямой: (y-1)/(3-1) = (x-3)/(1-3), или y+ x - 4 = 0.
Пример 1.8. Как расположены на плоскости точки, координаты которых удовлетворяют условиям (x-3) 2 + (y-3) 2 < 8, x > y?
Решение. Первое
неравенство системы определяет внутренность круга, не включая границу, т.е.
окружность с центром в точке (3,3) и радиуса ![]() .
Второе неравенство задает полуплоскость, определяемую прямой x = y, причем, так
как неравенство строгое, точки самой прямой не принадлежат полуплоскости, а все
точки ниже этой прямой принадлежат полуплоскости. Поскольку мы ищем точки, удовлетворяющие
обоим неравенствам, то искомая область - внутренность полукруга.
.
Второе неравенство задает полуплоскость, определяемую прямой x = y, причем, так
как неравенство строгое, точки самой прямой не принадлежат полуплоскости, а все
точки ниже этой прямой принадлежат полуплоскости. Поскольку мы ищем точки, удовлетворяющие
обоим неравенствам, то искомая область - внутренность полукруга.
Пример 1.9. Вычислить длину стороны квадрата, вписанного в эллипс x2/a2 + y2/b2 = 1.
Решение. Пусть
М(с, с) - вершина квадрата, лежащая в первой четверти. Тогда сторона
квадрата будет равна 2с. Т.к. точка М принадлежит эллипсу, ее
координаты удовлетворяют уравнению эллипса c2/a2 + c2/b2
= 1, откуда c = ab/ ![]() ; значит, сторона
квадрата - 2ab/
; значит, сторона
квадрата - 2ab/ ![]() .
.
Пример 1.10.
Зная уравнение асимптот гиперболы y = ± 0,5 x и одну из ее
точек М(12, 3![]() ), составить уравнение
гиперболы.
), составить уравнение
гиперболы.
Решение. Запишем каноническое уравнение гиперболы: x2/a2 - y2/b2 = 1. Асимптоты гиперболы задаются уравнениями y = ± 0,5 x, значит, b/a = 1/2, откуда a=2b. Поскольку М - точка гиперболы, то ее координаты удовлетворяют уравнению гиперболы, т.е. 144/a2 - 27/b2 = 1. Учитывая, что a = 2b, найдем b: b2=9 Þ b=3 и a=6. Тогда уравнение гиперболы - x2/36 - y2/9 = 1.
Пример 1.11. Вычислить длину стороны правильного треугольника ABC, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение. Каноническое
уравнение параболы с параметром р имеет вид y2 = 2рx, вершина
ее совпадает с началом координат, и парабола симметрична относительно оси
абсцисс. Так как прямая AB образует с осью Ox угол в 30o, то
уравнение прямой имеет вид: y = ![]() x.
x.
Следовательно, мы можем найти координаты точки B, решая систему уравнений
y2=2рx, y = ![]() x,
откуда x = 6р, y = 2
x,
откуда x = 6р, y = 2 ![]() р. Значит,
расстояние между точками A(0,0) и B(6р,2
р. Значит,
расстояние между точками A(0,0) и B(6р,2![]() р)
равно 4
р)
равно 4![]() р.
р.
Пример 1.12. Со станции ежедневно можно отправлять пассажирские и скорые поезда. Данные приведены в таблице.
| Тип поезда | Количество вагонов в составе | ||
| плацкартных | купейных | мягких | |
| Пассажирский | 5 | 6 | 3 |
| Скорый | 8 | 4 | 1 |
| Резерв вагонов | 80 | 72 | 21 |
Записать в математической форме условия, не позволяющие превысить наличный парк вагонов при формировании пассажирских и скорых поездов, ежедневно отправляемых со станции. Построить на плоскости Oxy область допустимых вариантов формирования поездов.
Решение. Обозначим через x количество пассажирских поездов, а через y - количество скорых. Получим систему линейных неравенств: 5x + 8y £ 80, 6x + 4y £ 72, 3x + y £ 21, x ³ 0, y ³ 0.
Построим соответствующие прямые:
5x + 8y = 80, 6x +4y = 72, 3x + y = 21, x = 0, y = 0,
записав их уравнения в виде уравнений прямых в отрезках: x/16 + y/10 = 1, x/12 + y/18 = 1, x/7 + y/21 = 1, x = 0, y = 0.
Заштрихуем полуплоскости, удовлетворяющие данным неравенствам, и получим область допустимых значений:
![]() y
y
 21
21
 18
18
 10
10
 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 7
12 16 x
0 7
12 16 x
Рис. 2
Итак, количество скорых поездов не превышает 10, а пассажирских должно быть не более 7.
Пример 1.13. Имеются два пункта производства (A и B) некоторого вида продукции и три пункта (I, II, III) его потребления. В пункте А производится 250 единиц продукции, а в пункте В - 350 единиц. В пункте I требуется 150 единиц, в пункте II -240 единиц и в пункте III - 210 единиц. Стоимость перевозки одной единицы продукции из пункта производства в пункт потребления дается следующей таблицей.
Таблица 1
| Пункт | Пункт потребления | ||
| производства | I | II | III |
| A | 4 | 3 | 5 |
| B | 5 | 6 | 4 |
Требуется составить план перевозки продукции, при котором сумма расходов на перевозку будет наименьшей.
Решение. Обозначим количество продукции, перевозимой из пункта А в пункт I через x, а из пункта А в пункт II - через y. Так как полная потребность в пункте I равна 150 единицам, то из пункта В надо завезти (150 - x) единиц. Точно так же из пункта В в пункт II надо завезти (240 - y) единиц. Далее: производительность пункта А равна 250 единицам, а мы уже распределили (x + y) единиц. Значит, в пункт III идет из пункта А (250 - x -y) единиц. Чтобы полностью обеспечить потребность пункта III, осталось завезти 210 - (250 - x -y) = x + y - 40 единиц из пункта В. Итак, план перевозок задается следующей таблицей.
Таблица 2
| Пункт | Пункт потребления | ||
| производства | I | II | III |
| A | x | y | 250 - x - y |
| B | 150 - x | 240 - y | x + y - 40 |
Чтобы найти полную стоимость перевозки, надо умножить каждый элемент этой таблицы на соответствующий элемент предыдущей таблицы и сложить полученные произведения. Получим выражение:
S(x,y) = 4x + 3y + 5 (250 - x - y) + 5 (150 - x) + + 6 (240 -y) + 4 (x + y - 40) = - 2x - 4y +3280.
По условию задачи требуется найти минимум этого выражения. Но величины x и y не могут принимать произвольных значений. Ведь количество перевозимой продукции не может быть отрицательным. Поэтому все числа таблицы 2 неотрицательны:
x ³ 0, y ³ 0, 250 - x - y ³ 0, 150 -x ³ 0, 240 - y ³ 0, x + y - 40 ³ 0. (2.12)
Итак, нам надо найти минимум функции S(x,y) в области, задаваемой системой неравенств (2.12). Эта область изображена на рис.3 - она является многоугольником, ограниченным прямыми:
x = 0, y = 0, 250 - x - y = 0, 150 - x = 0, 240 - y = 0, x + y - 40 = 0.
y

![]() F (0,240) E (10,240)
F (0,240) E (10,240)
D (150,100)
(0,40)
О B (40,0) C (150,0) x
Рис. 3.
Находим координаты вершин многоугольника: A (0,40), B (40,0), C (150,0), D (150,100), E (10,240), F (0,240). Очевидно, что функция S(x,y) принимает наименьшее значение в одной из вершин многоугольника CDEFKL.
В самом деле, выясним, где располагаются точки, в которых значения этой функции одинаковы (так называемые линии уровня функции S (x,y) = -2x - 4y + 3280). Если значение функции S (x,y) равно c, где с - вещественная константа, то - 2x - 4y + 3280 = c. Но это уравнение прямой линии. Значит, для функции S линиями уровня являются прямые линии, которые параллельны друг другу при различных значениях c. Если линия уровня пересекает многоугольник, то соответствующее значение c не является ни наибольшим, ни наименьшим. Ведь немного изменив c, мы получим прямую, которая также пересекает многоугольник. Если же линия уровня проходит через одну из вершин, причем весь многоугольник остается по одну сторону от этой линии, то соответствующее значение c является наибольшим или наименьшим.
Итак, функция S (x,y) = -2x - 4y + 3280 принимает наименьшее значение на многоугольнике в одной из его вершин. Поскольку мы уже знаем эти вершины, то подставим соответствующие значения координат и найдем, что
S (0,40) = 3120, S (40,0) = 3200, S (1,500) = 2980,
S (150,100) = 2580, S (10,240) = 2300, S (0,240) = 2320.
Наименьшим из этих значений является 2300. Это значение функция принимает в точке E (10, 240). Значит, x = 10, y = 240. Подставляя эти значения в план перевозок (см. таблицу 2), получаем:
Таблица 3
| Пункт | Пункт потребления | ||
| производства | I | II | III |
| A | 10 | 240 | 0 |
| B | 140 | 0 | 210 |
Таким образом, из пункта А в пункт I надо перевезти 10 единиц продукции, из пункта А в пункт II - 240 единиц и т. д. Стоимость намеченного плана равна 2300.
Рассмотренная задача относится к большому классу задач, возникающих не только в экономике, но и в других областях человеческой деятельности. Задачи такого типа называются задачами линейного программирования.
Пример 1.14.
Рассмотрим формулу простых процентов: S = P + I = P ( 1 + ni ).
В этой формуле I - это проценты за весь срок, P - первоначальная сумма, S - сумма, образованная к концу срока ссуды, i - ставка процентов в виде десятичной дроби. Начисленные проценты за один период ( месяц, квартал, год ) составят величину, равную Pi, за n периодов - Pni. Процесс роста суммы долга по формуле простых процентов легко представить графически. Перепишем S в виде S = P + Pni, откуда легко увидеть линейную зависимость между S и n, т. е. это уравнение прямой с угловым коэффициентом. Поскольку n - это независимая переменная, то, совместив ось On с горизонтальной осью, как это обычно и делается, а ось OS - c вертикальной осью, построим график функции S.
3. Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат x, y, z
Ax + By + Cz +D = 0 (3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; (3.2)
2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями:
![]() =
=![]() ; (3.3)
; (3.3)
3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
![]() . (3.4)
. (3.4)
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор a называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x1 +mt, y = y1 + nt, z = z1 + рt. (3.5)
Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:
x = mz + a, y = nz + b. (3.6)
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
![]() .
.
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n1, n2], где n1(A1, B1, C1) и n2(A2, B2, C2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
![]()
равносильна системе x = x1, ![]() ; такая прямая
перпендикулярна к оси Ох.
; такая прямая
перпендикулярна к оси Ох.
Система ![]() равносильна
системе x = x1, y = y1; прямая параллельна оси
Oz.
равносильна
системе x = x1, y = y1; прямая параллельна оси
Oz.
Пример 1.15. Cоставьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение. По условию задачи вектор ОА(1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде x-y+3z+D=0. Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 1-(-1)+3×3+D = 0 Þ D = -11. Итак, x-y+3z-11=0.
Пример 1.16.
Составьте уравнение плоскости, проходящей через ось Оz и образующей с
плоскостью 2x+y-![]() z-7=0 угол 60о.
z-7=0 угол 60о.
Решение. Плоскость, проходящая через ось Oz, задается уравнением Ax+By=0, где А и В одновременно не обращаются в нуль. Пусть В не равно 0, A/Bx+y=0. По формуле косинуса угла между двумя плоскостями
![]() = cos 60о, где m = A/B.
= cos 60о, где m = A/B.
Решая квадратное уравнение 3m2 + 8m - 3 = 0, находим его корни m1 = 1/3, m2 = -3, откуда получаем две плоскости 1/3x+y = 0 и -3x+y = 0.
Пример 1.17. Составьте канонические уравнения прямой: 5x + y + z = 0, 2x + 3y - 2z + 5 = 0.
Решение. Канонические уравнения прямой имеют вид:
![]()
где m, n, р - координаты направляющего вектора
прямой, x1, y1, z1 - координаты
какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения
двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из
координат (проще всего положить, например, x=0) и полученную систему решают как
систему линейных уравнений с двумя неизвестными. Итак, пусть x=0, тогда y + z =
0, 3y - 2z+ 5 = 0, откуда y=-1, z=1. Координаты точки М(x1, y1,
z1 ), принадлежащей данной прямой, мы нашли: M (0,-1,1).
Направляющий вектор прямой легко найти, зная нормальные векторы исходных
плоскостей n1(5,1,1) и n2(2,3,-2). Тогда n
= [n1, n2] = 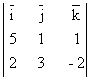 = (-2-3)i - (-10-2)j
+ (15-2)k = -5i+12j+13k.
= (-2-3)i - (-10-2)j
+ (15-2)k = -5i+12j+13k.
Канонические уравнения прямой имеют вид: x/(-5) = (y + 1)/12 = = (z - 1)/13.
Пример 1.18. В пучке, определяемом плоскостями 2х-у+5z-3=0 и х+у+2z+1=0, найти две перпендикулярные плоскости, одна из которых проходит через точку М(1,0,1).
Решение. Уравнение пучка, определяемого данными плоскостями, имеет вид u(2х-у+5z-3) + v(х+у+2z+1)=0, где u и v не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:
(2u +v)x + (- u + v)y + (5u +2v)z - 3u + v = 0.
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
(2u+v)×1 + ( -u + v)×0 + (5u + 2v )×1 -3u + v =0, или v = - u.
Тогда уравнение плоскости, содержащей M, найдем, подставив v = - u в уравнение пучка:
u(2x-y +5z - 3) - u (x + y +2z +1) = 0.
Т.к. u¹0 ( иначе v=0, а это противоречит определению пучка ), то имеем уравнение плоскости x-2y+3z-4=0. Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:
(2u+ v)×1 + (v - u)×(-2) + (5u +2v)×3 = 0, или v = - 19/5u.
Значит, уравнение второй плоскости имеет вид:
u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 или 9x +24y + 13z + 34 = 0.
II. ЛИНЕЙНАЯ АЛГЕБРА
4. Матрицы и определители
4.1 Матрицы. Операции над матрицами
Прямоугольной матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде
A =  (4.1)
(4.1)
или сокращенно в виде A = (ai j) (i =![]() ; j =
; j = ![]() ). Числа ai j,
составляющие данную матрицу, называются ее элементами; первый индекс
указывает на номер строки, второй - на номер столбца. Две матрицы A = (ai
j) и B = (bi j) одинакового размера называются равными,
если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B,
если ai j = bi j.
). Числа ai j,
составляющие данную матрицу, называются ее элементами; первый индекс
указывает на номер строки, второй - на номер столбца. Две матрицы A = (ai
j) и B = (bi j) одинакового размера называются равными,
если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B,
если ai j = bi j.
Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.
Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:
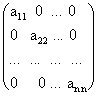 .
.
Если все элементы ai i диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:
E = 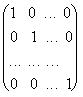 .
.
Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.
Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу
AT = ,
,
которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
Произведением матрицы А на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число l: l A = (l ai j).
Суммой двух матриц А = (ai j) и B = (bi j) одного размера называется матрица C = (ci j) того же размера, элементы которой определяются по формуле ci j = ai j + bi j.
Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
Произведением
двух матриц А = (ai j) и B = (bj k), где i =![]() , j=
, j=![]() , k=
, k=![]() , заданных в определенном
порядке АВ, называется матрица С = (c i k), элементы которой
определяются по следующему правилу:
, заданных в определенном
порядке АВ, называется матрица С = (c i k), элементы которой
определяются по следующему правилу:
c i k =
ai 1 b1 k + ai 2 b2 k +... + ai
m bm k = ![]() ai
s bs k. (4.2)
ai
s bs k. (4.2)
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Пример 2.1. Найти
произведение матриц А= ![]() и В =
и В = 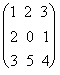 .
.
Решение. Имеем: матрица А размера 2´3, матрица В размера 3´3, тогда произведение АВ = С существует и элементы матрицы С равны с11 = 1×1 +2×2 + 1×3 = 8, с21 = 3×1 + 1×2 + 0×3 = 5, с12 = 1×2 + 2×0 + 1×5 = 7,
с22 =3×2 + 1×0 + 0×5 = 6, с13 = 1×3 + 2×1 + 1×4 = 9, с23 = 3×3 + 1×1 + 0×4 = 10.
AB =![]() , а произведение BA не
существует.
, а произведение BA не
существует.
Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70, а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
|
М1 |
М2 |
М3 |
|
| 1 | 20 | 35 | 10 |
| 2 | 15 | 27 | 8 |
Решение. Обозначим через А матрицу, данную нам в условии, а через В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
А =![]() , В = (50, 70, 130).
, В = (50, 70, 130).
Тогда матрица затрат на перевозки будет иметь вид:
АВT
= ![]()
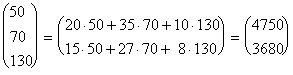 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Пример 2.3. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а вектор P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
|
Т1 |
Т2 |
Т3 |
Т4 |
|
| Зимнее пальто | 5 | 1 | 0 | 3 |
| Демисезонное пальто | 3 | 2 | 0 | 2 |
| Плащ | 0 | 0 | 4 | 3 |
1. Сколько метров ткани каждого типа потребуется для выполнения плана ?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Решение. Обозначим через А матрицу, данную нам в условии, т. е.,
A = 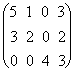 ,
,
тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор X умножить на матрицу А:
X А =
(10,15, 23)  =
= ![]() = = (95, 40, 92, 129).
= = (95, 40, 92, 129).
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу А и вектор CT:
А CT
= 
![]() =
=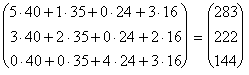 .
.
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
X А C T = (10,15,23)![]() =
=![]() .
.
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
X А P T = (95, 40, 92, 129)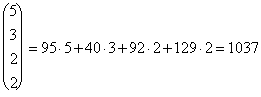 .
.
Итак, X А C T + X А P T = 9472 + 1037 = 10509 (ден. ед).
4.2 Определители
Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12...n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка, переводящая одну перестановку в другую, записывается двумя
строками в общих скобках, причем числа, занимающие одинаковые места в
рассматриваемых перестановках, называются соответствующими и пишутся
одно под другим. Например, символ ![]() обозначает
подстановку, в которой 3 переходит в 4, 1 ® 2, 2 ® 1, 4 ® 3. Подстановка называется четной (или
нечетной), если общее число инверсий в обеих строках подстановки четно
(нечетно). Всякая подстановка n-ой степени может быть записана в виде
обозначает
подстановку, в которой 3 переходит в 4, 1 ® 2, 2 ® 1, 4 ® 3. Подстановка называется четной (или
нечетной), если общее число инверсий в обеих строках подстановки четно
(нечетно). Всякая подстановка n-ой степени может быть записана в виде 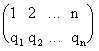 ,т.е. с натуральным
расположением чисел в верхней строке.
,т.е. с натуральным
расположением чисел в верхней строке.
Пусть нам дана квадратная матрица порядка n
 . (4.3)
. (4.3)
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
![]() , (4.4)
, (4.4)
где индексы q1, q2,..., qn составляют некоторую перестановку из чисел 1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (- 1)q, где q - число инверсий в перестановке вторых индексов элементов.
Определителем
n -го порядка, соответствующим матрице (4.3), называется алгебраическая сумма
n! членов вида (4.4). Для записи определителя употребляется символ êA ê=  или det A=
или det A=  (детерминант, или
определитель, матрицы А).
(детерминант, или
определитель, матрицы А).
Свойства определителей
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы
двух слагаемых ai j = bj + cj (j=![]() ), то определитель равен
сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном
определителе, а i-я строка в одном из слагаемых состоит из элементов bj,
в другом - из элементов cj.
), то определитель равен
сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном
определителе, а i-я строка в одном из слагаемых состоит из элементов bj,
в другом - из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором Mi j элемента ai j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j.
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d
= ai 1 Ai 1 + ai 2 Ai 2 +... + ai
n Ai n (i = ![]() )
)
или j- го столбца
d
= a1 j A1 j + a2 j A2 j +... + an j An j (j = ![]() ).
).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример 2.4. Не
вычисляя определителя 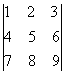 , показать, что
он равен нулю.
, показать, что
он равен нулю.
Решение. Вычтем
из второй строки первую, получим определитель 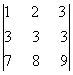 ,
равный исходному. Если из третьей строки также вычесть первую, то получится
определитель
,
равный исходному. Если из третьей строки также вычесть первую, то получится
определитель 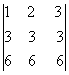 , в котором две
строки пропорциональны. Такой определитель равен нулю.
, в котором две
строки пропорциональны. Такой определитель равен нулю.
Пример 2.5. Вычислить
определитель D = 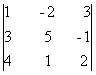 , разложив его по
элементам второго столбца.
, разложив его по
элементам второго столбца.
Решение. Разложим определитель по элементам второго столбца:
D = a12A12 + a22A22+a32A32=
= ![]() .
.
Пример 2.6. Вычислить определитель
A =  ,
,
в котором все элементы по одну сторону от главной диагонали равны
нулю.
Решение. Разложим определитель А по первой строке:
A = a11
A11 =  .
.
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
A = 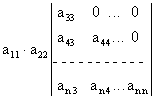 .
.
И так далее. После n шагов придем к равенству A = а11 а22... ann.
Пример 2.7.
Вычислить определитель 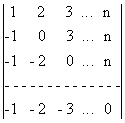 .
.
Решение. Если
к каждой строке определителя, начиная со второй, прибавить первую строку, то
получится определитель, в котором все элементы, находящиеся ниже главной
диагонали, будут равны нулю. А именно, получим определитель:  , равный исходному.
, равный исходному.
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.
4.3 Ранг матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение
0 £ r(A) £ min (m, n).
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.
Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
Канонической
матрицей называется матрица, у которой в начале главной диагонали стоят подряд
несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,  .
.
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример 2.8.
Найти методом окаймления миноров ранг матрицы 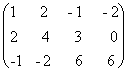 .
.
Решение. Начинаем
с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор
(элемент) М1 = 1, расположенный в первой строке и первом столбце.
Окаймляя при помощи второй строки и третьего столбца, получаем минор M2 =
![]() , отличный от нуля.
Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего
два (можно добавить второй столбец или четвертый). Вычисляем их:
, отличный от нуля.
Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего
два (можно добавить второй столбец или четвертый). Вычисляем их: 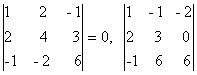 = 0. Таким образом, все окаймляющие миноры третьего порядка оказались
равными нулю. Ранг матрицы А равен двум.
= 0. Таким образом, все окаймляющие миноры третьего порядка оказались
равными нулю. Ранг матрицы А равен двум.
Пример 2.9.
Найти ранг матрицы А=  и
привести ее к каноническому виду.
и
привести ее к каноническому виду.
Решение. Из
второй строки вычтем первую и переставим эти строки:  .Теперь из второй и третьей
строк вычтем первую, умноженную соответственно на 2 и 5:
.Теперь из второй и третьей
строк вычтем первую, умноженную соответственно на 2 и 5: 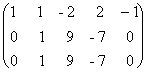 ; из третьей строки вычтем
первую; получим матрицу В =
; из третьей строки вычтем
первую; получим матрицу В =  ,
которая эквивалентна матрице А, так как получена из нее с помощью конечного
множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а
следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая
первый столбец, умноженный на подходящие числа, из всех последующих, обратим в
нуль все элементы первой строки, кроме первого, причем элементы остальных строк
не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа,
из всех последующих, обратим в нуль все элементы второй строки, кроме второго,
и получим каноническую матрицу:
,
которая эквивалентна матрице А, так как получена из нее с помощью конечного
множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а
следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая
первый столбец, умноженный на подходящие числа, из всех последующих, обратим в
нуль все элементы первой строки, кроме первого, причем элементы остальных строк
не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа,
из всех последующих, обратим в нуль все элементы второй строки, кроме второго,
и получим каноническую матрицу:  .
.
4.4 Обратная матрица
Рассмотрим квадратную матрицу
A =  .
.
Обозначим D =det A.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле
А-1 = 1/D  , (4.5)
, (4.5)
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 2.10.
Для матрицы А =  найти обратную.
найти обратную.
Решение. Находим
сначала детерминант матрицы А D = det А =  = 27 ¹ 0, значит, обратная матрица существует и мы ее можем
найти по формуле: А-1 = 1/D
= 27 ¹ 0, значит, обратная матрица существует и мы ее можем
найти по формуле: А-1 = 1/D 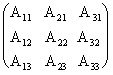 , где Аi j
(i,j=1,2,3) - алгебраические дополнения элементов аi j исходной
матрицы. Имеем:
, где Аi j
(i,j=1,2,3) - алгебраические дополнения элементов аi j исходной
матрицы. Имеем: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() откуда А-1 =
откуда А-1 = 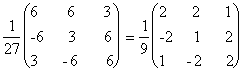 .
.
Пример 2.11.
Методом элементарных преобразований найти обратную матрицу для матрицы: А= 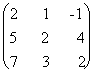 .
.
Решение. Приписываем
к исходной матрице справа единичную матрицу того же порядка: 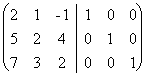 . С помощью элементарных
преобразований столбцов приведем левую “половину” к единичной, совершая
одновременно точно такие преобразования над правой матрицей. Для этого поменяем
местами первый и второй столбцы:
. С помощью элементарных
преобразований столбцов приведем левую “половину” к единичной, совершая
одновременно точно такие преобразования над правой матрицей. Для этого поменяем
местами первый и второй столбцы:  ~
~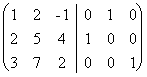 . К третьему столбцу прибавим первый, а ко второму - первый, умноженный
на -2:
. К третьему столбцу прибавим первый, а ко второму - первый, умноженный
на -2: 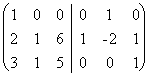 . Из первого столбца вычтем
удвоенный второй, а из третьего - умноженный на 6 второй;
. Из первого столбца вычтем
удвоенный второй, а из третьего - умноженный на 6 второй; 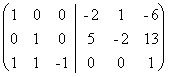 . Прибавим третий столбец к
первому и второму:
. Прибавим третий столбец к
первому и второму:  . Умножим
последний столбец на -1:
. Умножим
последний столбец на -1: 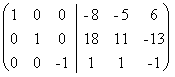 .
Полученная справа от вертикальной черты квадратная матрица является обратной к
данной матрице А. Итак, А-1 =
.
Полученная справа от вертикальной черты квадратная матрица является обратной к
данной матрице А. Итак, А-1 =  .
.
5. Системы линейных уравнений
5.1 Критерий совместности
Система линейных уравнений имеет вид:
a11 x1 + a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2, (5.1)
... ... ... ...
am1 x1 + am1 x2 +... + amn xn = bm.
Здесь аi j и bi (i = ![]() ;
j =
;
j = ![]() ) - заданные, а xj
- неизвестные действительные числа. Используя понятие произведения матриц, можно
переписать систему (5.1) в виде:
) - заданные, а xj
- неизвестные действительные числа. Используя понятие произведения матриц, можно
переписать систему (5.1) в виде:
AX = B, (5.2)
где A = (аi j) - матрица, состоящая из коэффициентов при неизвестных системы (5.1), которая называется матрицей системы, X = (x1, x2,..., xn)T, B = (b1, b2,..., bm)T - векторы-столбцы, составленные соответственно из неизвестных xj и из свободных членов bi.
Упорядоченная совокупность n вещественных чисел (c1, c2,..., cn) называется решением системы (5.1), если в результате подстановки этих чисел вместо соответствующих переменных x1, x2,..., xn каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c1, c2,..., cn)T такой, что AC º B.
Система (5.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
Матрица
`A =  ,
,
образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.
Вопрос о совместности системы (5.1) решается следующей теоремой.
Теорема Кронекера- Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A и`A совпадают, т.е. r(A) = r(`A) = r.
Для множества М решений системы (5.1) имеются три возможности:
1) M = Æ (в этом случае система несовместна);
2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);
3) M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.
Система имеет единственное решение только в том случае, когда r(A) = n. При этом число уравнений - не меньше числа неизвестных (m³n); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:
a11 x1 + a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2, (5.3)
... ... ... ... ... ...
an1 x1 + an1 x2 +... + ann xn = bn.
Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера; 3) матричным методом.
Пример 2.12. Исследовать систему уравнений и решить ее, если она совместна:
5x1 - x2 + 2x3 + x4 = 7,
2x1 + x2 + 4x3 - 2x4 = 1,
x1 - 3x2 - 6x3 + 5x4 = 0.
Решение. Выписываем расширенную матрицу системы:
`A = 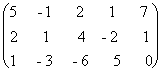 .
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор
второго порядка в левом верхнем углу ![]() = 7 ¹ 0; содержащие его миноры третьего порядка равны нулю:
= 7 ¹ 0; содержащие его миноры третьего порядка равны нулю:
M¢3 = 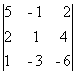 = 0, M²3 =
= 0, M²3 =  = 0.
= 0.
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы `A рассмотрим окаймляющий минор
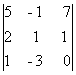 =
= 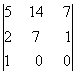 = -35 ¹ 0,
= -35 ¹ 0,
значит, ранг расширенной матрицы r(`A) = 3. Поскольку r(A) ¹ r(`A), то система несовместна.
5.2 Метод Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 2.13. Решить систему уравнений методом Гаусса:
x + y - 3z = 2,
3x - 2y + z = - 1,
2x + y - 2z = 0.
Решение. Выпишем расширенную матрицу данной системы

и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
 ~
~  ;
;
б) третью строку умножим на (-5) и прибавим к ней вторую:
 .
.
В результате всех этих преобразований данная система приводится к треугольному виду:
x + y - 3z = 2,
-5y + 10z = -7,
- 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = - 0,7.
5.3 Формулы Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
D = det (ai j)
и n вспомогательных определителей D i (i=![]() ), которые получаются из
определителя D заменой i-го столбца столбцом свободных членов.
), которые получаются из
определителя D заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
D × x i = D i (i = ![]() ). (5.4)
). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i = D i / D.
Если главный определитель системы D и все
вспомогательные определители D i = 0 (i= ![]() ), то система имеет
бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то
система несовместна.
), то система имеет
бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то
система несовместна.
Пример 2.14. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5,
x1 + 2x2 - x3 + 4x4 = -2,
2x1 - 3x2 - x3 - 5x4 = -2,
3x1 + x2 +2x3 + 11 x4 = 0.
Решение. Главный определитель этой системы
D =  = -142 ¹ 0,
= -142 ¹ 0,
значит, система имеет единственное решение. Вычислим вспомогательные
определители D i (i=![]() ),
получающиеся из определителя D путем замены в нем столбца,
состоящего из коэффициентов при xi, столбцом из свободных членов:
),
получающиеся из определителя D путем замены в нем столбца,
состоящего из коэффициентов при xi, столбцом из свободных членов:
D 1 =
 = - 142, D 2 =
= - 142, D 2 =  = -
284,
= -
284,
D 3 =
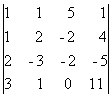 = - 426, D 4 =
= - 426, D 4 =  = 142.
= 142.
Отсюда x1 = D 1/D = 1, x2 = D 2/D = 2, x3 = D 3/D = 3, x4 = D 4/D = -1, решение системы - вектор С=(1, 2, 3, -1)T.
5.4 Матричный метод
Если матрица А системы линейных уравнений невырожденная, т.е. det A ¹ 0, то матрица А имеет обратную, и решение системы (5.3) совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A-1B называют матричным способом решения системы, или решением по методу обратной матрицы.
Пример 2.15. Решить матричным способом систему уравнений
x1 - x2 + x3 = 6,
2x1 + x2 + x3 = 3,
x1 + x2 +2x3 = 5.
Решение. Обозначим
A = 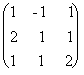 , X = (x1, x2,
x3)T, B = (6, 3, 5) T.
, X = (x1, x2,
x3)T, B = (6, 3, 5) T.
Тогда данная система уравнений запишется матричным уравнением AX=B.
Поскольку D = det 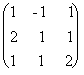 =5 ¹ 0, то матрица A невырождена и поэтому имеет обратную:
=5 ¹ 0, то матрица A невырождена и поэтому имеет обратную:
А-1 = 1/D 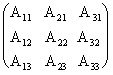 .
.
Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A-1B. В данном случае
A-1 = 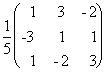
и, следовательно,
![]() =
= 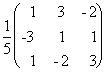
![]() .
.
Выполняя действия над матрицами, получим:
x1 = 1/5(1×6+3×3-2×5) = 1/5 (6+9-10) = 1,
x2 = 1/5 (-3×6 +1×3 - 1×5) = 1/5 (- 18 + 3 + 5) = -2,
x3 = 1/5 (1×6 - 2×3 + 3×5) = 1/5 (6 -6 + 15) = 3.
Итак, С = (1, -2, 3)T.
5.5 Системы линейных уравнений общего вида
Если система (5.1) оказалась совместной, т. е. матрицы A и `A имеют один и тот же ранг, то могут представиться две возможности - a) r = n; б) r < n:
а) если r = n, то имеем n независимых уравнений с n неизвестными, причем определитель D этой системы отличен от нуля. Такая система имеет единственное решение, получаемое по формулам Крамера;
б) если r < n, то число независимых уравнений меньше числа неизвестных.
Перенесем лишние неизвестные x r+1, x r+2,..., xn, которые принято называть свободными, в правые части; наша система линейных уравнений примет вид:
a11 x1 + a12 x2 +... + a1r xr = b1 - a1,r+1 xr+1 -... - a1nxn,
a21 x1 + a22 x2 +... + a2r xr = b2 - a2,r+1 xr+1 -... - a2nxn,
... ... ... ... ... ... ... ... ... ...
ar1 x1 + ar2 x2 +... + arr xr = br - ar,r+1 xr+1 -... - arnxn.
Ее можно решить относительно x1, x2,..., xr, так как определитель этой системы (r-го порядка) отличен от нуля. Придавая свободным неизвестным произвольные числовые значения, получим по формулам Крамера соответствующие числовые значения для x1, x2,..., xr. Таким образом, при r < n имеем бесчисленное множество решений.
Система (5.1) называется однородной, если все bi = 0, т. е. она имеет вид:
a 11 x1 + a12 x2 +... + a1n xn = 0,
a21 x1 + a22 x2 +... + a2n xn = 0, (5.5)
... ... ... ... ... ...
am1 x1 + am1 x2 +... + amn xn = 0.
Из теоремы Кронекера-Капелли следует, что она всегда совместна, так как добавление столбца из нулей не может повысить ранга матрицы. Это, впрочем, видно и непосредственно - система (5.5) заведомо обладает нулевым, или тривиальным, решением x1 = x2 =... = xn = 0. Пусть матрица А системы (5.5) имеет ранг r.
Если r = n, то нулевое решение будет единственным решением системы (5.5); при r < n система обладает решениями, отличными от нулевого, и для их разыскания применяют тот же прием, как и в случае произвольной системы уравнений.
Всякий ненулевой вектор - столбец X = (x1, x2,..., xn)T называется собственным вектором линейного преобразования (квадратной матрицы A), если найдется такое число l, что будет выполняться равенство
AX = lX.
Число l называется собственным значением линейного преобразования (матрицы A), соответствующим вектору X. Матрица A имеет порядок n.
В математической экономике большую роль играют так называемые продуктивные матрицы. Доказано, что матрица A является продуктивной тогда и только тогда, когда все собственные значения матрицы A по модулю меньше единицы.
Для нахождения собственных значений матрицы A перепишем равенство AX = lX в виде (A - lE)X = 0, где E- единичная матрица n-го порядка или в координатной форме:
(a11 -l)x1 + a12x2 +... + a1nxn =0,
a21x1 + (a22 -l)x2 +... + a2nxn = 0,
... ... ... ... ... ... ... ... (5.6)
an1x1 + an2x2 +... + (ann-l)xn = 0.
Получили систему линейных однородных уравнений, которая имеет ненулевые решения тогда и только тогда, когда определитель этой системы равен нулю, т.е.
![]() =
=  .
.
Получили уравнение n-ой степени относительно неизвестной l, которое называется характеристическим уравнением матрицы A,
многочлен ![]() называется характеристическим
многочленом матрицы A, а его корни - характеристическими числами, или
собственными значениями, матрицы A.
называется характеристическим
многочленом матрицы A, а его корни - характеристическими числами, или
собственными значениями, матрицы A.
Для нахождения собственных векторов матрицы A в векторное уравнение (A - lE)X = 0 или в соответствующую систему однородных уравнений (5.6) нужно подставить найденные значения l и решать обычным образом.
Пример 2.16. Исследовать систему уравнений и решить ее, если она совместна.
x1 + x2 - 2x3 - x4 + x5 =1,
3x1 - x2 + x3 + 4x4 + 3x5 =4,
x1 + 5x2 - 9x3 - 8x4 + x5 =0.
Решение. Будем находить ранги матриц A и `A методом элементарных преобразований, приводя одновременно систему к ступенчатому виду:
 ~
~  ~
~  .
.
Очевидно, что r(A) = r(`A) = 2. Исходная система равносильна следующей, приведенной к ступенчатому виду:
x1 + x2 - 2x3 - x4 + x5 = 1,
- 4x2 + 7x3 + 7x4 = 1.
Поскольку определитель при неизвестных x1 и x2 отличен от нуля, то их можно принять в качестве главных и переписать систему в виде:
x1 + x2 = 2x3 + x4 - x5 + 1,
- 4x2 = - 7x3 - 7x4 + 1,
откуда x2 = 7/4 x3 + 7/4 x4 -1/4, x1 = 1/4 x3 -3/4 x4 - x5 + 5/4 - общее решение системы, имеющей бесчисленное множество решений. Придавая свободным неизвестным x3, x4, x5 конкретные числовые значения, будем получать частные решения. Например, при x3 = x4 = x5 = 0 x1= 5/4, x2 = - 1/4. Вектор C(5/4, - 1/4, 0, 0, 0) является частным решением данной системы.
Пример 2.17. Исследовать систему уравнений и найти общее решение в зависимости от значения параметра а.
2x1 - x2 + x3 + x4 = 1,
x1 + 2x2 - x3 + 4x4 = 2,
x1 + 7x2 - 4x3 + 11x4 = a.
Решение.
Данной системе соответствует матрица`А= . Имеем `А ~
. Имеем `А ~  ~
~  , следовательно, исходная
система равносильна такой:
, следовательно, исходная
система равносильна такой:
x1 + 2x2 - x3 + 4x4 = 2,
5x2 - 3x3 + 7x4 = a-2,
0 = a-5.
Отсюда видно, что система совместна только при a=5. Общее решение в этом случае имеет вид:
x2 = 3/5 + 3/5x3 - 7/5x4, x1 = 4/5 - 1/5x3 - 6/5x4.
Пример 2.18. Выяснить, будет ли линейно зависимой система векторов:
a1 = (1, 1, 4, 2),
a2 = (1, -1, -2, 4),
a3 = (0, 2, 6, -2),
a4 = (-3, -1, 3, 4),
a5 = (-1, 0, - 4, -7).
Решение. Система векторов является линейно зависимой, если найдутся такие числа x1, x2, x3, x4, x5, из которых хотя бы одно отлично от нуля (см. п. 1. разд. I), что выполняется векторное равенство:
x1 a1 + x2 a2 + x3 a3 + x4 a4 + x5 a5 = 0.
В координатной записи оно равносильно системе уравнений:
x1 + x2 - 3x4 - x5 = 0,
x1 - x2 + 2x3 - x4 = 0,
4x1 - 2x2 + 6x3 +3x4 - 4x5 = 0,
2x1 + 4x2 - 2x3 + 4x4 - 7x5 = 0.
Итак, получили систему линейных однородных уравнений. Решаем ее методом исключения неизвестных:
 ~
~ ~
~  ~
~
~  ~
~  ~
~  .
.
Система приведена к ступенчатому виду, ранг матрицы равен 3, значит, однородная система уравнений имеет решения, отличные от нулевого (r < n). Определитель при неизвестных x1, x2, x4 отличен от нуля, поэтому их можно выбрать в качестве главных и переписать систему в виде:
x1 + x2 - 3x4 = x5,
-2x2 + 2x4 = -2x3 - x5,
- 3x4 = - x5.
Имеем: x4 = 1/3 x5, x2 = 5/6x5+x3, x1 = 7/6 x5 -x3.
Система имеет бесчисленное множество решений; если свободные неизвестные x3 и x5 не равны нулю одновременно, то и главные неизвестные отличны от нуля. Следовательно, векторное уравнение
x1 a1 + x2 a2 + x3 a3 + x4 a4 + x5 a5 = 0
имеет коэффициенты, не равные нулю одновременно; пусть например, x5 = 6, x3 = 1. Тогда x4=2, x2 = 6, x1=6 и мы получим соотношение
6a1 + 6a2 + a3 + 2a4 + 6a5 = 0,
т.е. данная система векторов линейно независима.
Пример 2.19. Найти собственные значения и собственные векторы матрицы
A =  .
.
Решение. Вычислим определитель матрицы A - lE:
![]() = det
= det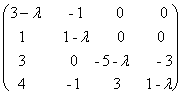 = det
= det 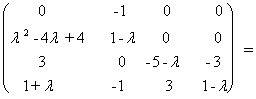
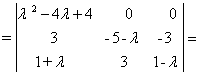
![]() .
.
Итак, ![]() = (l - 2)2 × (l+2)2. Корни
характеристического уравнения
= (l - 2)2 × (l+2)2. Корни
характеристического уравнения ![]() =0 - это
числа l1 = 2 и l2 = -2.
Другими словами, мы нашли собственные значения матрицы A. Для нахождения
собственных векторов матрицы A подставим найденные значения l в систему (5.6): при l = 2 имеем систему линейных
однородных уравнений
=0 - это
числа l1 = 2 и l2 = -2.
Другими словами, мы нашли собственные значения матрицы A. Для нахождения
собственных векторов матрицы A подставим найденные значения l в систему (5.6): при l = 2 имеем систему линейных
однородных уравнений
x1 - x2 = 0, x1 - x2 = 0,
x1 - x2 = 0, Þ 3x2 -7x3 - 3x4 = 0,
3x1 - 7x3 - 3x4 = 0, 5x3 + x4 = 0.
4x1 - x2 + 3x3 - x4 = 0,
Следовательно, собственному значению l = 2 отвечают собственные векторы вида a (8, 8, -3, 15), где a - любое отличное от нуля действительное число. При l = -2 имеем:
A - lE = A +2E =  ~
~  ,
,
и поэтому координаты собственных векторов должны удовлетворять системе уравнений
x1+3x2 = 0,
x2 = 0,
x3+x4= 0.
Поэтому собственному значению l = -2 отвечают собственные векторы вида b (0, 0,-1, 1), где b - любое отличное от нуля действительное число.
5.6 Использование систем линейных уравнений при решении экономических задач
Пример 2.20. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:
| Тип | Способ раскроя | ||
| заготовки | 1 | 2 | 3 |
| А | 3 | 2 | 1 |
| Б | 1 | 6 | 2 |
| В | 4 | 1 | 5 |
Записать в математической форме условия выполнения задания.
Решение. Обозначим через x, y, z количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя x листов будет получено 3x заготовок типа А, при втором - 2y, при третьем - z.
Для полного выполнения задания по заготовкам типа А сумма 3x +2y +z должна равняться 360, т.е.
3x +2y + z =360.
Аналогично получаем уравнения
x + 6y +2z = 300
4x + y + 5z = 675,
которым должны удовлетворять неизвестные x, y, z для того, чтобы выполнить задание по заготовкам Б и В. Полученная система линейных уравнений и выражает в математической форме условия выполнения всего задания по заготовкам А, Б и В. Решим систему методом исключения неизвестных. Запишем расширенную матрицу системы и приведем ее с помощью элементарных преобразований к треугольному виду.
 ~
~ 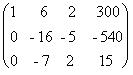 ~
~  ~ ~
~ ~ ~
~  ~
~  .
.
Следовательно, исходная система равносильна следующей:
x + 6y +2z = 300,
2y +9z = 570,
-67z = - 4020.
Из последнего уравнения находим z = 60; подставляя найденное значение z во второе уравнение, получим y = 15 и, наконец, из первого имеем x = 90. Итак, вектор C (90, 15, 60) есть решение системы.
Пример 2.21. Три судна доставили в порт 6000 т чугуна, 4000 т железной руды и 3000 т апатитов. Разгрузку можно производить как непосредственно в железнодорожные вагоны для последующей доставки потребителям, так и на портовые склады. В вагоны можно разгрузить 8000 т, а остаток груза придется направить на склады. Необходимо учесть, что поданные в порт вагоны не приспособлены для перевозки апатитов. Стоимость выгрузки 1 т в вагоны составляет соответственно 4,30, 5,25 и 2,20 ден. ед.
Записать в математической форме условия полной разгрузки судов, если затраты на нее должны составить 58850 ден. ед.
Решение. По условию задачи, доставленные в порт чугун, железную руду и апатиты можно разгрузить двумя способами: либо в железнодорожные вагоны, либо в портовые склады. Обозначим через x i j количество груза (в тоннах) i-го вида (i= 1,2,3), которое предполагается разгрузить j-м способом (j = 1, 2). Таким образом, задача содержит шесть неизвестных. Условие полной разгрузки чугуна можно записать в виде
x 11 + x 12 = 6000, (5.7)
где x 11, x 12 - части чугуна, разгружаемого соответственно в вагоны и на склады. Аналогичное условие должно выполняться и для железной руды:
x2 1 + x22 = 4000. (5.8)
Что же касается апатитов, то их можно разгружать только на склады, а поэтому неизвестное x 31 = 0, и условие полной разгрузки апатитов принимает вид
x 32 =3000. (5.9)
Условие полной загрузки всех поданных в порт вагонов запишется так:
x 11 + x 21 = 8000. (5.10)
Затраты на разгрузку, по условию, определены в 58850 ден. ед., что можно выразить записью:
4,3x 11 + 7,8 x 12 + 5,25 x 21 + 6,4x 22 + 3,25x 32 = 58850. (5.11)
Итак, с учетом сложившейся в порту ситуации условия полной разгрузки судов выражаются в математической форме системой линейных уравнений (5.7) - (5.11). С учетом (5.9) уравнение (5.11) перепишется в виде:
4,3x 11 + 7,8x 12 +5,25x 21 +6,4x 22 = 49100,
и теперь мы имеем систему из четырех уравнений с четырьмя неизвестными x 11, x 12, x 21, x 22, расширенная матрица которой имеет вид:
`A =  .
.
Преобразуем ее к треугольному виду:
`A ~  ~
~  ~ ~
~ ~  ~
~  .
.
Наша система равносильна следующей:
x 11 + x 12 = 6000,
- x 12 + x 21 = 2000,
x 21 + x 22 = 4000,
-2,35 x 22 = - 4700,
откуда x 22 = 2000, x 21 = 2000, x 12 = 0, x 11 = 6000.
Пример 2.22.На предприятии имеется четыре технологических способа изготовления изделий А и Б из некоторого сырья. В таблице указано количество изделий, которое может быть произведено из единицы сырья каждым из технологических способов.
Записать в математической форме условия выбора технологий при производстве из 94 ед. сырья 574 изделий А и 328 изделий Б.
| Изделие | Выход из единицы сырья | |||
| I | II | III | IV | |
| А | 2 | 1 | 7 | 4 |
| Б | 6 | 12 | 2 | 3 |
Решение. Обозначим через x1, x2, x3, x4 количество сырья, которое следует переработать по каждой технологии, чтобы выполнить плановое задание. Получим систему трех линейных уравнений с четырьмя неизвестными:
x1 + x2 + x3 + x4 = 94,
2x1 + x2 + 7x3 + 4x4 = 574,
6x1 +12x2 +2x3 + 3x4 = 328.
Решаем ее методом Гаусса:
 ~
~ ~
~  .
.
Имеем: r (А) = r (А) = 3, следовательно, число главных неизвестных равно трем, одно неизвестное x4 - свободное. Исходная система равносильна следующей:
x1 + x2 + x3 = 94 - x4,
- x2 + 5x3 = 386 - 2x4,
26x3 = 2080- 9x4.
Из последнего уравнения находим x3 = 80 - 9/26 x4, подставляя x3 во второе уравнение, будем иметь: x2 = 14 + 7/26x4 и, наконец, из первого уравнения получим: x1 = - 12/13 x4. С математической точки зрения система имеет бесчисленное множество решений, т. е. неопределенна. С учетом реального экономического содержания величины x1 и x4 не могут быть отрицательными, тогда из соотношения x1 = - 12/13 x4 получим: x1 = x4 = 0. Тогда вектор (0, 14, 80, 0) является решением данной системы.
Пример 2.23. Математическая модель межотраслевого баланса.
Модель межотраслевого баланса, разработанная профессором В. Леонтьевым (Гарвардский университет, США), имеет вид:
![]() , (5.12)
, (5.12)
или, в матричной форме,
AX + Y = X, (5.13)
где А = (a i j) - матрица коэффициентов прямых затрат, Х - вектор валовых выпусков, Y - вектор конечного продукта.
Перепишем систему (5.13) в виде
(E - A) X = Y, (5.14)
где E - единичная матрица n-го порядка, тогда решение системы (5.14) относительно неизвестных значений объемов производства продукции при заданном векторе конечного продукта находится по формуле
X = (E - A) -1 Y. (5.15)
Здесь (E - A) -1 - матрица коэффициентов полных затрат. Элемент b i j матрицы (E - A) -1 характеризует потребность в валовом выпуске отрасли i, который необходим для получения в процессе материального производства единицы конечного продукта отрасли j. Благодаря этому имеется возможность рассматривать валовые выпуски x i в виде функций планируемых значений y j конечных продуктов отраслей:
![]() .
.
Пример 2.24. Пусть дана леонтьевская балансовая модель “затраты - выпуск” X = AX +Y. Найти вектор конечной продукции Y при заданном X, где
A = 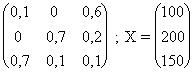 ;
;
Решение. Имеем: Y = (E - A) X, где E - единичная матрица третьего порядка.
E - A = 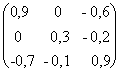 ,
,
значит,
Y= 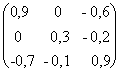
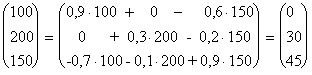 .
.
Пример 2.25. Пусть дана леонтьевская балансовая модель “затраты-выпуск”. Определить, будет ли продуктивной матрица технологических коэффициентов A. Найти вектор валовой продукции X при заданном Y, где
A=![]() .
.
Решение. Для решения вопроса о продуктивности матрицы A следует найти собственные значения этой матрицы. Составим характеристическое уравнение:
![]() ,
,
или
(0,125 -l)2 - 0,140625 = 0 Þ 0,125 - l = ± 0,375.
Следовательно, l1 = 0,5; l2 = - 0,25. Оба корня по модулю меньше единицы, значит, матрица технологических коэффициентов A продуктивная. Для определения вектора валовой продукции X имеем формулу X = (E - A) -1 Y. Найдем обратную матрицу для матрицы
E - A=![]() .
.
Обозначим B = E-A, тогда 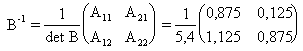 .
.
Следовательно,
X = ![]()
![]() .
.
III. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
6. Предел функции
6.1 Предел последовательности и функции. Теоремы о пределах
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
êxn - a ê < e. (6.1)
Записывают это следующим образом: ![]() или
xn ® a.
или
xn ® a.
Неравенство (6.1) равносильно двойному неравенству
a- e < xn < a + e, (6.2)
которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-e, a+e), т.е. попадают в какую угодно малую e-окрестность точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n.
Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется пределом функции f(x) при x®a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А.
Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.
Определение 2. Постоянное число А называется пределом функции f(x) при x®a, если, задав произвольное как угодно малое положительное число e, можно найти такое d >0 (зависящее от e), что для всех x, лежащих в d-окрестности числа а, т.е. для x, удовлетворяющих неравенству 0 < ½x-a½ < d, значения функции f(x) будут лежать в e-окрестности числа А, т.е. êf(x)-A ê < e.
Это определение называют определением предела функции по Коши, или “на языке e - d“.
Определения 1 и 2 равносильны. Если функция f(x) при x ® a имеет предел, равный А, это записывается в виде
![]() f(x) = A. (6.3)
f(x) = A. (6.3)
В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
![]() f(x) = ¥ (
f(x) = ¥ (![]() f(x)
= - ¥).
f(x)
= - ¥).
Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной.
Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
Для нахождения пределов на практике пользуются следующими теоремами.
Теорема 1.
Если существуют пределы ![]() f(x)=A,
f(x)=A,
![]() g(x)=B, то
g(x)=B, то
![]() (f(x)+(g(x)) = A + B, (6.4)
(f(x)+(g(x)) = A + B, (6.4)
![]() f(x) g(x) = AB, (6.5)
f(x) g(x) = AB, (6.5)
![]() f(x)/g(x) = A/B (B ¹ 0). (6.6)
f(x)/g(x) = A/B (B ¹ 0). (6.6)
Замечание. Выражения вида 0/0, ¥ /¥, 0 × ¥, ¥ - ¥ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и нахождение пределов такого вида носит название “раскрытие неопределенностей”.
Теорема 2.
![]() (f(x))a = (
(f(x))a = (![]() f(x))
a, где a = const, (6.7)
f(x))
a, где a = const, (6.7)
т.е. можно переходить к пределу в основании степени при постоянном
показателе, в частности, ![]() ;
;
![]() bf(x) =bA, где b
= const,
bf(x) =bA, где b
= const, ![]() f(x)=A; (6.8)
f(x)=A; (6.8)
![]() logc f(x) = logc
logc f(x) = logc![]() f(x), где c
= const. (6.9)
f(x), где c
= const. (6.9)
Теорема 3. ![]()
![]() = 1,
= 1, ![]()
![]() =
1, a = const, a >0,
=
1, a = const, a >0,
![]()
![]() = 1, (6.10)
= 1, (6.10)
![]() (1 + a)1/ a = e,
(6.11)
(1 + a)1/ a = e,
(6.11)
где e » 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первого и второго замечательного пределов.
Используются на практике и следствия формулы (6.11):
![]()
![]() = logc e, (6.12)
= logc e, (6.12)
![]() (aa - 1)/a = ln a, (6.13)
(aa - 1)/a = ln a, (6.13)
![]() ((1 + a) m - 1)/a = m, (6.14)
((1 + a) m - 1)/a = m, (6.14)
в частности,
![]()
![]() = 1.
= 1.
Eсли x® a и при этом x > a, то пишут x® a+0. Если, в частности, a=0, то вместо символа 0+0 пишут +0. Аналогично
если x®a и при этом x<a, то пишут x®a-0. Числа ![]() и
и ![]() называются соответственно пределом
справа и пределом слева функции f(x) в точке а.
Для существования предела функции f(x) при x®a необходимо и
достаточно, чтобы
называются соответственно пределом
справа и пределом слева функции f(x) в точке а.
Для существования предела функции f(x) при x®a необходимо и
достаточно, чтобы ![]() =
=![]() .
.
Функция f(x) называется непрерывной в точке x0, если
![]() . (6.15)
. (6.15)
Условие (6.15) можно переписать в виде:
![]() ,
,
то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.
Если равенство (6.15) нарушено, то говорят, что при x = xo функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(xo)= f(0) не определено, поэтому в точке xo = 0 функция имеет разрыв.
Функция f(x) называется непрерывной справа в точке xo, если
![]() ,
,
и непрерывной слева в точке xo, если
![]() .
.
Непрерывность функции в точке xo равносильна ее непрерывности в этой точке одновременно и справа и слева.
Для того, чтобы функция была непрерывна в точке xo,
например, справа, необходимо, во-первых, чтобы существовал конечный предел ![]() , а во-вторых, чтобы этот
предел был равен f(xo). Следовательно, если хотя бы одно из этих
двух условий не выполняется, то функция будет иметь разрыв.
, а во-вторых, чтобы этот
предел был равен f(xo). Следовательно, если хотя бы одно из этих
двух условий не выполняется, то функция будет иметь разрыв.
1. Если ![]() существует и не
равен f(xo), то говорят, что функция f(x) в точке xo
имеет разрыв первого рода, или скачок.
существует и не
равен f(xo), то говорят, что функция f(x) в точке xo
имеет разрыв первого рода, или скачок.
2. Если ![]() равен ¥ или не существует, то говорят, что в точке xo
функция имеет разрыв второго рода.
равен ¥ или не существует, то говорят, что в точке xo
функция имеет разрыв второго рода.
Например, функция y = ctg x при x® +0 имеет предел, равный +¥, значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.
Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой.
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.
Рассмотрим пример Я.И. Перельмана, дающий интерпретацию числа e
в задаче о сложных процентах. Число e есть предел e = ![]() . В сбербанках процентные
деньги присоединяются к основному капиталу ежегодно. Если присоединение
совершается чаще, то капитал растет быстрее, так как в образовании процентов
участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример.
Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные
деньги будут присоединены к основному капиталу лишь по истечении года, то к
этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что
превратятся 100 ден. ед., если процентные деньги присоединять к основному
капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода - в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать
каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3)3 »237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1
года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год
получится:
. В сбербанках процентные
деньги присоединяются к основному капиталу ежегодно. Если присоединение
совершается чаще, то капитал растет быстрее, так как в образовании процентов
участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример.
Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные
деньги будут присоединены к основному капиталу лишь по истечении года, то к
этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что
превратятся 100 ден. ед., если процентные деньги присоединять к основному
капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода - в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать
каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3)3 »237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1
года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год
получится:
100 × (1 +1/10)10 » 259 (ден. ед.),
100 × (1+1/100)100 » 270 (ден. ед.),
100 × (1+1/1000)1000 » 271 (ден. ед.).
При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что
![]() = e.
= e.
Пример 3.1. Пользуясь определением предела числовой последовательности, доказать, что последовательность xn =(n-1)/n имеет предел, равный 1.
Решение. Нам надо доказать, что, какое бы e>0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство ½ xn -1 ½<e.
Возьмем любое e >0. Так как ½ xn
-1 ½=½(n+1)/n - 1½= 1/n, то для отыскания N достаточно решить
неравенство 1/n<e. Отсюда n>1/e и, следовательно,
за N можно принять целую часть от 1/e, N = E(1/e). Мы тем самым доказали, что ![]() xn
= 1.
xn
= 1.
Пример 3.2.
Найти предел последовательности, заданной общим членом xn = ![]() .
.
Решение. Применим теорему о пределе суммы и найдем предел каждого слагаемого. При n ®¥ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему о пределе частного. Поэтому сначала преобразуем xn, разделив числитель и знаменатель первого слагаемого на n2, а второго на n. Затем, применяя теорему о пределе частного и о пределе суммы, найдем:
xn =
![]() .
.
Пример 3.3.
xn = ![]() . Найти
. Найти ![]() xn.
xn.
Решение. ![]() =
=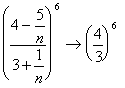 .
.
Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.
Пример 3.4.
Найти ![]() (
(![]() ).
).
Решение. Применять теорему о пределе разности нельзя, поскольку имеем неопределенность вида ¥ - ¥. Преобразуем формулу общего члена:
![]() =
= 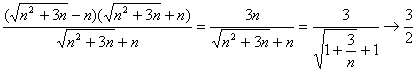 .
.
Пример 3.5.
Дана функция f(x)=21/x. Доказать, что ![]() не
существует.
не
существует.
Решение. Воспользуемся
определением 1 предела функции через последовательность. Возьмем
последовательность { xn }, сходящуюся к 0, т.е. ![]() xn =0. Покажем,
что величина f(xn)=
xn =0. Покажем,
что величина f(xn)= ![]() для
разных последовательностей ведет себя по-разному. Пусть xn = 1/n.
Очевидно, что
для
разных последовательностей ведет себя по-разному. Пусть xn = 1/n.
Очевидно, что ![]() 1/n =0, тогда
1/n =0, тогда ![]()
![]() =
= ![]() 2n = +¥. Выберем теперь в качестве xn последовательность с
общим членом xn = -1/n, также стремящуюся к нулю.
2n = +¥. Выберем теперь в качестве xn последовательность с
общим членом xn = -1/n, также стремящуюся к нулю. ![]()
![]() =
= ![]() 2- n=
2- n= ![]() 1/2n = 0.
Поэтому
1/2n = 0.
Поэтому ![]() 2 1/x не
существует.
2 1/x не
существует.
Пример 3.6.
Доказать, что ![]() sin x не
существует.
sin x не
существует.
Решение. Пусть
x1, x2,..., xn,... - последовательность, для
которой ![]() xn = ¥. Как ведет себя последовательность {f(xn)} = {sin xn
} при различных xn ®¥ ?
xn = ¥. Как ведет себя последовательность {f(xn)} = {sin xn
} при различных xn ®¥ ?
Если xn= pn, то sin xn= sin pn = 0 при всех n и ![]() sin xn
=0. Если же xn=2pn+p/2, то sin xn=
sin(2pn+p/2) = sin p/2 = 1 для всех n и следовательно
sin xn
=0. Если же xn=2pn+p/2, то sin xn=
sin(2pn+p/2) = sin p/2 = 1 для всех n и следовательно ![]() sin
xn =1. Таким образом,
sin
xn =1. Таким образом, ![]() sin x
не существует.
sin x
не существует.
Пример 3.7.
Найти ![]()
![]() .
.
Решение. Имеем:
![]() = 5
= 5![]() . Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу (3.10), получим 5
. Обозначим t = 5x. При x®0 имеем: t®0. Применяя формулу (3.10), получим 5![]() .
.
Пример 3.8.
Вычислить ![]()
![]() .
.
Решение. Обозначим y=p-x. Тогда при x®p, y®0.Имеем:
sin 3x = sin 3(p-y) = sin (3p-3y) = sin 3y.
sin 4x = sin 4(p-y) = sin (4p-4y)= - sin 4y.
![]()
![]() =-
=- ![]() .
.
Пример 3.9.
Найти ![]()
![]() .
.
Решение. Обозначим
arcsin x=t. Тогда x=sin t и при x®0 t®0. ![]() =
=![]() .
.
Пример 3.10.
Найти 1) ![]()
![]() ; 2)
; 2) ![]()
![]() ; 3)
; 3) ![]()
![]() .
.
Решение.
1. Применяя теорему 1 о пределе разности и произведения, находим предел
знаменателя: ![]()
![]() .
.
Предел знаменателя не равен нулю, поэтому, по теореме 1 о пределе
частного, получаем: ![]()
![]() =
=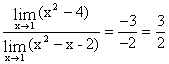 .
.
2. Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ¹ 2 равенство:
![]() =
=![]() .
.
Так как ![]() (x+1) ¹ 0, то, по теореме о пределе частного, найдем
(x+1) ¹ 0, то, по теореме о пределе частного, найдем
![]()
![]() =
= ![]()
![]() =
= 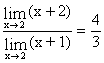 .
.
3. Числитель и знаменатель при x®¥ являются бесконечно большими функциями. Поэтому теорема о пределе частного непосредственно не применима. Разделим числитель и знаменатель на x2 и к полученной функции применим теорему о пределе частного:
![]() =
=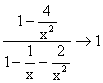 .
.
Пример 3.11.
Найти ![]()
![]() .
.
Решение. Здесь
числитель и знаменатель стремятся к нулю:![]() ,
x-9®0, т.е. имеем неопределенность вида
,
x-9®0, т.е. имеем неопределенность вида ![]() .
.
Преобразуем данную функцию, умножив числитель и знаменатель на неполный
квадрат суммы выражения ![]() ,
получим
,
получим
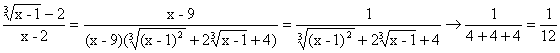 .
.
Пример 3.12.
Найти ![]()
![]() .
.
Решение. ![]() =
=![]() .
.
6.2 Применение пределов в экономических расчетах
Сложные проценты
В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т. д.). Время - дискретная переменная. В некоторых случаях - в доказательствах и расчетах, связанных с непрерывными процессами, возникает необходимость в применении непрерывных процентов. Рассмотрим формулу сложных процентов:
S = P(1 + i)n. (6.16)
Здесь P - первоначальная сумма, i - ставка процентов (в виде десятичной дроби), S - сумма, образовавшаяся к концу срока ссуды в конце n-го года. Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется, а проценты в виде разности S - P называются дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной, величиной S. Имеем:
P = ![]() Þ
Þ ![]() P =
P = ![]()
![]() =
0.
=
0.
Таким образом, при очень больших сроках платежа современная величина последнего будет крайне незначительна.
В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется прежде всего тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году:
S =P (1 + i/m) mn.
Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, i - годовая или номинальная ставка. Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m ®¥ имеем:
`S = ![]() P
(1 + i/m) mn = P
P
(1 + i/m) mn = P![]() ((1 +
i/m) m) n.
((1 +
i/m) m) n.
Поскольку ![]() (1 + i/m)
m = e i, то `S = P e in.
(1 + i/m)
m = e i, то `S = P e in.
При непрерывном наращении процентов применяют особый вид процентной
ставки - силу роста, которая характеризует относительный прирост
наращенной суммы в бесконечно малом промежутке времени. При непрерывной
капитализации процентов наращенная сумма равна конечной величине, зависящей от
первоначальной суммы, срока наращения и номинальной ставки процентов. Для того,
чтобы отличить ставки непрерывных процентов от ставки дискретных процентов,
обозначим первую через d, тогда `S = Pe![]() .
.
Сила роста d представляет собой номинальную ставку процентов при m®¥. Множитель наращения рассчитывается с помощью ЭВМ или по таблицам функции.
Потоки платежей. Финансовая рента
Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей. Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой. Ренты делятся на годовые и р-срочные, где р характеризует число выплат на протяжении года. Это дискретные ренты. В финансово-экономической практике встречаются и с последовательностями платежей, которые производятся так часто, что практически их можно рассматривать как непрерывные. Такие платежи описываются непрерывными рентами.
Пример 3.13. Пусть в конце каждого года в течение четырех лет в банк вносится по 1 млн. рублей, проценты начисляются в конце года, ставка - 5% годовых. В этом случае первый взнос обратится к концу срока ренты в величину 10 6 ´ 1,053 так как соответствующая сумма была на счете в течение 3 лет, второй взнос увеличится до 10 6 ´ 1,052, так как был на счете 2 года. Последний взнос процентов не приносит. Таким образом, в конце срока ренты взносы с начисленными на них процентами представляют ряд чисел: 10 6 ´ 1,053; 10 6 ´ 1,052; 10 6 ´ 1,05; 10 6. Наращенная к концу срока ренты величина будет равна сумме членов этого ряда. Обобщим сказанное, выведем соответствующую формулу для наращенной суммы годовой ренты. Обозначим: S - наращенная сумма ренты, R - размер члена ренты, i - ставка процентов (десятичная дробь), n - срок ренты (число лет). Члены ренты будут приносить проценты в течение n - 1, n - 2,..., 2, 1 и 0 лет, а наращенная величина членов ренты составит
R (1 + i)n - 1, R (1 + i)n - 2,..., R (1 + i), R.
Перепишем этот ряд в обратном порядке. Он представляет собой геометрическую прогрессию со знаменателем (1+i) и первым членом R. Найдем сумму членов прогрессии. Получим: S = R´((1 + i)n - 1)/((1 + i) - 1) = = R´((1 + i)n - 1)/ i. Обозначим S n; i = ((1 + i)n - 1)/ i и будем называть его коэффициентом наращения ренты. Если же проценты начисляются m раз в году, то S = R´((1 + i/m)mn - 1)/((1 + i/m) m - 1), где i - номинальная ставка процентов.
Величина a n; i = (1 - (1 + i) - n)/ i называется коэффициентом приведения ренты. Коэффициент приведения ренты при n ®¥ показывает, во сколько раз современная величина ренты больше ее члена:
![]() a n; i =
a n; i = ![]() (1
- (1 + i) - n)/ i =1/i.
(1
- (1 + i) - n)/ i =1/i.
Пример 3.14. Под вечной рентой понимается последовательность платежей, число членов которой не ограничено - она выплачивается в течение бесконечного числа лет. Вечная рента не является чистой абстракцией - на практике это некоторые виды облигационных займов, оценка способности пенсионных фондов отвечать по своим обязательствам. Исходя из сущности вечной ренты можно полагать, что ее наращенная сумма равна бесконечно большой величине, что легко доказать по формуле: R´((1 + i)n - 1)/ i ® ¥ при n ® ¥.
Коэффициент приведения для вечной ренты a n; i ® 1/i, откуда A = R/i, т. е. современная величина зависит только от величины члена ренты и принятой ставки процентов.
7. Производная
7.1 Производная, правила и формулы дифференцирования
Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке хo называется предел
![]() =
= ![]() .
.
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке xo; при этом она оказывается обязательно и непрерывной в этой точке.
Если же рассматриваемый предел равен ¥ (или - ¥), то при условии, что функция в точке хo непрерывна, будем говорить, что функция f(x) имеет в точке хo бесконечную производную.
Производная обозначается символами
y ¢, f ¢(xo), ![]() ,
, ![]() .
.
Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том,что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке хo; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент to.
Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) ' = 0, (cu) ' = cu';
2) (u+v)' = u'+v';
3) (uv)' = u'v+v'u;
4) (u/v)' = (u'v-v'u)/v2;
5) если y = f(u), u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из
дифференцируемых функций j и f, то ![]() , или
, или
![]() ;
;
6) если для функции y = f(x) существует обратная дифференцируемая функция
x = g(y), причем ![]() ¹ 0, то
¹ 0, то ![]() .
.
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (um)' = m um-1 u' (m Î R).
2. (au)' = au lna× u'.
3. (eu)' = eu u'.
4. (loga u)' = u'/(u ln a).
5. (ln u)' = u'/u.
6. (sin u)' = cos u× u'.
7. (cos u)' = - sin u× u'.
8. (tg u)' = 1/ cos2u× u'.
9. (ctg u)' = - u' / sin2u.
10. (arcsin u)' = u' /![]() .
.
11. (arccos u)' = - u' /![]() .
.
12. (arctg u)' = u'/(1 + u2).
13. (arcctg u)' = - u'/(1 + u2).
Вычислим производную степенно-показательного выражения y=uv, (u>0), где u и v суть функции от х, имеющие в данной точке производные u', v'.
Прологарифмировав равенство y=u v, получим ln y = v ln u.
Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:
y'/y = vu'/u +v' ln u, откуда y' = y (vu'/u +v' ln u).
Итак,
(u v)'=u v (vu'/u+v' ln u), u > 0.
Например, если y = x sin x, то y' = x sin x (sin x/x + cos x× ln x).
Если функция y = f(x) дифференцируема в точке x, т.е. имеет в этой
точке конечную производную y', то ![]() =
y'+a, где a®0 при Dх® 0; отсюда D y = y' Dх + a x.
=
y'+a, где a®0 при Dх® 0; отсюда D y = y' Dх + a x.
Главная часть приращения функции, линейная относительно Dх, называется дифференциалом функции и обозначается dy: dy
= y' Dх. Если положить в этой формуле y=x, то получим dx =
x'Dх = 1×Dх =Dх, поэтому dy=y'dx, т. е. символ
для обозначения производной ![]() можно
рассматривать как дробь.
можно
рассматривать как дробь.
Приращение функции D y есть приращение ординаты кривой, а дифференциал dy есть приращение ординаты касательной.
Пусть мы нашли для функции y=f(x) ее производную y ¢= f ¢(x). Производная от этой
производной называется производной второго порядка функции f(x), или второй
производной, и обозначается ![]() .
.
Аналогично определяются и обозначаются:
производная третьего порядка - ![]() ,
,
производная четвертого порядка - ![]()
и вообще производная n-го порядка - ![]() .
.
Пример 3.15. Вычислить производную функции y=(3x3-2x+1)×sin x.
Решение. По правилу 3, y'=(3x3-2x+1)'×sin x + (3x3-2x+1)×(sin x)' = = (9x2-2)sin x + (3x3-2x+1)cos x.
Пример 3.16.
Найти y', y = tg x +![]() .
.
Решение. Используя
правила дифференцирования суммы и частного, получим: y'=(tgx + ![]() )' = (tgx)' + (
)' = (tgx)' + (![]() )' =
)' = ![]() +
+ ![]() =
= ![]()
![]() .
.
Пример 3.17.
Найти производную сложной функции y=![]() , u=x4
+1.
, u=x4
+1.
Решение. По
правилу дифференцирования сложной функции, получим: y'x =y 'u
u'x =(![]() )'u(x4
+1)'x =(2u +
)'u(x4
+1)'x =(2u +![]() . Так
как u=x4 +1,то (2 x4 +2+
. Так
как u=x4 +1,то (2 x4 +2+![]() .
.
Пример 3.18.
Найти производную функции y=![]() .
.
Решение. Представим
функцию y= ![]() в виде суперпозиции двух
функций: y = eu и u = x2. Имеем: y'x =y 'u
u'x = (eu)'u(x2)'x = eu
×2x. Подставляя x2 вместо u,
получим y=2x
в виде суперпозиции двух
функций: y = eu и u = x2. Имеем: y'x =y 'u
u'x = (eu)'u(x2)'x = eu
×2x. Подставляя x2 вместо u,
получим y=2x![]() .
.
Пример 3.19. Найти производную функции y=ln sin x.
Решение. Обозначим
u=sin x, тогда производная сложной функции y=ln u вычисляется по формуле y' =
(ln u)'u(sin x)'x= ![]() .
.
Пример 3.20.
Найти производную функции y=![]() .
.
Решение. Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила 5:
![]()
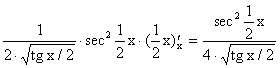 .
.
Пример 3.21.
Вычислить производную y=ln 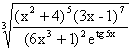 .
.
Решение. Логарифмируя и используя свойства логарифмов, получим:
y=5/3ln(x2+4) +7/3ln(3x-1)-2/3ln(6x3+1)-1/3tg 5x.
Дифференцируя обе части последнего равенства, получим:
![]() .
.
7.2 Предельный анализ в экономике. Эластичность функции
В экономических исследованиях для обозначения производных часто пользуются специфической терминологией. Например, если f(x) есть производственная функция, выражающая зависимость выпуска какой-либо продукции от затрат фактора x, то f '(x) называют предельным продуктом; если g(x) есть функция издержек, т. е. функция g(x) выражает зависимость общих затрат от объема продукции x, то g'(x) называют предельными издержками.
Предельный анализ в экономике - совокупность приемов исследования изменяющихся величин затрат или результатов при изменении объемов производства, потребления и т.п. на основе анализа их предельных значений. Большей частью плановые расчеты, основывающиеся на обычных статистических данных, ведутся в форме суммарных показателей. При этом анализ заключается главным образом в вычислении средних величин. Однако в некоторых случаях оказывается необходимым более детальное исследование с учетом предельных значений. Например, при выяснении издержек производства зерна в районе на перспективу принимают во внимание, что издержки могут быть различными в зависимости, при прочих равных условиях, от предполагаемых объемов сбора зерна, так как на вновь вовлекаемых в обработку худших землях издержки производства будут выше, чем по району в среднем.
Если зависимость между двумя показателями v и x задана
аналитически: v = f(x) - то средняя величина представляет собой
отношение v/x, а предельная - производную ![]() .
.
Нахождение производительности труда. Пусть известна функция u = u(t), выражающая количество произведенной продукции u за время работы t. Вычислим количество произведенной продукции за время Dt = t1 - t0: Du = u(t1) - u(t0) = u(t0+Dt) - u(t0). Средней производительностью труда называется отношение количества произведенной продукции к затраченному времени, т.е. z ср.= Du/Dt.
Производительностью труда рабочего z(t0) в момент t0 называется
предел, к которому стремится z ср. при Dt®0: ![]() .
Вычисление производительности труда, таким образом, сводится к вычислению производной:
z(t0) = u'(t0).
.
Вычисление производительности труда, таким образом, сводится к вычислению производной:
z(t0) = u'(t0).
Издержки производства K однородной продукции есть функция количества продукции x. Поэтому можно записать K = K(x). Предположим, что количество продукции увеличивается на Dх. Количеству продукции x+ Dх соответствуют издержки производства K(x + Dх). Следовательно, приращению количества продукции Dх соответствует приращение издержек производства продукции DK = K(x + Dх) - K(x).
Среднее приращение издержек производства есть DK/Dх. Это приращение издержек производства на единицу приращения количества продукции.
Предел ![]() называется
предельными издержками производства.
называется
предельными издержками производства.
Если обозначить через u(x) выручку от продажи x единиц
товара, то ![]() и называется предельной
выручкой.
и называется предельной
выручкой.
С помощью производной можно вычислить приращение функции, соответствующее приращению аргумента. Во многих задачах удобнее вычислять процент прироста (относительное приращение) зависимой переменной, соответствующий проценту прироста независимой переменной. Это приводит нас к понятию эластичности функции (иногда ее называют относительной производной). Итак, пусть дана функция y = f(x), для которой существует производная y ¢ = f ¢(x). Эластичностью функции y = f(x) относительно переменной x называют предел
![]() .
.
Его обозначают Ex (y) = x/y f ¢ (x) = ![]() .
.
Эластичность относительно x есть приближенный процентный прирост функции (повышение или понижение), соответствующий приращению независимой переменной на 1%. Экономисты измеряют степень чуткости, или чувствительности, потребителей к изменению цены продукции, используя концепцию ценовой эластичности. Для спроса на некоторые продукты характерна относительная чуткость потребителей к изменениям цен, небольшие изменения в цене приводят к значительным изменениям в количестве покупаемой продукции. Спрос на такие продукты принято называть относительно эластичным или просто эластичным. Что касается других продуктов, потребители относительно нечутки к изменению цен на них, то есть существенное изменение в цене ведет лишь к небольшому изменению в количестве покупок. В таких случаях спрос относительно неэластичен или просто неэластичен. Термин совершенно неэластичный спрос означает крайний случай, когда изменение цены не приводит ни к какому изменению количества спрашиваемой продукции. Примером может служить спрос больных острой формой диабета на инсулин или спрос наркоманов на героин. И наоборот, когда при самом малом снижении цены покупатели увеличивают покупки до предела своих возможностей - тогда мы говорим, что спрос является совершенно эластичным.
7.3 Экстремум функции
Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство f(x1) < f (x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ¢(x) > 0 (f ¢(x) < 0).
Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) £ f(xо) (f(x) ³ f(xо)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f ¢(xо) = 0, либо f ¢(xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть xо - критическая точка. Если f ¢ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет производную f ¢ (x) в окрестности точки xо и
вторую производную ![]() в самой точке xо.
Если f ¢(xо) = 0,
в самой точке xо.
Если f ¢(xо) = 0, ![]() >0
(
>0
(![]() <0), то точка xо
является точкой локального минимума (максимума) функции f(x). Если же
<0), то точка xо
является точкой локального минимума (максимума) функции f(x). Если же ![]() =0, то нужно либо
пользоваться первым достаточным условием, либо привлекать высшие производные.
=0, то нужно либо
пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Пример 3.22. Найти экстремумы функции f(x) = 2x3 - 15x2+ 36x - 14.
Решение. Так как f ¢ (x) = 6x2 - 30x +36 = 6(x -2)(x - 3), то критические точки функции x1 = 2 и x2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x2 = 3 производная меняет знак минус на плюс, поэтому в точке x2 = 3 у функции минимум. Вычислив значения функции в точках x1 = 2 и x2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
Пример 3.23. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение. Обозначим стороны площадки через x и y. Площадь площадки равна S = xy. Пусть y - это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x + y = a. Поэтому y = a - 2x и S = x(a - 2x), где 0 £ x £ a/2 (длина и ширина площадки не могут быть отрицательными). S ¢ = a - 4x, a - 4x = 0 при x = a/4, откуда y = a - 2×a/4 =a/2. Поскольку x = a/4 - единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При x < a/4 S ¢ >0, а при x >a/4 S ¢ <0, значит, в точке x=a/4 функция S имеет максимум. Значение функции S(a/4) = a/4(a - a/2) = a2 /8 (кв. ед).
Поскольку S непрерывна на [0, a/2] и ее значения на концах S(0) и S(a/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.
Пример 3.24. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p » 50 м3. Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR2Н Þ Н = V/pR2 =16p/ pR2 = 16/ R2. Значит, S(R) = 2p(R2+16/R). Находим производную этой функции: S ¢(R) = 2p(2R- 16/R2) = 4p (R- 8/R2). S ¢(R) = 0 при R3 = 8, следовательно, R = 2, Н = 16/4 = 4.
7.4 Раскрытие неопределенностей. Правило Лопиталя
1. Неопределенность вида 0/0. Первое правило Лопиталя.
Если ![]() = 0, то
= 0, то ![]() , когда последний существует.
, когда последний существует.
2. Неопределенность вида ¥/¥. Второе правило Лопиталя.
Если ![]() = ¥, то
= ¥, то ![]() , когда последний существует.
, когда последний существует.
3. Неопределенности вида 0× ¥, ¥ - ¥, 1¥ и 00 сводятся к неопределенностям 0/0 и ¥/¥ путем алгебраических преобразований.
Пример 3.25.
Найти предел функции y =![]() при x ® 0.
при x ® 0.
Решение. Имеем неопределенность вида ¥-¥. Сначала преобразуем ее к неопределенности вида 0/0, для чего достаточно привести дроби к общему знаменателю. К полученному выражению два раза применим правило Лопиталя. Записывая последовательно все промежуточные вычисления, будем иметь:
![]() =
= ![]() =
= ![]() =
=![]() = =
= =![]() =
=![]() .
.
Пример 3.26.
Найти ![]() .
.
Решение. Раскрывая неопределенность вида ¥/¥ по правилу Лопиталя, получаем:
![]() =
= ![]() =
= ![]() =0.
=0.
Пример 3.27.
Вычислить ![]() .
.
Решение. Имеем
неопределенность вида 1¥. Обозначим искомый предел
через A. A = ![]() .
.
Тогда ln A = ![]() =
= ![]() =
= ![]() = 2, Þ A = e2.
= 2, Þ A = e2.
7.5 Частные производные. Метод наименьших квадратов
Пусть D(x, y) - некоторое множество точек плоскости Oxy. Если каждой упорядоченной паре чисел (x, y) из области D соответствует определенное число z Î Z Ì R, то говорят, что z есть функция двух независимых переменных x и y. Переменные x и y называются независимыми переменными, или аргументами, D - областью определения, или существования, функции, а множество Z всех значений функции - областью ее значений. Функциональную зависимость z от x и y записывают в виде z = f(x, y), z = z(x, y), z = F(x, y) и т.д. Например, объем цилиндра V = pR2Н есть функция от радиуса R его основания и от высоты Н, т.е. V = f(R, Н), которая дает возможность, зная значения независимых переменных R и Н, установить соответствующее значение для V.
В экономических исследованиях часто используется производственная функция
Кобба-Дугласа ![]() , где z -
величина общественного продукта, x - затраты труда, y - объем
производственных фондов (обычно z и y измеряются в стоимостных
единицах, x - в человеко-часах); A, a, b - постоянные. Функция Кобба-Дугласа является функцией двух независимых
переменных: z = f(x, y). Частное значение функции z = f(x, y) при x = xo,
y=yo обозначается zo= f(xo, yo).
Геометрически область определения функции D представляет собой конечную или
бесконечную часть плоскости, ограниченную линиями, которые могут принадлежать
или не принадлежать этой области. В первом случае область D называется замкнутой
и обозначается D, во втором случае - открытой. Наподобие того, как
функция y = f(x) геометрически иллюстрируется своим графиком, можно
геометрически истолковать и уравнение z = f(x, y). Возьмем в пространстве R3
прямоугольную систему координат и изобразим на плоскости Oxy область D.
В каждой точке M(x, y)ÎD восстановим перпендикуляр к плоскости Oxy и
отложим на нем значение z = f(x, y). Геометрическое место полученных таким
образом точек и явится своего рода пространственным графиком нашей функции. Это
будет, вообще говоря, некоторая поверхность, поэтому уравнение z = f(x, y)
называется уравнением поверхности. Пара значений x и y
определяет на плоскости Oxy точку M(x, y), а z = f(x, y) - аппликату
соответствующей точки P(x, y, z) на поверхности. Поэтому говорят, что z
есть функция точки M(x, y) и пишут z = f(M).
, где z -
величина общественного продукта, x - затраты труда, y - объем
производственных фондов (обычно z и y измеряются в стоимостных
единицах, x - в человеко-часах); A, a, b - постоянные. Функция Кобба-Дугласа является функцией двух независимых
переменных: z = f(x, y). Частное значение функции z = f(x, y) при x = xo,
y=yo обозначается zo= f(xo, yo).
Геометрически область определения функции D представляет собой конечную или
бесконечную часть плоскости, ограниченную линиями, которые могут принадлежать
или не принадлежать этой области. В первом случае область D называется замкнутой
и обозначается D, во втором случае - открытой. Наподобие того, как
функция y = f(x) геометрически иллюстрируется своим графиком, можно
геометрически истолковать и уравнение z = f(x, y). Возьмем в пространстве R3
прямоугольную систему координат и изобразим на плоскости Oxy область D.
В каждой точке M(x, y)ÎD восстановим перпендикуляр к плоскости Oxy и
отложим на нем значение z = f(x, y). Геометрическое место полученных таким
образом точек и явится своего рода пространственным графиком нашей функции. Это
будет, вообще говоря, некоторая поверхность, поэтому уравнение z = f(x, y)
называется уравнением поверхности. Пара значений x и y
определяет на плоскости Oxy точку M(x, y), а z = f(x, y) - аппликату
соответствующей точки P(x, y, z) на поверхности. Поэтому говорят, что z
есть функция точки M(x, y) и пишут z = f(M).
Функция f(M) имеет предел A, ![]() ,
если разность f(M) - A есть бесконечно малая, когда r = MoM ® 0 при любом способе приближения M к Mo (например,
по любой линии).
,
если разность f(M) - A есть бесконечно малая, когда r = MoM ® 0 при любом способе приближения M к Mo (например,
по любой линии).
Функция f(x, y) называется непрерывной в точке Mo, если
![]() .
.
В экономике рассматриваются функции не только от двух, но и большего числа независимых переменных. Например, уровень рентабельности R зависит от прибыли П на реализованную продукцию, величин основных (a) и оборотных (b) фондов, R = П/(a+b), т.е. R является функцией трех независимых переменных R = f(П, a, b). Областью определения функции трех переменных является множество точек пространства R3, но непосредственной геометрической интерпретации для функций с числом аргументов больше двух не существует, однако для них вводятся по аналогии все определения (частные производные, предел, непрерывность и т.д.), сформулированнные для f(x,y).
Аналогично определяется функция n независимых переменных z = f(x1, x2,..., xn).
Областью определения такой функции будет множество D Ì Rn. Примером функций многих переменных в экономике являются производственные функции. При рассмотрении любого производственного комплекса как открытой системы (входами которой служат затраты ресурсов - людских и материальных, а выходами - продукция) производственная функция выражает устойчивое количественное соотношение между входами и выходами. Производственная функция обычно задается уравнением z = f(x1, x2,..., xn), где все компоненты выпуска объединены (по стоимости или в натуре) в одну скалярную величину z, а разнородные производственные ресурсы обозначены как xi.
Частной производной функции нескольких переменных по одной из этих переменных называется
производная, взятая по этой переменной при условии, что все остальные
переменные остаются постоянными. Для функции двух переменных z = f(x, y) частной
производной по переменной x называется производная этой функции по x
при постоянном y. Обозначается частная производная по x следующим
образом: ![]()
![]() .
.
Аналогично частной производной функции z = f(x, y) по аргументу y называется производная этой функции по y при постоянном x. Обозначения:
![]() .
.
Частными производными второго порядка функции z = f(x, y) называются частные производные от ее
частных производных первого порядка. Если первая производная была взята,
например, по аргументу x, то вторые производные обозначаются символами ![]() .
.
Пусть функция z = f(x, y) определена в области D и точка Mo(xo, yo) будет внутренней точкой этой области. Говорят, что функция f(x, y) в точке Mo(xo, yo) имеет максимум (минимум), если ее можно окружить такой окрестностью
(xo - d, xo + d; yo - e, yo+ e),
чтобы для всех точек этой окрестности выполнялось неравенство
f(x,y) £ f(xo,yo) ( f(x,y) ³ f(xo,yo)).
Функция многих переменных может иметь максимум или минимум (экстремум)
только в точках, лежащих внутри области определения функции, в которой все ее
частные производные первого порядка равны нулю или не существует хотя бы одна
из них. Такие точки называются критическими. Названные условия являются
необходимыми условиями экстремума, но еще не достаточными (они могут
выполняться и в точках, где нет экстремума). Чтобы критическая точка была
точкой экстремума, должны выполняться достаточные условия. Сформулируем
достаточные условия экcтремума для функции двух переменных. Пусть точка Mo(xo,
yo) - критическая точка функции z = f(x, y), т.е. ![]() , и функция z = f(x, y)
имеет непрерывные вторые частные производные в некоторой окрестности точки Mo(xo,
yo). Обозначим
, и функция z = f(x, y)
имеет непрерывные вторые частные производные в некоторой окрестности точки Mo(xo,
yo). Обозначим ![]()
![]() . Тогда:
. Тогда:
1) если D > 0, то функция z имеет экстремум в точке Mo: максимум при A < 0, минимум при A > 0;
2) если D < 0, то экстремума в точке Mo нет;
3) если D = 0, то требуется дополнительное исследование.
Пример 3.28. Исследовать функцию z = y4 - 2xy2 + x2 + 2y + y2 на экстремум.
Решение. Находим
частные производные: ![]() = - 2y2
+ 2x,
= - 2y2
+ 2x, ![]() = 4y3 - 4xy +2
+2y. Для отыскания критических точек решим систему уравнений:
= 4y3 - 4xy +2
+2y. Для отыскания критических точек решим систему уравнений: 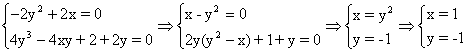 .
.
Итак, Mo(1,-1) -единственная точка, “подозрительная на
экстремум”. Находим вторые частные производные: ![]() ,
следовательно, A=2, B=4, С=10, D = 4, т.е. D > 0, функция имеет экстремум в точке Mo -
минимум (A>0). Вычислим z min = (-1)4 - 2×1×(-1)2 +1 - 2 +1
= -1.
,
следовательно, A=2, B=4, С=10, D = 4, т.е. D > 0, функция имеет экстремум в точке Mo -
минимум (A>0). Вычислим z min = (-1)4 - 2×1×(-1)2 +1 - 2 +1
= -1.
В естествознании, технике и экономике часто приходится иметь дело с эмпирическими формулами, т.е. формулами, составленными на основе обработки статистических данных или результатов опытов. Одним из распространенных приемов построения таких формул является метод наименьших квадратов. Изложим идею этого способа, ограничиваясь случаями линейной и квадратичной зависимости. Пусть требуется установить зависимость между двумя величинами x и y, например, между стоимостью потребляемого сырья и стоимостью выпущенной продукции. Произведем обследование n видов продукции и представим результаты исследования в виде таблицы:
| x |
x1 |
x2 |
... |
xn |
| y |
y1 |
y2 |
... |
yn |
Из анализа таблицы нелегко обнаружить наличие и характер зависимости между x и y. Поэтому обратимся к графику. Допустим, что точки, взятые из таблицы (опытные точки) группируются около некоторой прямой линии. Тогда можно предположить,что между x и y существует линейная зависимость`y= ax+b, где a и b - коэффициенты, подлежащие определению,`y - теоретическое значение ординаты. Проведя прямую “на глаз”, можно графически найти b и a=tg a, однако это будут весьма неточные результаты. Для нахождения a, b применяют метод наименьших квадратов.
Перепишем уравнение искомой прямой в виде ax + b -`y=0. Точки, построенные на основе опытных данных, вообще говоря, не лежат
на этой прямой. Поэтому если подставить в уравнение прямой вместо x и`y заданные величины xi
и yi, то окажется, что левая часть уравнения равна
какой-то малой величине ei=`yi -yi; а именно: для первой точки ax1 +
b - y1 = e1, для
второй - ax2 + b - y2 = e2, для последней - axn + b - yn = en.
Величины e1, e2,..., en, не
равные нулю, называются погрешностями. Геометрически это разность между
ординатой точки на прямой и ординатой опытной точки с той же абсциссой.
Погрешности зависят от выбранного положения прямой, т.е. от a и b.
Требуется подобрать a и b таким образом, чтобы эти погрешности
были возможно меньшими по абсолютной величине. Способ наименьших квадратов состоит
в том, что a и b выбираются из условия, чтобы сумма квадратов
погрешностей u = ![]() была
минимальной. Если эта сумма квадратов окажется минимальной, то и сами
погрешности будут в среднем малыми по абсолютной величине. Подставим в
выражение для u вместо ei их
значения.
была
минимальной. Если эта сумма квадратов окажется минимальной, то и сами
погрешности будут в среднем малыми по абсолютной величине. Подставим в
выражение для u вместо ei их
значения.
u = (ax1 + b - y1) 2 + (ax2 + b - y2) 2 +... + ( axn + b - yn)2, или u = u(a,b),
где xi, yi известные
величины, a и b - неизвестные, подлежащие определению. Выберем a
и b так, чтобы u(a,b) имело наименьшее значение. Необходимые
условия экстремума ![]() ,
, ![]() . Имеем:
. Имеем: ![]() = 2(ax1 + b - y1)x1
+... +2 (ax1 + b - y1)xn,
= 2(ax1 + b - y1)x1
+... +2 (ax1 + b - y1)xn, ![]() = 2(ax1 + b - y1)
+... + + 2 (ax1 + b - y1). Получаем
систему:
= 2(ax1 + b - y1)
+... + + 2 (ax1 + b - y1). Получаем
систему:
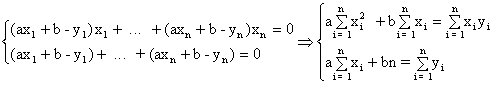 .
.
Эта система называется нормальной системой метода наименьших квадратов.
Из нее находим a и b и затем подставляем их в эмпирическую
формулу `y = ax + b. Пусть теперь точки на графике
располагаются вблизи некоторой параболы так, что между x и y
можно предположить квадратичную зависимость:`y=ax2 +
bx + c, тогда ![]()
![]() . Тогда u =
. Тогда u = ![]() =
= ![]()
![]() . Здесь u = u(a, b, c) -
функция трех независимых переменных a, b, c. Необходимые условия
экстремума
. Здесь u = u(a, b, c) -
функция трех независимых переменных a, b, c. Необходимые условия
экстремума ![]() ,
, ![]() ,
, ![]() в этом случае примут
следующий вид:
в этом случае примут
следующий вид:
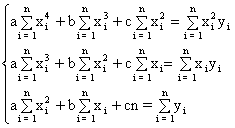 .
.
Получили нормальные уравнения способа наименьших квадратов для квадратичной зависимости `y = ax2 + bx + c, коэффициенты которой находим, решая систему трех линейных уравнений с тремя неизвестными.
Отыскание уравнения прямой по эмпирическим данным называется выравниванием по прямой, а отыскание уравнения параболы - выравниванием по параболе. В экономических расчетах могут встретиться также и другие функции. Довольно часто встречаются эмпирические формулы, выражающие обратно пропорциональную зависимость, графически изображаемую гиперболой. Тогда говорят о выравнивании по гиперболе и т.д.
Метод наименьших квадратов оказывается весьма эффективным при исследовании качества промышленной продукции в зависимости от определяющих его факторов на основе статистических данных текущего контроля качества продукции, в задачах моделирования потребительского спроса.
Пример 3.29. Темпы роста y производительности труда по годам в промышленности республики приведены в таблице.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 100 | 156 | 170 | 184 | 194 | 295 | 220 | 229 |
Предполагая, что зависимость y от x линейная: y = ax + b, найти a и b.
Решение. Вычислим
коэффициенты нормальной системы уравнений: ![]() .
.
Следовательно, имеем систему![]() , решая
которую, получим: a » 15,93; b » 110,57. Итак,
получили уравнение искомой прямой: y = 15,93x + 110,57.
, решая
которую, получим: a » 15,93; b » 110,57. Итак,
получили уравнение искомой прямой: y = 15,93x + 110,57.
8. Интегралы
8.1 Основные методы интегрирования
Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x Î X справедливо равенство:
F¢ (x) = f(x). (8.1)
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -
ò f(x) dx.
Если F(x) - какая-нибудь первобразная для функции f(x), то
ò f(x)dx = F(x) + C, (8.2)
где С - произвольная постоянная.
Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:
1) d ò f(x)=f(x)dx,
2) ò df(x)=f(x)+C,
3) ò af(x)dx=aò f(x)dx (a=const),
4) ò(f(x)+g(x))dx= ò f(x)dx+ ò g(x)dx.
Список табличных интегралов
1. ò xm dx = xm+1/(m + 1) +C (m ¹ -1).
2.![]() = ln êx ê +C.
= ln êx ê +C.
3. ò ax dx = ax/ln a + C (a>0, a¹1).
4. ò ex dx = ex + C.
5. ò sin x dx = cos x + C.
6. ò cos x dx = - sin x + C.
7.![]() = arctg
x + C.
= arctg
x + C.
8.![]() =
arcsin x + C.
=
arcsin x + C.
9.![]() = tg x + C.
= tg x + C.
10.![]() = - ctg x + C.
= - ctg x + C.
Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.
Если функция f(z) непрерывна на [a, b], функция z=g(x) имеет на [a,b] непрерывную производную и a £ g(x) £b, то
ò f(g(x)) g¢ (x) dx = ò f(z) dz, (8.3)
причем после интегрирования в правой части следует сделать подстановку z=g(x).
Для доказательства достаточно записать исходный интеграл в виде:
ò f(g(x)) g¢ (x) dx = ò f(g(x)) dg(x).
Например:
1) ![]() ;
;
2)![]() .
.
Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные производные. Тогда, по правилу дифференцирования произведения,
d(uv)= udv + vdu или udv = d(uv) -vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
ò udv = uv - ò vdu. (8.4)
Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.
Пусть, например, требуется найти ò x cosx dx. Положим u = x, dv = cos x dx, так что du=dx, v=sinx. Тогда
ò x cos x dx = ò x d(sin x) = x sin x - ò sin x dx = x sin x + cos x + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,
ò xk lnmx dx, ò xk sin bx dx, ò xk cos bx dx, ò xk e ax dx
и другие, которые вычисляются именно с помощью интегрирования по частям.
Понятие определенного интеграла вводится следующим образом. Пусть на
отрезке [a, b] определена функция f(x). Разобьем отрезок [a, b] на n
частей точками a = x0 < x1 <...<xn =
b. Из каждого интервала (xi-1, xi) возьмем произвольную точку xi и
составим сумму ![]() f(xi)D xi, где D xi = xi -
xi-1. Сумма
вида
f(xi)D xi, где D xi = xi -
xi-1. Сумма
вида ![]() f(xi)D xi называется интегральной суммой, а ее предел при l = max D xi ®0, если он
существует и конечен, называется определенным интегралом функции f(x) от
a до b и обозначается:
f(xi)D xi называется интегральной суммой, а ее предел при l = max D xi ®0, если он
существует и конечен, называется определенным интегралом функции f(x) от
a до b и обозначается:
![]()
![]()
![]() f(xi)D xi. (8.5)
f(xi)D xi. (8.5)
Функция f(x) в этом случае называется интегрируемой на отрезке [a, b], числа a и b носят название нижнего и верхнего предела интеграла.
Для определенного интеграла справедливы следующие свойства:
1) ![]()
![]()
![]() ;
;
2) ![]() ;
;
3) ![]() -
- ![]() ;
;
4) ![]()
![]() , (k = const, kÎR);
, (k = const, kÎR);
5) ![]() ;
;
6) ![]()
![]() ;
;
7) ![]() f(x)(b-a) (xÎ[a,b]).
f(x)(b-a) (xÎ[a,b]).
Последнее свойство называется теоремой о среднем значении.
Пусть f(x) непрерывна на [a, b]. Тогда на этом отрезке существует неопределенный интеграл
ò f(x) dx = F(x) + C
и имеет место формула Ньютона-Лейбница, cвязывающая определенный интеграл с неопределенным:
![]() F(b) - F(a). (8.6)
F(b) - F(a). (8.6)
Геометрическая интерпретация: определенный интеграл ![]() представляет собой площадь
криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x =
b и отрезком оси Ox.
представляет собой площадь
криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x =
b и отрезком оси Ox.
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:
![]() . (8.7)
. (8.7)
Если этот предел существует и конечен, то ![]() называется
сходящимся несобственным интегралом от f(x) на интервале [а,+¥), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+¥). В противном случае про интеграл
называется
сходящимся несобственным интегралом от f(x) на интервале [а,+¥), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+¥). В противном случае про интеграл ![]() говорят,
что он не существует, или расходится.
говорят,
что он не существует, или расходится.
Аналогично определяются несобственные интегралы на интервалах (-¥, b] и (-¥, +¥):
![]() .
.
Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка [a,b], кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:
![]() ,
,
если эти пределы существуют и конечны. Обозначение:
![]() =
= ![]() .
(8.8)
.
(8.8)
Пример 3.30. Вычислить ò dx/(x+2).
Решение. Обозначим t=x+2, тогда dx=dt, ò dx/(x+2) = ò dt/t = lnïtï+C = = lnïx+2ï+C.
Пример 3.31. Найти ò tg x dx.
Решение. ò tg x dx = ò sin x/cos x dx = - ò d(cos x)/ cos x. Пусть t=cos x, тогда ò tg x dx = - ò dt/t = - lnïtï+C = - lnïcos xï+C.
Пример 3.32. Найти ò dx/sin x.
Решение.
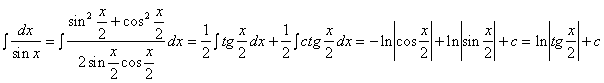
Пример 3.33.
Найти ![]() .
.
Решение. ![]() =
= ![]()
![]()
Пример 3.34. Найти ò arctg x dx.
Решение. Обозначим u=arctg x, dv=dx. Тогда du = dx/(x2+1), v=x, откуда ò arctg x dx = x arctg x - ò x dx/(x2+1) = x arctg x + 1/2 ln(x2+1) +C; так как ò x dx/(x2+1) = 1/2 ò d(x2+1)/(x2+1) = 1/2 ln(x2+1) +C.
Пример 3.35. Вычислить ò ln x dx.
Решение. Применяя формулу интегрирования по частям, получим: u=ln x, dv=dx, du= 1/x dx, v=x. Тогда ò ln x dx = x lnx - ò x 1/x dx = = x lnx - ò dx = x lnx - x + C.
Пример 3.36. Вычислить ò ex sin x dx.
Решение. Обозначим u = ex, dv = sin x dx, тогда du = ex dx, v=ò sin x dx= - cos x Þ ò ex sin x dx = - ex cos x + ò ex cos x dx. Интеграл ò ex cos x dx также интегрируем по частям: u = ex, dv = cos x dx Þ du=exdx, v=sin x. Имеем: ò ex cos x dx = ex sin x - ò ex sin x dx. Получили соотношение ò ex sin x dx = - ex cos x + ex sin x - ò ex sin x dx, откуда 2 ò ex sin x dx = - ex cos x + ex sin x + С.
Пример 3.37. Вычислить J = ò cos(ln x)dx/x.
Решение. Так как dx/x = d(ln x), то J= ò cos(ln x)d(ln x). Заменяя ln x через t, приходим к табличному интегралу J = ò cos t dt = sin t + C = sin(ln x) + C.
Пример 3.38.
Вычислить J = ![]() .
.
Решение. Учитывая,
что ![]() = d(ln x), производим
подстановку ln x = t. Тогда J =
= d(ln x), производим
подстановку ln x = t. Тогда J = ![]() .
.
Пример 3.39.
Вычислить интеграл J = ![]() .
.
Решение. Имеем:
![]() . Поэтому
. Поэтому ![]() = =
= =![]() =
=![]() .
.
Пример 3.40.
Можно ли применить формулу Ньютона-Лейбница к интегралу ![]() ?
?
Решение. Нет,
нельзя. Если формально вычислять этот интеграл по формуле Ньютона-Лейбница, то
получим неверный результат. Действительно, ![]() =
=
![]() .
.
Но подынтегральная функция f(x) = ![]() >
0 и, следовательно, интеграл не может равняться отрицательному числу. Суть дела
заключается в том, что подынтегральная функция f(x) =
>
0 и, следовательно, интеграл не может равняться отрицательному числу. Суть дела
заключается в том, что подынтегральная функция f(x) = ![]() имеет бесконечный разрыв в
точке x = 4, принадлежащей промежутку интегрирования. Следовательно, здесь
формула Ньютона-Лейбница неприменима.
имеет бесконечный разрыв в
точке x = 4, принадлежащей промежутку интегрирования. Следовательно, здесь
формула Ньютона-Лейбница неприменима.
Пример 3.41.
Вычислить интеграл ![]() .
.
Решение. Подынтегральная
функция определена и непрерывна при всех значениях х и, следовательно,
имеет первообразную F(x)= ![]() .
.
По определению имеем: ![]() =
= ![]() .
.
По формуле Ньютона-Лейбница,
![]() = F(b) - F(0) =
= F(b) - F(0) = ![]() +
+![]() =
= ![]() ;
;
![]() =
= ![]() =
= ![]() .
.
8.2Использование интегралов в экономических расчетах
Пример 3.42. Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией
f(t) = 3/(3t +1) + 4.
Решение. Если непрерывная функция f(t) характеризует производительность труда рабочего в зависимости от времени t, то объем продукции, произведенной рабочим за промежуток времени от t1 до t2 будет выражаться формулой
V =![]() .
.
В нашем случае
V =![]() = ln 10 + 12 - ln 7 - 8 =
ln 10/7 + 4.
= ln 10 + 12 - ln 7 - 8 =
ln 10/7 + 4.
Пример 3.43. Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией f(t) = 2t + 5.
Решение. Имеем:
V =![]() .
.
Пример 3.44. Пусть сила роста (см.6.1) описывается некоторой непрерывной функцией времени d t = f(t), тогда наращенная сумма находится как
S = P exр ![]() d t dt,
d t dt,
а современная величина платежа P = S exр(-![]() d t dt).
d t dt).
Если, в чаcтности, d t является линейной функцией времени: d t = d o + at, где d o - величина силы роста для t = 0, a - годовой прирост, то
![]() d t dt =
d t dt = ![]() (d o + at)dt = d o n + an2/2;
(d o + at)dt = d o n + an2/2;
множитель наращения exр(d o n + an2/2). Если сила роста изменяется по геометрической прогрессии d t = d o at, где d o - начальное значение процентной ставки, a - годовой коэффициент роста, тогда
![]() d t dt =
d t dt = ![]() d o at dt =
d o
at /lna
d o at dt =
d o
at /lna![]() = d o(an -1)/lna;
= d o(an -1)/lna;
множитель наращения exр(d o(an -1) / lna).
Предположим, что начальный уровень силы роста равен 8%, процентная ставка ежегодно увеличивается на 20% (a=1,2), срок ссуды 5 лет. Множитель наращения в этом случае составит exр (0,08 (1,25-1) / ln1,2) » » exр 0,653953 » 1,921397.
Пример 3.45. Выше
при анализе непрерывных потоков платежей предполагалось, что годовая сумма
ренты R равномерно распределяется на протяжении года. На практике, особенно в
инвестиционных процессах, этот поток может существенно изменяться во времени,
следуя какому-либо закону. Если этот поток непрерывен и описывается некоторой
функцией R t = f (t), то общая сумма поступлений за время n
равна ![]() .
.
В этом случае наращенная по непрерывной ставке за период от 0 до n сумма составит:
S = ![]() .
.
Современная величина такого потока равна
A = ![]() .
.
Пусть функция потока платежей является линейной: Rt = Ro + at, где Ro - начальная величина платежа, выплачиваемого за единицу времени, в которой измеряется срок ренты. Вычислим современную величину A, пользуясь правилами интегрирования определенного интеграла:
A = ![]() =
= ![]() +
+ ![]() .
.
Обозначим A1
= ![]() , A2 =
, A2 = ![]() .
.
Имеем: A1 = ![]() = - Ro/d
= - Ro/d![]() ê
ê![]() = - Ro/d(
= - Ro/d(![]() -eo) = - Ro/d(
-eo) = - Ro/d(![]() -1) = =
Ro(
-1) = =
Ro(![]() -1)/d. A2
=
-1)/d. A2
= ![]() . Вычислим неопределенный
интеграл
. Вычислим неопределенный
интеграл ![]() по частям: u = t, dv =
по частям: u = t, dv = ![]() dt Þ du = dt, v =
dt Þ du = dt, v = ![]() =
-
=
- ![]() /d, тогда
/d, тогда ![]() = - t
= - t![]() /d + 1/d
/d + 1/d ![]() = - t
= - t![]() /d (t+1/d) +C. Следовательно, A2 = -a t
/d (t+1/d) +C. Следовательно, A2 = -a t![]() /d (t+1/d)ê
/d (t+1/d)ê![]() = ((1-
= ((1- ![]() )/d - n
)/d - n![]() )a/d.
)a/d.
Итак, исходный интеграл
A = A1
+ A2 = Ro(![]() -1)/d + ((1-
-1)/d + ((1- ![]() )/d - n
)/d - n![]() )a/d.
)a/d.
9. Дифференциальные уравнения
При изучении интегралов перед нами стояла задача: найти y, если
y¢ = f(x),
или dy = f(x)dx. Решение, как известно, дается формулой
y = ò f(x)dx
и сводится, таким образом, к вычислению неопределенного интеграла. Однако на практике значительно чаще встречается гораздо более сложная задача: найти функцию y, если известно, что она удовлетворяет данному соотношению вида
F(x, y, y¢, y¢¢,..., y(n)) = 0. (9.1)
Такого рода соотношения, связывающие независимую переменную x, неизвестную функцию y и ее производные до некоторого порядка n включительно, называются дифференциальными уравнениями.
В дифференциальном уравнении, таким образом, неизвестной является функция, входящая в уравнение под знаком производных (или дифференциалов) того или иного порядка. Порядок наивысшей производной, входящей в дифференциальное уравнение, называется порядком этого дифференциального уравнения.
Например:
y¢ - x2y + x3 = 0 - уравнение первого порядка,
y¢¢ + 4y¢ + cos x = 0 - уравнение второго порядка,
x y(5) + yy¢¢¢ = 1 - уравнение пятого порядка и т. д.
Всякая функция, удовлетворяющая данному дифференциальному уравнению, называется его решением, или интегралом. Решить дифференциальное уравнение - это значит найти все его решения. Если для искомой функции y нам удалось получить формулу, дающую все решения данного дифференциального уравнения и только их, то мы говорим, что нашли его общее решение, или общий интеграл.
Общее решение дифференциального уравнения n-го порядка содержит n произвольных постоянных с1, с2,..., cn и имеет вид
y = j(x, с1, с2,..., cn).
Если соотношение, связывающее x, y и n произвольных постоянных, получено в виде, не разрешенном относительно y -
Ф(x, y, с1, с2,..., cn) = 0,
то будем называть такое соотношение общим интегралом уравнения (9.1).
В противовес общему решению каждое конкретное решение, т. е. каждая конкретная функция, удовлетворяющая данному дифференциальному уравнению и не зависящая от произвольных постоянных, называется частным решением, или частным интегралом. Частные решения (интегралы) получаются из общего, когда постоянным с1, с2,..., cn придают конкретные числовые значения.
График каждого частного решения называется интегральной кривой. Поэтому общее решение, содержащее все частные решения, представляет собой семейство интегральных кривых. В случае уравнения первого порядка это семейство зависит от одной произвольной постоянной, в случае уравнения n-го порядка - от n произвольных постоянных.
В задаче Коши (начальной задаче) требуется найти частное решение для уравнения n-го порядка, удовлетворяющее n начальным условиям:
y(xo) = yo, y¢(xo) = yo¢,..., y(n-1)(xo) = yo(n-1),
по которым определяются n постоянных с1, с2,..., cn. Дифференциальное уравнение 1-го порядка имеет общий вид
F(x, y, y¢) = 0,
или вид, разрешенный относительно y¢:
y¢ = f(x, y).
Пример 3.46. Найти общее решение уравнения y¢ = 3x.
Решение. Интегрируя, находим
y = ò 3x dx, y = 3x2/2 + C,
где С - произвольная постоянная. Придавая С конкретные числовые значения, будем получать частные решения, например,
y = 3x2/2 (С= 0),
y = 3x2/2 + 5 (С = 5)
и т.д.
Пример 3.47. Рассмотрим процесс возрастания денежной суммы, положенной в банк при условии начисления 100 r сложных процентов в год. Пусть Yo обозначает начальную денежную сумму, а Yx - денежную сумму по истечении x лет. Если бы проценты начислялись один раз в год, мы бы имели
Yx+1 = (1+r)Yx,
где x = 0, 1, 2, 3,.... Если бы проценты начислялись два раза в год (по истечении каждого полугодия), то мы имели бы
Yx+1/2 = (1 + r/2)Yx,
где x = 0, 1/2, 1, 3/2,.... Вообще, если проценты начисляются n раз в год и x принимает последовательно значения 0, 1/n, 2/n, 3/n,..., тогда
Yx+1/n = (1 + r/n)Yx,
то есть
![]() .
.
Если обозначить 1/n = h, то предыдущее равенство перепишется так:
![]() .
.
Неограниченно увеличивая n (при n®¥, h®0) мы в пределе приходим к процессу возрастания денежной суммы при непрерывном начислении процентов:
![]() ,
,
то есть при непрерывном изменении x закон возрастания выражен дифференциальным уравнением 1- го порядка. Отметим для четкости, что Yx - неизвестная функция, x - независимая переменная, r - постоянная. Для решения данного уравнения перепишем его следующим образом:
![]()
откуда Yx = e r x+C, или Yx = P e r x, где через P обозначено eC.
Учитывая начальное условие Y(0) = Yo, найдем P: Yo = Peo, следовательно, Yo = P. Решение имеет вид:
Yx =Yo e r x.
Рассмотрим еще одну экономическую задачу. Простейшие макроэкономические модели также приводят к линейным дифференциальным уравнениям 1-го порядка, описывающим изменение дохода или выпуска продукции Y как функций времени.
Пример 3.48. Пусть национальный доход Y возрастает со скоростью, пропорциональной его величине:
![]() ,
,
и пусть, кроме того, дефицит в расходах правительства прямо пропорционален доходу Y (при коэффициенте пропорциональности q). Дефицит в расходах приводит к возрастанию национального долга D:
dD/dt = qY.
Здесь мы считаем переменные Y и D непрерывными и дифференцируемыми функциями времени t. Пусть начальные условия имеют вид Y = Yo и D = Do при t = 0. Из первого уравнения мы получаем, учитывая начальные условия, Y= Yo e k t. Подставляя Y во второе уравнение, получаем dD/dt = qYo e k t. Общее решение этого уравнения имеет вид D = (q/ k) Yo e k t +С, где С = const, которую мы определим из начальных условий. Подставляя начальные условия в полученное решение, мы получаем Do = (q/ k)Yo + С. Итак, окончательно,
D = Do+(q/ k)Yo (e k t -1),
то есть, национальный долг возрастает с той же относительной скоростью k, что и национальный доход.
Простейшим дифференциальным уравнением n-го порядка является уравнение
y(n) = f(x).
Его общее решение можно получить с помощью n интегрирований.
Пример 3.49. Решить уравнение y¢¢¢ = cos x.
Решение. Интегрируя, находим
y¢¢ = ò cos x dx = sin x + C1,
y¢ = ò (sin x + C1)dx = - cos x + C1x + С2,
y = ò (- cos x + C1x +C2)dx = - sin x + C1x2/2 +C2x+C3.
Итак, общее решение
y = - sin x + C1x2/2 +C2x+C3.
В математической экономике большое применение находят линейные дифференциальные уравнения, и поэтому мы рассмотрим решение таких уравнений. Дифференциальное уравнение (9.1) называется линейным, если имеет вид:
рo(x)y(n)(x) + р1(x)y(n- 1)(x) +... + рn - 1(x)y¢(x) + рn(x)y(x) = f(x), (9.2)
где рo(x), р1(x),..., рn(x), f(x) - данные функции. Если f(x) º 0, то уравнение (9.2) называется однородным, в противном случае - неоднородным. Общее решение уравнения (9.2) есть сумма какого-либо его частного решения y(x) и общего решения соответствующего однородного уравнения:
рo(x)y(n)(x) + р1(x)y(n- 1)(x) +... + рn - 1(x)y¢(x) + рn(x)y(x) = 0. (9.3)
Если коэффициенты рo(x), р1(x),..., рn(x) постоянные, то уравнение (9.2) принимает вид:
рoy(n)(x) + р1y(n- 1)(x) +... + рn - 1y¢(x) + рny(x) = f(x) (9.4)
и называется линейным дифференциальным уравнением порядка n с постоянными коэффициентами.
Соответствующее уравнению (9.4) однородное уравнение выглядит так:
рoy(n)(x) + р1y(n- 1)(x) +... + рn - 1y¢(x) + рny(x) = 0. (9.5)
Без ограничения общности можно положить рo = 1 и записать уравнение (9.5) в виде
y(n)(x) + р1y(n- 1)(x) +... + рn - 1y¢(x) + рny(x) = 0. (9.6)
Решение уравнения (9.6) будем искать в виде y = e kx, где k - постоянная. Имеем: y¢ = ke kx, y¢¢ = k2 e kx,..., y(n) = kn e kx. Подставляя полученные выражения в (9.6), будем иметь:
e kx (kn + р1kn-1 +... + рn-1k + рn) = 0.
Т.к. e kx ¹ 0, то
kn + р1kn-1 +... + рn-1k + рn = 0. (9.7)
Равенство (9.7) есть алгебраическое уравнение с неизвестным k. Оно
называется характеристическим уравнением для дифференциального уравнения (9.6).
Характеристическое уравнение есть уравнение n-й степени, следовательно,
оно имеет n корней, среди которых могут быть кратные и комплексные. Если
k1, k2,..., kn - действительные и различные
корни уравнения (9.7), то ![]() -
частные решения уравнения (9.7), а общее имеет вид
-
частные решения уравнения (9.7), а общее имеет вид
y = ![]() .
.
Рассмотрим подробно линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
y¢¢ + рy¢ +qy = 0. (9.8)
Его характеристическое уравнение имеет вид
k2 + рk + q=0 (9.9)
и в зависимости от значения дискриминанта D = р2 - 4q возможны три случая.
1. Если D>0, то корни k1 и k2 уравнения (9.9) действительны и различны, тогда общее решение имеет вид:
y = c1 exр(k1x) + c2 exр(k2x).
2. Если D = 0, т.е. корни k1 и k2 действительные и равные, то общее решение находится по формуле:
y = (c1 + c2x) exр (k1x).
3. Если D<0, то корни комплексные, k1 = a + bi, k2 = a - bi, где i - мнимая единица. Тогда общее решение таково:
y = (c1 cos bx+c2 sin bx) exр (ax).
Пример 3.50. Решить уравнение y¢¢ - y = 0.
Решение. Характеристическое уравнение имеет вид k2 - 1 = 0, корни которого k1 = 1, k2 = -1 действительны и различны. Общее решение:
y = c1e x + c2e -x.
Пример 3.51. Найти общее решение уравнения y¢¢- 4y¢ + 4y = 0.
Решение. Характеристическое уравнение запишется в виде: k2 -4k +4 = 0 или (k - 2)2 = 0, т.е. имеет равные корни k1= k2 =2, значит, общее решение данного уравнения находится по формуле:
y = e2x(c1+c2x).
Пример 3.52. Найти общее решение уравнения y¢¢+9y = 0.
Решение. Имеем следующее уравнение для нахождения k: k2+9 = 0, откуда k = ±3i, Þ a = 0, b = 3, значит, общее решение имеет вид:
y = c1 cos 3x + c2 sin 3x.
Линейные дифференциальные уравнения 2-го порядка находят применение при изучении, например, экономической модели паутинообразного типа с запасами товаров, в которой скорость изменения цены P зависит от величины запаса (см. о паутинообразной модели в параграфе 10). Если спрос и предложение являются линейными функциями цены, то есть
D = a +aP, S =b+bP,
а l есть постоянная, определяющая скорость реакции (то есть изменения цены при изменении запасов товара), то процесс изменения цены описывается дифференциальным уравнением:
![]() + l (b - a) P = l (a - b).
+ l (b - a) P = l (a - b).
В качестве частного решения можно взять постоянную
P =`P = (a - b)/(b - a),
имеющую смысл цены равновесия. Отклонение р = P -`P удовлетворяет тогда однородному уравнению
![]() + l (b - a) р = 0. (9.10)
+ l (b - a) р = 0. (9.10)
Найдем общее решение этого уравнения. Характеристическое уравнение, в котором неизвестная обозначена через k, будет следующее:
k2 + l (b - a) = 0.
В обычном случае (a<0, b>0, l>0) член l (b - a) положителен. Введем обозначение w =![]() . Тогда корни
характеристического уравнения будут k 1,2 = ± i w. Следовательно, общее решение уравнения (9.10) имеет
вид:
. Тогда корни
характеристического уравнения будут k 1,2 = ± i w. Следовательно, общее решение уравнения (9.10) имеет
вид:
р = C cos (wt-e),
где C и e представляют собой произвольные постоянные, которые определяются единственным образом, если заданы начальные условия. Следовательно, присоединив `P, получим закон изменения цены во времени:
P = `P+ C cos (wt-e).
10. Разностные уравнения
На практике простейшие разностные уравнения возникают при исследовании например величины банковского вклада. Эта величина является переменной Yx, представляющей сумму, которая накапливается по установленному закону при целочисленных значениях аргумента x. Пусть сумма Yo положена в банк при условии начисления 100 r сложных процентов в год. Пусть начисление процентов производится один раз в год и x обозначает число лет с момента помещения вклада (x = 0, 1, 2,...). Обозначим величину вклада по истечении x лет через Yx. Мы получаем
Yx = (1+r)Yx-1.
Если начальная сумма составляет Yo, мы приходим к задаче отыскания решения полученного разностного уравнения, подчиненного начальному условию Yx = Yo при x = 0. Полученное разностное уравнение содержит Yx и значение этой переменной на один год раньше, т.е. Yx-1; в данном случае аргумент x явно не входит в разностное уравнение.
Вообще говоря, обыкновенное разностное уравнение устанавливает связь между значениями функции Y = Y(x), рассматриваемой для ряда равноотстоящих значений аргумента x, но можно без ограничения общности считать, что искомая функция определена для равноотстоящих значений аргумента с шагом, равным единице. Таким образом, если начальное значение аргумента есть x, то ряд его равноотстоящих значений будет x, x+1, x+2,... и в обратном направлении: x, x-1, x-2,.... Соответствующие значения функции будем обозначать Yx,Yx+1,Yx+2,... или Yx, Yx-1, Yx-2,.... Определим так называемые разности различных порядков функции Yx с помощью следующих формул:
Разности первого порядка
D Yx = Yx+1 - Yx,
D Yx+1 =Yx+2 - Yx+1,
DYx+2 = Yx+3 - Yx+2,
... ... ... ... ...
Разности второго порядка
D2Yx= DYx+1 - D Yx,
D2Yx+1= D Yx+2 - DYx+1,
D2Yx+2= D Yx+3 - DYx+2,
... ... ... ... ...
Разности третьего порядка
D3Yx= D2Yx+1 - D2Yx,
D3Yx+1= D2Yx+2 - D2Yx+1,
... ... ... ... ...
Обыкновенным разностным уравнением называется уравнение, связывающее значения одного независимого аргумента x, его функцииYx и разностей различных порядков этой функции DYx, D2Yx, D3Yx,.... Такое уравнение можно записать в общем виде следующим образом:
j(x, Yx, DYx, D2Yx D3Yx, DnYx) = 0, (10.1)
которое по форме аналогично дифференциальному уравнению.
Порядком разностного уравнения называется порядок наивысшей разности, входящей в это уравнение. Разностное уравнение (10.1) часто удобнее записать, пользуясь не разностями неизвестной функции, а ее значениями при последовательных значениях аргумента, то есть выразить DYx, D2Yx, D3Yx,... через Yx, Yx+1, Yx+2,.... Уравнение (10.1) можно привести к одной из двух форм:
y(x, Yx, Yx+1,...,Yx+n) = 0, (10.2)
x(x, Yx, Yx-1,...,Yx-n) = 0. (10.3)
Общее дискретное решение Yx обыкновенного разностного уравнения n-го порядка представляет функцию x (x = 0, 1. 2,...), содержащую ровно n произвольных постоянных:
Yx = Y(x, C1, C2,..., Cn).
Паутинообразная модель. Пусть рынок какого-либо отдельного товара характеризуется следующими функциями спроса и предложения:
D = D(P), S = S(P).
Для существования равновесия цена должна быть такой, чтобы товар на рынке был распродан, или
D(P) = S(P).
Цена равновесия `P задается этим уравнением (которое может иметь множество решений), а соответствующий объем покупок-продаж, обозначаемый через `X, - следующим уравнением:
`X = D (`P) = S(`P).
Динамическая модель получается при наличии запаздывания спроса или предложения. Простейшая модель в дискретном анализе включает неизменное запаздывание или отставание предложения на один интервал:
Dt = D (Pt) и St = S (Pt-1).
Это может случиться, если для производства рассматриваемого товара требуется определенный период времени, выбранный за интервал. Действие модели таково: при заданном Pt-1 предшествующего периода объем предложения на рынке в текущем периоде будет S (Pt-1), и величина Pt должна установиться так, чтобы был куплен весь объем предложенного товара. Иными словами, Pt и объем покупок-продаж Xt характеризуются уравнением:
Xt = D (Pt) = S (Pt-1).
Итак, зная исходную цену Po, с помощью этих уравнений мы можем получить значения P1 и X1. Затем, используя имеющуюся цену P1, из соответствующих уравнений получим значения P2 и X2 и т.д. В общем изменение Pt характеризуется разностным уравнением первого порядка (одноинтервальное отставание):
D (Pt) = S (Pt-1).
Решение можно проиллюстрировать диаграммой, представленной на рис.5, где D и S - соответственно кривые спроса и предложения, а положение равновесия (со значениями `P и `X) соответствует точке их пересечения Q. Цена в начальный момент времени равна Po. Соответствующая точка Qo на кривой S дает объем предложения в период 1. Весь этот предложенный объем товара раскупается при цене P1, заданной точкой Q1 на кривой D с той же ординатой (X1), что и Qo. Во второй период времени движение происходит сначала по вертикали от точки Q1 к точке на кривой S, дающей X2, а затем по горизонтали - к точке Q2 на кривой D. Последняя точка характеризует P2. Продолжение этого процесса и дает график паутины, показанный на рис. 5. Цены и объемы (покупок - продаж) в последовательные периоды времени являются соответственно координатами точек Q1, Q2, Q3,... на кривой спроса D. В рассматриваемом случае последовательность точек стремится к Q. При этом точки поочередно располагаются на левой и правой стороне от Q. Следовательно, и значения цены Pt стремятся к `P, располагаясь поочередно по обе стороны от`P. Точно так же обстоит дело и с объемами покупок - продаж (X t).
Решение можно получить алгебраически для случая линейных функций спроса и предложения: D = a +aP, S = b +bP. Значения равновесия `P и `X будут заданы уравнениями
`X = a +a`P = b +b`P,
то есть
`P = (a - b)/(b - a), `X = (ba - ab)/(b - a). (10.4)
Дискретная динамическая модель задается уравнением
X t = a +aP t = b +bP t-1. (10.5)
Ищем сначала решение, дающее равновесие. Для этого положим P t = `P, X t = `X для всех значений t:
`X = a +a`P = b +b`P. (10.6)
Получаем те же значения `P и `X, что и в (10.4). Следовательно, если в каком-либо периоде существовали цены и объемы, обеспечивающие равновесие, то в динамической модели (10.5) они сохранятся и в последующих периодах.
Вычтем уравнение (10.6) из (10.5) и положим р t = P t -`P, x t = X t -`X. Тогда
x t = aр t = bр t-1. (10.7)
Уравнения (10.7) аналогичны (10.5), за исключением того, что они описывают отклонения от уровней равновесия (теперь уже известно, что таковые существуют). Оба эти уравнения являются разностными уравнениями первого порядка. Положим c = b/a и подставим его в уравнение (10.7), так что разностное уравнение относительно р t будет
р t = c р t-1. (10.8)
При данном значении р o в момент t = 0 из (10.8) получаем решение:
р t = рo c t,
или
P t = `P + (Po - `P) c t.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Аллен Р. Математическая экономия. М.: Изд-во иностранной литературы, 1963.
2. Баврин И. И., Матросов В. Л. Общий курс высшей математики. М.: Просвещение, 1995.
3. Белинский В. А., Калихман В. А., Майстров Л. Е., Митькин А. М. Высшая математика с основами математической статистики. М.: Высшая школа, 1965.
4. Высшая математика: Общий курс / Под ред. А. И. Яблонского. Минск: Вышейш. школа, 1993.
5. Ланкастер К. Математическая экономика. М.: Советское радио, 1972.
6. Макконелл К., Брю С. Экономикс: принципы, проблемы, политика. М.: Республика, 1992. Т. 1-2.
7. Математика и кибернетика в экономике: Словарь - справочник / Под ред. Н. П. Федоренко. М.: Экономика, 1975.
8. Минорский В. П. Сборник задач по высшей математике. М.: Наука, 1987.
9. Рублев А. Н. Линейная алгебра. М.: Высшая школа, 1968.
10. Сборник задач и упражнений по высшей математике: Общий курс: Учеб. пособие / А. В. Кузнецов, Д. С. Кузнецова, Е. И. Шилкина и др. - Минск: Вышейш. шк., 1994.
11. Сборник задач по математическому анализу. Предел, непрерывность, дифференцируемость / Л. Д. Кудрявцев, А. Д. Кутасов, В. И. Чехлов, М. И. Шабунин; Под ред. Л. Д. Кудрявцева. - М.: Наука, 1984.
12. Тышкевич Р. И., Феденко А. С. Линейная алгебра и аналитическая геометрия. Минск: Вышейш. школа, 1968.
13. Фихтенгольц Г. М. Основы математического анализа. М.: Наука, 1968. Т. 1-2.
14. Четыркин Е. М. Методы финансовых и коммерческих расчетов. М.: Дело, Business Речь, 1992.
15. Шипачев В. С. Основы высшей математики / Под ред. А. Н. Тихонова. М.: Высш. шк., 1994.
16. Mathematische Proрadeutik fur Wirtshaftswissenschaftler / W. Wetzel, Н. Skarabis, P. Naeve, Н. Buening. Berlin, New York: Walter de Gruyter, 1981.
17. Mathematik fur Wirtshafts-Kaufleute / E. Forster, Н. Korth. Munchen: Wilhelm Нeyne Verlag, 1976.
ОГЛАВЛЕНИЕ
| ПРЕДИСЛОВИЕ ................................................................................................. | 3 |
| I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ ................................................................ | 5 |
| 1. Векторы ..................................................................................................... | 5 |
| 2. Линии на плоскости .................................................................................. | 7 |
| 3. Плоскость и прямая в пространстве ........................................................ | 17 |
| II. ЛИНЕЙНАЯ АЛГЕБРА .................................................................................. | 21 |
| 4. Матрицы и определители ......................................................................... | 21 |
| 4.1. Матрицы. Операции над матрицами .............................................. | 21 |
| 4.2. Определители ................................................................................... | 24 |
| 4.3. Ранг матрицы ................................................................................... | 28 |
| 4.4. Обратная матрица ............................................................................ | 30 |
| 5. Системы линейных уравнений ................................................................. | 33 |
| 5.1. Критерий совместности .................................................................. | 33 |
| 5.2. Метод Гаусса ................................................................................... | 35 |
| 5.3. Формулы Крамера ........................................................................... | 36 |
| 5.4. Матричный метод ............................................................................ | 38 |
| 5.5. Системы линейных уравнений общего вида .................................. | 39 |
| 5.6. Использование систем линейных уравнений при решении экономических задач ............................................................................. | 44 |
| III. МАТЕМАТИЧЕСКИЙ АНАЛИЗ .................................................................. | 50 |
| 6. Предел функции ........................................................................................ | 50 |
| 6.1. Предел последовательности и функции. Теоремы о пределах ...... | 50 |
| 6.2. Применение пределов в экономических расчетах ......................... | 57 |
| 7. Производная .............................................................................................. | 60 |
| 7.1. Производная, правила и формулы дифференцирования ............... | 60 |
| 7.2. Предельный анализ в экономике. Эластичность функции ............ | 64 |
| 7.3. Экстремум функции ........................................................................ | 66 |
| 7.4. Раскрытие неопределенностей. Правило Лопиталя ....................... | 67 |
| 7.5. Частные производные. Метод наименьших квадратов ................. | 68 |
| 8. Интегралы ................................................................................................. | 76 |
| 8.1. Основные методы интегрирования ................................................. | 76 |
| 8.2. Использование интегралов в экономических расчетах ................. | 81 |
| 9. Дифференциальные уравнения ................................................................ | 83 |
| 10. Разностные уравнения ............................................................................ | 90 |
| Список рекомендуемой литературы ................................................................... | 95 |
[