Контрольная работа: Высшая математика. Матрица
Министерство образования
Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
КОНТРОЛЬНАЯ РАБОТА
2003
1(Т85.РП). Найдите матрицу D=(AC-AB), если
А= 1 0 ,C= 3 4 4 , B= -3 1 4 .
2 -2 1 -3 5 2 -3 4
(В ответ ввести вторую строку матрицы D.)
Решение:
Размеры матриц А и С согласованны, т.к. число
элементов в строке матрицы А равно числу элементов в столбце матрицы В.
а*с= 1 0 * 3 4 4 = 1*3+0*1 1*4+0*(-3) 1*4+0*5 = 3 4 4
2 -2 1 -3 5 2*3+(-2)*1 2*4-2*(-3) 2*4-2*5 4 14 -2
А*В= 1 0 * -3 1 4 =
1*(-3)+0*2 1*1+0*(-3) 1*4+0*4 = -3 1 4
2 -2 2 -3 4 2*(-3)-2*2 2*1-2*(-3) 2*4-2*4 -10 8 0
 |
|
 |
 |
D=А*С-А*В= 3 4 4 _ -3 1 4 = 3-(-3) 4-1 4-4 = 6 3 0
4 14 -2 -10 8 0 4-(-10) 14-8 -2-0 14 6 -2
Ответ :14 , 6 , -2.
2(3ТО).Вычислите определитель D= 2 2 1 0
1 1 1 0
1 2 2 1
0 3 2 2
Решение:
2 2 1 0
1 1 1 0
1 2 2 1 =
0 3 2 2
Умножим третью строку на (-2) и сложим с четвёртой строкой , результат запишем
в четвёртую строку:
2 2 1 0
1 1 1 0
= 1 2 2 1 =
-2 -1 -2 0
Данный определитель разложим по элементам четвёртого столбца :
3+4 2 2 1
= 1*(-1) * 1 1 1 =
-2 -1 -2
Умножим вторую строку на (-2) и сложим с первой, результат запишем в первую строку . Умножим вторую строку на 2 и сложим с третьей , результат запишем в третью строку .
0 0 -1
= - 1 1 1 = - (-1) 1+3 * (-1) * 1 1 = 1-0 =1;
0 1 0 0 1
Ответ: D = 1.
3(598.Р7).Решите матричное уравнение
1 2 1 1 1 -1
X* 4 3 -2 = 16* -1 2 3
-5 -4 -1 0 -1 -2 .
Решение:
A*X=B , X=A-1 *B
Найдём det A:
1 2 1
det A= 4 3 -2 = 1*3*(-1)+1*4*(-4)+2*(-2)*(-5)-1*3*(-5)-2*4*(-1)-1*(-2)*(-4)=
-5 -4 -1
=-19+20+15-8+8=16 ;
det= 16 ≠ 0;
Составим матрицу А -1 ,
обратную матрицы А:
А1 1 = 3 -2 = -3 –8 = -11
-4 -1
А12 = - 4 -2 = -(-4-10) = 14
-5 -1
А13 = 4 3 = -16+15 = -1
-5 -4
A21 = - 2 1 = -(-2+4) = -2
-4 -1
A22
= 1 1 = -1+5 = 4
-5 -1
A23 =
- 1 2 = - (-4+10) = -6
-5 -4
A31
= 2 1 = - 4-3 = -7
3 -2
A32 = - 1 1 = - (-2-4) = 6
–2
A33 = 1 2 = 3 –8 = -5
4 3
-11/16
-2/16 -7/16
А-1 = 14/16 4/16 6/16
-1/16 -6/16 -5/16
 |
 |
-11/16 -2/16 -7/16 1*16 1*16 -1*16
Х = 14/16 4/16 6/16 * -1*16 2*16 3*16 =
-1/16 -6/16 -5/16 0*16 -1*16 2*16
-11*1+(-2*(-1))+(-7*0) -11*1+(-2*2)+(-7*(-1)) -11*(-1)+(-2*3)+(-7*2)
= 14*1+4*(-1)+6*0 14*1+4*2+6*(-1) 14*(-1)+4*3+6*2 =
-1*1+(-6*(-1))+(-5*0)
-1*1+(-6*2)+(-5*(-1)) -1*(-1)+(-6*3)+(-5*2)
-9 -8 -9
= 10 16 10
5 -8 -27
Ответ : Х = : -9 , -8 , -9 : 10 , 16 , 10 : 5 , -8 , -27 .
4(4П5).При каком значении параметра p , если он существует ,
1 2 -2 1
последняя строка матрицы А = 2 -3 3 2 является линейной комбинацией первых
1 -1 1 2
8 -7 p 11
трёх строк?
Решение :
Вычислим det A:
1 2 -2
1 1 2 -2 1 -7 7 0
-7 7 0
det A = 2 -3 3 2 = 0 -7 7 0 = 3 -3 -1 = 3 -3 -1 =
1 -1 1 2 0 3 -3 -1 23 -16-p -3 14 -7-p 0
8 -7 p 11 0 23 -16-p -3
-1*(-1) 2+3
* -7 7 = 49 + 7p – 98 = 7p - 49
14 -7-p
Если det A=0 , то ранг матрицы А равен двум , т.е. 7p – 49 = 0 , p = 7.
Третья строка по теореме о базисном миноре является комбинацией первых двух .
Обозначим коэффициенты этой комбинации через λ1 и λ2 , λ3 ,тогда (8,-7,7,11) = λ1(1,2,-2,1)+ + λ2 (2,-3,3,2) + λ3 (1,-1,1,2);
Имеем систему : λ1 + 2λ2
+ λ3 = 8 * 2
2λ1- 3λ2 - λ3 = -7
-2λ1 + 3λ2 + λ3 = 7
λ1 + 2λ2 + 2λ3 = 11
Решим данную систему методом Гаусса :
λ1 + 2λ2 +
λ3 = 8 1) λ3 = 3
7λ2 + 3λ3 = 23 2) 7λ2 + 9 = 23
7λ2 + 3λ3 = 23 7λ2 = 14
λ3 = 3 λ2 = 2
3) λ1 + 2*2 + 3 =8
λ1 = 1
коэффициенты линейных комбинаций λ1 = 1 ; λ2 = 2 ; λ3 = 3 ;
Ответ : (8,-7,7,11) = 1(1,2,-2,1)+ 2(2,-3,3,2) + 3(1,-1,1,2) .
5. Относительно канонического базиса в R3 даны четыре вектора f1(1,1,1) , f2 (1,2,3) , f3 (1,3,6), x(4,7,10). Докажите, что векторы f1, f2 , f3 можно принять за новый базис в R3 . (ТР0.РП) . Найдите координаты вектора x в базисе fi .
Составим определитель из компонент векторов и f1, f2 , f3 вычислим его :
1 1 1 1 1 1
∆ = 1 2 3 = 0 1 2 =
1*(-1)1+1 * 1 2 = 5 – 4 = 1
1 3 6 0 2 5 2 5
Так как ∆ ≠ 0 , то векторы f1, f2 , f3 образуют базис трёхмерного пространства R3
Для вычисления координат вектора x в этом базисе составим систему линейных уравнений :
х1 + х2 + х3 =
4 *(-1)
х1 + 2х2 + 3х3 = 7
х1 + 3х2 + 6х3 = 10
х1 + х2 + х3
= 4
х2 + 2х3 =
3 *(-2)
2х2 + 5х3 = 6
х1 + х2 + х3
= 4 1) х3 = 0 3) х1 + 3 +
0 = 4
х2 + 2х3 = 3 2) х2 + 0 = 3 х1 = 4 - 3
х3 = 0 х2 = 0 х1 = 1
х1 = 1 , х2 = 0 , х3 = 0 .
Решение этой системы образует совокупность координат вектора x в базисе f1, f2 , f3
x(1;3;0);
x = f1 + 3f2 + 0f3;
x = f1 + 3f2 .
Ответ : координаты вектора x (1;3;0).
6. Докажите , что система
2х1 + 2х2 +
х3 = 8,
х1 + х2 + х3 = 3,
х1 + 2х2 + 2х3 + х4 = 3,
3х2 + 2х3 +2х4 = 3
имеет единственное решение . (362).Неизвестное х2 найдите по формулам Крамера . (0М1.РЛ) . Решите систему методом Гаусса .
Решение:
Составим матрицу из коэффициентов при переменных
2 2 1 0
А = 1 1 1 0
1 2 2 1
0 3 2 2
Вычислим определитель матрицы А
2 2 1 0 2 2 1 0 2 2 1 1 1 0
∆ = 1 1 1 0 = 1 1 1 0 = (-1)3+4 * 1 1 1 = - 1 1 1 =
1 2 2 1 1 2 2 1 -2 -1 -2 0 1 0
0 3 2 2 -2 -1 -2 0
= - (-1)2+3 * 1 1
= 1
0 1
∆ ≠ 0, тогда система имеет решение х2 = ∆ х2 /∆
2 8 1 0 2 8 1
0 2 8 1 2 8 1
∆ х2 = 1 3 1 0 = 1 3 1 0 = (-1)3+4 * 1 3 1 = - 1 5 0 =
1 3 2 1 1 3 2 1 -2 -3 -2 0 3 0
0 3 2
2 -2 -3 -2 0
= -(-1)1+3 * 1 5 = ( 3 + 0 ) = 3
0 8
х2 = 3 /1 = 3.
Решим систему методом Гаусса
2х1 + 2х2 +
х3 = 8 *(-2) *(-1)
х1 + х2 + х3 = 3
х1 + 2х2 + 2х3 + х4 = 3
3х2 + 2х3 +2х4 = 3
х1 + х2 +
х3 = 3
- х3 = 2
х2 + х3
+ х4 = 0 *(-3)
3х2 + 2х3 +2х4 = 3
х1 + х2 +
х3 = 3
х2 + х3 + х4 = 0
- х3 - х4 = 3
х3 = -2
1) х3 = - 2 3) х2 - 2 - 1 = 0
2) 2 - х4 = 3 х2 = 3
х4 = -1 4) х1 + 3 - 2 = 3
х1 = 2
Проверка :
2 + 3 – 2 =3, 3 = 3
4 + 3*3 – 2 = 8, 8 = 8
2 + 6 – 4 – 2 = 3, 3 =3
9 – 4 – 2 = 3 , 3 = 3.
Ответ : х1 = 2 , х2 = 3 , х3 = - 2 , х4 = -1.
7. Дана система линейных уравнений
3х1 + х2 - х3
- х4 = 2,
9х1 + х2 - 2х3 - х4 = 7,
х1 - х2 - х4 = -1,
х1 + х2 - х3 -3х4 = -2.
Докажите ,что система совместна . Найдите её общее решение . (392.БЛ). Найдите частное решение , если х4 = 1 .
Доказательство :
Система линейных уравнений совместна тогда и только тогда , когда ранг основной матрицы
системы равен рангу расширенной матрицы .
Составим расширенную матрицу :
3 1 -1 -1 2
0 -2 2 8 8 0 0 1 6
7
А = 9 1 -2 -1 7 → 0 -8 7 26 25 → 0 0 3 18 21 =0
1 -1 0 -1 -1 0 -2 1 2 1 0 -2 1 2 1
1 1 -1 -3 -2 1 1 -1 -3 -2 1 1 -1 -3 -2
Первая и вторая строка пропорциональны следовательно А = 0. Поэтому ранг матрицы и расширенной матрицы равны 3 поэтому система является совместной .
Решим систему методом Гаусса :
запишем последнее уравнение на первое место :
х1 + х2 - х3
-3х4 = -2
3х1 + х2 - х3 - х4 = 2
9х1 + х2 - 2х3 - х4 = 7
х1 - х2
- х4 = -1
1 1 -1
-3 -2 1 1 -1 -3 -2 1
1 -1 -3 -2
С = 3 1 -1 -1 2 → 0 2 -2 -8 -8 → 0 2 -2 -8 -8 →
9 1 -2 -1 7 0 8 -7 -26 -25 0 0 -1 -6 -7
1 -1 0 -1 -1 0 2 -1 -2 -1 0 0 -1 -6 -7
х1 + х2 -
х3 -3х4 = -2
→ 2х2- 2х3 -8х4 = -8
- х3 -6х4 = -7.
1) х3 = 7 - 6х4
2) х2 - х3 -4х4 = -4
х2 = х3 + 4х4 - 4
х2 = 7 - 6х4 + 4х4 - 4
х2 = 3 - 2х4
3) х1 = - х2 + х3 + 3х4 - 2
х1 = - 3 + 2х4 + 7 - 6х4 + 3х4 – 2
х1 = 2 -х4 .
Получаем общее решение системы :
х1 = 2 -х4
х2 = 3 - 2х4
х3 = 7 - 6х4.
Найдём частное решение , если х4 = 1 тогда
х1 = 2 – 1 = 1;
х2 = 3 – 2*1 = 1;
х3 = 7 – 6*1 =1.
Ответ : (1;1;1;1) – частное решение .
8. Дана система линейных однородных уравнений
2х1 +3х2 -
х3 - х4 + х5 = 0,
3х1 - 2х2 - 3х3 -3х5 = 0,
х1 - 3х2 + 2х3 -5х4 -2х5 = 0.
Докажите , что система имеет нетривиальное решение . Найдите общее решение системы . Найдите какую-нибудь фундаментальную систему решений Доказательство :
Система имеет нетривиальное решение тогда и только тогда , когда ранг её матрицы меньше числа неизвестных .В этом случае ранг матрицы не больше трёх , а переменных в системе пять .
Решим систему методом Гаусса .
Запишем матрицу системы :
2 3 -1 -1 1 1
-3 2 -5 -2
А = 3 -2 3 0 -3 → 0 9 -5 9 5 │*7 →
1 -3 2 -5 -2 0 7 -3 15 3 │*(-9)
1 -3 2
-5 -2
→ 0 9 -5 9 5
0 0 -8 -72 8
х1 -3х2 +
2х3 - 5х4 -2х5 = 0
9х2 - 5х3 + 9х4 +5х5 = 0
-8х3 -72х4 +8х5 = 0
1) 8х3 = -72х4 + 8х5
х3 = - 9х4 + х5
2) 9х2 + 45х4 - 5х5 + 9х4 +5х5 = 0
9х2 + 36х4 = 0
х2= - 4х4
3) х1 +12х4 - 18х4 + 2 х5 - 5х4 -2х5 = 0
х1 - 11х4 = 0
х1 =11х4
Общее решение системы :
х1 =11х4
х2= - 4х4
х3 = - 9х4 + х5
Найдём фундаментальную систему решений , положив х4 = 1 , х5 = 0.
х1 =11*1 = 11,
х2= - 4*1 = -4,
х3 = - 9*1 + 0 = -9.
Пусть х4 = 0, х5 = 1.
х1 =11*0 = 0,
х2= - 4*0 = 0,
х3 = - 9*0 + 1 = 1.
Ответ : (11;-4;-9;1;0)
(0; 0; 1; 0; 1).
9 (3СА). Найдите площадь параллелограмма , построенного на векторах а = 2р + 3r, b = p –2r , | p | = √2 , | r | = 3, (p,^r) = 45° .
Решение :
S =| [а , b] | = | [2р + 3r , p –2r] | = | 2[p , p] - 4[p, r ] + 3[r , p] -6[r , r] |
[p , p] = 0 , [r , r] = 0 , [r , p] = - [p, r ] .
S = | 7[r , p] | = 7| r | * | p | * sinφ
S = 7 * 3 * √2 * sin 45° = 21 * √2 * √2 / 2 =21 .
Ответ :S =21 .
10 (78Т). Вычислите ПрBD[BC ,CD] , если B(6,3,3) ; C(6,4,2) ; D(4,1,4) .
Решение :
Найдём координаты векторов
BD = ( 4 – 6 , 1 – 3 , 4 – 3 ) = ( - 2 ; - 2 ; 1 ),
BC = ( 6 – 6 , 4 – 3 , 2 – 3 ) = ( 0 ; 1 ; - 1 ),
CD = ( 4 – 6 , 1 – 4 , 4 – 2 ) = ( - 2 ; - 3 ; 2 ).
Найдём векторное произведение :
i j k
[BC ,CD] = 0 1 -1 = i (2 – 3) – j (0 –2) + k (0 + 2) = - i + 2j + 2k .
-2 -3 2
Пусть [BC ,CD] = а , тогда а = ( -1 ; 2 ; 2 )
ПрBD а = ( BD , a ) /| BD |
( BD , a ) = -2*( -1 ) – 2*2 + 1*2 = 2 –4 + 2 = 0 .
ПрBD а = 0 .
Ответ : ПрBD а = 0 .
11. Линейный оператор А действует в R3 → R3 по закону Ax = (- х1 + 2х2 + x3 , 5х2 , 3х1 + 2х2 + х3 ), где х( х1, х2, х3 ) – произвольный вектор .(125.РП). Найдите матрицу А этого оператора в каноническом базисе . Докажите , что вектор х(1,0 ,3) является собственным для матрицы А .(Т56). Найдите собственное число λ0 , соответствующее вектору х . (Д25.РП). Найдите другие собственные числа , отличные от λ0 . Найдите все собственные векторы матрицы А и сделайте проверку .
Решение :
Ax = (- х1 + 2х2 + x3 ; 5х2 ; 3х1 + 2х2 + х3 )
Найдём матрицу в базисе l1 , l2 , l3
A l1 = (-1 ; 2 ;1)
A l2 = (0 ; 5 ; 0)
A l3 = (3 ; 2 ; 1)
-1 2 1
A = 0 5 0
3 2 1 .
Докажем , что вектор х = (1 ,0 ,3) является собственным для матрицы А.
Имеем
-1 2 1
1 -1 + 0 + 3 2 1
Aх = 0 5 0 * 0 = 0 + 0 + 0 = 0 = 2 * 0
3 2 1 3 3 + 0 + 3 6 3 .
Отсюда следует , что вектор х = (1 ,0 ,3) собственный и отвечает собственному числу λ = 2 .
Составляем характеристическое уравнение :
-1 – λ 2 1
0 5 – λ 0 = 0
3 2 1 – λ
(5 – λ)*((-1 – λ)*(1 – λ) – 3) = 0
5 – λ = 0 или λ2 –1 – 3 = 0
λ2 = 4
λ = ±2
λ1 = 2 , λ2 = -2 , λ3 = 5 .
Запишем систему для определения собственного вектора, отвечающего собственному числу λ = -2.
х1 + 2х2 +
х3 = 0 х2 = 0
7х2 = 0
3х1 + 2х2 + 3х3 = 0
х1 + х3 = 0
х1 = -х3
3х1 + 3х3 = 0
Пусть х3 = 1 ,тогда х1 = -1 , имеем собственный вектор х1 = (-1 ;0 ;1) .
Проверка :
-1 2 1 -1 1 + 0 + 1 2 -1
A = 0 5 0 * 0 = 0 + 0 + 0 = 0 = -2 * 0
3 2 1 1 -3 + 0 + 1 -2 1
Следовательно , х1 = (-1 ;0 ;1) собственный вектор и отвечает собственному числу λ = -2.
Найдём собственный вектор для λ = 5
-6х1 + 2х2 + х3 =
0
3х1 + 2х2 - 4х3 = 0
-9х1 + 5х3 = 0
х1 = 5/9 х3
-6*(5/9 х3) + 2х2 + х3 = 0
-10/3 х3 + х3 + 2х2 = 0
2х2 = 7/3 х3
х2 = 7/6 х3 .
Пусть х3 = 18 , тогда х1 = 10 , х2 = 21 .
Вектор х2 = (10 ;21 ;18) собственный вектор .
Проверка
-1 2 1 10 -10 + 42 + 18 50 10
A = 0 5 0 * 21 = 0 + 105 + 0 = 105 = 5 * 21
3 2 1 18 30 + 42 + 18 90 18 .
Следовательно , х2 = (10 ;21 ;18) собственный и отвечает собственному числу λ = 5 .
Ответ : матрица в каноническом базисе : -1 , 2 , 1 : 0 , 5 , 0 : 3 , 2 , 1; вектор х = (1 ,0 ,3) собственный и отвечает собственному числу λ = 2 , х1 = (-1 ;0 ;1) собственный вектор и отвечает собственному числу λ = -2 , х2 = (10 ;21 ;18) собственный и отвечает собственному числу λ = 5 .
12(Д01.РП).Составьте общее уравнение прямой , проходящей через точку М(1,4) параллельно прямой 2х + 3y + 5 = 0.
Решение :
Найдём угловой коэффициент прямой 2х + 3y + 5 = 0.
3y = -2x –5
y = -2/3 x – 5/3
κ = -2/3
Так как исходная прямая параллельна данной , то её угловой коэффициент равен κ = -2/3 .
Уравнение прямой имеющей угловой коэффициент κ и проходящей через точку М(х0,y0) записывается в виде
y – y0 = κ(x – x0).
Имеем
y – 4 = -2/3 (x – 1)
3y – 12 = -2x + 2
2х + 3y - 14 = 0.
Ответ : 2х + 3y - 14 = 0 – уравнение искомой прямой .
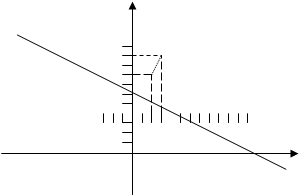
13(3А2.РП).Найдите координаты проекции точки М(3,6) на прямую х + 2y – 10 = 0.
Решение :
Пусть N – проекция точки М на данную прямую .
Составим уравнение прямой MN угловой коэффициент заданной прямой х + 2y – 10 = 0 равен κ1 = -1/2 , тогда угловой коэффициент прямой MN равен κ2 = 2 .
Тогда уравнение MN имеет вид y – y0 = 2(x – x0) .
Для определения координат точки N решим систему уравнений
х + 2y – 10 = 0
y – y0 = 2(x – x0) , x0 = 3 , y0 = 6 .
х + 2y – 10 = 0 2х + 4y – 20 = 0
y – 6 = 2(x – 3) -2х + y = 0
4y = 20
y = 4
2х = y
х = ½ y
х = ½ * 4 = 2
х = 2 .
 |
|||
 |
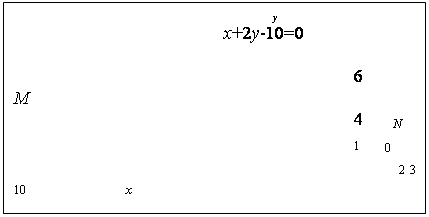
Ответ : координаты проекции точки М(3,6) на прямую х + 2y – 10 = 0 N(2,4).
14(103.БЛ). Запишите общее уравнение плоскости , походящей через три заданные точки M1(-6,1,-5) , M2(7,-2,-1) , M3(10,-7,1) .
Решение :
Уравнение плоскости , проходящей через 3 точки имеет вид
x-x1 y-y1 z-z1
x2-x1 y2-y1 z2-z1 = 0
x3-x1 y3-y1 z3-z1
x-6 y-1 z+5
7+6 -2-1 -1+5 = 0
10+6 -7-1 1-5
x-6 y-1 z+5
13 -3 4 = 0
16 -8 -4
(x –6)* -3 4 - (y – 1)*
13 4 + (z + 5)* 13 -3 = (x –6)*(12+32) – (y – 1)*(-52-64)+
-8 -4 16 -4 16 -8
+ (z + 5)*(-104+48) = 0
(x –6)*44 - (y – 1)*(-116) + (z + 5)*(-56) = 0
11*(x –6) + 29*(y – 1) – 14*(z + 5) = 0
11x – 66 + 29y – 29 – 14z – 70 = 0
11x + 29y – 14z – 165 = 0 .
Ответ : общее уравнение плоскости 11x + 29y – 14z – 165 = 0 .
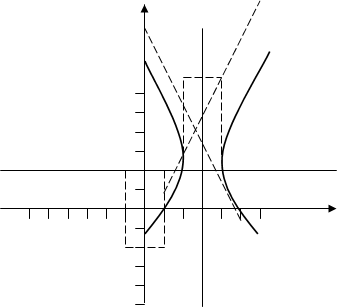
15.Дана кривая 4x2 – y2 – 24x + 4y + 28 = 0 .
8.1.Докажите , что эта кривая – гипербола .
8.2 (325.Б7).Найдите координаты её центра симметрии .
8.3 (Д06.РП).Найдите действительную и мнимую полуоси .
8.4 (267.БЛ). Запишите уравнение фокальной оси .
8.5. Постройте данную гиперболу .
Решение :
Выделим полные квадраты
4(x2 – 6x + 9) – 36 – (y2 – 4y + 4) + 4 + 28 = 0
4(x – 3)2 – (y – 2)2 – 4 = 0
4(x – 3)2 – (y – 2)2 = 4
((x – 3)2/1) – ((y – 2)2/4) = 1
Положим x1 = x – 3 , y1 = y – 2 , тогда x12/1 – y12/4 =1 .
Данная кривая является гиперболой .
Определим её центр
x1 = x – 3 = 0 , x = 3
y1 = y – 2 = 0 , y = 2
(3 ; 2) - центр .
Действительная полуось a =1 .
Мнимая полуось b =2 .
Уравнение асимптот гиперболы
y1 = ± b/a x1
(y – 2) = (± 2/1)*(x – 3)
y –2 = 2x – 6 и y – 2 = -2(x – 8)
2x – y – 4 = 0 2x + 2y – 8 = 0
x + y – 4 = 0 .
Определим фокусы гиперболы
F1(-c ; 0) , F2(c ; 0)
c2 = a2 + b2 ; c2 = 1 + 4 = 5
c = ±√5
F1(-√5; 0) , F2(√5 ; 0).
F1′(3 - √5; 2) , F2′ (3 + √5; 2).
Уравнение F1′ F2′ (x – 3 + √5) / (3 + √5 – 3 + √5) = (y – 2) /(2 – 2) ; y = 2
 |
|||
 |
Ответ: (3 ; 2) , действительная полуось a =1 , мнимая полуось b =2, (x – 3 + √5) / (3 + √5 – 3 + √5) = (y – 2) /(2 – 2) ; y = 2 .
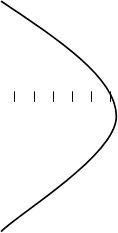
16.Дана кривая y2 + 6x + 6y + 15 = 0.
16.1.Докажите , что эта кривая – гипербола .
16.2(058.РП). Найдите координаты её вершины .
16.3(2П9). Найдите значения её параметра p .
16.4(289.РП). Запишите уравнение её оси симметрии .
16.5.Постройте данную параболу .
Решение :
Выделим полный квадрат при переменной y
(y2 + 6y + 9) + 6x + 6 = 0
(y + 3)2 = - 6(x + 1) .
Положим y1 = y + 3 , x1 = x + 1 .
Получим
y12 = ±6x1 .
Это уравнение параболы вида y2 = 2px , где p = -3 .
Данная кривая является гиперболой .
Так как p<0 , то ветви параболы в отрицательную сторону. Координаты вершины параболы y + 3 = 0 x + 1 = 0
y = -3 x = -1
(-1 ; -3) – вершина параболы .
Уравнение оси симметрии y = -3.
 |
|||||||||||||
 |
|||||||||||||
 |
|
 |
|
|
|||||||||
 |
||
 |
Ответ : (-1 ; -3) – вершина параболы , p = -3 , уравнение оси симметрии y = -3 .