Реферат: Конечные разности. Погрешности
Реферат
«Конечные разности. Погрешности»
1. Погрешности
1.1 Действительные и конечно-разрядные числа
Представление действительных чисел в вычислительных машинах с фиксированной разрядной сеткой влечет появление инструментальной погрешности в обрабатываемых числах и результатах арифметических действий.
Принятое при вводе преобразование исходных действительных чисел в нормализованную экспоненциальную форму и размещение их в ограниченной разрядной сетке ЭВМ с порядком и дробной частью (мантиссой) в общем случае вносит в этот операнд относительную инструментальную погрешность, величина которой не превышает
где n – число значащих дробных двоичных разрядов, отведенных для хранения мантиссы.
Приближенное
конечно-разрядное число a – это действительное число, занимающее заданное
количество разрядов и округленное до числа с ближайшим значением достоверного
младшего разряда. Приближенные действительные числа имеют абсолютную 
и относительную 
погрешности. Эти
погрешности при анализе распространения ошибки при вычислениях приписываются к приближенному
числу результата и связываются между собой следующим образом:
Если число a = 5,3812
имеет все разряды достоверные, то его абсолютная погрешность принимается
равной половине единицы младшего разряда, т.е. =0.00005,
а относительная погрешность, округляемая обычно до одного-двух значащих
достоверных разрядов, будет 
Всякие арифметические операции с операндами, представленными в системе с плавающей точкой, в общем случае вносят в результат аналогичную относительную инструментальную погрешность:
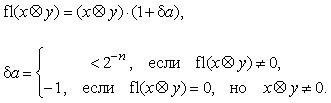
где fl(•) – указание на арифметику с плавающей точкой,
– арифметическая
операция из множества 
.
Значение результата, равное нулю принудительно устанавливается в машинах при операциях умножения с двумя операндами, приводящее к исчезновению порядка (отрицательный порядок по модулю не умещается на отведенном для него количестве разрядов).
Несколько иначе обстоит дело при вычитании чисел с плавающей точкой и одинаковым порядком:
,
.
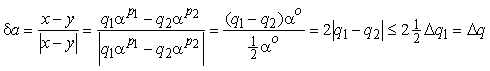Из последнего можно
заключить, что для операции вычитания относительная погрешность численно
определяется количеством значащих разрядов в результате, которое из-за
выполнения нормализации не может быть меньше 
.
Т.е. погрешность приближается к 100% последовательно. Это предупреждение
адресуется составителям вычислительных алгоритмов, которым необходимо
выискивать эквивалентные формулы с контролем величины операндов, в определенных
ситуациях можно использовать программный переход к вычислениям с удвоенной
точностью.
При выполнении аддитивных операций с приближенными операндами погрешность результата равна сумме абсолютных погрешностей всех чисел, участвовавших в операции. Выполнение мультипликативных операций вносит в результат относительную погрешность, равную сумме относительных погрешностей каждого из операндов.
1.2 Погрешность алгоритмов
Инструментальные погрешности арифметических машинных команд из-за различия и непредсказуемости величины ошибки результата нарушают дистрибутивный, ассоциативный и коммутативный законы арифметики. Каждый же программист, составляя программу, уже на уровне интуиции пользуется ими, как незыблемыми. Отсюда различие в точности тех или иных вычислительных алгоритмов и трудно уловимые ошибки.
Проследить накопление вычислительной
погрешности алгоритма для операндов, которые имеют производные, удобно, если результат
r каждой двуместной арифметической операции умножать на множитель 
с последующим разложением
результирующей функции алгоритма по степеням этого множителя или этих
множителей, если 
в группах
операторов отличаются по величине. Например, для алгоритма вычисления значения
полинома 
третьей степени по схеме
Горнера с псевдокодом:
P:=0; j:=3;
repeat
S:=a[j]*x+a [j-1];
P:=P+S*x;
j:=j-1;
until j=1;
функция алгоритма будет:
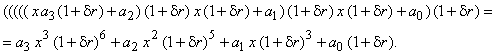
Учитывая, что 
, последнее выражение дает
возможность после раскрытия скобок выделить из суммы и оценить сначала
абсолютную погрешность, а по абсолютной погрешности – относительную:
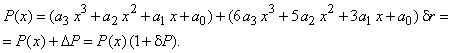
Условные арифметические
операторы с проверкой равенства операндов необходимо заменять проверкой вида: 
.
2. Конечные разности
2.1 Определение конечных разностей
Конечная разность «вперед»
для таблично заданной функции в i-той точке определяется выражением: 
, где функция 
задана, как функция
целочисленного аргумента с единичным шагом по аргументу i.
Для аналитически заданной
и протабулированной с постоянным шагом h функции 
определяющее соотношение
имеет вид:
.
Преобразование таблицы
функции в функцию целочисленного
аргумента осуществляют при помощи
линейного соотношения между аргументами x и i: 
.
Коэффициенты a и b
находят из системы уравнений, получаемой в результате подстановки в пределах
заданной таблицы вместо x и i сначала начальных значений
аргументов 
, а затем конечных 
. При этом начало таблицы
удобно совместить с началом координат функции с целочисленным аргументом
(
). Тогда для таблицы с (n+1) –
й строками:
,
Повторные конечные
разности n-го порядка в i-той точке для табличной функции определяются соотношением
.
2.2 Конечно-разностные операторы
Линейность
конечно-разностного оператора 
позволяет
ввести конечно-разностный оператор сдвига 
и
многочлены от оператора с
целыми коэффициентами, такие, как 
, где 
должно рассматриваться как
оператор повторной разности k-того порядка.
Действие любого
многочлена 
на функцию g(i)
определяется как
.
Применение оператора сдвига к g(i) преобразует последнее в g (i+1):
g (i+1)
= E g(i) = (1+) g(i)=
g(i) + g(i).
Повторное применение оператора сдвига позволяет выразить (i+n) – е значение ординаты функции g через конечные разности различных порядков:
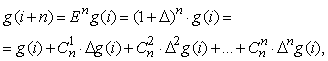
где 
– число сочетаний из n
элементов по k;
– многочлен степени k
от целой переменной n (
),
имеющий k сомножителей. При k=n 
.
В силу линейности
оператора сдвига можно конечно-разностный оператор выразить, как 
, и определить повторные
конечные разности через многочлены от операторов сдвига так 
.
Последнее позволяет формульно выражать n-ную повторную разность через (n+1) ординату табличной функции, начиная с i-той строки:
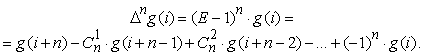
Если в выражении для g
(i+n) положить i=0 и вместо 
подставить
их факториальные представления, то после несложных преобразований получится разложение
функции целочисленного аргумента по многочленам 
,
которые в литературе называют факториальными:
.
Можно поставить задачу
разложения и функции действительной переменной f(x) по
многочленам 
относительно начала
координат (аналогично ряду Маклорена), т.е. 
.
Если последовательно находить конечные разности от левой и правой частей, то,
зная, что 
и 
, после подстановки x=0
будем получать выражения для коэффициентов разложения 
. У многочленов k-той
степени, 
, поэтому
.
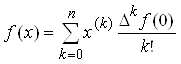Такое разложение табличной функции f(x) в литературе называют интерполяционным многочленом Ньютона для равных интервалов.
2.3 Взаимосвязь операторов разности и дифференцирования
Значение функции на
удалении h от некоторой точки 
можно
выразить через значения производных в этой точке, разложив ее в ряд Тейлора:
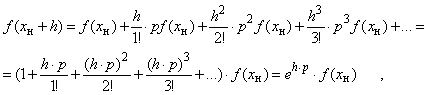
где 
– оператор
дифференцирования,
– оператор сдвига,
выраженный через оператор p.
h – шаг по оси действительной переменной
Из равенства операторов
сдвига, выраженных через p и , можно
получить взаимосвязь этих линейных операторов:
,
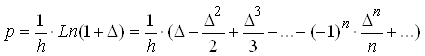Оператор дифференцирования порядка n, перенесенный в точку, удаленную от текущей, например, на 2 шага вперед представляется так:
.
Выполнив алгебраическое
перемножение многочленов с конечно-разностными операторами и ограничившись
операторами со степенью не выше n, получим одну из возможных
аппроксимаций оператора дифференцирования. Действуя таким сложным конечно-разностным
оператором на ординату f(x), получаем формулу для
вычисления n-й производной в точке 
по
значениям ее конечных разностей. Например, для n=2, отбрасывая все
повторные разности выше третьего порядка, получим:
.
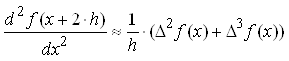Если f(x) является многочленом степени n, то повторные разности (n+1) – го порядка тождественно равны нулю. Приравнивая нулю повторные разности порядков выше n мы фактически аппроксимируем f(x) многочленом степени n.
В предыдущем выражении, выразив повторные разности через ординаты табличной функции, получим еще один вид формулы для вычисления значения производной:
.
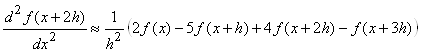Для целочисленного
аргумента табличной функции запись выражения можно упростить, если положить h=1
и 
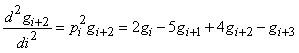
2.4 Исчисление конечных разностей
Разложение функций в ряд по факториальным многочленам (интерполяционным многочленам Ньютона в частности) дает возможность получать формулы суммирования функциональных рядов в виде аналитических выражений, зависящих от пределов. Эта возможность открывается в связи с тем, что суммировать конечные разности не представляет большой сложности, а выразить конечную разность от факториального многочлена через факториальный же многочлен можно, воспользовавшись соотношением:
Факториальные многочлены по отношению к исчислению разностей ведут себя так же, как степенные функции в исчислении производных: дифференцирование тоже понижает степень многочлена на единицу. Это свойство позволяет в факториальном разложении заменить факториальные многочлены своими конечными разностями следующего вида:
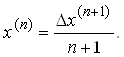
Замена хороша тем, что суммирование конечных разностей в заданных пределах мнемонически весьма напоминает вычисление определенного интеграла от функции по ее первообразной:
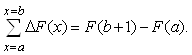
Если 
, то
.
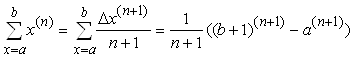Процедуру суммирования
функционального ряда продемонстрируем на примере получения суммы квадратов
натурального ряда чисел в пределах от a=1 до b=5 (Для проверки: 
):
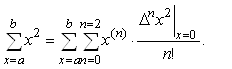
Вторая сумма по
переменной n представляет разложение 
по
факториальным многочленам, в которое входят значения конечных разностей 0, 1 и
2-го порядков, вычисленные в начале координат целочисленной переменной, т.е.
при x=0. Они соответственно равны:
,
,
.
После подстановки значений разностей во второй сумме останутся два факториальных полинома: первой и второй степеней:
Если распределить вычисление сумм по слагаемым, то мы перейдем к суммированию конечных разностей от факториальных многочленов:
Литература
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие. – М.: Наука, 1987. – 600 с.
2. Воеводин В.В. Численные методы алгебры. Теория и алгорифмы. – М.: Наука, 1966. – 248 с.
3. Воеводин В.В. Вычислительные основы линейной алгебры. – М.: Наука, 1977. – 304 с.
4. Волков Е.А. Численные методы. – М.: Наука, 1987. – 248 с.
5. Калашников В.И. Аналоговые и гибридные вычислительные устройства: Учеб. пособие. – Харьков: НТУ «ХПИ», 2002. – 196 с.
6. Вержбицкий, В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш.шк., 2001. 383 с.
7. Волков, Е.А. Численные методы. СПб.: Лань, 2004. 248 с.
8. Мудров, А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП «РАСКО», 1991. 272 с.
9. Шуп, Т.Е. Прикладные численные методы в физике и технике. М.: Высш. шк., 1990. 255 с.
10. Бахвалов, Н.С. Численные методы в задачах и упражнениях / Н.С. Бахвалов, А.В. Лапин, Е.В. Чижонков. М.: Высш. шк., 2000. 192 с.