Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления
СОДЕРЖАНИЕ
1. Анализ объекта управления
1.1 Анализ линейного стационарного объекта управления, заданного передаточной функцией
1.2 Получение математической модели в пространстве состояний линейного стационарного объекта управления, заданного передаточной функцией
1.2.1 Матрица Фробениуса
1.2.2 Метод параллельной декомпозиции
2. Решение задачи быстродействия симплекс-методом
3. Оптимальная l – проблема моментов
3.1 Оптимальная l – проблема моментов в пространстве «вход-выход»
3.2 Оптимальная l – проблема моментов в пространстве состояний
4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)
5. Аналитическое конструирование оптимальных регуляторов (акор)
5.1 Стабилизации объекта управления на полубесконечном интервале времени
5.1.1 Решение алгебраического уравнения Риккати методом диагонализации
5.1.2 Решение алгебраического уравнения Риккати интегрированием в обратном времени до установившегося состояния
5.2 Стабилизации объекта управления на конечном интервале времени
5.3 Задача акор – стабилизации для компенсации известного возмущающего воздействия.
5.4 Задача акор для отслеживания известного задающего воздействия. i подход
5.5 Задача акор для отслеживания известного задающего воздействия. ii подход (линейный сервомеханизм)
5.6 Задача акор – слежения со скользящими интервалами.
6. Синтез наблюдателя полного порядка
Литература
Приложение
PlotTimeFrHaract.m
ProstranstvoSostoyanii.m
SimplexMetod2.m
Optimal_L_problem_moments.m
Gramian_Uprav.m
AKOR_stabilizaciya_na_polybeskon_interval.m
AKOR_stabilizaciya_na_konech_interval.m
Sravnenie_stabilizacii.m
AKOR_stabilizaciya_pri_vozmusheniyah.m
AKOR_slegenie_na_konech_interval_I_podxod.m
AKOR_slegenie_na_konech_interval_II_podxod.m
AKOR_slegenie_so_skolz_intervalami_Modern.m
Sintez_nablyud_polnogo_poryadka.m
Solve_Riccati_Method_Diag.m
Solve_Riccati_Method_Revers_Integr.m
Vozmyshyayushee_Vozdeistvie_Discrete_Revers.m
Zadayushee_Vozdeistvie_Discrete_Revers_Modern.m
1. Анализ объекта управления
1.1 Анализ линейного стационарного объекта управления, заданного передаточной функцией
Передаточная функция данного объекта имеет вид:
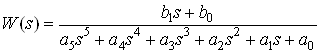 ,
,
где:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
или
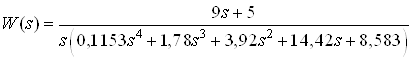 .
.
Нули передаточной функции:
![]()
Полюса передаточной функции (полученные стандартными функциями среды Matlab 7.4):
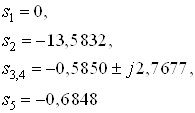
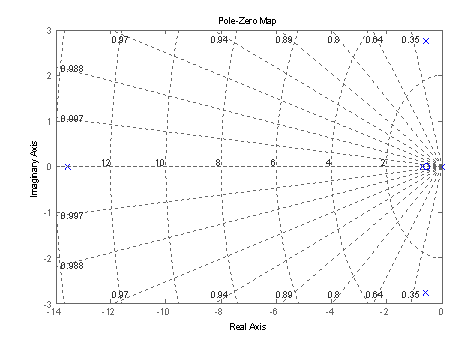
Рис.1. График расположения нулей и полюсов передаточной функции объекта на комплексной плоскости.
Найдем временные характеристики объекта управления.
К временным
характеристикам относятся ![]() и
и
![]() .
.
![]() – переходная характеристика;
– переходная характеристика;
![]() – импульсная переходная функция;
– импульсная переходная функция;
Для нахождения ![]() и
и ![]() воспользуемся пакетом Matlab 7.4.
воспользуемся пакетом Matlab 7.4.
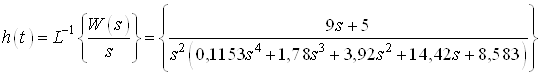 ,
,
Аналитическое выражение
для ![]() :
:
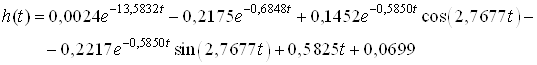
В этом случае ![]() имеет вид
имеет вид
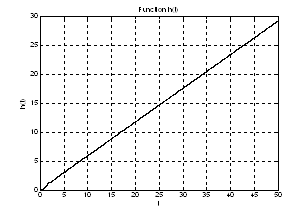
Рис.2. График переходной характеристики ![]() .
.
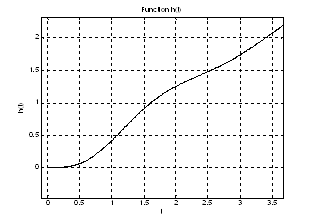
Рис.3. График переходной характеристики ![]() на интервале
на интервале ![]() (увеличенное).
(увеличенное).
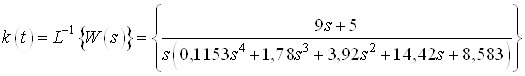 ,
,
Аналитическое выражение
для ![]() :
:
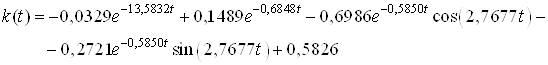 .
.
В этом случае ![]() имеет вид
имеет вид
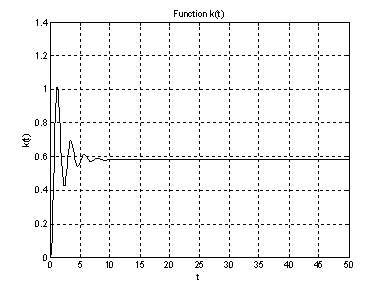
Рис.4. График импульсной переходной
характеристики ![]() .
.

Рис.5. График импульсной переходной
характеристики ![]() на интервале
на интервале ![]() (увеличенное).
(увеличенное).
Найдем частотные характеристики объекта управления.
К частотным характеристикам относятся:
амплитудно – частотная характеристика (АЧХ),
фазо – частотная характеристика (ФЧХ),
амплитудно – фазовая частотная характеристика (АФЧХ),
Аналитическое выражение для АЧХ:
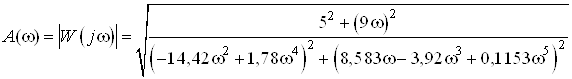 .
.
В этом случае АЧХ имеет вид
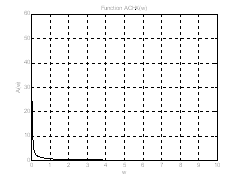
Рис.6. График АЧХ
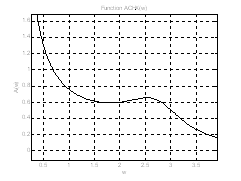
Рис.7. График АЧХ на интервале ![]() (увеличенное). Аналитическое
выражение для ФЧХ:
(увеличенное). Аналитическое
выражение для ФЧХ:

В этом случае ФЧХ имеет вид
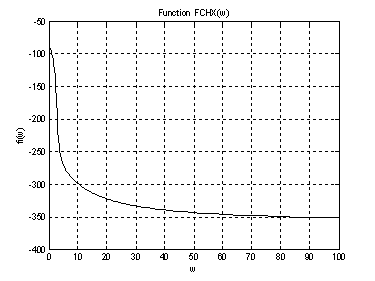
Рис.8. График ФЧХ .
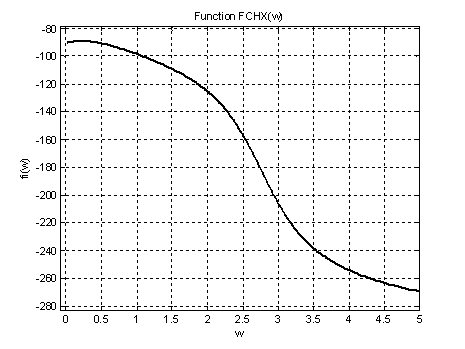
Рис.9. График ФЧХ на интервале ![]() (увеличенное).
(увеличенное).
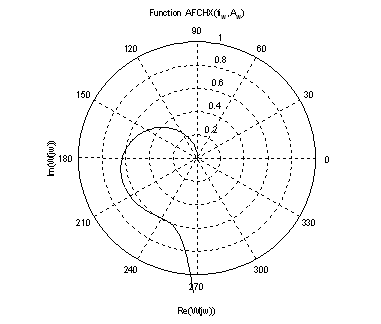
Рис.10. График АФЧХ.
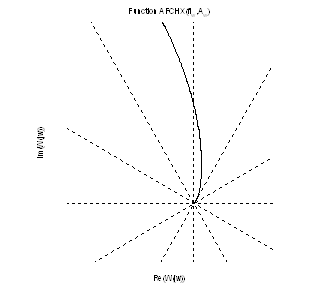
Рис.11. График АФЧХ (увеличенное).
Аналитическое выражение для ЛАЧХ:
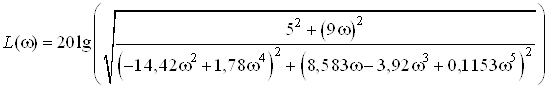 .
.
В этом случае ЛАЧХ имеет вид
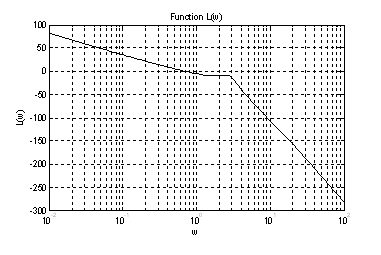
Рис.12. График ЛАЧХ.
Аналитическое выражение для ЛФЧХ:
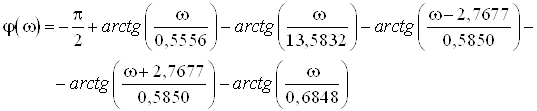
В этом случае ЛФЧХ имеет вид
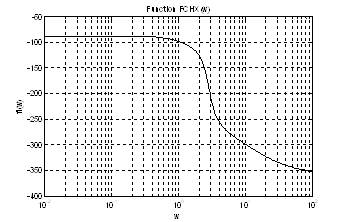
Рис.13. График ЛФЧХ.
1.2 Получение математической модели в пространстве состояний линейного стационарного объекта управления, заданного передаточной функцией
Передаточная функция данного объекта имеет вид:
![]()
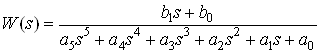 ,
,
где:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
или
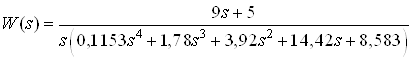
Описание системы в пространстве состояний имеет следующий вид:
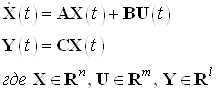
Переходя в область изображений описание системы в пространстве состояний будет иметь следующий вид:
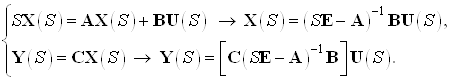
1.2.1 Матрица Фробениуса
Получим выражения, которые определяют вектор состояний и выход заданного объекта в общем виде:
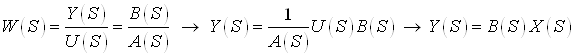 .
.
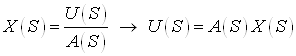 .
.
Тогда получим:
![]() (1)
(1)
![]() (2)
(2)
Числитель передаточной
функции имеет вид: ![]() .
.
Знаменатель передаточной функции:
![]() .
.
Тогда согласно равенству (1) и (2) имеем
![]() ,
,
![]() .
.
Перейдем из области изображений в область оригиналов
![]() ,
,
![]()
и затем перейдем к нормальной форме Коши


![]() .
.
Запишем матрицы состояний
 ,
, 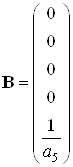 ,
, ![]()
Численное значение матриц состояний:
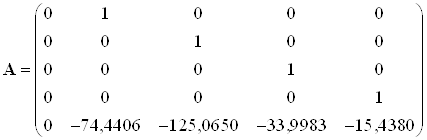 ,
,  ,
,
![]()
1.2.2 Метод параллельной декомпозиции
Запишем передаточную функцию объекта в другом виде, а именно:
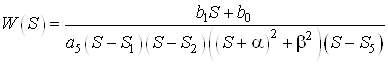
или
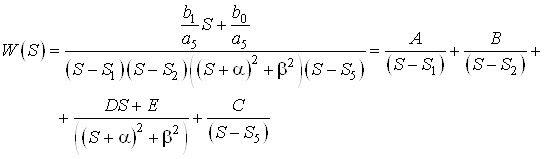 .
.
Согласно формуле ![]() получим
получим
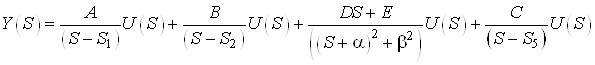
Рассмотрим каждое из слагаемых в отдельности согласно принципу параллельной декомпозиции.
a.
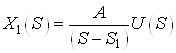 ,
,
![]() .
.
b.
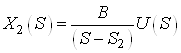 ,
,
![]() .
.
c.
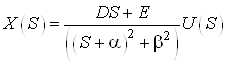 ,
,
![]() ,
,
![]() ,
,
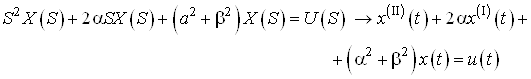
![]()
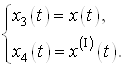
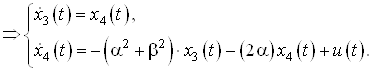
![]()
d.
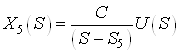 ,
,
![]()
Получим выход системы:
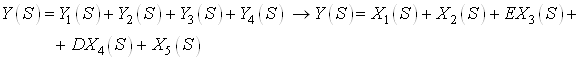
![]()
Запишем матрицы состояний
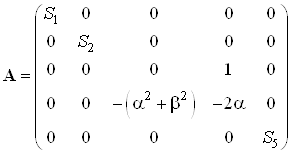 ,
, 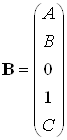 ,
, ![]()
Вычисление коэффициентов
разложения дробной рациональной функции ![]() на
сумму элементарных дробей и проверка правильности получения матриц состояния сделано
с помощью пакета Matlab 7.4 (скрипт
ProstranstvoSostoyanii.m)
на
сумму элементарных дробей и проверка правильности получения матриц состояния сделано
с помощью пакета Matlab 7.4 (скрипт
ProstranstvoSostoyanii.m)
Получены следующие результаты:Матрица СЛАУ:
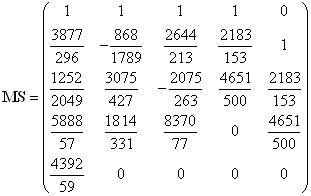 ,
, 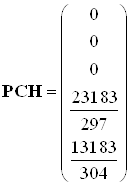 ,
,
![]() ,
,
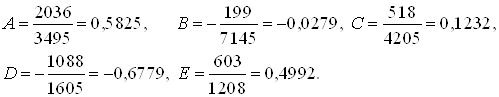
Численное значение матриц состояний:
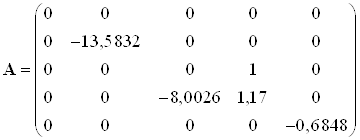 ,
,  ,
,
![]() .
.
2. Решение задачи быстродействия симплекс-методом
Дана система:
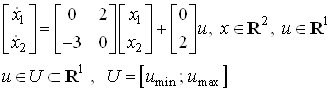 (3)
(3)
1. Проверим управляемость данной системы.
Запишем систему ДУ в матричном виде:
![]() ,
,
где 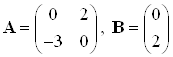 .
.
Данная система является
стационарной, её порядок ![]() ,
поэтому матрица управляемости имеет вид:
,
поэтому матрица управляемости имеет вид:
![]()
Найдем матрицу управляемости:

Ранг матрицы управляемости равен порядку системы, следовательно, данная система является управляемой.
![]() следовательно
следовательно ![]() .
.
Собственные числа матрицы
![]() найдем из уравнения
найдем из уравнения
![]() :
:
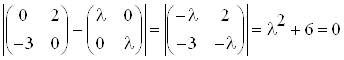
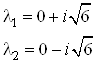
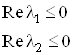
Действительные части
собственных значений матрицы ![]() являются
неположительными, следовательно, все условия управляемости выполнены.
являются
неположительными, следовательно, все условия управляемости выполнены.
2. Ссылаясь на решение задачи быстродействия из ДЗ№2 по СУЛА «Решение задачи быстродействия» имеем:
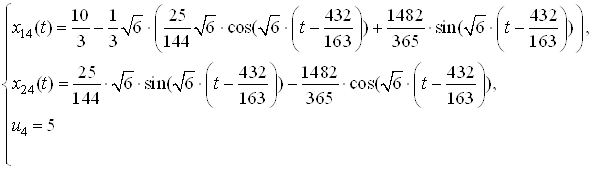
Запишем зависимости ![]() ,
, ![]() , полученные при решении
систем дифференциальных уравнений:
, полученные при решении
систем дифференциальных уравнений:
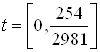 :
:
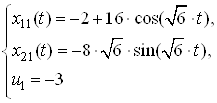
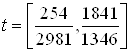 :
:

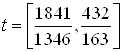 :
:
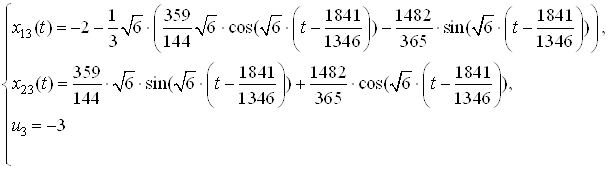
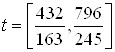 :
:
Перейдем к дискретной модели заданной системы. Имеем
![]() (4)
(4)
где ![]() шаг дискретизации и
соответствующие матрицы
шаг дискретизации и
соответствующие матрицы
 (5)
(5)
Пусть управление ограничено интервальным ограничением
![]() (6)
(6)
Тогда на ![]() шаге имеем
шаге имеем
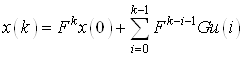 (7)
(7)
Известны начальная и конечная точки
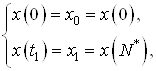
где ![]() – оптимальное число шагов в
задаче быстродействия.
– оптимальное число шагов в
задаче быстродействия.
Решается задача быстродействия
![]()
а) Формирование задачи быстродействия как задачи линейного программирования
Конечная точка ![]() в дискретной модели
представлена в виде
в дискретной модели
представлена в виде
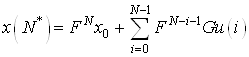 (8)
(8)
Получаем ![]() – равенств
– равенств
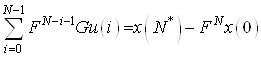 (9)
(9)
Для приведения ограничений (9) к канонической форме сделаем необходимое преобразование в правой и левой частях, чтобы правые части были неотрицательными (если правая часть меньше нуля, то домножаем на (-1) левую и правую части). Отметим проведенные изменения точкой в правом верхнем углу соответствующих векторов
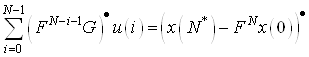 . (10)
. (10)
Для того чтобы получить
необходимый допустимый базис для задачи линейного программирования, добавим
формально остаточные искусственные переменные (![]() ).
Таким образом, уравнения (10) представляются в виде
).
Таким образом, уравнения (10) представляются в виде
 (11)
(11)
Так как текущее
управление ![]() – управление имеет любой
знак,
– управление имеет любой
знак, ![]() то сделаем необходимую
замену
то сделаем необходимую
замену
![]()
Тогда уравнения (11) примут вид
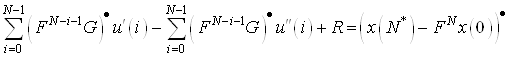 (12)
(12)
Введем остаточные переменные в ограничения на управление
![]()
![]()
 (13)
(13)
При объединении выражений
(12) и (13) получаем ![]() ограничений.
ограничений.
Начальный допустимый базис состоит из остаточных и остаточных искусственных переменных
![]()
Формируем целевую функцию (по второму методу выбора начального допустимого базиса)
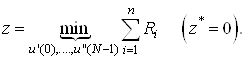 (14)
(14)
б) Решение задачи быстродействия
Предположим, что ![]() , где
, где ![]() – оптимальное число шагов.
Так как значение
– оптимальное число шагов.
Так как значение ![]() нам неизвестно
(но
нам неизвестно
(но ![]() известно точно), выбираем
некоторое начальное
известно точно), выбираем
некоторое начальное ![]() и решаем задачу
линейного программирования (12)-(14).
и решаем задачу
линейного программирования (12)-(14).
При этом
Общее число столбцов в
симплекс-таблице: ![]()
Число базисных переменных:
![]()
Сформируем ![]() строку. Имеем
строку. Имеем
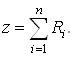
Выразим из уравнения (12)
начальные базисные переменные ![]()
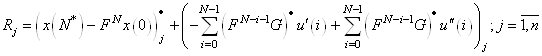
и подставим в целевую
функцию. Получим ![]() – строку
– строку
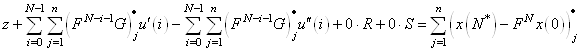 (15)
(15)
Решаем задачу (12) – (14) симплекс-методом.
В случае,
если ![]() ,
, ![]() – малое число
– малое число ![]()
иначе
1) если ![]() увеличить
увеличить ![]() и целое,рвернуться к первому
шагу формирования задачи линейного программирования;
и целое,рвернуться к первому
шагу формирования задачи линейного программирования;
2) если ![]() (не все управления будут
равны предельным, могут быть, в том числе нулевые)),
(не все управления будут
равны предельным, могут быть, в том числе нулевые)), ![]() , уменьшить
, уменьшить ![]() , вернуться к первому шагу
формирования задачи линейного программирования.
, вернуться к первому шагу
формирования задачи линейного программирования.
Решения данной задачи
получено с помощью пакета Matlab
7.4 (скрипт SimplexMetod2.m): ![]()
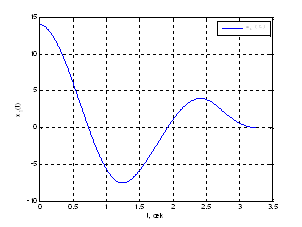
Рис. 14. График фазовой координаты ![]() .
.
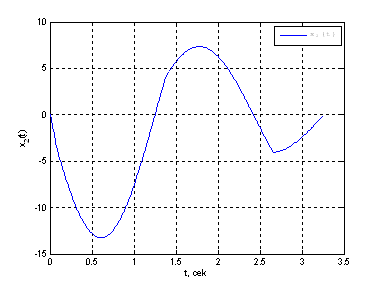
Рис. 15. График фазовой координаты ![]() .
.
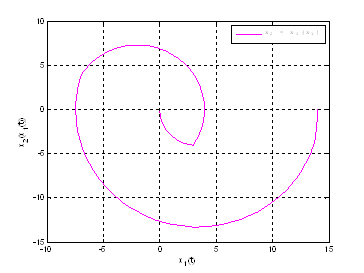
Рис. 16. График ![]() .
.
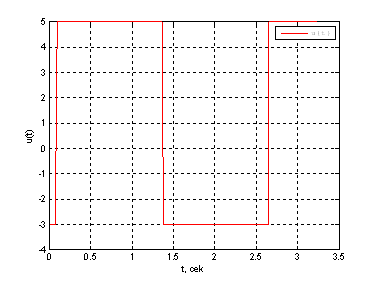
Рис. 17. График оптимального управления ![]() .
.
Выводы: Сравнивая полученные результаты с
результатами полученными в ДЗ№2 по СУЛА, можно сделать вывод, что решения
совпадают, с точностью до ![]() .
.
3. Оптимальная L – проблема моментов
Укороченная система данного объекта имеет вид:
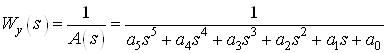 ,
,
где:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Полюса укороченной передаточной функции:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Заданы начальные и конечные условия:
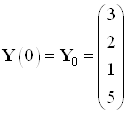 ,
,  ,
, ![]() .
.
Для
определения начальных и конечных условий для ![]() воспользуемся
следующей формулой:
воспользуемся
следующей формулой:
![]() ,
,
Где
матрица ![]() имеет следующий вид
имеет следующий вид
 ,
,
где ![]() ,
, ![]() .
.
ИПФ укороченной системы:
![]()
Составим фундаментальную систему решений:
ФСР:  .
.
Составим матрицу ![]() .
.
![]() , где
, где ![]() –
матрица Вронского
–
матрица Вронского
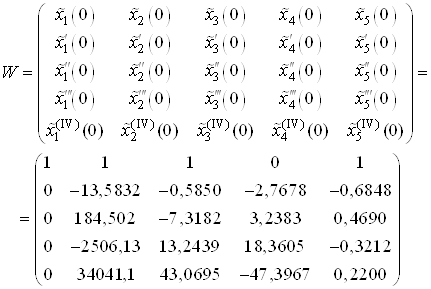
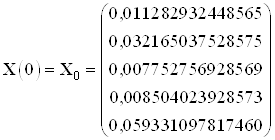 ,
,
Тогда
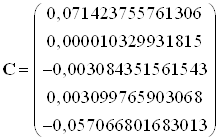 .
.
Составим моментные уравнения (связь между входом и выходом):
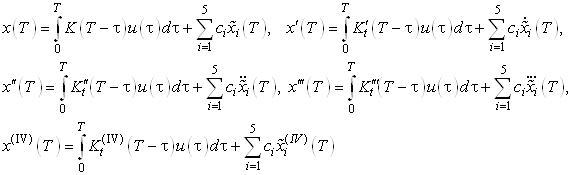
Моментные функции определяются по следующей формуле
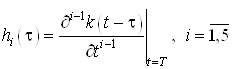
Составим моментные функции:
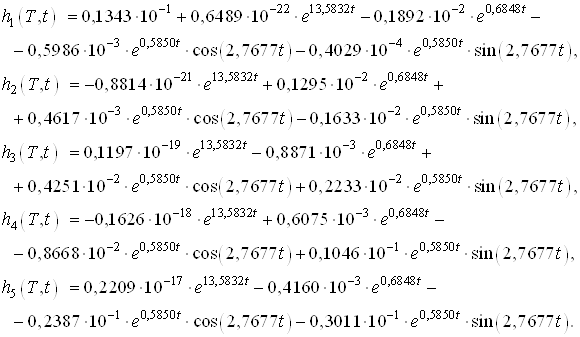
Найдем моменты по следующей формуле:
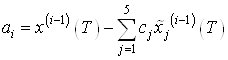 .
.
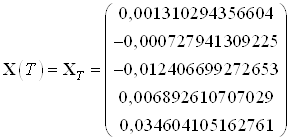
Числовое значение найденных моментов:
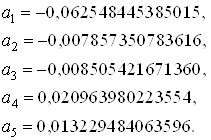
Составим функционал качества, который имеет следующий вид:
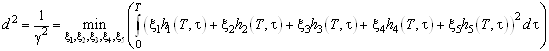
при условии, что :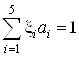 , т.е.
, т.е. ![]()
Выразим из данного
условия ![]() , тогда получим следующее
равенство:
, тогда получим следующее
равенство:
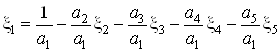 .
.
Подставляя полученное
равенство в функционал и заменяя ![]() их
правыми частями получаем
их
правыми частями получаем
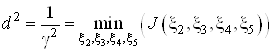
Найдем частные производные
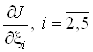 и приравняем их к нулю.
Решая полученную систему уравнений, определяем оптимальные значения
коэффициентов
и приравняем их к нулю.
Решая полученную систему уравнений, определяем оптимальные значения
коэффициентов ![]() , а
, а ![]() вычислим по формуле
вычислим по формуле
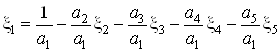 .
.
Т.о. имеем:
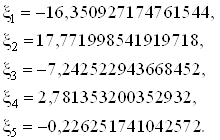
Минимальная энергия:
![]()
Найдем управление по следующей формуле:
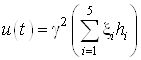
Тогда оптимальное управление
 .
.
3.2 Оптимальная L – проблема моментов в пространстве состояний
Система задана в виде:
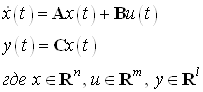
Решение ДУ имеет вид:
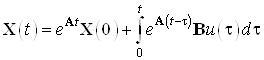 , при
, при ![]() имеем:
имеем:
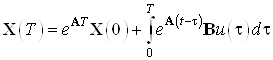 .
.
Составим моментные уравнения:
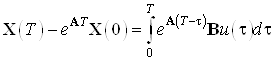
![]()
Подставляя необходимые данные в выше приведенные формулы, получим следующие моменты и моментные функции:
Числовое значение найденных моментов:
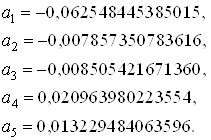
Моментные функции:
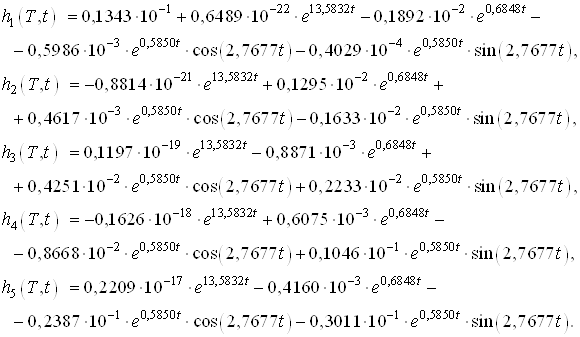
Заметим, что моменты и моментные функции совпадают с моментами и моментными функциями, найденными в пункте (а).
Из этого следует,
что функционал, значения ![]() ,
управление и минимальная энергия будут иметь точно такие же числовые значения и
аналитические выражения, как и в пункте (3.1).
,
управление и минимальная энергия будут иметь точно такие же числовые значения и
аналитические выражения, как и в пункте (3.1).
Оптимальное управление имеет вид:
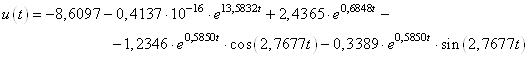
Проверим правильность полученного решения.
Эталонные значения координат в начальный и конечный момент времени:
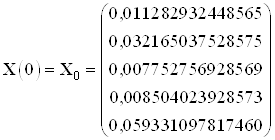 ,
, 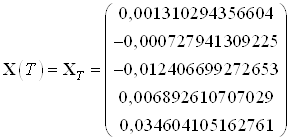
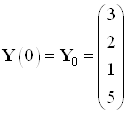 ,
, 
Найденные значения координат в начальный и конечный момент времени:
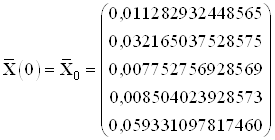 ,
, 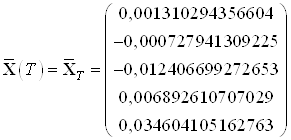
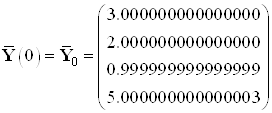 ,
, 
Вычислим погрешность полученных результатов:
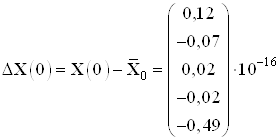 ,
, 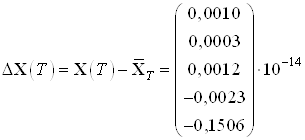
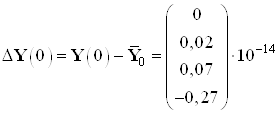 ,
, 
Ниже представлены графики полученного решения с помощью скрипта Optimal_L_problem_moments.m.
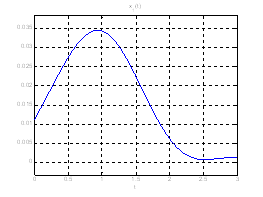
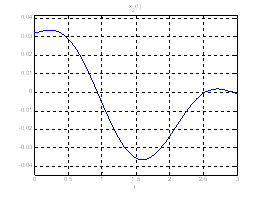
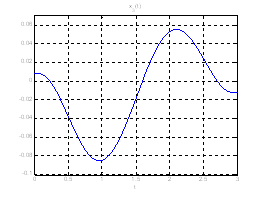
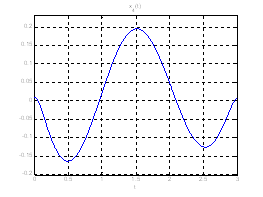
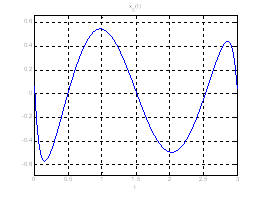
Рис. 18. Графики фазовых координат системы при переходе из ![]() в
в ![]() .
.
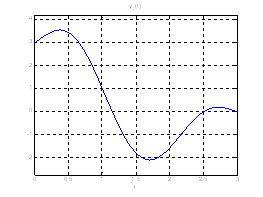
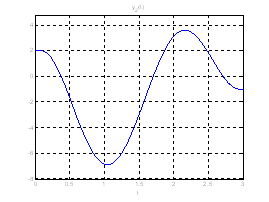
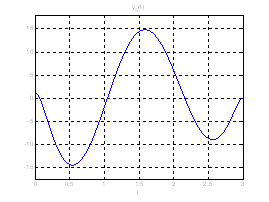
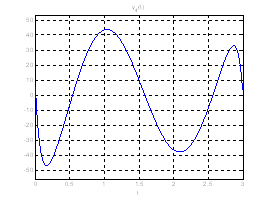
Рис. 19. Графики выходных координат системы при переходе из ![]() в
в ![]() .
.
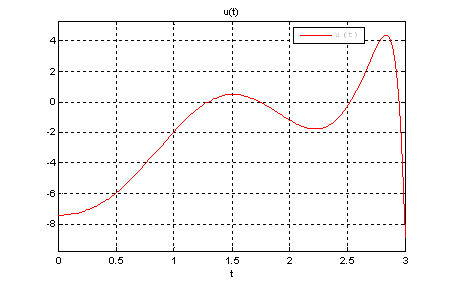
Рис.20. График оптимального управления ![]() .
.
Выводы: Задача перевода системы из начальной точки в конечную с помощью L-проблемы моментов в пространстве состояний и в пространстве вход-выход была решена с точностью до 12-го знака после запятой. Результаты, полученные при переводе системы из начальной точки в конечную, полностью совпадают.
4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)
Система имеет вид:
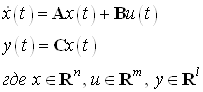
с начальными условиями:
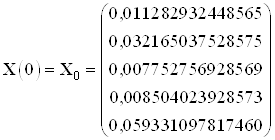 ,
, 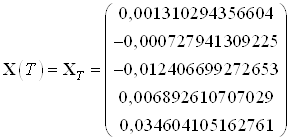
![]() .
.
Составим матрицу управляемости и проверим управляемость системы:
![]()

![]() .
.
Составим грамиан управляемости для данной системы:
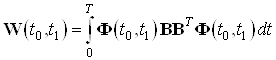
Найдем грамиан по формуле:
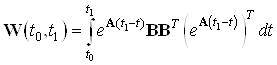

Тогда управление имеет вид:
![]() .
.
или
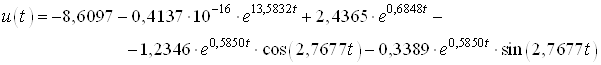
Ниже представлен график оптимального управления полученного с помощью скрипта Gramian_Uprav.m.:
Рис.21. График оптимального управления ![]() .
.
Графики фазовых координат аналогичны, как и в оптимальной L – проблеме моментов.
Сравним управление, полученное в начальной и конечной точках в пунктах 3 и 4 соответственно:
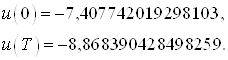 и
и 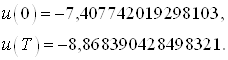
Выводы: Как видно, значения граничных управлений совпадают. А это значит, что задача перевода объекта из начального состояния в конечное решена с высокой степенью точности и с минимальной энергией.
Графическое сравнение оптимальных управлений из пунктов 3 и 4:
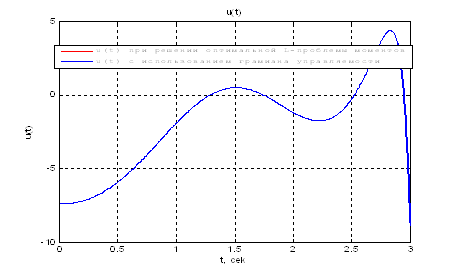
Рис.21. Сравнение графиков оптимального
управления ![]() .
.
5. Аналитическое конструирование оптимальных регуляторов (АКОР)
Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме
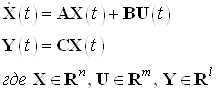
Необходимо получить закон управления
![]()
минимизирующий функционал вида
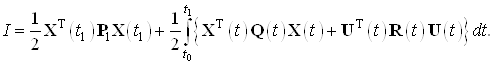
Начальные условия для заданной
системы ![]()
Моменты времени ![]() фиксированы. Матрицы
фиксированы. Матрицы ![]() — симметричные неотрицательно
определенные:
— симметричные неотрицательно
определенные:
![]()
матрица ![]() —
положительно определенная:
—
положительно определенная:
![]()
Матричное дифференциальное уравнение Риккати имеет вид:
![]()
Если линейная стационарная
система является полностью управляемой и наблюдаемой, то решение
уравнения Риккати при ![]() стремится к
установившемуся решению
стремится к
установившемуся решению ![]() не
зависящему от
не
зависящему от ![]() и определяется
следующим алгебраическим уравнением:
и определяется
следующим алгебраическим уравнением:
![]()
В рассматриваемом случае
весовые матрицы ![]() и
и ![]() в функционале не зависят
от времени.
в функционале не зависят
от времени.
Оптимальное значение функционала равно
![]()
и является квадратичной функцией от начальных значений отклонения вектора состояния.
Таким образом, получаем,
что при ![]() оптимальное управление
приобретает форму стационарной обратной связи по состоянию
оптимальное управление
приобретает форму стационарной обратной связи по состоянию
![]()
где ![]() —
решение алгебраического матричного уравнения Риккати.
—
решение алгебраического матричного уравнения Риккати.
5.1.1. Решение алгебраического уравнения Риккати методом диагонализации
Для решения данной задачи
найдем весовые матрицы ![]() и
и ![]() :
:
Выберем произвольно ![]() , тогда
, тогда

Взяв значения ![]() из решения задачи L – проблемы моментов получим:
из решения задачи L – проблемы моментов получим:


Матрицы системы имеют вид:
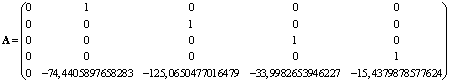
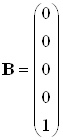 ,
, ![]() .
.
Введем расширенный вектор
состояния 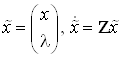 .
.
Тогда матрица Z будет иметь следующий вид: 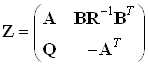 ,
,
или в численном виде
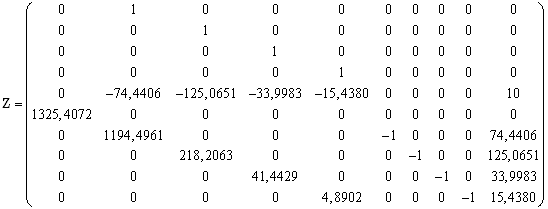 .
.
Собственные значения матрицы
![]() :
:  .
.
Зная собственные значения
и собственные вектора матрицы Z,
построим матрицу ![]()
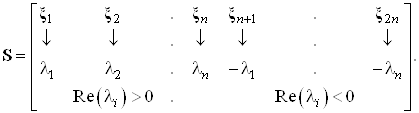
По определению все
решения должны быть устойчивы при любых начальных условиях ![]() , т.е. при
, т.е. при ![]() . Чтобы не оперировать
комплексными числами, осуществим следующий переход. Пусть:
. Чтобы не оперировать
комплексными числами, осуществим следующий переход. Пусть:

Тогда матрица ![]() формируется следующим
образом:
формируется следующим
образом:
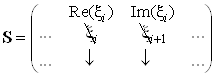 .
.
Можно показать, что матрицу можно получить из прямой матрицы собственных векторов:
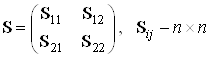 ,
,
![]() .
.
Установившееся решение уравнения Риккати, полученное с помощью скрипта Solve_Riccati_Method_Diag.m. имеет вид:
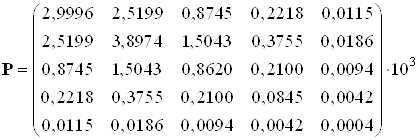
5.1.2 Решение алгебраического уравнения Риккати интегрированием в обратном времени до установившегося состояния
Весовые матрицы ![]() и
и ![]() такие же как и в пункте
(5.1.1).
такие же как и в пункте
(5.1.1).
Матрицы ![]() тоже аналогичны.
тоже аналогичны.
Запишем уравнение Риккати
![]() .
.
Зная, что ![]() , решаем уравнение методом
обратного интегрирования на достаточно большом интервале (примерно 10 с.),
получим установившееся решение с помощью скрипта
, решаем уравнение методом
обратного интегрирования на достаточно большом интервале (примерно 10 с.),
получим установившееся решение с помощью скрипта
Solve_Riccati_Method_Revers_Integr.m.:
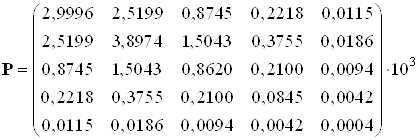
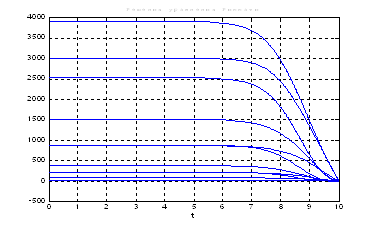
Рис.22. Графики решения уравнения Риккати.
Найдем разницу между решениями уравнения Риккати в пунктах 5.1.1 и 5.1.2:
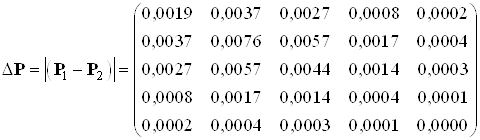
Выводы: сравнивая решения полученные в пунктах 5.1.1 и 5.1.2 можно сказать, что решения уравнения Риккати первым и вторым методами совпадают с заданной точностью. Погрешность расхождения решений невелика.
Используя скрипт AKOR_stabilizaciya_na_polybeskon_interval.m получим коэффициенты регулятора, фазовые координаты системы и управление.
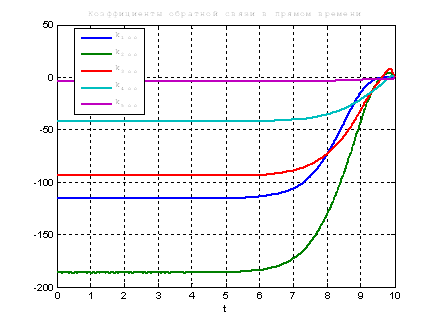
Рис.23. Графики коэффициентов регулятора обратной связи.
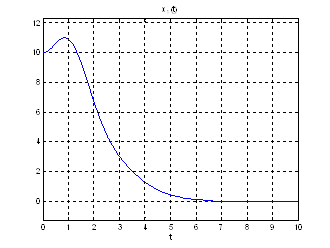
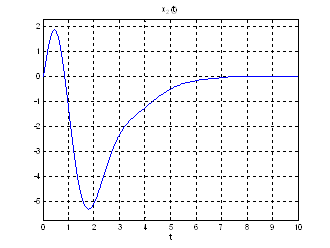
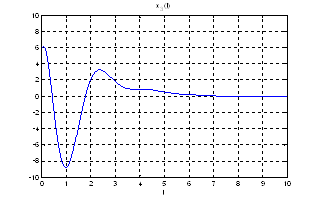
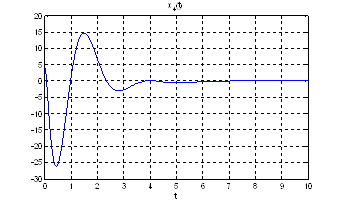
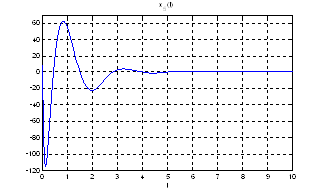
Рис.24. Графики фазовых координат.
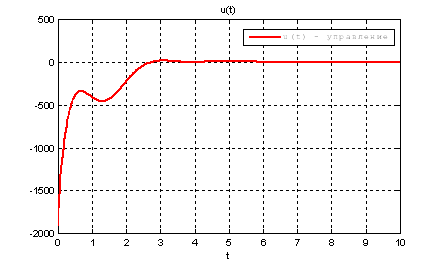
Рис.25. График управления.
Выводы: т.к. решения уравнения Риккати методом диагонализации и интегрирования в обратном времени дают практически одинаковый результат, то можно считать, что задача АКОР – стабилизации на полубесконечном интервале решена с заданной точностью.
5.2 Стабилизации объекта управления на конечном интервале времени
Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме
Начальные условия для заданной
системы ![]()
Время стабилизации ![]() .
.
Необходимо получить закон управления
![]()
минимизирующий функционал вида
Закон оптимального управления в данной задаче имеет вид
![]()
Матричное дифференциальное уравнение Риккати будет иметь следующий вид:
![]()
Если
обозначить ![]() то можно записать
то можно записать
![]()
Уравнение замкнутой скорректированной системы примет вид
![]()
Матрицы ![]() заданы
в пункте 5.1.1.
заданы
в пункте 5.1.1.
Весовые матрицы ![]() и
и ![]() имеют следующий вид:
имеют следующий вид:
 ,
, ![]() .
.
Используя скрипт AKOR_stabilizaciya_na_konech_interval.m получили следующие результаты:
Рис.26. Графики решения уравнения Риккати.
Рис.27. Графики коэффициентов регулятора обратной связи.
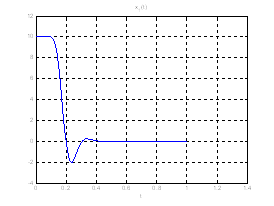
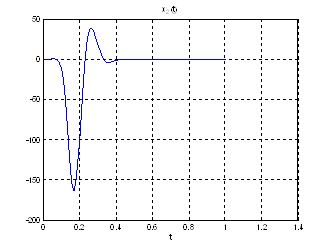
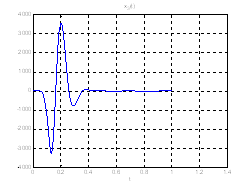

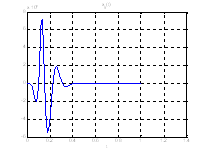
Рис.28. Графики фазовых координат.
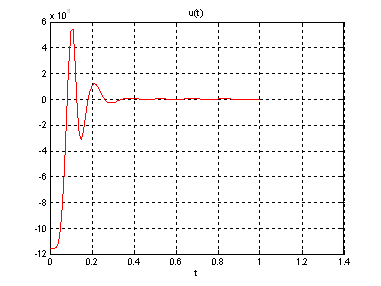
Рис.29. График управления.
Сравним, как стабилизируется система управления с постоянными и переменными коэффициентами регулятора обратной связи на начальном этапе:
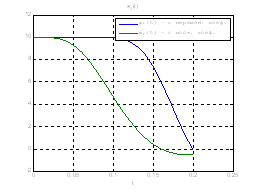
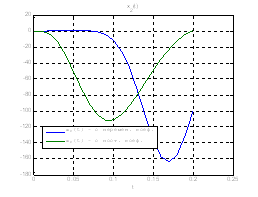
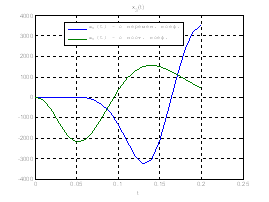
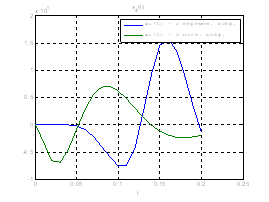
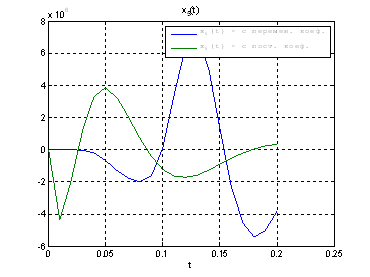
Рис.30. Графики фазовых координат.
Выводы: из графиков видно, что система, у которой коэффициенты регулятора меняются со временем, стабилизируется не хуже, чем, система, у которой коэффициенты регулятора не изменяются.
5.3 Задача АКОР – стабилизации для
компенсации
известного возмущающего воздействия
Рассмотрим систему вида
![]() ,
,
где ![]() – возмущающее
воздействие.
– возмущающее
воздействие.
Матрицы ![]() заданы в пункте 5.1.1.
заданы в пункте 5.1.1.
Весовые матрицы ![]() и
и ![]() имеют следующий вид:
имеют следующий вид:
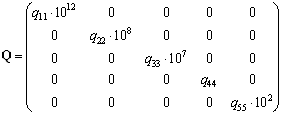 ,
, ![]() .
.
Начальные условия для заданной
системы ![]() .
.
Время стабилизации ![]() .
.
Задаем возмущающее воздействие только на первую координату, так как только она имеет значение
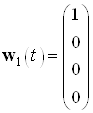 и
и  .
.
Решение задачи стабилизации сводится к решению уравнения Риккати
![]()
с начальными условиями: ![]()
Введём вспомогательную
вектор-функцию ![]() , ДУ которой имеет
вид:
, ДУ которой имеет
вид:
![]()
с начальными условиями: ![]() .
.
Управление определяется по формуле:
![]() .
.
Используя скрипт AKOR_stabilizaciya_pri_vozmusheniyah.m, получили следующие результаты:
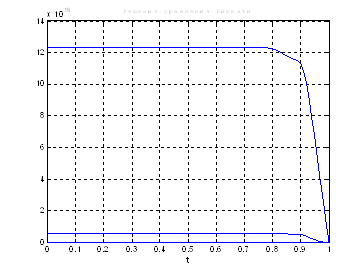
Рис.31. Графики решения уравнения Риккати.
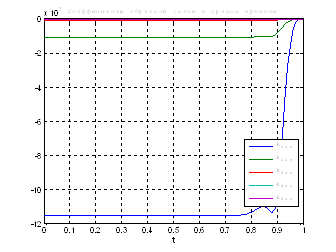
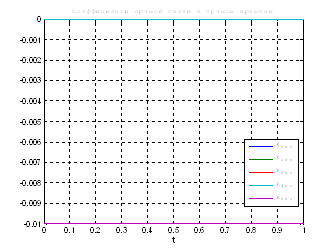
Рис.32. Графики коэффициентов регулятора обратной и прямой связи.
Рис.33. График возмущающего воздействия.
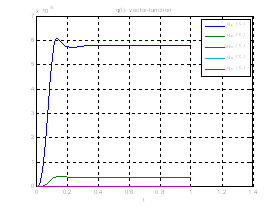
Рис.34. График вспомогательной вектор – функции.
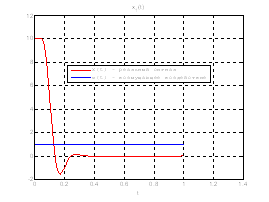
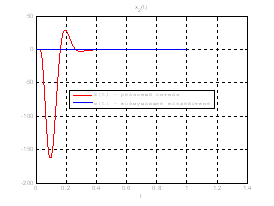
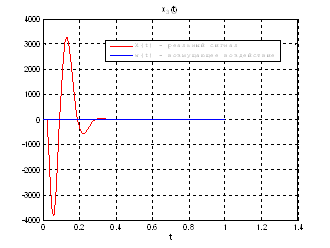
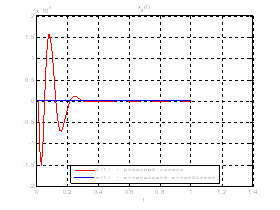
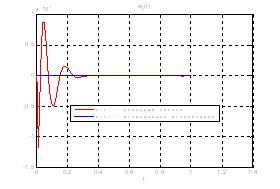
Рис.35. Графики фазовых координат.
Рис.36. График управления.
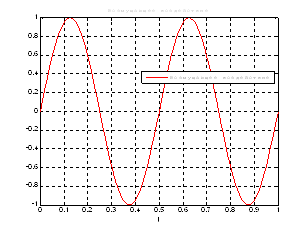
Рис.37. График возмущающего воздействия.
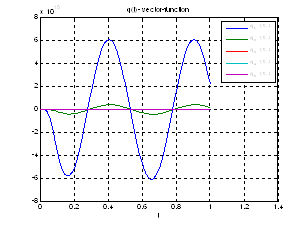
Рис.38. График вспомогательной вектор – функции.
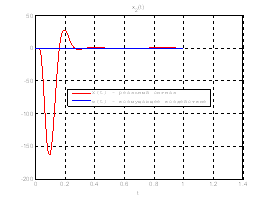
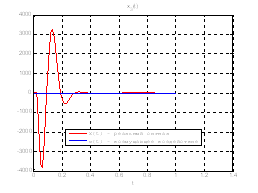
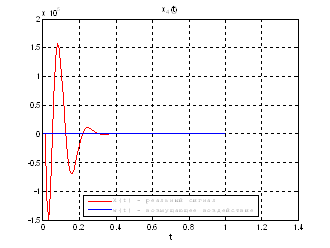
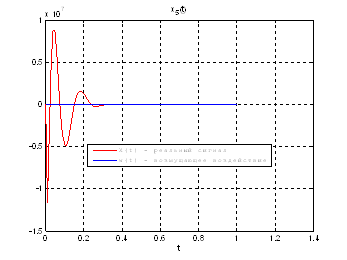
Рис.39. Графики фазовых координат.
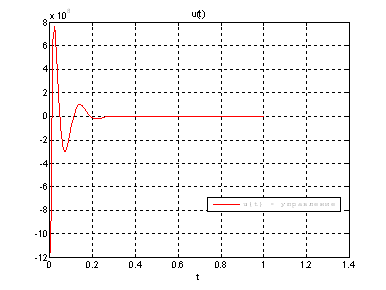
Рис.40. График управления.
Выводы: По графикам фазовых координат при различных воздействиях видно, что влияние возмущающего воздействия не существенно и фазовые координаты устанавливаются в ноль. При этом видно, что графики первой фазовой координаты при различных воздействиях мало отличаются друг от друга, т.е. система отрабатывает любое возмущение.
5.4 Задача АКОР для отслеживания известного задающего воздействия. I подход
Система задана в виде:
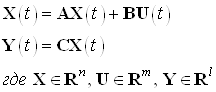
Матрицы ![]() заданы в пункте 5.1.1.
заданы в пункте 5.1.1.
Весовые матрицы ![]() и
и ![]() имеют следующий вид:
имеют следующий вид:
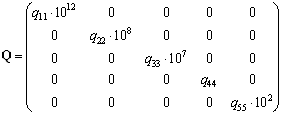 ,
, ![]() .
.
Начальные условия для заданной
системы ![]() .
.
Время слежения ![]() .
.
Задающее воздействие в виде системы ДУ
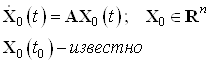
Начальные условия для воздействия:
![]() .
.
Введем расширенный вектор
состояния и расширенные матрицы ![]()
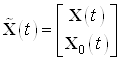 ,
,
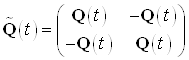 ,
,
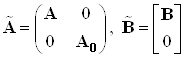 .
.
Тогда новое описание системы имеет вид:
![]()
с начальными условиями: 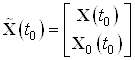 .
.
Решением уравнения Риккати будет матрица:
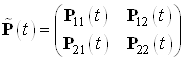
с н.у.![]()
Тогда оптимальное управление, находится по формуле:
![]()
Используя скрипт AKOR_slegenie_na_konech_interval_I_podxod, получили следующие результаты:
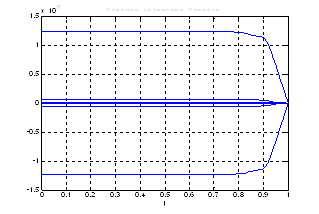
Рис.41. Графики решения уравнения Риккати.
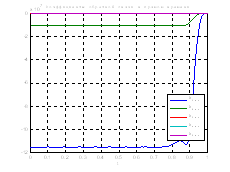
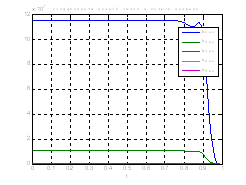
Рис.42. Графики коэффициентов регулятора обратной и прямой связи.
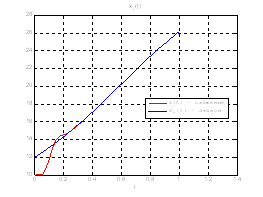
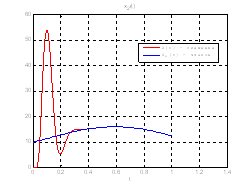
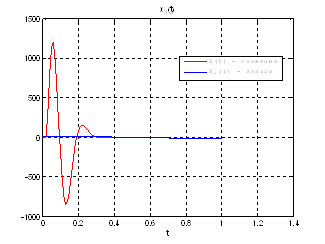
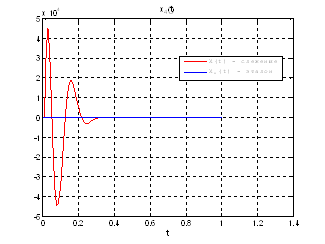
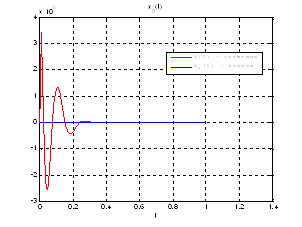
Рис.43. Графики фазовых координат.
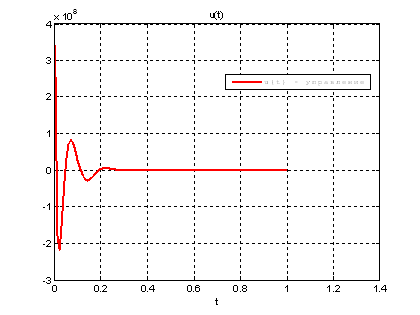
Рис.44. График управления.
Выводы: На данном этапе была решена задача АКОР-слежения. В качестве отслеживаемого воздействия была взята исходная система, но с другими начальными условиями, поэтому графики фазовых координат отличаются от заданных, но только на начальном участке движения.
5.5 Задача АКОР для отслеживания известного задающего воздействия. II подход (линейный сервомеханизм)
Система задана в виде:
Матрицы ![]() заданы в пункте 5.1.1.
заданы в пункте 5.1.1.
Весовые матрицы ![]() и
и ![]() имеют следующий вид:
имеют следующий вид:
 ,
, ![]() .
.
Начальные условия для заданной
системы ![]() .
.
Задающее воздействие имеет вид:
![]() ,
, ![]() .
.
Время слежения ![]()
Введём вспомогательную
вектор-функцию ![]() , ДУ которой
определяется
, ДУ которой
определяется ![]()
![]() ,
,
![]() ,
,
НУ определяются из соотношения
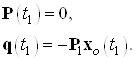
Зная закон изменения ![]() и
и ![]() , можно определить
управление:
, можно определить
управление:
![]() .
.
Используя скрипт AKOR_slegenie_na_konech_interval_II_podxod, получили следующие результаты:
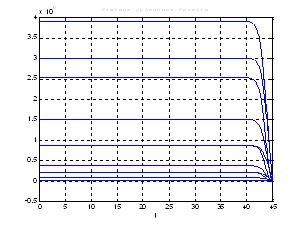
Рис.45. Графики решения уравнения Риккати.
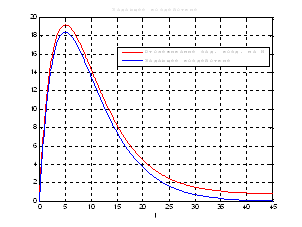
Рис.46. График задающего воздействия.
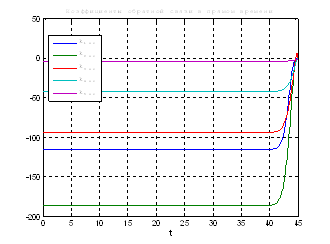
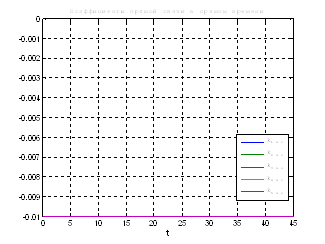
Рис.47. Графики коэффициентов регулятора обратной и прямой связи.
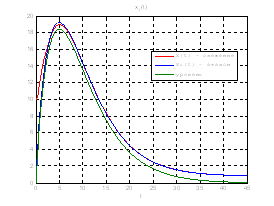
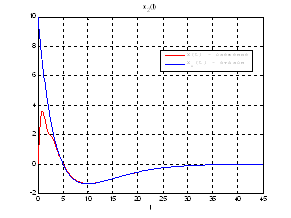
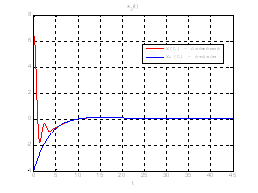
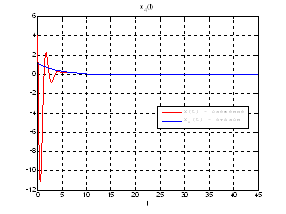
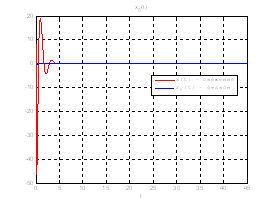
Рис.48. Графики фазовых координат.
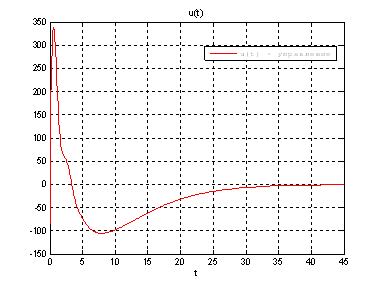
Рис.49. График управления.
Выводы: На данном этапе была решена задача построения линейного сервомеханизма. В качестве отслеживаемого воздействия была задана экспоненциальная функция. Анализируя выше приведенные графики, можно сказать, что все состояния заданной системы, особенно первая фазовая координата, отслеживается с заданной точностью.
5.6 Задача АКОР – слежения со скользящими интервалами
Пусть интервал времени ![]() является объединением
нескольких отрезков. Известно некоторое задающее воздействие
является объединением
нескольких отрезков. Известно некоторое задающее воздействие ![]() заданное аналитическим
выражением, причем информация о задающем сигнале на следующем отрезке времени
поступает только в конце предыдущего. Таким образом, зная задающий сигнал
только на одном отрезке времени, мы будем синтезировать управление на этом
отрезке.
заданное аналитическим
выражением, причем информация о задающем сигнале на следующем отрезке времени
поступает только в конце предыдущего. Таким образом, зная задающий сигнал
только на одном отрезке времени, мы будем синтезировать управление на этом
отрезке.
Разобьем весь интервал на 3 равных отрезка.
Данная задача похожа на задачу отслеживания известного задающего воздействия, заданного аналитическим выражением, но с некоторыми изменениями:
1. Поскольку в уравнение Риккати
относительно матрицы ![]() входят только
параметры системы и функционала качества, то решать его будем один раз на
первом отрезке, так как на остальных отрезках решение будет иметь тот же вид, но
будет смещено по времени:
входят только
параметры системы и функционала качества, то решать его будем один раз на
первом отрезке, так как на остальных отрезках решение будет иметь тот же вид, но
будет смещено по времени:
![]()
![]()
![]()
![]()
2. Начальными условиями для системы на каждом отрезке будет точка, в которую пришла система на предыдущем отрезке:
![]()
![]()
![]()
![]()
3. Вектор ![]() необходимо пересчитывать
на каждом отрезке.
необходимо пересчитывать
на каждом отрезке.
4. В остальном данная задача аналогична задаче построения линейного сервомеханизма (пункт 5.5).
Используя скрипт AKOR_slegenie_so_skolz_intervalami_Modern, получили следующие результаты:
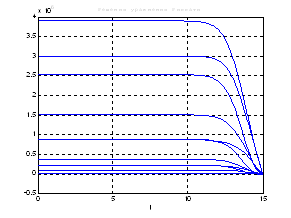
Рис.50. Графики решения уравнения Риккати.
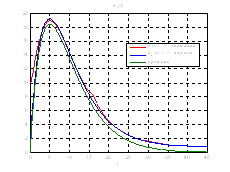
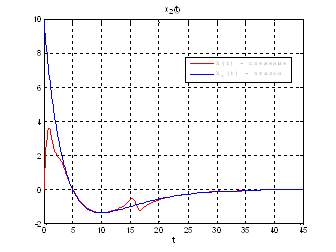

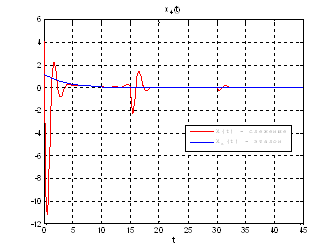
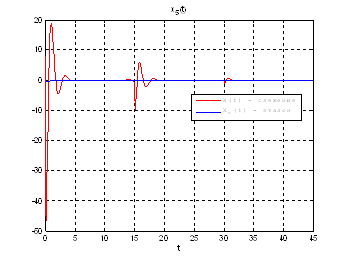
Рис.51. Графики фазовых координат.
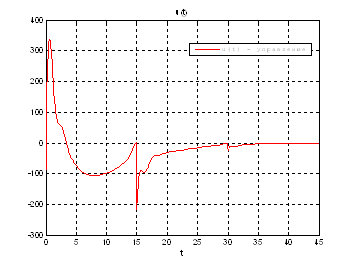
Рис.52. График управления.
Выводы: при сравнении полученных результатов, можно сказать, что различия в фазовых координатах при наличии трех участков и при наличии одного участка несущественные. Если сравнивать скорость вычислений и используемые ресурсы, то скорость увеличивается почти в 3 раза, а памяти требуется в 3 раза меньше для решения поставленной задачи. В точках соединения участков наблюдаются скачки, связанные с тем, что требуется значительные затраты на управление, но для первой координаты этот скачок незначительный.
6. Синтез наблюдателя полного порядка
Наблюдателями называются
динамические устройства, которые позволяют по известному входному и выходному
сигналу системы управления получить оценку вектора состояния. Причем ошибка
восстановления ![]() .
.
Система задана в виде:
Начальные условия для заданной
системы ![]() .
.
Матрицы ![]() заданы в пункте 5.1.1.
заданы в пункте 5.1.1.
Весовые матрицы ![]() и
и ![]() имеют следующий вид:
имеют следующий вид:
 ,
, ![]() .
.
Построим наблюдатель
полного порядка и получим значения наблюдаемых координат ![]() таких, что:
таких, что: ![]()
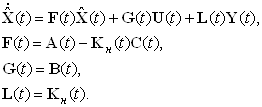
В качестве начальных условий для наблюдателя выберем нулевые н.у.:
![]()
Ранг матрицы наблюдаемости:
![]() - матрица
- матрица
наблюдаемости.
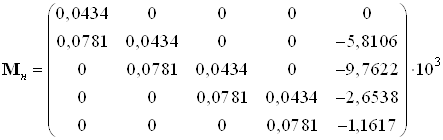 .
.
![]() .
.
Т. е. система является наблюдаемой.
Коэффициенты регулятора:
![]() ,
,
тогда

Собственные значения
матрицы ![]() :
:
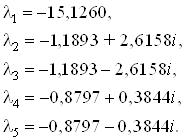
Коэффициенты наблюдателя
выберем из условия того, чтобы наблюдатель был устойчивым, и ближайший к началу
координат корень матрицы ![]() лежал
в 3 – 5 раз левее, чем наиболее быстрый корень матрицы
лежал
в 3 – 5 раз левее, чем наиболее быстрый корень матрицы ![]() . Выберем корни матрицы
. Выберем корни матрицы
![]()
Коэффициенты матрицы наблюдателя:
![]() .
.
Используя скрипт Sintez_nablyud_polnogo_poryadka, получили следующие результаты:
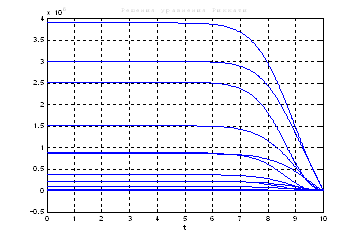
Рис.53. Графики решения уравнения Риккати.
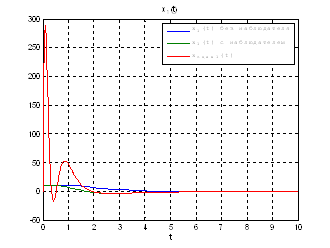
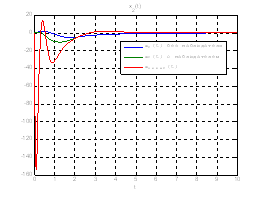
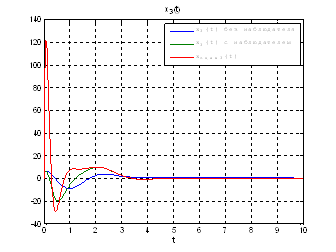
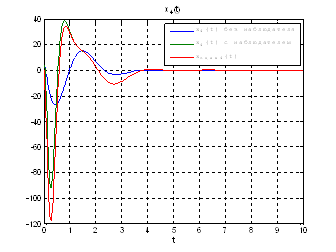
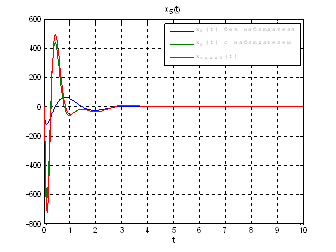
Рис.54. Графики фазовых координат.
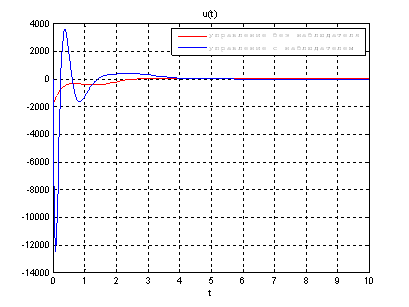
Рис.55. Графики управлений.
Выводы: Так как система является полностью
наблюдаема и полностью управляема, то спектр матрицы ![]() может располагаться
произвольно. Перемещая собственные значения матрицы
может располагаться
произвольно. Перемещая собственные значения матрицы ![]() левее,
относительно собственных значений матрицы
левее,
относительно собственных значений матрицы ![]() мы улучшаем динамику
системы, однако, наблюдатель становится более чувствителен к шумам.
мы улучшаем динамику
системы, однако, наблюдатель становится более чувствителен к шумам.
Литература
1. Методы классической и современной теории автоматического управления: Учебник в 5 – и т. Т.4: Теория оптимизации систем автоматического управления / Под ред. Н.Д. Егупова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 748 с.
2. Краснощёченко В.И.: Методическое пособие: «Методы теории оптимального управления».
Приложение .
PlotTimeFrHaract.m
clc
clear all
close all
b1 = 9;
b0 = 5;
a4 = 0.1153;
a3 = 1.78;
a2 = 3.92;
a1 = 14.42;
a0 = 8.583;
% syms s w
% W_s_chislit = b1 * s + b0;
% W_s_znamen = s * (a4 * s^4 + a3 * s^3 + a2 * s^2 + a1 * s + a0);
%
% W_s_obj = W_s_chislit/W_s_znamen;
%A_w = collect(simplify(abs(subs(W_s_obj, s, i*w))))
%----------------------Построение АЧХ-------------------------------------%
figure('Name', '[0,10]');
w = 0 : 0.01 : 10;
A_w = sqrt((b0^2 + b1^2.*w.^2)./((-a1*w.^2+a3*w.^4).^2+(a0*w-a2*w.^3+a4*w.^5).^2));
plot(w,A_w,'k', 'LineWidth', 2);
grid on
xlabel('w')
ylabel('A(w)')
title('Function ACHX(w)')
%-------------------------------------------------------------------------%
r_ch = roots([b1 b0])
r_zn = roots([a4 a3 a2 a1 a0 0])
%----------------------Построение ФЧХ-------------------------------------%
figure('Name', '[0,100]');
w = 0 : 0.01 : 100;
fi_w = (atan(w/0.5556)-atan(w/0)-atan(w/13.5832)-atan((w-2.7677)/0.5850)...
-atan((w+2.7677)/0.5850) - atan(w/(0.6848)))*180/pi;
plot(w,fi_w, 'k', 'LineWidth', 2);
grid on
xlabel('w')
ylabel('fi(w)')
title('Function FCHX(w)')
%-------------------------------------------------------------------------%
%----------------------Построение АФЧХ------------------------------------%
figure('Name', '[0,100]');
w = 0 : 0.01 : 100;
A_w = sqrt((b0^2 + b1^2.*w.^2)./((-a1*w.^2+a3*w.^4).^2+(a0*w-a2*w.^3+a4*w.^5).^2));
fi_w = (atan(w/0.5556)-atan(w/0)-atan(w/13.5832)-atan((w-2.7677)/0.5850)...
-atan((w+2.7677)/0.5850) - atan(w/(0.6848)));
polar(fi_w,A_w, 'k');
grid on
xlabel('Re(W(jw))')
ylabel('Im(W(jw))')
title('Function AFCHX(fi_w,A_w)')
%-------------------------------------------------------------------------%
%----------------------Построение ЛАЧХ------------------------------------%
figure('Name', '[0,100]');
w = -100 : 0.01 : 100;
LA_w = 20*log(sqrt((b0^2 + b1^2.*w.^2)./((-a1*w.^2+a3*w.^4).^2+(a0*w-a2*w.^3+a4*w.^5).^2)));
plot(w,LA_w,'k', 'LineWidth', 2);
grid on
xlabel('w')
ylabel('L(w)')
title('Function L(w)')
%-------------------------------------------------------------------------%
%----------------------Построение ФАЧХ------------------------------------%
%-------------------------------------------------------------------------%
%----------------------Построение h(t)------------------------------------%
figure('Name', '[0,50]');
t = 0 : 0.01 : 50;
h_t = 0.0024 * exp(-13.5832.*t) - 0.2175 * exp(-0.6848.*t)...
+ 0.1452 * exp(-0.5850.*t).* cos(2.7677.*t)...
- 0.2217 * exp(-0.5850.*t).* sin(2.7677.*t)...
+ 0.5825 .* t + 0.0699;
plot(t,h_t, 'k', 'LineWidth', 2);
grid on
xlabel('t')
ylabel('h(t)')
title('Function h(t)')
%-------------------------------------------------------------------------%
%----------------------Построение k(t)------------------------------------%
figure('Name', '[0,50]');
t = 0 : 0.01 : 50;
k_t = - 0.0329 * exp(-13.5832.*t) + 0.1489 * exp(-0.6848.*t)...
- 0.6986 * exp(-0.5850.*t).* cos(2.7677.*t)...
- 0.2721 * exp(-0.5850.*t).* sin(2.7677.*t)...
+ 0.5826;
plot(t,k_t, 'k', 'LineWidth', 2);
grid on
xlabel('t')
ylabel('k(t)')
title('Function k(t)')
%-------------------------------------------------------------------------%
x1=tf([b1 b0],[a4 a3 a2 a1 a0 0]);
ltiview(x1)
ProstranstvoSostoyanii.m
clc
clear all
%format rational
b1 = 9;
b0 = 5;
a5 = 0.1153;
a4 = 1.78;
a3 = 3.92;
a2 = 14.42;
a1 = 8.583;
a0 = 0;
%1. Матрица Фробениуса
A=[0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0;
0 0 0 0 1;
0 -a1/a5 -a2/a5 -a3/a5 -a4/a5]
B=[0; 0; 0; 0; 1/a5]
C=[b0 b1 0 0 0]
%Проверка
syms s
W_s = collect(simplify(C*(s.*eye(5)-A)^(-1)*B),s)
pretty(W_s)
%2. Параллельная декомпозиция
b1 = b1/a5;
b0 = b0/a5;
s1 = 0;
s2 = -6615/487;
s3 = -1022/1747 + 4016/1451*i;
s4 = -1022/1747 - 4016/1451*i;
s5 = -415/606;
alfa = real(s3);
beta = imag(s3);
syms s A B C D E
W_s_etal = collect(((b1*s+b0)/((s-s1)*(s-s2)*((s+alfa)^2+beta^2)*(s-s5))),s)
%pretty(W_s_etal)
Slag_1 = simplify(collect(A*(s-s2)*((s+alfa)^2+beta^2)*(s-s5),s));
Slag_2 = simplify(collect(B*(s-s1)*((s+alfa)^2+beta^2)*(s-s5),s));
Slag_3 = simplify(collect(C*(s-s1)*((s+alfa)^2+beta^2)*(s-s2),s));
Slag_4 = simplify(collect((D*s+E)*(s-s1)*(s-s2)*(s-s5),s));
Chislit_W_s =collect(Slag_1 + Slag_2 + Slag_3 + Slag_4,s);
%Решение системы линейных уравнений
MS =double( [1 1 1 1 0;
6753029497/515578134 -513659/1058682 10560977/850789 4210795/295122 1;
77456808434995506239663107/126764366837761533378822144 1874500571398143988939141/260296441145300889894912 -3300780600401725219142291/418364246989311991349248 915075/98374 4210795/295122;
26189071674868424275768861465/253528733675523066757644288 2853037197681682345182805/520592882290601779789824 45476725452203201718998205/418364246989311991349248 0 915075/98374;
6290947020888109571128085025/84509577891841022252548096 0 0 0 0])
PCH = [0; 0; 0; b1; b0];
Koeff = MS^(-1)*PCH
%Проверка
MS*[Koeff(1);Koeff(2);Koeff(3);Koeff(4);Koeff(5)];
Slag_1 = simplify(collect(Koeff(1)*(s-s2)*((s+alfa)^2+beta^2)*(s-s5),s));
Slag_2 = simplify(collect(Koeff(2)*(s-s1)*((s+alfa)^2+beta^2)*(s-s5),s));
Slag_3 = simplify(collect(Koeff(3)*(s-s1)*((s+alfa)^2+beta^2)*(s-s2),s));
Slag_4 = simplify(collect((Koeff(4)*s+Koeff(5))*(s-s1)*(s-s2)*(s-s5),s));
Chislit_W_s =collect((Slag_1 + Slag_2 + Slag_3 + Slag_4),s);
Znamena_W_s = collect((s-s1)*(s-s2)*((s+alfa)^2+beta^2)*(s-s5),s);
W_s = collect(simplify(Koeff(1)/(s-s1)+Koeff(2)/(s-s2)+(Koeff(4)*s+Koeff(5))/((s+alfa)^2+beta^2)+Koeff(3)/(s-s5)),s)
pretty(W_s)
%Расчет матриц состояния
A = [s1 0 0 0 0;
0 s2 0 0 0 ;
0 0 0 1 0;
0 0 -(alfa^2+beta^2) -2*alfa 0;
0 0 0 0 s5]
B = [Koeff(1); Koeff(2); 0; 1; Koeff(3)]
C = [1 1 Koeff(5) Koeff(4) 1]
%Проверка
W_s = collect(simplify(C*(s.*eye(5)-A)^(-1)*B),s)
pretty(W_s)
%ВСЕ ПОДСЧИТАНО ВЕРНО!!!
SimplexMetod2.m
function SimplexMetod2
clc
clear all
close all
format short
% Матрицы системы
A = [0 2;
-3 0];
B = [0; 2];
% Координаты начальной и конечной точки
X_0 = [14; 0];
X_N = [0; 0];
% Ограничение на управление
u_m = -3;
u_p = 5;
eps = 1e-10;% погрешность сравнения с нулем
N = 195;% число шагов
%h = t1/N;% шаг дискретизации
h = 0.0162;
alfa = 1;
a = 0;
b = 0;
%t1 = 796/245;% время перехода в конечное состояние
n = size(A);
n = n(1);% порядок системы
% Нахождение матричного экспоненциала
syms s t
MatrEx = ilaplace((s*eye(n)-A)^(-1));
MatrEx_B = MatrEx*B;
% Вычисление матриц F и G
F = subs(MatrEx, t, h);
G = double(int(MatrEx_B, t, 0, h));
ФОРМИРОВАНИЕ ЗАДАЧИ БЫСТРОДЕЙСТВИЯ КАК ЗАДАЧИ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
for index = 1 : 1e+10
% Вычисление правой части
PravChast = X_N - F^N * X_0;
% Вычисление произведения F на G
FG = zeros(n, N);% формирование матрицы для хранения данных
for j = 1 : n
for i = 0 : N - 1
fg = F^(N-i-1) * G;
if PravChast(j) < 0
fg = -fg;
end
FG(j, i+1) = fg(j);
end
end
% Построение z-строки
z_stroka = zeros(1, 4*N+n+2);% формирование матрицы для хранения данных
% Первый элемент z-строки
z_stroka(1) = 1;
% Суммирование правых частей
for j = 1 : n
z_stroka(4*N+n+2) = z_stroka(4*N+n+2) + abs(PravChast(j));
end
% Формирование элементов z-строки между 1-м и последним элементами
%при 2N небазисных переменных, т.е. при управлениях
for i = 2 : 2 : 2 * N
for j = 1 : n
z_stroka(i) = z_stroka(i) + FG(j, i/2);
end
for j = 1 : n
z_stroka(i+1) = z_stroka(i+1) - FG(j, i/2);
end
end
% Формирование симплекс-таблицы
CT = zeros(n+2*N+1, 4*N+n+2);
% Построение симплекс-таблицы начиная с z-строки
CT(1,:) = z_stroka(1,:);
% Формирование R-строк в симплекс-таблице
for j = 2 : n + 1
% Формирование правой части в R-строках
CT(j, 4*N+n+2) = abs(PravChast(j-1));
% Формирование элементов R-строк между 1-м и последним элементами
%при 2N небазисных переменных, т.е. при управлениях
for i = 2 : 2 : 2 * N
CT(j, i) = FG(j-1, i/2);
CT(j, i+1) = -FG(j-1, i/2);
end
end
% Формирование S-строк в симплекс-таблице
l = 2;
for j = n + 2 : 2 : n + 2 * N + 1
% Формирование правой части в S-строках
CT(j, 4*N+n+2) = u_p;
CT(j+1, 4*N+n+2) = abs(u_m);
% Формирование элементов S-строк между 1-м и последним элементами
%при 2N небазисных переменных, т.е. при управлениях
CT(j, l : l+1) = [1 -1];
CT(j+1, l : l+1) = [-1 1];
l = l + 2;
end
% Формирование базиса в симплекс-таблице, т.е коэффициентов, стоящих при
%базисных переменных от 2N небазисных переменных до правой части (до 4*N+n+1)
CT(2 : n+2*N+1, 2*N+2 : 4*N+n+1) = eye(n+2*N, n+2*N);
РЕШЕНИЕ ЗАДАЧИ БЫСТРОДЕЙСТВИЯ
% Цикл смены базисных переменных
nn = size(find(CT(1,2:2*N+1) >= eps));
while nn > 0
[znach, N_stolb] = max(CT(1, 2 : 2*N+1));
N_stolb = N_stolb + 1; % т.к. при небазисн. перемен.
PravChast = CT(:, 4*N+n+2);
for j = 2 : n + 2 * N + 1
if CT(j, N_stolb) > 0
PravChast(j) = PravChast(j) / CT(j, N_stolb);
else
PravChast(j) = inf;
end
end
[znach, N_str] = min(PravChast(2 : n+2*N+1));
N_str = N_str + 1;
% Формирование матрицы перехода B
B = eye(n+2*N+1, n+2*N+1);
B(:, N_str) = CT(:, N_stolb);
% Обращение матрицы B
RE = B(N_str, N_str);
for j = 1 : n + 2 * N + 1
if j == N_str
B(j, N_str) = 1 / RE;
else
B(j, N_str) = -B(j, N_str) / RE;
end
end
%B = inv(B);
% Получение новой симплекс таблицы
CT = B * CT;
nn = size(find(CT(1,2:2*N+1) >= eps));
end
u = zeros(1,N);
% Формирование управления
for j = 2 : n + 2 * N + 1
for i = 2 : 2 * N + 1
if CT(j, i) >= eps
if mod(i, 2) < eps
u(i/2) = CT(j, 4*N+n+2);
else
u((i-1)/2) = -CT(j, 4*N+n+2);
end
end
end
end
% Формирование x1 и x2
X = zeros(n, N);
X(:, 1) = F * X_0 + G * u(1);
for i = 2 : N
X(:, i) = F * X(:, i-1) + G * u(i);
end
% Объединение с начальными условиями
X1 = [X_0(1) X(1, :)];
X2 = [X_0(2) X(2, :)];
% проверка на окончание выбора количества шагов
XX = [X_0 X];
% Вычисление нормы вектора состояния
normaXX = norm(XX(:,N))
% Вычисление значения переменной R
R = abs(X_N - F^N * X_0) - FG * u';
R = R';
z = sum(R);
% Погрешность приближения к точному решению
pogresh = 0.3;
if (normaXX < pogresh)
N_opt = N;
break;
else
if (z > h)
if a == 1
alfa = ceil(alfa/2);
end
N = N + alfa;
a = 0;
b = 1;
else
if b == 1
alfa = ceil(alfa/2);
end
N = N - alfa;
a = 1;
b = 0;
end
end
t_perevoda = N * h;
end
N_opt
h
t_perevoda
ОФОРМЛЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
В ГРАФИЧЕСКОМ ВИДЕ
% Построение графика x1(t);
figure(1)
t = (0 : 1 : length(X1)-1) * h;
plot(t, X1, 'b', 'LineWidth', 2);
hl=legend('x_1(t)');
set(hl, 'FontName', 'Courier');
xlabel('t, cek'); ylabel('x_1(t)');
grid on
% Построение графика x2(t);
figure(2)
t = (0 : 1 : length(X2)-1) * h;
plot(t, X2, 'b', 'LineWidth', 2);
hl=legend('x_2(t)');
set(hl, 'FontName', 'Courier');
xlabel('t, cek'); ylabel('x_2(t)');
grid on
% Построение графика x2 = x2(x1);
figure(3)
plot(X1, X2, 'm', 'LineWidth', 2);
hl=legend('x_2 = x_2(x_1)');
set(hl, 'FontName', 'Courier');
xlabel('x_1(t)'); ylabel('x_2(x_1(t))');
grid on
% Построение графика u(t)
figure(4)
t = (0 : 1 : length(u)-1) * h;
plot(t, u, 'r', 'LineWidth', 2);
hl=legend('u(t)');
set(hl, 'FontName', 'Courier');
xlabel('t, cek'); ylabel('u(t)');
grid on
Optimal_L_problem_moments.m
clc
close all
clear all
format long
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% Порядок системы
poryadok = 5;
% Начальные и конечные условия относительно вектора Y
Y_0 = [3 2 1 5]';
Y_T = [0 -1 0 3]';
% Конечное время перехода
T = 3;
% Матрица перехода от Н.У. Y к Н.У. X
B_ = [b0 b1 0 0 0;
0 b0 b1 0 0;
0 0 b0 b1 0;
0 0 0 b0 b1];
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Начальные условия для упорядоченной системы
X_0 = B_' * inv(B_ * B_') * Y_0
X_T = B_' * inv(B_ * B_') * Y_T
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4]
B = [0; 0; 0; 0; 1]
C = [b0 b1 0 0 0]
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Вычисление матричной экспоненты
syms s t
MatrEx = simplify (vpa(ilaplace(inv(s*eye(5) - A)), 50))
% ------------------------------------------------------------------------%
RETURN = 1;
while RETURN == 1
disp('L - проблема моментов в пространстве вход-выход: 1')
disp('L - проблема моментов в пространстве состояний : 2')
reply = input('Выберете метод решения [1 или 2]: ', 's');
switch reply
case '1'
disp('L - проблема моментов в пространстве вход-выход')
% ------------------------L - проблема моментов---------------------------%
% ----------------------в пространстве вход-выход-------------------------%
% ------------------------------------------------------------------------%
% Передаточная функция
W_obj_s = 1/(a5*s^5 + a4*s^4 + a3*s^3 + a2*s^2 + a1*s + a0);
% Полюса передаточной функции
polyusa_TF = roots([a5 a4 a3 a2 a1 a0]);
% ИПФ
K_t = simplify (vpa (ilaplace(1 / (a5*s^5 + a4*s^4 + a3*s^3 + ...
a2*s^2 + a1*s + a0)),50))
% K_t = vpa(K_t,6)
% ------------------------------------------------------------------------%
% Составление матрицы Вронского
for i = 1 : poryadok
Matrix_Vron (i, 1) = diff (exp (polyusa_TF(1) *t), t, i - 1);
Matrix_Vron (i, 2) = diff (exp (polyusa_TF(2) *t), t, i - 1);
Matrix_Vron (i, 3) = diff (exp (real(polyusa_TF(3))*t) * ...
cos(imag(polyusa_TF(3))*t), t, i - 1);
Matrix_Vron (i, 4) = diff (exp (real(polyusa_TF(4))*t) * ...
sin(imag(polyusa_TF(4))*t), t, i - 1);
Matrix_Vron (i, 5) = diff (exp (polyusa_TF(5) *t), t, i - 1);
end
% Матрица Вронского при t = 0;
Matrix_Vron_t_0 = double(subs(Matrix_Vron,t,0));
% Матрица Вронского при t = T;
T = 3;
Matrix_Vron_t_T = double(subs(Matrix_Vron,t,T));
% vpa(Matrix_Vron_t_0,6)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Определение неизвестных коэффициентов C
C_ = inv(Matrix_Vron_t_0) * X_0;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение моментных функций
K_Tt_1 = subs (K_t,t, T - t);
K_Tt = diff (K_t);
K_Tt_2 = subs (K_Tt, t, T - t);
K_Ttt = diff (K_Tt);
K_Tt_3 = subs (K_Ttt, t, T - t);
K_Tttt = diff (K_Ttt);
K_Tt_4 = subs (K_Tttt, t, T - t);
K_Ttttt = diff (K_Tttt);
K_Tt_5 = subs (K_Ttttt, t, T - t);
h1_Tt = K_Tt_1
h2_Tt = K_Tt_2
h3_Tt = K_Tt_3
h4_Tt = K_Tt_4
h5_Tt = K_Tt_5
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение моментов
for i = 1 : poryadok
Matrix_a(i) = X_T(i) - C_' * Matrix_Vron_t_T(i,:)';
end
Matrix_a = Matrix_a'
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
RETURN = 2;
case '2'
disp('L - проблема моментов в пространстве состояний')
% ------------------------L - проблема моментов---------------------------%
% ----------------------в пространстве состояний--------------------------%
% ------------------------------------------------------------------------%
Matr_Ex_T = subs(MatrEx, t, T);
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение моментов
for i = 1 : poryadok
Matrix_a(i) = X_T(i) - Matr_Ex_T(i,:) * X_0;
end
Matrix_a = Matrix_a'
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение моментных функций
Matr_Ex_Tt = subs(MatrEx, t, T - t);
h_Tt = vpa(expand(simplify(Matr_Ex_Tt * B)),50);
h1_Tt = h_Tt(1)
h2_Tt = h_Tt(2)
h3_Tt = h_Tt(3)
h4_Tt = h_Tt(4)
h5_Tt = h_Tt(5)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
RETURN = 2;
otherwise
disp('Неизвестный метод.')
RETURN = 1;
end
end
% h1_Tt = vpa(h1_Tt,6)
% h2_Tt = vpa(h2_Tt,6)
% h3_Tt = vpa(h3_Tt,6)
% h4_Tt = vpa(h4_Tt,6)
% h5_Tt = vpa(h5_Tt,6)
% ------------------------------------------------------------------------%
% --------Нахождение управления и вычисление минимальной энергии----------%
% ------------------------------------------------------------------------%
syms ks1 ks2 ks3 ks4 ks5
% ------------------------------------------------------------------------%
% Формирование функционала
d_v_2 = vpa (simplify (int ((ks1*h1_Tt + ks2*h2_Tt + ks3*h3_Tt + ...
ks4*h4_Tt + ks5*h5_Tt)^2, t, 0, T)), 50);
% Выражаем ks1 через остальные
ks1 = vpa ((1 - ks2*Matrix_a(2) - ks3*Matrix_a(3) - ...
ks4*Matrix_a(4) - ks5*Matrix_a(5))/Matrix_a(1), 50);
% Подставляем в функционал ks1
d_v_2 = vpa (expand (subs (d_v_2, ks1)), 50);
% Находим частные производные по ksi
eq_1= diff(d_v_2, ks2);
eq_2= diff(d_v_2, ks3);
eq_3= diff(d_v_2, ks4);
eq_4= diff(d_v_2, ks5);
% Решаем СЛАУ относительно ksi
ksi= solve(eq_1, eq_2, eq_3, eq_4);
% Полученные значения ksi
ks2= double(ksi.ks2)
ks3= double(ksi.ks3)
ks4= double(ksi.ks4)
ks5= double(ksi.ks5)
ks1 = double(vpa ((1 -ks2*Matrix_a(2) -ks3*Matrix_a(3) -ks4*Matrix_a(4) - ...
ks5*Matrix_a(5))/Matrix_a(1), 50))
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Проверка условия полученного результата
ks1*Matrix_a(1) + ks2*Matrix_a(2) + ks3*Matrix_a(3) + ...
ks4*Matrix_a(4) + ks5*Matrix_a(5)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Вычисление управления и минимальной энергии
d_v_2 = vpa (simplify (int ((ks1*h1_Tt + ks2*h2_Tt + ks3*h3_Tt + ...
ks4*h4_Tt + ks5*h5_Tt)^2, t, 0, T)), 50)
% d_v_2 = double(d_v_2)
gamma_v_2 = 1/d_v_2
% gamma_v_2 = double(gamma_v_2)
u = vpa (expand(simplify(gamma_v_2 * (ks1*h1_Tt + ks2*h2_Tt + ks3*h3_Tt + ...
ks4*h4_Tt + ks5*h5_Tt))), 50)
% u = vpa(u,6)
u_0 = subs(u,t,0)
u_T = subs(u,t,T)
ezplot(u, [0 T], 1)
hl=legend('u(t)');
set(hl, 'FontName', 'Courier');
title ('u(t)');
xlabel('t')
grid on
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождения X
% Вычисление матричной экспоненты
MatrEx = simplify (vpa(ilaplace(inv(s*eye(5) - A)), 50));
syms t tay
X_svob = MatrEx * X_0;
X_vinyg = int ((subs(MatrEx, t, t - tay))*B*(subs (u, t, tay)), tay, 0,t);
X_real = X_svob + X_vinyg;
save Sostoyaniya X_real u
X_real = vpa (expand (simplify(X_real)), 50)
X_real_0 = double(subs (X_real, t, 0))
X_real_T = double(subs (X_real, t, T))
% Погрешность X
delta_X_T = double(vpa(X_T - X_real_T, 50))
delta_X_0 = double(vpa(X_0 - X_real_0, 50))
% Нахождение Y
for i = 1 : poryadok - 1
Y_real(i) = B_(i,:) * X_real;
end
Y_real = vpa (expand(simplify(Y_real')), 50)
Y_real_0 = double(subs (Y_real, t, 0))
Y_real_T = double(subs (Y_real, t, T))
% Погрешность Y
delta_Y_T = double(vpa(Y_T - Y_real_T, 50))
delta_Y_0 = double(vpa(Y_0 - Y_real_0, 50))
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Вычисление max значений для задачи АКОР
h = 0.01;
tic
tt = 0 : h : T;
for i = 1 : poryadok
X_max(i) = max(abs(subs(X_real(i),t,tt)));
end
U_max = max(abs(subs(u,t,tt)));
toc
save Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Построение результатов X(t)
ezplot (X_real(1), [0 T],2)
title ('x_1(t)');
grid on
ezplot (X_real(2), [0 T],3)
title ('x_2(t)');
grid on
ezplot (X_real(3), [0 T],4)
title ('x_3(t)');
grid on
ezplot (X_real(4), [0 T],5)
title ('x_4(t)');
grid on
ezplot (X_real(5), [0 T],6)
title ('x_5(t)');
grid on
% Построение результатов Y(t)
ezplot (Y_real(1), [0 T],7)
title ('y_1(t)');
grid on
ezplot (Y_real(2), [0 T],8)
title ('y_2(t)');
grid on
ezplot (Y_real(3), [0 T],9)
title ('y_3(t)');
grid on
ezplot (Y_real(4), [0 T],10)
title ('y_4(t)');
grid on
% ------------------------------------------------------------------------%
Gramian_Uprav.m
clc
close all
clear all
format long
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% Порядок системы
poryadok = 5;
% Начальные и конечные условия относительно вектора Y
Y_0 = [3 2 1 5]';
Y_T = [0 -1 0 3]';
% Конечное время перехода
T = 3;
% Матрица перехода от Н.У. Y к Н.У. X
B_ = [b0 b1 0 0 0;
0 b0 b1 0 0;
0 0 b0 b1 0;
0 0 0 b0 b1];
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Начальные условия для упорядоченной системы
X_0 = B_' * inv(B_ * B_') * Y_0
X_T = B_' * inv(B_ * B_') * Y_T
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4];
B = [0; 0; 0; 0; 1];
C = [b0 b1 0 0 0];
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Вычисление матричной экспоненты
syms s t
MatrEx = simplify (vpa(ilaplace(inv(s*eye(5) - A)), 50));
MatrEx_T = vpa(subs(MatrEx, t, T),50);
MatrEx_Tt = vpa(subs(MatrEx, t, T-t),50);
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Вычисление матрицы управляемости
M_c = [B A*B A^2*B A^3*B A^4*B]
rank_M_c = rank(M_c); %ранк = 5 - система управляема
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Вычисление грамиана управляемости
W_Tt = double(vpa(simplify(int(MatrEx_Tt*B*B'*MatrEx_Tt',t,0,T)),50))
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Формирование управления
u = vpa(expand(simplify(B'*MatrEx_Tt'*inv(W_Tt)*(X_T-MatrEx_T*X_0))),50)
u_0 = subs(u,t,0)
u_T = subs(u,t,T)
u = vpa(u,6)
% ------------------------------------------------------------------------%
ezplot(u, [0 T], 1)
title ('u(t)');
xlabel('t')
grid on
tt = 0 : 0.01 : T;
u2 = -20.605579750692850622177761310569*exp(-40.749492463732569440253455897187+13.583164154577523146751151965729*t)+19.011167813350479567880663060491*exp(-2.0544534472800777280645828326668+.68481781576002590935486094422228*t)+1.3356706538317879679656856470126*exp(-1.7550088311372150108106250409710+.58500294371240500360354168032368*t)*cos(-8.3032397968812277095785721047505+2.7677465989604092365261907015835*t)+7.2830359327562658520685140088852*exp(-1.7550088311372150108106250409710+.58500294371240500360354168032368*t)*sin(-8.3032397968812277095785721047505+2.7677465989604092365261907015835*t)-8.6096491449877801097840179781687;
u1 = subs(u2, t, tt);
u2 = subs(u, t, tt);
figure(2)
plot(tt,u1,'r',tt,u2,'b','LineWidth',2)
hl=legend('u(t) при решении оптимальной L-проблемы моментов','u(t) с использованием грамиана управляемости');
set(hl, 'FontName', 'Courier');
xlabel('t, cek'); ylabel('u(t)');
title('u(t)')
grid on
AKOR_stabilizaciya_na_polybeskon_interval.m
clc
clear all
close all
poryadok = 5;
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0;
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4]
B = [0; 0; 0; 0; 1]
C = [b0 b1 0 0 0]
% Начальные условия
X_0 = [10; 0; 6; 4; 8]
%T = 1;
Time = 1;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Получение max значений из файла
load Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% Нахождение элементов матриц Q и R
r(1) = 0.1;
q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;
for i = 2 : poryadok
q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;
end
Q = diag(q)
R = diag(r)
% Для изменения коэффициентов
% Q(1,1) = Q(1,1);
% Q(2,2) = Q(2,2);
% Q(3,3) = Q(3,3);
% Q(4,4) = Q(4,4);
% Q(5,5) = Q(5,5);
Q(1,1) = Q(1,1)*1e+12;
Q(2,2) = Q(2,2)*1e+8;
Q(3,3) = Q(3,3)*1e+7;
Q(4,4) = Q(4,4)*1e+0;
Q(5,5) = Q(5,5)*1e+2;
R(1,1) = R(1,1);
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом диагонализации
P1 = Solve_Riccati_Method_Diag(A,B,Q,R)
% ------------------------------------------------------------------------%
P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом обратного интегрирования
P2 = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach)
% ------------------------------------------------------------------------%
% Сравнение расхождения методов
Delta_P = abs(P1-P2)
% Построение графика коэффициентов регулятора
load Solve_Riccati_Method_Revers_Integr Time_R P N_str
PP = P;
for i = 1 : N_str
P = reshape(PP(i, :), poryadok, poryadok);
K(i, :) = -inv(R)*B'*P;
end
figure(2)
plot(Time_R,K(:,1),'-',Time_R,K(:,2),'-',Time_R,K(:,3),'-',Time_R,K(:,4),'-',Time_R,K(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты обратной связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
% Решение уравнения Риккати с помощью встроенной функции
% P = vpa(care(A,B,Q,R), 10)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение коэффициентов регулятора
disp('Коэффициенты регулятора:')
K1 = -inv(R) * B' * P1
K2 = -inv(R) * B' * P2
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
A1_ = A + B * K1;
A2_ = A + B * K2;
% Вычисление матричной экспоненты
syms s t
MatrEx1 = simplify (vpa(ilaplace(inv(s*eye(5) - A1_)), 50));
MatrEx2 = simplify (vpa(ilaplace(inv(s*eye(5) - A2_)), 50));
% Нахождение координат состояния
X1 = vpa(simplify(MatrEx1 * X_0), 50);
X2 = vpa(simplify(MatrEx2 * X_0), 50);
% Нахождение управления
u1 = vpa(simplify(K1 * X1),50)
u2 = vpa(simplify(K2 * X2),50)
% ------------------------------------------------------------------------%
% Построение u(t) и X(t)
T_sravneniya = 0.2;
figure(3);
tt = 0 : 0.01 : T_sravneniya;
uu1 = subs(u1,t,tt);
uu2 = subs(u2,t,tt);
plot(tt, uu1, tt, uu2, 'LineWidth', 2)
title ('u(t)');
xlabel('t')
hl=legend('u(t) - управление',0);
set(hl,'FontName','Courier');
grid on
ezplot(X1(1), [0 Time], 4)
hold on
title ('x_1(t)');
xlabel('t')
grid on
ezplot(X1(2), [0 Time], 5)
title ('x_2(t)');
xlabel('t')
grid on
ezplot(X1(3), [0 Time], 6)
title ('x_3(t)');
xlabel('t')
grid on
ezplot(X1(4), [0 Time], 7)
title ('x_4(t)');
xlabel('t')
grid on
ezplot(X1(5), [0 Time], 8)
title ('x_5(t)');
xlabel('t')
grid on
tt = 0 : 0.01 : T_sravneniya;
X21 = subs(X1(1), t, tt);
X22= subs(X1(2), t, tt);
X23= subs(X1(3), t, tt);
X24= subs(X1(4), t, tt);
X25= subs(X1(5), t, tt);
save Sravnenie_stabilizacii_1 X21 X22 X23 X24 X25 uu1
AKOR_stabilizaciya_na_konech_interval.m
clc
clear all
close all
poryadok = 5;
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4];
B = [0; 0; 0; 0; 1];
C = [b0 b1 0 0 0];
% Начальные условия
X_0 = [10; 0; 6; 4; 8];
Time = 0.2;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Получение max значений из файла
load Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% Нахождение элементов матриц Q и R
% r(1) = 100;
r(1) = 0.1;
q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;
for i = 2 : poryadok
q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;
end
Q = diag(q);
R = diag(r);
% Для изменения коэффициентов
Q(1,1) = Q(1,1)*1e+12;
Q(2,2) = Q(2,2)*1e+8;
Q(3,3) = Q(3,3)*1e+7;
Q(4,4) = Q(4,4)*1e+0;
Q(5,5) = Q(5,5)*1e+2;
R(1,1) = R(1,1);
% P_prib = eye(poryadok, poryadok);
% P_prib(1,1) = 100;
% P_prib(2,2) = 10;
% % P_prib(3,3) = 1000;
% % P_prib(4,4) = 10;
% % P_prib(5,5) = 1;
% ------------------------------------------------------------------------%
P_nach = zeros(poryadok, poryadok);% + P_prib;
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом обратного интегрирования
P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach)
% ------------------------------------------------------------------------%
% Нахождение переменных коэффициентов регулятора
load Solve_Riccati_Method_Revers_Integr Time_R P N_str
PP = P;
for i = 1 : N_str
P = reshape(PP(i, :), poryadok, poryadok);
K(i, :) = -inv(R)*B'*P;
end
% ------------------------------------------------------------------------%
% Формирование вектора коэффициентов регулятора
% и решения уравнения Риккати в прямом порядке
load Solve_Riccati_Method_Revers_Integr P
size(K)
i = 1;
len_K = length(K(:,1))
for j = len_K : -1 : 1
K_pr(i,:) = K(j,:);
i = i + 1;
end
% ------------------------------------------------------------------------%
% Построение графика переменных коэффициентов регулятора в прямом времени
figure(2)
plot(Time_R,K(:,1),'-',Time_R,K(:,2),'-',Time_R,K(:,3),'-',...
Time_R,K(:,4),'-',Time_R,K(:,5),'-', 'LineWidth', 2);
grid on;
title('K(t)')
xlabel('t')
legend('k_1','k_2','k_3','k_4','k_5');
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
for k = 1 : len_K
A_(:,:,k) = A + B * K(k,:);
end
size(A_);
% ------------------------------------------------------------------------%
% Нахождение фазовых координат
X(:,1) = X_0;
h = 0.01;
time_X(1) = 0;
for k = 1 : len_K
X(:, k+1) = X(:, k) + h * A_(:,:,k) * X(:, k);
time_X(k+1) = time_X(k) + h;
end
X(:, k+1) = [];
time_X(k+1) = [];
% ------------------------------------------------------------------------%
% Нахождение управления
for k = 1 : len_K
u(k) = K_pr(k,:) * X(:,k);
end
% ------------------------------------------------------------------------%
% Построение u(t) и X(t)
figure(3);
plot(time_X, u, 'r-', 'LineWidth', 2)
title ('u(t)');
xlabel('t')
grid on
figure(4);
plot(time_X, X(1,:), 'LineWidth', 2)
hold on
title ('x_1(t)');
xlabel('t')
grid on
figure(5);
plot(time_X, X(2,:), 'LineWidth', 2)
title ('x_2(t)');
xlabel('t')
grid on
figure(6);
plot(time_X, X(3,:), 'LineWidth', 2)
title ('x_3(t)');
xlabel('t')
grid on
figure(7);
plot(time_X, X(4,:), 'LineWidth', 2)
title ('x_4(t)');
xlabel('t')
grid on
figure(8);
plot(time_X, X(5,:), 'LineWidth', 2)
title ('x_5(t)');
xlabel('t')
grid on
save Sravnenie_stabilizacii_2 time_X X u
Sravnenie_stabilizacii.m
close all
load Sravnenie_stabilizacii_1 X21 X22 X23 X24 X25 uu1
load Sravnenie_stabilizacii_2 time_X X u
figure(31);
plot(time_X, u, time_X, uu1, 'LineWidth', 2)
title ('u(t)');
xlabel('t')
hl=legend('u(t) - управление с перемен. коеф.','u(t) - управление с пост. коеф.');
set(hl,'FontName','Courier');
grid on
figure(41);
plot(time_X, X(1,:), time_X, X21, 'LineWidth', 2)
hold on
title ('x_1(t)');
xlabel('t')
hl=legend('x_1(t) - с перемен. коеф.','x_1(t) - с пост. коеф.');
set(hl,'FontName','Courier');
grid on
figure(51);
plot(time_X, X(2,:), time_X, X22,'LineWidth', 2)
title ('x_2(t)');
xlabel('t')
hl=legend('x_2(t) - с перемен. коеф.','x_2(t) - с пост. коеф.');
set(hl,'FontName','Courier');
grid on
figure(61);
plot(time_X, X(3,:), time_X, X23,'LineWidth', 2)
title ('x_3(t)');
xlabel('t')
hl=legend('x_3(t) - с перемен. коеф.','x_3(t) - с пост. коеф.');
set(hl,'FontName','Courier');
grid on
figure(71);
plot(time_X, X(4,:), time_X, X24,'LineWidth', 2)
title ('x_4(t)');
xlabel('t')
hl=legend('x_4(t) - с перемен. коеф.','x_4(t) - с пост. коеф.');
set(hl,'FontName','Courier');
grid on
figure(81);
plot(time_X, X(5,:), time_X, X25,'LineWidth', 2)
title ('x_5(t)');
xlabel('t')
hl=legend('x_5(t) - с перемен. коеф.','x_5(t) - с пост. коеф.');
set(hl,'FontName','Courier');
grid on
AKOR_stabilizaciya_pri_vozmusheniyah.m
clc
clear all
close all
warning off
poryadok = 5;
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4];
B = [0; 0; 0; 0; 1];
C = [b0 b1 0 0 0];
% Начальные условия
X_0 = [10; 0; 6; 4; 8];
Time = 1;
h = 0.01;
% ------------------------------------------------------------------------%
tic
% ------------------------------------------------------------------------%
% Получение max значений из файла
load Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% Нахождение элементов матриц Q и R
r(1) = 100;
q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;
for i = 2 : poryadok
q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;
end
Q = diag(q);
R = diag(r);
% Для изменения коэффициентов
Q(1,1) = Q(1,1)*1e+12;
Q(2,2) = Q(2,2)*1e+8;
Q(3,3) = Q(3,3)*1e+7;
Q(4,4) = Q(4,4)*1e+0;
Q(5,5) = Q(5,5)*1e+2;
R(1,1) = R(1,1);
% P_0 = ones(poryadok, poryadok);
% P_0(1,1) = P_0(1,1)*1e12;
% P_0(2,2) = P_0(2,2)*1e8;
% P_0(3,3) = P_0(3,3)*1e7;
% P_0(4,4) = P_0(4,4)*1e0;
% P_0(5,5) = P_0(5,5)*1e2;
% ------------------------------------------------------------------------%
P_nach = zeros(poryadok, poryadok);%+P_0;
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом обратного интегрирования
P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach);
load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str
PP = P;
for k = 1 : N_str
P1 = reshape(PP(k, :), poryadok, poryadok);
for i = 1 : poryadok
for j = 1 : poryadok
P2(i,j,k) = P1(i,j);
end
end
end
size_P = size(P2);
% ------------------------------------------------------------------------%
tic
% ------------------------------------------------------------------------%
% Получение дискретных значений задающего воздействия в обратном времени
% для нахождения вспомогательной функции q(t)
Vozmyshyayushee_Vozdeistvie_Discrete_Revers(h, 0, Time);
% ------------------------------------------------------------------------%
load Vozmyshyayushee_Vozdeistvie_Discrete_Revers w_discrete_rev
% ------------------------------------------------------------------------%
size(w_discrete_rev);
% Начальное значение q(t)
q = zeros(poryadok,1);
% Интегрирование q(t) в обратном времени
for k = 1 : N_str
q(:, k+1) = q(:, k) - h * ((P2(:,:,k)*B*inv(R)*B'-A') * q(:, k) - P2(:,:,k)*w_discrete_rev(:,k));
end
q(:, k+1) = [];
size_q = size(q);
% ------------------------------------------------------------------------%
% Нахождение переменных коэффициентов регулятора
for k = 1 : N_str
K_o(k, :) = -inv(R) * B' * P2(:,:,k);
K_pr(k, :) = -inv(R) * B';
end
% Формирование вектора коэффициентов регулятора, значений задающего
% воздействия, значений вспомогательной функции в прямом порядке
size(K_o);
size(K_pr);
K_pr_p = K_pr;
i = 1;
len_K = length(K_o(:,1));
for j = len_K : -1 : 1
K_o_p(i,:) = K_o(j,:);
w_discrete(:,i) = w_discrete_rev(:,j);
q_pr(:, i) = q(:, j);
i = i + 1;
end
% ------------------------------------------------------------------------%
% Построение графика переменных коэффициентов регулятора обратной связи
% в прямом времени
toc
figure(3)
plot(Time_R,K_o(:,1),'-',Time_R,K_o(:,2),'-',Time_R,K_o(:,3),'-',...
Time_R,K_o(:,4),'-',Time_R,K_o(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты обратной связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Построение графика переменных коэффициентов регулятора прямой связи
% в прямом времени
figure(4)
plot(Time_R,K_pr(:,1),'-',Time_R,K_pr(:,2),'-',Time_R,K_pr(:,3),'-',...
Time_R,K_pr(:,4),'-',Time_R,K_pr(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты прямой связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_п_с','k_2_п_с','k_3_п_с','k_4_п_с','k_5_п_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
tic
% ------------------------------------------------------------------------%
for k = 1 : len_K
A_(:,:,k) = A + B * K_o_p(k,:);
end
size_A_ = size(A_);
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение фазовых координат
X(:,1) = X_0;
time_X(1) = 0;
for k = 1 : len_K
X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * q_pr(:,k) + w_discrete(:,k));
time_X(k+1) = time_X(k) + h;
end
X(:, k+1) = [];
time_X(k+1) = [];
size_X = size(X);
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение управления
for k = 1 : len_K
u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * q_pr(:,k);
end
size_u = size(u);
% ------------------------------------------------------------------------%
toc
% Построение u(t) и X(t)
figure(5);
plot(time_X, u, 'r-', 'LineWidth', 2)
title ('u(t)');
xlabel('t')
hl=legend('u(t) - управление',0);
set(hl,'FontName','Courier');
grid on
figure(6);
plot(time_X, X(1,:),'r-', time_X, w_discrete(1,:), 'LineWidth', 2)
hold on
title ('x_1(t)');
xlabel('t');
hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);
set(hl,'FontName','Courier');
grid on
figure(7);
plot(time_X, X(2,:),'r-', time_X, w_discrete(2,:), 'LineWidth', 2)
title ('x_2(t)');
xlabel('t');
hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);
set(hl,'FontName','Courier');
grid on
figure(8);
plot(time_X, X(3,:),'r-', time_X, w_discrete(3,:), 'LineWidth', 2)
title ('x_3(t)');
xlabel('t');
hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);
set(hl,'FontName','Courier');
grid on
figure(9);
plot(time_X, X(4,:),'r-', time_X, w_discrete(4,:), 'LineWidth', 2)
title ('x_4(t)');
xlabel('t');
hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);
set(hl,'FontName','Courier');
grid on
figure(10);
plot(time_X, X(5,:),'r-', time_X, w_discrete(5,:), 'LineWidth', 2)
title ('x_5(t)');
xlabel('t');
hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);
set(hl,'FontName','Courier');
grid on
figure(11);
plot(time_X, q(1,:), time_X, q(2,:), time_X, q(3,:), time_X, q(4,:), time_X, q(5,:), 'LineWidth', 2)
title ('q(t)- vector-function');
xlabel('t');
hl=legend('q_1(t)', 'q_2(t)', 'q_3(t)', 'q_4(t)', 'q_5(t)');
set(hl,'FontName','Courier');
grid on
AKOR_slegenie_na_konech_interval_I_podxod.m
clc
clear all
close all
poryadok = 5;
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4];
B = [0; 0; 0; 0; 1];
C = [b0 b1 0 0 0];
% Начальные условия
X_0 = [10; 0; 6; 4; 8;];
Time = 1;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Получение max значений из файла
load Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% Нахождение элементов матриц Q и R
r(1) = 100;
q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;
for i = 2 : poryadok
q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;
end
Q = diag(q);
R = diag(r);
% Для изменения коэффициентов
% Q(1,1) = Q(1,1)*1e+10;
% Q(2,2) = Q(2,2)*1e+8;
% Q(3,3) = Q(3,3)*1e+6;
% Q(4,4) = Q(4,4)*1e+2;
% Q(5,5) = Q(5,5)*1e+2;
Q(1,1) = Q(1,1)*1e+12;
Q(2,2) = Q(2,2)*1e+8;
Q(3,3) = Q(3,3)*1e+7;
Q(4,4) = Q(4,4)*1e+0;
Q(5,5) = Q(5,5)*1e+2;
R(1,1) = R(1,1);
% ------------------------------------------------------------------------%
% Задающее воздействие
A_o = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4];
X_o_0 = [12; 10; 14; 8; 16];
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Расширенный вектор состояния и расширенные матрицы A,B,Q
%X_rassh = [X_0; X_o];
NULL_M1 = zeros(size(A));
A_rassh = [A NULL_M1;
NULL_M1 A_o];
NULL_M2 = zeros(length(A(:,1)), 1);
B_rassh = [B; NULL_M2];
Q_rassh = [Q -Q;
-Q Q];
X_rassh_0 = [X_0; X_o_0]
% ------------------------------------------------------------------------%
P_nach = zeros(2*poryadok, 2*poryadok);%+ones(poryadok, poryadok);
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом обратного интегрирования
P = Solve_Riccati_Method_Revers_Integr(A_rassh,B_rassh,Q_rassh,R,Time,2*poryadok, P_nach)
% ------------------------------------------------------------------------%
% Нахождение переменных коэффициентов регулятора
load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str
% ------------------------------------------------------------------------%
% % Формирование матриц P11 и P12
PP = P;
for k = 1 : N_str
P = reshape(PP(k, :), 2*poryadok, 2*poryadok);
for i = 1 : poryadok
for j = 1 : poryadok
P11(i,j,k) = P(i,j);
end
end
for i = 1 : poryadok
for j = (poryadok+1) : (2*poryadok)
P12(i,j-poryadok,k) = P(i,j);
end
end
end
P11(:,:,k)
P12(:,:,k)
% ------------------------------------------------------------------------%
for k = 1 : N_str
K_o(k, :) = -inv(R) * B' * P11(:,:,k);
K_pr(k, :) = -inv(R) * B' * P12(:,:,k);
end
% Формирование вектора коэффициентов регулятора
% в прямом порядке
size(K_o)
size(K_pr)
i = 1;
len_K = length(K_o(:,1))
for j = len_K : -1 : 1
K_o_p(i,:) = K_o(j,:)
K_pr_p(i,:) = K_pr(j,:);
i = i + 1;
end
% ------------------------------------------------------------------------%
% Построение графика переменных коэффициентов регулятора обратной связи
% в прямом времени
figure(2)
plot(Time_R,K_o(:,1),'-',Time_R,K_o(:,2),'-',Time_R,K_o(:,3),'-',...
Time_R,K_o(:,4),'-',Time_R,K_o(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты обратной связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Построение графика переменных коэффициентов регулятора прямой связи
% в прямом времени
figure(3)
plot(Time_R,K_pr(:,1),'-',Time_R,K_pr(:,2),'-',Time_R,K_pr(:,3),'-',...
Time_R,K_pr(:,4),'-',Time_R,K_pr(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты прямой связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_п_с','k_2_п_с','k_3_п_с','k_4_п_с','k_5_п_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение отслеживаемого сигнала
X_o(:,1) = X_o_0;
h = 0.01;
for k = 1 : len_K
X_o(:, k+1) = X_o(:, k) + h * A_o * X_o(:, k);
end
X_o(:, k+1) = [];
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
for k = 1 : len_K
A_(:,:,k) = A + B * K_o_p(k,:);
end
size(A_)
% ------------------------------------------------------------------------%
% Нахождение фазовых координат
X(:,1) = X_0;
time_X(1) = 0;
for k = 1 : len_K
X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * X_o(:,k));
time_X(k+1) = time_X(k) + h;
end
X(:, k+1) = [];
time_X(k+1) = [];
% ---------------------------------------------------------------------%
% Нахождение управления
for k = 1 : len_K
u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * X_o(:,k);
end
% ------------------------------------------------------------------------%
% Построение u(t) и X(t)
figure(4);
plot(time_X, u, 'r-', 'LineWidth', 2)
title ('u(t)');
xlabel('t')
hl=legend('u(t) - управление',0);
set(hl,'FontName','Courier');
grid on
figure(5);
plot(time_X, X(1,:),'r-', time_X, X_o(1,:), 'LineWidth', 2)
hold on
title ('x_1(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(6);
plot(time_X, X(2,:),'r-', time_X, X_o(2,:), 'LineWidth', 2)
title ('x_2(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(7);
plot(time_X, X(3,:),'r-', time_X, X_o(3,:), 'LineWidth', 2)
title ('x_3(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(8);
plot(time_X, X(4,:),'r-', time_X, X_o(4,:), 'LineWidth', 2)
title ('x_4(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(9);
plot(time_X, X(5,:),'r-', time_X, X_o(5,:), 'LineWidth', 2)
title ('x_5(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
AKOR_slegenie_na_konech_interval_II_podxod.m
clc
clear all
close all
poryadok = 5;
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4];
B = [0; 0; 0; 0; 1];
C = [b0 b1 0 0 0];
% Начальные условия
X_0 = [10; 0; 6; 4; 8];
Time = 45;
h = 0.01;
H = 0.8;
% ------------------------------------------------------------------------%
tic
% ------------------------------------------------------------------------%
% Получение max значений из файла
load Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% Нахождение элементов матриц Q и R
r(1) = 100;
q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;
for i = 2 : poryadok
q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;
end
Q = diag(q);
R = diag(r);
% Для изменения коэффициентов
% Q(1,1) = Q(1,1)*1e+12;
% Q(2,2) = Q(2,2)*1e+8;
% Q(3,3) = Q(3,3)*1e+7;
% Q(4,4) = Q(4,4)*1e+0;
% Q(5,5) = Q(5,5)*1e+2;
R(1,1) = R(1,1);
% ------------------------------------------------------------------------%
P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом обратного интегрирования
P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach);
load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str
PP = P;
for k = 1 : N_str
P1 = reshape(PP(k, :), poryadok, poryadok);
for i = 1 : poryadok
for j = 1 : poryadok
P2(i,j,k) = P1(i,j);
end
end
end
size_P = size(P2)
% ------------------------------------------------------------------------%
tic
% ------------------------------------------------------------------------%
% Получение дискретных значений задающего воздействия в обратном времени
% для нахождения вспомогательной функции q(t)
Zadayushee_Vozdeistvie_Discrete_Revers_Modern(h, 0, Time);
% ------------------------------------------------------------------------%
load Zadayushee_Vozdeistvie_Discrete_Revers X_o_discrete_rev
% ------------------------------------------------------------------------%
size(X_o_discrete_rev);
% Нахождение q(t)
for i = 1 : poryadok
qq = -P_nach(:,:,1) * X_o_discrete_rev(i,1);
q(i,1) = qq(i,1);
end
% Интегрирование q(t) в обратном времени
for k = 1 : N_str
q(:, k+1) = q(:, k) - h * ((P2(:,:,k)*B*inv(R)*B'-A') * q(:, k) + Q*X_o_discrete_rev(:,k));
end
q(:, k+1) = [];
size_q = size(q)
% ------------------------------------------------------------------------%
% Нахождение переменных коэффициентов регулятора
for k = 1 : N_str
K_o(k, :) = -inv(R) * B' * P2(:,:,k);
K_pr(k, :) = -inv(R) * B';
end
% Формирование вектора коэффициентов регулятора, значений задающего
% воздействия, значений вспомогательной функции в прямом порядке
size(K_o);
size(K_pr);
K_pr_p = K_pr;
i = 1;
len_K = length(K_o(:,1));
for j = len_K : -1 : 1
K_o_p(i,:) = K_o(j,:);
X_o_discrete(:,i) = X_o_discrete_rev(:,j);
q_pr(:, i) = q(:, j);
i = i + 1;
end
% ------------------------------------------------------------------------%
% Построение графика переменных коэффициентов регулятора обратной связи
% в прямом времени
toc
figure(3)
plot(Time_R,K_o(:,1),'-',Time_R,K_o(:,2),'-',Time_R,K_o(:,3),'-',...
Time_R,K_o(:,4),'-',Time_R,K_o(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты обратной связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Построение графика переменных коэффициентов регулятора прямой связи
% в прямом времени
figure(4)
plot(Time_R,K_pr(:,1),'-',Time_R,K_pr(:,2),'-',Time_R,K_pr(:,3),'-',...
Time_R,K_pr(:,4),'-',Time_R,K_pr(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты прямой связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_п_с','k_2_п_с','k_3_п_с','k_4_п_с','k_5_п_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
tic
% ------------------------------------------------------------------------%
for k = 1 : len_K
A_(:,:,k) = A + B * K_o_p(k,:);
end
size_A_ = size(A_)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение фазовых координат
X(:,1) = X_0;
time_X(1) = 0;
for k = 1 : len_K
X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * q_pr(:,k));
time_X(k+1) = time_X(k) + h;
end
X(:, k+1) = [];
time_X(k+1) = [];
size_X = size(X)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение управления
for k = 1 : len_K
u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * q_pr(:,k);
end
size_u = size(u)
% ------------------------------------------------------------------------%
toc
% Построение u(t) и X(t)
figure(5);
plot(time_X, u, 'r-', 'LineWidth', 2)
title ('u(t)');
xlabel('t')
hl=legend('u(t) - управление',0);
set(hl,'FontName','Courier');
grid on
figure(6);
plot(time_X, X(1,:),'r-', time_X, X_o_discrete(1,:), time_X, X_o_discrete(1,:)-0.8,'LineWidth', 2)
hold on
title ('x_1(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон', 'уровень',0);
set(hl,'FontName','Courier');
grid on
figure(7);
plot(time_X, X(2,:),'r-', time_X, X_o_discrete(2,:), 'LineWidth', 2)
title ('x_2(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(8);
plot(time_X, X(3,:),'r-', time_X, X_o_discrete(3,:), 'LineWidth', 2)
title ('x_3(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(9);
plot(time_X, X(4,:),'r-', time_X, X_o_discrete(4,:), 'LineWidth', 2)
title ('x_4(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(10);
plot(time_X, X(5,:),'r-', time_X, X_o_discrete(5,:), 'LineWidth', 2)
title ('x_5(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
AKOR_slegenie_so_skolz_intervalami_Modern.m
function AKOR_slegenie_so_skolz_intervalami_Modern
clc
clear all
close all
poryadok = 5;
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4];
B = [0; 0; 0; 0; 1];
C = [b0 b1 0 0 0];
% Начальные условия
X_0 = [10; 0; 6; 4; 8];
Time = 45;
Kolvo_intervalov = 3;
h = 0.01;
H = 0.8;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Получение max значений из файла
load Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% Нахождение элементов матриц Q и R
r(1) = 100;
q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;
for i = 2 : poryadok
q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;
end
Q = diag(q);
R = diag(r);
% Для изменения коэффициентов
% Q(1,1) = Q(1,1)*1e+13;
% Q(2,2) = Q(2,2)*1e+10;
% Q(3,3) = Q(3,3)*1e+8;
% Q(4,4) = Q(4,4)*1e+5;
% Q(5,5) = Q(5,5)*1e+2;
R(1,1) = R(1,1);
% ------------------------------------------------------------------------%
% ------------------Скользящие интервалы----------------------------------%
shag = Time/Kolvo_intervalov;
Time1 = shag
Time2 = 2*shag
Time3 = Time
% ------------------------------------------------------------------------%
P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом обратного интегрирования
P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time1,poryadok, P_nach);
load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str
PP = P;
for k = 1 : N_str
P1 = reshape(PP(k, :), poryadok, poryadok);
for i = 1 : poryadok
for j = 1 : poryadok
P2(i,j,k) = P1(i,j);
end
end
end
size_P = size(P2)
% ------------------------------------------------------------------------%
% Нахождение переменных коэффициентов регулятора
for k = 1 : N_str
K_o(k, :) = -inv(R) * B' * P2(:,:,k);
K_pr(k, :) = -inv(R) * B';
end
% ------------------------------------------------------------------------%
tic
% 1 интервал
Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, 0, Time1, X_0, poryadok, K_o, K_pr);
load Solve_Interval time_X X u X_o_discrete
time_X1 = time_X;
X1 = X;
u1 = u;
X_o_discrete1 = X_o_discrete;
% 2 интервал
Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, Time1, Time2, X1(:,N_str), poryadok, K_o, K_pr);
load Solve_Interval time_X X u X_o_discrete
time_X2 = time_X;
X2 = X;
u2 = u;
X_o_discrete2 = X_o_discrete;
% 3 интервал
Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, Time2, Time3, X2(:,N_str), poryadok, K_o, K_pr);
load Solve_Interval time_X X u X_o_discrete
time_X3 = time_X;
X3 = X;
u3 = u;
X_o_discrete3 = X_o_discrete;
toc
% ------------------------------------------------------------------------%
% Объединение интервалов
time_X = [time_X1 time_X2 time_X3];
u = [u1 u2 u3];
X = [X1 X2 X3];
X_o_discrete = [X_o_discrete1 X_o_discrete2 X_o_discrete3];
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Построение u(t) и X(t)
figure(3);
plot(time_X, u, 'r-','LineWidth', 2);
title ('u(t)');
xlabel('t')
hl=legend('u(t) - управление',0);
set(hl,'FontName','Courier');
grid on
figure(4);
plot(time_X, X(1,:),'r-', time_X, X_o_discrete(1,:), time_X, X_o_discrete(1,:)-0.8,'LineWidth', 2)
hold on
title ('x_1(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон', 'уровень',0);
set(hl,'FontName','Courier');
grid on
figure(5);
plot(time_X, X(2,:),'r-', time_X, X_o_discrete(2,:), 'LineWidth', 2)
title ('x_2(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(6);
plot(time_X, X(3,:),'r-', time_X, X_o_discrete(3,:), 'LineWidth', 2)
title ('x_3(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(7);
plot(time_X, X(4,:),'r-', time_X, X_o_discrete(4,:), 'LineWidth', 2)
title ('x_4(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
figure(8);
plot(time_X, X(5,:),'r-', time_X, X_o_discrete(5,:), 'LineWidth', 2)
title ('x_5(t)');
xlabel('t');
hl=legend('X(t) - слежение','X_o(t) - эталон',0);
set(hl,'FontName','Courier');
grid on
function Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, T_nach, T_konech, X_0, poryadok, K_o, K_pr)
Zadayushee_Vozdeistvie_Discrete_Revers_Modern(h, T_nach, T_konech);
load Zadayushee_Vozdeistvie_Discrete_Revers X_o_discrete_rev
% ------------------------------------------------------------------------%
% Нахождение q(t)
for i = 1 : poryadok
qq = -P_nach(:,:,1) * X_o_discrete_rev(i,1);
q(i,1) = qq(i,1);
end
% Интегрирование q(t) в обратном времени
for k = 1 : N_str
q(:, k+1) = q(:, k) - h * ((P2(:,:,k)*B*inv(R)*B'-A') * q(:, k) + Q*X_o_discrete_rev(:,k));
end
q(:, k+1) = [];
size_q = size(q)
% ------------------------------------------------------------------------%
% Формирование вектора коэффициентов регулятора, значений задающего
% воздействия, значений вспомогательной функции в прямом порядке
K_pr_p = K_pr;
i = 1;
for j = N_str : -1 : 1
K_o_p(i,:) = K_o(j,:);
X_o_discrete(:,i) = X_o_discrete_rev(:,j);
q_pr(:, i) = q(:, j);
i = i + 1;
end
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
for k = 1 : N_str
A_(:,:,k) = A + B * K_o_p(k,:);
end
size_A_ = size(A_)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение фазовых координат
X(:,1) = X_0;
time_X(1) = T_nach;
for k = 1 : N_str
X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * q_pr(:,k));
time_X(k+1) = time_X(k) + h;
end
X(:, k+1) = [];
time_X(k+1) = [];
size_X = size(X)
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение управления
for k = 1 : N_str
u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * q_pr(:,k);
end
size_u = size(u)
save Solve_Interval time_X X u X_o_discrete
Sintez_nablyud_polnogo_poryadka.m
clc
clear all
close all
poryadok = 5;
% ------------------------------------------------------------------------%
b_0 = 5;
b_1 = 9;
% Укороченная система данного объекта
a_5 = 0.1153;
a_4 = 1.78;
a_3 = 3.92;
a_2 = 14.42;
a_1 = 8.583;
a_0 = 0;
% ------------------------------------------------------------------------%
% Приведение системы
b0 = b_0/a_5;
b1 = b_1/a_5;
a5 = a_5/a_5;
a4 = a_4/a_5;
a3 = a_3/a_5;
a2 = a_2/a_5;
a1 = a_1/a_5;
a0 = a_0/a_5;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Представление системы в пространстве состояний
A = [0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0;
0 0 0 0 1;
-a0 -a1 -a2 -a3 -a4]
B = [0; 0; 0; 0; 1]
C = [b0 b1 0 0 0]
% Начальные условия
X_0 = [10; 0; 6; 4; 8]
Time = 10;
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Получение max значений из файла
load Sostoyaniya X_max U_max
% ------------------------------------------------------------------------%
% Нахождение элементов матриц Q и R
r(1) = 100;
q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;
for i = 2 : poryadok
q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;
end
Q = diag(q)
R = diag(r)
% Для изменения коэффициентов
Q(1,1) = Q(1,1);
Q(2,2) = Q(2,2);
Q(3,3) = Q(3,3);
Q(4,4) = Q(4,4);
Q(5,5) = Q(5,5);
% Q(1,1) = Q(1,1)*1e+12;
% Q(2,2) = Q(2,2)*1e+8;
% Q(3,3) = Q(3,3)*1e+7;
% Q(4,4) = Q(4,4)*1e+0;
% Q(5,5) = Q(5,5)*1e+2;
R(1,1) = R(1,1);
% ------------------------------------------------------------------------%
P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);
% ------------------------------------------------------------------------%
% Решение уравнения Риккати методом обратного интегрирования
P1 = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach)
% ------------------------------------------------------------------------%
% Построение графика коэффициентов регулятора
load Solve_Riccati_Method_Revers_Integr Time_R P N_str
PP = P;
for i = 1 : N_str
P = reshape(PP(i, :), poryadok, poryadok);
K(i, :) = -inv(R)*B'*P;
end
figure(2)
plot(Time_R,K(:,1),'-',Time_R,K(:,2),'-',Time_R,K(:,3),'-',Time_R,K(:,4),'-',Time_R,K(:,5),'-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Коэффициенты обратной связи в прямом времени');
set(tit1,'FontName','Courier');
hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);
set(hl,'FontName','Courier');
grid on;
% ------------------------------------------------------------------------%
% Нахождение коэффициентов регулятора
disp('Коэффициенты регулятора:')
K = -inv(R) * B' * P1
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
A_ = A + B * K;
% ------------------------------------------------------------------------%
% Нахождение фазовых координат
X(:,1) = X_0;
h = 0.01;
time_X(1) = 0;
for k = 1 : N_str
X(:, k+1) = X(:, k) + h * A_ * X(:, k);
time_X(k+1) = time_X(k) + h;
end
X(:, k+1) = [];
time_X(k+1) = [];
% ------------------------------------------------------------------------%
% Нахождение управления
for k = 1 : N_str
u(k) = K * X(:,k);
end
% ------------------------------------------------------------------------%
% Нахождение коэффициентов наблюдателя
M_n = [C' A'*C' (A^2)'*C' (A^3)'*C' (A^4)'*C']
rank_M_n = rank(M_n)
A_r = A_
disp('Спектр матрицы регулятора:')
spektr_A_r = eig(A_r)
koeff = 1;
min_lyamda_A_r = min(real(spektr_A_r))
% lyamda = min_lyamda_A_r * koeff;
lyamda = -5;
disp('Спектр матрицы наблюдателя эталонный:')
lyamda_A_n = [lyamda - koeff * 4; lyamda - koeff * 3; lyamda - koeff * 2;...
lyamda - koeff; lyamda]'
syms k_n1 k_n2 k_n3 k_n4 k_n5 lyam
K_n = [k_n1; k_n2; k_n3; k_n4; k_n5];
Koeff_poly_n_etalon = poly(lyamda_A_n)
disp('Характеристический полином наблюдателя эталонный:')
poly_n_etalon = poly2sym(Koeff_poly_n_etalon, lyam)
disp('Характеристический полином наблюдателя реальный:')
poly_n_real = collect(expand(simplify(det(lyam*eye(poryadok) - (A - K_n*C)))),lyam)
raznost_poly = collect(poly_n_etalon-poly_n_real,lyam)
for i = 1 : poryadok
Koeff_raznost_poly(i) = subs(diff(raznost_poly,poryadok-i,lyam)/factorial(poryadok-i),lyam,0);
end
Koeff_raznost_poly
[Kn1 Kn2 Kn3 Kn4 Kn5]= solve(Koeff_raznost_poly(5), Koeff_raznost_poly(4),...
Koeff_raznost_poly(3), Koeff_raznost_poly(2), Koeff_raznost_poly(1), ...
k_n1, k_n2, k_n3, k_n4, k_n5)
Kn = [Kn1; Kn2; Kn3; Kn4; Kn5];
Kn = vpa(Kn,50)
% Проверка
Proverka = solve(det(lyam*eye(poryadok)-(A-Kn*C)))
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение x и x_оценочного
X_ocen_0 = [0 0 0 0 0]';
A_rash = [A B*K;
Kn*C A-Kn*C+B*K]
X_rash_0 = [X_0;X_ocen_0]
X_rash(:,1) = X_rash_0;
for k = 1 : N_str
X_rash(:,k+1) = X_rash(:,k) + h * A_rash * X_rash(:,k);
end
X_rash(:,k+1) = [];
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Разделение x и x_оценочного
for i = 1 : poryadok
X_n(i,:) = X_rash(i,:);
end
for i = poryadok + 1 : 2*poryadok
X_n_ocen(i - poryadok,:) = X_rash(i,:);
end
% ------------------------------------------------------------------------%
% ------------------------------------------------------------------------%
% Нахождение управления
for i = 1 : N_str
u_n(i) = K * X_n_ocen(:,i);
end
% Построение u(t) и X(t)
figure(3);
plot(time_X, u, 'r-', time_X, u_n, 'b-', 'LineWidth', 2)
title ('u(t)');
xlabel('t')
hl=legend('управление без наблюдателя','управление c наблюдателем');
set(hl,'FontName','Courier');
grid on
figure(4);
plot(time_X, X(1,:), time_X, X_n(1,:), time_X, X_n_ocen(1,:),'LineWidth', 2)
hold on
title ('x_1(t)');
xlabel('t')
hl=legend('x_1(t) без наблюдателя','x_1(t) c наблюдателем', 'x_о_ц_е_н_1(t)');
set(hl,'FontName','Courier');
grid on
figure(5);
plot(time_X, X(2,:), time_X, X_n(2,:), time_X, X_n_ocen(2,:),'LineWidth', 2)
title ('x_2(t)');
xlabel('t')
hl=legend('x_2(t) без наблюдателя','x_2(t) c наблюдателем', 'x_о_ц_е_н_2(t)');
set(hl,'FontName','Courier');
grid on
figure(6);
plot(time_X, X(3,:), time_X, X_n(3,:), time_X, X_n_ocen(3,:),'LineWidth', 2)
title ('x_3(t)');
xlabel('t')
hl=legend('x_3(t) без наблюдателя','x_3(t) c наблюдателем', 'x_о_ц_е_н_3(t)');
set(hl,'FontName','Courier');
grid on
figure(7);
plot(time_X, X(4,:), time_X, X_n(4,:), time_X, X_n_ocen(4,:),'LineWidth', 2)
title ('x_4(t)');
xlabel('t')
hl=legend('x_4(t) без наблюдателя','x_4(t) c наблюдателем', 'x_о_ц_е_н_4(t)');
set(hl,'FontName','Courier');
grid on
figure(8);
plot(time_X, X(5,:), time_X, X_n(5,:), time_X, X_n_ocen(5,:),'LineWidth', 2)
title ('x_5(t)');
xlabel('t')
hl=legend('x_5(t) без наблюдателя','x_5(t) c наблюдателем', 'x_о_ц_е_н_5(t)');
set(hl,'FontName','Courier');
grid on
Solve_Riccati_Method_Diag.m
% ------------------------------------------------------------------------%
% Метод диагонализации для решения алгебраического уравнения Риккати
function P = Solve_Riccati_Method_Diag(A,B,Q,R)
% Расширенная матрица системы
Z = [A B*inv(R)*B';
Q -A']
% Нахождение собственных векторов и собственных чисел матрицы Z
[V,D] = eig(Z)
% ------------------------------------------------------------------------%
% Построение матрицы S
% Индексы столбцов собственных значений Re(lyamda) > 0
Ind_Re_plus = find(sum(real(D)) > 0);
% Индексы столбцов собственных значений Re(lyamda) < 0
Ind_Re_minus = find(sum(real(D)) < 0);
% Формирование матрицы D в виде Re(lyamda) > 0 -> Re(lyamda) < 0
D1 = sum(D(:, Ind_Re_plus));
D2 = sum(D(:, Ind_Re_minus));
D = [D1 D2];
% Формирование матрицы S в виде Re(lyamda) > 0 -> Re(lyamda) < 0
S1 = V(:, Ind_Re_plus);
S2 = V(:, Ind_Re_minus);
S = [S1 S2];
% Поиск столбцов с комплексными корнями в матрице D
Ind_Complex_D = find(imag(D) ~= 0);
% Формирование конечной матрицы S
for i = 1 : 2 : length(Ind_Complex_D)
S (:, Ind_Complex_D(i) + 1) = imag(S(:, Ind_Complex_D(i)));
S (:, Ind_Complex_D(i)) = real(S(:, Ind_Complex_D(i)));
end
S = S
% ------------------------------------------------------------------------%
poryadok = length(A(1,:));
S12 = S(1 : poryadok, poryadok+1 : 2*poryadok);
S22 = S(poryadok+1 : 2*poryadok, poryadok+1 : 2*poryadok);
% ------------------------------------------------------------------------%
% Вычисление матрицы P
P = -S22 * inv(S12);
Solve_Riccati_Method_Revers_Integr.m
% ------------------------------------------------------------------------%
% Решение уравнения Риккати интегрированием в обратном времени
function P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P1)
save For_Riccati A B Q R poryadok
% Решение дифференциального уравнения Риккати
P1 = reshape(P1, poryadok^2, 1);
[Time_R, P] = ode45(@Riccati, [Time : -0.01 : 0], P1);
[N_str, N_stolb] = size(P);
% Построение полученного решения
figure(1)
for i = 1 : poryadok^2
plot(Time_R, P(:,i),'-')
hold on
end
% plot(Time_R,P(:,1),'-',Time_R,P(:,2),'-',Time_R,P(:,3),'-',Time_R,P(:,4),'-',Time_R,P(:,5),'-',Time_R,P(:,6),'-',...
% Time_R,P(:,7),'-',Time_R,P(:,8),'-',Time_R,P(:,9),'-',Time_R,P(:,10),'-',Time_R,P(:,11),'-',Time_R,P(:,12),'-',...
% Time_R,P(:,13),'-',Time_R,P(:,14),'-',Time_R,P(:,15),'-',Time_R,P(:,16),'-',Time_R,P(:,17),'-',Time_R,P(:,18),'-',...
% Time_R,P(:,19),'-',Time_R,P(:,20),'-',Time_R,P(:,21),'-',Time_R,P(:,22),'-',Time_R,P(:,23),'-',Time_R,P(:,24),'-',...
% Time_R,P(:,25),'-', 'lineWidth', 2);
grid on;
tit1 = title('Решения уравнения Риккати');
set(tit1,'FontName','Courier');
xlabel('t');
% legend('p_1','p_2','p_3','p_4','p_5','p_6','p_7','p_8','p_9','p_1_0','p_1_1','p_1_2','p_1_3','p_1_4','p_1_5','p_1_6',...
% 'p_1_7','p_1_8','p_1_9','p_2_0','p_2_1','p_2_2','p_2_3','p_2_4','p_2_5');
save Solve_Riccati_Method_Revers_Integr Time_R P N_str
save Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str
P = reshape(P(N_str,:), poryadok, poryadok);
function dP = Riccati(Time,P)
load For_Riccati A B Q R poryadok
P = reshape(P, poryadok, poryadok);
% Дифференциальное уравнение Риккати
dP = -P*A - A'*P + P*B*inv(R)*B'*P - Q;
dP = reshape(dP, poryadok^2, 1);
Vozmyshyayushee_Vozdeistvie_Discrete_Revers.m
% Получение дискретных значений возмущающего воздействия в обратном времени
% для нахождения вспомогательной функции q(t)
function Vozmyshyayushee_Vozdeistvie_Discrete_Revers(h, T_nach, T_konech)
% ------------------------------------------------------------------------%
% Возмущающее воздействие
A = 1;
w = 4*pi;
k = 1;
RETURN = 1;
while RETURN == 1
disp('Возмущающее воздействие - const: 1')
disp('Возмущающее воздействие - A*sin(w*t): 2')
reply = input('Выберете возмущающее воздействие [1 или 2]: ', 's');
switch reply
case '1'
disp('Возмущающее воздействие - const')
for t = T_konech: -h : T_nach
w_discrete_rev(:, k) = [A + 0 * t; 0; 0; 0; 0];
k = k + 1;
end
RETURN = 2;
case '2'
disp('Возмущающее воздействие - A*sin(w*t)')
for t = T_konech: -h : T_nach
w_discrete_rev(:, k) = [A * sin(w * t); 0; 0; 0; 0];
k = k + 1;
end
RETURN = 2;
otherwise
disp('Неизвестное воздействие.')
RETURN = 1;
end
end
figure(2)
t = T_konech : -h : T_nach;
plot(t, w_discrete_rev(1,:), 'r-', 'LineWidth', 2);
xlabel('t')
tit1 = title('Возмущающее воздействие');
set(tit1,'FontName','Courier');
hl=legend('Возмущающее воздействие',0);
set(hl,'FontName','Courier');
grid on;
save Vozmyshyayushee_Vozdeistvie_Discrete_Revers w_discrete_rev
% ------------------------------------------------------------------------%
Zadayushee_Vozdeistvie_Discrete_Revers_Modern.m
% Получение дискретных значений задающего воздействия в обратном времени
% для нахождения вспомогательной функции q(t)
function Zadayushee_Vozdeistvie_Discrete_Revers_Modern(h, T_nach, T_konech)
% ------------------------------------------------------------------------%
% Задающее воздействие
alfa = 0.2;
beta = 10;
H = 0.8;
k = 1;
for t = T_konech: -h : T_nach
X_o_1 = 10*exp(-1/5*t)*t+4/5;
X_o_2 = -2*exp(-1/5*t)*t+10*exp(-1/5*t);
X_o_3 = 2/5*exp(-1/5*t)*t-4*exp(-1/5*t);
X_o_4 = -2/25*exp(-1/5*t)*t+6/5*exp(-1/5*t);
X_o_5 = 2/125*exp(-1/5*t)*t-8/25*exp(-1/5*t);
X_o_discrete_rev(:, k) = [X_o_1; X_o_2; X_o_3; X_o_4; X_o_5];
k = k + 1;
end
figure(2)
t = T_konech : -h : T_nach;
plot(t, X_o_discrete_rev(1,:), 'r-', t, X_o_discrete_rev(1,:)-H, 'LineWidth', 2);
xlabel('t')
tit1 = title('Задающее воздействие');
set(tit1,'FontName','Courier');
hl=legend('Отслеживание зад. возд. на H ','Задающее воздействие',0);
set(hl,'FontName','Courier');
grid on;
save Zadayushee_Vozdeistvie_Discrete_Revers X_o_discrete_rev
% ------------------------------------------------------------------------%