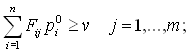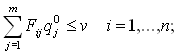Реферат: Математические методы экономики
В условиях рыночной системы управления производственной и сбытовой деятельностью предприятий и фирм в основе принятия хозяйственных решений лежит рыночная информация, а обоснованность решений проверяется рынком в ходе реализации товаров и услуг. При таком подходе основой предпринимательской деятельности становится изучение потребительского спроса.
Рассмотрим некоторые вопросы моделирования спроса и потребления.
Уровень потребления общества можно выразить целевой
функцией потребления U = U(Y), где Y ![]() О - вектор переменных разнообразных
товаров и услуг. Ряд свойств этой функции удобно изучать, используя геометрическую
интерпретацию уравнений U(Y) = С, где С - меняющийся параметр,
характеризующий значение (уровень) целевой функции потребления (например, доход
или уровень материального благосостояния).
О - вектор переменных разнообразных
товаров и услуг. Ряд свойств этой функции удобно изучать, используя геометрическую
интерпретацию уравнений U(Y) = С, где С - меняющийся параметр,
характеризующий значение (уровень) целевой функции потребления (например, доход
или уровень материального благосостояния).
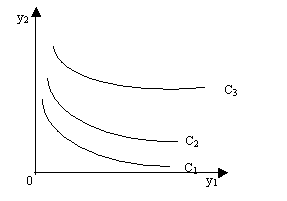
В совокупности потребительских благ каждому уравнению U(Y) = С соответствует определенная поверхность равноценных, или безразличных, наборов благ, которая называется поверхностью безразличия. Для наглядности рассмотрим пространство двух благ, например, в виде двух агрегированных групп товаров: продукты питания (y1) и непродовольственные товары, включая услуги (у2 ). Тогда уровни целевой функции потребления можно изобразить на плоскости в виде кривых безразличия, соответствующих различным значениям С (рис. 8.1, где С1 < С2 < Сз).
|
|
Рис. 8.1. График кривых безразличия
Из основных свойств целевой функции потребления можно отметит следующие:
1. функция U(Y) является возрастающей функцией всех своих аргументов, т.е. увеличение потребления любого блага при неизменном уровне потребления всех других благ увеличивает значение данной функции;
2. кривые безразличия не могут пересекаться, т.е. через одну точку совокупности благ (товаров, услуг) можно провести только одну поверхность безразличия;
3. кривые безразличия имеют отрицательный наклон к каждой оси координат, при этом абсолютный наклон кривых уменьшается при движении в положительном направлении по каждой оси, т.е. кривые безразличия являются выпуклыми кривыми.
Методы построения целевой функции потребления основаны на обобщении опыта поведения потребителей и тенденций покупательского спроса в зависимости от уровня благосостояния.
Рассмотрим моделирование поведения потребителей в условиях товарно-денежных отношений на базе целевой функции потребления. В основе модели поведения потребителей лежит гипотеза, что потребители, осуществляя выбор товаров при установленных ценах и имеющемся доходе, стремятся максимизировать уровень удовлетворения своих потребностей.
Пусть в совокупности п видов товаров исследуется поведение
потребителей. Обозначим спрос потребителей через вектор Y = (y1, у2,...,yn),
а цены на различные товары - через вектор Р = (р1, р2,…,pп).
Пусть D - величина дохода. Тогда потребители могут выбирать
только такие комбинации товаров, которые удовлетворяют ограничению 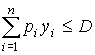 , называемому
бюджетным ограничением.
, называемому
бюджетным ограничением.
Пусть U(Y) целевая функция потребления. Тогда простейшая модель поведения потребителей в векторной форме можно записать в виде:
![]() (8.1)
(8.1)
Геометрическая интерпретация модели (8.1) для двух агрегированных групп товаров представлена на рис. 8.2.
Линия АВ (в других вариантах А1В1, А2В2) соответствует бюджетному ограничению и называется бюджетной линией. Выбор потребителей ограничен треугольником АОВ (A1OB1, A2OB2).
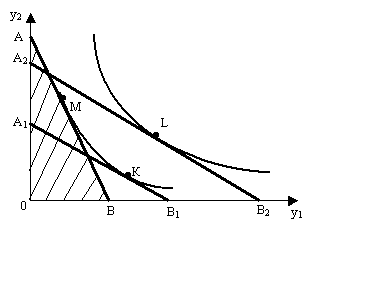
Рис. 8.2. График простейшей модели поведения потребителя
Набор товаров М, соответствующий точке касания прямой АВ с наиболее отдаленной кривой безразличия, является оптимальным решением (в других вариантах это точки К и L). Легко заметить, что линии АВ и A1B1 соответствуют одному и тому же размеру дохода и разным ценам на товары y1 и у2; линия A2B2 соответствует большему размеру дохода.
На основе теории нелинейного программирования, можно определить математические условия оптимальности решений для модели (8.1). С задачей нелинейного программирования связывается так называемая функция Лагранжа, которая для задачи (8.1) имеет вид
L(Y, l,) = U(Y) + l(D - PY),
где множитель Лагранжа l является оптимальной оценкой дохода.
Обозначим частные производные функции U(Y) через Ui:
![]()
Они представляют собой предельные полезные эффекты (предельные полезности) соответствующих потребительских благ и показывает на сколько единиц увеличивается целевая функция потребления при увеличении использования i-гоблага (товара) на некоторую условную «малую единицу».
Необходимыми условиями того что вектор Y0 будет оптимальным решением, является условия Куна-Таккера:
![]()
при этом![]()
![]() (товар
приобретается)
(товар
приобретается)
![]() (товар не
приобретается)
(8.2)
(товар не
приобретается)
(8.2)
![]()
Последнее из соотношений (8.2) соответствует полному
использованию дохода, и для этого случая очевидно неравенство ![]() .
.
Из условий оптимальности (8.2) следует, что
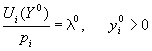
Это означает, что потребители должны выбрать товары таким образом, чтобы отношение предельной полезности к цене товара было одинаковым для всех приобретаемых товаров, т.е. в оптимальном наборе предельные полезности выбираемых товаров должны быть пропорциональны ценам.
Функциями спроса называются функции, отражающие зависимость объема спроса на отдельные товары и услуг от совокупности факторов, влияющих на него. Рассмотрим построение функций спроса в зависимости от двух факторов – дохода и цен.
Пусть в модели (8.1) цены и доход рассматриваются как
меняющиеся параметры. Переменную дохода будем обозначать Z. Тогда решением
оптимизационной задачи (8.1) будет векторная функция ![]() компонентами
которой являются функции спроса на определенный товар от цен и дохода:
компонентами
которой являются функции спроса на определенный товар от цен и дохода:
![]()
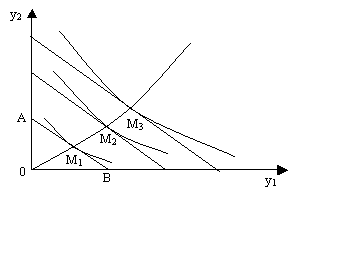
Рассмотрим частный случай, когда вектор цен является неизменным, а доход изменяется. Для двух товаров этот случай представлен на рис. 8.3. Если по оси абсцисс отложить количество единиц товара y1, которое можно приобрести на имеющий доход Z (точка В), а по оси ординат – то же самое для товара y2 (точка А), то прямая линия АВ, называемой бюджетной линией, показывает любую комбинацию количеств этих двух товаров, которую можно купить за сумму денег Z. При увеличении дохода бюджетные линии перемещаются параллельно самим себе, удаляясь от начала координат. Вместе с ними перемещаются соответствующие кривые безразличия. Точками оптимума спроса потребителей для соответствующих размеров дохода будут в данном случае точки M1, M2, M3. При нулевом доходе спрос на оба товара нулевой. Кривая, соединяющая точки 0, M1, M2, M3, является графическим отображением векторной функции спроса и дохода при заданном векторе цен.
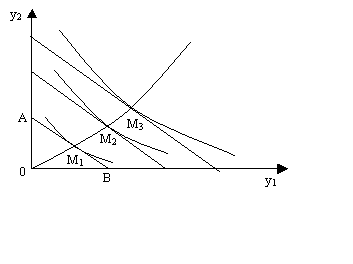
Рис. 8.3. График функции спроса и дохода (для двух товаров у1 и у2)
Однофакторные функции спроса от дохода широко применяются
при анализе покупательского спроса. Соответствующие этим функциям кривые ![]() называются
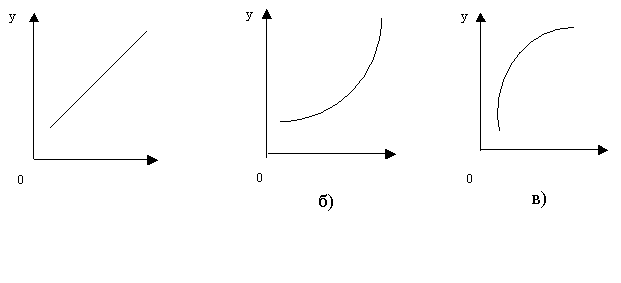
кривыми Энгеля (по имени немецкого экономиста). Формы этих кривых для
различных товаров могут быть различны. Если спрос на данный товар возрастает
примерно пропорционально доходу, то функция будет линейной (рис. 8.4а). Если по
мере роста дохода спрос на данную группу товаров возрастает все более высокими
темпами, то кривая Энгеля будет выпуклой (рис. 8.4б). Если рост значений
спроса, начиная с определенного момента, по мере насыщения спроса отстает от
роста дохода, то кривая Энгеля имеет вид вогнутой кривой (рис. 8.4в).
называются
кривыми Энгеля (по имени немецкого экономиста). Формы этих кривых для
различных товаров могут быть различны. Если спрос на данный товар возрастает
примерно пропорционально доходу, то функция будет линейной (рис. 8.4а). Если по
мере роста дохода спрос на данную группу товаров возрастает все более высокими
темпами, то кривая Энгеля будет выпуклой (рис. 8.4б). Если рост значений
спроса, начиная с определенного момента, по мере насыщения спроса отстает от
роста дохода, то кривая Энгеля имеет вид вогнутой кривой (рис. 8.4в).
предложил специальные виды функции спроса (функции Торнквиста) для трех групп товаров: первой необходимости, второй необходимости, предметов роскоши.
Важным показателем функции спроса является коэффициент эластичности. Коэффициент эластичности спроса от дохода показывает на сколько процентов, изменится спрос, если доход увеличится на 1% (при прочих не изменяющихся факторах), и вычисляется по формуле:
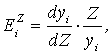
где ![]() - коэффициент
эластичности для i-го товара (группы товаров) по доходу Z;yi
- спрос на i-й товар, являющийся функцией дохода:
- коэффициент
эластичности для i-го товара (группы товаров) по доходу Z;yi
- спрос на i-й товар, являющийся функцией дохода: ![]() .
.
|
|
Рис. 8.4. Кривые Энгеля
Аналогичный принцип разграничения групп товаров по типам функций спроса от дохода использовал шведский экономист Л. Торнквист, который
Коэффициенты эластичности спроса от дохода различны по величине для разных товаров, вплоть до отрицательных значений, когда с ростом доходов потребление уменьшается. Принято выделять четыре группы товаров в зависимости от коэффициента эластичности спроса на них от дохода:
·
малоценные товары (![]() );
);
·
товары с малой эластичностью (![]() );
);
·
товары со средней эластичностью (![]() близки к единице);
близки к единице);
·
товары с высокой эластичностью (![]() ).
).
К малоценным товарам (с отрицательной эластичностью спроса от дохода) относятся хлеб, а также низкосортные товары. По результатам обследований, коэффициенты эластичности для основных продуктов питания находятся в интервале от 0,4 до 0,8, по одежде, тканям, обуви - в интервале от 1,1 до 1,3 и т.д. По мере увеличения дохода спрос перемещается с товаров первой и второй групп на товары третьей и четвертой групп, при этом потребление товаров первой группы по абсолютным размерам сокращается.
Перейдем к рассмотрению и анализу функций покупательского
спроса от цен на товары. Из модели поведения потребителей (8.1) следует, что
спрос на каждый товар в общем случае зависит от цен на все товары (вектора Р),
однако построить функции общего вида ![]() очень сложно. Поэтому в
практических исследованиях ограничиваются построением и анализом функций
спроса для отдельных товаров в зависимости от изменения цен на этот же товар
или группу взаимозаменяемых товаров:
очень сложно. Поэтому в
практических исследованиях ограничиваются построением и анализом функций
спроса для отдельных товаров в зависимости от изменения цен на этот же товар
или группу взаимозаменяемых товаров: ![]() .
.
Для большинства товаров действует зависимость: чем выше цена, тем ниже спрос, и наоборот. Относительное изменение объема спроса при изменении цены данного товара или цен других связанных с ним товаров характеризует коэффициент эластичности спроса от цен.Этот коэффициент эластичности удобно трактовать как величину изменения спроса в процентах при изменении цены на 1%.
Для спроса yi на i-й товар относительно его собственной цены pi коэффициент эластичности исчисляется по формуле:
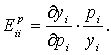 (8.4)
(8.4)
Значения коэффициентов эластичности спроса от цен практически всегда отрицательны. Однако по абсолютным значениям этих коэффициентов товары могут существенно различаться друг от друга. Их можно разделить на три группы:
- товары с неэластичным спросом в отношении цены ![]() ;
;
- товары со средней эластичностью спроса от цены (![]() близки к
-1);
близки к
-1);
- товар с высокой эластичностью спроса ![]() .
.
В товарах эластичного спроса повышение цены на 1% приводит к снижению спроса более чем на 1% и, наоборот, понижение цены на 1% приводит к росту покупок больше чем на 1%. Если повышение цены на 1% влечет за собой понижение спроса менее чем на 1%, то говорят, что этот товар неэластичного спроса.
Рассмотрим влияние на спрос на какой-либо товар изменения
цен на другие товары. Коэффициент, показывающий, на сколько процентов изменится
спрос на данный товар при изменении на 1% цены на другой товар при условии, что
другие цены и доходы покупателей остаются прежними, называется перекрестным
коэффициентом эластичности. Для спроса уi на i-й товар относительно
цены pj на j-й товар (![]() ) перекрестный коэффициент
эластичности рассчитывается по формуле:
) перекрестный коэффициент
эластичности рассчитывается по формуле:
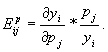 (8.5)
(8.5)
По знаку перекрестных коэффициентов эластичности товары
можно разделить на взаимозаменяемые и взаимодополняемые. Если ![]() , это
означает, что i-й товар заменяет в потреблении товар j, т.е. на товар i
переключается спрос при увеличении цены на товар j. Примером взаимозаменяемых
товаров могут служить многие продукты питания.
, это
означает, что i-й товар заменяет в потреблении товар j, т.е. на товар i
переключается спрос при увеличении цены на товар j. Примером взаимозаменяемых
товаров могут служить многие продукты питания.
Если ![]() , это служит признаком того,
что i-й товар в процессе потребления дополняет товар j, т.е. увеличение цены на
товар j приводит к уменьшению спроса на товар i. В качестве примера можно
привести такие взаимодополняемые товары, как автомобили и бензин, чай и сахар.
, это служит признаком того,
что i-й товар в процессе потребления дополняет товар j, т.е. увеличение цены на
товар j приводит к уменьшению спроса на товар i. В качестве примера можно
привести такие взаимодополняемые товары, как автомобили и бензин, чай и сахар.
Спрос во многом определяет стратегию и тактику организации производства и сбыта товаров и услуг. Учет спроса, обоснованное прогнозирование его на краткосрочную и долгосрочную перспективу - одна из важнейших задач различных организаций и фирм.
Состав и уровень спроса на тот или иной товар зависят от многих факторов, как экономических, так и естественных. К экономическим факторам относятся уровень производства (предложения) товаров и услуг (обозначим этот фактор в общем виде П), уровень денежных доходов отдельных групп населения (D), уровень и соотношение цен (Р). К естественным факторам относятся демографический состав населения, в первую очередь размер и состав семьи (S), а также привычки и традиции, уровень культуры, природно-климатические условия и т.д.
Экономические факторы очень мобильны, особенно распределение населения по уровню денежных доходов. Естественные же факторы меняются сравнительно медленно и в течение небольшого периода (до 3-5 лет) не оказывают заметного влияния на спрос. Исключение составляет демографический состав населения. Поэтому в текущих и перспективных прогнозах спроса все естественные факторы, кроме демографических, целесообразно учитывать сообща, введя фактор времени (t).
Общем виде спрос определяется в виде функции перечисленных выше факторов:
у = f(П,D,P, S,t). (8.6)
Поскольку наибольшее влияние на спрос оказывает фактор дохода, многие расчеты спроса и потребления осуществляются в виде функции от душевого денежного дохода: у = f(D).
Наиболее простой подход к прогнозированию спроса на небольшой период времени связан с использованием так называемых структурных моделей спроса. При построении модели исходят из того, что для каждой экономической группы населения по статистическим бюджетным данным может быть рассчитана присущая ей структура потребления. При этом предполагается, что на изучаемом отрезке времени заметные изменения претерпевает лишь доход, а цены, размер семьи и прочие факторы принимаются неизменными. Изменение дохода, например его рост, можно рассматривать как перемещение определенного количества семей из низших доходных групп в высшие. Другими словами, изменяются частоты в различных интервалах дохода: они уменьшаются в нижних и увеличиваются в верхних интервалах. Семьи, которые попадают в новый интервал, будут иметь ту же структуру потребления и спроса, какая сложилась у семей с таким же доходом к настоящему времени.
Таким образом, структурные модели рассматривают спрос как
функцию только распределения потребителей по уровню дохода. Имея
соответствующие структуры спроса, рассчитанные по данным статистики бюджетов, и
частоты распределения потребителей по уровню дохода, можно рассчитать общую
структуру спроса. Если обозначить структуру спроса в группе семей со средним
доходом Di через r(Di), а частоты семей с доходом
Di через ![]() , то общая структура
спроса R может быть рассчитана по формуле:
, то общая структура
спроса R может быть рассчитана по формуле:
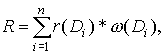 (8.7)
(8.7)
где п - количество интервалов дохода семей.
Структурные модели спроса - один из основных видов экономико-математических моделей планирования и прогнозирования спроса и потребления. В частности, широко распространены так называемые компаративные (сравнительные) структурные модели, в которых сопоставляются структуры спроса данного исследуемого объекта и некоторого аналогового объекта. Аналогом обычно считаются регион или группа населения с оптимальными потребительскими характеристиками.
Наряду со структурными моделями в планировании и прогнозировании спроса используются конструктивные модели спроса. В основе их лежат уравнения бюджета населения, т.е. такие уравнения, которые выражают очевидное равенство общего денежного расхода (другими словами, объема потребления) и суммы произведений количества каждого потребленного товара на его цену. Если Z - объем потребления, т - количество разных видов благ, qi - размер потребления i-го блага, pi - цена i-го блага, то конструктивная модель спроса может быть записана следующим образом:
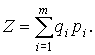
Эти модели, называемые также моделями бюджетов потребителей, играют важную роль в планировании потребления. Одной из таких моделей является, например, всем известный прожиточный минимум. К таким моделям относятся также рациональные бюджеты, основанные на научных нормах потребления, прежде всего продуктов питания, перспективные бюджеты (например, так называемый бюджет достатка) и др.
В практике планирования и прогнозирования спроса кроме структурных и конструктивных моделей применяются также аналитические модели спроса и потребления, которые строятся в виде однофакторных и многофакторных уравнений, характеризующих зависимость потребления товаров и услуг от тех или иных факторов
Моделирование конфликтов в финансово-экономической сфере. Основные понятия и определения теории игр. Классификация игр. Решение матричных игр с седловой точкой. Решение матричных игр без седловой точки. Смешанные стратегии. Теорема Дж. фон Неймана о существовании решения в смешанных стратегиях.
При управлении производством принимать решения очень часто приходится не имея достаточной информации, то есть в условиях неопределенности и риска.
Методами обоснования решений в условиях неопределенности и риска занимается математическая теория игр.
В теории игр рассматриваются такие ситуации, когда имеются два участника выполнения операции, каждый из которых преследует противоположные цели. В качестве участников могут выступать коллективы, конкурирующие предприятия и т. д. Во всех случаях предполагается, что операция проводится против разумного противника (конкурента), преследующего свои собственные цели и сознательно противодействующего достижению цели другим участником.
Так как цели противоположны, а результат мероприятия каждой из сторон зависит от действий конкурента, то эти действия называют конфликтными ситуациями. В конфликтной ситуации сталкиваются противоположные интересы двух участников. Формализованная (схематизированная) модель конфликтной ситуации называется игрой. Результат игры - победа или поражение, которые не всегда имеют количественное выражение, можно выразить (условно) числами (например, в шахматах: 1, 0, 1/2).
Игра называется игрой с нулевой суммой, если один из игроков выигрывает ровно столько, сколько проигрывает другой.
Развитие игры во времени представляется как ряд последовательных «ходов». Ходы могут быть сознательные и случайные. Случайный ход - результат, получаемый не решением игрока, а каким-либо механизмом случайного выбора (покупательский спрос, задержка с поставкой материалов и т.п.). Сознательный ход - выбор игроком одного из возможных вариантов действия (стратегии) и принятие решения об его осуществлении.
Возможные варианты (исходы) игры сводятся в прямоугольную
таблицу (табл. 5.1.1) - платежную матрицу, в которой строки соответствуют
различным стратегиям игрока А, столбцы - стратегиям игрока ![]() . Для
условности предположим, что игрок А – выигрывает, а игрок В – проигрывает.
. Для
условности предположим, что игрок А – выигрывает, а игрок В – проигрывает.
В результате выбора игроками любой пары стратегий Ai и Bj (i =1,…, m j = 1,…,n) однозначно определяется исход игры qij.
Цель теории игр - выработка рекомендаций для различного поведения игроков в конфликтной ситуации, то есть выбор оптимальной стратегии для каждого из них.
Для нахождения оптимальной стратегии необходимо
проанализировать все возможные стратегии и рассчитывать на то, что разумный
противник на каждую из них будет отвечать такой, при которой выигрыш игрока А
минимален. Обычно минимальные числа в каждой строке обозначаются ![]() и
выписываются в виде добавочного столбца матрицы (табл. 5.1.2).
и
выписываются в виде добавочного столбца матрицы (табл. 5.1.2).
Они обозначают минимально-возможный выигрыш игрока А при
соответствующей стратегии Аi. В каждой строке будет свое![]() . Так как
игрок А выигрывает, то предпочтительной для игрока А является стратегия,
при которой
. Так как
игрок А выигрывает, то предпочтительной для игрока А является стратегия,
при которой ![]() обращается в максимум,
то есть
обращается в максимум,
то есть ![]() или
или ![]() ,
,
где ![]() - максиминный выигрыш
(максимин), а соответствующая ей стратегия - максиминная.
- максиминный выигрыш
(максимин), а соответствующая ей стратегия - максиминная.
Таблица 5.1.1
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
| … | … | … | … | … |
|
|
|
|
… |
|
Таблица 5.2.2
|
|
|
… |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
… | … | … | … | … |
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Если придерживаться максиминной стратегии, то при любом
поведении стороны В (конкурента) гарантирован выигрыш, во всяком случае
не меньше ![]() . Поэтому
. Поэтому ![]() называют
также ценой игры - тот гарантированный минимум, который можно обеспечить при
наиболее осторожной (перестраховочной) стратегии.
называют
также ценой игры - тот гарантированный минимум, который можно обеспечить при
наиболее осторожной (перестраховочной) стратегии.
Очевидно, что аналогичные распределения можно провести и для
конкурента В, который должен рассмотреть все свои стратегии, выделяя
для каждой из них максимальные значения проигрыша: ![]() (последняя
строка матрицы).
(последняя
строка матрицы).
Из всех значений ![]() находят минимальное:
находят минимальное:
![]() ,
,
которое дает минимаксный выигрыш или минимакс.
Такая ![]() -стратегия - минимаксная,
придерживаясь которой сторона В гарантировано, что в любом случае
проиграет не больше
-стратегия - минимаксная,
придерживаясь которой сторона В гарантировано, что в любом случае
проиграет не больше ![]() . Поэтому
. Поэтому ![]() называют
верхней ценой игры.
называют
верхней ценой игры.
Если ![]() , то число С
называют чистой ценой игры или седловой точкой.
, то число С
называют чистой ценой игры или седловой точкой.
Для игры с седловой точкой нахождение решения состоит в выборе пары максиминной и минимаксной стратегий, которые являются оптимальными, так как любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго игрока по сравнению с ценой игры С.
Однако не все матрицы имеют седловую точку. Тогда решение находят, применяя смешанные стратегии, то есть чередуя случайным образом несколько чистых стратегий (гибкая тактика).
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называют смешанной стратегией данного игрока.
Из этого определения следует, что сумма компонент этого вектора равна единице, а сами компоненты не отрицательны.
Обычно смешанную стратегию первого игрока обозначают как вектор
![]() , а второго игрока - как
вектор
, а второго игрока - как
вектор ![]() , где
, где 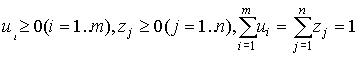 .
(5.1.1).
.
(5.1.1).
Если u° - оптимальная стратегия первого игрока, z° -
оптимальная стратегия второго игрока, то число 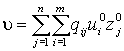 -
называют ценой игры.
-
называют ценой игры.
Для того чтобы число ![]() - было ценой игры, а u° и z°
— оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
- было ценой игры, а u° и z°
— оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
![]() ,
(5.1.2)
,
(5.1.2)
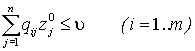 .
(5.1.3)
.
(5.1.3)
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры и вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, в том числе и чистые стратегии
Внимание к седловым точкам в теории игр традиционно. Объясняется это недоверием к максимину, как к принципу оптимального выбора в том случае, когда нет седловой точки. Поэтому естественно стремление заполнить промежуток между максимином и минимаксом путем применения смешанных стратегий.
Однако, не следует забывать, что:
1) применение смешанных стратегий рисковано, когда игра не повторяется;
2) если игра повторяется, надо иметь уверенность, что у противника нет
информации о конкретных решениях другого игрока;
3) противник не обязан применять смешанные стратегии, равно как и стремиться к
цели, противоположной цели другого игрока.
Обозначим смешанную стратегию первого игрока p = {pi},
![]() где pi
- вероятность применения i-й стратегии,
где pi
- вероятность применения i-й стратегии, 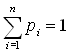 ,
, ![]() . Пусть смешанная стратегия
второго игрока
. Пусть смешанная стратегия
второго игрока ![]() ,
, ![]() , qj -
вероятность применения j-й стратегии,
, qj -
вероятность применения j-й стратегии, 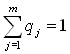 ,
, ![]() . Р и Q определяют
математическое ожидание платежа:
. Р и Q определяют
математическое ожидание платежа:
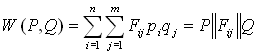 .
.
Теорема фон Неймана. Любая матричная игра имеет седловую точку в смешанных стратегиях.
Доказательство. Множества M и N ограничены
и замкнуты, так как ![]() ,
, ![]() , а функция W непрерывна по
P и Q . W линейна по P при фиксированных Q,
следовательно, вогнута по P при фиксированных Q. Аналогично W
выпукла по Q при фиксированных P. M и N выпуклы.
, а функция W непрерывна по
P и Q . W линейна по P при фиксированных Q,
следовательно, вогнута по P при фиксированных Q. Аналогично W
выпукла по Q при фиксированных P. M и N выпуклы.
Действительно, рассмотрим такие ![]() и
и ![]() , что
, что 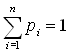 ,
, 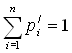 , тогда
, тогда ![]() ,
, ![]() .
.
Складывая, получим ![]() .
.
Кроме того, ![]() .
.
Следовательно, при![]() и
и ![]()
![]()
тоже смешанная стратегия.
Применяя фундаментальную теорему, получим то, что требуется доказать:
![]() .
.
Опираясь на доказанную теорему, можно быть уверенным, что решение игры в смешанных стратегиях всегда существует (если только вообще их можно применять). В теории игр доказывается теорема, указывающая на эквивалентность решения матричной игры в смешанных стратегиях и двойственной задачи линейного программирования.
Пусть Po и Qo оптимальные смешанные стратегии, v - цена игры, тогда
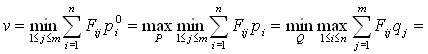
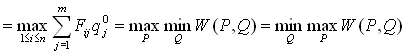 .
.
Из теорема следует, что
|
|
(4) |
|
|
(5) |
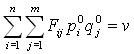 .
.
Обозначим ![]() .
.
Поделим (4) на v , получим
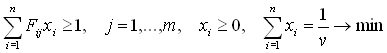 .
.
Из этой задачи линейного программирования можно получить оптимальные стратегии первого игрока (оперирующей стороны).
Аналогично, если 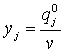 , получится задача линейного
программирования для получения оптимальных стратегий второго игрока:
, получится задача линейного
программирования для получения оптимальных стратегий второго игрока: 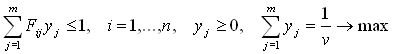 .
.
Игры с природой. Оптимальная стратегия в игре с природой при известном распределении её состояний. Максиминный критерий Вальда выбора стратегии в игре с природой при неизвестном распределении её состояний. Критерий минимаксного риска Сэвиджа выбора стратегии в игре с природой при неизвестном распределении её состояний. Критерий пессимизма-оптимизма Гурвица выбора стратегии в игре с природой при неизвестном распределении её состояний.
В случае, когда между сторонами (участниками) отсутствует «антагонизм» (например, в процессе работы предприятий и торговых посредников), такие ситуации называют «играми с природой».
Здесь первая сторона принимает решение, а вторая сторона — «природа» не оказывает первой стороне сознательного, агрессивного противодействия, но ее реальное поведение неизвестно.
Пусть торговое предприятие имеет т стратегий: ![]() и имеется
n возможных состояний природы:
и имеется
n возможных состояний природы: ![]() . Так как природа не
является заинтересованной стороной, исход любого сочетания поведения сторон
можно оценить выигрышем
. Так как природа не
является заинтересованной стороной, исход любого сочетания поведения сторон
можно оценить выигрышем ![]() первой стороны для
каждой пары стратегий
первой стороны для
каждой пары стратегий ![]() и
и ![]() . Все показатели
игры заданы платежной матрицей
. Все показатели
игры заданы платежной матрицей ![]() .
.
По платежной матрице можно принять ряд решений. Например, оценить возможные исходы: минимальный выигрыш
![]()
то есть наименьшая из величин в каждой i-й строке как пессимистическая оценка; максимальный выигрыш – то наилучшее, что дает выбор i-го варианта
![]()
При анализе «игры с природой» вводится показатель, по которому оценивают, насколько то или иное состояние «природы» влияет на исход ситуации. Этот показатель называют риском.
Риск ![]() при пользовании
стратегией
при пользовании
стратегией ![]() и состоянии «природы»
и состоянии «природы» ![]() оценивается
разностью между максимально возможным выигрышем при данном состоянии «природы»
оценивается
разностью между максимально возможным выигрышем при данном состоянии «природы»
![]() и
выигрышем
и
выигрышем ![]() при выбранной
стратегии
при выбранной
стратегии ![]() .
.
![]() .
.
Исходя из этого определения можно оценить максимальный риск каждого решения:
![]() .
.
Решения могут приниматься по результатам анализа ряда критериев.
Критерий, основанный на известных вероятностных состояниях «природы».
Если известны вероятности состояний «природы» (например, спроса по данным анализа за прошлые годы):
![]()
где ![]() ,
,
то в качестве показателя эффективности (рациональности,
обоснованности) стратегии ![]() берется средний
(математическое ожидание) - выигрыш применения этой стратегии:
берется средний
(математическое ожидание) - выигрыш применения этой стратегии:
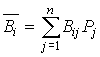 ,
,
а оптимальной считают стратегию, для которой этот показатель эффективности имеет максимальное значение, то есть
![]() .
.
Если каждому решению ![]() соответствует
множество возможных результатов
соответствует
множество возможных результатов ![]() с вероятностями
с вероятностями ![]() ,
то среднее значение выигрыша можно определить по формуле
,
то среднее значение выигрыша можно определить по формуле
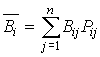 ,
,
а оптимальная стратегия выбирается по условию
![]() .
.
В этом случае можно воспользоваться и стратегией минимального среднего риска для каждого i-го состояния «природы»
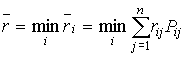 .
.
Максиминный критерий Вальда предполагает выбор решения, при котором гарантируется максимальный выигрыш в наихудших условиях внешней среды (состояния «природы»):
![]() .
.
Согласно критерия пессимизма-оптимизма Гурвица при выборе решения вместо двух крайностей в оценке ситуации (оптимум-пессимизм) придерживаются некоторого компромисса, учитывающего возможность как наихудшего, так и наилучшего поведения «природы»:
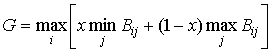 ,
,
где x - показатель пессимизма-оптимизма (чаще всего 0,5).
Если х = 1 критерий слишком пессимистичный, если х = 0 – слишком отптимистичный.
По критерию минимаксного риска Сэвиджа выбирают ту стратегию, при которой величина риска имеет минимальное значение в самой неблагоприятной ситуации:
![]()
чтобы избежать слишком большого риска при выборе решения.
Комплексный анализ всех этих критериев позволяет в какой-то мере оценить возможные последствия принимаемых решений
Модели поведения фирмы в условиях конкуренции. Модель поведения фирмы в условиях совершенной конкуренции. Исследование модели в зависимости от показателя степени однородности производственной функции. Модели поведения фирмы в условиях несовершенной конкуренции. Монополия и монопсония. Конкуренция среди немногих. Олигополия. Модели дуополии.
Поведение фирмы в условиях совершенной конкуренции
Существуют модели:
· Описание общей модели Вальраса
· Модель Эрроу-Дебре. Существование конкурентного равновесия
· Модель регулирования цен и устойчивость конкурентного равновесия
Опишем общие понятия.
Обозначим через S множество потребителей и в
пространстве товаров ![]() введем понятие коллективного
предпочтения (
введем понятие коллективного
предпочтения (![]() ) с помощью следующих аксиом
(некоторые из них соответствуют аксиомам индивидуального предпочтения (см. §3.1
)):
) с помощью следующих аксиом
(некоторые из них соответствуют аксиомам индивидуального предпочтения (см. §3.1
)):
A1) полнота: для любых ![]() либо
либо ![]() , либо
, либо ![]() , либо
, либо ![]() (
( ![]() - отношение безразличия);
- отношение безразличия);
A2) транзитивность: для любых ![]() , таких, что
, таких, что ![]() ,
, ![]() , справедливо
, справедливо ![]() ;
;
A3) единогласие: если ![]() для всех
для всех ![]() , то
, то ![]() ;
;
A4) независимость: для любых ![]() из
из ![]() ,
, ![]() ,
,![]() , следует
, следует ![]() (
( ![]() - любое отношение).
- любое отношение).
Обоснование неоспоримости этих аксиом можно найти, например, в книге [ 18 ].
Главный вопрос теперь заключается в том, существует ли отношение предпочтения, удовлетворяющее этим четырем аксиомам? К сожалению, в общем случае ответ будет отрицательным. Более или менее известные способы определения коллективного предпочтения, такие, как "правило большинства", "правило уравновешивания", "правило диктатора" (см. [ 18 ]), во-первых, более применимы в области политики, чем экономики, во-вторых, приводят к нарушению некоторых из аксиом A1-A4. Это вполне понятно. С одной стороны, легче согласовать идеи, чем потребности, с другой - участники экономики поступают главным образом эгоистически, и не существует единственного способа приспособления их потребностей друг к другу. Во избежание неправильных выводов здесь нужно пояснить: сказанное не означает, что в каждом отдельном случае коллектив не придет к соглашению. Речь идет лишь об отсутствии общих адекватных методов получения коллективного предпочтения.
Теперь проанализируем возможность построения коллективной
функции полезности, исходя из индивидуальных функций полезности всех
потребителей. Последние, как мы видели в §3.2 , вполне реально определяются и
существуют. Искомую функцию для потребительского сектора S естественно
определить как ![]() , где
, где ![]() - функция полезности потребителя i
. По определению 3.1 , с этой функцией должно быть связано некоторое отношение
предпочтения
- функция полезности потребителя i
. По определению 3.1 , с этой функцией должно быть связано некоторое отношение
предпочтения ![]() :
: ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() . Оказывается,
такое отношение предпочтения удовлетворяет аксиоме единогласия, но противоречит
аксиоме независимости (установите это самостоятельно).
. Оказывается,
такое отношение предпочтения удовлетворяет аксиоме единогласия, но противоречит
аксиоме независимости (установите это самостоятельно).
Для выявления еще более серьезного возражения против функции
![]() представим
ее в виде
представим
ее в виде ![]() ,
где
,
где ![]() ,
,![]() , s -
число всех потребителей. Тогда по теореме 3.2 любая функция вида
, s -
число всех потребителей. Тогда по теореме 3.2 любая функция вида
![]()
где ![]() , является также функцией
коллективной полезности. Положим
, является также функцией
коллективной полезности. Положим ![]() . Легко видеть, что функция
. Легко видеть, что функция ![]() в этом случае
порождает отношение предпочтения, дающее приоритетный вес только первому
потребителю. Такое отношение предпочтения явно не совпадает с отношением
предпочтения, порожденным исходной функцией
в этом случае
порождает отношение предпочтения, дающее приоритетный вес только первому
потребителю. Такое отношение предпочтения явно не совпадает с отношением
предпочтения, порожденным исходной функцией ![]() . Можно доказать, что только в
одном случае все функции вида (5.2.1) будут соответствовать одному и тому же
отношению предпочтения, а именно, когда выполнено дополнительное условие
. Можно доказать, что только в
одном случае все функции вида (5.2.1) будут соответствовать одному и тому же
отношению предпочтения, а именно, когда выполнено дополнительное условие ![]() . Каждому
набору коэффициентов
. Каждому
набору коэффициентов ![]() из этого условия будет
соответствовать своя функция полезности
из этого условия будет
соответствовать своя функция полезности ![]() . Возникает новая проблема: какую
из этого бесконечно большого числа функций предпочтут потребители?
. Возникает новая проблема: какую
из этого бесконечно большого числа функций предпочтут потребители?
Резюмируя, можно говорить, что попытка определения
коллективной функции полезности на основе индивидуальных функций полезности не
решает проблему, так как вопрос существования коллективно предпочитаемых весов ![]() возвращает
проблему к исходной точке. Вообще, задача коллективного предпочтения требует
принципиально иных подходов, о которых речь пойдет в главе VII .
возвращает
проблему к исходной точке. Вообще, задача коллективного предпочтения требует
принципиально иных подходов, о которых речь пойдет в главе VII .
Напомним, что мы анализировали возможность построения коллективной функции полезности и пришли к отрицательному заключению: с одной стороны, ее нельзя построить непосредственно, так как нельзя определить строго понятие коллективного предпочтения; с другой - ее не удается построить, используя индивидуальные функции полезности, из-за проблемы неоднозначности.
Теперь проанализируем возможность определения рыночного
спроса, исходя из решений индивидуальных оптимизационных задач вида (3.4.1)-(3.4.2)
для всех потребителей. Такой анализ проведем нестрого, так, как это делают
экономисты, на языке кривых спроса. 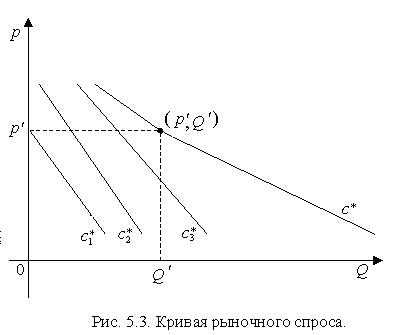 А именно,
покажем, что кривую рыночного спроса (
А именно,
покажем, что кривую рыночного спроса (![]() ) можно получить как сумму кривых
индивидуального спроса (
) можно получить как сумму кривых
индивидуального спроса (![]() ) всех потребителей. На рис. 5.3
показаны линейные графики спроса
) всех потребителей. На рис. 5.3
показаны линейные графики спроса ![]() для трех потребителей. Любая точка
на кривой рыночного спроса получается для данной цены как сумма по
горизонтальной оси координат соответствующих этой же цене точек всех
индивидуальных кривых спроса. Аналитически это означает, что
для трех потребителей. Любая точка
на кривой рыночного спроса получается для данной цены как сумма по
горизонтальной оси координат соответствующих этой же цене точек всех
индивидуальных кривых спроса. Аналитически это означает, что ![]() . При этом рыночная
кривая спроса не обязательно имеет такой же вид, что и индивидуальные кривые.
Как видно из рис. 5.3 , даже для линейных кривых индивидуального спроса
рыночная кривая получается нелинейной (изгиб в точке
. При этом рыночная
кривая спроса не обязательно имеет такой же вид, что и индивидуальные кривые.
Как видно из рис. 5.3 , даже для линейных кривых индивидуального спроса
рыночная кривая получается нелинейной (изгиб в точке ![]() ). Изменению подвергаются и другие
свойства индивидуальных кривых, в частности, такие характеристики, как
эластичность спроса, предельная норма замещения и др.
). Изменению подвергаются и другие
свойства индивидуальных кривых, в частности, такие характеристики, как
эластичность спроса, предельная норма замещения и др.
Для теоретического обоснования приведенного выше "графического способа" определения рыночного спроса сформулируем без доказательства следующее утверждение.
Теорема 5.1. Пусть области
определения ![]() ,
,
![]() , функций
полезности индивидуальных потребителей есть конусы с вершинами в нуле
пространства товаров. Пусть, далее, каждая индивидуальная функция полезности
, функций
полезности индивидуальных потребителей есть конусы с вершинами в нуле
пространства товаров. Пусть, далее, каждая индивидуальная функция полезности ![]() положительно
однородна и принимает на
положительно
однородна и принимает на ![]() хотя бы одно положительное
значение. Тогда существует такая функция
хотя бы одно положительное
значение. Тогда существует такая функция ![]() , что при любых ценах
, что при любых ценах ![]() решение задачи
решение задачи ![]() ,
, ![]() , совпадает с
суммой решений s оптимизационных задач:
, совпадает с
суммой решений s оптимизационных задач: ![]() .
.
Напомним, что множество ![]() называется конусом с вершиной в
нуле пространства
называется конусом с вершиной в
нуле пространства ![]() , если оно вместе с каждой точкой
, если оно вместе с каждой точкой ![]() содержит луч
содержит луч ![]() .
.
По существу, в теореме 5.1 сформулированы те условия, при
выполнении которых существует коллективная функция полезности (![]() ) и с помощью которых
всех потребителей можно представить как одно лицо.
) и с помощью которых
всех потребителей можно представить как одно лицо.
Как и в случае с потребителями, путем суммирования кривых предложения отдельных фирм, полученных в результате решения их оптимизационных задач из главы IV , можно получить понятие кривой рыночного предложения.
Общий вывод такой, что можно найти, во всяком случае, приемлемые для экономической практики способы формализации понятий рыночного спроса и рыночного предложения. Последнее дает моральное право оперировать понятиями совокупного спроса и совокупного предложения.
Представляется необходимым обратить внимание читателя на следующий момент. Совокупный спрос (совокупное предложение) не является результатом кооперирования между потребителями (производителями). Более того, кооперация вообще исключена условиями совершенной конкуренции (см. ниже). Совокупный спрос характеризует суммарную потребность общества в товарах, а совокупное предложение - суммарные возможности производителей этих товаров.
Любая функция ![]() , ставящая в соответствие каждому
вектору затрат x вектор
, ставящая в соответствие каждому
вектору затрат x вектор ![]() максимального выпуска, который
может быть получен при этих затратах, называется производственной функцией.
максимального выпуска, который
может быть получен при этих затратах, называется производственной функцией.
Монополия.
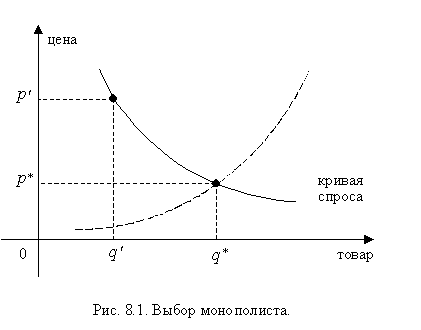 Так
как монополист является единственным производителем товара, исходя из кривой
спроса, он самостоятельно определяет объем продаж и цену товара (рис. 8.1).
Предположим, что в условиях совершенной конкуренции равновесие достигается в
точке
Так
как монополист является единственным производителем товара, исходя из кривой
спроса, он самостоятельно определяет объем продаж и цену товара (рис. 8.1).
Предположим, что в условиях совершенной конкуренции равновесие достигается в
точке ![]() , а
доход данной фирмы, как участника рынка совершенной конкуренции, есть
, а
доход данной фирмы, как участника рынка совершенной конкуренции, есть ![]() (
(![]() ). Будучи монополистом,
при том же уровне спроса эта фирма добьется данного уровня дохода при меньшем
выпуске (
). Будучи монополистом,
при том же уровне спроса эта фирма добьется данного уровня дохода при меньшем
выпуске (![]() )
за счет более высокой цены (
)
за счет более высокой цены (![]() ). Именно в этом заключается
приоритетность положения монополиста.
). Именно в этом заключается
приоритетность положения монополиста.
До какого уровня монополист будет повышать цену товара и снижать объем продаж, чтобы получить максимальную прибыль с учетом издержек на производство товара?
Кривая спроса и оценка собственных издержек являются
главными ориентирами для фирмы-монополиста при принятии экономического решения.
Она принимает решение относительно объема выпуска (или продажи) товара, а его
цена определяется с помощью кривой спроса (см. рис. 8.1). Следовательно, в
условиях монополии цена (![]() ) является функцией от выпуска (
) является функцией от выпуска (![]() ), т.е. , и,
располагая информацией о спросе, фирма может добиться получения максимальной
прибыли.
), т.е. , и,
располагая информацией о спросе, фирма может добиться получения максимальной
прибыли.
Монополист может увеличить прибыль двумя путями: либо за счет повышения цены на товар, не изменяя при этом объема выпуска, либо за счет сокращения объема выпуска (снизив тем самым издержки на производство), не изменяя цену товара. Каково же оптимальное действие монополиста?
Чтобы ответить на этот вопрос, обратимся опять к конкурентному рынку и рассмотрим долгосрочную задачу фирмы (4.5.1). Так как мы хотим узнать именно об оптимальном объеме производства, переформулируем эту задачу на языке выпуска. Обозначим доход как функцию от выпуска:
![]()
Так как издержки фирмы зависят от объема производства, они также являются функциями от выпуска:
![]()
Теперь задачу (4.5.1) можно записать так:
![]()
Условие первого порядка для максимизации прибыли ![]() есть
есть
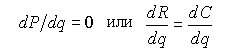
Следовательно, чтобы максимизировать прибыль, фирма должна
достичь такого объема выпуска, при котором предельный доход равен предельным
издержкам. Далее, учитывая тот факт, что ![]() , получаем
, получаем ![]() , т.е. равновесная цена,
если она существует, должна равняться предельным издержкам:
, т.е. равновесная цена,
если она существует, должна равняться предельным издержкам:

Графическая иллюстрация этого равенства показана на рис. 8.2,
где предельные издержки есть возрастающая функция от объема производства, 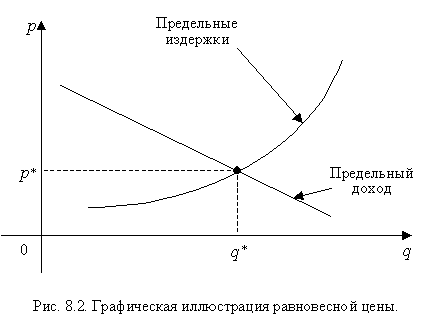 а предельный доход
(цена) - убывающая функция того же аргумента.
а предельный доход
(цена) - убывающая функция того же аргумента.
Вернемся к монополии и проверим, будет ли цена, максимизирующая прибыль монополиста, подчиняться закону (8.1.2)?
В монополии ![]() , поэтому
, поэтому
![]()
Далее без потери общности будем считать ![]() .
.
Вычислим предельный доход
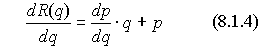
Заметим, что и в монополии цена убывает с ростом объема
продаж, потому что фирма снижает цену, чтобы продать больше продукции. Поэтому ![]() и из (8.1.4)
следует
и из (8.1.4)
следует
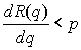
Как видим, в случае монополии предельный доход меньше цены товара.
Проанализируем теперь издержки монополиста. Как и на
конкурентном рынке, цены затрат являются функциями от объема затрат, т.е. ![]() ,
, ![]() . Поэтому
издержки на факторы производства выражаются как
. Поэтому
издержки на факторы производства выражаются как
![]()
Будем предполагать, что ![]() для всех
для всех ![]() .
.
Вычислим предельные издержки:

По рыночным законам фирма может покупать большее количество
данного фактора производства, только предложив более высокую плату. Поэтому ![]() . Тогда из (8.1.6)
следует
. Тогда из (8.1.6)
следует
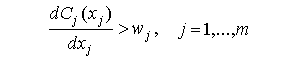
Таким образом, в случае монополии предельные издержки на факторы производства оказываются больше их цен.
Подставляя (8.1.3) и (8.1.5) в (8.1.1), получим оптимизационную задачу монополиста:
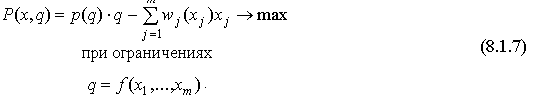
Подчеркнем еще раз, в отличие от задачи (8.1.1) фирмы на конкурентном рынке, в условиях задачи монополиста (8.1.7) все цены зависят от объемов продуктов.
Максимум функции прибыли P в задаче (8.1.7) вычисляется по m+1
переменной ![]() .
Поэтому составим функцию Лагранжа
.
Поэтому составим функцию Лагранжа
![]()
где ![]() - множитель Лагранжа. Выпишем
необходимые условия оптимальности точки
- множитель Лагранжа. Выпишем
необходимые условия оптимальности точки ![]() :
:
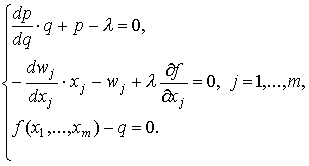
Отсюда имеем, в частности,
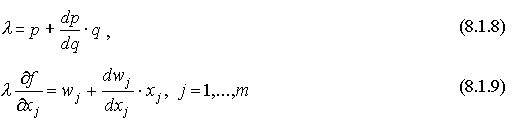
Сумма, стоящая в правой части равенства (8.1.8), есть
предельный доход (см. (8.1.4)), а сумма, стоящая в правой части (8.1.9), -
предельные издержки по производственному фактору j-го вида (см. (8.1.6)).
Поэтому величина, стоящая в левой части (8.1.9), представляет собой
произведение предельного дохода (![]() ) на предельный продукт j-го вида
затрат (
) на предельный продукт j-го вида
затрат (![]() ).
Это произведение можно трактовать как предельный доход j-го вида затрат.
).
Это произведение можно трактовать как предельный доход j-го вида затрат.
Исключая из системы необходимых условий множитель Лагранжа ![]() , получаем
, получаем
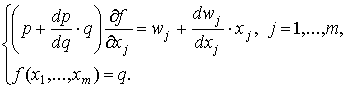
Пользуясь равенствами (8.1.4) и (8.1.6), перепишем эту систему в виде
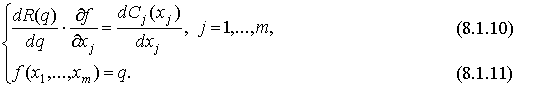
Оценим отношение предельной стоимости затрат на предельный продукт
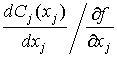
Во-первых, как следует из (8.1.10), эта величина для всех j
одна и та же. Во-вторых, издержки можно представить как функцию от выпуска,
т.е. ![]() .
Поэтому, пользуясь равенством (8.1.11), можно формально написать
.
Поэтому, пользуясь равенством (8.1.11), можно формально написать
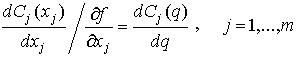
Так как эта величина одна и та же для всех j, то, опуская индекс, из системы (8.1.10)-(8.1.11) получаем

Следовательно, чтобы максимизировать прибыль, монополист должен достичь такого уровня выпуска, при котором предельный доход равен предельным издержкам.
Для монополиста мы получили такое же правило оптимального поведения, что и любая фирма в условиях конкурентного рынка. Однако в случае монополии
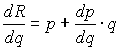
и поэтому оптимальная цена товара отличается от выражения (8.1.2) в сторону повышения. А именно, через предельный доход она выражается как
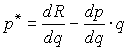
а через предельные издержки -
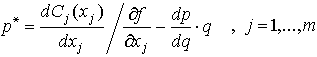
Олигополия.
На практике рыночной властью, т.е. властью над ценообразованием, обладают не только фирмы, являющиеся чистыми монополистами. Во многих отраслях экономики конкурирует небольщое число фирм, каждая из которых обладает некоторой рыночной властью. Таковы, например, крупные металлургические комбинаты России (КМК, Запсиб, Магнитка и др.).
В этом и следующих параграфах мы изучим рыночные механизмы в условиях олигополии, т.е. когда на рынке товара конкурирует небольшое число фирм. Рыночная власть и прибыль олигополистов частично зависят от того, как они взаимодействуют между собой. В некоторых олигопольных отраслях фирмы агрессивно конкурируют, а в других сотрудничают. Естественно, конкуренция приводит к снижению цен, а имея тенденцию к сотрудничеству, фирмы могут назначить цены выше предельных издержек и получить большую прибыль.
Крайнюю форму сотрудничества представляет собой картель. На картельном рынке некоторые или все фирмы вступают в сговор по поводу захвата рынка. Определяя сообща цены товара и объемы продаж, они максимизируют свои прибыли. Картель отличается от монополии тем, что не может контролировать весь рынок товара по причине наличия фирм, не входящих в картель. Другая причина отличия - в нестабильности картеля как структуры, состоящей из фирм, преследующих каждая свои интересы.
Олигополия является преобладающей формой современной рыночной структуры. На олигопольных рынках несколько фирм производят всю или почти всю продукцию. Чем шире олигополия, тем сложнее принятие экономических решений для фирм. Поэтому они могут предпринять стратегические усилия, чтобы затруднить вступление на рынок новых фирм.
Олигополист принимает решение по установлению цены и объема выпускаемой им продукции. Экономическое решение олигополиста складывается сложнее, чем монополиста, так как имеет место конкуренция между несколькими фирмами. Поэтому фирма должна тщательно взвесить свои решения с точки зрения реакции соперников. Стратегические соображения должны быть глубокими и всесторонними. Каждая фирма учитывает реакцию конкурентов, зная, что те, в свою очередь, тоже будут взвешивать ее реакцию на их собственные решения. При этом фирма должна принимать во внимание возможность восстановления ее стратегических рассуждений конкурентами, и потому она должна поставить себя на место конкурентов и поразмыслить, какова бы была их реакция. Именно с позиций такой рекомендации разрабатываются принципы оптимального поведения олигополистов. Некоторые из них мы рассмотрим в следующих параграфах. Здесь мы займемся моделированием задачи олигополиста и олигопольного рынка в целом.
Определяющим свойством олигопольного рынка является то, что все конкурирующие фирмы могут влиять на цены продукции и затрат. Следовательно, прибыль каждой фирмы зависит и от экономических решений всех остальных фирм. Каково будет в этих условиях оптимальное решение олигополиста по объему выпуска и цене товара? Для получения ответа на этот вопрос необходимо построить математическую модель олигополиста и решить совместно систему, состоящую из задач всех конкурирующих между собой фирм.
Обозначим через n число олигополистов и предположим, что все они выпускают один и тот же товар, применяя m видов затрат. Заметим, что при этом продукции разных фирм могут отличаться рядом признаков (качеством, оформлением и т.д.).
Согласно описания олигополии, цена товара (p) определяется
объемом всех выпусков ![]() , а цена затрат (
, а цена затрат (![]() ) - объемом затрат всех
фирм
) - объемом затрат всех
фирм ![]() :
:
![]()
При возрастании выпусков цены понизятся. Поэтому
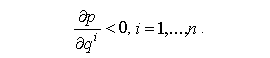
Аналогично, если фирмы увеличат покупки производственных факторов, произойдет повышение их цен. Поэтому
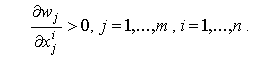
Пусть ![]() - производственная функция i-го олигополиста.
Тогда производство описывается системой из n уравнений
- производственная функция i-го олигополиста.
Тогда производство описывается системой из n уравнений
![]()
Так как все олигополисты действуют на рынках одних и тех же товаров, то
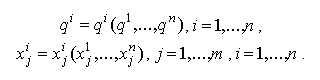
Задача i-го олигополиста может быть сформулирована следующим образом:
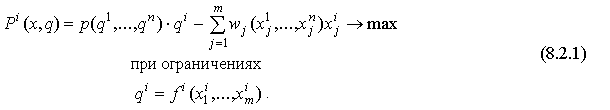
Здесь ![]() - матрица затрат,
- матрица затрат, ![]() - вектор выпусков.
Максимизация функции прибыли
- вектор выпусков.
Максимизация функции прибыли ![]() осуществляется только по
переменным
осуществляется только по
переменным ![]() ,
выбором значений которых распоряжается i-ый олигополист.
,
выбором значений которых распоряжается i-ый олигополист.
Из вида целевой функции задачи (8.2.1)
приходим к выводу, что максимизация прибыли ![]() зависит не только от
экономического решения i-го олигополиста, но и от действий его конкурентов,
распоряжающихся выбором
зависит не только от
экономического решения i-го олигополиста, но и от действий его конкурентов,
распоряжающихся выбором ![]() .
.
Модель олигополии в целом имеет вид:
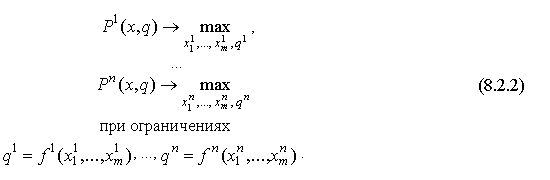
Такого рода модели называются конфликтными задачами принятия
решения или играми n лиц. Конфликтный характер принятия решения здесь
заключается в том, что каждая целевая функция ![]() зависит от экономических решений
всех олигополистов. Поэтому для нахождения оптимальных решений олигополистов
наиболее подходящим аппаратом является теория игр. В частности, при отсутствии
как антагонистического противостояния, так и сговора между фирмами, их
оптимальные стратегии могут быть определены, исходя из принципа равновесия по
Нэшу.
зависит от экономических решений
всех олигополистов. Поэтому для нахождения оптимальных решений олигополистов
наиболее подходящим аппаратом является теория игр. В частности, при отсутствии
как антагонистического противостояния, так и сговора между фирмами, их
оптимальные стратегии могут быть определены, исходя из принципа равновесия по
Нэшу.
Дуополия.
Предположим, что имеется всего две конкурирующих по выпуску одного и того же товара фирмы. Это есть частный случай олигополии, называемый дуополией. Обе фирмы принимают решения по объему выпуска одновременно и тайно друг от друга, и конечная цена товара зависит от совокупного объема производства этих фирм. То есть, как и в олигополии, дуополисты имеют частичную рыночную власть (частичное влияние на цену товара).
Модель дуополии впервые рассматривал французский экономист О. Курно еще в тридцатых годах прошлого столетия. Подход Курно основывается на гипотезе о том, что свое экономическое решение каждая фирма принимает в предположении о постоянном объеме производства своего конкурента. Иными словами, дуополист считает, что конкурент не реагирует на его выпуск. Чтобы лучше понять, как это происходит, рассмотрим пример. Предварительно заметим, что в дуополии фирма ориентируется на ту часть рыночного спроса, которая не обеспечена предложением другой фирмы. Поэтому для фирмы очень важно правильно оценить спрос населения на ее товар и объем производства конкурента.
Математическую модель дуополии получим как частный случай задачи (8.2.2) при n=2 :
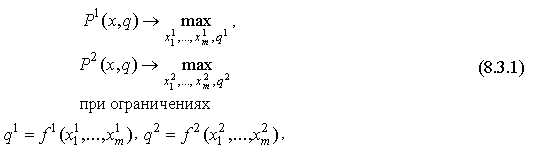
где ![]() - матрица затрат,
- матрица затрат, ![]() - вектор выпусков,
- вектор выпусков,
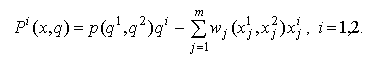
Как и в олигополии,
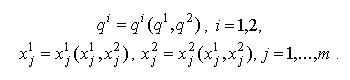
Для вычисления оптимальных выпусков дуополистов имеется 2(m+1) условий вида (8.2.3):
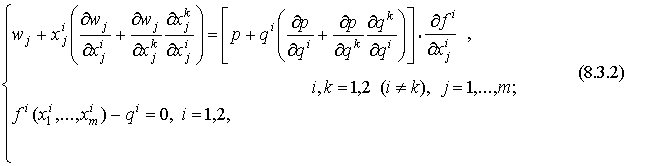
где
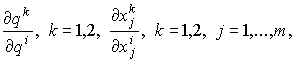
- предположительные вариации дуополиста i, i=1,2 (![]() ).
).
Модель (8.3.1) называется дуополией Курно, если в (8.3.2) выполнены условия

Как видно из определения, в дуополии Курно каждая фирма считает, что изменения объема ее собственного выпуска не повлияют на решение конкурента.
Равновесие Штакельберга. Рассмотренная в предыдущем параграфе модель Курно описывает лишь один из возможных способов формирования экономической стратегии дуополистов. Причем исходная гипотеза (8.3.3) относительно предположительных вариаций, на основе которой строится равновесие Курно, оказалась, по существу, не соответствующей реальности, так как не выдерживает испытания временем.
В этом параграфе мы отказываемся от гипотезы Курно и анализируем другую гипотезу, которая порождает так называемую дуополию Штакельберга.
Фирму 1 (2) будем называть дуополистом Курно, если
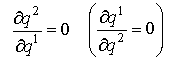
Далее фирму 1 (2) будем называть S-стратегом, если она
считает, что фирма 2 (1) будет вести себя как дуополист Курно, т.е. что она
будет определять свой выпуск, пользуясь кривой реакции ![]() (
(![]() ) (см. рис. 8.7).
) (см. рис. 8.7).
Определение 8.4. Модель (8.3.1) называется дуополией Штакельберга, если одна или обе фирмы являются S-стратегами.
Тройка ![]() , где
, где ![]() - решение задачи (8.3.1) при
условиях дуополии Штакельберга,
- решение задачи (8.3.1) при
условиях дуополии Штакельберга, ![]() - соответствующая этим выпускам (в
силу системы (8.3.1)) цена товара, называется равновесием Штакельберга.
- соответствующая этим выпускам (в
силу системы (8.3.1)) цена товара, называется равновесием Штакельберга.
Равновесие Нэша. В рассмотренных моделях мы исходили из того, что свои экономические решения по поводу объемов выпуска дуополисты принимают лишь на основе информации (гипотезы) об объемах выпуска конкурента. Замечая узость такого подхода, все же надо понимать, что, во-первых, всегда можно обобщить эти подходы на основе более разнообразной информации, во-вторых, как уже было сказано, объем выпуска партнера для конкурирующих фирм является основным и определяющим ориентиром для принятия решения дуополистами.
Обобщая экономические решения, анализированные в дуополиях Курно и Штакельберга, можно сказать, что у каждой фирмы есть два варианта поведения: либо действовать как дуополист Курно, либо действовать как дуополист Штакельберга (т.е. быть S-стратегом).
Экономическое решение i-ой фирмы, характеризующее ее
как дуополиста Курно, будем называть ее K-стратегией и обозначать ![]() . Аналогично,
экономическое решение i-ой фирмы, характеризующее ее как дуополиста
Штакельберга, будем называть ее S-стратегией и обозначать
. Аналогично,
экономическое решение i-ой фирмы, характеризующее ее как дуополиста
Штакельберга, будем называть ее S-стратегией и обозначать ![]() .
.
Таким образом, у каждого дуополиста имеется две стратегии: у
фирмы 1 - ![]() и
и
![]() , у фирмы
2 -
, у фирмы
2 - ![]() и
и ![]() , и потому
может быть реализована одна из четырех ситуаций:
, и потому
может быть реализована одна из четырех ситуаций: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Разместим соответствующие этим
ситуациям объемы выпусков фирмы 1 и фирмы 2 в следующую таблицу (рис. 8.8).
. Разместим соответствующие этим
ситуациям объемы выпусков фирмы 1 и фирмы 2 в следующую таблицу (рис. 8.8).
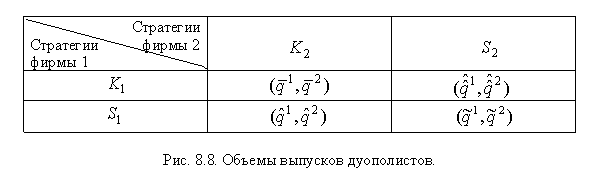
На рис. 8.8 ![]() - равновесие Курно,
- равновесие Курно, ![]() - 1-равновесие Штакельберга,
- 1-равновесие Штакельберга,
![]() -
2-равновесие Штакельберга,
-
2-равновесие Штакельберга, ![]() - неравновесие Штакельберга.
- неравновесие Штакельберга.
Матрицу

можно рассматривать как математическую модель принятия
решения с двумя участниками, имеющими каждый только две стратегии. Каждой из
перечисленных четырех ситуаций соответствует одна из пар выпусков ![]() . Например,
если первый участник выбрал стратегию
. Например,
если первый участник выбрал стратегию ![]() , а второй - стратегию
, а второй - стратегию ![]() , то в
создавшейся ситуации
, то в
создавшейся ситуации ![]() выпуск первого участника равен
выпуск первого участника равен ![]() , а второго -
, а второго - ![]() . Каждый
участник выбирает свою стратегию с целью получения как можно большего выпуска.
. Каждый
участник выбирает свою стратегию с целью получения как можно большего выпуска.
Модель (8.4.6) называется бескоалиционной игрой двух лиц или
биматричной игрой; участники называются игроками, а выпуск ![]() - выигрышем
первого игрока,
- выигрышем
первого игрока, ![]() - выигрышем второго игрока.
- выигрышем второго игрока.
Таким образом, биматричная игра (8.4.6) может рассматриваться как еще одна (обобщенная) модель дуополии. По построению этой игры оптимальные стратегии (стратегии, максимизирующие выигрыши) игроков являются наилучшими экономическими решениями дуополистов.
Специфика модели (8.4.6), и вообще игровых моделей, в том, что по причине конфликтного характера принятия решения нет ситуаций, доставляющих игрокам их максимальные выигрыши. Объясним это на числовых значениях элементов матрицы Q, положив в примере 8.2 a=30 , b=2, c=6, d=0 . В этом случае матрица Q принимает вид:

Видно, что максимальный выигрыш первого игрока (36) может
реализоваться в ситуации ![]() , а максимальный выигрыш второго
игрока (36) может реализоваться в ситуации
, а максимальный выигрыш второго
игрока (36) может реализоваться в ситуации ![]() . Так как эти ситуации не
совместимы, т.е. не могут реализоваться одновременно, то добиться максимальных
выигрышей оба игрока одновременно не смогут.
. Так как эти ситуации не
совместимы, т.е. не могут реализоваться одновременно, то добиться максимальных
выигрышей оба игрока одновременно не смогут.
Единственным приемлемым принципом оптимального поведения игроков в биматричной игре является принцип равновесия по Нэшу (см. определение 8.1). Фактически этот принцип отражает известную поговорку: "из двух зол выбирают меньшее". Применяя это мудрое правило, и найдем ситуацию равновесия Нэша в игре Q.
Выбирая стратегию K1, первый игрок в
худшем случае получит ![]() , а, применяя стратегию S1,
-
, а, применяя стратегию S1,
- ![]() .
Лучший из двух худших выигрышей равен
.
Лучший из двух худших выигрышей равен ![]() . Этот выигрыш соответствует
стратегии S1. Рассуждая так же, найдем для второго игрока
выигрыш 23 и стратегию S2. Как легко проверить, ситуация
. Этот выигрыш соответствует
стратегии S1. Рассуждая так же, найдем для второго игрока
выигрыш 23 и стратегию S2. Как легко проверить, ситуация ![]() и является
равновесием Нэша. Действительно, отклоняясь односторонне от ситуации
и является
равновесием Нэша. Действительно, отклоняясь односторонне от ситуации ![]() , любой игрок
разве что уменьшает свой же выигрыш.
, любой игрок
разве что уменьшает свой же выигрыш.
Напомним, что эта же ситуация ![]() в дуополии была названа
неравновесием Штакельберга, так как существует доминирующая над ней ситуация
в дуополии была названа
неравновесием Штакельберга, так как существует доминирующая над ней ситуация ![]() , в которой оба
дуополиста получают большие прибыли. Но в модели (8.4.7) в условиях отсутствия
обмена информацией между игроками ситуация
, в которой оба
дуополиста получают большие прибыли. Но в модели (8.4.7) в условиях отсутствия
обмена информацией между игроками ситуация ![]() реализована не будет ввиду
рискованности одностороннего отклонения игроков от ситуации равновесия Нэша.
Этот факт говорит в пользу кооперации между дуополистами, так как согласованный
выбор привел бы их к гораздо лучшей ситуации
реализована не будет ввиду
рискованности одностороннего отклонения игроков от ситуации равновесия Нэша.
Этот факт говорит в пользу кооперации между дуополистами, так как согласованный
выбор привел бы их к гораздо лучшей ситуации ![]() .
.
Статическая модель межотраслевого баланса. Коэффициенты прямых материальных затрат. Достаточное условие продуктивности матрицы коэффициентов прямых материальных затрат. Структурная форма линейной модели баланса межотраслевых материально-вещественных связей.
Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе.
Балансы бывают отчетные и плановые. Отчетные фиксируют сложившиеся пропорции, а плановые отражают некоторое желательное состояние и получаются в результате расчета по моделям, о которых и пойдет речь в этой главе.
В зависимости от того, в каких единицах измеряются межотраслевые потоки, различают балансы натуральные и стоимостные. Далее мы будем иметь в виду в основном стоимостные балансы.
Предположим, что народное хозяйство представлено совокупностью п отраслей. Будем считать, что каждая отрасль производит только один продукт и каждый продукт производится только одной отраслью, т. е. между отраслями и продукцией существует взаимно однозначное соответствие. В действительности это не так, поэтому в МОБ фигурируют не реальные, а так называемые "чистые", или "технологические", отрасли.
Общий вид межотраслевого баланса представлен в таблице. Она
состоит из четырех разделов. Первый раздел образуется перечнем
"чистых" отраслей. Каждая отрасль представлена в МОБ дважды: как
производящая и как потребляющая. Отрасли как производителю
соответствует строка таблицы, отрасли как потребителю соответствует столбец.
На пересечении i-й строки и j-го столбца
находится величина xij -
количество продукции
i-й отрасли (в денежном выражении), израсходованной на производственные
нужды j-й отрасли. Таким образом, первый раздел характеризует межотраслевые
потоки сырья, материалов, энергии и т. д., обусловленные производственной
деятельностью отраслей.
| 1 | 2 | … |
n |
У |
Х |
|
| 1 |
x11 |
x12 |
… |
x1n |
y1 |
x1 |
| 2 |
х21 |
x22 |
x2n |
y2 |
x2 |
|
| … | … | … | … | … | … | … |
|
n |
xn1 |
xn2 |
… |
xnn |
yn |
xn |
|
V |
v 1 |
v2 |
… |
vn |
||
|
Х |
x1 |
x2 |
. . . |
xn |
Второй раздел МОБ состоит из двух столбцов. Столбец
Y - это конечная продукция отраслей. Конечная продукция включает
в себя непроизводственное потребление (личное и общественное), возмещение
выбытия основных фондов и накопление. Столбец Х содержит величины валового
производства отраслей.
Третий раздел представлен двумя нижними строками. Строка Х содержит те же самые величины, что и соответствующий столбец второго раздела. Строка V содержит величины условно-чистой продукции отраслей. Условно-чистая продукция включает в себя амортизационные отчисления и вновь созданную стоимость (заработную плату и прибыль).
Четвертый раздел МОБ не имеет непосредственного отношения к анализу межотраслевых связей. Он характеризует перераспределительные отношения в народном хозяйстве и здесь рассматриваться не будет.
Строки показывают распределение продукции. Для любой i-й строки первого раздела справедливо соотношение
![]()
т.е. вся произведенная i-й отраслью продукция хi (валовая продукция в денежном выражении) делится на промежуточную и конечную. Промежуточная продукция - это та часть валовой продукции i-й отрасли, которая расходуется другими отраслями в процессе осуществления ими собственных производственных функций.
Столбцы МОБ показывают структуру затрат. Для любого j-го столбца можно записать:
![]()
![]()
т.е. стоимость всей произведенной j-й отраслью продукции хj состоит из текущих производственных затрат и условно-чистой продукции vj.
Суммарный конечный продукт равен суммарной условно-чистой продукции. Действительно,
![]()
![]()
Сравнивая правые части этих соотношений, видим, что
![]()
Зная суммарный конечный продукт или, что то же, суммарную условно-чистую продукцию, можно определить национальный доход. Он равен разности суммарного конечного продукта и амортизационных отчислений, направляемых на возмещение выбытия основных фондов.
Рассмотренная таблица МОБ всего лишь форма представления статистической информации о взаимосвязи отраслей. Перейдем теперь к построению математической модели. Для этого введем понятие коэффициентов прямых материальных затрат:
![]() (1)
(1)
Коэффициент aij показывает, какое количество i-го продукта затрачивается на производство единицы j-го продукта.
Поскольку продукция измеряется в стоимостных единицах, коэффициенты прямых затрат являются величинами безразмерными. Кроме того, из (1) следует, что
![]() (2)
(2)
Считая коэффициенты прямых материальных затрат постоянными, запишем систему балансовых соотношений
![]()
следующим образом:
![]()
Перенося yi в правую часть, а xi в левую и меняя знаки на противоположные, получаем
![]()
В матричной форме эта система уравнений выглядит следующим образом:
X - AX = Y или (E - A) X = Y,
где Е - единичная матрица n-го порядка;
![]() - матрица
коэффициентов прямых материальных затрат.
- матрица
коэффициентов прямых материальных затрат.
Итак, мы получили систему уравнений межотраслевого баланса, которую называют моделью Леонтьева. Используя эту модель, можно ответить на основной вопрос межотраслевого анализа - каким должно быть валовое производство каждой отрасли для того, чтобы экономическая система в целом произвела заданное количество конечной продукции?
Следует отметить одно важное свойство матрицы А - сумма элементов любого ее столбца меньше единицы:
![]() (3)
(3)
Для доказательства разделим обе части балансового соотношения
![]()
![]()
на хj и, выполнив простейшие преобразования, получим
![]()
где vj / xj= ![]() -
доля условно-чистой продукции в единице валового выпуска.
-
доля условно-чистой продукции в единице валового выпуска.
Очевидно, что ![]() >0,
так как в процессе производства не может не создаваться новой стоимости. Из
этого следует справедливость соотношения (3).
>0,
так как в процессе производства не может не создаваться новой стоимости. Из
этого следует справедливость соотношения (3).
Свойства (2) и (3) матрицы А играют ключевую роль в доказательстве ее продуктивности, т. е. в доказательстве того, что при любом неотрицательном Y система
X - AX = Y или (E - A) X = Y,
имеет единственное и неотрицательное решение Х=(Е-А)-1Y. Матрицу (Е-А)-1 обозначают через В и называют матрицей коэффициентов полных материальных затрат, или обратной матрицей Леонтьева. Коэффициент bij этой матрицы показывает, каким должен быть валовой выпуск i-й отрасли для того, чтобы обеспечить производство единицы конечного продукта j-й отрасли. Используя матрицу В, можем записать
Х = ВY
или в развернутом виде
![]()
Преимущество такой формы записи балансовой модели состоит в том, что, вычислив матрицу В лишь однажды, мы можем многократно использовать ее для вычисления Х прямым счетом, т.е. умножением В на Y. Это гораздо проще, чем каждый раз решать систему линейных уравнений.
Обратную матрицу В можно вычислить, используя метод обращения с применением формулы разложения ее в матричный ряд:
В=Е+А+А2+...+Аk+... (4)
Число членов ряда, необходимое для получения достаточно точного приближения, зависит от матрицы А, но в любом случае приемлемый результат достигается при k³ 30.
Формула (4) имеет строгое математическое доказательство. Но мы ограничимся тем, что попытаемся осмыслить ее, рассматривая Х как результат некоторого гипотетического процесса последовательного уточнения промежуточной продукции, необходимой для создания заданного конечного продукта.
Итак, вектор конечной продукции, которую должна произвести экономическая система, равен Y. Будем считать, что это и есть первоначальное задание отраслям, т. е. Х0 =Y. Для выполнения собственного задания каждая отрасль нуждается в продукции других отраслей. Если бы все отрасли подсчитали потребности и подали заявки в некоторый центр, то оказалось бы, что суммарная потребность составляет X1 =АХ0=АY. Вектор X1 можно рассматривать как промежуточную продукцию, необходимую для производства Х0. Но под обеспечение производства X1 тоже нужна промежуточная продукция: X2 =АХ1 =А2Y. Рассуждая так и далее, мы приходим к выводу, что
Х=Х0+Х1+Х2+...+Хk+... = Y+АY+А2Y+...+AkY+... =
= (е+а+а2+…+аk+...)Y.
Полные затраты можно разложить на прямую и косвенную составляющие. Прямые затраты осуществляются непосредственно при производстве данного продукта, а косвенные А2+А3+…+Аk+... относятся к предшествующим стадиям производства. Они осуществляются не прямо, а через посредство других ингредиентов, входящих в данный продукт. Элементы матрицы А2 представляют собой косвенные затраты первого порядка, элементы матрицы А3 - косвенные затраты второго порядка и т. д.
Статическая модель межотраслевого баланса, расширенная балансом труда. Коэффициенты полных затрат труда. Коэффициенты фондоёмкости отраслей. Баланс основных производственных фондов. Статическая модель межотраслевого баланса, расширенная балансом основных производственных фондов.
Показатели использования трудовых ресурсов и основных производственных фондов также могут быть исследованы в межотраслевом контексте.
Пусть L - среднегодовая численность работников i-й отрасли. По аналогии с коэффициентами прямых материальных затрат вводятся коэффициенты прямых затрат труда:
![]()
Зная эти коэффициенты, можем вычислить суммарную потребность в трудовых ресурсах при заданном объеме валового производства:
![]()
Валовое производство можно выразить через конечную продукцию по формуле
![]()
Воспользуемся этой формулой и запишем предыдущее соотношение так:
![]()
Величина ![]() показывает, какое количество
трудовых ресурсов i-й отрасли необходимо для того, чтобы обеспечить i-й
продукцией выпуск единицы j-го конечного продукта. Суммируя по всем
отраслям, получаем
показывает, какое количество
трудовых ресурсов i-й отрасли необходимо для того, чтобы обеспечить i-й
продукцией выпуск единицы j-го конечного продукта. Суммируя по всем
отраслям, получаем
![]()
или в векторной форме:
Т=ВTt.
Тj - коэффициент полных затрат труда (полная трудоемкость). Он показывает, какое количество трудовых ресурсов всех отраслей необходимо для производства единицы j-го конечного продукта.
Таким образом, суммарная потребность в трудовых ресурсах может быть вычислена двумя способами:
![]() (1)
(1)
Аналогично определяются коэффициенты прямой и полной фондоемкости. Пусть Fi - среднегодовое количество используемых основных фондов. Тогда коэффициент прямой фондоемкости
![]()
Коэффициент полной фондоемкости
![]()
То же в векторной форме:
Ф = ВTt.
Коэффициент Фj показывает, какое количество основных фондов всех отраслей необходимо для производства единицы j-го конечного продукта.
По аналогии с (1) суммарная потребность в основных фондах вычисляется так:
![]()
Коэффициенты полной трудоемкости и фондоемкости можно подобно коэффициентам полных материальных затрат рассматривать как сумму прямой и косвенной составляющих. Например, для полной фондоемкости:
Ф=(Е+А+А2+...+Ак+...)Т, f=f+(А+А2+...+Аk+...)Тf.
Косвенная составляющая полной фондоемкости (так же, как и полной трудоемкости) сравнительно невелика в сырьевых отраслях и возрастает в "завершающих" отраслях до 90¸95%.
Пример. Вычислить общую потребность в трудовых ресурсах, если известны коэффициенты прямых материальных затрат, коэффициенты прямых затрат труда и задан вектор конечного продукта:
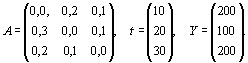
Для решения этой задачи нужно воспользоваться формулой
![]()
Как видим, возможны два способа: 1) вычислить Х = ВY, а затем применить формулу L=(t,x); 2) вычислить коэффициенты полных затрат труда Т =BTt и далее L=(Т,Y). Но в обоих случаях необходимо сначала вычислить
матрицу В.
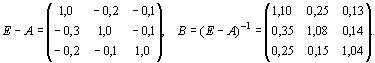
Первый способ:
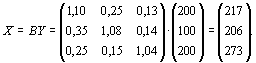
![]()
Второй способ:
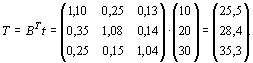
![]()
Важнейшую часть национального богатства составляют основные производственные фонды, представляющие собой материально-техническую базу народного хозяйства. Основные производственные фонды - это средства труда, функционирующие во всех отраслях материального производства. К основным производственным фондам относят только продукты общественного труда, начавшие функционирование в производстве.
Основные производственные фонды весьма различны по своему вещественно-материальному составу и назначению. Одни создают условия для осуществления производственного процесса, другие выполняют транспортные функции, при помощи третьих осуществляется производственный процесс и т.д. В настоящее время в практике нашей статистики принята следующая единая типовая классификация основных производственных фондов по всему народному хозяйству.
· Здания.
· Сооружения.
· Передаточные устройства.
· Машины и оборудование, в том числе: силовые машины и оборудование, из них автоматические, рабочие машины и оборудование, из них автоматические, измерительные и регулирующие приборы и устройства и лабораторное оборудование, из них автоматические, вычислительная техника, в том числе автоматическая, прочие машины, из них автоматические.
· Транспортные средства.
· Инструменты.
· Производственный инвентарь и принадлежности.
· Хозяйственный инвентарь.
· Рабочий и продуктивный скот.
· Многолетние насаждения
· Капитальные затраты по улучшению земель.
· Прочие основные фонды.
По отдельным отраслям материального производства эта типовая классификация конкретизируется с учетом особенностей отрасли.
Основные фонды занимают, как правило, основной удельный вес в общей сумме основного капитала предприятия. От их количества, стоимости, технического уровня, эффективности использования во многом зависят конечные результаты деятельности предприятия: выпуск продукции, ее себестоимость, прибыль, рентабельность, устойчивость финансового состояния.
Для обобщающей характеристики эффективности использования основных средств служат показатели рентабельности (отношение прибыли к среднегодовой стоимости основных производственных фондов), фондоотдачи (отношение стоимости произведенной или реализованной продукции после вычета НДС, акцизов к среднегодовой стоимости основных производственных фондов), фондоемкости (обратный показатель фондоотдачи), удельных капитальных вложений на один рубль прироста продукции
Динамическая модель межотраслевого баланса. Открытая и замкнутая динамические модели. Сбалансированная траектория развития экономики в линейной модели с продуктивной матрицей коэффициентов прямых материальных затрат.
Следующим представителем класса линейных моделей экономики является модель, построенная в середине 1930-х годов австрийским математиком Джоном фон Нейманом. По сравнению с моделью Леонтьева, которую можно использовать для планирования производства на одном плановом периоде в целом (год, пятилетка и т.д.), модель Неймана отслеживает производственный процесс внутри планового периода, т.е. затраты и выпуск, осуществляемые в каждый период времени (от квартала в квартал, от года в год и т.д.). Поэтому она обобщает модель Леонтьева в двух аспектах: в динамическом плане и в плане многопродуктовых отраслей. В модели Неймана предполагается, что экономика функционирует эффективным образом сколь угодно долго. Логическим следствием такой предпосылки является рост производственных возможностей во времени с нарастающими темпами. Поэтому модель Неймана описывает "расширяющуюся" экономику.
Для вывода этой схемы рассмотрим функционирование экономики
на некотором конечном периоде времени [0,T] . Отрезок [0,T]
разобьем точками ![]() , k=0,1,...,T, так, чтобы
получилась возрастающая последовательность моментов времени
, k=0,1,...,T, так, чтобы
получилась возрастающая последовательность моментов времени
![]()
Тогда получаем последовательность полуинтервалов ![]() длины
длины ![]() , покрывающих
весь отрезок [0,T] . Момент
, покрывающих
весь отрезок [0,T] . Момент ![]() будем трактовать как начальный
момент планирования производства товаров, а момент
будем трактовать как начальный
момент планирования производства товаров, а момент ![]() - как плановый горизонт. В
дальнейшем во всех отношениях удобно полагать
- как плановый горизонт. В
дальнейшем во всех отношениях удобно полагать ![]() и трактовать моменты
и трактовать моменты ![]() как годы. При
этих обозначениях мы будем писать
как годы. При
этих обозначениях мы будем писать ![]() .
.
В этом параграфе, как и в модели Леонтьева, будем предполагать, что экономика состоит из n чистых отраслей с постоянными технологиями, описываемыми матрицей A. Планирование опять будем понимать по схеме затраты-выпуск при известном спросе на товары, но теперь уже с учетом фактора времени.
Под планом производства на отрезке времени [0,T] будем понимать совокупность
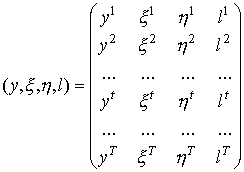
Здесь каждая строка соответствует плану ![]() в год t ;
в год t ; ![]() - вектор
запасов товаров,
- вектор
запасов товаров, ![]() - вектор валового выпуска. Каждая
компонента
- вектор валового выпуска. Каждая
компонента ![]() считается
максимально возможным при существующих основных фондах выпуском отрасли j.
Валовый выпуск отрасли может быть увеличен путем дополнительных вложений, и
этот показатель также включается в план. Вектор
считается
максимально возможным при существующих основных фондах выпуском отрасли j.
Валовый выпуск отрасли может быть увеличен путем дополнительных вложений, и
этот показатель также включается в план. Вектор ![]() обозначает планируемое в год t
увеличение (приращение) валового выпуска. Наконец, число lt
показывает общее количество нанятых во всех отраслях рабочих в год t.
обозначает планируемое в год t
увеличение (приращение) валового выпуска. Наконец, число lt
показывает общее количество нанятых во всех отраслях рабочих в год t.
Труд, как вид товара, не рассматривался в исходной модели
Леонтьева. Особенность данного товара заключается в том, что он, во-первых,
являясь воспроизводимым ресурсом, в то же время не является продуктом
какой-либо отрасли, во-вторых, как фактор в производственном процессе, занимает
промежуточное положение между материальными ресурсами и готовой продукцией.
Никакое производство не может обходиться без трудовых затрат. Единицей ее
измерения является рабочая сила. Необходимое для отрасли количество рабочей
силы определяется трудовыми затратами, вложенными в выпуск одной единицы
продукции. Данный параметр для отрасли j обозначим ![]() . Тогда число рабочих в
отрасли j в год t равно
. Тогда число рабочих в
отрасли j в год t равно ![]() . Вектор
. Вектор ![]() называется вектором трудовых
затрат.
называется вектором трудовых
затрат.
Обозначим через ![]() , j=1,...,n, объемы материальных
затрат, необходимых для приращения на одну единицу выпуска товара i.
Тогда материальные затраты на одновременное приращение выпусков всех отраслей
на величины
, j=1,...,n, объемы материальных
затрат, необходимых для приращения на одну единицу выпуска товара i.
Тогда материальные затраты на одновременное приращение выпусков всех отраслей
на величины ![]() будут
исчисляться как
будут
исчисляться как ![]() , где
, где ![]() - технологическая матрица
приращения производства.
- технологическая матрица
приращения производства.
Наглядную картину межотраслевых связей во времени при плане
производства ![]() , плане конечного потребления на
одного работающего на весь плановый период
, плане конечного потребления на
одного работающего на весь плановый период ![]() и при постоянных технологиях
производства и его приращения показывает схема динамического межотраслевого
баланса (рис. 6.2). Эта схема составляется для каждого года
и при постоянных технологиях
производства и его приращения показывает схема динамического межотраслевого
баланса (рис. 6.2). Эта схема составляется для каждого года ![]() , причем при
, причем при ![]() есть валовый
выпуск отрасли j к началу планового периода.
есть валовый
выпуск отрасли j к началу планового периода.

Балансовый характер этой схемы заключается в том, что ее элементы должны удовлетворять следующим (балансовым) соотношениям:
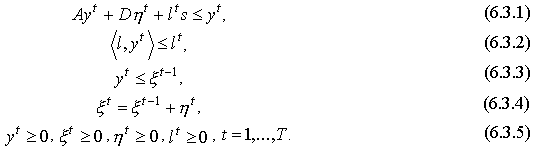
Здесь ![]() - производственные затраты,
- производственные затраты, ![]() -
дополнительные затраты, соответствующие приращению производства на вектор
-
дополнительные затраты, соответствующие приращению производства на вектор ![]() , а
, а ![]() - конечное
потребление в год t. Поэтому условие (6.3.1) требует, чтобы весь
годичный запас товаров покрывал все годичные затраты ежегодно. Неравенство (6.3.2)
задает условие на необходимый объем трудовых ресурсов, неравенство (6.3.3)
говорит о том, что запасы на данный год не могут превышать результатов
производства предыдущего года, и, наконец, уравнение (6.3.4) описывает динамику
роста валового выпуска из года в год.
- конечное
потребление в год t. Поэтому условие (6.3.1) требует, чтобы весь
годичный запас товаров покрывал все годичные затраты ежегодно. Неравенство (6.3.2)
задает условие на необходимый объем трудовых ресурсов, неравенство (6.3.3)
говорит о том, что запасы на данный год не могут превышать результатов
производства предыдущего года, и, наконец, уравнение (6.3.4) описывает динамику
роста валового выпуска из года в год.
Если сравнить систему (6.3.1)-(6.3.5) с моделью Леонтьева (6.2.1),
то можно заметить, что последняя получается из (6.3.1) при отсутствии
приращения производства, т.е. когда ![]() . Дополнительные условия (6.3.2)-(6.3.4)
вызваны необходимостью учета трудовых ресурсов и динамического характера
развития производства. Как и модель Леонтьева, данная схема может быть обобщена
и детализирована по ряду параметров. В приведенном здесь виде наиболее
нереальным является условие (6.3.4), которое предполагает (при
. Дополнительные условия (6.3.2)-(6.3.4)
вызваны необходимостью учета трудовых ресурсов и динамического характера
развития производства. Как и модель Леонтьева, данная схема может быть обобщена
и детализирована по ряду параметров. В приведенном здесь виде наиболее
нереальным является условие (6.3.4), которое предполагает (при ![]() ) получение результатов
от затрат, осуществляемых в начале периода
) получение результатов
от затрат, осуществляемых в начале периода ![]() , уже к концу этого периода.
Условие (6.3.4) можно переписать так:
, уже к концу этого периода.
Условие (6.3.4) можно переписать так:
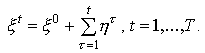
В этом равенстве последнее слагаемое имеет смысл приращения производства за первые t лет по сравнению с начальным объемом выпуска. Доля такого приращения, приходящаяся на одну единицу начального валового выпуска, есть
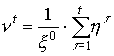
Введем величину ![]() . Тогда уравнение (6.3.4) можно
написать в виде
. Тогда уравнение (6.3.4) можно
написать в виде
![]()
Представление динамики производства в подобном виде будет использовано нами в следующем параграфе. Здесь заметим только, что более адекватным описанием динамики производства, чем (6.3.4), представляется равенство
![]()
где ![]() - отнесенный к моменту t
временной лаг,
- отнесенный к моменту t
временной лаг, ![]() (
(![]() ).
).
Обозначим ![]() и составим матрицы
и составим матрицы
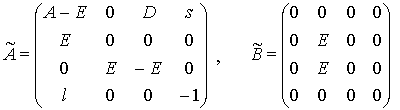
с помощью которых систему (6.3.1)-(6.3.5) перепишем в виде
![]()
В математической экономике магистралью называется траектория экономического роста, на которой пропорции производственных показателей (такие как темп роста производства, темп снижения цен) неизменны, а сами показатели (такие как интенсивность производства, валовый выпуск) растут с постоянным максимально возможным темпом. Таким образом, магистраль - это траектория или луч максимального сбалансированного роста. Ее часто сравнивают со скоростной автострадой. Так, например, для того чтобы добраться из Кемерово в Киселевск как можно быстрее, наиболее целесообразно сначала проехать по автостраде Кемерово-Новокузнецк, а затем уже съехать на ответвляющуюся от нее дорогу в районе Киселевска. Так мы потеряем на дорогу меньше времени и доедем до конечного пункта с большим комфортом, чем если бы мы ехали по обычному шоссе через Ленинск-Кузнецкий и Белово.
Поскольку "оптимальное" или
"эффективное" развитие экономики в любом смысле так или иначе связано
и должно сопровождаться экономическим ростом, то для достижения любой конечной
цели следует поступать аналогичным образом: сначала вывести производство на
магистральный путь, т.е. на траекторию (или луч) Неймана, характеризующуюся
максимальным темпом роста ![]() и минимальной нормой процента
и минимальной нормой процента ![]() (см. (6.4.14)),
а по истечении определенного срока времени вывести ее к задуманной цели. Такими
целями могут быть максимизация прибыли, минимизация затрат, максимизация
полезности от потребления товаров, достижение конкурентного равновесия при
наиболее благоприятных условиях, т.е. на более высоком уровне благосостояния
населения, и т.д.
(см. (6.4.14)),
а по истечении определенного срока времени вывести ее к задуманной цели. Такими
целями могут быть максимизация прибыли, минимизация затрат, максимизация
полезности от потребления товаров, достижение конкурентного равновесия при
наиболее благоприятных условиях, т.е. на более высоком уровне благосостояния
населения, и т.д.
Итак, с одной стороны мы имеем магистральные модели, а с
другой - оптимизационные или еще шире - нормативные модели экономики. Изучение
этих двух моделей во взаимосвязи, т.е. изучение связи между магистральными и
оптимальными (в том или ином смысле) траекториями и является предметом
магистральной теории. Можно говорить, что магистральная теория является одним
из средств качественного анализа оптимальных траекторий. Основной целью этой
теории является исследование условий так называемых "слабой" и
"сильной" теорем о магистралях. Слабая теорема утверждает, что за
исключением некоторого малого периода ![]() (или некоторого числа дискретных
моментов из
(или некоторого числа дискретных
моментов из ![]() ),
не зависящего от продолжительности T планового периода, все оптимальные
траектории сосредотачиваются в относительной близости к магистральной
траектории. Сильная теорема говорит о том, что те небольшие промежутки времени
),
не зависящего от продолжительности T планового периода, все оптимальные
траектории сосредотачиваются в относительной близости к магистральной
траектории. Сильная теорема говорит о том, что те небольшие промежутки времени ![]() , на которых
оптимальные траектории удалены от магистральной, если они существуют, то разве
лишь в начале периода
, на которых
оптимальные траектории удалены от магистральной, если они существуют, то разве
лишь в начале периода ![]() , т.е.
, т.е. ![]() , или в конце периода
, или в конце периода ![]() , т.е.
, т.е. ![]() ; а в середине
периода оптимальные траектории расположены в относительной близости к
магистральной.
; а в середине
периода оптимальные траектории расположены в относительной близости к
магистральной.
В общем случае в моделях экономической динамики даже при неизменности технологических возможностей утверждения теорем о магистрали не выполняются. Для их выполнения приходится вводить различные дополнительные предположения о свойствах исходной модели экономики. Другой путь состоит в изучении реальных отраслевых пропорций и сравнении их с магистральными. Благодаря техническому прогрессу и изменчивости во времени общественных предпочтений различных благ, реальное состояние экономики при детальном (дезагрегированном) ее описании всегда значительно отличается от магистрального. В то же время, как показывают полученные в этом направлении результаты исследований, при высоком уровне агрегирования экономические пропорции близки к магистральным.
Теоремы о магистралях доказываются для ряда оптимизационных моделей расширяющейся экономики. Наиболее общей из них является известная теорема Раднера для нелинейных моделей расширения (см. §7.2). Здесь мы приведем подобные теоремы для линейных моделей Леонтьева и Неймана. Единственная наша цель - дать читателю начальное представление о магистральной теории. Поэтому приводить сложные доказательства теорем и заниматься подробным и строгим анализом их условий не будем. Для более углубленного изучения магистральной теории можно рекомендовать книги [2, 16].
Три этапа построения производственной функции. Спецификация ПФ, идентификация параметров. Проверка на адекватность.
По существу, производственная функция f есть совокупность "правил", с помощью которых для каждого набора затрат определяется соответствующий выпуск. Поэтому построение производственной функции означает нахождение математической формулы, отражающей эти правила или, иначе говоря, закономерности превращения набора ресурсов в конечный продукт. Этот процесс условно можно представить схемой:
В блоке f (см. рис. 4.2 ), образно говоря, происходит
"смешивание" ресурсов ![]() в определенных
"пропорциях" таким образом, чтобы получился требуемый продукт. Эти
"пропорции" определяются спецификой производства и математически
выражаются с помощью различных коэффициентов и показателей степени для величин
в определенных
"пропорциях" таким образом, чтобы получился требуемый продукт. Эти
"пропорции" определяются спецификой производства и математически
выражаются с помощью различных коэффициентов и показателей степени для величин ![]() .
"Смешивание" их математически выражается с помощью разных формальных
операций между ними (суммирования, произведения, логарифмирования и т.д.), вид
и сочетание которых также определяется спецификой моделируемого производства.
Так что вопрос построения производственной функции в каждом конкретном случае
сводится к нахождению этих "пропорций" и к определению характера их
"смешивания".
.
"Смешивание" их математически выражается с помощью разных формальных
операций между ними (суммирования, произведения, логарифмирования и т.д.), вид
и сочетание которых также определяется спецификой моделируемого производства.
Так что вопрос построения производственной функции в каждом конкретном случае
сводится к нахождению этих "пропорций" и к определению характера их
"смешивания".
Из сказанного выше следует, что для построения производственных функций нужно знать технологию производства, ее структуру и организацию, а также принципы работы сложных машин и оборудования, т.е. надо быть одновременно и технологом, и инженером, и математиком. Оказывается, что знание всего этого сложного производственного механизма не требуется, если владеть подходящими математическими приемами. Речь идет об использовании методов регрессионного анализа на основе статистических (опытных, экспертных) данных о затратах и выпуске. Не умаляя достоинства других математических и иных методов построения производственных функций, можно сказать, что именно методы регрессионного анализа наилучшим образом оправдали себя на практике и потому являются наиболее популярными. Вопросы построения производственных функций на основе экспериментальных данных являются предметом изучения специального раздела – эконометрики. . Здесь же мы коснемся лишь содержательной стороны построения конкретных видов производственных функций.
Идею применения статистических данных для построения производственной
функции можно объяснить так: Имеются известные величины (реальные результаты
производства) и одно неизвестное выражение f, их связующее. Наблюдая в
течение достаточно большого периода времени функционирования производства за
различными значениями затрат ![]() и соответствующими им значениями
выпуска y, можно выявить закономерность f :
и соответствующими им значениями
выпуска y, можно выявить закономерность f :
![]()
Кратко остановимся на этапах построения производственной
функции. Пусть нам известны виды ресурсов (![]() ), используемых для выпуска данной
продукции, и имеется необходимое количество статистических данных по объемам
затрат
), используемых для выпуска данной
продукции, и имеется необходимое количество статистических данных по объемам
затрат ![]() и
выпуска y. Требуется установить зависимость
и
выпуска y. Требуется установить зависимость ![]() , т.е. найти аналитический вид
производственной функции f. Эта задача распадается на два этапа:
, т.е. найти аналитический вид
производственной функции f. Эта задача распадается на два этапа:
спецификация функции f, т.е. выявление общего вида функции f
от аргументов ![]() с неопределенными параметрами
(коэффициентами и показателями степеней при
с неопределенными параметрами
(коэффициентами и показателями степеней при ![]() и свободным членом);
и свободным членом);
оценка параметров - определение конкретных числовых значений неизвестных параметров.
Картина "расположения" статистических данных в
пространстве затраты-выпуск может подсказать линейный или нелинейный характер
зависимости функции f от аргументов ![]() . Например, в случае линейной
производственной функции результатом спецификации будет гипотеза о линейной
зависимости вида
. Например, в случае линейной
производственной функции результатом спецификации будет гипотеза о линейной
зависимости вида
![]()
в случае производственной функции Кобба-Дугласа - в виде мультипликативной функции

в случае производственной функции CES - в виде степенного многочлена

и т.д. Здесь ![]() являются неизвестными параметрами,
подлежащими определению (оценке).
являются неизвестными параметрами,
подлежащими определению (оценке).
Чаще остальных на практике применяется аппроксимация вида (4.4.1) , называемая линейной регрессией (см. §9.2 ). Для определения ее параметров используется (линейный) метод наименьших квадратов (см. §9.3 ). В некоторых случаях к линейной аппроксимации удается свести и нелинейные относительно ресурсов производственные функции. Например, логарифмируя функцию (4.4.2) , получим:
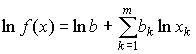
Далее, вводя обозначения
![]()
приходим к линейной регрессии вида (4.4.1) :
![]()
Применяя такой способ на основе статистических данных упомянутого выше периода, Кобб и Дуглас получили следующую оценку параметров для своей функции:
![]()
и, следовательно, их производственная функция выглядела так:
![]()
Дальнейший анализ показал, что за исключением некоторых
случаев (например, учета технического прогресса), имеет место соотношение ![]() . Так как
величина
. Так как
величина ![]() показывает
эластичность производства, равенство
показывает
эластичность производства, равенство ![]() является признаком линейной
однородности производственной функции (см. §4.3
и пример 4.1 ). Этот факт позволяет
записывать функцию Кобба-Дугласа в виде
является признаком линейной
однородности производственной функции (см. §4.3
и пример 4.1 ). Этот факт позволяет
записывать функцию Кобба-Дугласа в виде ![]() , где
, где ![]() .
.
В отличие от функции Кобба-Дугласа, функция (4.4.3) даже после логарифмирования остается нелинейной. Поэтому для оценки параметров функции CES применяется более сложный нелинейный метод наименьших квадратов. Изложение этого метода и реализацию его алгоритма на языке программирования Бейсик интересующийся читатель может найти в книге [ 14 ].
При спецификации производственной функции, т.е. при решении
вопроса о ее принадлежности к тому или иному классу известных функций, может
быть полезным знание тех или иных числовых характеристик этих классов функций
(отношение средних и предельных показателей, предельная норма замещения,
эластичность и др.). Например, при моделировании двухфакторного производства (![]() ) на основе
имеющейся статистики
) на основе
имеющейся статистики ![]() можно составить дискретный
(разностный) аналог показателя эластичности по капиталу
можно составить дискретный
(разностный) аналог показателя эластичности по капиталу
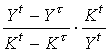
Если эта величина приблизительно равна постоянному числу для
всех t и ![]() ,
для которых разность
,
для которых разность ![]() достаточно мала, то искомая
функция может принадлежать классу функций Кобба-Дугласа. Точно так же,
дискретный аналог эластичности замещения может внести ясность относительно
принадлежности искомой функции к классу функций CES.
достаточно мала, то искомая
функция может принадлежать классу функций Кобба-Дугласа. Точно так же,
дискретный аналог эластичности замещения может внести ясность относительно
принадлежности искомой функции к классу функций CES.
Выделение существенных видов ресурсов (факторов производства) и выбор аналитической формы ПФ называется спецификацией ПФ.
Преобразование реальных и экспертных данных в модельную информацию, т.е. расчет численных значений параметров ПФ на базе статистических данных с помощью регрессионного и корреляционного анализа, называется параметризацией ПФ.
Проверка истинности (адекватности) ПФ называется ее верификацией.
Спецификация определяется, прежде всего, теоретическими соображениями, которые учитывают макро и микроэкономические особенности объекта исследования, параметризация также использует для сглаживания результатов ряда лет методы наименьших квадратов.
Моделирование производственных процессов. Факторы производства. Неоклассическая производственная функция, и её свойства. Предельные и средние продукты факторов производства. Эластичность выпуска по факторам производства. Изокванты. Предельные нормы и эластичность замещения факторов производства. Основные виды ПФ выпуска. Равновесие производителя.
Под производством понимается процесс взаимодействия экономических факторов, завершаемый выпуском какой-либо продукции. Правила, предписывающие определенный порядок взаимодействия экономических факторов, составляют способ производства или, иначе говоря, технологию производства. Производство - основная область деятельности фирмы (или предприятия). Фирма - это организация, производящая затраты экономических ресурсов для изготовления продукции и услуг, которые она продает потребителям, в том числе, другим фирмам. Производственными единицами являются не только заводы и фабрики, но и отдельные лица - фермеры, ремесленники и др.
Производство можно представить как систему "затраты-выпуск", в которой выпуском является то, что фактически произведено, а затратами - то, что потребляется с целью выпуска (капитал, труд, энергия, сырье). Поэтому формально можно сказать, что производство - это функция, которая каждому набору затрат и конкретной технологии ставит в соответствие определенный выпуск. Именно такое упрощенное понимание производства как "черного ящика" заложено в математической модели производства. Во "вход" этого черного ящика подаются затраты, а на "выходе" получаем выпуск (произведенную продукцию).
Подобное описание производства на первый взгляд кажется сильно абстрактным, так как в нем не отражены технологические процессы, происходящие внутри черного ящика. В математической модели технология производства учитывается обычно посредством задания соотношений между затратами и выпуском т.е. нормой затрат каждого из ресурсов, необходимых для получения одной единицы выпускаемой продукции. Такой подход объясняется тем, что математическая экономика изучает суть экономических процессов, а сугубо технические операции как таковые (а не их экономические следствия) остаются за рамками этой науки.
Задача фирмы, как производственной единицы, сложна и многогранна - начиная от организации производства и кончая благотворительной деятельностью. Естественно, математической моделью нельзя охватить весь спектр деятельности фирмы и отразить все преследуемые цели. Поэтому при формализации задачи рационального функционирования фирмы учитываются лишь основные конечные цели.
Конечной целью фирмы является получение наибольшей прибыли от реализации своей продукции. Напомним в этой связи, что прибыль понимается как разность двух величин: выручки от реализации продукции (дохода) и издержек производства. Издержки производства равны общим выплатам за все виды затрат, иначе говоря, издержки - это денежный эквивалент материальных затрат. В общем случае издержки состоят из двух слагаемых: постоянных издержек и переменных издержек. Постоянные издержки (расходы на закупку и ремонт оборудования, содержание фирмы, страховку и пр.) фирма несет независимо от объема выпуска. Переменные издержки (расходы на заработную плату, сырье и пр.) касаются использования уже имеющихся в распоряжении фирмы ресурсов, производственных мощностей и меняются вместе с объемом выпуска.
Согласно с поставленной целью, задача фирмы сводится к поиску такого способа производства (сочетания затрат и выпуска), который обеспечивает ей наибольшую прибыль с учетом и в рамках имеющихся у нее ограниченных ресурсов. Данная трактовка цели фирмы и наилучшего способа производства не является единственно возможной. Речь идет о некоторой гипотезе относительно предпочтений производителя, а не о логической необходимости. В действительности же мотивы принимаемых руководителями фирм решений могут быть продиктованы другими соображениями, например, гуманного или социально-политического характера. Поэтому в отличие от математической теории потребления, где существовала единственная, логически оправданная оптимизационная модель потребителя, здесь нецелесообразно говорить об "оптимизационной модели фирмы" как таковой. Задачи фирмы могут существенно отличаться как преследуемой целью, так и временным периодом ее решения.
Обсужденную выше задачу будем называть задачей фирмы на максимизацию прибыли. Двойственной к ней (в некотором смысле) является задача фирмы на минимизацию издержек при фиксированном уровне планируемого выпуска (дохода). Именно такая формализация цели производства в последнее время становится более популярной в связи с глобальной проблемой "устойчивого развития" общества, так как она созвучна с задачами рационального использования природных ресурсов.
Предположим, что фирма производит n видов продуктов.
Виды продуктов будем обозначать индексом j, а их количества - через ![]() . Технология
производства каждого вида продукта требует использования ряда ресурсов в
некоторых количествах. Двойными индексами
. Технология
производства каждого вида продукта требует использования ряда ресурсов в
некоторых количествах. Двойными индексами ![]() обозначим виды ресурсов,
используемых для выпуска продукта вида j. Пусть
обозначим виды ресурсов,
используемых для выпуска продукта вида j. Пусть ![]() . . Обозначим через
. . Обозначим через ![]() - количества
этих ресурсов,
- количества
этих ресурсов, ![]() . Следовательно, имеется всего
. Следовательно, имеется всего ![]() видов ресурсов.
видов ресурсов.
Использование такой двойной индексации привлекательно с
точки зрения информативности (видно, какой ресурс относится к какому продукту),
но неудобно чисто технически. Во-первых, усложняется запись формул; во-вторых,
увеличивается размерность задачи (т.к. среди ![]() могут быть одни и те же
наименования) и, в-третьих, такие операции как сложение, вычитание затрат в
векторной форме, а также составление уравнений становятся невозможными без
дополнительных преобразований индексов (идентификация, упорядочение и т.д.).
могут быть одни и те же
наименования) и, в-третьих, такие операции как сложение, вычитание затрат в
векторной форме, а также составление уравнений становятся невозможными без
дополнительных преобразований индексов (идентификация, упорядочение и т.д.).
Поэтому в дальнейшем виды ресурсов будем обозначать
одинарными индексами k, их количества - ![]() , где
, где ![]() . Здесь m - достаточно
большое число (равное сумме
. Здесь m - достаточно
большое число (равное сумме ![]() , где каждый ресурс считается
только один раз). Теперь можно говорить, что для производства n видов продуктов
фирма использует m видов затрат. Это не приводит к недоразумениям, так как в
случае неиспользования k-го ресурса для выпуска данного продукта
полагаем
, где каждый ресурс считается
только один раз). Теперь можно говорить, что для производства n видов продуктов
фирма использует m видов затрат. Это не приводит к недоразумениям, так как в
случае неиспользования k-го ресурса для выпуска данного продукта
полагаем ![]() .
.
Введем в рассмотрение два вида векторов: ![]() - вектор затрат и
- вектор затрат и
![]() - вектор
выпуска. Положительный ортант
- вектор
выпуска. Положительный ортант
![]()
называется пространством затрат. Аналогично определяется пространство выпуска:
![]()
Для отражения реальных возможностей фирмы в математических
моделях часто применяются более узкие множества ![]() .
.
Технологическая связь между затратами и выпуском описывается с помощью производственной функции.
Определение 4.1. Любая функция ![]() , ставящая в
соответствие каждому вектору затрат x вектор
, ставящая в
соответствие каждому вектору затрат x вектор ![]() максимального выпуска, который
может быть получен при этих затратах, называется производственной функцией.
максимального выпуска, который
может быть получен при этих затратах, называется производственной функцией.
Это есть определение производственной функции для
многопродуктовой фирмы, т.е. векторной производственной функции. Если фирма
выпускает только один вид продукта, то производственная функция является
скалярной: ![]() или
или
![]()
В общем случае производственную функцию можно записать в
неявной форме: ![]() , где A -
, где A - ![]() -матрица параметров
(технологическая матрица). В некоторых моделях применяется следующее выражение
для производственной функции:
-матрица параметров
(технологическая матрица). В некоторых моделях применяется следующее выражение
для производственной функции: ![]() , где переменные
, где переменные ![]() со знаком "-"
обозначают затраты, а со знаком "+" - выпуски.
со знаком "-"
обозначают затраты, а со знаком "+" - выпуски.
Если в качестве независимых переменных (аргументов)
выступают затраты (см. (4.2.1) ), то производственную функцию иногда называют функцией
выпуска, если же фиксирована величина выпуска (y), то
производственная функция является функцией затрат (![]() ). Таким образом,
функция выпуска и функция затрат являются взаимно обратными друг другу
функциями.
). Таким образом,
функция выпуска и функция затрат являются взаимно обратными друг другу
функциями.
Применение производственных функций не ограничивается выявлением зависимости затраты-выпуск. Различные приемы математического аппарата позволяют использовать их для вычисления численных характеристик производства, анализа эффективности изменения масштаба производства и технологического прогресса, исследования эластичности производственных факторов, рационального ведения хозяйства, оптимального планирования и прогнозирования вариантов развития фирмы и др.
Поэтому очень важно, чтобы производственная функция объективно отражала моделируемую действительность, т.е. чтобы она удовлетворяла содержательно-логическим и экономическим требованиям. Основные из них следующие:
- в число аргументов производственной функции должны быть включены все существенные для данного процесса факторы;
- все величины должны иметь отчетливый экономический смысл;
- все экономические величины, входящие в производственную функцию, должны быть измеримы;
- выпуск продукции без затрат невозможен;
- если величина какого-либо ресурса ограничена, то выпуск не может расти бесконечно;
- увеличение затрат не может привести к уменьшению выпуска.
Вопрос об адекватном описании экономической реальности на языке производственных функций тесно связан с их математическими свойствами. Ради простоты эти свойства приведем для однопродуктового производства, т.е. для производственной функции вида (4.2.1) .
- Монотонность: из
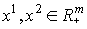 и
и 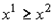 следует
следует 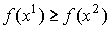 .
. - Вогнутость: для любых
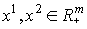 и
и 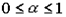 справедливо
неравенство
справедливо
неравенство 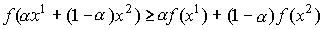 .
. - Поведение в начале координат:
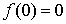 .
. - Однородность:
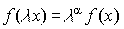 , где
, где 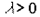 -
масштабное число,
-
масштабное число, 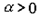 - степень однородности.
- степень однородности.
Если производственная функция дифференцируема по всем аргументам, то свойства 1 и 2 соответственно могут быть заменены следующими неравенствами:

Частные производные ![]() называются предельными
продуктами. Условие (4.2.2) , как и свойство 1, означает, что увеличение
любого вида затрат не приводит к уменьшению выпуска. Условие (4.2.3)
показывает, что увеличение затрат одного вида ресурса (при постоянном уровне
затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство
в экономической теории называется законом убывающей доходности (отдачи).
называются предельными
продуктами. Условие (4.2.2) , как и свойство 1, означает, что увеличение
любого вида затрат не приводит к уменьшению выпуска. Условие (4.2.3)
показывает, что увеличение затрат одного вида ресурса (при постоянном уровне
затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство
в экономической теории называется законом убывающей доходности (отдачи).
Свойство 3 является отражением бездеятельности, так как без
затрат нет и выпуска. Свойство 4 описывает реакцию производства на изменение
затрат. Параметр ![]() показывает масштаб изменения
производства (расширения производства - если
показывает масштаб изменения
производства (расширения производства - если ![]() , сужения производства - если
, сужения производства - если ![]() ), а
), а ![]() - эффект от изменения
масштабов производства. Если
- эффект от изменения
масштабов производства. Если ![]() , то одновременное увеличение всех
факторов в
, то одновременное увеличение всех
факторов в ![]() раз
приводит к возрастанию объема выпуска больше, чем в
раз
приводит к возрастанию объема выпуска больше, чем в ![]() раз (
раз (![]() ), т.е. эффект от расширения
масштаба производства положителен. При
), т.е. эффект от расширения
масштаба производства положителен. При ![]() получаем:
получаем: ![]() - выпуск возрастает в
той же пропорции, что и затраты. Такие функции называются линейно-однородными
(или однородными в первой степени).
- выпуск возрастает в
той же пропорции, что и затраты. Такие функции называются линейно-однородными
(или однородными в первой степени).
Если
![]()
то говорят о возрастающем (убывающем) доходе от расширения масштаба производства. Заметим, что свойство 4 определено в точке, тогда как свойства 1 и 2 - во всем пространстве затрат.
Как мы видим, перечисленные (желательные) свойства производственной функции вполне согласуются с ее определением, так как они касаются только соотношения затраты-выпуск. Действительно, здесь нет никаких требований на бесперебойную работу станков, нормирования движения конвейера и т.д. Поэтому производственная функция, как отображение количественной связи между затратами и выпуском, представляет собой регрессионную модель (см. §2.5 ). Следовательно, она может быть построена на основе статистических данных и с применением методов математической статистики. Оставляя подробное обсуждение этого вопроса до §4.4 , сейчас мы приведем примеры наиболее удачно построенных и потому часто применяемых на практике производственных функций. При этом для простоты будем рассматривать двухфакторную однопродуктовую производственную функцию вида
![]()
Средним продуктом по k-му виду затрат называется объем выпуска, приходящийся на единицу затрат k-го вида при фиксированном уровне затрат других видов:
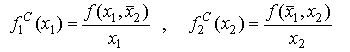
Сначала остановимся на понятии эластичности производства.
Уже знакомое нам из §4.2 свойство однородности производственной функции
оценивает технологию производства в различных точках пространства затрат. А
именно, производственная функция в одних точках этого пространства может
характеризоваться постоянным доходом от расширения масштаба производства, а в
других - его увеличением или, наоборот, уменьшением. Локальным показателем
измерения дохода от расширения масштаба производства и служит эластичность
производства. Ее мы будем обозначать символом ![]() ("эластичность f по
("эластичность f по ![]() в точке x").
Формально (см. (3.3.2) ) мы можем написать:
в точке x").
Формально (см. (3.3.2) ) мы можем написать:
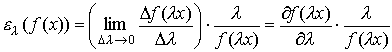
Однако это соотношение не отражает изменение масштаба производства в точке x. Поэтому вычислительная формула эластичности производства выглядит так:

или, что то же самое,
![]()
В случае постоянства дохода при расширении масштаба производства (т.е. для линейно-однородной производственной функции) эластичность производства равна единице.
Эластичность производства, описываемого дифференцируемой линейно-однородной функцией, в любой точке пространства затрат равна сумме эластичностей выпуска по всем видам затрат.
На практике по разным причинам часто возникает необходимость замены одних ресурсов другими. Например, при расширении производства фирма должна решить: либо полностью автоматизировать производство за счет дорогостоящего оборудования и сократить количество рабочих мест (сократить фонд заработной платы), либо использовать предназначенные для этого средства для частичной модернизации технологии и увеличения фонда заработной платы. Что выгодно для фирмы? Для получения ответа на этот вопрос вводят понятия предельной нормы замещения одних ресурсов другими и эластичности замещения одних ресурсов другими.
Возможности замещения характеризуют производственную функцию
с точки зрения различных комбинаций затрат, порождающих одинаковые уровни
выпуска. Предположим, что двухфакторное производство описывается
производственной функцией ![]() , где Y - выпуск, K
- капитал (основные фонды), L - трудовые ресурсы. Предположим, часть
рабочих (
, где Y - выпуск, K
- капитал (основные фонды), L - трудовые ресурсы. Предположим, часть
рабочих (![]() )
уволилась. На какую величину
)
уволилась. На какую величину ![]() следует увеличить основные фонды,
чтобы выпуск остался на прежнем уровне, т.е. чтобы имело место равенство
следует увеличить основные фонды,
чтобы выпуск остался на прежнем уровне, т.е. чтобы имело место равенство ![]() ? Рассуждая
как в §3.3 (см. (3.3.5)-(3.3.10) ), получаем, что количество основных фондов
надо увеличить на величину
? Рассуждая
как в §3.3 (см. (3.3.5)-(3.3.10) ), получаем, что количество основных фондов
надо увеличить на величину
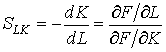
Число ![]() называется предельной нормой
замещения трудовых ресурсов основными фондами.
называется предельной нормой
замещения трудовых ресурсов основными фондами.
Итак, предельная норма замещения показывает величину ресурса
одного вида, которой производитель готов пожертвовать ради одной единицы
ресурса другого вида. Поставим теперь "обратный" вопрос: как
изменится величина ![]() при изменении предельной нормы
замещения
при изменении предельной нормы
замещения ![]() на
1%? Согласно определения эластичности, это есть "эластичность
на
1%? Согласно определения эластичности, это есть "эластичность ![]() по
по ![]() ". По
формуле вычисления эластичности (3.3.2) имеем:
". По
формуле вычисления эластичности (3.3.2) имеем:
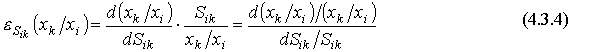
Эта величина называется эластичностью предельной нормы
замещения (или просто эластичностью замещения). Введем более простое
обозначение ![]() . С учетом известной формулы
. С учетом известной формулы
Определим производственную деятельность как процесс, в ходе которого предприятия затрачивают различные ресурсы — вещественные блага и услуги (факторы производства) и в результате выпускают разнообразную, ориентированную на рынок продукцию (продукты производства). Отправной точкой микроэкономической теории производства является идея о том, что технологически эффективная производственная деятельность предприятия, в ходе которой для выпуска, например, для одного вида продукции Y затрачивается два вида ресурсов X1, X2 может быть описана с помощью производственной функции Y=F(X1,X2). Если для фиксированного выпуска Y изобразить на плоскости (X1, X2) все возможные сочетания необходимых ресурсов (X1, X2), мы получим кривую, называемую изоквантой. Можно выделить по крайней мере четыре типа производственных функций и изоквант.
1. Функции с полным взаимозамещением ресурсов, например,
Y=a1* X1+a2* X2.
2. Неоклассическая производственная функция, например,
Y=X1a1* X2a2; a1+a2Ј1.
3. Функции с полным взаимодополнением ресурсов, например,
Y = min(X1/a1, X2/a2).
4. Функции смешанного типа, например,
Y = y1+y2: Xiіai*y1+bi*y2, i=1,2.
Производственная функция Кобба-Дугласа — самая известная из всех производственных функций неоклассического типа — была открыта в 20-х годах нашего века экономистом Дугласом в сотрудничестве с математиком Коббом и получила широкое применение в эмпирических исследованиях. В нашу программу включена производственная функция, оцененная Дугласом на основе данных по обрабатывающей промышленности США. Y — индекс производства, X1 и X2 — соответственно индексы наемной рабочей силы и капитального оборудования.
Моделирование НТП. Автономный, управляемый, материализованный (овеществленный), индуцированный, нейтральный виды НТП.
НТП – научно технический прогресс.
Различают автономный, материализованный, нейтральный и не нейтральный технический прогресс.
Автономный (экзогенный) технический прогресс представлен производственной функцией, описывающей изменение технологии во времени независимо от изменений переменных состояния экономики (капитала, земли, труда, времени). Речь здесь идет об изменениях в специализации, кооперации, управлении и т.д.
Материализованный (овеществленный) технический прогрессхарактеризуется переменными, которые принимают активное участие в изменении производственной функции (капитала, земли, труда, времени).
Нейтральный технический прогрессопределяется такими техническими изменениями (автономного или материального вида), которые не нарушают равновесия, то есть экономически и социально «безопасны» для общества.
Общепризнанным следует считать тот факт, что с течением времени на предприятии, сохраняющем фиксированную численность работников и постоянный объем основных фондов, выпуск продукции увеличивается. Это означает, что помимо обычных производственных факторов, связанных с затратами ресурсов, существует фактор, который обычно называют научно-техническим прогрессом (НТП) . Этот фактор можно рассматривать как синтетическую характеристику, отражающую совместное влияние на экономический рост многих существенных явлений, среди которых нужно отметить следующие:
а) улучшение со временем качества рабочей силы вследствие повышения квалификации работников и освоения ими методов использования более совершенной техники;
б) улучшение качества машин и оборудования приводит к тому, что определенная сумма капитальных вложений (в неизменных ценах) позволяет по прошествии времени приобрести более эффективную машину;
в) улучшение многих сторон организации производства, в том числе снабжения и сбыта, банковских операций и других взаимных расчетов, развитие информационной базы, образование различного рода объединений, развитие международной специализации и торговли и т.п.
В связи с этим термин научно-технический прогресс можно интерпретировать как совокупность всех явлений, которые при фиксированных количествах затрачиваемых производственных факторов дают возможность увеличить выпуск качественной, конкурентоспособной продукции. Весьма расплывчатый характер такого определения приводит к тому, что исследование влияния НТП проводится лишь как анализ того дополнительного увеличения продукции, которое не может быть объяснено чисто количественным ростом производственных факторов. Главный подход к учету НТП сводится к тому, что в совокупность характеристик выпуска или затрат вводится время ( t ) как независимый производственный фактор и рассматривается преобразование во времени либо производственной функции, либо технологического множества.
Остановимся на способах учета НТП путем преобразования производственной функции (ПФ), причем за основу примем двухфакторную ПФ:
![]()
где в качестве производственных факторов выступают капитал ( К ) и труд ( L ). Модифицированная ПФ в общем случае имеет вид
![]()
причем выполняется условие
![]()
которое и отражает факт роста производства во времени при фиксированных затратах труда и капитала. Геометрическая иллюстрация такого процесса дана на рис. 4.13, где показано, что изокванта, соответствующая выпуску продукции в объеме Q , смещается с течением времени ( t 2 > t 1 ) вниз и налево.
При разработке конкретных модифицированных ПФ обычно стремятся отразить характер НТП в наблюдаемой ситуации. При этом различают четыре случая:
а) существенное улучшение со временем качества рабочей силы позволяет добиться прежних результатов с меньшим количеством занятых; подобный вид НТП часто называют трудосберегающим. Модифицированная ПФ имеет вид
![]() где монотонная функция l
( t ) характеризует рост производительности труда;
где монотонная функция l
( t ) характеризует рост производительности труда;
б) преимущественное улучшение качества машин и оборудования повышает фондоотдачу, имеет место капиталосберегающий НТП и соответствующая ПФ:
![]()
где возрастающая функция k ( t ) отражает изменение фондоотдачи;
в) если имеет место значительное влияние обоих упомянутых явлений, то используется ПФ в форме
![]()
г) если же нет возможности выявить влияние НТП на производственные факторы, то применяется ПФ в виде
![]()
где a ( t ) возрастающая функция, выражающая рост продукции при неизменных значениях затрат факторов. Для исследования свойств и особенностей НТП используются некоторые соотношения между результатами производства и затратами факторов. К их числу относятся:
а) средняя производительность труда
![]()
б) средняя фондоотдача
![]()
в) коэффициент фондовооруженности работника
![]()
г) равенство между уровнем оплаты труда и предельной (маргинальной) производительности труда
![]()
д) равенство между предельной фондоотдачей и нормой банковского процента
![]()
Говорят, что НТП является нейтральным, если он не изменяет с течением времени определенных связей между приведенными величинами.
Рассмотрим далее три случая:
1) прогресс называется нейтральным по Хиксу, если в течение времени остается неизменным соотношение между фондовооруженностью ( x ) и предельной нормой замены факторов ( w / r ). В частности, если w / r = const, то замена труда на капитал и наоборот не принесет никакой выгоды и фондовооруженность x = K / L также останется постоянной. Можно показать, что в этом случае модифицированная ПФ имеет вид
![]() ,
,
и нейтральность по Хиксу эквивалентна рассмотренному выше влиянию НТП непосредственно на выпуск продукции. В рассматриваемой ситуации изокванта с течением времени смещается налево вниз путем преобразования подобия, т.е. остается в точности той же формы, что и в исходном положении;
2) прогресс называется нейтральным по Харроду, если в течение рассматриваемого периода времени норма банковского процента ( r ) зависит лишь от фондоотдачи ( k ), т.е. на нее не влияет НТП. Это означает, что предельная фондоотдача установлена на уровне нормы процента и дальнейшее увеличение капитала нецелесообразно. Можно показать, что такой тип НТП соответствует производственной функции
![]()
т.е. технический прогресс является трудосберегающим;
3) прогресс является нейтральным по Солоу, если сохраняется неизменным равенство между уровнем оплаты труда ( w ) и предельной производительностью труда и дальнейшее увеличение затрат труда невыгодно. Можно показать, что в этом случае ПФ имеет вид
![]()
т.е. НТП оказывается фондосберегающим
Однако в долгосрочном плане НТП является и результатом развития, и, в значительной мере, его причиной. Поскольку именно экономическое развитие позволяет богатым обществам финансировать создание новых образцов техники, а затем уже пожинать плоды научно-технической революции. Поэтому вполне правомерен подход к НТП как эндогенному явлению, вызванному (индуцированному) экономическим ростом.
Здесь выделяются два основных направления моделирования НТП:
1) модель индуцированного прогресса основана на формуле
![]()
причем предполагается, что общество может распределять предназначенные для НТП инвестиции между его различными направлениями. Например, между ростом фондоотдачи ( k ( t )) (улучшение качества машин) и ростом производительности труда ( l ( t )) (повышение квалификации работников) или выбором наилучшего (оптимального) направления технического развития при данном объеме выделенных капитальных вложений;
2) модель процесса обучения в ходе производства, предложенная К. Эрроу, основана на наблюдаемом факте взаимного влияния роста производительности труда и количества новых изобретений. В ходе производства работники приобретают опыт и время на изготовление изделия уменьшается, т.е. производительность труда и сам трудовой вклад зависят от объема производства
![]()
В свою очередь, рост трудового фактора, согласно производственной функции
![]()
приводит к росту производства. В простейшем варианте модели используются формулы:
![]()
(производственная функция КоббаДугласа).
Отсюда имеем соотношение
![]()
которое при заданных функциях K ( t ) и L 0 ( t ) показывает более быстрый рост y , обусловленный отмеченным выше взаимным влиянием НТП и экономического развития.
Виды производственных функций ПФ Кобба – Дугласа, ПФ Леонтьева, ПФ Солоу, Линейная ПФ.
Предположим, что фирма производит n видов продуктов.
Виды продуктов будем обозначать индексом j, а их количества - через ![]() . Технология
производства каждого вида продукта требует использования ряда ресурсов в
некоторых количествах. Двойными индексами
. Технология
производства каждого вида продукта требует использования ряда ресурсов в
некоторых количествах. Двойными индексами ![]() обозначим виды ресурсов,
используемых для выпуска продукта вида j. Пусть
обозначим виды ресурсов,
используемых для выпуска продукта вида j. Пусть ![]() . . Обозначим через
. . Обозначим через ![]() - количества
этих ресурсов,
- количества
этих ресурсов, ![]() . Следовательно, имеется всего
. Следовательно, имеется всего ![]() видов ресурсов.
видов ресурсов.
Использование такой двойной индексации привлекательно с
точки зрения информативности (видно, какой ресурс относится к какому продукту),
но неудобно чисто технически. Во-первых, усложняется запись формул; во-вторых,
увеличивается размерность задачи (т.к. среди ![]() могут быть одни и те же
наименования) и, в-третьих, такие операции как сложение, вычитание затрат в
векторной форме, а также составление уравнений становятся невозможными без
дополнительных преобразований индексов (идентификация, упорядочение и т.д.).
могут быть одни и те же
наименования) и, в-третьих, такие операции как сложение, вычитание затрат в
векторной форме, а также составление уравнений становятся невозможными без
дополнительных преобразований индексов (идентификация, упорядочение и т.д.).
Поэтому в дальнейшем виды ресурсов будем обозначать
одинарными индексами k, их количества - ![]() , где
, где ![]() . Здесь m - достаточно
большое число (равное сумме
. Здесь m - достаточно
большое число (равное сумме ![]() , где каждый ресурс считается
только один раз). Теперь можно говорить, что для производства n видов продуктов
фирма использует m видов затрат. Это не приводит к недоразумениям, так как в
случае неиспользования k-го ресурса для выпуска данного продукта
полагаем
, где каждый ресурс считается
только один раз). Теперь можно говорить, что для производства n видов продуктов
фирма использует m видов затрат. Это не приводит к недоразумениям, так как в
случае неиспользования k-го ресурса для выпуска данного продукта
полагаем ![]() .
.
Введем в рассмотрение два вида векторов: ![]() - вектор затрат и
- вектор затрат и
![]() - вектор
выпуска. Положительный ортант
- вектор
выпуска. Положительный ортант
![]()
называется пространством затрат. Аналогично определяется пространство выпуска:
![]()
Для отражения реальных возможностей фирмы в математических
моделях часто применяются более узкие множества ![]() .
.
Технологическая связь между затратами и выпуском описывается с помощью производственной функции.
Определение 4.1. Любая функция ![]() , ставящая в
соответствие каждому вектору затрат x вектор
, ставящая в
соответствие каждому вектору затрат x вектор ![]() максимального выпуска, который
может быть получен при этих затратах, называется производственной функцией.
максимального выпуска, который
может быть получен при этих затратах, называется производственной функцией.
Это есть определение производственной функции для
многопродуктовой фирмы, т.е. векторной производственной функции. Если фирма
выпускает только один вид продукта, то производственная функция является
скалярной: ![]() или
или
![]()
В общем случае производственную функцию можно записать в
неявной форме: ![]() , где A -
, где A - ![]() -матрица параметров
(технологическая матрица). В некоторых моделях применяется следующее выражение
для производственной функции:
-матрица параметров
(технологическая матрица). В некоторых моделях применяется следующее выражение
для производственной функции: ![]() , где переменные
, где переменные ![]() со знаком "-"
обозначают затраты, а со знаком "+" - выпуски.
со знаком "-"
обозначают затраты, а со знаком "+" - выпуски.
Если в качестве независимых переменных (аргументов)
выступают затраты (см. (4.2.1) ), то производственную функцию иногда называют функцией
выпуска, если же фиксирована величина выпуска (y), то
производственная функция является функцией затрат (![]() ). Таким образом,
функция выпуска и функция затрат являются взаимно обратными друг другу
функциями.
). Таким образом,
функция выпуска и функция затрат являются взаимно обратными друг другу
функциями.
Применение производственных функций не ограничивается выявлением зависимости затраты-выпуск. Различные приемы математического аппарата позволяют использовать их для вычисления численных характеристик производства, анализа эффективности изменения масштаба производства и технологического прогресса, исследования эластичности производственных факторов, рационального ведения хозяйства, оптимального планирования и прогнозирования вариантов развития фирмы и др.
Поэтому очень важно, чтобы производственная функция объективно отражала моделируемую действительность, т.е. чтобы она удовлетворяла содержательно-логическим и экономическим требованиям. Основные из них следующие:
- в число аргументов производственной функции должны быть включены все существенные для данного процесса факторы;
- все величины должны иметь отчетливый экономический смысл;
- все экономические величины, входящие в производственную функцию, должны быть измеримы;
- выпуск продукции без затрат невозможен;
- если величина какого-либо ресурса ограничена, то выпуск не может расти бесконечно;
- увеличение затрат не может привести к уменьшению выпуска.
Вопрос об адекватном описании экономической реальности на языке производственных функций тесно связан с их математическими свойствами. Ради простоты эти свойства приведем для однопродуктового производства, т.е. для производственной функции вида (4.2.1) .
1.
Монотонность: из ![]() и
и ![]() следует
следует ![]() .
.
2.
Вогнутость: для любых ![]() и
и ![]() справедливо неравенство
справедливо неравенство ![]() .
.
3.
Поведение в начале координат: ![]() .
.
4.
Однородность: ![]() , где
, где ![]() - масштабное число,
- масштабное число, ![]() - степень однородности.
- степень однородности.
Если производственная функция дифференцируема по всем аргументам, то свойства 1 и 2 соответственно могут быть заменены следующими неравенствами:

Частные производные ![]() называются предельными
продуктами. Условие (4.2.2) , как и свойство 1, означает, что увеличение
любого вида затрат не приводит к уменьшению выпуска. Условие (4.2.3)
показывает, что увеличение затрат одного вида ресурса (при постоянном уровне
затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство
в экономической теории называется законом убывающей доходности (отдачи).
называются предельными
продуктами. Условие (4.2.2) , как и свойство 1, означает, что увеличение
любого вида затрат не приводит к уменьшению выпуска. Условие (4.2.3)
показывает, что увеличение затрат одного вида ресурса (при постоянном уровне
затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство
в экономической теории называется законом убывающей доходности (отдачи).
Свойство 3 является отражением бездеятельности, так как без
затрат нет и выпуска. Свойство 4 описывает реакцию производства на изменение
затрат. Параметр ![]() показывает масштаб изменения
производства (расширения производства - если
показывает масштаб изменения
производства (расширения производства - если ![]() , сужения производства - если
, сужения производства - если ![]() ), а
), а ![]() - эффект от
изменения масштабов производства. Если
- эффект от
изменения масштабов производства. Если ![]() , то одновременное увеличение всех
факторов в
, то одновременное увеличение всех
факторов в ![]() раз
приводит к возрастанию объема выпуска больше, чем в
раз
приводит к возрастанию объема выпуска больше, чем в ![]() раз (
раз (![]() ), т.е. эффект от расширения
масштаба производства положителен. При
), т.е. эффект от расширения
масштаба производства положителен. При ![]() получаем:
получаем: ![]() - выпуск возрастает в той
же пропорции, что и затраты. Такие функции называются линейно-однородными
(или однородными в первой степени).
- выпуск возрастает в той
же пропорции, что и затраты. Такие функции называются линейно-однородными
(или однородными в первой степени).
Если
![]()
то говорят о возрастающем (убывающем) доходе от расширения масштаба производства. Заметим, что свойство 4 определено в точке, тогда как свойства 1 и 2 - во всем пространстве затрат.
Как мы видим, перечисленные (желательные) свойства производственной функции вполне согласуются с ее определением, так как они касаются только соотношения затраты-выпуск. Действительно, здесь нет никаких требований на бесперебойную работу станков, нормирования движения конвейера и т.д. Поэтому производственная функция, как отображение количественной связи между затратами и выпуском, представляет собой регрессионную модель (см. §2.5 ). Следовательно, она может быть построена на основе статистических данных и с применением методов математической статистики. Оставляя подробное обсуждение этого вопроса до §4.4 , сейчас мы приведем примеры наиболее удачно построенных и потому часто применяемых на практике производственных функций. При этом для простоты будем рассматривать двухфакторную однопродуктовую производственную функцию вида
![]()
Производственная функция Кобба-Дугласа. Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году. Предложенная ими функция изначально имела вид:
![]()
где Y - объем выпуска, K - величина
производственных фондов (капитал), L - затраты труда, ![]() - числовые параметры
(масштабное число и показатель эластичности). Благодаря своей простоте и
рациональности, эта функция широко применяется до сих пор и получила дальнейшие
обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем
записывать в виде
- числовые параметры
(масштабное число и показатель эластичности). Благодаря своей простоте и
рациональности, эта функция широко применяется до сих пор и получила дальнейшие
обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем
записывать в виде
![]()
Легко проверить, что ![]() и
и
![]()
Кроме того, функция (4.2.4) линейно-однородна:
![]() .
.
Таким образом, функция Кобба-Дугласа (4.2.4) обладает всеми вышеуказанными свойствами.
Для многофакторного производства функция Кобба-Дугласа имеет вид:
![]()
Для учета технического прогресса в функцию Кобба-Дугласа
вводят специальный множитель (технического прогресса)![]() , где t - параметр
времени,
, где t - параметр
времени, ![]() -
постоянное число, характеризующее темп развития. В результате функция принимает
"динамический" вид:
-
постоянное число, характеризующее темп развития. В результате функция принимает
"динамический" вид:
![]()
где не обязательно ![]() . Как будет показано в следующем
параграфе, показатели степени в функции (4.2.4) имеют смысл эластичности
выпуска по капиталу и труду.
. Как будет показано в следующем
параграфе, показатели степени в функции (4.2.4) имеют смысл эластичности
выпуска по капиталу и труду.
Производственная функция CES (с постоянной эластичностью замещения) имеет вид:
![]()
где ![]() - коэффициент шкалы,
- коэффициент шкалы, ![]() - коэффициент
распределения,
- коэффициент
распределения, ![]() - коэффициент замещения,
- коэффициент замещения, ![]() - степень
однородности. Если выполнены условия
- степень
однородности. Если выполнены условия
![]()
то функция (4.2.5) удовлетворяет неравенствам (4.2.2) и (4.2.3) (проверьте это самостоятельно). С учетом технического прогресса функция CES записывается:
![]()
Название данной функции следует из того факта, что для нее эластичность замещения постоянна (см. §4.3 ).
Производственная функция с фиксированными пропорциями.
Эта функция получается из (4.2.5) при ![]() и имеет вид:
и имеет вид:
![]()
Производственная функция затрат-выпуска (функция
Леонтьева) получается из (4.2.6) при ![]() :
:
![]()
Содержательно эта функция задает пропорцию, с помощью которой определяется количество затрат каждого вида, необходимое для производства одной единицы выпускаемой продукции. Поэтому в литературе часто встречаются другие формы записи:

или
![]()
Здесь ![]() - количество затрат вида k,
необходимое для производства одной единицы продукции, а y - выпуск.
- количество затрат вида k,
необходимое для производства одной единицы продукции, а y - выпуск.
Производственная функция анализа способов производственной деятельности. Данная функция обобщает производственную функцию затрат-выпуска на случай, когда существует некоторое число (r) базовых процессов (способов производственной деятельности), каждый из которых может протекать с любой неотрицательной интенсивностью. Она имеет вид "оптимизационной задачи"
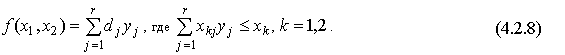
Здесь ![]() - выпуск продукции при единичной
интенсивности j-го базового процесса,
- выпуск продукции при единичной
интенсивности j-го базового процесса, ![]() - уровень интенсивности,
- уровень интенсивности, ![]() - количество
затрат вида k, необходимых при единичной интенсивности способа j.
Как видно из (4.2.8) , если выпуск, произведенный при единичной интенсивности и
затраты, необходимые на единицу интенсивности, известны, то общий выпуск и
общие затраты находятся путем сложения выпуска и затрат соответственно для каждого
базового процесса при выбранных интенсивностях. Заметим, что задача
максимизации функции f по
- количество
затрат вида k, необходимых при единичной интенсивности способа j.
Как видно из (4.2.8) , если выпуск, произведенный при единичной интенсивности и
затраты, необходимые на единицу интенсивности, известны, то общий выпуск и
общие затраты находятся путем сложения выпуска и затрат соответственно для каждого
базового процесса при выбранных интенсивностях. Заметим, что задача
максимизации функции f по ![]() в (4.2.8) при заданных
ограничениях-неравенствах является моделью анализа производственной
деятельности (максимизация выпуска при ограниченных ресурсах).
в (4.2.8) при заданных
ограничениях-неравенствах является моделью анализа производственной
деятельности (максимизация выпуска при ограниченных ресурсах).
Линейная производственная функция (функция с взаимозамещением ресурсов) применяется при наличии линейной зависимости выпуска от затрат:
![]()
где ![]() - норма затрат k-го вида
для производства единицы продукции (предельный физический продукт затрат).
- норма затрат k-го вида
для производства единицы продукции (предельный физический продукт затрат).
Методы математического моделирования рисковых ситуаций. Риск и неопределенность в осуществлении экономической деятельности. Место методов математического моделирования в общей схеме управления риском. Основные механизмы управления риском — прямое воздействие на факторы риска и диверсификация. Цели моделирования механизмов управления риском. Методы моделирования неопределенности и риска экономической деятельности.
Любая сфера человеческой деятельности, в особенности экономика или бизнес, связана с принятием решений в условиях неполноты информации. Источники неопределенности могут быть самые разнообразные: нестабильность экономической и/или политической ситуации, неопределенность действий партнеров по бизнесу, случайные факторы, т.е. большое число обстоятельств, учесть которые не представляется возможным (например, погодные условия, неопределенность спроса на товары, неабсолютная надежность процессов производства, неточность информации и др.). Экономические решения с учетом перечисленных и множества других неопределенных факторов принимаются в рамках так называемой теории принятия решений - аналитического подхода к выбору наилучшего действия (альтернативы) или последовательности действий. В зависимости от степени определенности возможных исходов или последствий различных действий, с которыми сталкивается лицо, принимающее решение (ЛПР), в теории принятия решений рассматриваются три типа моделей:
• выбор решений в условиях определенности, если относительно каждого действия известно, что оно неизменно приводит к некоторому конкретному исходу;
• выбор решения при риске, если каждое действие приводит к одному из множества возможных частных исходов, причем каждый исход имеет вычисляемую или экспертно оцениваемую вероятность появления. Предполагается, что ЛПР эти вероятности известны или их можно определить путем экспертных оценок;
• выбор решений при неопределенности, когда то или иное действие или несколько действий имеют своим следствием множество частных исходов, но их вероятности совершенно не известны или не имеют смысла.
Проблема риска и прибыли - одна из ключевых в экономической деятельности, в частности в управлении производством и финансами. Под риском принято понимать вероятность (угрозу) потери лицом или организацией части своих ресурсов, недополучения доходов или появления дополнительных расходов в результате осуществления определенной производственной и финансовой политики.
Различают следующие виды рисков:
- производственный, связанный с возможностью невыполнения фирмой своих обязательств перед заказчиком;
- кредитный, обусловленный возможностью невыполнения фирмой своих финансовых обязательств перед инвестором;
- процентный, возникающий вследствие непредвиденного изменения процентных ставок;
- риск ликвидности, обусловленный неожиданным изменением кредитных и депозитных потоков;
- инвестиционный, вызванный возможным обесцениванием инвестиционно-финансового портфеля, состоящего из собственных и приобретенных ценных бумаг;
- рыночный, связанный с вероятным колебанием как рыночных процентных ставок собственной национальной денежной единицы, так и курса зарубежных валют.
Риск подразделяется на динамический и статический. Динамический риск связан с возникновением непредвиденных изменений стоимости основного капитала вследствие принятия управленческих решений, а также рыночных или политических обстоятельств. Такие изменения могут привести как к потерям, так и к дополнительным доходам. Статический риск обусловлен возможностью потерь реальных активов вследствие нанесения ущерба собственности и потерь дохода из-за недееспособности организации.
Все участники проекта заинтересованы в том, чтобы не допустить возможность полного провала проекта или хотя бы избежать убытка. В условиях нестабильной, быстро меняющейся ситуации необходимо учитывать все возможные последствия от действий конкурентов, а также изменения конъюнктуры рынка. Поэтому основное назначение анализа риска состоит в том, чтобы обеспечить партнеров информацией, необходимой для принятия решений о целесообразности участия в некотором проекте, и предусмотреть меры по защите от возможных финансовых потерь.
При анализе риска могут использоваться следующие условия или предположения:
• потери от риска не зависят друг от друга;
• потери по одному из некоторого перечня рисков не обязательно увеличивают вероятность потерь по другим;
• максимально возможный ущерб не должен превышать финансовых возможностей участников проекта.
Все факторы, влияющие на рост степени риска в проекте, можно условно разделить на объективные и субъективные. Объективные факторы непосредственно не зависят от самой фирмы: это инфляция, конкуренция, политические и экономические кризисы, экология, налоги и т.д. Субъективные факторы непосредственно характеризуют данную фирму: это производственный потенциал, техническое оснащение, уровень производительности труда, проводимая финансовая, техническая и производственная политика, в частности выбор типа контракта между инвестором и заказчиком. Последний фактор играет особо важную роль для фирмы, поскольку от типа контракта зависят степень риска и величина вознаграждения по окончании проекта.
Исследование риска целесообразно проводить в следующей последовательности:
• выявление объективных и субъективных факторов, влияющих на конкретный вид риска;
• анализ выявленных факторов;
• оценка конкретного вида риска с финансовых позиций, определяющая либо финансовую состоятельность проекта, либо его экономическую целесообразность;
• установка допустимого уровня риска;
• анализ отдельных операций по выбранному уровню риска;
• разработка мероприятий по снижению риска.
Финансирование проекта, являясь одним из наиболее важных условий обеспечения эффективности его выполнения, должно быть нацелено на обеспечение потока инвестиций для планомерного выполнения проекта, на снижение капитальных затрат и риска проекта за счет оптимальной структуры инвестиций и получения налоговых преимуществ. В плане финансирования проекта должны учитываться следующие виды рисков:
• нежизнеспособности проекта;
• налоговый;
• неуплаты задолженностей;
• незавершения строительства.
Высокая степень риска проекта приводит к необходимости поиска путей искусственного снижения его (риска) возможных последствий на состояние дел фирмы.
В существующей практике применяются главным образом четыре основных способа управления риском: распределение риска между всеми участниками проекта (передача части риска соисполнителям), страхование, резервирование средств на покрытие непредвиденных расходов и диверсификация.
Анализ рисков подразделяется на два взаимно дополняющих друг друга вида: качественный, главная задача которого состоит в определении факторов риска и обстоятельств, приводящих к рисковым ситуациям, и количественный, позволяющий вычислить размеры отдельных рисков и риска проекта в целом.
Меры риска
Наиболее распространена точка зрения, согласно которой мерой риска коммерческого (финансового) решения или операции следует считать среднеквадратичное отклонение (положительный квадратный корень из дисперсии) значения показателя эффективности этого решения или операции. Действительно, поскольку риск обусловлен недетерминированностью исхода решения (операции), то, чем меньше разброс (дисперсия) результата решения, тем более он предсказуем, т.е. меньше риск. Если вариация (дисперсия) результата равна нулю, риск полностью отсутствует. Например, в условиях стабильной экономики операции с государственными ценными бумагами считаются безрисковыми.
Чаще всего показателем эффективности финансового решения (операции) служит прибыль.
Рассмотрим в качестве иллюстрации выбор некоторым лицом одного из двух вариантов инвестиций в условиях риска. Пусть имеются два проекта Л и В, в которые указанное лицо может вложить средства. Проект А в определенный момент в будущем обеспечивает случайную величину прибыли. Предположим, что ее среднее ожидаемое значение, математическое ожидание, равно тА с дисперсией SA . Для проекта В эти числовые характеристики прибыли как случайной величины предполагаются равными соответственно тв и SB~. Среднеквадратичные отклонения равны соответственно SA и SB.
Возможны следующие случаи:
a) тА = тв, SA < SB, следует выбрать проект Л;
b) тА > тв, SA < sb, следует выбрать проект А;
c) тА > тв, SA = sb, следует выбрать проект Л;
d) тА > тв, SA >SB;
e) тА < тв, SA <SB.
В последних двух случаях решение о выборе проекта А или В зависит от отношения к риску ЛПР. В частности, в случае d) проект А обеспечивает более высокую среднюю прибыль, однако он и более рискован. Выбор при этом определяется тем, какой дополнительной величиной средней прибыли компенсируется для ЛПР заданное увеличение риска. В случае е) для проекта А риск меньший, но и ожидаемая прибыль меньше.
Магистральные модели экономики. Магистральная модель накопления основных производственных фондов в конце планового периода. Модель фон Неймана расширяющейся экономики.
Классическая (исходная) модель Неймана строится при следующих предпосылках:
- экономика, характеризуемая линейной технологией, состоит из отраслей, каждая из которых обладает конечным числом производственных процессов, т.е. выпускается несколько видов товаров, причем допускается совместная деятельность отраслей;
- производственные процессы разворачиваются во времени, причем осуществление затрат и выпуск готовой продукции разделены временным лагом;
- для производства в данный период можно тратить только те продукты, которые были произведены в предыдущем периоде времени, первичные факторы не участвуют;
- спрос населения на товары и, соответственно, конечное потребление в явном виде не выделяются;
- цены товаров изменяются во времени.
Перейдем к описанию модели Неймана. На дискретном временном
интервале ![]() с
точками
с
точками ![]() рассматривается
производство, в котором n видов затрат с помощью m
технологических процессов превращаются в n видов продукции. Мы не будем
указывать число отраслей, так как в дальнейшем не понадобится подчеркивать
принадлежность товаров или технологий к конкретным отраслям. В модели Леонтьева
технологические коэффициенты были отнесены к единице продукта. В модели
Неймана, принимая в качестве производственных единиц не отрасли, а
технологические процессы, удобно отнести эти коэффициенты к интенсивности производственных
процессов.
рассматривается
производство, в котором n видов затрат с помощью m
технологических процессов превращаются в n видов продукции. Мы не будем
указывать число отраслей, так как в дальнейшем не понадобится подчеркивать
принадлежность товаров или технологий к конкретным отраслям. В модели Леонтьева
технологические коэффициенты были отнесены к единице продукта. В модели
Неймана, принимая в качестве производственных единиц не отрасли, а
технологические процессы, удобно отнести эти коэффициенты к интенсивности производственных
процессов.
Интенсивностью производственного процесса j
называется объем продуктов, выпускаемых этим процессом за единицу времени. Уровень
интенсивности j-го процесса в момент времени t обозначим через ![]() (
(![]() ). Заметим, что
). Заметим, что ![]() является
вектором, число компонент которого соответствует числу выпускаемых j-ым
процессом видов товаров и
является
вектором, число компонент которого соответствует числу выпускаемых j-ым
процессом видов товаров и ![]() .
.
Предположим, что функционирование j-го процесса (![]() ) с единичной
интенсивностью требует затрат продуктов в количестве
) с единичной
интенсивностью требует затрат продуктов в количестве
![]()
и дает выпуск товаров в количестве
![]()
Введем обозначения ![]() . Пара
. Пара ![]() характеризует технологический
потенциал, заложенный в j-ом процессе (его функционирование с единичной
интенсивностью). Поэтому пару
характеризует технологический
потенциал, заложенный в j-ом процессе (его функционирование с единичной
интенсивностью). Поэтому пару ![]() можно назвать базисом j-го
производственного процесса, имея в виду, что для любой интенсивности
можно назвать базисом j-го
производственного процесса, имея в виду, что для любой интенсивности ![]() соответствующую
пару затраты-выпуск можно выразить как
соответствующую
пару затраты-выпуск можно выразить как ![]() . Поэтому последовательность пар
. Поэтому последовательность пар
![]()
представляющих собой затраты и выпуски всех производственных процессов в условиях их функционирования с единичными интенсивностями, будем называть базисными процессами.
Все m базисных процессов описываются двумя матрицами
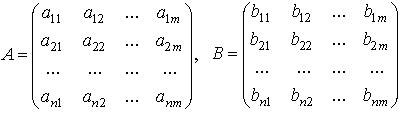
где A- матрица затрат, B- матрица
выпуска. Вектор ![]() называется вектором
интенсивностей. Соответствующие этому вектору затраты и выпуски по всем m
процессам можно получить как линейную комбинацию базисных процессов (6.4.1) с
коэффициентами
называется вектором
интенсивностей. Соответствующие этому вектору затраты и выпуски по всем m
процессам можно получить как линейную комбинацию базисных процессов (6.4.1) с
коэффициентами ![]() :
:
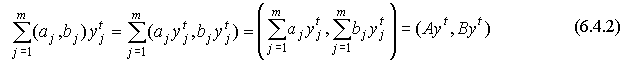
Говорят, что в производственном процессе ![]() базисные процессы (6.4.1)
участвуют с интенсивностями
базисные процессы (6.4.1)
участвуют с интенсивностями ![]() . Как видно из (6.4.2) ,
неймановская технология, описываемая двумя матрицами A и B
единичных уровней затрат и выпуска, является линейной (см. предпосылку 1) в
начале параграфа). Рассматривая все допустимые "смеси" базисных
процессов, получаем расширенное множество производственных процессов
. Как видно из (6.4.2) ,
неймановская технология, описываемая двумя матрицами A и B
единичных уровней затрат и выпуска, является линейной (см. предпосылку 1) в
начале параграфа). Рассматривая все допустимые "смеси" базисных
процессов, получаем расширенное множество производственных процессов
![]()
которое и отражает допустимость совместной деятельности
отраслей. Возможность совместного производства нескольких продуктов в одном
процессе следует из того, что в каждом процессе j может быть отличной от
нуля более чем одна из величин ![]() . Множество (6.4.3) представляет
собой неймановскую технологию в статике (в момент t ). Если в матрице A
положить n=m, матрицу B отождествить с единичной матрицей, а
. Множество (6.4.3) представляет
собой неймановскую технологию в статике (в момент t ). Если в матрице A
положить n=m, матрицу B отождествить с единичной матрицей, а ![]() интерпретировать
как вектор валового выпуска, то (6.4.2) превращается в леонтьевскую технологию.
интерпретировать
как вектор валового выпуска, то (6.4.2) превращается в леонтьевскую технологию.
Продолжим описание модели Неймана. Согласно предпосылок 2) и
3), затраты ![]() в
момент t не могут превышать выпуска
в
момент t не могут превышать выпуска ![]() , соответствующего предыдущему
моменту t-1 (рис. 6.3).
, соответствующего предыдущему
моменту t-1 (рис. 6.3).
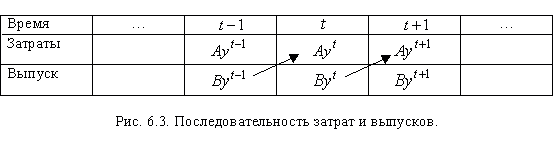
Поэтому должны выполняться условия:
![]()
где ![]() - вектор запаса товаров к началу
планируемого периода.
- вектор запаса товаров к началу
планируемого периода.
Обозначим через ![]() , вектор цен товаров. Неравенство (6.4.4)
можно трактовать как непревышение спроса над предложением в момент t.
Поэтому в стоимостном выражении (в ценах момента t) должно быть:
, вектор цен товаров. Неравенство (6.4.4)
можно трактовать как непревышение спроса над предложением в момент t.
Поэтому в стоимостном выражении (в ценах момента t) должно быть:
![]()
По предположению 5) прибыль базисного процесса ![]() на отрезке [t-1,T]
равна величине
на отрезке [t-1,T]
равна величине ![]() , т.е. затраты осуществляются по
цене начала периода, а готовая продукция - по цене момента ее реализации. Таким
образом, издержки по всем базисным процессам можно записать как
, т.е. затраты осуществляются по
цене начала периода, а готовая продукция - по цене момента ее реализации. Таким
образом, издержки по всем базисным процессам можно записать как ![]() , а выручку - как
, а выручку - как ![]() (рис. 6.4).
(рис. 6.4).
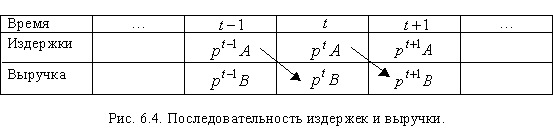
Будем говорить, что базисные процессы неубыточны, если ![]() , неприбыльны -
если
, неприбыльны -
если
![]()
В модели Неймана предполагается неприбыльность базисных
процессов. Это объясняется тем, что издержки и выручки разведены во времени,
т.е. относятся к разным моментам времени, и в условиях расширяющейся экономики
"характерен случай падения цен (![]() )", т.е. покупательская
способность денег в момент t будет выше, чем в момент t-1. С
таким обоснованием можно согласиться или не согласиться. Главная же причина
неприбыльности базисных процессов заложена в определении экономического
равновесия. Поясним это чуть подробнее.
)", т.е. покупательская
способность денег в момент t будет выше, чем в момент t-1. С
таким обоснованием можно согласиться или не согласиться. Главная же причина
неприбыльности базисных процессов заложена в определении экономического
равновесия. Поясним это чуть подробнее.
Основной предмет исследования Дж. фон Неймана - это возможность существования равновесия в рассматриваемой им динамической модели экономики при заданных в каждый момент ценах. Как следует из определения 5.2, при равновесии в условиях совершенной конкуренции имеет место стоимостной баланс (см. (5.3.8)). Таким образом, в условиях равновесия не создается никакой прибыли, и неравенство http://www.csu.ac.ru/%7Erusear/ME_Ruda/Chapter6/par6_4.php - %286.4.6.%29(6.4.6) является отражением этого факта. Поэтому, если в (6.4.6) для некоторого базисного процесса j имеет место строгое неравенство, т.е. предложение превышает спрос:
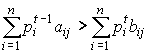
то должно быть ![]() . Иначе говоря, отсутствие
"отрицательной прибыли" обеспечивается нулевой интенсивностью. Отсюда
получаем
. Иначе говоря, отсутствие
"отрицательной прибыли" обеспечивается нулевой интенсивностью. Отсюда
получаем
![]()
Описание модели Неймана завершено. Совокупность неравенств и уравнений (6.4.4) -(6.4.7) :
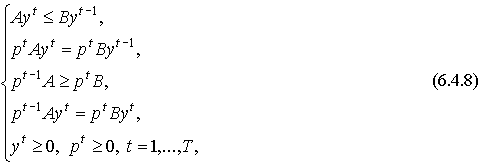
где ![]() и
и ![]() - матрицы затрат и выпуска
соответственно, называется (динамической) моделью Неймана.
- матрицы затрат и выпуска
соответственно, называется (динамической) моделью Неймана.
Определение 6.2. Говорят, что в
экономике наблюдается сбалансированный рост производства, если
существует такое постоянное число ![]() , что для всех m
производственных процессов
, что для всех m
производственных процессов
![]()
Постоянное число ![]() называется темпом
сбалансированного роста производства.
называется темпом
сбалансированного роста производства.
Содержательно (6.4.9) означает, что все уровни интенсивности возрастают одинаковыми темпами
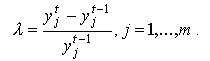
Раскрывая рекуррентно правую часть (6.4.9), получаем
![]()
где ![]() - интенсивность процесса j
, установившаяся к началу планового периода. Заметим, что t в правой
части (6.4.10) является показателем степени, а в левой - индексом.
- интенсивность процесса j
, установившаяся к началу планового периода. Заметим, что t в правой
части (6.4.10) является показателем степени, а в левой - индексом.
В случае сбалансированного роста производства, с учетом
постоянства темпа роста, последовательность ![]() называется стационарной
траекторией производства.
называется стационарной
траекторией производства.
Определение 6.3. Говорят, что в
экономике наблюдается сбалансированное снижение цен, если существует такое
постоянное число ![]() , что для всех n товаров
, что для всех n товаров
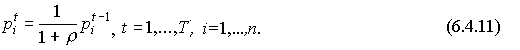
Постоянное число ![]() называется нормой процента.
называется нормой процента.
Содержательно (6.4.11) означает, что цены на все товары снижаются одинаковыми темпами
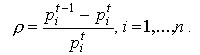
Название "норма процента" для темпа снижения ![]() принято по
ассоциации с показателем нормы процента (нормы доходности) в формуле сложного
процента
принято по
ассоциации с показателем нормы процента (нормы доходности) в формуле сложного
процента ![]() ,
где R0 - сумма начального вложения, Rn - получаемая через n
периодов конечная сумма,
,
где R0 - сумма начального вложения, Rn - получаемая через n
периодов конечная сумма, ![]() - норма процента. Так как в определении
6.3 речь идет о снижении, то "норма процента" в (6.4.11) входит с
отрицательным знаком (
- норма процента. Так как в определении
6.3 речь идет о снижении, то "норма процента" в (6.4.11) входит с
отрицательным знаком (![]() ).
).
Из равенства (6.4.10) получаем
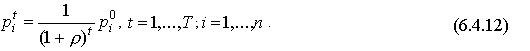
где ![]() - цены, установившиеся к началу
планового периода.
- цены, установившиеся к началу
планового периода.
В случае сбалансированного снижения цен последовательность ![]() называется стационарной
траекторией цен.
называется стационарной
траекторией цен.
Подставляя (6.4.10) и (6.4.12) в модель Неймана (6.4.8), получаем ее "стационарную" форму:
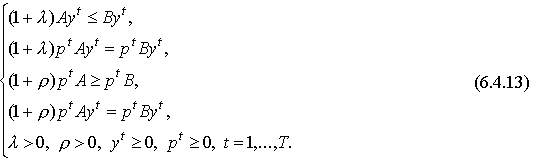
Эта система соотношений показывает, что по стационарным траекториям y и p экономика развивается согласно неизменному динамическому закону. Поэтому такую ситуацию естественно назвать равновесной.
http://www.csu.ac.ru/%7Erusear/ME_Ruda/Chapter6/def6.4.Определение
6.4. Четверка ![]() , где y - стационарная
траектория производства, p- стационарная траектория цен, а
, где y - стационарная
траектория производства, p- стационарная траектория цен, а ![]() и
и ![]() -
соответствующие им темп сбалансированного роста производства и норма процента
(темп сбалансированного снижения цен), называется состоянием
(динамического) равновесия в модели Неймана (6.4.8).
-
соответствующие им темп сбалансированного роста производства и норма процента
(темп сбалансированного снижения цен), называется состоянием
(динамического) равновесия в модели Неймана (6.4.8).
Сделаем следующие предположения:
а) ![]()
в) для каждого j существует хотя бы одно i , такое что ![]() ;
;
г) для каждого i существует хотя бы одно j , такое что ![]() ;
;
д) для каждого t ![]() .
.
Теорема 6.4. Если выполнены условия а)-д), то в модели Неймана (6.4.8) существует состояние равновесия.
Условия в) и г) говорят о наличии в каждом столбце матрицы A и каждой строке матрицы B по крайней мере одного положительного элемента. Содержательно это означает, что среди всех производственных процессов нет таких, которые ничего не тратят, и каждый из n видов продуктов действительно производится. Условие д) имеет чисто техническое предназначение.
Определение 6.5. Число
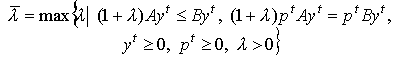
называется максимальным темпом сбалансированного роста, а число
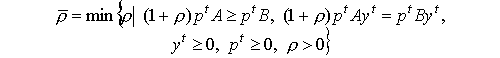
называется минимальной нормой процента.
Оказывается, что в состоянии равновесия числа ![]() и
и ![]() существуют и равны между
собой:
существуют и равны между
собой:

если только начальные точки y0 и p0 также удовлетворяют этому равенству.
Траектория производства ![]() , удовлетворяющая условиям (6.4.13)
при
, удовлетворяющая условиям (6.4.13)
при ![]() и
и ![]() и
соответствующая максимальному сбалансированному росту, т.е.
и
соответствующая максимальному сбалансированному росту, т.е. ![]() , называется траекторией
равновесного роста (или траекторией Неймана, или магистралью).
Поскольку эту траекторию можно представить в виде
, называется траекторией
равновесного роста (или траекторией Неймана, или магистралью).
Поскольку эту траекторию можно представить в виде ![]() , где
, где ![]() , то ее еще называют лучом
Неймана а цены (6.4.12), соответствующие минимальной норме процента
, то ее еще называют лучом
Неймана а цены (6.4.12), соответствующие минимальной норме процента ![]() , называют неймановскими
ценами .
, называют неймановскими
ценами .
В математической экономике магистралью называется траектория экономического роста, на которой пропорции производственных показателей (такие как темп роста производства, темп снижения цен) неизменны, а сами показатели (такие как интенсивность производства, валовый выпуск) растут с постоянным максимально возможным темпом. Таким образом, магистраль - это траектория или луч максимального сбалансированного роста. Ее часто сравнивают со скоростной автострадой. Так, например, для того чтобы добраться из Кемерово в Киселевск как можно быстрее, наиболее целесообразно сначала проехать по автостраде Кемерово-Новокузнецк, а затем уже съехать на ответвляющуюся от нее дорогу в районе Киселевска. Так мы потеряем на дорогу меньше времени и доедем до конечного пункта с большим комфортом, чем если бы мы ехали по обычному шоссе через Ленинск-Кузнецкий и Белово.
Поскольку "оптимальное" или
"эффективное" развитие экономики в любом смысле так или иначе связано
и должно сопровождаться экономическим ростом, то для достижения любой конечной
цели следует поступать аналогичным образом: сначала вывести производство на
магистральный путь, т.е. на траекторию (или луч) Неймана, характеризующуюся
максимальным темпом роста ![]() и минимальной нормой процента
и минимальной нормой процента ![]() (см. (6.4.14)),
а по истечении определенного срока времени вывести ее к задуманной цели. Такими
целями могут быть максимизация прибыли, минимизация затрат, максимизация
полезности от потребления товаров, достижение конкурентного равновесия при
наиболее благоприятных условиях, т.е. на более высоком уровне благосостояния
населения, и т.д.
(см. (6.4.14)),
а по истечении определенного срока времени вывести ее к задуманной цели. Такими
целями могут быть максимизация прибыли, минимизация затрат, максимизация
полезности от потребления товаров, достижение конкурентного равновесия при
наиболее благоприятных условиях, т.е. на более высоком уровне благосостояния
населения, и т.д.
Итак, с одной стороны мы имеем магистральные модели, а с
другой - оптимизационные или еще шире - нормативные модели экономики. Изучение
этих двух моделей во взаимосвязи, т.е. изучение связи между магистральными и
оптимальными (в том или ином смысле) траекториями и является предметом
магистральной теории. Можно говорить, что магистральная теория является одним
из средств качественного анализа оптимальных траекторий. Основной целью этой
теории является исследование условий так называемых "слабой" и
"сильной" теорем о магистралях. Слабая теорема утверждает, что за
исключением некоторого малого периода ![]() (или некоторого числа дискретных
моментов из
(или некоторого числа дискретных
моментов из ![]() ),
не зависящего от продолжительности T планового периода, все оптимальные
траектории сосредотачиваются в относительной близости к магистральной
траектории. Сильная теорема говорит о том, что те небольшие промежутки времени
),
не зависящего от продолжительности T планового периода, все оптимальные
траектории сосредотачиваются в относительной близости к магистральной
траектории. Сильная теорема говорит о том, что те небольшие промежутки времени ![]() , на которых
оптимальные траектории удалены от магистральной, если они существуют, то разве
лишь в начале периода
, на которых
оптимальные траектории удалены от магистральной, если они существуют, то разве
лишь в начале периода ![]() , т.е.
, т.е. ![]() , или в конце периода
, или в конце периода ![]() , т.е.
, т.е. ![]() ; а в середине
периода оптимальные траектории расположены в относительной близости к
магистральной.
; а в середине
периода оптимальные траектории расположены в относительной близости к
магистральной.
В общем случае в моделях экономической динамики даже при неизменности технологических возможностей утверждения теорем о магистрали не выполняются. Для их выполнения приходится вводить различные дополнительные предположения о свойствах исходной модели экономики. Другой путь состоит в изучении реальных отраслевых пропорций и сравнении их с магистральными. Благодаря техническому прогрессу и изменчивости во времени общественных предпочтений различных благ, реальное состояние экономики при детальном (дезагрегированном) ее описании всегда значительно отличается от магистрального. В то же время, как показывают полученные в этом направлении результаты исследований, при высоком уровне агрегирования экономические пропорции близки к магистральным.
Модель общего экономического равновесия в долгосрочном периоде. Факторы валового национального продукта (ВНП) и его представление при помощи производственной функции макроэкономического анализа. Распределение ВНП по факторам производства. Функция потребления.
Ценность моделей МОБа для анализа макроэкономического равновесия велика, так ведущие факторы и показатели экономики, в частности: сферы и сектора; валовой выпуск; валовой национальный продукт; промежуточный продукт; национальный доход; все национальные потоки; импортно-экспортные связи.
С помощью этой модели могут быть получены данные для анализа основных макроэкономических пропорций, сделан их прогноз.
Модель Леонтьева называется «затраты-выпуск» потому, что отдельные отрасли рассматриваются в балансе двояко:
1. как выразители совокупного спроса и покупатели материальных благ и услуг, предложенных другими отраслями (затраты) – это столбцы баланса;
2. как выразители совокупного предложения и продавцы материальных благ и услуг, которые они предоставляют сами другим отраслям (выпуск) – это строки баланса.
Модель затраты – выпуск связана с системой национальных счетов (СНС), принятой в странах с рыночной экономикой.
Баланс Леонтьева (в свернутом виде).
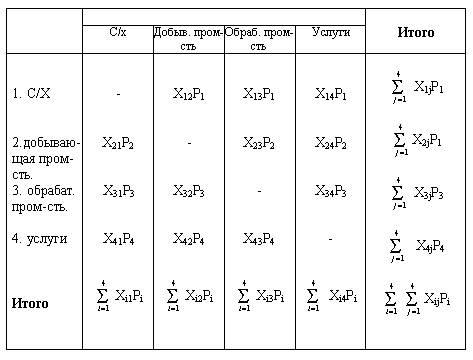
По вертикали отражаются счета наступлений (покупок), а по горизонтали счета выпуска (продаж).[метка3]
Из этой модели в идеале можно получить следующие виды равновесия:
1. отраслевое равновесие
Напр., для отрасли (1):
![]()
Или: сумма счетов затрат отрасли равна сумме счетов выпуска ее продукции.
2. межотраслевое равновесие, например для обрабатывающей и добывающей промышленности.
Х32Р3=Х23Р2
Или: итог предложения продукции отраслью (3) для отрасли (2) равен итогу спроса отрасли (3) на продукцию отрасли (2). Обычно в реальной жизни такой тип равновесия отсутствует.
3. Общее равновесие
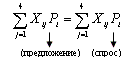
или: совокупное предложение и совокупный спрос на товары равны.
В ряде случаев может отсутствовать и отраслевое равновесие. Однако в модели Леонтьева в итого все сбалансировано потому, что МОБ отражает факт состоявшихся сделок, реальные рыночные потоки. А это означает, что в модели Леонтьева отражена лишь часть проблем макроэкономического равновесия. Не учитываются факторы, нарушающие это равновесие, например, предприятия-банкроты; склады; дефицитное состояние экономики, экономические циклы.
С помощью МОБ можно проанализировать основные макроэкономические показатели: ВНП, потребление, накопление, ВОП, его структуру, эффективность использования ресурсов, рассчитать форму накопления и т.д.
Приведённая (функциональная) форма статической модели межотраслевого баланса. Мультипликатор Леонтьева (матрица коэффициентов полных материальных затрат). Коэффициенты прямых затрат труда. Баланс трудовых ресурсов.
Для более глубокого изучения межотраслевых связей и совершенствования прогнозирования народного хозяйства, наряду с коэффициентами прямых затрат, большое научное и практическое значение приобретает исчисление так называемых коэффициентов полных затрат, т.е. затрат, связанных с производством того или иного продукта не только прямо, но и косвенно через другие продукты.
Коэффициенты полных затрат тесно связаны с алгебраическим решением системы уравнений межотраслевого баланса. Решая эти уравнения относительно Yi, после того как вместо аij поставлены конкретные числа, а y1,y2,…,yn оставлены в алгебраической форме, получим для каждого Yi выражение следующего вида
Yi = bi1y1 + bi2y2 + … + bijyj + … + bimyn ,
где bij – коэффициенты полных затрат.
Если теперь положить yj = 1, а все остальные значения y равными нулю, то есть y1 = y2 =…= yj-1 = yj+1 =…= yn = 0, то получим Yi = bij.
Таким образом, b1j, b2j,…
являются полными затратами 1-го,
2-го,… продуктов на единицу j-го продукта.
Получение коэффициентов полных затрат bij
математически отвечает получению матрицы, обратной матрице E-A, т.е.
матрицы (E-A)![]() .
.
Дискретная динамическая модель межотраслевого баланса с учетом ввода мощностей. Постановка оптимизационной модели.
Структурная форма модели общего экономического равновесия в долгосрочном периоде. Равновесие и ставка процента.
Виды целевых функций в экономическом анализе.
Функция, связывающая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации.