Контрольная работа: Методы решения уравнений линейной регрессии
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
ФИЛИАЛ В Г. ЛИПЕЦКЕ
Контрольная работа
по эконометрике
Липецк, 2009 г.
Задача
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (Х, млн.руб.)
| Y | 31 | 23 | 38 | 47 | 46 | 49 | 20 | 32 | 46 | 24 |
| Х | 38 | 26 | 40 | 45 | 51 | 49 | 34 | 35 | 42 | 24 |
Требуется:
1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
2.
Вычислить
остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ![]() ; построить график
остатков.
; построить график
остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве.
6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,01 при Х=80% от его максимального значения.
7. Представить графически фактических и модельных значений Y, точки прогноза.
8. Составить уравнения нелинейной регрессии:
· Гиперболической;
· Степенной;
· Показательной.
Привести графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
Решение
1. Уравнение линейной регрессии имеет вид:
![]() = а0 + а1x.
= а0 + а1x.
Построим линейную модель.
Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( рис. 1).
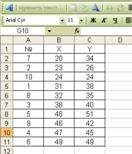
Рис.1
Используем программу РЕГРЕССИЯ и найдем коэффициенты модели (рис.2)
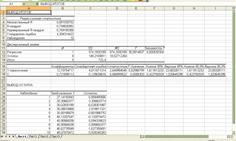
Рис.2
Коэффициенты модели содержатся в таблице 3 (столбец Коэффициенты).
Таким образом, модель построена и ее уравнение имеет вид
Yт = 12,70755+0,721698Х.
Коэффициент регрессии b=0,721698, следовательно, при увеличении объема капиталовложений (Х) на 1 млн руб. объем выпуска продукции (Y) увеличивается в среднем на 0,721698 млн руб.
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков S²e; построить график остатков.
Остатки содержатся в столбце Остатки итогов программы РЕГРЕССИЯ (таблица 4).
Программой РЕГРЕССИЯ найдены также остаточная сумма квадратов SSост=148,217 и дисперсия остатков MS=18,52712 (таблица 2).
Для построения графика остатков нужно выполнить следующие действия:
· Вызвать Матер Диаграмм, выбрать тип диаграммы Точечная (с соединенными точками).
· Для указания данных для построения диаграммы зайти во вкладку Ряд, нажать кнопку Добавить; в качестве значений Х указать исходные данные Х (таблица 1);значения Y - остатки (таблица 4).
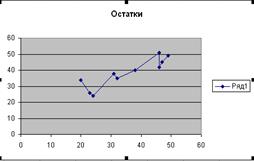
Рис.3 График остатков
3. Проверить выполнение предпосылок МНК.
Предпосылками построения классической линейной регрессионной модели являются четыре условия, известные как условия Гаусса-Маркова.
· В уравнении линейной модели Y=a+b*X+ε слагаемое ε - случайная величина, которая выражает случайный характер результирующей переменной Y.
· Математическое ожидание случайного члена в любом наблюдении равно нулю, а дисперсия постоянна.
· Случайные члены для любых двух разных наблюдений независимы (некоррелированы).
· Распределение случайного члена является нормальными.
1) Проведем проверку случайности остаточной компоненты по критерию повторных точек.
Количество повторных точек определим по графику остатков: p=5
Вычислим критическое значение по формуле:
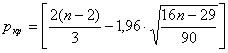 .
.
При
![]() найдем
найдем ![]()
Схема критерия:

Сравним
![]() , следовательно, свойство
случайности для ряда остатков выполняется.
, следовательно, свойство
случайности для ряда остатков выполняется.
1.
Равенство
нулю математического ожидания остаточной компоненты для линейной модели,
коэффициенты которой определены по МНК, выполняется автоматически. С помощью
функции СРЗНАЧ для ряда остатков можно проверить: ![]() .
.
Свойство постоянства дисперсии остаточной компоненты проверим по критерию Гольдфельда–Квандта.
В
упорядоченных по возрастанию переменной X
исходных данных (![]() ) выделим первые
4 и последние 4 уровня, средние 2 уровня не рассматриваем.
) выделим первые
4 и последние 4 уровня, средние 2 уровня не рассматриваем.
С
помощью программы РЕГРЕССИЯ построим модель по первым четырем наблюдениям
(регрессия-1), для этой модели остаточная сумма квадратов ![]() .
.
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 107,7894737 | 107,7894737 | 15,67347 | 0,15751 | |
| Остаток | 1 | 6,877192982 | 6,877192982 | |||
| Итого | 2 | 114,6666667 |
С
помощью программы РЕГРЕССИЯ построим модель по последним четырем наблюдениям
(регрессия-2), для этой модели остаточная сумма квадратов ![]() .
.
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 4,166666667 | 4,166666667 | 0,186916 | 0,707647 | |
| Остаток | 2 | 44,58333333 | 22,29166667 | |||
| Итого | 3 | 48,75 |
Рассчитаем статистику критерия:
![]() .
.
Критическое
значение при уровне значимости ![]() и числах
степеней свободы
и числах
степеней свободы ![]() составляет
составляет ![]() .
.
Схема критерия:
![]()
Сравним
![]() , следовательно, свойство
постоянства дисперсии остатков выполняется, модель гомоскедастичная.
, следовательно, свойство
постоянства дисперсии остатков выполняется, модель гомоскедастичная.
2. Для проверки независимости уровней ряда остатков используем критерий Дарбина–Уотсона
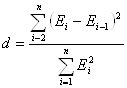 .
.
Предварительно
по столбцу остатков с помощью функции СУММКВРАЗН определим ![]() ; используем найденную
программой РЕГРЕССИЯ сумму квадратов остаточной компоненты
; используем найденную
программой РЕГРЕССИЯ сумму квадратов остаточной компоненты ![]() .
.
Таким образом,
![]()
Схема критерия:

Полученное значение d=2,375, что свидетельствует об отрицательной корреляции. Перейдем к d’=4-d=1,62 и сравним ее с двумя критическими уровнями d1=0,88 и d2=1,32.
D’=1,62 лежит в интервале от d2=1,32 до 2, следовательно, свойство независимости остаточной компоненты выполняются.
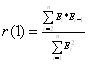
С
помощью функции СУММПРОИЗВ найдем для остатков ![]() , следовательно r(1)=2,4869Е-14/148,217=1,67788Е-16.
, следовательно r(1)=2,4869Е-14/148,217=1,67788Е-16.
Критическое
значение для коэффициента автокорреляции определяется как отношение ![]() Ön
и составляет для данной задачи
Ön
и составляет для данной задачи ![]()
Сравнения показывает, что çr(1)= 1,67788Е-16<0,62, следовательно, ряд остатков некоррелирован.
4)
Соответствие ряда остатков нормальному закону распределения проверим с помощью ![]() критерия:
критерия:
![]() .
.
С
помощью функций МАКС и МИН для ряда остатков определим ![]() ,
, ![]() . Стандартная ошибка модели
найдена программой РЕГРЕССИЯ и составляет
. Стандартная ошибка модели
найдена программой РЕГРЕССИЯ и составляет ![]() .
Тогда:
.
Тогда:
![]()
Критический
интервал определяется по таблице критических границ отношения ![]() и при
и при ![]() составляет (2,67; 3,57).
составляет (2,67; 3,57).
Схема критерия:
![]()
2,995
![]() (2,67; 3,57), значит, для
построенной модели свойство нормального распределения остаточной компоненты
выполняется.
(2,67; 3,57), значит, для
построенной модели свойство нормального распределения остаточной компоненты
выполняется.
Проведенная проверка предпосылок регрессионного анализа показала, что для модели выполняются все условия Гаусса–Маркова.
4.
Осуществить проверку значимости параметров уравнения регрессии с помощью t–критерия
Стьюдента (![]() ).
).
t–статистика для коэффициентов уравнения приведены в таблице 4.
Для
свободного коэффициента ![]() определена
статистика
определена
статистика ![]() .
.
Для
коэффициента регрессии ![]() определена
статистика
определена
статистика ![]() .
.
Критическое
значение ![]() найдено для уравнения
значимости
найдено для уравнения
значимости ![]() и числа степеней свободы
и числа степеней свободы ![]() с помощью функции
СТЬЮДРАСПОБР.
с помощью функции
СТЬЮДРАСПОБР.
Схема критерия:
![]()
Сравнение показывает:
![]() , следовательно,
свободный коэффициент a
является значимым.
, следовательно,
свободный коэффициент a
является значимым.
![]() , значит,
коэффициент регрессии b
является значимым.
, значит,
коэффициент регрессии b
является значимым.
5.
Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с
помощью F–критерия Фишера (![]() ), найти среднюю
относительную ошибку аппроксимации. Сделать вывод о качестве модели.
), найти среднюю
относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Коэффициент
детерминации R–квадрат определен
программой РЕГРЕССИЯ и составляет ![]() .
.
Таким образом, вариация объема выпуска продукции Y на 79,5% объясняется по полученному уравнению вариацией объема капиталовложений X.
Проверим значимость полученного уравнения с помощью F–критерия Фишера.
F–статистика определена программой РЕГРЕССИЯ
(таблица 2) и составляет ![]() .
.
Критическое
значение ![]() найдено для уровня значимости
найдено для уровня значимости
![]() и чисел степеней свободы
и чисел степеней свободы ![]() ,
, ![]() .
.
Схема критерия:
![]()
Сравнение
показывает: ![]() ; следовательно, уравнение
модели является значимым, его использование целесообразно, зависимая переменная
Y достаточно хорошо описывается
включенной в модель факторной переменной Х.
; следовательно, уравнение
модели является значимым, его использование целесообразно, зависимая переменная
Y достаточно хорошо описывается
включенной в модель факторной переменной Х.
Для вычисления средней относительной ошибки аппроксимации рассчитаем дополнительный столбец относительных погрешностей, которые вычислим по формуле
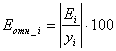
с помощью функции ABS (таблица 5).
ВЫВОД ОСТАТКА |
|||
| Наблюдение | Предсказанное Y | Остатки | Отн. Погр-ти |
| 1 | 27,14150943 | 6,858490566 | 20,17% |
| 2 | 29,30660377 | -3,306603774 | 12,72% |
| 3 | 30,02830189 | -6,028301887 | 25,12% |
| 4 | 35,08018868 | 2,919811321 | 7,68% |
| 5 | 35,80188679 | -0,801886792 | 2,29% |
| 6 | 40,13207547 | -0,132075472 | 0,33% |
| 7 | 45,90566038 | -3,905660377 | 9,30% |
| 8 | 45,90566038 | 5,094339623 | 9,99% |
| 9 | 46,62735849 | -1,627358491 | 3,62% |
| 10 | 48,07075472 | 0,929245283 | 1,90% |
По
столбцу относительных погрешностей найдем среднее значение ![]() (функция СРЗНАЧ).
(функция СРЗНАЧ).
Схема проверки:
![]()
Сравним: 9,31% < 15%, следовательно, модель является точной.
Вывод: на основании проверки предпосылок МНК, критериев Стьюдента и Фишера и величины коэффициента детерминации модель можно считать полностью адекватной. Дальнейшее использование такой модели для прогнозирования в реальных условиях целесообразно.
6.
Осуществить прогнозирование среднего значения показателя Y
при уровне значимости ![]() , если прогнозное
значение фактора X составит 80% от
его максимального значения.
, если прогнозное
значение фактора X составит 80% от
его максимального значения.
Согласно
условию задачи прогнозное значение факторной переменной Х составит 80% от 49,
следовательно, ![]() . Рассчитаем по
уравнению модели прогнозное значение показателя У:
. Рассчитаем по
уравнению модели прогнозное значение показателя У:
![]() .
.
Таким образом, если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции составит около 48 млн. руб.
Зададим
доверительную вероятность ![]() и
построим доверительный прогнозный интервал для среднего значения Y.
и
построим доверительный прогнозный интервал для среднего значения Y.
Для этого нужно рассчитать стандартную ошибку прогнозирования:
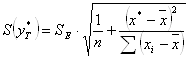
Предварительно подготовим:
-
стандартную ошибку модели ![]() (Таблица
2);
(Таблица
2);
-
по столбцу исходных данных Х найдем среднее значение ![]() (функция СРЗНАЧ) и
определим
(функция СРЗНАЧ) и
определим ![]() (функция КВАДРОТКЛ).
(функция КВАДРОТКЛ).
Следовательно, стандартная ошибка прогнозирования для среднего значения составляет:
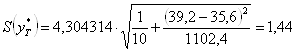
При
![]() размах доверительного
интервала для среднего значения
размах доверительного
интервала для среднего значения
![]()
Границами прогнозного интервала будут
![]()
![]()
Таким образом, с надежностью 90% можно утверждать, что если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции будет от 45,3 млн. руб. до 50,67 млн. руб.
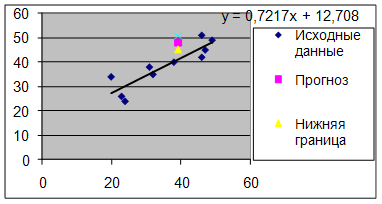
7. Представить графически фактические и модальные значения Y точки прогноза.
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции).
Затем с помощью опции Добавить линию тренда… построим линию модели:
тип → линейная; параметры → показывать уравнение на диаграмме.
Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:
Имя
→ прогноз; значения ![]() ; значения
; значения
![]() ;
;
Имя
→ нижняя граница; значения ![]() ; значения
; значения
![]() ;
;
Имя
→ верхняя граница; значения ![]() ;
значения
;
значения ![]()
8. Составить уравнения нелинейной регрессии: гиперболической; степенной; показательной.
8.1 Гиперболическая модель
Уравнение гиперболической функции:
![]() = a + b/x.
= a + b/x.
Произведем линеаризацию модели путем замены X = 1/x. В результате получим линейное уравнение
![]() = a + bX.
= a + bX.
Рассчитаем параметры уравнения по данным таблицы 2.
b =![]() =
=![]()
а = ![]() =38,4+704,48*0,03=60,25.
=38,4+704,48*0,03=60,25.
Получим следующее уравнение гиперболической модели:
![]() = 60,25-704,48/х.
= 60,25-704,48/х.
8.2 Степенная модель
Уравнение степенной
модели имеет вид: ![]() =аxb
=аxb
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
lg ![]() = lg a + b lg x.
= lg a + b lg x.
Обозначим через
Y=lg ![]() , X=lg x, A=lg a.
, X=lg x, A=lg a.
Тогда уравнение примет вид: Y = A + bX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.
b = ![]() =
=![]()
A = ![]() = 1,57-0,64*1,53=0,59
= 1,57-0,64*1,53=0,59
Уравнение регрессии будет иметь вид: Y = 0,59+0,64* Х.
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.
![]() = 100,59* х0,64.
= 100,59* х0,64.
Получим уравнение степенной модели регрессии:
![]() = 3,87* х0,64.
= 3,87* х0,64.
8.3 Показательная модель
Уравнение показательной
кривой: ![]() =abx.
=abx.
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
lg ![]() = lg a + x lg b.
= lg a + x lg b.
Обозначим: Y = lg ![]() , B = lg b, A = lg a. Получим линейное уравнение регрессии: Y = A + B x. Рассчитаем его параметры, используя
данные таблицы 4.
, B = lg b, A = lg a. Получим линейное уравнение регрессии: Y = A + B x. Рассчитаем его параметры, используя
данные таблицы 4.
В =![]() =
=![]()
А =![]() = 1,57-0,01*35,6=1,27
= 1,57-0,01*35,6=1,27
Уравнение будет иметь вид: Y = 1,27+0,01х.
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
![]() =101,27* ( 100,01)х
= 18,55*1,02х.
=101,27* ( 100,01)х
= 18,55*1,02х.
Графики построенных моделей:

Рис.3. Гиперболическая
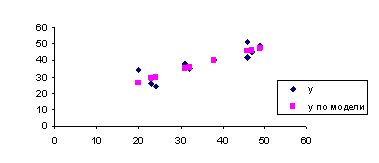
Рис.4. Степенная
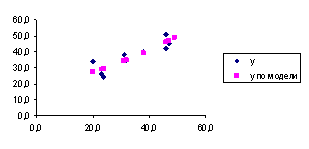
Рис.5. Показательная
9. Сравнение моделей по характеристикам: коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Вывод.
9.1 Гиперболическая модель
Коэффициент детерминации:
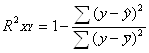 =
=![]()
Вариация результата Y на 70,9% объясняется вариацией фактора Х.
Коэффициент эластичности:
![]() =
=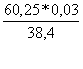 =
0,05.
=
0,05.
Это означает, что при увеличении фактора Х на 1 % результирующий показатель изменится на 0,05 %.
Бета-коэффициент:
Sx=![]() =0,01
Sy=
=0,01
Sy=![]() =8,5
=8,5
![]() 60,25*0,01/8,5=0,07.
60,25*0,01/8,5=0,07.
Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,07 среднеквадратического отклонения этого показателя.
Средняя относительная ошибка аппроксимации:
![]() отн = 109,7/ 10= 10,97 %.
отн = 109,7/ 10= 10,97 %.
В среднем расчетные
значения ![]() для гиперболической модели
отличаются от фактических значений на 10,97%.
для гиперболической модели
отличаются от фактических значений на 10,97%.
9.2 Степенная модель
Коэффициент детерминации:
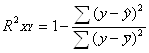 =
=![]()
Вариация результата Y на 73,6% объясняется вариацией фактора Х. Коэффициент эластичности:
![]() =
=![]() =
0,57.
=
0,57.
Это означает, что при увеличении факторного признака на 1 % результирующий показатель увеличится на 0,57%.
Бета-коэффициент:
![]() , Sy=
, Sy=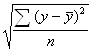 и
Sx=
и
Sx=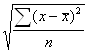 .
.
Sx=![]() =0,14
Sy=
=0,14
Sy=![]() =0,10
=0,10
![]() 0,59*0,14/0,1=0,78.
0,59*0,14/0,1=0,78.
Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,78 среднеквадратического отклонения этого показателя.
![]() отн=
отн= ![]() = 93,77/10 = 9,34%.
= 93,77/10 = 9,34%.
В среднем расчетные
значения ![]() для степенной модели
отличаются от фактических значений на 9,34%.
для степенной модели
отличаются от фактических значений на 9,34%.
9.3 Показательная модель
Коэффициент детерминации:
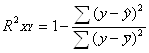 =
=![]()
Вариация результата Y на 75,7% объясняется вариацией фактора Х. Коэффициент эластичности:
![]()
![]() =
28,71.
=
28,71.
Это означает, что при росте фактора Х на 1 % результирующий показатель Y изменится на 28,71 %.
Бета-коэффициент:
Sx=![]() =10,5
Sy=
=10,5
Sy=![]() =0,10
=0,10
![]() 1,27*10,5/0,10=129,10.
1,27*10,5/0,10=129,10.
Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 129,1 среднеквадратического отклонения этого показателя.
![]() отн= 91,9/ 10 = 9,19%.
отн= 91,9/ 10 = 9,19%.
В среднем расчетные
значения ![]() для показательной модели
отличаются от фактических значений на 9,19%.
для показательной модели
отличаются от фактических значений на 9,19%.
Вывод
Лучшей из уравнений нелинейной регрессии является показательная: выше коэффициент детерминации, наименьшая относительная ошибка. Модель можно использовать для прогнозирования.