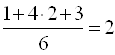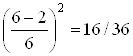Книга: Прикладной системный анализ: сетевой анализ и календарное планирование проектов, метод прогнозного графа
В.К. Буторин, В. В. Карпов
ПРИКЛАДНОЙ СИСТЕМНЫЙ АНАЛИЗ:
СЕТЕВОЙ АНАЛИЗ И КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ ПРОЕКТОВ,
МЕТОД ПРОГНОЗНОГО ГРАФА
Кемерово 2002
УДК 681.51
ISBN 5-87057-123-1
Рецензенты:
В.К. Буторин, В. В. Карпов
Прикладной системный анализ: сетевой анализ и календарное планирование проектов, метод прогнозного графа: Учеб. пособие. /Под ред. к. т. н. В.К. Буторина. НФИ КемГУ. – Новокузнецк, 2002. 59 с.
ISBN 5-87057-123-1
Рассматриваются постановки задач и практические аспекты использования методов сетевого анализа и календарного планирования проектов с использованием теории графов. Описывается минимизация времени выполнения и общей стоимости проекта. Рассматривается метод прогнозного графа. Алгоритмы принятия решений иллюстрируются на конкретных примерах. Приведены упражнения для выполнения практических работ.
Предназначено для студентов специальностей “Прикладная информатика в экономике”(351400), “Автоматизированные системы обработки информации и управления”(220200).
УДК 681.51
ISBN 5-87057-123-1
ã Новокузнецкий филиал-институт
Кемеровского государственного
университета, 2002
ã К.К. Буторин, В. В. Карпов, 2002
Содержание
1. Сетевой анализ и календарное управление
Введение
1.1. Сетевые графы
1.2. Стрелочные графы
1.3. Вершинные графы
1.4. Анализ критического пути
1.5. Анализ критического пути с применением вершинных графов
1.6. Анализ критического пути с применением стрелочных графов
1.7. Стоимость проекта
1.8. Минимизация общей стоимости проекта
1.9. Выполнение проекта с минимальными издержками
1.10. Неопределённость времени выполнения проекта
1.11. Распределение ресурсов
1.12. Графики ресурсов
Заключение
Упражнения
2. Метод прогнозного графа
Список литературы
1.СЕТЕВОЙ АНАЛИЗ И КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ ПРОЕКТОВ
Введение
Сетевой анализ - это метод планирования работ проектного характера, т.е. работ, операции в которых, как правило, не повторяются. Этот метод применим например, при составлении календарного плана выполнения операций, входящих в программу инсталлирования компьютерной системы в некоторой компании, или операций, являющихся составными частями улучшения обстановки офиса. Процессы инсталлирования компьютерных систем или улучшения обстановки офиса в данной компании могут протекать непрерывно, однако, вряд ли два любых проекта окажутся совершенно одинаковыми.
Методы сетевого анализа позволяют осуществить анализ проекта, которых включает в себя большое число взаимосвязанных операций. Мы можем определить вероятную продолжительность выполнения работ, их стоимость, возможные размеры экономии времени или денежных средств, а также то, выполнение каких операций нельзя отсрочить, не задержав при этом срок выполнения проекта в целом. Немаловажной является и проблема обеспечения ресурсами. Методы сетевого анализа могут быть использованы при составлении календарного плана выполнения операций, удовлетворяющего существующим ограничениям на обеспечение ресурсами.
Анализ любого проекта осуществляется в три этапа:
1. Расчленение проекта на ряд отдельных работ (или операций), из которых затем составляется логическая схема. Под операцией понимается деятельность или процесс, выполнение которых требует затрат временных и/или иных ресурсов.
2. Оценка продолжительности выполнения каждой операции; составление календарного плана выполнения проекта и выделение работ, которые определяют завершение выполнения проекта в целом.
3. Оценка потребностей каждой операции в ресурсах; пересмотр плана выполнения операций с учетом обеспечения ресурсами либо перераспределение денежных или других ресурсов, которое улучшит план. Рассмотрим каждый из этих этапов в отдельности.
1.1 Сетевые графы
Первым шагом в анализе любого проекта является составление списка входящих в него операций. Детали такого списка зависят от специфики конкретного проекта. Тем не менее во всех случаях необходимо выделить непосредственно предшествующую операцию или операции. Непосредственно предшествующими называются операции, выполнение которых должно быть закончено прежде, чем может начаться данная операция. Например, при постройке дома крыша не может быть построена до того момента, пока не закончится возведение стен.
После того как составлен список, логическая последовательность выполнения операций может быть проиллюстрирована с помощью графа. Существуют различные типы графов, но наиболее широкое применение получили так называемые вершинные и стрелочные графы. Однако каждый из них имеет свои преимущества и недостатки, и выбор того или иного графа является вопросом личных предпочтений или же определяется целью создания и использования данного графа.
1.2 Стрелочные графы
В этом типе графов (рис. 1) каждая операция представлена стрелкой. Длина стрелок значения не имеет. Направление стрелки отражает ход времени и обычно указывается слева направо. Начало и окончание каждой операции называются событиями и изображаются на графе кружочками или узлом.
|
|
![]()
Предшествующее Операции Последующее
событие (начало) событие (окончание)
Рис. 1. Изображение операции на стрелочном графе
Операции обозначают буквой или словом, а события - числом. Поскольку любая операция характеризуется парой событий, ее можно также обозначать с помощью чисел, соответствующих этим событиям. Например, на рис. 1 операция А означает то же самое, что и операция (1, 2). Одному узлу может соответствовать (входить или выходить из него) несколько операций. Событие, изображаемое на графе с помощью узла, не считается свершившимся до тех пор, пока не окончены все входящие в него операции. Операция, выходящая из некоторого узла, Не может начаться до тех пор, пока не будет достигнуто начальное событие, т.е. пока не будут завершены все операции, входящие в узловое начальное событие.
Если операция С не может быть начата до момента окончания работ А и В, логическую схему данной ситуации можно представить графически следующим образом (см. рис. 2).
Начальным событием для С является конечное событие для А и В. Существенно, что в стрелочном графе сохраняется логическая зависимость операций. Иногда, чтобы достичь этого, необходимо включить в граф одну или более фиктивных логических операций.
Фиктивная логическая стрелка вводится в граф, если необходимо отразить, что некоторое событие не может появиться раньше другого события, а с помощью обычных стрелок, соответствующих операциям, этого сделать нельзя. Функция фиктивной логической операции состоит в том, чтобы показать последовательность появления событий.
![]()
|
|
|
![]()
![]()
![]()
|
Рис. 2. Логические взаимосвязи в стрелочном графе
Фиктивным логическим операциям ставится в соответствие нулевая продолжительность выполнения, а изображаются они обычно пунктиром. Например, если работу С нельзя начать прежде, чем завершится операция А, а работу О нельзя начать до тех пор, пока не завершатся работы А и В, соответствующий стрелочный граф будет выглядеть следующим образом:
Кроме того, в стрелочных графах для избежания неоднозначности используются фиктивные операции идентификации. В некоторых пакетах прикладных программ, используемых в сетевом анализе, операции обозначаются не с помощью букв или слов, а числами, обозначающими соответствующие им события. Если же две или более операций выполняются одновременно и имеют одни и те же начальное и конечное события, то компьютер не сможет отличить их друг от друга и не воспримет вводимую исходную информацию. Как показано на рис. 4, включение фиктивной операции идентификации позволяет решить данную проблему. На практике принято нумеровать события таким образом, чтобы номер конечного события был больше, чем номер начального события.
|
|
|
![]() Фиктивная
логическая
Фиктивная
логическая
операция
![]()
|
|
|
![]()
![]()
Рис. 3. Использование в стрелочном графе
фиктивной логической операции
Первый шаг после составления списка операций, входящих в проект, состоит в том, чтобы создать таблицу операций, в которой отражаются все операции, а также операции, непосредственно им предшествующие.
В данный список не включаются фиктивные логические операции или операции идентификации. На основе полученного списка строится стрелочный сетевой граф, включающий действительные и фиктивные операции и отражающий установленные взаимосвязи между ними. После того, как закончено построение исходного графа, можно выявить и исключить из рассмотрения ненужные фиктивные операции. Затем для улучшения логической схемы исходный граф можно модифицировать и перекомпоновать.
![]()
![]()
 Фиктивная операция
Фиктивная операция
![]() идентификации
идентификации
|
|
|
|

 Заменяется на
Заменяется на
Рис. 4. Использование в стрелочном графе фиктивной операции идентификации
Ненужные фиктивные логические операции можно выявить с помощью простого практического правила. Если единственной операцией, выходящей из некоторого узла, является фиктивная логическая операция, то по всей вероятности без нее можно обойтись.
Пример 1. Компания "Эвриком" - это промышленная фирма, которая заключила контракт о производстве партии станков, предназначенных к использованию крупным предприятием обувной промышленности для массового производства обуви. Ниже перечислены операции, которые необходимо выполнить в процессе разработки и производства этих станков (табл. 1).
Нужно изобразить операции с помощью стрелочного графа.
Решение.
Сетевой граф должен начинаться с единственного начального события, которое показано на рис. 5 кружочком, и заканчиваться единственным конечным событием. Построение графа мы начали с первого события. С этого события начинаются все операции, которым не предшествуют никакие виды работ. Начинать построение полезно с примерного эскиза будущего графа:
![]()
![]()
![]()
![]() F
G
F
G
![]()
![]()
![]() 5 9 10 12
5 9 10 12
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() А B C E
K L
А B C E
K L
![]()
![]()
![]()
![]()
![]()
![]() 1 2 3 4 7 13
14
1 2 3 4 7 13
14
![]()
![]()
![]()
![]()
![]()
![]() D H I
D H I
![]()
![]() 6 8 11
6 8 11
J
Рис. 5. Примерный эскиз графа для примера 1
Таблица 1. Таблица операций для задачи из примера 1
| ОПЕРАЦИИ |
Непосредственно предшествующая операция |
|
А Составление сметы затрат В Согласованные оценки С Покупка собственного оборудования D Подготовка конструкторских проектов E Строительство основного цеха F Монтаж оборудования G Испытания оборудования H Определение типа модели I Проектирование внешнего корпуса J Создание внешнего корпуса K Конечная сборка L Контрольная проверка |
- A B B D C,E F D D H,I G,J K |
В соответствии с приведенной выше таблицей необходимо тщательно, переходя от одной операции к другой, проверить построенный в первом приближении граф.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() A B C F G K L
A B C F G K L
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 2 3 5 8 9 10 11
1 2 3 5 8 9 10 11
![]()
![]()
![]()
![]()
![]() D E J
D E J
![]() 4
7 Фиктивная операция
4
7 Фиктивная операция
![]()
![]()
![]() H
I идентификации
H
I идентификации
6
Рис.6. Новый чертеж стрелочного графа для примера 1
Пример 2. Компания "Эвриком" является участником другого проекта, детали которого приведены ниже. Изобразим данный проект при помощи стрелочного графа.
Решение
Построение начинаем с начального события, обозначенного кружком 1. Из таблицы следует, что существуют три операции - А, В и С, которым не предшествует ни одна из операций. Поэтому из начального события выходят три стрелки. На первый взгляд таблица операций выглядит чрезвычайно простой, однако отразить присущую ей логику с помощью сетевого графа достаточно трудно, вследствие чего мы вынуждены использовать три фиктивные логические операции (см. рис. 7).
Таблица 2. Таблица операций для примера 2
| Операция |
Непосредственно Предшествующая операция |
Операция |
Непосредственно предшествующая операция |
|
A B C D |
- - - A,B |
E F G H |
B,C C D,E F,G |
 4
4
![]()
![]() 2
2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 5 6 7 8
1 5 6 7 8
![]()
![]()
3
Рис. 7. Стрелочный граф для примера 2
1.2 Вершинные графы
В этом типе сетевых графов операции представлены узлами графа, а стрелками изображаются их взаимосвязи. В таких графах не возникает необходимости вводить фиктивные операции. Как и в предыдущем случае, течение времени следует изображать в направлении слева направо.
Пример 3. Обратившись к данным из примера 2, модифицируем полученную в этом примере схему, поставив в соответствие операциям узлы графа.
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]() D
D
![]()
![]()
![]()
![]()
![]()
![]() Начальный B G
Начальный B G
![]()
![]()
![]()
![]()
![]() узел E H
узел E H
![]() C F
C F
Рис. 8. Вершинный граф
Каждый из описанных типов графов имеет свои преимущества и недостатки. Обычно не имеет принципиального значения, какая из систем используется. Если в стрелочные графы приходится вводить достаточно большое число фиктивных операций, то гораздо более предпочтительным является выбор вершинного графа. Ниже приведено сравнение двух видов изображения операций и их основных особенностей (см. рис. 9).
Ситуация Строчный граф Вершинный граф
![]()
![]()
![]()
![]()
![]() Операция Q P Q
Операция Q P Q
![]()
![]()
![]() зависит 1 2 3 P
Q
зависит 1 2 3 P
Q
![]()
![]() от операций P,Q
от операций P,Q
![]()
![]()
![]()
![]()
![]() Операция Х 1 Р X Р
Операция Х 1 Р X Р
![]()
![]()
![]()
![]()
![]() зависит 3 4
X
зависит 3 4
X
от операций P,Q 2 Q Q
![]()
![]()
![]()
![]()
![]() Операция Х,Y 1 Р X 4 Р
X
Операция Х,Y 1 Р X 4 Р
X
![]()
![]()
![]()
![]()
![]()
![]()
![]() зависит 3
зависит 3
![]() от операций P,Q 2 Q Y 5 Q
Y
от операций P,Q 2 Q Y 5 Q
Y
![]()
![]()
![]()
![]() Операция Х 1 Р 2 X 5 Р
X
Операция Х 1 Р 2 X 5 Р
X
![]()
![]()
![]()
![]()
![]()
![]() зависит
зависит
![]()
![]()
![]() от операции P; 3 Q 4 Y 6 Q Y
от операции P; 3 Q 4 Y 6 Q Y
oперация Y зависит от
операций Р и Q
Рис. 9. Сравнение сетевых стрелочного и вершинного графов
1.3 Анализ критического пути
После того как проведена идентификация операций, можно оценить их продолжительность. На основе продолжительности выполнения каждой операции и руководствуясь логической схемой, можно найти время выполнения проекта в целом. На данном этапе предполагается, что продолжительность выполнения каждой операции является фиксированной величиной, не испытывающей влияний неопределенности. В последнем разделе главы мы рассмотрим вопрос о том, какие поправки следует внести в этот анализ, чтобы учесть неопределенность времени выполнения операций. В каждом графе существует несколько возможных путей. Общее время, необходимое для того, чтобы пройти какой-либо путь, есть сумма времени выполнения всех операций, принадлежащих данному пути. Продолжительность выполнения всего проекта занимает наибольшее время. Более длительные операции называются критическими. Любая задержка срока начала или окончания выполнения этих работ повлечет за собой задержку срока выполнения проекта в целом. Критические операции образуют непрерывную цепь, проходящую через весь граф. Эта цепь критических операций называется критическим путем. В каждом графе найдется, по крайней мере, один критический путь.
Для того чтобы найти общую продолжительность выполнения проекта, нужно определить продолжительность критического пути. В большинстве графов идентифицировать все идущие сквозь граф пути, чтобы выявить среди них тот, который занимает наибольшее время, достаточно трудно. Существуют два возможных метода, позволяющих отследить движение времени в графе:
1. Определение для каждой операции наиболее ранних сроков начала и окончания ее выполнения.
2. Определение для каждого события наиболее раннего срока его наступления. Следует отметить, что второй метод может использоваться только в стрелочных графах.
1.4 Анализ критического пути с применением вершинных графов
Пример 4. В табл. 3 указана продолжительность выполнения каждой операции проекта, о котором шла речь в примерах 2 и 3 Определим общую продолжительность выполнения проекта. Вершинный граф, соответствующий данному проекту, был построен в примере 3.
Таблица 3. Операции и их продолжительность для примера 4
| Операция |
Непосредственно Предшествующая Операция |
Время, дней |
|
A B C D T F G H |
- - - A,B B,C C D,E F,G |
8 10 6 8 9 14 14 6 |
Решение
Предположим, что каждая из исходных операций А, В и С начинается в нулевой момент времени. Это наиболее ранний срок начала этих Е5 операций. Наиболее ранний срок, к которому их выполнение может быть завершено, определяется следующим образом:
Наиболее ранний срок окончания ЕР=ЕS+Продолжительность операции.
Обычно найденные значения этих сроков наносятся непосредственно на граф, однако, мы занесем их сначала в таблицу, чтобы продемонстрировать методику проведения расчетов.
Таблица 4. Расчет наиболее ранних сроков начала окончания операций для примера 4
| Операция | Продолжи-тельность, дней | Наиболее ранний срок начала | Наиболее ранний срок окончания | Комментарии |
|
A B C D E F G H |
8 10 6 8 9 14 14 6 |
0 0 0 10 10 6 19 33 |
0+8=8 0+10=10 0+6=6 10+8=18 10+9=19 6+14=20 19+14=33 33+6=39 |
Нельзя начать, пока не завершены А и В Нельзя начать, пока не завершены В и С Нельзя начать, пока не завершена С Нельзя начать, пока не завершены D и E Нельзя начать, пока не завершены F и G |
Ключ

![]()
![]()
 0
8 обозначение ЕS EF
0
8 обозначение ЕS EF
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() A 8 операции
продолжительность
A 8 операции
продолжительность
3 11 10 16 LS LF
![]()
![]()
![]()
![]()
![]()
![]()

 D 8
D 8
 0
10 11 19 19 33
0
10 11 19 19 33
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 Начальный B 10 G 14
Начальный B 10 G 14
 Узел 0
10 10 19 19 33 33 39
Узел 0
10 10 19 19 33 33 39
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 E 9
H 6
E 9
H 6
0 6 10 19 6 20 33 39
![]()
![]()
![]()
![]()
![]() C 6
F 14
C 6
F 14
4 10 19 33
Рис. 10 Вершинный граф для примера 4
Наиболее ранние сроки начала и окончания операций занесены в вершинный граф, изображенный на рис. Нетрудно заметить, что операция Н завершится на 39-й день, следовательно, это значение дает нам искомую продолжительность выполнения проекта в целом.
Таблица 5. Расчет наиболее поздних сроков начала и окончания
операций для примера 4
| Операция |
Продолжительность, дней |
Наиболее Поздний срок окончания |
Наиболее Поздний Срок Начала |
Комментарии |
|
H G F E D C B A |
6 14 14 9 8 6 10 8 |
39 33 33 19 19 10 10 11 |
39-6=33 33-14=19 33-14=19 19-9=10 19-8=11 10-6=4 10-10=0 11-8=3 |
G нужно завершить до наступления наиболее позднего срока начала H F нужно завершить до наступления наиболее позднего срока начала H E нужно завершить до наступления наиболее позднего срока начала G D нужно завершить до наступления наиболее позднего срока начала G C нужно завершить до наступления наиболее позднего срока начала Е и F. В нужно завершить до наступления наиболее позднего срока начала D и E. Нужно использовать наименьший из этих сроков, равным 10 дням. А нужно завершить до наступления наиболее позднего срока начала D |
На данном этапе мы еще не можем определить критические операции. Чтобы это осуществить, необходимо для каждой операции рассчитать два срока, ей соответствующие, а именно наиболее поздний срок начала LS и наиболее поздний срок окончания LF операции. В данном случае процедуру расчетов мы начнем с последней операции в графе и предположим, что наиболее поздний и наиболее ранний сроки ее окончания совпадают. Затем вычитанием из этой величины продолжительности выполнения операций находим наиболее поздний срок ее начала. Ход выполнения расчетов показан в табл. 5.
Критической является операция, для которой справедливы следующие соотношения:
ЕS = LS и ЕF = LF,
т. е. операция, для которой не существует резерва времени между наиболее ранним сроком ее начала и наиболее поздним сроком ее окончания. Нетрудно, заметить, что в нашем примере критическими являются операции В, Е, G и Н. Путь в вершинном графе, соединяющий эти операции, называется критическим путем. В нашем примере критическим является путь В-Е-G-Н.
1.5 Анализ критического пути с применением стрелочных графов
Приведенная выше методика анализа аналогичным образом может использоваться. и для стрелочных графов. Значения сроков ЕS, ЕF, LS и LF записываются в графе вдоль стрелок, соответствующих операциям:
![]()
![]() [ES,EF] A
[ES,EF] A
1
![]() 2
2
[LS,EF]
Рис. 11. Нанесение на стрелочный граф сроков, соответствующих операциям
Можно провести подобный анализ в терминах сроков наступления каждой события. Производится расчет наиболее раннего срока, к которому может завершиться каждое событие. Этот срок называется наиболее ранним сроком события (earliest event time - ЕЕТ). Общая продолжительность выполнения проекта определяется ЕЕТ конечного узла графа. ЕЕТ исходного события равен нулю.
Для того чтобы выявить критические операции, необходимо, начиная с конца графа, вычислить наиболее поздние сроки событий (1аtest еvent time - LЕТ), к которым события могут закончиться. События, для которых выполняются соотношения
LEТ начала- ЕЕTокончания + продолжительность = О или
ЕЕТначала - LETокончания + продолжительность = О,
являются критическими.
Пример 5. Применив ЕЕТ и LЕТ, повторим задачу из примера 4 при условии, что продолжительность выполнения фиктивных операций равна нулю. Решение
В первую очередь для каждого события вычислим значение наиболее раннего срока. Если некоторому событию соответствует более одной операции, появляется проблема выбора соответствующего значения. Поскольку событие считается незавершенным до тех пор, пока не будет завершено выполнение всех составляющих его операций, следует выбрать наибольшее из значений.
Таблица 6. Расчет значений ЕЕТ для примера 5
| Узел | ЕЕТ, дней | Комментарии |
|
1 2 3 4 5 6 7 8 |
0 0+10=10 0+6=6 0+8=8 или 10+0=10* 10+0=10* или 6+0=6 10+8=18 или 10+9=19* 19+14=33* или 6+14=20 33+6=39 |
Начальное событие ЕЕТ узла 1 + продолжительность операции В ЕЕТ узла 1 + продолжительность операции С ЕЕТ узла 1 + продолжительность операции А. ЕЕТ узла 2 + продолжительность фиктивной операции. Выбирается максимальный срок, т. е. 10 дней ЕЕТ узла 2 + продолжительность фиктивной операции. ЕЕТ узла 3 + продолжительность фиктивной операции. Выбирается максимальный срок, т. е. 10 дней ЕЕТ узла 4 + продолжительность операции D ЕЕТ узла 5 + продолжительность операции Е. Выбирается максимальный срок, т. е. 19 дней ЕЕТ узла б + продолжительность операции С ЕЕТ узла 3 + продолжительность операции Р. Выбирается максимальный срок, т. е. 33 дня ЕЕТ узла 7 + продолжительность операции Н |
*Выбранное значение ЕЕТ
Полученные значения сроков наносятся на стрелочный граф, как это показано на рис. 12.
ЕЕТ последнего события равно 39 дням, которые также определяют общую продолжительность выполнения проекта.
Чтобы определить критические операции, будем двигаться по графу начиная с конечного узла и вычисляя LЕТ каждого события. Предположим, что для конечного события ЕЕТ = LЕТ. Если в некоторый узел входит более одной стрелки, то возникает проблема выбора значения LЕТ. Так как событие должно завершиться к сроку, удовлетворяющему всем наиболее поздним срокам начала событий, которые выходят из данного узла для LЕТ, следует выбрать наименьшее значение.
Найденные значения сроков наносятся на стрелочный граф, изображенный на рис. 12.
|
|
|
|
|
|
|
![]()
 2
2
![]()
![]()
|
|
|
 |
|
||||||||||||
|
|||||||||||||
![]()
![]()
|

![]()
![]()
|
|
![]()
![]()
|
Рис. 12. Стрелочный граф для примера 5 с указанием ЕЕТ и событий
Операция является критической, если для нее справедливы следующие соотношения:
ЕЕТначала = LETначала и ЕЕТокончания = LЕТокончания
LEТокончания - EETначала - Продолжительность = 0.
Из рисунка 12 видно, что критическими, как и ранее, являются операции В, Е, G и Н. Любые замедления на критическом пути приведут к задержке срока выполнения, всего проекта. Между тем для некритических путей можно допустить некоторые задержки при выполнении составляющих их операций или пересмотреть график их выполнения. Запас времени, который существует в схеме проекта, называется резервом времени.
Различают несколько видов резерва времени, возникающих под влиянием различных воздействий, которые оказывает запас времени на схему выполнения проекта.
Общим резервом называется количество времени, на которое можно увеличить продолжительность операции в результате продления срока ее выполнения или пересмотра плана, не влияющего на продолжительность выполнения проекта в целом. Свободным резервом называется количество времени, на которое можно увеличить продолжительность операции в результате продления срока ее выполнения или пересмотра плана, не оказывающего воздействия на наиболее ранний срок выполнения любой последующей операции. Иногда используют третий вид, так называемый независимый резерв времени. Он не оказывает никакого влияния на предшествующие или последующие операции. Для любой операции
Общий резерв времени = LЕTокончания - ЕЕТначала - Продолжительность, также
Свободный резерв времени = ЕЕТокончания - ЕЕТначала – Продолжительность
Независимый резерв = ЕЕТокончания-LETначала – Продолжительность.
Иногда бывает полезно изобразить на графе имеющийся в наличии резерв времени, особенно если план выполнения операций необходимо пересмотреть. В этом случае одним из возможных методов является график Ганта.
Таблица 7. Расчет значений ЕЕТ для примера 5
| Узел | LET,дней | Комментарий |
|
8 7 6 5 4 3 2 1 |
39 39-6=33 33-14=19 19-9=10 19-8=11 10-0=0* или 33-14=19 10-0=10* или 11-0=11 11-8=3 или 10-10=0* или 10-6=4 |
Конечный узел LЕТ = ЕЕТ LЕТ узла 8 – продолжительность операции Н LЕТ узла 7 – продолжительность операции G LЕТ узла б – продолжительность операции Е LЕТ узла 6 – продолжительность операции D LЕТ узла 5 – продолжительность фиктивной операции или LЕТ узла 7 – продолжительность операции F. Выбирается минимальный срок, т.е. 10 дней LЕТ узла 5 – продолжительность фиктивной операции или LЕТ узла 4 - продолжительность фиктивной операции Выбирается минимальный срок, т.е. 10 дней LЕТ узла 4 – продолжительность операции А или LЕТ узла 2 продолжительность операции В или LЕТ узла 3 – продолжительность операции С Выбирается минимальный срок, т.е. О дней |
*Выбранное значение LЕТ.
Пример 6. По данным примера 5 для каждой операции найдем общий резерв времени.
Операции, общий резерв времени которых равен нулю, являются критическими. На рис. 13 построен график Ганта, и отмечены, возможно наиболее ранние сроки начала операций.
Таблица 8. Расчет резерва времени операций для примера 5 (дней)
| операция | LET окончания | LET начала | продолжительность | Общий резерв времени |
|
A B C D E F G H |
11 10 10 19 19 33 33 39 |
0 0 0 10 10 6 19 33 |
8 10 6 8 9 14 14 6 |
3 0 4 1 0 13 0 0 |
Стандартные сроки
Стандартные сроки
![]()
|
![]()
|
|
Рис. 13. График Ганта для примера 5
1.6 Стоимость проекта
Общая стоимость проекта зависит от стоимости выполнения каждой операция, а также от любых дополнительных переменных или постоянных расходов. Так как необходимо завершить все операции, независимо от того, являются они критическими или нет, общая стоимость выполнения операций представляет собой арифметическую сумму отдельных значений стоимости каждой операции.
Можно снижать продолжительность выполнения некоторых операций с помощью дополнительных ресурсов. Косвенным последствием такой меры является увеличение стоимости данных операций. Однако если операция критическая, то экономия времени ее выполнения может привести к общей экономии времени выполнения проекта в целом, а следовательно, и к снижению общей стоимости проекта.
Возможный наименьший срок, к которому можно завершить операцию, получил название критического срока. В некоторых случаях завершить операцию можно только либо к стандартному, либо к критическому сроку их выполнения, но не между ними. Иногда, напротив, существует возможность постепенно уменьшать время выполнения операции до того момента, пока не будет достигнут критический срок ее выполнения. Рассмотрим, как действует уменьшение времени выполнения операций на календарный план, и стоимость выполнения проекта, принимая во внимание две различные цели:
1. Минимизацию общего времени выполнения проекта;
2. Минимизацию общей стоимости проекта.
1.7 Минимизация общей продолжительности проекта с минимальными дополнительными расходами
Для этой цели необходимо обладать информацией о стоимости каждой операции, любом возможном уменьшении времени ее выполнения и о дополнительных издержках, связанных со снижением времени выполнения операции.
Пример 7. Обратимся к данным примера 2. Ниже приводится дополнительная информация о стоимости операций и возможном уменьшении времени их выполнения.
Показатели критических значений отражают минимальное время, за которое можно выполнить операцию, и общую стоимость выполнения операции в течение этого времени. Необходимо сделать выбор между стандартными значениями времени и издержек и их критическими значениями. Практически невозможно получить экономию времени выполнения операции в один день при пропорциональном возрастании ее стоимости. Помимо стоимости каждой операции необходимо учесть стоимость строительной площадки, составляющую 1000 руб. в день.
1. Каково минимальное время, в течение которого можно завершить проект?
2. Какова соответствующая минимальная дополнительная стоимость?
Решение
Минимальное время можно найти, рассчитав для всех, как критических, так и некритических операций, критическое время их выполнения. Ниже изображен стрелочный граф, построенный в примере 2. На граф нанесены значения ЕЕТ и LЕТ, найденные на основе критических значений времени выполнения операций.
Нетрудно заметить, что ЕЕТ узла 8 равно 28 дням, поэтому минимальное время выполнения проекта также составляет 28 дней. Критический путь остается неизменным: В-Е-G-Н.
Общую стоимость можно найти из следующего уравнения:
Общая стоимость = Критическая стоимость операций + 28 х
х Стоимость строительной площадки в день = 102 750 руб. +
+ 28 х 1000 руб. = 130750 руб.
Таблица 9. Значения стандартных и критических сроков и соответствующих издержек выполнения операций для примера 7
| ОПЕРА-ЦИЯ | НЕПОСРЕДСТ-ВЕННО ПРЕДШЕ-СТВУЮЩИЕ ОПЕРАЦИИ | СТАНДАРТНОЕ ЗНАЧЕНИЕ | Критическое значение | ||
| ВРЕМЕ-НИ, ДНЕЙ | СТОИМО-СТИ, РУБ. | Времени, дней | Стоимости, руб. | ||
|
A B C D E F G H |
- - - A,B B,C C D,E F,G |
8 10 6 8 9 14 14 6 |
7500 8500 6000 13000 14000 14500 13500 5500 |
4 8 5 5 6 11 10 4 |
9000 11000 7000 16000 16500 18000 18750 6500 |
| ОБЩИЕ ИЗДЕРЖКИ ВЫ-ПОЛНЕНИЯ ОПЕРАЦИЙ | 82500 | 102750 |
|
|
|
|
|
![]()
|
|
![]()
![]() 2
2
![]()
|
|
|
 |
|
||||||||||||
|
|||||||||||||
![]()
![]()
|


![]()
![]()
|
|
![]()
![]()
|
Рис. 14. Стрелочный граф для примера 7 с указанием критического времени
Между тем найденное значение стоимости выполнения проекта в указанное время не является минимальным, поскольку необходимости использовать критические значения для некритических операций нет. Некритическими являются операции А, С, D и F. Поэтому необходимо найти эффект от использования соответствующих этим операциям некритических значений показателей. В случае, если существует возможность восстановить их стандартную продолжительность, не увеличивая при этом общую продолжительность выполнения проекта, можно будет одновременно достичь и экономию стоимости в результате использования ее некритических значений.
Критические значения для операции А можно не использовать, поскольку увеличение продолжительности ее выполнения до 8 дней не меняет ЕЕТ узла 4, и, следовательно, не оказывает воздействия на выполнение остальных операций календарного плана. Использование некритических значений для операции А позволяет достичь экономии, составляющей 1500 руб.
Увеличение продолжительности операции С с 5 до 6 дней приведет к увеличению значения ЕЕТ узла 3 до 6, однако не окажет воздействия на ЕЕТ узлов 5 и 7. Вследствие этого продолжительность выполнения проекта останется неизменной. Использование некритических значений, соответствующих операции С, позволит получить экономию 1000 руб.
Если использовать некритические значения показателей операции D, то ЕЕТ узла 6 возрастет до 16 дней. Узел 6 принадлежит критическому пути, поэтому для того, чтобы достичь минимального общего времени выполнения проекта, составляющего 28 дней, необходимо применять критические значения времени и стоимости операции D.
Использование некритических значений для операции F не изменит ЕЕТ узла 7 и не приведет к увеличению продолжительности проекта в целом. Используя для F некритические значения, мы сможем достичь экономии, составляющей 3500 руб.
Минимальная стоимость выполнения проекта за 28 дней составит:
130750 - 1500 (А) - 1000 (С) - 3500 (Р) = 124750 руб.
Стоимость выполнения проекта в стандартные сроки равна:
82500 (стоимость операций) + 39000 (стоимость строительной площадки)= = 121500 руб
Следовательно, дополнительная стоимость, связанная с завершением выполнения проекта на 11 дней раньше, будет равна:
124750 - 121500 = 3250 руб.
Пример 8. Обратимся к данным примера 1. В табл. 10 приводится дополнительная информация о стоимости операций и возможном сокращении времени их выполнения.
Переменные накладные расходы составляют 300 руб. в неделю в течение всего времени выполнения проекта.
1. Определить стандартные значения общего времени выполнения и общей стоимости проекта.
2. Найти минимальное время, за которое можно выполнить данный проект, и соответствующее ему минимальное значение стоимости.
Таблица 10. Стандартные и критические значения сроков выполнения и стоимости операций для примера 8
| Операция | Стандартное значение | Возможное сокращение времени, недель | Критичес-кое время, недель | Дополнительные издержки сокращения времени на неделю, руб. | ||
| Времени, недели |
Стои-мость, руб. |
|||||
|
A B C D E F G H I J K L |
2 1 4 6 3 3 4 2 3 8 2 2 |
400 0 200 450 700 200 600 0 250 600 450 200 |
1 0 2 4 2 2 3 0 1 4 1 1 |
1 1 2 2 1 1 1 2 2 4 1 1 |
400 0 125 175 250 200 125 0 200 100 250 150 |
|
| Стоимость операций 4050 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
Рис. 15. Стрелочный граф для примера 8 с указанием стандартных сроков
|
|
срок события, срок события (стандартный срок, дней)
Решение
На рис. 15 воспроизведен стрелочный граф, построенный в примере 1. Для каждой операции на графе указаны значения ЕЕТ и LЕТ. Стандартный срок выполнения проекта составляет 24 недели, а соответствующий ему критический путь имеет следующий вид:
А-B-D-1-]-К-L.
Общая стоимость проекта составляет:
4050 (стоимость операций) + 24х300 (переменные накладные расходы) = 11250руб.
Чтобы определить минимальное время, требующееся для выполнения проекта в целом, каждой операции поставим в соответствие минимальный срок ее завершения. На рис. 16 показаны значения этих сроков и итоговые значения ЕЕТ и LЕТ.
Минимальная продолжительность проекта составляет 12 недель. В данном случае критическими оказываются следующие пути:
А-B-D-1-]-К-L и А-B-D-Н-]-К-L.
Проверим, можно ли, используя некритические значения для некоторых некритических операций, получить экономию денежных средств.
Таблица 11. Использование некритических значений показателей для некритических операций из примера 8
| Опера-ция | Изменение продолжитель-ности | Эффект |
|
Е F G С |
Увеличение на 2 недели Увеличение на1 неделю Увеличение невозможно Увеличение на 2 недели |
ЕЕТ узла 5 становится равным 7 неделям; ЕЕТ узла 8 становится равным 8 неделям, не влияя при этом на ЕЕТ узла 9, принадлежащего критическому пути; других воздействий нет. Е выполняется в стандартный срок ЕЕТ узла 8 становится равным 9 неделям. Операции Е, F и G становится критическими. На узел 5 не оказывается никакого воздействия. С выполняется в стандартный срок. |
Некритическими являются операции С, Е, F и G. Продолжительность операций в данном примере можно изменять по интервалам в одну неделю, так как единицей измерения продолжительности является неделя. В первую очередь рассмотрим операции, которые, если использовать их некритические значения, |могут принести наибольшую экономию денежных средств. Операции будем рассматривать в следующем порядке: Е (250 руб.), F (200 руб.), и С (125 руб.) или G (125 руб.).
Минимальная стоимость выполнения проекта за 12 недель составила:
(4050 (стандартная стоимость операций) + 1 • 400 (А) + 4 • 175 (В) + 1 • 200 (F) + 3 • 125 (G) + 1 • 200 (I) + 4 • 100 (J) + 1 • 250 (К) + 1 • 150 (L) (предельные издержки) + 12 • 300 ( переменные накладные расходы) = 4050 + 2675 + 3600 = 10325 руб.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
Рис. 16. Стрелочный граф для примера 8 с указанием критических сроков
|
|
срок события, срок события (стандартный срок, дней)
1.8 Выполнение проекта с минимальными издержками
Если выполнение проекта требует оплаты переменных накладных расходов, таких, например, как расходы, связанные с оборудованием строительной площадки, то может оказаться выгодным снижение продолжительности выполнения проекта. Поскольку сами эти сокращения влекут за собой определенные издержки, необходимо подвести баланс. Экономия времени может быть достигнута только в том случае, если сократить продолжительность критических операций. Критические значения должны использоваться только по тем критическим операциям, по которым величина экономии накладных расходов превышает стоимость выполнения операции за критическое время.
Пример 9. Обратившись к данным примера 7, определим минимальную стоимость проекта и соответствующее время его выполнения. Предполагается, что операции можно выполнять либо в стандартные, либо в критические сроки, но не в промежутке между ними.
Решение
Используя граф, построенный в примере 5 для стандартных сроков выполнения операций, перечислим все критические операции и соответствующие им показатели максимально возможной экономии времени и чистой экономии стоимости.
Таблица 12. Расчет минимальной стоимости проекта для примера 9
| Опера-ция | Число дней экономии для критиче-ского времени | Дополни-тельная стоимость критичес-кого времени, руб. | Экономия, руб. | Чистая экономия, руб. | Комментарии |
|
В Либо Е Либо Е и D G Н |
2 1* 3 4 2 |
2500 2500 5500 5250 1000 |
2·1000 1·1000 3·1000 4·1000 2·1000 |
-500 -1500 -2500 -1250 +1000 |
Критические значения не используются Критические значения не используются Критические значения не используются Критические значения не используются Используются критические значения. Снижение продолжительности проекта с 39 до 37 дней |
*Достичь экономии, равной 3 дням, нельзя, поскольку в этом случае путь А-D-G-Н становится критическим. Поэтому общая продолжительность снижается только на один день. Если же использовать критические значения одновременно для Е и О, достигается экономия времени, равная 3 дням. Однако соответствующая стоимость становится равной: 2500 руб. + 3000 руб., т.е. такая экономия времени не целесообразна.
Минимальная стоимость проекта равна: 121500 - 1000 = 120500 руб. Соответствующее время его выполнения составляет 37 дней.
1.9 Неопределённость времени выполнения операций
В приведенных выше методах анализа предполагалось, что время выполнении операций точно известно. Однако на практике сроки выполнения операций обычней являются довольно неопределенными. Управляющий производством может выдвинуть некоторые предположения о том, сколько времени потребуется для выполнения каждой работы, но не может предусмотреть возможные трудности или задержки выполнения. Неопределенность сроков выполнения операций означает, что общая продолжительность проекта также подвержена неопределенности.
Выбор метода, позволяющего учесть эту неопределенность, зависит от типа проекта и природы неопределенности. Если можно определить минимальную и максимальную продолжительности каждой операции, то их рассчитывают с помощью показателей ожидаемой (средней) продолжительности и ожидаемого времени выполнения проекта. Алгоритм, получивший наиболее широкое применение, называется методом оценки и пересмотра проектов (Project Еvа1uation and Reiew Technique -- PERT). При вычислении ожидаемого времени выполнения проекта методом РЕRТ используются показатели ожидаемого времени выполнения операций. Оставшаяся часть алгоритма аналогична описанным выше алгоритмам, применяемым в случаях, когда время выполнения операций является фиксированной величиной.
Если время выполнения операций подвержено влиянию неопределенности, то большое значение приобретают некритические пути в графе, когда могут изменяться сроки выполнения всех операций. На практике может оказаться, что путь, который на основе ожидаемых значений сроков считался некритическим, становится критическим в соответствии с результатами метода определения критического пути.
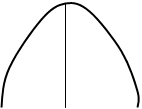
В основу метода РЕRТ положена предпосылка о проведении продолжительности операции. Предполагается, что время выполнения каждой отдельно взятой операции аппроксимируется p-распределением. Если это верно, то распределение времени выполнения проекта в целом является нормальным. Метод РЕRТ может применяться при анализе конкретного проекта только в случае выполнения данной предпосылки. График р-распределения изображен на рис. 17. Возможное наименьшее время выполнения операции называют оптимистическим сроком (а), а возможное наибольшее время ее выполнения - пессимистическим сроком (b).
Пику распределения соответствует наиболее вероятное время выполнения операции (m). Необходимо произвести оценку каждого из этих трех сроков для всех операций, входящих в граф.
Исходя из этих трех значений можно найти ожидаемую продолжительность операции (t) и ее дисперсию. Ожидаемая продолжительность операции определяется следующим образом:
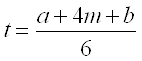
Соответствующая дисперсия ожидаемой продолжительности определяется по формуле:
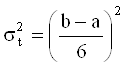
![]()
![]() Плотность
Плотность
вероятности
![]() Срок
выполнения
Срок
выполнения
а m b
Оптимистический Пессимистический
Наиболее вероятный
Рис. 17. Стандартное b-распределение для времени выполнения операций
Время выполнения проекта можно найти непосредственно из графа, используя для этого ожидаемые значения продолжительности операций. Предполагается, что время выполнения проекта в целом распределено по нормальному закону.
В предположении, что сроки выполнения операций не зависят друг от друга, среднее значение нормального распределения определяется как сумма математических ожиданий продолжительности критических операций, а дисперсия - как сумма их дисперсий. Полученное нормальное распределение можно использовать для оценки вероятности завершения проекта к заранее установленной дате.
Алгоритм метода РЕRТ аналогичен анализу сетевого графа с фиксированными значениями продолжительности операций.
1.Составить список всех операций, входящих в проект, с указанием непосредственно предшествующих операций, а также оптимистического, наиболее вероятного и пессимистического сроков их выполнения.
2. Построить сетевой граф.
3.В предположении, что время выполнения любой операции аппроксимируется р-распределением, оценить для каждой операции ожидаемое время ее выполнения и его дисперсию.
4. Используя ожидаемые значения сроков выполнения операций, найти продолжительность проекта в целом.
5. Определить критические операции и критический путь.
6. С помощью значений дисперсии для критических операций оценить дисперсию ожидаемой продолжительности всего проекта.
Пример: Процесс создания и серийного производства нового вида продукта компаний "НЕВА" включает в себя следующие операции (см. табл. 13).
1. Определим ожидаемое число недель, необходимое для выполнения проекта.
Какие операции являются критическими?
2. Какова вероятность того, что выполнение проекта займет более 16 недель?
Таблица 13. Таблица операций и сроков их выполнения для примера 10
| Опера-ция |
Непосред-ственно, предшест-вующие операции |
Сроки выполнения операций, недель | ||
| Оптимисти-ческий, a | Наиболее вероятный, m | Пессимисти-ческий,b | ||
|
A B C D E F G H I |
- A - C B,D E B,D G F,H |
1,5 2 1 1,5 0,5 1 3 3 1,5 |
2 2,5 2 2 1 2 3,5 4 2 |
2,5 6 3 2,5 1,5 3 7 5 2,5 |
Решение
Ожидаемые сроки выполнения операций и соответствующие дисперсии приведены в таблице 14.
Ниже приведен сетевой граф с указанием ожидаемой продолжительности каждой операции (см. рис. 18).
Расчет ожидаемого срока выполнения проекта в целом производится обычным способом. Как показано на рис. 18, выполнение проекта предполагается осуществить за 15 недель. Критическими являются операции А, В, G, Н и I. Приведем для сравнения другие возможные пути в графе:
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
![]()
![]()
|
|
Рис. 18. Стрелочный граф с указанием ожидаемых сроков выполнения операций для примера 10
|
|
срок события, срок события (ожидаемый срок, дней)
А, В, Е, F, I - занимает 10 недель,
С, D, Е, F, I - занимает 9 недель,
С, D, G, H, I - занимает 14 недель.
Следует отметить, что путь - С,D,G,Н, I - занимает время, которое меньше выполнения критического пути всего на одну неделю. Поэтому небольшие изменения времени выполнения некоторых операций могут привести к изменению критического пути.
Дисперсия ожидаемого времени выполнения всего проекта определяется как сумма дисперсий критических операций:
s2=s2A+s2B+s2G+s2H+s2I
следовательно,
s2= 1/36 + 16/36 + 6/36 +4/36 + 1/36 = 38/36 =1,11 недель2
Стандартное отклонение времени выполнения проекта составит:
![]() =1,03 недель
=1,03 недель
Вероятность того, что выполнение проекта займет более 16 недель, можно найти следующим образом: Шестнадцать недель составляют z стандартных отклонений от среднего, где:
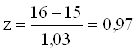
По таблице стандартного нормального распределения находим:
Р (z > 0,97) =0,166.
Следовательно, вероятность того, что выполнение проекта займет более 16 недель, равна 16,6%.
Таблица 14. Расчет ожидаемых сроков выполнения операций и их дисперсий по данным примера 10
| Операция | Ожидаемый срок выполнения |
Дисперсия, недель2 |
|
A B С D E F G I |
2 1 2 4 4 2 |
=1/36 =1/36 =4/36 =16/36 =4/36 =1/36 |
f(T)
 |
|||
15 16 T,недель
Рис. 19. Распределение времени выполнения проекта для примера 10
1.10 Распределение ресурсов
Сетевой граф отражает логическую последовательность выполнения операций, входящих в проект. Ни в одном из видов анализа, рассмотренных нами выше, не принимались во внимание какие-либо ограничения на обеспечение ресурсами. Исходный календарный план выполнения операций составлялся при условии, что все необходимые ресурсы имеются в достаточном количестве. Однако такая ситуация имеет место далеко не всегда, а если это так, то использование ресурсов в соответствии с потребностями, указанными в исходном календарном плане, может оказаться неэкономичным.
Метод составления календарного плана с учетом обеспечения ресурсами зависит от конкретных целей лиц, осуществляющих контроль за ходом выполнения проекта. Например, вопросом первостепенной важности может оказаться завершение проекта к определенному сроку безотносительно к затратам ресурсов - такие планы ограничены по времени. И наоборот, в условиях ограниченности в денежных средствах на выполнение проекта отводится определенное количество ресурсов, тогда как срок выполнения не принимается в расчет - такие планы ограничены по ресурсам. В данном контексте к ресурсам можно отнести рабочую силу, оборудование, сырье, денежные средства, производственные площади и т.д.
Перед тем как приступить к выполнение проекта, управляющий производством должен четко сформулировать критерий, в соответствии с которым будет осуществляться распределение ресурсов. В качестве такого критерия можно выбрать:
1. Максимальное использование ресурсов. Оценить использование ресурсов можно через соответствующий коэффициент:
Коэффициент использования = Общее количество используемых ресурсов
Общее количество наличных ресурсов
2. Минимизацию максимальных потребностей в ресурсах.
3. Минимизацию максимальных изменений потребностей в ресурсах.
Кроме названных, существует множество других критериев. Существует также множество возможных методов решения проблемы распределения ресурсов, таких, как, например, эвристические методы, методы линейного и других видов математического программирования. Рассмотрим один из простейших алгоритмов, в котором используются графики ресурсов и "метод проб и ошибок".
1.11 Графики ресурсов
Если общая потребность в некотором ресурсе определяется на основе постоянных интервалов, например, за один день или за одну неделю, то можно построить график ресурса. Ресурсы, требуемые для осуществления каждой работы, складываются по всем работам, выполняемым одновременно, в предположении, что каждая работа начинается в наиболее ранний срок ее выполнения. Необходимо построить отдельные графики по каждому виду ресурса. На рис. 20 схематично изображен график ресурса "рабочая сила". Как следует из приведенного графика, иногда потребности в рабочей силе превышают ее наличие, но в то же время общее число требуемых человеко-часов не превосходит их наличного количества.
Если потребность в ресурсе превысила его лимит, необходимо либо вложить в проект дополнительное количество ресурса, либо пересмотреть календарный план выполнения операций. Иногда в таких ситуациях необходимо задержать срок выполнения проекта. Несмотря на то, что некоторые операции проекта не имеют явной логически последовательной взаимосвязи, одновременное их выполнение часто оказывается невозможным вследствие ограничений на ресурсы. Это ограничение можно отразить на графике ресурса, если провести линию, соответствующую наличному количеству данного ресурса. Такой прием позволит не планировать выполнение определенных операций на один и тот же период.
![]()
![]() Потребности
Потребности
в рабочей силе
![]()
![]() 20
20
![]()
![]()
![]() 15
15
10 Наличие
![]()
![]()
![]()
![]() 5
5
![]()
5 10 15 20 Время, недели
Рис. 20. График ресурса "рабочая сила"
Пример 11. Компания с ограниченной ответственностью "ТРАСТ" заключила контракт на проведение работ по асфальтированию стоянки автомобилей. Менеджер проекта установил, что данная работа состоит из восьми основных операций. Приведем детальное описание этих операций:
Таблица 15. Операции для примера 11, с указанием сроков выполнения и потребностей в рабочей силе
| Операция |
Предшествующие Операции |
Время, дней | Число человек, требуемое для выполнения операции |
|
A B C D E F G H |
- - - A C B,E C F,G |
3 6 7 8 4 3 10 3 |
1 1 2 2 1 2 2 1 |
Ввиду необходимости срочного выполнения работ на других участках, "ТРАСТ" может выделить только четырех человек для проведения работ на автомобильной стоянке. Определим, сколько времени займет проведение работ и как следует распределить рабочих. Предположим, что каждый из рабочих может выполнять любую операцию.
Решение
Предположив, что все операции начинаются в наиболее ранний срок, построим соответствующий график "рабочей силы". После этого можно составить календарный план выполнения операций, удовлетворяющий ограничению на количество работников. Сначала построим сетевой граф и определим критический путь.
|
|||||
|
|
 4
4
 |
|||||||||||||||||
|
|
||||||||||||||||
|
|
||||||||||||||||
![]()
|
|

 |
|||||
|
|||||
![]()
|
Рис. 21. Стрелочный граф для примера 11
|
|
срок события, срок события (стандартные сроки, дней)
Время выполнения проекта в целом, если не принимать во внимание обеспечение ресурсами, составляет 20 дней. Критический путь выглядит следующим образом: С - G - Н.
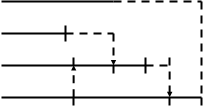
В предположении, что выполнение всех операций начинается в наиболее ранние сроки, посмотрим график Ганта и соответствующий график ресурса. График Ганта отражает распределение резерва времени на момент окончания каждой операции. С его помощью мы можем определить, какие операции выполняются одновременно и по каким операциям можно изменить календарный план их выполнения таким образом, чтобы эти изменения не привели к задержке выполнения проекта в целом.
|
![]()
![]()
![]()
![]()
![]() 5
10 15 20 день
5
10 15 20 день
Рис. 22. График Ганга для примера 11
Из графика ресурса следует, что лимит, равный четырем рабочим, превышается, когда выполнение операции D попадает в промежуток между 3 и 11 днями осуществления проекта. Пересмотреть календарный план и полностью удовлетворить потребности в рабочей силе, соответствующие операции D, нельзя. Для выполнения критических операций С и D требуются два человека, поэтому операция D не может быть начата в течение 17 дней, т.е. до тех пор, пока не закончится выполнение остальных некритических операций.
Если операцию D отложить на 12 дней, то в дни с 12 по 14 потребность в рабочих все еще будет превышать их наличие: в эти дни будут выполняться операции G(2 человека), F(2 человека) и (2 человека). В этом случае придется либо привлечь к работе: одного рабочего дополнительно на указанный период, либо отложить операцию D до момента, когда будет завершена операция F, т.е. до 14-го дня. При последнем варианте будет иметь место задержка в выполнении проекта, равная двум дням. Таким образом, его продолжительность возрастает с 20 до 22 дней.
Потребности
![]()
![]()
![]() в
рабочей силе 5
в
рабочей силе 5
![]()

|
![]() сроков
начала операций 3
сроков
начала операций 3
![]()
![]() 2
2
![]()
![]() 1
1
![]()
5 10 15 20 Дни
Рис. 23. График ресурса для примера 11, соответствующий наиболее ранним срокам начала выполнения операций.
Заключение
Сетевой анализ используется при разработке и планировании проектов. Он предполагает разбиение проекта на отдельные виды работ или операции. Логическая взаимосвязь между операциями изображается с помощью сетевого графа. На основе значений сроков выполнения операций производится расчет общей продолжительности проекта, возможных сроков начала и окончания каждого вида работ и определяются операции, принадлежащие критическому пути.
Операции в сетевых графах можно изображать либо с помощью стрелок, либо с помощью узлов. Альтернативным методом изображения сети операций является график Ганта, в котором используется шкала времени.
В большинстве проектов определенные виды работ могут быть выполнены в более сжатые сроки, однако, это требует дополнительных затрат. Соответствующие показатели называются критическими сроками и критическими затратами. Они могут использоваться при составлении календарных планов реализации проектов за "минимальное время" или с "минимальной стоимостью".
Сроки выполнения операций могут быть подвержены влиянию неопределенности. В этом случае для анализа проекта можно использовать метод оценки и пересмотра проектов (РЕRТ), основанный на предпосылке об аппроксимации сроков выполнения операций р-распределением с минимальным значением а, наиболее вероятным значением m и максимальным значением b. Ожидаемая продолжительность операции в методе РЕRТ рассчитывается по следующей формуле:
![]() , а соответствующая дисперсия равна
, а соответствующая дисперсия равна 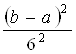
Продолжительность выполнения проекта имеет нормальное распределение, среднее значение которого равно сумме значений ожидаемых сроков выполнения операций, принадлежащих критическому пути. Дисперсия данного нормального распределения есть сумма дисперсий критических операций. Распределение времени выполнения проекта в целом используют в расчетах вероятности завершения проекта к заранее заданному сроку.
В анализ проектов можно включить также вопросы, связанные с наличием и распределением ресурсов. Для определения направлений пересмотра календарного плана выполнения операций и достижения конкретной цели применяются графики Ганга и графики ресурсов.
Упражнения
Упражнение 1
Компания с ограниченной ответственностью "МR" разрабатывает строительный проект небольшого масштаба. Основные операции проекта, соответствующие им непосредственно предшествующие операции и время их выполнения приведены в таблице:
| операция | Непосредственно предшествующая операция | Продолжительность, недель |
|
A B C D E F G |
- - A,B B C D E,F |
4 6 7 3 4 5 3 |
Требуется:
1. Дать иллюстрацию проекта с помощью стрелочного сетевого графа.
2. Определить критические операции и общую продолжительность выполнения проекта.
Упражнение 2
Используя данные упражнения 1:
1. Дать иллюстрацию проекта с помощью вершинного графа;
2. На основе графа, построенного в п.1, определить влияние на ход выполнения проекта задержки операции D на четыре недели.
Упражнение 3
В Чартерском Институте подготовки специалистов по принятию количественных решений (СIQDМ) действует ежегодная программа чтения лекций сотрудникам института. Подготовка программы на следующий год ведется сотрудниками ректората института, начиная с осени предыдущего года. Эта программа содержит детальные сведения о лекторах и их лекциях, а также список членов института. Ниже перечислены операции, входящие в процесс подготовки программы, с указанием соответствующих непосредственно предшествующих операций.
Операция |
Носредствен-но предшест-вующая операция | Стан-дартное время, дней | Крити-ческое время, дней | Дополни-тельные издежки, руб. |
|
А Выбор дат проведения лекций В Назначение лекторов и согласование лекционных тем С Подготовка для программы рекламных материалов D Обновление списка студентов, обучающихся заочно Е Подготовка списка оплачиваемых сотрудников F Распечатка программы и списка членов на принтере G Корректировка напечатанных программы и списка членов Н Печать и раскладка программы по экземплярам I Получение распечатанного на компьютере списка адресов членов института J Рассылка программы |
- A - - D B,C,E F G E H,I |
5 20 15 15 30 10 10 15 5 5 |
5 10 10 5 25 5 5 10 2 2 |
- 100 150 200 50 100 50 75 50 50 |
Если в процессе подготовки программы будет занято стандартное число сотрудников ректората, соответствующее штатному расписанию, то, как было оценено, каждая операция будет выполнена в указанные выше стандартные сроки. При этом предполагается, что управленческий персонал работает 5 дней в неделю. Сколько существует возможность принять на работу несколько временных работников дополнительно в помощь основному персоналу на этот период. Продолжительность выполнения операций в этих условиях определяется критическими сроками, значения которых, а также соответствующие значения дополнительных издержек, связанных с выполнением операций в критические сроки, указаны выше. Для простоты расчетов предполагается, что все операции могут быть выполнены только либо в стандартные, либо в критические сроки.
Требуется:
1. Изобразить данный проект с помощью сетевого графа.
2. Определить общее время, требуемое для подготовки и рассылки программы, при условии, что временные работники не будут приняты на работу в этот период. Какие операции являются критическими?
3. Каково влияет на общую продолжительность проекта тот факт, что время, необходимое, мое для получения рекламных материалов, было оценено неправильно, и на самом деле данная операция занимает 30 дней?
4. Каково значение возможного наименьшего срока, к которому можно закончить подготовку и рассылку программы? Какова минимальная дополнительная стоимость завершения проекта к этому сроку?
Упражнение 4
Компания с ограниченной ответственностью "Верикс" выполняет заказ, полученный от ее потребителя. Необходимая информация приведена ниже
Операция |
Непосредст-венно предшест-вующие операции | Срок, дней | Стоимость для ожидаемой продолжительности, руб. | ||
| Оптимистический | Наиболее вероятный | Пессимистический | |||
|
A B C D E F G H |
- - - A B C D,E G,F |
3 4 4 5 2 10 3 1 |
4 7 5 6 2,5 10,5 4 2 |
5 10 6 7 6 14 5 9 |
1000 1400 2000 1200 900 2500 800 300 |
Косвенные издержки, связанные с выполнением проекта, составляют 300 руб. в день. В контракте, заключенном с потребителем, оговорено, что если заказ не будет выполнен в течение 15 дней, сумма штрафа составит 100 руб. за каждый последующий день.
Требуется:
1. Построить сетевой граф. Каково ожидаемое значение времени выполнения всего проекта? Каково значение соответствующей стоимости?
2. Какой путь в графе является критическим? Прокомментируйте продолжительности некритических путей.
3. Какова вероятность того, что проект будет завершен без выплаты штрафов?
Упражнение 5
Компания "Гомер" намерена учредить дочернюю издательскую компанию. В нижеследующей таблице приведены необходимые операции, их взаимозависимости и продолжительность.
| операция |
Непосредственно предшествующая операция |
Продолжитель-ность, недель |
|
A B C D E F G H I J |
- A A A B D D G C,E,F G,I |
3 4 2 6 3 2 4 7 5 3 |
Требуется:
1. Определить ожидаемое время выполнения проекта в целом.
2. В предположении, что для выполнения каждой операции в установленные сроки требуется один человек, определить скорректированную ожидаемую продолжительность проекта при условии, что в распоряжении компании для выполнения данной работы имеются только два человека, каждый из которых может выполнить любую из операций.
Упражнение 6
Администрация компании "Сатурн" собирается реализовать исследовательский проект по изучению характеристик нового продукта. Итогом выполнения проекта должен быть отчет, содержащий рекомендации по выпуску нового продукта. Ниже приведены операции, которые необходимо осуществить в процессе выполнения исследовательского проекта.
Требуется:
1. Построить сетевой граф, отражающий приведенные выше операции и их взаимосвязи. Определить критический путь и наименьшую продолжительность выполнения проекта.
2. В предположении, что началом выполнения проекта служит нулевой момент времени, а каждая операция начинается с наиболее раннего срока, построить график, изображающий потребности в персонале на любой момент времени.
3. Администрация компании приняла решение, что на выполнение изложенного проекта в любой момент времени будет выделено не более 9 человек персонала. Опишите, как следует выполнять проект в данных условиях за наименьшее время. В течение какого количества недель в выполнении проекта будут участвовать все 9 человек персонала?
| Операция | Описание | Непосредст-венно предшест-вующие операции | Ожидаемое время выполнения, недель | Потребности в персонале |
|
A B C D E F G H I J |
Первичные разработки Исследование рынка Получение технических стандартов Создание образца Подготовка рыночной базы Расчет стоимости Испытание продукта Выборочный контроль Оценки цены Итоговый отчет |
- - A A A C D B,E H F,G,I |
5 3 2 5 3 2 4 6 2 6 |
3 2 2 5 3 2 5 4 1 2 |
Упражнение 7
1 сентября каждого года администрация компании с ограниченной ответственностью "Селком" составляет бюджет на следующий год. Было установлено, что процесс составления бюджета включает в себя следующие этапы (см. таблицу).
Составление бюджета необходимо закончить к концу декабря, таким образом, администрация располагает периодом в 17 рабочих недель.
Требуется:
1. Построить сетевой граф, отражающий последовательность выполнения этапов, включенных в подготовку бюджетов. Можно ли закончить данный процесс в течение 17 недель?
2. Если бы потребовалось сократить время, отведенное на составление бюджетов, на какие этапы следовало бы обратить внимание и почему?
3. Объясните различие между понятиями общего, свободного и независимого резерва времени. Докажите, что свободный резерв времени этапа 1 равен трем неделям, причем две из них - это независимый резерв времени.
| Этап | Предшествующие этапы | Время, недель |
|
А Оценка ставок заработной платы В Разработка прогнозов рынка С Определение цен продаж D Составление бюджета для объемов продаж Е Составление бюджета доходов от продажи F Составление бюджета расходов по продаже G Составление бюджета объемов производства Н Составление бюджета накладных расходов I Составление бюджета трудовых ресурсов J Составление бюджета сырья К Составление бюджета производственных площадей и оборудования L Выработка прогноза общей прибыли |
- - - B C,D A,D D A A,G G G E,F,H,I,J,K |
2 4 3 3 1 3 6 4 2 3 5 1 |
Упражнение 8
Некоторый проект включает в себя 10 операций, продолжительность и взаимосвязи которых указаны ниже.
Продолжительность операций F и Н является неопределенной, поскольку на данной стадии её оценка вызывает некоторые затруднения.
Требуется:
1. Построить соответствующий сетевой граф, отражающий взаимосвязи между 10 операциями.
2. Определить минимальное время, требующееся для реализации проекта, не учитывая при этом влияние операций F и Н.
3. Если бы возникла необходимость закончить выполнение проекта за 19 дней, какие ограничения накладывало бы это условие на продолжительность операций F и H?
4. После проведения дальнейших исследований было установлено, что ожидаемыми сроками выполнения операций F и Н являются два дня и один день соответственно. Кроме того, можно предположить, что неопределенность в продолжительности этих двух операций можно аппроксимировать с помощью распределения Пуассона. Исходя из этой информации, найдите вероятность того, что выполнение проекта займет не более 19 дней. В нижеследующей таблице приведены некоторые значения вероятностей, соответствующие распределению Пуассона:
Среднее значение, m |
Вероятность | ||||
| 0 | 1 | 2 | 3 | 4 и более | |
|
1 2 |
0,368 0,135 |
0,368 0,271 |
0,184 0.271 |
0,061 0,180 |
0,019 0,143 |
Операция |
Продолжительность, дней | Непосредственно предшествующие операции |
|
A B C D E F G H I J |
6 1 2 1 1 1 4 5 |
- A A B D B C F,G E,H I |
Упражнение 9
Фирма "Джилет" выпускает ряд средств для ухода за волосами и для бритья, включая опасные бритвы. Ее конкурент организовал недавно производство нового вида опасных бритв, которые за последние шесть месяцев приобрели большую популярность на потребительском рынке, что оказало обратное воздействие на объемы продаж фирмы "Джилет". Администрация приняла решение о скорейшем внедрении в производство конкурентоспособной продукции и поручила главному бухгалтеру составить план разработки нового продукта и внедрения его на потребительский рынок.
Первый шаг, предпринятый бухгалтером при разработке этого проекта, состоял в определении основных задач, которые необходимо решить в процессе создания нового продукта. Эти задачи перечислены ниже. Он произвел также оценку времени, которое займет решение каждой задачи, и выявил задачи, которые ей предшествуют.
1. Постройте сетевой граф, отражающий логическую последовательность решения указанных задач, и определите, какой период времени пройдет с момента разработки плана до налаживания серийного выпуска новой продукции (можно предположить, что выпуск продукции на национальном уровне будет иметь место сразу же после составления его плана).
| Задача | Время, недель | Предшествующие задачи |
|
А Создание новой продукции В Создание упаковки С Подготовка производственных мощностей D Получение сырья и материалов Е Выпуск опытной партии продукции F Упаковка G Принятие решения о выборе пробного рынка сбыта Н Упаковка опытной партии I Поставка продукции на пробный рынок сбыта J Продажа продукции на пробном рынке сбыта К Оценка результатов внедрения продукции на рынок L Планирование выпуска продукции на национальном уровне |
8 4 4 2 3 2 1 2 3 4 3 4 |
- - A A C,D B - E,F H,G I J K |
2. Рассчитайте значения резерва времени, соответствующие каждой из некритических операций.
3. Время, которое потребуется для выполнения задач А, В, D, К и L, подвержено влиянию неопределенности, поэтому для получения наиболее вероятных значений сроков выполнения этих операций, которые приведены выше, были разработаны следующие оценки оптимистических и пессимистических сроков:
| Задача | Оптимистический срок, недель | Пессимистический срок, недель |
|
A B D K L |
5 2 1 2 2 |
13 6 4 6 8 |
С учетом приведенной выше информации определите ожидаемое время, которое пройдет до момента серийного выпуска продукции, и вероятность того, что этот период превысит 35 недель (следует ввести предпосылку о том, что продолжительность проекта в целом аппроксимируется нормальным распределением).
2. МЕТОД ПРОГНОЗНОГО ГРАФА
Этот метод предложен академиком В. М. Глушковым на основе обобщения, с одной стороны, упомянутого выше метода Дельфы, а с другой — метода сетевого планирования и служит для определения вероятности наступления тех или иных событий и оценки вероятного их наступления. Практическую реализацию он получил в методике, разработанной коллективом авторов и утвержденной Госкомитетом по науке и технике Совета Министров СССР.
Метод прошел проверку при прогнозировании развития широкого комплекса научно-технических работ в области технических средств систем обработки информации.
Согласно ему строится сеть взаимосвязанных событий (целей) — прогнозный граф, служащий основным материалом для выявления и анализа возможных путей решения генеральной цели научно-технической политики в той или иной области, сформулированной исходя из общегосударственных интересов.
Рассмотрим последовательность разработки научно-технического программного прогноза с помощью данного метода.
Прежде всего, составляется перечень конечных целей (набор проблем или типов событий) S1, S2,....,Sm, оценка достижения которых составляет задачу прогноза.
Всем целям априорно ( способом, изложенным ниже ) придаются веса a1, a2,..., ak в соответствии с их относительной значимостью для достижения генеральной цели.
Затем составляется предварительный список промежуточных целей Sm+1, Sm+2,..., Sm+n и предварительный граф их соподчиненности. Для этого экспертам в отношении каждой из целей Sl (l=l,2,..,m) задается вопрос: укажите промежуточные цели Sl1 , Sl2,.. ., Slnj, которые было бы полезно достичь для ускорения достижения цели Sl. Здесь nj- означает число промежуточных целей, выдвинутых экспертом j для решения цели l, причем j=1,2,... , Si, где ki — количество экспертов, оценивающих цель Sl. Для каждой из целей количество промежуточных целей равняется:
kl
ni =∑ nj
j=1
![]() С расширением списка
промежуточных целей такой же вопрос задается в отношении каждой из них,
поскольку каждая промежуточная цель в свою очередь является исходной проблемой
для промежуточных целей следующего уровня.
С расширением списка
промежуточных целей такой же вопрос задается в отношении каждой из них,
поскольку каждая промежуточная цель в свою очередь является исходной проблемой
для промежуточных целей следующего уровня.
Определение промежуточных целей для каждой цели Si (i=l, 2,...,m,m+1,...,m+n) продолжается до тех пор, пока не появятся цели, для которых нет соответствующих промежуточных целей (либо проблема решена, либо не может быть решена — не видно путей ее решения).
В итоге составляется предварительный список промежуточных целей.
Соединяя стрелками каждую из промежуточных целей Sl1 , Sl2,.. ., Slnj, полезных для достижения цели Si (i=l, 2,...,m+n), с этой последней целью, получаем предварительный граф подчиненности. Основой построения его служат логические связи: промежуточные цели Sl1 , Sl2,.. ., Slni —>эксперт Эj (который выдвинул эти промежуточные цели для решения цели Si)——> цель Si.
Графически эти связи изображаются в виде ориентированных дуг, направленных от промежуточных целей к эксперту (выдвинувшему эти цели) и от эксперта к соответствующей исходной проблеме.
Ориентированные дуги графа интерпретируют работы, а вершины графа — цели экспертов. Таким образом, предварительный граф соподчиненности промежуточных целей; другими словами, множество предварительных предпосылок для всех целей Si (i=l,2, ...,m+n) представляет собой многоуровневую иерархическую структуру с общим числом вершин:
M=m+n+k,
где М — общее число вершин в графе;
m+n — число исходных проблем и промежуточных целей;
k — количество экспертов.
На следующем этапе привлекается широкий коллектив экспертов, который разбивается на относительно небольшие подгруппы для оценки каждой из целей S1, S2,...,Sm+n. Каждому из экспертов, оценивающему цель Si посылается анкета с формулировкой этой цели и списком всех ее предварительных предпосылок. Из этого списка эксперт должен выбрать те цели, достижение которых он считает непременным условием для достижения цели Si(i= 1,2, . . . ,m+n), и дополнить его недостающими на его взгляд целями.
Назовем совокупность всех промежуточных целей, выставленных экспертом j для цели i, предпосылкой ij.
Эксперт оценивает время, необходимое для достижения цели Si при условии, что все цели предпосылки ij уже достигнуты. Эта оценка (обозначим ее через tij), как и в методе Дельфы, предполагает возможность бесконечного значения, т. е. цель никогда не может быть достигнута. Разумеется, в этом случае предпосылка ij предполагается пустой. Кроме того, эксперт дает качественную оценку своей компетентности (применительно к данной цели) и степени уверенности в своем прогнозе. Эти оценки переводятся в весовые коэффициенты βij и γij, произведение которых βij - γij = δij представляет собой вес данного единичного прогноза.
Эксперту предлагается также назвать фамилии нескольких специалистов, которых он считает целесообразным привлечь для прогноза по событию Si (i=1,2,...,m+n). Те эксперты, фамилии которых были указаны их коллегами, получают добавку Δβij к самооценке своей собственной компетентности βij тем большую, чем чаще упоминались их фамилии. Теперь необходимо для каждой цели Si определить предпосылки с набором оценок. В общем это должно выполняться периодически (например, один раз в полтора года).
Заполненные анкеты обрабатываются, строится граф соподчиненности целей. Для любого эксперта j, оценивавшего цель Si, все цели предпосылки ij соединяются стрелками с целью Si аналогично тому, как было описано.
Построенный граф проверяется на отсутствие циклов. Если в нем оказываются петли, то их устраняют, проведя дополнительную работу с экспертами (хотя в ряде случаев можно работать и с неустранёнными петлями). Так в конце концов получается прогнозный граф.
Систематизируя полученный в результате проведения экспертизы массив исходных данных, выявляют адекватные условия, объединяют некоторые условия в одно, а также искусственно заземляют часть условий в графе, после чего начальные данные и связи в графе кодируются для машинной обработки.
Анализ прогнозного графа включает в себя:
1) поиск циклов и тупиковых событий в прогнозном графе;
2) ранжирование событий в прогнозном графе;
3) вычисление вероятностных и временных характеристик;
4) варьирование вероятностных и временных характеристик.
События в прогнозном графе (т. е. вершины его, соединенные дугами) — это проблемы (исходные и промежуточные цели) и эксперты.
Граф должен удовлетворять следующим условиям:
- в нем не должно быть событий, из которых не выходит ни одной связи, если только эти события не завершающие (имеющие пустые предпосылки ij);
- в нем не должно быть событий, в которые не входит ни одной связи, если только эти события не исходные цели (проблемы);
- в нем не должно быть замкнутых контуров, т. е. не должно быть связей, соединяющих какое-либо событие с ним же самим;
- в нем не должно быть событий, имеющих одинаковые шифры. Поэтому первое, что следует сделать при анализе графа, — выявить все ошибки, допущенные при его составлении.
Рассмотрим порядок поиска тупиковых событий и циклов. Событие, в которое не входит ни одна работа и которое не является исходным событием для данного графа, называется тупиковым событием первого рода. Событие же, из которого не выходит ни одна работа и которое не является конечным для данного графа, является тупиковым событием второго рода.
Исходная информация формируется в виде некоторого массива (событие и связи — работы), затем путем последовательного выбора кодов связи и выделения из них кодов начальных событий создается новый массив, содержащий начальные события с признаками работ, исходящих из этих событий. Наконец, выделяются конечные события, их включают в сформированный массив с признаками работ, входящих в данные события.
После пересмотра всех связей-работ входной информации сформированный массив будет включать все события графа с соответствующими признаками входящих и исходящих связей. При этом признаки тупиковых событий первого и второго рода примут, например, соответственно следующий вид: 01 и 10. Признаком кодов всех нетупиковых условий будет в этом случае сочетание 11. В результате просмотра признаков всех событий, записанных в сформированный массив, выявятся тупиковые события первого и второго рода.
Согласно данному алгоритму начальные и конечные события графа снабжены соответствующими признаками.
Допустим, имеется прогнозный граф с М вершинами и N дугами. На вершинах m=l,2,... , М данного графа определяется функция
![]() 1, если вершина принадлежит контуру или пути,
начинающемуся
1, если вершина принадлежит контуру или пути,
начинающемуся
φ(m)= на контуре;
0, в противном случае.
Вычисляют φ(m) рекуррентным образом при пoмощи последовательности
Вспомогательных функций ψk(m) ≤ ψk-1,m=1,2,…,M сходящейся к φ(m): ψk0(m)≡ ψk0(m)≡ φ(m) при некотором конечном k0. Строится функция ψk(m) следующим образом.
Положим ψ0(m) ≡ 1, a ψk-1(m) вычислена. Вычисляем ψk(m) следующим образом: последовательно просматриваем список дуг (i, j), i и j — начало и конец дуги. Если ψk-1(i) = 0, то переходим к следующей дуге. В противном случае если ψk-1(i)=1, то ψk(j)=1. Всем ψk(m), не определенным после полного просмотра списка дуг, приписывают значение 0.
Рассмотрим геометрический смысл этого рекуррентного построения. Первоначально значение ψ1(m) = l получает каждая вершина, в которую входит хотя бы одна дуга. Следовательно, ψ1(m) = 0 на тех вершинах, куда не входит ни одна дуга. Эти вершины исключаются из дальнейшего рассмотрения, так как они не могут лежать на контуре или на пути, выходящем из контура.
Граф сокращается за счет исключения дуг, выходящих из начальных вершин (т. е. вершин, не имеющих входящих в них дуг). Но в нем появляются новые начальные вершины, поскольку из графа исключаются все незамкнутые пути, выходящие из начальных вершин (т. е. мы подойдем к контуру, если он имеется в графе).
Если φ(m)=0 (т=1, 2,...,М), то контуров в графе нет. Если же φ(m)≠0, то граф содержит контуры. В этом случае строится функция:
![]() 1, если вершина принадлежит контуру или пути,
начинающемуся
1, если вершина принадлежит контуру или пути,
начинающемуся
φ*(m) = на контуре;
0, в противном случае.
Чтобы вычислить функции φ*k, нужно построить последовательность по дугам с обратной ориентацией точно так же, как последовательность ψk.
Вершины, в которых ф(т)=ф*(т)=*1, принадлежат одному из контуров.
Рассмотрим порядок ранжирования событий в графе с целью преобразования исходной информации к виду, удобному для вычисления временных и вероятностных характеристик. Используем для этого одну из модификаций стандартных способов ранжирования событий, применяемых в сетевом планировании.
Множество событий в графе разбивается на слои, начиная с уровня событий, не имеющих предпосылок i,j (так называемая «земля» — события класса ko). Событие Si принадлежит уровню ρ, если все его предпосылки принадлежат меньшим уровням и хотя бы одна — в точности уровню ρ — 1 (ρ = 1, 2, . . . , q, . . . ), начиная с «заземленного уровня» (класс k0), q — число уровней в графе).
Вычисление временных характеристик производят по следующей формуле:

![]() где t(Si) — время свершения
события S,
графа;
где t(Si) — время свершения
события S,
графа;
tj — время свершения события Si согласно варианту эксперта j (j=l, 2, . . ., Ri);
Vj — вес эксперта j;
Ri — количество экспертов, оценивающих событие Si в графе (i= 1, 2, . . . , т+п).
Временные характеристики для каждого варианта (эксперта j) определяются так:
tj(Si) =max t(Sir)+tij ,
где tj(Si) — время реализации проблемы Si согласно варианту эксперта j;
t (Sir) — время свершения выдвинутых экспертом j условий SirÎj предпосылке;
tij — условное время, заданное экспертом;
Sir — событие, входящее в предпосылку i,j цели Si (r =l, 2,..., nj).
Аналогично (с незначительными изменениями) вычисляются и стоимостные характеристики.
Вероятностные характеристики рассчитывают следующим образом.
1. Вероятность свершения условий, выдвинутых Эj экспертом при наличии значения абсолютных вероятностей событий «заземленного уровня» (пустые ij — предпосылки):
Pэj (Sir) =P(Si1 Λ Si2 Λ … Λ Sinj)=pi1 · pi2 ·… ·pinj ,
где pi1 , pi2 ,… ,pinj — абсолютные вероятности свершения отдельных условий, выдвинутых экспертом j;
nij — количество условий, выдвинутых j-м экспертом; Pэj (Sir) — вероятность выполнения ij предпосылки.
2. Pэj (Sir) — вероятность свершения события Si анализируемого экспертом j при предпосылке ij;
pij — условная вероятность, выставленная Эj экспертом:
pэj (Si)= pэj (Sir) pij .
3. Для всех пар экспертов определяются условные вероятности:
![]()
где p(Эp/Эl) вычисляется по общим формулам теории вероятностей. Например:
Si=(Э1 (S2 , S3 , S4) , Э2 (S3 , S4, S5) ) ;
p (Э1 Λ Э2) =p ( (S2 Λ S3 Λ S4) Λ (S3 Λ S4 Λ S5) ) = p(S2Λ S3 Λ S4Λ S5) =
= p2 ·p3 ·p4 ·p5;
![]()
Если для какой-либо пары экспертов p(Эр / Эl) или р(Эl/Эр) ≥0,5, то производится усреднение вероятностей по формуле:
V рÚ l = min(Vр, Vl)

(p, l = 1, 2, … ,k).
После этого присваивается
![]() p(Эp), если p(Эp/Эl)£ р(Эl/Эр) ;
p(Эp), если p(Эp/Эl)£ р(Эl/Эр) ;
p(Эр Ú Эl) =
p(Эl) в противном случае.
Заметим , что усреднение начинается с тех пар экспертов , которые имеют максимальное значение условных взаимных вероятностей (среди равнозначных порядок безразличен).
Значение p Э рVЭ l и Vp Vl рассматривается как данные нового эксперта (вероятность и вес эксперта). Оценка p(Эр Ú Эl) служит для переноса ранее полученных значений условных вероятностей на нового эксперта. Оба первичных эксперта из процедуры исключаются. Если после проведения всех усреднений остается один эксперт, то значение p Э рVЭ l , полученное после усреднения последней пары, присваивается p(Si). Если остается более одного эксперта, то оценка p(Si ) вычисляется по формуле
r
p(Si ) = 1-П (1- pρ ),
ρ=1
где r - число оставшихся экспертов;
pρ - вероятности оставшихся экспертов (ρ = 1, 2, . . . ,r), что в предыдущих обозначениях соответствует рЭру Эl (не надо путать ее с оценкой p(Эp v Эl);
p(Si )- вероятность свершения события Si , анализируемого экспертами j (j=1, 2, . . . , ki ).
На практике при проведении экспертизы по методу прогнозного графа оказалось, что экспертам довольно трудно осуществить оценку вероятности, поэтому было признано целесообразным перейти к одной оценке — по времени, сделав оценку производной от него.
Для каждой цели Si(i=l,2,...,т+п) находится экспериментальный закон распределения вероятности Pi(t) ее достижения не позже, чем на время t (считая от настоящего момента).
С этой целью должна быть решена система уравнений

где pi (t) — закон распределения вероятности достижения цели S к времени t;
pijr(t) — закон распределения вероятности времени достижения промежуточных целей Sir, входящих в ij предпосылки цели Si;
tij — относительная оценка времени свершения целей при условии выполнения ij предпосылок;
i = 1, 2,..., (m + n) (m + n — количество событий в графе);
j =1, 2, . . ., Ri (Ri — количество экспертов, участвующих в оценке цели);
r=1, 2, . .., пj (пj — число промежуточных целей, входящих в предпосылку ij);
δij = βij - γij — вес соответствующего предсказания;
βij — оценка собственной компетентности эксперта;
γij — степень уверенности в прогнозе.
Суммы в числителе и знаменателе распространены на всех экспертов, принимавших участие в оценке цели Si. Граф соподчиненности называется правильным, если из этой системы уравнений однозначным образом могут быть найдены все функции pi (t).
Так, в частности, будет, если все цели разбиваются на непересекающиеся классы k0, k1,..., ki таким образом, что предпосылки ij для цели Si из некоторого класса kr (r=0,1,...,l) могут состоять лишь из целей, принадлежащих kp<p<_r. Для класса k0 это означает, очевидно, отсутствие каких-либо предпосылок. Зависимость pijr(t - tij) определяют исходя из абсолютных оценок вероятности свершения, которые задаются для заземленных событий (класса k0). Данное уравнение для событий этого класса приобретает форму:
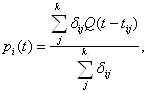
где Q(x) — функция, равная нулю при отрицательных значениях аргумента и равная единице при нулевом или положительном аргументе.
Член δijQ(t - tij) появляется в сумме всякий раз, когда эксперт j дает оценку времени tij достижения цели Si, не сопровождая ее никакими условиями (с пустой предпосылкой ij).
Оценки времени в прогнозах обычно даются лишь целыми числами (дней, месяцев или лет). При этом функцию распределения pi (t) удобно задавать векторами pi (1), pi (2),..., pi (τ), где τ — первое значение tij , для которого pi (t) достигает максимального значения (обычно это значение равно единице).
Для найденных экспериментальных распределений находятся обычные статистические характеристики: средние значения (или медианы), среднеквадратичные отклонения (или квартили). Так как распределение несимметрично, в ряде случаев необходимо рассматривать левые и правые среднеквадратичные отклонения.
Среднее значение для распределения pi(t) вычисляется по формуле
∞
Ei = ∑ τ (pi (τ) - pi (τ - 1)),
τ =1
Для нахождения медианы Mi и расстояний от медианы до квартилей pi ' и qi" предполагается, что между указанными значениями в целочисленных точках функции распределения меняются по линейному закону.
Мерой уточнения прогноза по какой-либо цели Si может служить абсолютная величина приращения какой-либо меры разброса распределения pi(t) , например его среднеквадратичного отклонения σi. Минимальный разброс получается, если распределение pi(t) заменить распределением p'i(t)=Q(t — Ei), т. е. таким распределением, что pi'(t)=0 при t< Ei и pi'= 1 при t ≥ E.
Коэффициентом информационной значимости цели Si служит величина

где Disk — приращение, получаемое среднеквадратичным отклонением распределения pk(t) при замене распределения pi(t) на распределение
p'i (t) =Q(t - Et).
Сумма берется по всем конечным целям.
К понятию информационной значимости приближается понятие важности (по срокам) промежуточной цели. Коэффициентом важности (по срокам) цели t называют величину

где ak — относительный вес конечных событий,
DiEk — приращение математического ожидания времени достижения Sk – й (конечной) цели при условии сдвига на одну единицу влево распределения pi(t), т. е. при замене функции pi(t) функцией pi(t+1).
Приведенные коэффициенты имеют большое значение при переводе прогнозов в план. Планом достижения цели является любой подграф прогнозного графа, построенный следующим образом: первая вершина плана — цель Si ; далее выбирается одна из предпосылок ij; Si1, Si2,..., Sinj и для каждой из них повторяется тот же процесс, что и для вершины Si, пока не перестанут получаться новые вершины. Все построенные таким образом вершины (кроме Si) называют промежуточными целями данного плана.
Поскольку в общем случае цель может обладать многими планами для ее достижения, то на множество планов для достижения любой данной цели вводят понятие близости, определив тем или иным методом расстояние между планами. В работе дается одно из возможных определений: расстояние z (А1,A2) между двумя планами А1 и А2 принимается равным
z(А1 , А2) = 1 – N1 / N2 ,
где N1 — число элементов в пересечении множеств целей планов А1 и А2;
N2 – число элементов в их объединении.
Получив близкие планы, производят повторную экспертизу, направленную на то, чтобы сделать их полностью совпадающими. Если в результате подобных действий для какой-нибудь конечной цели удалось получить единственный план, то можно принять его в качестве обобщенного сетевого графика для организации фактической работы (достижения данной цели).
Когда же получить единственный план не удается, возникает проблема выборов в множестве активных планов. Критерием такого выбора может послужить, например, то, что подавляющее большинство экспертов склонилось к какому-то одному плану, причем между ними имеется и большее согласие по срокам достижения цели. Признаком такого согласия может служить малая величина разброса распределения pi(t) для конечной цели данного плана, вычисленного по тем предсказаниям, которые укладываются в рамки рассматриваемого плана.
Если проблему выбора решить не удается, то можно осуществить частичный перевод прогноза в план, в каком-то смысле наилучший с точки зрения достижения поставленных целей. Для этого во множестве промежуточных целей, для которых проблема выбора может быть решена, выбираются цели с максимальными значениями коэффициентов важности и для них осуществляется перевод частей прогнозного графа в сетевые графики.
Коэффициент информационной значимости необходим для выбора тех промежуточных целей, на которые в первую очередь следует обратить внимание с точки зрения уточнения прогноза. В соответствии с этим коэффициентом строится и вся последующая работа с экспертами: увеличивается, скажем, число экспертов по целям с большой информационной значимостью; экспертов снабжают дополнительной информацией и так далее.
Основой получения исходных данных для проведения соответствующих прогностических расчетов служат таблицы экспертных оценок. Их форма должна обеспечить наиболее быстрый и полный сбор информации. Состоят они из нескольких частей.
Первая часть содержит обращение к эксперту с целью ввести эксперта в сущность работы, к которой он привлекается. Кратко описываются цель и задачи применяемой методики прогнозирования, роль эксперта в ее реализации. Желательно, чтобы эксперт поставил себя в положение непосредственного участника событий. Следует порекомендовать эксперту, не ограничиваться лишь сферой своей специальности, смело выдвигать предложения и требования даже за рамками компетентности. Строго оговаривается необходимость четкости и ясности формулировок.
Вторая часть содержит описание проблемы, предлагаемой эксперту для анализа.
Третья представляет собой набор научно-технических условий и оценок, выдвигаемых экспертом. Тут же эксперту предлагается назвать других специалистов, которые могли бы взяться за осуществление сформулированных условий, для каждого условия в отдельности. Каждое условие или набор условий, выдвинутых экспертом, оценивается им по нескольким параметрам.
Рекомендуется оценивать следующие основные параметры:
1) промежуток времени (Т) в годах от момента выполнения выдвинутых экспертом условий до решения рассматриваемой проблемы;
2) затраты на решение предложенной проблемы без учета затрат на осуществление условий: форма задания оценок затрат должна позволять экспертам однозначно понимать смысл этих оценок, что значительно уменьшает разброс значений экспертных оценок;
3) степень уверенности эксперта в решении прогнозируемой проблемы на основе выдвинутых им условий;
4) стадия разработки предложенной для оценки проблемы.
Временные оценки (1 и 4), оценки затрат (2) служат критериями выбора путей решения проблем. Оценка степени уверенности (3) используется как весовой коэффициент при оценке вероятности реализации какой-либо проблемы к определенному сроку и также служит в известной мере критерием отбора путей решения проблем.
Конкретная прогнозная разработка определяет количество основных и дополнительных параметров и формы их задания.
Экспертные оценки условий и параметров объекта прогнозирования служат основными исходными данными для информационно-логических и количественных расчетов. Кроме того, эксперту предлагается сформулировать организационно-экономические условия, необходимые для решения проблемы, а также замечания и особое мнение.
Опрос экспертов с целью построения прогнозного графа проводится в несколько туров, в ходе которых события и логические связи уточняются и детализируются.
Задача первого тура экспертизы — составление предварительного списка промежуточных целей и предварительного графа их соподчиненности для реализации сформулированной исходной проблемы. Эксперты для решения этой задачи отбираются исходя из каталога специалистов, составленного в результате предварительного исследования предпрогнозной ориентировки. Этот отбор в зависимости от характера объекта прогнозирования может проводиться как эвристически, так и с привлечением формальных процедур.
В итоге проведения его получают набор условий, на основе анализа которых составляется предварительный список промежуточных целей.
В процессе обработки и сравнительного анализа дополнительных данных (зарубежных прогнозов, результатов других методов прогнозирования, например экстраполяции, и т. д.) список промежуточных целей может быть расширен. Окончательная форма, в которой должны быть представлены промежуточные цели, зависит от характера объекта прогнозирования. Такой формой может быть список промежуточных целей в виде классификатора первого тура как один из возможных вариантов структуры прогнозируемого объекта (системы, устройства и т. д.). В процессе формирования этого списка определяются диапазоны значений характеристик для каждой из промежуточных целей.
Таким образом, результатом первого тура экспертизы является граф соподчиненности и список промежуточных целей. Последние служат объектом при проведении экспертизы второго тура.
К участию во втором туре экспертизы привлекается более широкий круг экспертов, нежели в первом: ведущие специалисты в соответствующих областях науки и техники. Эта группа экспертов формируется на основе рекомендаций экспертов начальной группы; используются и данные вышеупомянутого каталога специалистов.
Проведение второго тура экспертизы вскрывает множество научно-технических и организационно-экономических условий для реализации промежуточных целей, полученных в результате проведения первого тура, первичной обработки и анализа этих условий. Составляется предварительный список промежуточных целей второго тура и соответствующий им граф соподчиненности. Повторно обращаясь к части экспертов, уточняют формулировки условий использования результатов других источников информации. После этого окончательно дорабатывается список промежуточных целей, служащих в свою очередь исходным материалом для формулирования проблем проведения экспертизы третьего тура и так далее.
Цепочка туров продолжается до тех пор, пока все выдвинутые экспертами условия (или достаточное их количество, например 75% всего количества не окажутся «заземленными»), т. е. условия уже выполнены или для их выполнения нет необходимости проводить научно-технические исследования и разработки. Количество туров экспертизы определяется конкретной прогнозной разработкой.
В результате всех туров экспертизы строится информационная модель решения исходной проблемы, служащая основой построения прогнозного графа. Это — сетевая схема, отражающая процесс опроса экспертов, т. е. эксперты первого тура оценивают исходную проблему, затем условия, выдвинутые ими после соответствующей обработки, оцениваются как проблемы экспертами второго тура и так далее до окончания экспертизы.
Чтобы построить прогнозный граф, проводят анализ адекватности условий, ищут циклы и тупики, выявляют «заземленные» условия, объединяют несколько условий в одно. Условия обрабатывают как после каждого тура экспертизы, так и после проведения всей экспертизы.
По окончании экспертизы формируется основной массив исходных данных для обработки графа (наборы условий и связи между условиями).
Итак, прогнозный граф представляет собой сетевую схему, отражающую процесс реализации условий. Первый уровень его охватывает условия, которые осуществлены или осуществляются («заземлены»), следующий включает условия, выполнение которых зависит от осуществления условий первого уровня, и т. д. Самый верхний уровень — это конечная цель, исходная проблема.
А теперь требуется произвести качественное исследование прогнозного графа с целью:
а) обобщения и анализа содержащихся в нем вариантов (альтернатив) решения отдельных проблем;
б) оценки выдвинутых условий на перспективность.
Это исследование осуществляется группой управления прогнозной разработкой с привлечением наиболее квалифицированных специалистов. В его задачи входят:
оценка возможных альтернатив решения проблемы, которые трудно определить на формальном уровне;
выделение научно-технических условий, общих для всех выявленных альтернатив;
выделение научно-технических условий, специфичных для каждой отдельной альтернативы;
дополнение условий реализации отдельных альтернатив в случае, если сведения о них по каким-либо причинам не удалось получить на этапах разработки прогноза.
Для дальнейшего анализа графа и принятия решений особое значение имеет процедура выделения общих условий в альтернативных путях достижения цели прогнозирования. Эти общие условия не зависят от альтернативы и их еще до окончательных выводов по прогнозу можно включать в план научно-исследовательских выводов и опытно-конструкторских работ.
Для формирования набора возможных вариантов, ведущих к решению исходной проблемы на основе временных, стоимостных и вероятностных характеристик и определения показателей относительной важности и информационной значимости отдельных научно-технических событий с точки зрения решения исходной проблемы, необходимо провести количественный анализ прогнозного графа. Он включает в себя:
поиск циклов и тупиковых условий в прогнозном графе (для первичной обработки массива исходных данных и подготовки его для последующей обработки);
ранжирование событий в прогнозном графе (для перевода предварительно обработанной информационной модели в прогнозный граф);
вычисление вероятностных, временных и стоимостных характеристик (для определения вероятности свершения условий к определенному сроку, минимальных, средних и максимальных временных и стоимостных оценок каждого условия, начиная с начальных);
варьирование вероятностных и временных характеристик (для оценки относительной важности каждого условия в прогнозном графе, чтобы решить исходную проблему по коэффициенту информационной значимости и коэффициенту важности).
Таковы четыре типа вопросов, ответа на которые и ждут от коллектива экспертов.
Полученные прогнозные данные должны быть тщательно проверены на внутреннюю непротиворечивость. Сопоставляя их с зарубежными прогнозами, судим о полноте охвата существенных факторов и ожидаемых возможностей в исследуемой области. В итоге формируется гипотеза о грядущем мировом уровне объекта прогнозирования (и его отдельных элементов).
Полученные посредством качественного анализа структурные и функциональные группировки последовательностей решений совмещаются с результатами количественного анализа прогнозного графа, осуществляется синтез вариантов научно-технической стратегии, направленных на решение исходной проблемы.
Синтез прогнозных данных (итоговая формулировка гипотез) должен вбирать в себя достаточно широкую гамму вариантов, находящихся между самой осторожной и самой смелой научно-технической стратегией, анализируя варианты вероятностных и временных характеристик научно-технических условий на прогнозном графе, учитывая положение различных событий в системе причинно-следственных связей и разное влияние их на достижение поставленной цели.
Список литературы
1. Эддоус М., Стэнсфилд Р. Методы принятия решений / Пер. с англ. под ред. Член-корр. РАН И.И. Елисеевой. – М.: Аудит, ЮНИТИ, 1997. – 590 с.
2. Введение в экономико-математическое моделирование. Лотов А.В. – М.: Наука. Главная редакция физико-математической литературы, 1984. – 392 с.
3. Экономико-математические методы и модели: Учеб. пособие / Н. И. Холод, А. В. Кузнецов, Я. Н. Жихар и др.; Под общ. Ред. А. В. Кузнецова. 2-е изд. – Мн.: БГЭУ, 2000. – 412 с.
4. Моделирование развивающихся систем. Глушкова В. М., Иванов В. В., Яненко В. М. – М.: Наука. Главная редакция физико-математической литературы, 1993. – 350 с.
Карпов Валерий Витальевич
ПРИКЛАДНОЙ СИСТЕМНЫЙ АНАЛИЗ:
СЕТЕВОЙ АНАЛИЗ И КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ ПРОЕКТОВ, МЕТОД ПРОГНОЗНОГО ГРАФА
Учебное пособие
Под рекдакцией В.К. Буторина
Изд. лиц. Серия ЛР №020464 от 09.06.1997г.
Лицензия выдана КемГУ (650043, г. Кемерово, ул. Красная,6)
Подписано в печать г.
Формат бумаги 60х90 1/16. Бумага писчая. Печать на ризографе GR3750.
Усл. печ. л. . Тираж 500 экз. Заказ
Новокузнецкий филиал-институт
Кемеровского государственного университета
654041, г. Новокузнецк, ул. Циолковского 15а.
Издательский центр НФИКемГУ
Цена договорная