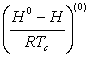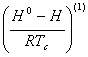Реферат: Прогнозирование энтальпии образования при нормальных и повышенных давлениях
При прогнозировании энтальпий образования органических веществ, находящихся при давлении 1 атм и температуре выше 298 К, используются:
*
значение ![]() вещества, вычисленное любым из
аддитивных методов или взятое из справочников;
вещества, вычисленное любым из
аддитивных методов или взятое из справочников;
* сведения о температурной зависимости теплоемкости вещества в виде аппроксимирующего уравнения или в табулированной форме;
* сведения о температурной зависимости теплоемкости простых веществ или элементов, которыми представлено данное вещество, в виде аппроксимирующего уравнения или в табулированной форме (прил. 3);
* уравнение Кирхгофа (1.1)
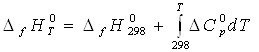 , (1.1)
, (1.1)
где ![]() - разность
между теплоемкостями соединения и простых веществ или элементов, которыми
представлено данное вещество, причем каждый элемент или простое вещество
находится в своем стандартном состоянии (как указано выше) и теплоемкость
каждого умножается на соответствующий стехиометрический коэффициент в реакции образования
вещества из элементов или простых веществ. Сведения о теплоемкостях простых
веществ приводятся в табл. прил. 3. Процедура расчета
- разность
между теплоемкостями соединения и простых веществ или элементов, которыми
представлено данное вещество, причем каждый элемент или простое вещество
находится в своем стандартном состоянии (как указано выше) и теплоемкость
каждого умножается на соответствующий стехиометрический коэффициент в реакции образования
вещества из элементов или простых веществ. Сведения о теплоемкостях простых
веществ приводятся в табл. прил. 3. Процедура расчета ![]() рассмотрена в примере 1.2, при
этом использованы справочные данные для теплоемкостей вещества, поскольку
вопросы прогнозирования
рассмотрена в примере 1.2, при
этом использованы справочные данные для теплоемкостей вещества, поскольку
вопросы прогнозирования ![]() обсуждаются позже (разд. 3
данного пособия).
обсуждаются позже (разд. 3
данного пособия).
Пример 1.2
Рассчитать ![]() циклогексана при 400, 500 и 600
К. Энтальпия образования
циклогексана при 400, 500 и 600
К. Энтальпия образования ![]() циклогексана составляет –123,34
кДж/моль [1], значения теплоемкостей
циклогексана составляет –123,34
кДж/моль [1], значения теплоемкостей ![]() при 400, 500 и 600 К заимствованы
из [1] и приведены в табл. 1.12.
при 400, 500 и 600 К заимствованы
из [1] и приведены в табл. 1.12.
Решение
С использованием уравнения Кирхгофа вычисляются энтальпии образования циклогексана при интересующих температурах. При этом средние величины теплоемкостей циклогексана, углерода и водорода в любом из интервалов температур (от 300 до 400 К, от 400 до 500 К, от 500 до 600 К) считаются величинами постоянными по условию создания таблиц, допускающих линейную интерполяцию соседних значений в них.
Таблица 1.12
|
кДж/моль [1] |
Теплоемкость, |
кДж/моль |
% отн. | ||||
|
Т, К | Циклогексан |
Углерод (графит) |
Водород (Н2) |
|||
| 300 | 107,03 | 8,72 | 28,85 | ||||
| 400 | -134,10 | 149,87 | 11,93 | 29,18 | -134,32 | 0,13 | |
| 500 | -142,59 | 190,25 | 14,63 | 29,26 | -142,81 | 0,15 | |
| 600 | -148,84 | 225,22 | 16,86 | 29,32 | -149,06 | 0,15 | |
Результаты расчета приведены ниже и в табл. 1.12 сопоставлены с рекомендуемыми значениями [1]. Температурная зависимость идеально-газовой энтальпии образования циклогексана иллюстрируется рис. 1.4.
![]() = –123,34+((149,87+107,03)/2·(400–298)
– 6·(11,93+8,72)/2·(400–298) –
= –123,34+((149,87+107,03)/2·(400–298)
– 6·(11,93+8,72)/2·(400–298) –
– 6·(29,18+28,85)/2·(400–298))/1000= – 134,32 кДж/моль.
![]() = –123,34+((149,87+107,03)/2·(400–298)
– 6·(11,93+8,72)/2·(400–298) –
= –123,34+((149,87+107,03)/2·(400–298)
– 6·(11,93+8,72)/2·(400–298) –
–6·(29,18+28,85)/2·(400–298))/1000+((190,25+149,85)/2·(500–400) – 6·(14,63+11,93)/2·
·(500-400)– 6·(29,26+29,18)/2·(500–400))/1000= – 142,81 кДж/моль.
![]() = –123,34+((149,87+107,03)/2·(400–298)
– 6 (11,93+8,72)/2·(400-298) –
= –123,34+((149,87+107,03)/2·(400–298)
– 6 (11,93+8,72)/2·(400-298) –
– 6·(29,18+28,85)/2·(400–298))/1000+((190,25+149,85)/2·(500–400) – 6·(14,63+11,93)/2
·(500–400)–6·(29,26+29,18)/2·(500–400))/1000+((225,22+190,25)/2·(600–500) –
– 6·(16,86+14,63)/2·(600–500)– 6·(29,32+29,26)/2·(600–500))/1000= –149,06 кДж/моль.
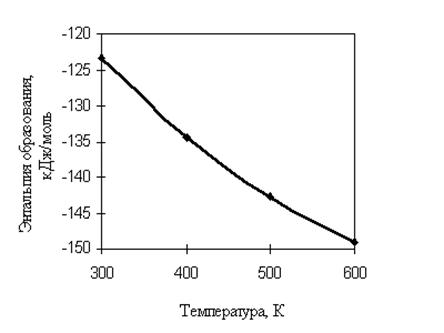
Р и с. 1.4. Температурная зависимость ![]() циклогексана
циклогексана
Прогнозирование энтальпий образования органических соединений при повышенных давлениях
Экспериментальные
сведения о ![]() органических
веществ при высоких давлениях практически отсутствуют. Поэтому их
прогнозирование оказывается неизбежным в большинстве практических расчетов.
Поскольку речь идет о свойстве вещества в реальном состоянии, методы
прогнозирования основаны на принципе соответственных состояний. При массовых
расчетах широко используется подход, основанный на разложении Питцера:
органических
веществ при высоких давлениях практически отсутствуют. Поэтому их
прогнозирование оказывается неизбежным в большинстве практических расчетов.
Поскольку речь идет о свойстве вещества в реальном состоянии, методы
прогнозирования основаны на принципе соответственных состояний. При массовых
расчетах широко используется подход, основанный на разложении Питцера:
 (1.2)
(1.2)
и таблицах Ли-Кеслера (табл. 1.13, 1.14.) для энтальпий.
Изотермические изменения энтальпии, рассчитанные по уравнению
Значения для простого вещества 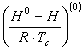
|
Tr |
Pr |
||||||
| 0,010 | 0,050 | 0,100 | 0,200 | 0,400 | 0,600 | 0,800 | |
| 0,30 | 6,045 | 6,043 | 6,040 | 6,034 | 6,022 | 6,011 | 5,999 |
| 0,35 | 5,906 | 5,904 | 5,901 | 5,895 | 5,882 | 5,870 | 5,858 |
| 0,40 | 5,763 | 5,761 | 5,757 | 5,751 | 5,738 | 5,726 | 5,713 |
| 0,45 | 5,615 | 5,612 | 5,609 | 5,603 | 5,590 | 5,577 | 5,564 |
| 0,50 | 5,465 | 5,463 | 5,459 | 5,453 | 5,440 | 5,427 | 5,414 |
| 0,55 | 0,032 | 5,312 | 5,309 | 5,303 | 5,290 | 5,278 | 5,265 |
| 0,60 | 0,027 | 5,162 | 5,159 | 5,153 | 5,141 | 5,129 | 5,116 |
| 0,65 | 0,023 | 0,118 | 5,008 | 5,002 | 4,991 | 4,980 | 4,968 |
| 0,70 | 0,020 | 0,101 | 0,213 | 4,848 | 4,838 | 4,828 | 4,818 |
| 0,75 | 0,017 | 0,088 | 0,183 | 4,687 | 4,679 | 4,672 | 4,664 |
| 0,80 | 0,015 | 0,078 | 0,160 | 0,345 | 4,507 | 4,504 | 4,499 |
| 0,85 | 0,014 | 0,069 | 0,141 | 0,300 | 4,309 | 4,313 | 4,316 |
| 0,90 | 0,012 | 0,062 | 0,126 | 0,264 | 0,596 | 4,074 | 4,094 |
| 0,93 | 0,011 | 0,058 | 0,118 | 0,246 | 0,545 | 0,960 | 3,920 |
| 0,95 | 0,011 | 0,056 | 0,113 | 0,235 | 0,516 | 0,885 | 3,763 |
| 0,97 | 0,011 | 0,054 | 0,109 | 0,225 | 0,490 | 0,824 | 1,356 |
| 0,98 | 0,010 | 0,053 | 0,107 | 0,221 | 0,478 | 0,797 | 1,273 |
| 0,99 | 0,010 | 0,052 | 0,105 | 0,216 | 0,466 | 0,773 | 1,206 |
| 1,00 | 0,010 | 0,051 | 0,103 | 0,212 | 0,455 | 0,750 | 1,151 |
| 1,01 | 0,010 | 0,050 | 0,101 | 0,208 | 0,445 | 0,728 | 1,102 |
| 1,02 | 0,010 | 0,049 | 0,099 | 0,203 | 0,434 | 0,708 | 1,060 |
| 1,05 | 0,009 | 0,046 | 0,094 | 0,192 | 0,407 | 0,654 | 0,955 |
| 1,10 | 0,008 | 0,042 | 0,086 | 0,175 | 0,367 | 0,581 | 0,827 |
| 1,15 | 0,008 | 0,039 | 0,079 | 0,160 | 0,334 | 0,523 | 0,732 |
| 1,20 | 0,007 | 0,036 | 0,073 | 0,148 | 0,305 | 0,474 | 0,657 |
| 1,30 | 0,006 | 0,031 | 0,063 | 0,127 | 0,259 | 0,399 | 0,545 |
| 1,40 | 0,005 | 0,027 | 0,055 | 0,110 | 0,224 | 0,341 | 0,463 |
| 1,50 | 0,005 | 0,024 | 0,048 | 0,097 | 0,196 | 0,297 | 0,400 |
| 1,60 | 0,004 | 0,021 | 0,043 | 0,086 | 0,173 | 0,261 | 0,350 |
| 1,70 | 0,004 | 0,019 | 0,038 | 0,076 | 0,153 | 0,231 | 0,309 |
| 1,80 | 0,003 | 0,017 | 0,034 | 0,068 | 0,137 | 0,206 | 0,275 |
| 1,90 | 0,003 | 0,015 | 0,031 | 0,062 | 0,123 | 0,185 | 0,246 |
| 2,00 | 0,003 | 0,014 | 0,028 | 0,056 | 0,111 | 0,167 | 0,222 |
| 2,20 | 0,002 | 0,012 | 0,023 | 0,046 | 0,092 | 0,137 | 0,182 |
| 2,40 | 0,002 | 0,010 | 0,019 | 0,038 | 0,076 | 0,114 | 0,150 |
| 2,60 | 0,002 | 0,008 | 0,016 | 0,032 | 0,064 | 0,095 | 0,125 |
| 2,80 | 0,001 | 0,007 | 0,014 | 0,027 | 0,054 | 0,080 | 0,105 |
| 3,00 | 0,001 | 0,006 | 0,011 | 0,023 | 0,045 | 0,067 | 0,088 |
| 3,50 | 0,001 | 0,004 | 0,007 | 0,015 | 0,029 | 0,043 | 0,056 |
| 4,00 | 0,000 | 0,002 | 0,005 | 0,009 | 0,017 | 0,026 | 0,033 |
Таблица 1.13
состояния Ли-Кеслера
|
Pr |
|||||||
| 1,000 | 1,200 | 1,500 | 2,000 | 3,000 | 5,000 | 7,000 | 10,000 |
| 5,987 | 5,975 | 5,957 | 5,927 | 5,868 | 5,748 | 5,628 | 5,446 |
| 5,845 | 5,833 | 5,814 | 5,783 | 5,721 | 5,595 | 5,469 | 5,278 |
| 5,700 | 5,687 | 5,668 | 5,636 | 5,572 | 5,442 | 5,311 | 5,113 |
| 5,551 | 5,538 | 5,519 | 5,486 | 5,421 | 5,288 | 5,154 | 4,950 |
| 5,401 | 5,388 | 5,369 | 5,336 | 5,270 | 5,135 | 4,999 | 4,791 |
| 5,252 | 5,239 | 5,220 | 5,187 | 5,121 | 4,986 | 4,849 | 4,638 |
| 5,104 | 5,091 | 5,073 | 5,041 | 4,976 | 4,842 | 4,704 | 4,492 |
| 4,956 | 4,945 | 4,927 | 4,896 | 4,833 | 4,702 | 4,565 | 4,353 |
| 4,808 | 4,797 | 4,781 | 4,752 | 4,693 | 4,566 | 4,432 | 4,221 |
| 4,655 | 4,646 | 4,632 | 4,607 | 4,554 | 4,434 | 4,303 | 4,095 |
| 4,494 | 4,488 | 4,478 | 4,459 | 4,413 | 4,303 | 4,178 | 3,974 |
| 4,316 | 4,316 | 4,312 | 4,302 | 4,269 | 4,173 | 4,056 | 3,857 |
| 4,108 | 4,118 | 4,127 | 4,132 | 4,119 | 4,043 | 3,935 | 3,744 |
| 3,953 | 3,976 | 4,000 | 4,020 | 4,024 | 3,963 | 3,863 | 3,678 |
| 3,825 | 3,865 | 3,904 | 3,940 | 3,958 | 3,910 | 3,815 | 3,634 |
| 3,658 | 3,732 | 3,796 | 3,853 | 3,890 | 3,856 | 3,767 | 3,591 |
| 3,544 | 3,652 | 3,736 | 3,806 | 3,854 | 3,829 | 3,743 | 3,569 |
| 3,376 | 3,558 | 3,670 | 3,758 | 3,818 | 3,801 | 3,719 | 3,548 |
| 2,584 | 3,441 | 3,598 | 3,706 | 3,782 | 3,774 | 3,695 | 3,526 |
| 1,796 | 3,283 | 3,516 | 3,652 | 3,744 | 3,746 | 3,671 | 3,505 |
| 1,627 | 3,039 | 3,422 | 3,595 | 3,705 | 3,718 | 3,647 | 3,484 |
| 1,359 | 2,034 | 3,030 | 3,398 | 3,583 | 3,632 | 3,575 | 3,420 |
| 1,120 | 1,487 | 2,203 | 2,965 | 3,353 | 3,484 | 3,453 | 3,315 |
| 0,968 | 1,239 | 1,719 | 2,479 | 3,091 | 3,329 | 3,329 | 3,211 |
| 0,857 | 1,076 | 1,443 | 2,079 | 2,807 | 3,166 | 3,202 | 3,107 |
| 0,698 | 0,860 | 1,116 | 1,560 | 2,274 | 2,825 | 2,942 | 2,899 |
| 0,588 | 0,716 | 0,915 | 1,253 | 1,857 | 2,486 | 2,679 | 2,692 |
| 0,505 | 0,611 | 0,774 | 1,046 | 1,549 | 2,175 | 2,421 | 2,486 |
| 0,440 | 0,531 | 0,667 | 0,894 | 1,318 | 1,904 | 2,177 | 2,285 |
| 0,387 | 0,466 | 0,583 | 0,777 | 1,139 | 1,672 | 1,953 | 2,091 |
| 0,344 | 0,413 | 0,515 | 0,683 | 0,996 | 1,476 | 1,751 | 1,908 |
| 0,307 | 0,368 | 0,458 | 0,606 | 0,880 | 1,309 | 1,571 | 1,736 |
| 0,276 | 0,330 | 0,411 | 0,541 | 0,782 | 1,167 | 1,411 | 1,577 |
| 0,226 | 0,269 | 0,334 | 0,437 | 0,629 | 0,937 | 1,143 | 1,295 |
| 0,187 | 0,222 | 0,275 | 0,359 | 0,513 | 0,761 | 0,929 | 1,058 |
| 0,155 | 0,185 | 0,228 | 0,297 | 0,422 | 0,621 | 0,756 | 0,858 |
| 0,130 | 0,154 | 0,190 | 0,246 | 0,348 | 0,508 | 0,614 | 0,689 |
| 0,109 | 0,129 | 0,159 | 0,205 | 0,288 | 0,415 | 0,495 | 0,545 |
| 0,069 | 0,081 | 0,099 | 0,127 | 0,174 | 0,239 | 0,270 | 0,264 |
| 0,041 | 0,048 | 0,058 | 0,072 | 0,095 | 0,116 | 0,110 | 0,061 |
Изотермические изменения энтальпии, рассчитанные по уравнению
Значения для простого вещества 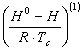
|
Tr |
Pr |
||||||
| 0,010 | 0,050 | 0,100 | 0,200 | 0,400 | 0,600 | 0,800 | |
| 0,30 | 11,098 | 11,096 | 11,095 | 11,091 | 11,083 | 11,076 | 11,069 |
| 0,35 | 10,656 | 10,655 | 10,654 | 10,653 | 10,650 | 10,646 | 10,643 |
| 0,40 | 10,121 | 10,121 | 10,121 | 10,120 | 10,121 | 10,121 | 10,121 |
| 0,45 | 9,515 | 9,515 | 9,516 | 9,517 | 9,519 | 9,521 | 9,523 |
| 0,50 | 8,868 | 8,869 | 8,870 | 8,872 | 8,876 | 8,880 | 8,884 |
| 0,55 | 0,080 | 8,211 | 8,212 | 8,215 | 8,221 | 8,226 | 8,232 |
| 0,60 | 0,059 | 7,568 | 7,570 | 7,573 | 7,579 | 7,585 | 7,591 |
| 0,65 | 0,045 | 0,247 | 6,949 | 6,952 | 6,959 | 6,966 | 6,973 |
| 0,70 | 0,034 | 0,185 | 0,415 | 6,360 | 6,367 | 6,373 | 6,381 |
| 0,75 | 0,027 | 0,142 | 0,306 | 5,796 | 5,802 | 5,809 | 5,816 |
| 0,80 | 0,021 | 0,110 | 0,234 | 0,542 | 5,266 | 5,271 | 5,278 |
| 0,85 | 0,017 | 0,087 | 0,182 | 0,401 | 4,753 | 4,754 | 4,758 |
| 0,90 | 0,014 | 0,070 | 0,144 | 0,308 | 0,751 | 4,254 | 4,248 |
| 0,93 | 0,012 | 0,061 | 0,126 | 0,265 | 0,612 | 1,236 | 3,942 |
| 0,95 | 0,011 | 0,056 | 0,115 | 0,241 | 0,542 | 0,994 | 3,737 |
| 0,97 | 0,010 | 0,052 | 0,105 | 0,219 | 0,483 | 0,837 | 1,616 |
| 0,98 | 0,010 | 0,050 | 0,101 | 0,209 | 0,457 | 0,776 | 1,324 |
| 0,99 | 0,009 | 0,048 | 0,097 | 0,200 | 0,433 | 0,722 | 1,154 |
| 1,00 | 0,009 | 0,046 | 0,093 | 0,191 | 0,410 | 0,675 | 1,034 |
| 1,01 | 0,009 | 0,044 | 0,089 | 0,183 | 0,389 | 0,632 | 0,940 |
| 1,02 | 0,008 | 0,042 | 0,085 | 0,175 | 0,370 | 0,594 | 0,863 |
| 1,05 | 0,007 | 0,037 | 0,075 | 0,153 | 0,318 | 0,498 | 0,691 |
| 1,10 | 0,006 | 0,030 | 0,061 | 0,123 | 0,251 | 0,381 | 0,507 |
| 1,15 | 0,005 | 0,025 | 0,050 | 0,099 | 0,199 | 0,296 | 0,385 |
| 1,20 | 0,004 | 0,020 | 0,040 | 0,080 | 0,158 | 0,232 | 0,297 |
| 1,30 | 0,003 | 0,013 | 0,026 | 0,052 | 0,100 | 0,142 | 0,177 |
| 1,40 | 0,002 | 0,008 | 0,016 | 0,032 | 0,060 | 0,083 | 0,100 |
| 1,50 | 0,001 | 0,005 | 0,009 | 0,018 | 0,032 | 0,042 | 0,048 |
| 1,60 | 0,000 | 0,002 | 0,004 | 0,007 | 0,012 | 0,013 | 0,011 |
| 1,70 | 0,000 | 0,000 | 0,000 | -0,000 | -0,003 | -0,009 | -0,017 |
| 1,80 | -0,000 | -0,001 | -0,003 | -0,006 | -0,015 | -0,025 | -0,037 |
| 1,90 | -0,001 | -0,003 | -0,005 | -0,011 | -0,023 | -0,037 | -0,053 |
| 2,00 | -0,001 | -0,003 | -0,007 | -0,015 | -0,030 | -0,047 | -0,065 |
| 2,20 | -0,001 | -0,005 | -0,010 | -0,020 | -0,040 | -0,062 | -0,083 |
| 2,40 | -0,001 | -0,006 | -0,012 | -0,023 | -0,047 | -0,071 | -0,095 |
| 2,60 | -0,001 | -0,006 | -0,013 | -0,026 | -0,052 | -0,078 | -0,104 |
| 2,80 | -0,001 | -0,007 | -0,014 | -0,028 | -0,055 | -0,082 | -0,110 |
| 3,00 | -0,001 | -0,007 | -0,014 | -0,029 | -0,058 | -0,086 | -0,114 |
| 3,50 | -0,002 | -0,008 | -0,016 | -0,031 | -0,062 | -0,092 | -0,122 |
| 4,00 | -0,002 | -0,008 | -0,016 | -0,032 | -0,064 | -0,096 | -0,127 |
Таблица 1.14
состояния Ли-Кеслера
|
Pr |
|||||||
| 1,000 | 1,200 | 1,500 | 2,000 | 3,000 | 5,000 | 7,000 | 10,000 |
| 11,062 | 11,055 | 11,044 | 11,027 | 10,992 | 10,935 | 10,872 | 10,781 |
| 10,640 | 10,637 | 10,632 | 10,624 | 10,609 | 10,581 | 10,554 | 10,529 |
| 10,121 | 10,121 | 10,121 | 10,122 | 10,123 | 10,128 | 10,135 | 10,150 |
| 9,525 | 9,527 | 9,531 | 9,537 | 9,549 | 9,576 | 9,611 | 9,663 |
| 8,888 | 8,892 | 8,899 | 8,909 | 8,932 | 8,978 | 9,030 | 9,111 |
| 8,238 | 8,243 | 8,252 | 8,267 | 8,928 | 8,360 | 8,425 | 8,531 |
| 7,596 | 7,603 | 7,614 | 7,632 | 7,669 | 7,745 | 7,824 | 7,950 |
| 6,980 | 6,987 | 6,997 | 7,017 | 7,059 | 7,147 | 7,239 | 7,381 |
| 6,388 | 6,395 | 6,407 | 6,429 | 6,475 | 6,574 | 6,677 | 6,837 |
| 5,824 | 5,832 | 5,845 | 5,868 | 5,918 | 6,027 | 6,142 | 6,318 |
| 5,285 | 5,293 | 5,306 | 5,330 | 5,385 | 5,506 | 5,632 | 5,824 |
| 4,763 | 4,771 | 4,784 | 4,810 | 4,872 | 5,008 | 5,149 | 5,358 |
| 4,249 | 4,255 | 4,268 | 4,298 | 4,371 | 4,530 | 4,688 | 4,916 |
| 3,934 | 3,937 | 3,951 | 3,987 | 4,073 | 4,251 | 4,422 | 4,662 |
| 3,712 | 3,713 | 3,730 | 3,773 | 3,873 | 4,068 | 4,248 | 4,497 |
| 3,470 | 3,467 | 3,492 | 3,551 | 3,670 | 3,885 | 4,077 | 4,336 |
| 3,332 | 3,327 | 3,363 | 3,434 | 3,568 | 3,795 | 3,992 | 4,257 |
| 3,164 | 3,164 | 3,223 | 3,313 | 3,464 | 3,705 | 3,909 | 4,178 |
| 2,471 | 2,952 | 3,065 | 3,186 | 3,358 | 3,615 | 3,825 | 4,100 |
| 1,375 | 2,595 | 2,880 | 3,051 | 3,251 | 3,525 | 3,742 | 4,023 |
| 1,180 | 1,723 | 2,650 | 2,906 | 3,142 | 3,435 | 3,661 | 3,947 |
| 0,877 | 0,878 | 1,496 | 2,381 | 2,800 | 3,167 | 3,418 | 3,722 |
| 0,617 | 0,673 | 0,617 | 1,261 | 2,167 | 2,720 | 3,023 | 3,362 |
| 0,459 | 0,503 | 0,487 | 0,604 | 1,497 | 2,275 | 2,641 | 3,019 |
| 0,349 | 0,381 | 0,381 | 0,361 | 0,934 | 1,840 | 2,273 | 2,692 |
| 0,203 | 0,218 | 0,218 | 0,178 | 0,300 | 1,066 | 1,592 | 2,086 |
| 0,111 | 0,115 | 0,108 | 0,070 | 0,044 | 0,504 | 1,012 | 1,547 |
| 0,049 | 0,046 | 0,032 | -0,008 | -0,078 | 0,142 | 0,556 | 1,080 |
| 0,005 | -0,004 | -0,023 | -0,065 | -0,151 | -0,082 | 0,217 | 0,689 |
| -0,027 | -0,040 | -0,063 | -0,109 | -0,202 | -0,223 | -0,028 | 0,369 |
| -0,051 | -0,067 | -0,094 | -0,143 | -0,241 | -0,317 | -0,203 | 0,112 |
| -0,070 | -0,088 | -0,117 | -0,169 | -0,271 | -0,381 | -0,330 | -0,092 |
| -0,085 | -0,105 | -0,136 | -0,190 | -0,295 | -0,428 | -0,424 | -0,255 |
| -0,106 | -0,128 | -0,163 | -0,221 | -0,331 | -0,493 | -0,551 | -0,489 |
| -0,120 | -0,144 | -0,181 | -0,242 | -0,356 | -0,535 | -0,631 | -0,645 |
| -0,130 | -0,156 | -0,194 | -0,257 | -0,376 | -0,567 | -0,687 | -0,754 |
| -0,137 | -0,164 | -0,204 | -0,269 | -0,391 | -0,591 | -0,729 | -0,836 |
| -0,142 | -0,170 | -0,211 | -0,278 | -0,403 | -0,611 | -0,763 | -0,899 |
| -0,152 | -0,181 | -0,224 | -0,294 | -0,425 | -0,650 | -0,827 | -1,015 |
| -0,158 | -0,188 | -0,233 | -0,306 | -0,442 | -0,680 | -0,874 | -1,097 |
В уравнении (1.2):
- ацентрический фактор;
 - поправка к энтальпии на
давление, характеризующая поведение простого вещества;
- поправка к энтальпии на
давление, характеризующая поведение простого вещества;
 - функция отклонения в поведении
рассматриваемого вещества от поведения простого вещества;
- функция отклонения в поведении
рассматриваемого вещества от поведения простого вещества;
![]() - идеально-газовая энтальпия
вещества при рассматриваемой температуре; в случае расчета энтальпий
образования органических соединений это
- идеально-газовая энтальпия
вещества при рассматриваемой температуре; в случае расчета энтальпий
образования органических соединений это ![]() ;
;
![]() - искомая энтальпия, в нашем
случае это
- искомая энтальпия, в нашем
случае это ![]() ;
;
![]() - газовая постоянная, равная
8,31441 Дж/(моль×К) или 1,98725 кал/(моль×К);
- газовая постоянная, равная
8,31441 Дж/(моль×К) или 1,98725 кал/(моль×К); ![]() - критическая температура вещества,
К.
- критическая температура вещества,
К.
Таблицы Ли-Кеслера составлены на основе достаточно универсального уравнения состояния вещества (уравнение Бенедикта-Уэбба-Рубина) с соблюдением общепринятых принципов, т.е. между любыми соседними значениями в столбцах или строках таблицы корректной является линейная интерполяция. В таблицах область над линией излома принадлежит жидкому состоянию вещества.
Расчет ![]() иллюстрируется примером
1.3.
иллюстрируется примером
1.3.
Пример 1.3
Рассчитать ![]() циклогексана при
давлении, изменяющемся от 0,4 до 120,6 атм, и при температурах 304,37, 415,05 и
581,07 К. Дать графическую зависимость изотерм и выполнить их анализ. Указать
фазовые состояния циклогексана при рассматриваемых параметрах. Критические
температура, давление и ацентрический фактор циклогексана равны: 553,4 К, 40,2
атм и 0,213.
циклогексана при
давлении, изменяющемся от 0,4 до 120,6 атм, и при температурах 304,37, 415,05 и
581,07 К. Дать графическую зависимость изотерм и выполнить их анализ. Указать
фазовые состояния циклогексана при рассматриваемых параметрах. Критические
температура, давление и ацентрический фактор циклогексана равны: 553,4 К, 40,2
атм и 0,213.
Решение
1. Рассчитываются ![]() при
интересующих температурах. Поскольку последние попадают в интервал,
рассмотренный в примере 1.2, и на каждом из участков возможна линейная
интерполяция теплоемкостей циклогексана и простых веществ, его образующих, то
корректной будет и линейная интерполяция вычисленных в примере 1.2 значений
при
интересующих температурах. Поскольку последние попадают в интервал,
рассмотренный в примере 1.2, и на каждом из участков возможна линейная
интерполяция теплоемкостей циклогексана и простых веществ, его образующих, то
корректной будет и линейная интерполяция вычисленных в примере 1.2 значений ![]() . Таким
образом, имеем
. Таким
образом, имеем
![]() = (–134,32– (– 123,34))/100 4,37+(
– 123,34) = –123,82 кДж/моль.
= (–134,32– (– 123,34))/100 4,37+(
– 123,34) = –123,82 кДж/моль.
Аналогично ![]() = (–142,81+134,32)/100 15,05–134,32
= –135,59 кДж/моль;
= (–142,81+134,32)/100 15,05–134,32
= –135,59 кДж/моль;
![]() = –147,87 кДж/моль.
= –147,87 кДж/моль.
2. Рассчитываются приведенные температуры:
![]() = 304,37/553,4 =0,55;
= 304,37/553,4 =0,55; ![]() = 415,05/553,4
=0,75;
= 415,05/553,4
=0,75; ![]() =
581,07/553,4 = 1,05.
=
581,07/553,4 = 1,05.
3. При полученных
приведенных температурах и значениях приведенных давлений c помощью таблиц
Ли-Кеслера и рассчитанных величин ![]() вычисляются значения
вычисляются значения ![]() .
.
Для ![]() и P = 2,01 атм имеем
и P = 2,01 атм имеем
![]() = –123,82–(5,312+0,213×8,211)×8,31441×553,4/1000 = –156,31 кДж/моль.
= –123,82–(5,312+0,213×8,211)×8,31441×553,4/1000 = –156,31 кДж/моль.
Фрагмент результатов расчета приведен в табл. 1.15 и 1.16, где жирным шрифтом выделены сведения, относящиеся к жидкому состоянию циклогексана.
Дело в том, что различие в энергиях конформеров, обусловленных взаимной ориентацией атомов и групп соседних заместителей в ароматическом ядре, оказывается достаточным, чтобы учесть этот фактор при формировании аддитивной схемы. Суть вопроса становится понятной при конформационном анализе соединений с относительно несложным строением молекул, например метилбензолов (МБ), проведенного с помощью программы Gaussian 03W методом B3LYP/6-311G++2d,2p. Указанный метод дает для о-ксилола два сосуществующих конформера (“А” и “В”, рис. 1.2)
Один из них
(“А”) характеризуется взаимным транс-расположением атомов водорода метильных
групп, лежащих в плоскости ароматического ядра, в другом (“В”) атомы водорода
метильных групп имеют шахматную ориентацию по отношению друг к другу. Различие
в энергиях этих конформеров по результатам расчета составляет для ![]() 5,2 кДж/моль.
Очевидно, что при таком соотношении в энергиях о-ксилол представлен при 298 К
преимущественно конформером “А”, и эффект взаимодействия заместителей
(орто-эффект типа “метил-метил” или C1-C1(транс-“Н-Н”)) для
5,2 кДж/моль.
Очевидно, что при таком соотношении в энергиях о-ксилол представлен при 298 К
преимущественно конформером “А”, и эффект взаимодействия заместителей
(орто-эффект типа “метил-метил” или C1-C1(транс-“Н-Н”)) для ![]() составляет 2,76
кДж/моль. Но очевидно также и то, что указанное расположение метильных групп
возможно только для двух соседних заместителей, третий и последующие
заместители уже не могут иметь транс-ориентации атомов водорода. Выполненный
нами конформационный анализ показал, что для 1,2,3-триМБ энергетически наиболее
выгодным конформером является “С” (рис. 1.3), который для двух соседних групп
имеет транс-ориентацию атомов водорода, лежащих в плоскости ароматического
ядра, а третья метильная группа подстроена к соседней “шахматно”. Таким
образом, суммарный эффект взаимодействия замести телей, дестабилизирующий
молекулу 1,2,3-триМБ, составляет для
составляет 2,76
кДж/моль. Но очевидно также и то, что указанное расположение метильных групп
возможно только для двух соседних заместителей, третий и последующие
заместители уже не могут иметь транс-ориентации атомов водорода. Выполненный
нами конформационный анализ показал, что для 1,2,3-триМБ энергетически наиболее
выгодным конформером является “С” (рис. 1.3), который для двух соседних групп
имеет транс-ориентацию атомов водорода, лежащих в плоскости ароматического
ядра, а третья метильная группа подстроена к соседней “шахматно”. Таким
образом, суммарный эффект взаимодействия замести телей, дестабилизирующий
молекулу 1,2,3-триМБ, составляет для ![]() 7,63 кДж/моль (2,76+4,87), а
величину 2,11 кДж/моль, равную 7,63-2·2,76 кДж/моль, можно было бы воспринять в
рамках схемы Кокса-Пилчера [2] как дополнительный “тройной” эффект (сверх удвоенного
орто-эффекта). Однако указанная ситуация в группе метилбензолов реализуется
только в случае 1,2,3,5-тетраМБ, т.е. носит довольно частный характер. Расчет
показывает, что для 1,2,3,4-тетраМБ и пента-МБ две группы транс-ориентированы,
а остальные шахматно подстроены. В случае гекса-МБ все заместители имеют
шахматную ориентацию.
7,63 кДж/моль (2,76+4,87), а
величину 2,11 кДж/моль, равную 7,63-2·2,76 кДж/моль, можно было бы воспринять в
рамках схемы Кокса-Пилчера [2] как дополнительный “тройной” эффект (сверх удвоенного
орто-эффекта). Однако указанная ситуация в группе метилбензолов реализуется
только в случае 1,2,3,5-тетраМБ, т.е. носит довольно частный характер. Расчет
показывает, что для 1,2,3,4-тетраМБ и пента-МБ две группы транс-ориентированы,
а остальные шахматно подстроены. В случае гекса-МБ все заместители имеют
шахматную ориентацию.
4. Зависимость ![]() от давления
при избранных температурах приведена на рис. 1.5. Характер полученных
графических зависимостей различен для изотерм, принадлежащих жидкому и
газообразному состояниям вещества. Энтальпия образования жидкости в меньшей
степени зависит от давления, от чем газа, что очевидно. Характер изменения
энтальпии в закритической области сложен, особенно вблизи критической точки.
Для докритической изотермы резкое изменение энтальпии сопряжено с изменением
фазового состояния вещества.
от давления
при избранных температурах приведена на рис. 1.5. Характер полученных
графических зависимостей различен для изотерм, принадлежащих жидкому и
газообразному состояниям вещества. Энтальпия образования жидкости в меньшей
степени зависит от давления, от чем газа, что очевидно. Характер изменения
энтальпии в закритической области сложен, особенно вблизи критической точки.
Для докритической изотермы резкое изменение энтальпии сопряжено с изменением
фазового состояния вещества.
Таблица 1.15
|
|
при
приведенном давлении, |
при
приведенном давлении, |
||||||||
| 0,010 | 0,050 | 0,100 | 0,200 | 0,400 | 0,010 | 0,050 | 0,100 | 0,200 | 0,400 | |
| 0,55 | 0,032 | 5,312 | 5,309 | 5,303 | 5,29 | 0,080 | 8,211 | 8,212 | 8,215 | 8,221 |
| 0,75 | 0,017 | 0,088 | 0,183 | 4,687 | 4,679 | 0,027 | 0,142 | 0,306 | 5,796 | 5,802 |
| 1,05 | 0,009 | 0,046 | 0,094 | 0,192 | 0,407 | 0,007 | 0,037 | 0,075 | 0,153 | 0,318 |
Таблица 1.16
| T, K |
|
|||||||||
| 0,402 | 2,01 | 4,02 | 8,04 | 16,08 | 24,12 | 32,16 | 40,2 | 48,24 | 60,3 | |
| 304,37 | -124,05 | -156,31 | -156,30 | -156,28 | -156,22 | -156,17 | -156,12 | -156,06 | -156,01 | -155,93 |
| 415,05 | -135,70 | -136,14 | -136,74 | -162,84 | -162,81 | -162,78 | -162,75 | -162,72 | -162,69 | -162,64 |
| 581,07 | -147,92 | -148,12 | -148,38 | -148,91 | -150,06 | -151,37 | -152,94 | -154,99 | -158,09 | -163,28 |
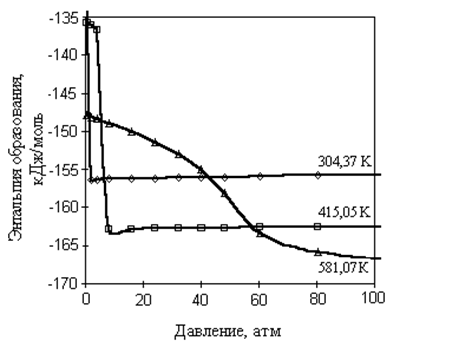
Р и с. 1.5. Зависимость энтальпии образования циклогексана от давления