Реферат: Формально–кинетический анализ гипотез
Кинетический анализ гипотез – важный этап рациональной стратегии, предшествующий планированию кинетического эксперимента с целью дискриминации гипотез. Каждую гипотезу необходимо проанализировать с учётом различных сочетаний быстрых и медленных стадий (приближения квазистационарности, квазиравновесия, возможных лимитирующих стадий), с учётом различной структуры материальных балансов по катализатору, а также природы поверхности в случае гетерогенных катализаторов и состояния комплексов в растворе в случае гомогенного катализа комплексами металлов.
Стехиометрический анализ механизмов.
Теория маршрутов
Первый этап формально-кинетического анализа гипотез о механизме – стехиометрический анализ механизмов. Основой такого анализа является теория маршрутов Хориути-Тёмкина. Важность теории (или метода) маршрутов, позволяющей найти итоговые уравнения реакций, исходя из механизма процесса, а не только на основе материального баланса, видна из следующего примера.
Пример 1. Материальный баланс процесса описывается уравнением (1), а схема механизма – уравнениями (2 – 3):
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
где М – катализатор, МА и МВ – промежуточные вещества.
Если сложить стадии механизма (для стационарных или квазистационарных режимов), промежуточные вещества и катализатор исчезают и получается итоговое уравнение
![]() (5)
(5)
С позиций стехиометрии и материального баланса уравнения (1) и (5) линейно зависимы. С позиций кинетических скорость реакции превращения А в В есть скорость по итоговому уравнению (5) и именно эта скорость R, как разность скоростей в прямом (R+) и обратном (R–) направлениях (R = R+ – R–) соответствует механизму (2 – 4). При [А], [В] >> [М]Σ и [М]Σ >> [МА], [МВ] ([М]Σ @ [М]) получаем для стационарного или квазистационарного режимов
![]() (6)
(6)
При равновесии (R+ = R–) из (6) получается константа равновесия реакции (5) К = [А]2 / [В]2. Если возникает задача найти скорость прямой реакции, используя скорость обратной реакции и соотношение (7)
![]() , (7)
, (7)
где DG – изменение изобарно-изотермического (химического) потенциала для итогового уравнения в ходе реакции, то для записи DG также следует использовать уравнение, вытекающее из механизма, в данном случае, уравнение (5). Соотношение (7) справедливо только для одномаршрутных реакций.
Напомним определения маршрута реакции. Маршрутом реакции называется такая последовательность стадий, входящих в механизм сложной реакции, которая при сложении уравнений стадий, умноженных на особые стехиометрические числа стадий νj, даёт итоговое уравнение, не содержащее промежуточных веществ (интермедиатов) – важнейших участников механизма сложной реакции.
Маршрутом реакции называется также и вектор, компонентами
которого являются стехиометрические числа стадий νj. Для механизма (2 – 4) таким вектором
являются набор из трёх компонент ν2 = 1, ν3
= 1, ν4 = 1: ![]() = (1, 1, 1). Другой набор стехиометрических чисел
= (1, 1, 1). Другой набор стехиометрических чисел ![]() = (0.5, 0.5,
0.5) даёт уравнение А = В, но как мы видели выше, такое итоговое уравнение
противоречит кинетике стационарного процесса.
= (0.5, 0.5,
0.5) даёт уравнение А = В, но как мы видели выше, такое итоговое уравнение
противоречит кинетике стационарного процесса.
Число линейно-независимых маршрутов определяется по уравнению Хориути (8)
P = S – I + W, (8)
где I – общее число интермедиатов, W – число независимых линейных законов сохранения (число линейных связей между интермедиатами) NI = I – W. Очевидно, что NI = rank BX, где BX – матрица стехиометрических коэффициентов для интермедиатов (BX – блок стехиометрической матрицы механизма ВМ).
Для каталитических реакций с одним типом катализатора (или активных центров) W = 1, т.е. имеется один стехиометрический закон сохранения – материальный баланс по катализатору. В случае двух катализаторов, участвующих в механизме реакции, W = 2.
Для нахождения векторов стехиометрических чисел ![]() ,т.е. матрицы
Г, решается система уравнений
,т.е. матрицы
Г, решается система уравнений
![]() (9)
(9)
Для решения системы (9) используем только линейно-независимые
столбцы матрицы ВХ и один вектор из матрицы Г.
Например, для двухмаршрутного каталитического процесса с катализатором М и
первым интермедиатом Х1 имеем матрицу ВХ (rank BX = 2) S = 4 и вектор ![]() .
.

![]()
Получим 2 уравнения:
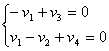 (10)
(10)
Для решения системы двух уравнений с четырьмя неизвестными разделим переменные на независимые, значения которых задаём, и зависимые
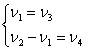 .
(11)
.
(11)
При таком разделении системы уравнений следует проверить, чтобы определитель левой части D ≠ 0, иначе система не будет иметь решения. Для удобства нахождения значений ν1 и ν2 (при заданных ν3 и ν4), систему (11) приводят к единичному базису (метод Жордано-Гаусса) так, чтобы каждое уравнение слева имело одно неизвестное. Так, сложив уравнения в системе (11), получим ν2 = ν3 + ν4 и система (11) примет вид (12)
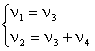 (12)
(12)
Задавая ν3
= 1 и ν4 = 0, получим ν1 = 1 и ν2
= 1, т.е. ![]() для
первого маршрута. При ν3 = 0 и ν4
= 1 ν1 = 0 и ν2 = 1 и
для
первого маршрута. При ν3 = 0 и ν4
= 1 ν1 = 0 и ν2 = 1 и ![]() для второго
маршрута. При ν3 = 0 и ν4 = 0 все
решения будут нулевыми.
для второго
маршрута. При ν3 = 0 и ν4 = 0 все
решения будут нулевыми.
Пример 2. Рассмотрим пример нелинейного механизма.
![]() (13)
(13)
![]()
Здесь одно линейно-независимое промежуточное соединение Х (NI = 1), 2 стадии (S = 2) и один маршрут Р = 2 – 1
= 1. Матрицу стехиометрических коэффициентов интермедиатов ВХ
запишем вектором-строкой ![]() . Поскольку
. Поскольку ![]() , умножим вектор-строку
, умножим вектор-строку![]() на вектор
столбец
на вектор
столбец ![]() .
Получим одно уравнение
.
Получим одно уравнение
ν1 – 2ν2 = 0, (14)
которое имеет одно
линейно-независимое решение. Задав ν1 = 1, получим ν2
= 0.5. При ν1 = 2 ν2 = 1 и т.д.
Если при сложении стадий (1) и (2) (для исключения Х из итогового
уравнения) умножим стадии (1) и (2) на наборы ![]() |1 0.5| или
|1 0.5| или ![]() |2 1|, получим итоговые уравнения,
соответственно, маршрутов N(1) и N(2):
|2 1|, получим итоговые уравнения,
соответственно, маршрутов N(1) и N(2):
N(1) А = 1/2 Р
N(2) 2А = Р
Очевидно, что ΔG(Р) (по маршруту N(Р)) определяется уравнением (15)
![]() (15)
(15)
В соответствии с уравнением (7) для ΔG(Р) и для ΔGj получаем:
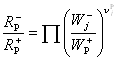 (16)
(16)
где ![]() –скорости элементарной
стадии в прямом и обратном направлениях.
–скорости элементарной
стадии в прямом и обратном направлениях.
Для маршрута N(1):
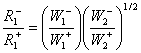 (17)
(17)
Для маршрута N(2):
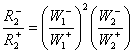 (18)
(18)
Примем стадию (1)
механизма (13) в качестве лимитирующей, а стадию (2) – квазиравновесной (![]() ). Тогда при
равновесии брутто-процесса (
). Тогда при
равновесии брутто-процесса (![]() ) получим из уравнения (17)
константу равновесия итогового уравнения для маршрута N(1)
) получим из уравнения (17)
константу равновесия итогового уравнения для маршрута N(1)
![]() ,
,
а из уравнения (18) – константу равновесия маршрута N(2)
![]() .
.
Такие уравнения для К(1) и К(2) получим и в случае лимитирующей второй стадии.
Если кинетические уравнения получены экспериментально, итоговые уравнения выбираются уже не произвольно. Так, например, для механизма (13), если R+ µ [A] (стадия (1) лимитирующая), итоговое уравнение, которое получится при равновесии, будет уравнением N(1). Если R+ µ [A]2, итоговое уравнение N(2). Поэтому для определения скорости R- по известной R+ (и наоборот) следует использовать соответствующие кинетике итоговые уравнения. Таким образом, кинетика реакции в случае нелинейного механизма может ограничивать выбор маршрута.
Для обратимых стационарных и квазистационарных процессов с
линейными механизмами нет ограничений при выборе базиса маршрутов и итоговых
уравнений.. Однако итоговое уравнение, как мы видели в случае 2А = 2В, не
должно противоречить кинетическому уравнению, следующему из механизма реакции.
Для механизмов с необратимыми стадиями формально также можно использовать любые
наборы ![]() ,
включая и отрицательные νj для необратимых стадий. Вместе с
тем, в согласии с физическим смыслом целесообразно выбирать такие базисы
маршрутов, чтобы и маршрут и скорость по маршруту относились к термодинамически
и кинетически разрешенному направлению реакции (направление необратимых
стадий).
,
включая и отрицательные νj для необратимых стадий. Вместе с
тем, в согласии с физическим смыслом целесообразно выбирать такие базисы
маршрутов, чтобы и маршрут и скорость по маршруту относились к термодинамически
и кинетически разрешенному направлению реакции (направление необратимых
стадий).
Для нелинейных одномаршрутных механизмов, имеющих лимитирующую стадию, можно получить выражения для скорости лимитирующей стадии в прямом и обратном направлениях, но в этом случае выбор итогового уравнения будет определяться природой лимитирующей стадии.
Получив матрицу Г, найдём итоговое уравнение, т.е. матрицу стехиометрических коэффициентов итоговых уравнений ВР,
![]() или
или ![]()
и уравнения, связывающие скорости по веществу RN и скорости по маршруту RP
![]() .
.
Поскольку ![]() , получим
, получим ![]() или
или ![]() . Домножив обе части
полученного матричного уравнения слева на ВN, получим уравнение (19)
. Домножив обе части
полученного матричного уравнения слева на ВN, получим уравнение (19)
ГRP = Wj, (19)
называемое условием стационарности стадий Хориути - Тёмкина. Это уравнение устанавливает связь между скоростью стадии и скоростью по маршруту и показывает, как стадии механизма перераспределяются по маршрутам. Кроме того, уравнение (19) можно использовать и для вывода уравнений для скоростей Ri и RP (аналогично методу Боденштейна), поскольку система (19) содержит S уравнений и S неизвестных (S = NI + P). Условие стационарности стадий (19) эквивалентно условию Боденштейна
![]() . (20)
. (20)
Из (20) и (19) получаем уравнение (9), используемое для нахождения базиса маршрутов
![]()
![]()
![]() .
.
Пример 3. Механизм гидрирования этилена (21) на поверхности твердого металлического катализатора опишем последовательностью четырех элементарных стадий:
![]() (21)
(21)
![]()
![]()
![]()
![]()

NI = rankBX = 2 (есть один закон сохранения, ![]() ). Следовательно,
P = S – NI = 2. Найдем матрицу Г. Для этого запишем систему
уравнений
). Следовательно,
P = S – NI = 2. Найдем матрицу Г. Для этого запишем систему
уравнений ![]() .
Возьмем два независимых столбца (Z, ZH2) (см. уравнения (10 – (12))
.
Возьмем два независимых столбца (Z, ZH2) (см. уравнения (10 – (12))
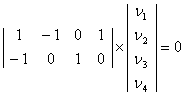
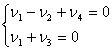
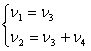
![]()
Задавая n3 и n4, получим два вектора nj для двух маршрутов, т.е. матрицу Г:

Зная Г, найдем BP и итоговые уравнения маршрутов BP = ГTBN.
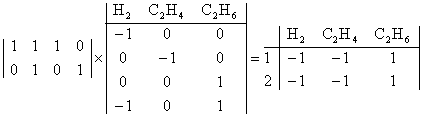
Итоговые уравнения для обоих маршрутов одинаковы
I) H2 + C2H4 = C2H6
II) H2 + C2H4 = C2H6
В этом случае
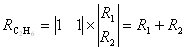
Поскольку стадия механизма (4) обратима, можно взять другую комбинацию маршрутов:
![]()

Получим другую матрицу BP:
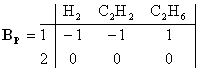
и новые итоговые уравнения:
I) H2 + C2H4 = C2H6
II*) 0 = 0
Второй маршрут (II*) называют пустым маршрутом. Скорость реакции по пустому маршруту не равна нулю. Это скорость перехода интермедиатов:
![]()
по циклической последовательности стадий. Скорости ![]() ,
, ![]() ,
, ![]() по пустому
маршруту равны нулям.
по пустому
маршруту равны нулям. ![]() ,
, ![]() ,
, ![]() .
.
Ранг матрицы BP, т.е. базис QP итоговых уравнений, для маршрутов I и II равен 1 (QP = rankBP = 1). Во втором случае (I и II*) число ненулевых итоговых уравнений равно QP. Такой базис маршрутов называется “стехиометрическим базисом” маршрутов (число пустых маршрутов равно P – QP).
На данном множестве реагентов и продуктов мы имеем максимальный базис итоговых (брутто) реакций по стехиометрическому правилу Гиббса
![]() , (22)
, (22)
где N – общее число участников, Н – атомная матрица. Сравнение Qmax с базисом итоговых уравнений маршрутов QP дает неравенство:
Qmax ≥ QP, (23)
при этом, QP ≤ P, Qmax ≥ P.
В рассмотренном выше примере №1 Qmax = 1, QP = 1, Р = 2.
Пример 4. Рассмотрим более сложный случай пятистадийного цепного процесса пиролиза этана.
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
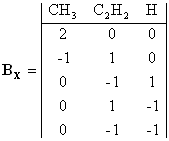
rankBX = 3 P = S – NI = 5 – 3 = 2
Произведение ![]() дает три уравнения:
дает три уравнения:
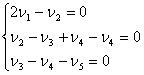
Возьмем n4 и n5 в качестве независимых переменных и преобразуем систему уравнений:
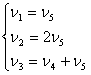
Определитель левой части D ¹ 0. Задавая n4 = 1, n5 = 0 и n4 = 0, n5 = 1, получаем матрицу Г для Р = 2 и матрицу BP:

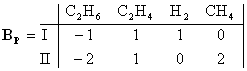
I) C2H6 = C2H4 + H2 QP = rankBP = 2
II) 2C2H6 = C2H4 + 2CH4 Qmax = 2
Приближения квазистационарности и квазиравновесия
При выводе кинетических уравнений часто используют различные допущения о соотношениях скоростей стадий, поскольку скорости элементарных стадий могут сильно различаться по величине. Например, скорости стадий адсорбции и химических превращений на поверхности катализатора. Важное допущение – о наличии медленных и быстрых стадий. Быстрые обратимые стадии являются квазиравновесными (РЕ – preequilibrium), а допущение о наличии таких стадий – приближением квазиравновесия. В закрытых системах особенно для каталитических реакций используют допущение о квазистационарности концентраций интермедиатов (SS – steady - state, допущение Боденштейна). Критерии применимости этих допущений рассмотрены в учебном пособии О.Н. Тёмкина, К.Ю. Одинцова и Л.Г. Брука “Приближения квазистационарности и квазиравновесия в химической кинетике”, М., МИТХТ, 2001г. Здесь приведем условия реализации различных приближений для простой схемы:
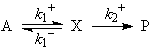 (24)
(24)
Необходимым и достаточным условием реализации приближения Боденштейна (SS) является условие СХ << СА (ΣСXi << CA). Из этого условия следует и условие
![]() (25)
(25)
которое реализуется при ![]() Условие SS может одновременно совпадать с
условием квазиравновесия первой стадии (PE).
Условие SS может одновременно совпадать с
условием квазиравновесия первой стадии (PE).
Для одномаршрутных механизмов единственную медленную стадию (все остальные квазиравновесные) называют лимитирующей стадией. Критерием условия квазиравновесия для механизма (24) является соотношение (26)
![]() (26)
(26)
Из анализа соотношений констант k1, k-1 и k2, приводящих к ε1<<1 и ε2<<1, сделан вывод, что при значительном различии ki (не менее, чем в 10 раз) имеется всего 6 вариантов соотношений констант и по 4 случая реализации режимов SS (ε1<<1) и РЕ (ε2<<1).
Таблица 1. Соотношения констант скорости и режимы протекания процесса (24).
|
№ варианта |
Соотношения ki |
|
|
Режим | Лимитирующая стадия |
| I |
k2>>k1>>k-1 |
<<1 | >>1 | SS | 1 |
| II |
k2>>k-1>>k1 |
<<1 | >>1 | SS | 1 |
| III |
k1>>k2>>k-1 |
>>1 | <<1 |
PE * |
2 |
| IV |
k1>>k-1>>k2 |
>>1 | <<1 | PE | 2 |
| V |
k-1>>k2>>k1 |
<<1 | <<1 | SS, PE | 2 |
| VI |
k-1>>k1>>k2 |
<<1 | <<1 | SS, PE | 2 |
Как мы видим, сильными условиями режима SS являются условия k2>>k1, k-1 (I, II) и k-1>>k1 (V, VI), делающие ε1<<1, в первом случае за счёт быстрого превращения Х, а во втором – за счёт очень маленькой К1 = k1/ k-1.
Вариант III является режимом PE*( ε2<<1), но при большой разнице констант. При десятикратном различии констант режим РЕ устанавливается позднее, чем в других случаях (при большом значении выхода продукта Р), по существу на завершающем этапе процесса.
Рассмотренные 6 крайних случаев полезно дополнить вариантами реализации режимов SS и РЕ при условии равенства (близости) констант. Случай близости всех констант k1 ≈ k-1 ≈ k2 не соответствует критериям SS и РЕ – приближений. При попарном равенстве констант имеем ещё 5 случаев (таблица 2).
Таблица 2. Соотношения констант скоростей и режимы протекания процесса.
|
№ варианта |
Близкие константы |
Соотношения ki |
|
|
Режим | Лимитирующая стадия |
| VII |
k1 ≈ k-1 |
k2 >> k1 ≈ k-1 |
<< 1 | >> 1 | SS | 1 |
| VIII |
k1 ≈ k-1 |
k2 >> k1 ≈ k-1 |
≈ 1 | << 1 | PE | 2 |
| IX |
k2 ≈ k-1 |
k1 << k-1 ≈ k2 |
<< 1 | ≈ 1 | SS | 1 |
| X |
k2 ≈ k-1 |
k1 << k-1 ≈ k2 |
>> 1 | << 1 |
PE * |
2 |
| XI |
k1 ≈ k2 |
k-1 >> k1 ≈ k2 |
<< 1 | << 1 | SS, PE | 2 |
* Режим РЕ при k1 / k-1 ≥ 100
При близости констант k2 и k-1 также, как и в варианте III, режим не является строго квазиравновесным (соотношение СХ / СА = α не постоянно в ходе процесса). При равенстве k1 = k2 достигается режим квазистационарности в условиях квазиравновесия. Таким образом, приближение SS выполняется:
- при k2 >> k1 (I, II, V, VII, VIII, IX);
- при k1>>k2 (VI);
- при k1 ≈ k2 (XI).
Приближение РЕ выполняется:
- при k2 >> k1 (V);
- при k1>>k2 (IV, VI, VIII и III, X при больших значениях k1 / k–1);
- при k1 ≈ k2 (XI).
Экспериментальными критериями режима SS являются следующие:
1) СХ / СА = α << 1 Проверяется экспериментально в результате анализа материального баланса, который должен выполняться с погрешностью эксперимента
![]()
2)
![]() Соотношение легко проверяется
экспериментально. Величина delta
Соотношение легко проверяется
экспериментально. Величина delta
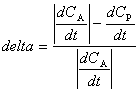
не должна превышать ошибки эксперимента на большом интервале времени при выходе продукта (на СА0) до 70 – 90%.
3)
В случае
гомогенных каталитических реакций при ![]() ошибка SS-приближения не превышает 1%.
ошибка SS-приближения не превышает 1%.
4)
В гетерогенном
катализе в закрытой и открытой системах количество молей вещества в газе (![]() ) должно быть
больше количества вещества на поверхности (
) должно быть
больше количества вещества на поверхности (![]() ):
):
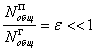 .
.
В этом случае ![]()