Курсовая работа: Топологические пространства

§1. Топологические пространства

(предварительные сведения)

1.1.  Непрерывные отображения топологических

пространств

Пусть Х и Y топологические пространства.

Определение 1. Отображение f : Х→Y называется непрерывным, если у всякого множества О, открытого в пространстве Y, полный прообраз  f ^–1(О) открыт  в пространстве Х.

Замечание 1. Для любого подмножества А пространства Y и отображения f: X→Y справедливо следующее равенство:

            (1).

Теорема 1.1. Отображение f : X→Y  является непрерывным тогда и только тогда, когда у всякого множества F, замкнутого в Y, полный прообраз f ^–1(F) замкнут в Х.

Доказательство. Необходимость. Пусть отображение f : X→Y является непрерывным, т.е. для любого множества О, открытого в Y, прообраз f ^–1(O) открыт в Х, и пусть F произвольное замкнутое в Y множество. Тогда множество CF открыто в Y, и множество открыто в Х, в силу непрерывности отображения f  и равенства (1). Следовательно, множество f ^–1(F) замкнуто в Х.

Достаточность. Пусть для любого множества F, замкнутого в Y, полный прообраз f ^–1(F) замкнут в Х. Рассмотрим произвольное открытое в Y множество О. Тогда множество CO будет замкнутым в Y. Поэтому  замкнутое в Х множество. Следовательно, множество открыто в Х. Таким образом, для любого множества О, открытого в Y, полный прообраз открыт в Х и отображение f : X→Y непрерывное по определению. €

1.2. Связность топологических пространств

Определение 4. Топологическое пространство Х называется несвязным, если его можно разбить на два непустых непересекающихся открытых множества:

Х = О₁  О₂.

Определение 5. Пространство Х называется связным, если такого разбиения не существует.

Заметим, что если несвязное пространство Х разбито на два непустых открытых множества О₁ и О₂, не имеющих общих точек, то О₁ = CO₂ и O₂ = CO₁. Поэтому можно дать другое определение связного пространства:

Определение 6. Топологическое пространство Х называется связным, если в нём одновременно открытым и замкнутым множеством является лишь само пространство или пустое множество.

Определение 7. Множество Н в топологическом пространстве Х называется связным, если оно является связным пространством относительно индуцированной топологии.

Теорема 1.2. Для топологического пространства Х следующие условия эквивалентны:

(1)  существуют непустые открытые множества О₁ и О₂, для которых О₁ ∩ О₂ = Æ  и  О₁  О₂ = Х;

(2)  существуют непустые замкнутые множества F₁ и F₂, для которых F₁ ∩ F₂ = Æ  и  F₁  F₂ = Х;

(3)  в  Х  существует нетривиальное открыто-замкнутое множество G;

(4)  существует непрерывная сюръективная функция φ : Х ® {1, 2}.

Доказательство. Из (1) следует (2). Пусть О₁ и О₂ непустые открытые множества, для которых О₁ ∩ О₂ = Æ и О₁  О₂ = Х. Рассмотрим множества F₁ = СО₁ и F₂ = СО₂. Они являются непустыми замкнутыми множествами, причём F₁ ∩ F₂ = Æ  и  F₁  F₂ = Х.

Из (2) следует (3). Пусть F₁ и F₂  непустые замкнутые множества, для которых F₁ ∩ F₂ = Æ  и  F₁  F₂ = Х. Рассмотрим множество  G = F₁ Ì Х. Множество F₁ замкнутое по условию и открытое, как дополнение до замкнутого множества F₂ (F₁ = CF₂). Поэтому множество G = F₁ является нетривиальным открыто-замкнутым множеством в Х.

Из (3) следует (4). Пусть G нетривиальное открыто-замкнутое множество в Х. Тогда множество Q = CG тоже нетривиальное открыто-замкнутое в Х.

Рассмотрим функцию φ : Х ® {1, 2}, при которой

φ(х) =  

Функция φ является непрерывной и сюръективной, т.к. для любых элементов 1 и 2 множества {1, 2} прообразы их соответственно равны множествам G и Q, открытым в Х.

Из (4) следует (1). Пусть φ : Х ® {1, 2} – непрерывная сюръективная функция и пусть множество M = {1, 2}, т.е. φ(Х) = М. Множества  A  = {1}  и  B = {2} – непустые, непересекающиеся открытые в М и . Функция φ сюръективная, поэтому справедливо следующее равенство:

Х = φ ^–1(М) = φ ^–1(А  В) = φ ^–1(А)  φ ^–1(В),

причём φ ^–1(А)  и  φ ^–1(В) непустые непересекающиеся множества. В силу того, что функция φ непрерывная, множества  О₁ = φ ^–1(А)  и  О₂ = φ ^–1(В) непустые, непересекающиеся открытые в  Х  и  Х = О₁  О₂ . €

Теорема 1.3. Пусть в топологическом пространстве Х даны два дизъюнктных замкнутых множества F₁  и  F₂ и непустое связное множество М, содержащееся в объединении F₁  F₂. Тогда М содержится только в одном из множеств, входящих в объединение, т.е. либо в F₁, либо в F₂.

Доказательство. Пусть F₁ и F₂ дизъюнктные замкнутые в Х множества и непустое связное множество М Í F₁  F₂. Тогда

М = (М ∩ F₁)  (M ∩ F₂).

Так как множества F₁ и F₂ замкнутые в Х, то множества М ∩ F₁ и M ∩ F₂ замкнутые в М. Но множество М связно, т.е. его нельзя разбить на два непустых непересекающихся замкнутых множества, поэтому одно из множеств, например M ∩ F₂, пустое. Тогда

М = М ∩ F₁ Í F₁. €

Аналогично доказывается

Теорема 1.4. Если связное множество М содержится в объединении двух дизъюнктных открытых множеств О₁ и О₂ топологического пространства Х, то оно целиком содержится только в одном из множеств, входящих в объединение.

Теорема 1.5. Пусть f : Х→Y непрерывное отображение и f (X) = Y. Тогда если Х связно, то Y связно.

Доказательство от противного. Предположим, что пространство Y несвязно. Тогда оно разбивается на два непустых открытых дизъюнктных множества

Y = O₁  O₂.

В силу того, что f  непрерывное отображение и f (X) = Y, прообразы G₁ = f ^–1(O₁)  и  G₂ = f ^–1(O₂) будут непустыми дизъюнктными открытыми множествами, которые в сумме дают всё пространство Х, что противоречит его связности. €

1.3. Компактность топологических пространств

Определение 8. Топологическое пространство называется компактным, если всякое покрытие этого пространства открытыми множествами содержит конечное подпокрытие.

Определение 9. Множество А в топологическом пространстве Х называется компактным, если оно компактно в индуцированной топологии как подпространство.

Теорема 1.6. Подмножество А топологического пространства Х компактно тогда и только тогда, когда из любого его покрытия множествами, открытыми в Х, можно выбрать конечное подпокрытие.

Теорема 1.7. Замкнутое подмножество А компактного пространства Х компактно.

Доказательство. В силу теоремы 1.6, достаточно из произвольного покрытия  множества А открытыми в Х множествами выбрать конечное подпокрытие. Для этого добавим к этим множествам открытое множество Х \ А и получим открытое покрытие всего пространства Х. В силу компактности пространства Х, из этого покрытия можно выделить конечное подпокрытие, причём мы всегда можно считать, что в это подпокрытие входит множество Х \ А. Пусть, например,

.

Очевидно, что множества  образуют искомое конечное подпокрытие множества А. €

Определение 10. Топологическое пространство называется хаусдорфовым, если любые две его различные точки обладают непересекающимися окрестностями.

Теорема 1.8. Компактное подмножество А хаусдорфова пространства Х замкнуто.

Теорема 1.9. Непрерывный образ компактного пространства компактен, т.е. если f : Х→Y – непрерывное отображение и пространство Х компактно, то и множество f (Х) компактно.

Доказательство теорем 1.6 – 1.9 можно найти в [2].

 §2. Связность непрерывных отображений

2.1. Определение связности отображения и простейшие свойства

Пусть f : Х→Y – непрерывное отображение. Для открытого в Y множества U и точки yÎY прообраз f ^–1(U) называется трубкой (над U), а прообраз f ^–1(y) называется слоем (над точкой y).

Определение 11.. Непрерывное отображение f : Х→Y называется несвязным над точкой yÎY, если существует такая окрестность Oy точки y, что трубка f ^–1(U) является несвязной над каждой окрестностью U Í Oy точки y.

Замечание 2. В данном определении достаточно рассматривать только связные окрестности U Í Oy, т.к., если U = U₁  U₂, где  U₁,  U₂ – непустые дизъюнктные открытые в U  (а значит и в Y ) множества, то

f  ^–1(U) = f  ^–1(U₁)  f  ^–1(U₂),        f ^–1(U₁) ∩ f  ^–1(U₂) = Æ,

т.е.  f ^–1(U) несвязно автоматически.

Определение 12. Непрерывное отображение f : Х→Y называется связным над точкой yÎY, если оно не является несвязным над точкой y, т.е. для любой окрестности Oy точки y существует такая связная окрестность U Í Oy точки y, что трубка  f  ^–1(U)  связна.

Определение 13. Непрерывное отображение f : Х→Y называется связным, если оно связно над каждой точкой y Î Y.

Теорема 2.1 (критерии несвязности). Пусть отображение f : Х→Y непрерывно и точка y Î Y. Тогда следующие условия эквивалентны:

(1)  отображение f  несвязно над точкой y Î Y;

(2)  существует такая окрестность Oy точки y Î Y, что каждая трубка f  ^–1(U) над окрестностью U Í Oy точки у распадается на два дизъюнктных непустых открытых в этой трубке множества;

(3)  существует такая окрестность Oy точки y Î Y, что каждая трубка f ^–1(U) над окрестностью U Í Oy точки у распадается на два дизъюнктных непустых замкнутых в этой трубке множества;

(4)  существует такая окрестность Oy точки y Î Y, что в каждой трубке f ^–1(U) над окрестностью U Í Oy точки у существует нетривиальное открыто-замкнутое в этой трубке множество;

(5)  существует такая окрестность Oy точки y Î Y, что для каждой трубки f  ^–1(U) над окрестностью U Í Oy точки у существует непрерывная сюръективная функция  φ : f  ^–1(U) ® {1, 2}.

Доказательство. Из (1) следует (2). Пусть непрерывное отображение f : Х→Y  несвязное над точкой y Î Y, т.е. существует такая окрестность Oy точки y, что трубка f ^–1(U) является несвязной над каждой окрестностью U Í Oy точки y. Таким образом, трубка f ^–1(U) над окрестностью U Í Oy распадается на два дизъюнктных непустых открытых в этой трубке множества, т.е.

f  ^–1(U) = О₁  О₂,  О₁ ∩ О₂ = Æ.

Из (2) следует (3). Пусть трубка f ^–1(U) распадается на два дизъюнктных непустых открытых в этой трубке множества. Тогда, по теореме 1.2, трубка f ^–1(U) распадается на два дизъюнктных непустых замкнутых в этой трубке множества.

Из (3) следует (4). Пусть трубка f ^–1(U) распадается на два дизъюнктных непустых замкнутых в этой трубке множества. Тогда, по теореме 1.2, в трубке f ^–1(U) существует нетривиальное открыто-замкнутое в этой трубке множество.

Из (4) следует (5). Пусть в трубке f ^–1(U) существует нетривиальное открыто-замкнутое в этой трубке множество. Тогда, по теореме 1.2, для трубки f ^–1(U) существует непрерывная сюръективная функция  φ : f  ^–1(U) ® {1, 2}.

Из (5) следует (1). Пусть существует такая окрестность Oy точки  y Î Y, что для трубки f ^–1(U) над некоторой окрестностью U Í Oy существует непрерывная сюръективная функция  φ : f  ^–1(U) ® {1, 2}. Тогда, по теореме 1.2, трубка f ^–1(U) распадается на два дизъюнктных непустых открытых в этой трубке множества. Отсюда, по определению несвязного над точкой отображения, следует, что отображение f  несвязно над точкой y Î Y. €

Определение 14. Отображение f : Х→Y называется послойно связным, если каждый слой f  ^–1(y), где y Î Y, этого отображения является связным множеством.

Теорема 2.2 (о сохранении связности). Пусть отображения  f : X ® Y  и  g : Z ® Y непрерывные и существует непрерывное сюръективное отображение φ : X ® Z, при котором  f = g  φ. Тогда, если отображение  f связно над точкой y Î Y (слой f ^–1(y) связен), то и отображение  g связно над точкой  y Î Y (слой g ^–1(y) связен). В частности, если отображнение f связно (послойно связно), то и отображение g связно (послойно связно).

Доказательство. Пусть отображения f : X ®Y связное над точкой  y Î Y, тогда для любой окрестности Oy точки y существует связная окрестность U Í Oy точки y, трубка над которой f ^–1(U) связна. Отображение φ непрерывное, значит (по теореме 1.5) образ связного множества  f ^–1(U) (связного слоя f ^–1(y)) связен, т.е. множество       φ(f ^–1(U)) (множество φ( f ^–1(y)))  – связное.

Предположим, что отображение g несвязно над точкой  y Î Y, т.е. существует такая связная окресность Oy точки y, что трубка g ^–1(U) является несвязной над каждой окрестностью U Í Oy точки y. (Предположим, что слой g ^–1(y) несвязен над точкой y Î Y).

По условию, f = g  φ, следовательно,

f ^–1(U) = (g  φ) ^–1(U) = φ ^–1(g^–1(U)).

Отсюда, 

φ(f ^–1(U)) = φ(φ^–1(g^–1(U))) =g^–1(U)

(для слоя  φ( f ^–1(y)) = g^–1(y)). Получили противоречие, т.к. множество φ( f ^–1(U)) связное (слой φ( f ^–1(y)) связен), а множество  g^–1(U) (слой g^–1(y)) – нет.

Пусть отображнение  f связно (послойно связное), тогда, по определению 10 (11), оно связно над каждой точкой y Î Y (каждый слой f ^–1(y) связен). Возьмём произвольную точку y Î Y. Если отображение  f связно над этой точкой y Î Y (слой f ^–1(y) связен), то и отображение g связно над этой же точкой (слой g^–1(y) связен). В силу произвольности выбора точки y, заключаем, что отображение g связно над каждой точкой  y Î Y (послойно связно). €

2.2. Замкнутые отображения. Связь связности и послойной связности

Определение 15. Отображение f : X→Y называется замкнутым, если для каждого замкнутого множества  F Í Х образ  f (F) является замкнутым множеством в Y.

Определение 16. Отображение f : X→Y называется замкнутым над точкой yÎY, если для всякой окрестности О слоя f ^–1(y) Ì Х найдётся окрестность Oy точки y, трубка над которой f ^–1(Oy) содержится в данной окрестности О слоя f ^–1(y):

f ^–1(y) Í f ^–1(Oy) Í О.

Связь между замкнутостью  в точке и общей замкнутостью устанавливает следующая

Лемма 2.1. Непрерывное отображение f : X→Y замкнуто тогда и только тогда, когда оно замкнуто над каждой точкой  yÎY.

Доказательство. Необходимость. Пусть отображение f : X→Y замкнуто. Возьмём произвольную точку  y Î Y  и рассмотрим окрестность О множества  f ^–1(y). Множество F = X \ О замкнуто в Х и F ∩ f ^–1(y) = Æ. Поэтому множество f (F) замкнуто в Y и точка y Ï f(F). Значит окрестность Oy = Y \ f (F) точки y обладает таким свойством  f ^–1(Oy) ∩ F = Æ, следовательно, f ^–1(Oy) Ì О. Таким образом, отображение f замкнуто над каждой точкой yÎY в силу того, что точка y взята произвольно.

Достаточность. Пусть непрерывное отображение f замкнуто над каждой точкой yÎY. Предположим, что образ f (F) некоторого замкнутого в Х множества F не замкнут в Y. Пусть точка  y Î [f(F)] \ f(F), т.е. принадлежит границе множества f (F). Множество X \ F является окрестностью множества f ^–1(y). Следовательно, существует такая окресность Oy точки y, что f ^–1(Oy) Ì X \ F. Но тогда  Oy ∩ f (F) = Æ и поэтому точка y Ï [f (F)].

Получили противоречие. Отсюда, отображение f замкнуто. €

Следующие утверждения указывают на некоторые важнейшие примеры замкнутых отображений.

Предложение 2.1. Непрерывное отображение f : X ® Y компактного пространства X в хаусдорфово пространство Y является замкнутым.

Доказательство. Рассмотрим произвольное множество F, замкнутое в Х. Оно будет компактным (по теореме 1.7). Тогда непрерывный образ f (F) компактного множества F будет компактен в Y (по теореме 1.9). Пространство Y хаусдорфово, следовательно, множество f (F) – замкнуто (в силу теоремы 1.8). Таким образом, отображение f является замкнутым. 

Следствие 2.1. Биективное непрерывное отображение f : X ® Y компактного пространства X на хаусдорфово пространство Y является гомеоморфизмом.

Доказательство. Рассмотрим произвольное замкнутое подмножество F компактного пространства X. В силу предложения 2.1, образ f (F) – замкнутое множество. Тогда, по теореме 1.1, отображение f  ^–1 является непрерывным, следовательно, f – гомеоморфизм.ÿ

Предложение 2.2. Пусть отображение f : X ® Y замкнуто над точкой y Î Y и пусть множество Z замкнуто в X. Тогда подотображение g = f |_Z : Z ® Y замкнуто над точкой y. В частности, если отображение f замкнуто (над каждой точкой y Î Y), то и отображение g замкнуто.

Доказательство. Возьмём произвольную точку y Î Y и рассмотрим окрестность U Ì Z слоя g^–1(y). Тогда в Х найдётся открытое множество  U¢  такое, что  U = U¢  Z.  Множество  O = U¢  (X \ Z)  будет окрестностью слоя  f ^–1(y) . Отображение f замкнутое над точкой  y Î Y,  поэтому найдётся такая окрестность Oy точки y, что       f ^–1(Oy) Ì O. Тогда g^–1(Oy) Ì Z  O = Z  U¢ = U.

В силу произвольности выбора точки y Î Y, можно заключить, что если отображение f замкнутое над каждой точкой y Î Y, то и отображение g замкнутое над каждой точкой y Î Y. 

Предложение 2.3. Пусть отображение f : X ® Y замкнуто над точкой y Î T Í Y, где T – произвольное множество в Y. Тогда под-отображение  g = f | : f ^–1(T) ® T замкнуто над точкой y. В частности, если отображение f замкнуто (над каждой точкой y Î T), то и отображение g тоже замкнуто (над каждой точкой  y Î T).

Доказательство. Возьмём произвольную точку y Î T Í Y и некоторую окрестность О слоя g^–1(y) = f ^–1(y), такую что

O = O'  f ^–1(T),

где О¢ – открытое в Х множество. Так как отображение f замкнутое над точкой y, найдётся такая окрестность O'y в Y точки y, что            f ^–1(O'y) Ì О'. Тогда в Т существует  такая окрестность Oy точки y, что Oy = Oy'  T, и  f ^–1(Oy) = g^–1(Oy) Ì O'  f ^–1(T) = О. Следовательно, отображение g будет замкнуто над y Î Y.

Если отображение  f  замкнутое над каждой точкой y, то и отображение g будет замкнутым над каждой точкой y. 

Установим теперь связь между связными и послойно связными замкнутыми отображениями.

Предложение 2.4. Пусть отображение f : X→Y замкнуто над точкой y Î Y  и слой f ^–1(y) является несвязным множеством. Тогда отображение f несвязное над точкой y. В частности, если отображение f замкнуто и каждый его слой несвязен, то оно несвязное над каждой точкой y Î Y.

Доказательство. Поскольку слой f ^–1(y) является несвязным множеством, то найдутся такие непустые открытые в f ^–1(y) множества О₁ и О₂, что О₁ ∩ О₂ = Æ и О₁  О₂ = f ^–1(y). Тогда в Х существуют открытые множества Q₁ и Q₂ такие, что

O₁ = Q₁  f ^–1(y),            O₂ = Q₂  f  ^–1(y).

Рассмотрим замыкание этих множеств  и  в Х. Их пересечение  есть замкнутое множество, и F  f ^–1(y) = Æ (т.к. О₁ и О₂ замкнутые в f  ^–1(y), как дополнения до открытых). Множество О = (Q₁  Q₂) \ F открыто в Х, причём  f  ^–1(y) Ì О. Для этой окрестности О (в силу замкнутости отображения f ) найдётся такая окрестность Oy точки y, что  f ^–1(Oy) Ì О. Пусть G₁ = f ^–1(Oy)  Q₁ и G₂ = f ^–1(Oy)  Q₂ – открытые в f ^–1(Oy) множества. Так как

 Ì Х \ f ^–1(Oy),

то G₁ ∩ G₂ = Æ. Тогда f ^–1(Oy) = G₁ G₂. Следовательно, трубка f ^–1(Oy) несвязна.

Пусть U Í Oy – произвольная окрестность точки y. Тогда  и  – дизъюнктные множества, открытые в f  ^–1(U),  и непустые, т.к. О₁ Ì  и О₂ Ì . Следовательно, для любой окрестности U Í Oy трубка f  ^–1(U) несвязна. Отображение f  несвязно над точкой y по определению.

Если отображение f замкнутое над каждой точкой  y Î Y  и каждый его слой несвязн, тогда, для произвольной точки y, отображение f  будет несвязным над ней, следовательно, и над каждой точкой y Î Y.

Из установленного предложения автоматически вытекает

Следствие 2.2. Пусть отображение f : X→Y замкнуто над точкой y Î Y и связно над точкой y. Тогда слой f  ^–1(y) является связным множеством. В частности, если f замкнутое и связное отображение, то оно послойно связное.

Предложение 2.5. Пусть отображение f : X→Y замкнутое и послойно связное. Тогда оно связное.

Доказательство. Возьмём произвольную точку y Î Y и предположим, что отображение f несвязно над точкой y. Тогда существует такая окрестность Oy точки y, что трубка f ^–1(U) является несвязной над каждой окрестностью U Í Oy точки y. Зафиксируем некоторую такую связную окрестность U, для которой выполняются следующие условия:

f ^–1(U) = О₁  О₂,       О₁ ∩ О₂ = Æ,

где О₁ и О₂ – непустые открытые в  f ^–1(U) множества.

Слой f ^–1(y) связен и f ^–1(y) Ì f ^–1(U), отсюда,  f ^–1(y) содержится либо в О₁, либо в О₂ (по теореме 1.4). Рассмотрим произвольную точку х₁ÎО₁. Образ этой точки f (x₁) = y₁ Ì U. По условию, слой f ^–1(y₁) связен и  f ^–1(y₁) Ì О₁ О₂ = f ^–1(U). Поскольку О₁ ∩ О₂ = Æ и х₁ÎО₁, следовательно (по теореме 1.4),  f ^–1(y₁) Ì О₁. (Другими словами, если одна точка слоя принадлежит множеству О₁, то и весь слой принадлежит этому множеству.)

Отсюда, так как точка х₁ произвольная, то О₁ = f ^–1( f (O₁)). Аналогично доказывается, что О₂ = f ^–1(f (O₂)).

Отображение f  замкнутое, тогда, по теореме 2.3, подотображение  g = f : f ^–1(Oy) ® Oy также замкнутое. Таким образом, множества f (O₁) = g (O₁)  и  f (O₂) = g (O₂) будут непересекающимися открыто-замкнутыми в U и U = f (O₁)  f (O₂), т.е. окрестность U несвязна. Это противоречит выбору окрестности U. 

Для замкнутых отображений итоговую взаимосвязь между послойной связностью и связностью теперь можно выразить в форме следующей теоремы:

Теорема 2.3. Замкнутое отображение f : X→Y связно тогда и только тогда, когда оно послойно связно.

(Вытекает из следствия 2.1 и предложения 2.5).

Из последней теоремы и предложений 2.2 – 2.3 получаются такие следствия:

Следствие 2.3. Пусть отображение f : X→Y замкнутое, Z Í X замкнуто в Х. Подотображение g = f |_Z : Z ® Y является связным тогда и только тогда, когда оно послойно связное.

Следствие 2.4. Пусть отображение f : X→Y замкнутое, T Í Y произвольное множество. Подотображение  g = f | : f ^–1(T) ® T является связным тогда и только тогда, когда оно послойно связное.

Рассмотренные здесь свойства будут использованы в следующих пунктах в качестве основы для построения примеров связных и несвязных отображений.

2.3. Связь между связностью пространств

и отображений

Пусть пространство Y = {*} – одноточечное. В этом случае отображение f : X→Y непрерывно и является связным (несвязным) тогда и только тогда, когда пространство Х связно (несвязно), т.к. трубки и слои над пространством Y совпадают со всем пространством Х.

Этот факт позволяет строить многочисленные примеры связных и несвязных отображений. Для этого достаточно взять связные и несвязные пространства и отображение их в одноточечные множества.

Пример. Рассмотрим отображение f : [-1;1] ® R, для которого f (х) = 0 при любом х Î [-1;1]. Отображение f связно тогда и только тогда, когда слой  f ^–1(y) над точкой y = 0 связен. Но f ^–1(0) = [-1;1] – связное множество. Причём, понятия трубки и слоя над точкой y = 0 совпадают, поэтому отображение f является связным и послойно связным.

Если отображение f : [-1;1]  [2;3] ® R задано условием  f (х) = 0 для любого х Î [-1;1]  [2;3], то оно несвязно (послойно несвязно) над точкой y = 0 в силу несвязности трубки (слоя) f ^–1(0) = [-1;1]   [2;3].

В рассмотренных примерах пространство Y является связным. Это условие и условие связности отображения f оказались необходимым и достаточным условием для связности пространства Х. Более того, имеет место

Теорема 2.4. Пусть сюръективное отображение f : X→Y непрерывно и связно. Пространство  X является связным тогда и только тогда, когда пространство Y связное.

Доказательство. Необходимость. По теореме 1.5 (§1), если  f : Х→Y непрерывное отображение,  f (X) = Y и  Х связно, то Y связно.

Достаточность. Пусть пространство Y связно. Предположим, что пространство Х несвязно. Тогда в Х найдутся такие непустые дизъюнктные открытые множества О₁ и О₂, что О₁  О₂ = Х. Допустим, что найдётся точка y Î . Тогда в любой окрестности слоя f ^–1(y) содержаться как точки множества О₁, так и точки множества О₂. С другой стороны,  f ^–1(y) Ì f ^–1(U), где трубка f ^–1(U) является связным множеством (в силу связности отображения f над точкой y) и должна содержаться либо в О₁, либо в О₂ (по теореме 1.4). Получили противоречие. Следовательно,

 = Æ,

т.е.   и   – непустые дизъюнктные замкнутые множества. Но f (О₁)  f (О₂) = Y, значит,

 = f (О₁)     и     = f (О₂),

т.е. эти множества открыто-замкнутые. Это противоречит связности пространства Y.

Таким образом, предположение о несвязности топологического пространства Х неверно, а верно то, что требуется доказать. €

Другой связи между связностью пространств и связностью отображений может и не быть.

f ^–1(U) = 

распадается на два непустых непересекающихся открытых в R множества, т.е. f ^–1(U) – несвязное множество. Таким образом, отображение f несвязно по определению.

Можно привести ещё пример такого рода. Пусть Oxy – прямоугольная декартова система координат. Рассмотрим кольцо ω с центром в начале координат и радиусами r = a, R = b (рис. 2). Пусть pr_X : ω → [– b; b] – проекция этого кольца на ось Ox, где pr_X (x; y) = х Î [– b; b] для любой точки (x; y) Î ω. Возьмём произвольную точку х Î (– a; a) Ì [– b; b]. Для любой окрестности       U Ì (– a; a)  точки х трубка  является несвязной, т.к. состоит из двух частей A и B (рис. 2). Таким образом, проекция pr_X  –  является несвязным отображением.

Пусть, например, отображение f : R \ {0} ® R \ {0} задано формулой  f (х) =  для любого х Î R \ {0} (рис. 3). Возьмём произвольную точку y Î R \ {0}. Для любой окрестности Oy Ì R \ {0} точки y найдётся связная окрестность U Í (0; + ¥) (или U Í (– ¥; 0)), трубка     f ^–1(U)  над которой связна (т.к. f ^–1(U) содержит часть ветви гиперболы или всю ветвь, которая связна и даже линейно связна).

Пусть Х = [0; 1], Y = [0; 1]  [2; 3]. Рассмотрим проекцию : X ´ Y ® Y (рис. 4), где pr_Y (x; y) = y Î Y для любой точки (x; y) Î X ´ Y. Множества X ´ Y  и Y являются несвязными, но проекция   – связное отображение (в силу теоремы 2.7, которая будет доказана в пункте 2.4).

Рассмотрим другие примеры связных отображений, связаные с непрерывными числовыми функциями.

Теорема 2.6. Непрерывная функция f : [a; b] → R является связной тогда и только тогда, когда она монотонна, т.е. когда для любых точек х, х¢ Î [a; b], где х £ х¢, выполняется только одно из двух свойств: f (x) £ f (x¢ ) либо f (x) ³ f (x¢ ).

Доказательство. Необходимость. Функция f является отображением компактного множества в хаусдорфово пространство, поэтому она замкнута (в силу предложения 2.1). Тогда, по теореме 2.3, функция  f  является послойно связной.

Предположим, что f – не монотонна. Тогда найдутся такие точки х₁, х₂, х₃ Î [a; b] и х₁ <  х₂ <  х₃, для которых выполняется система неревенств:

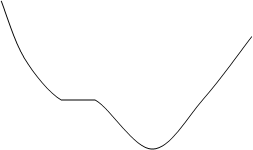
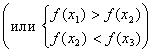Положим f (x₁) = y₁, f (x₂) = y₂, f (x₃) = y₃ и y₃ ³ y₁ (или y₁ ³ y₃). Тогда слой f ^–1(y₃) является связным замкнутым подмножеством прямой y = y₃ (рис. 5), т.е. отрезком. По теореме о промежуточном значении функции, существует точка х¢ Î [x₁; x₂) и f (x¢ ) = y₃. В силу связности слоя f ^–1(y₃), отрезок [А ; В] (см. рис. 5) должен целиком лежать в слое f ^–1(y₃). Но точка (x₂; y₂), где x¢ < x₂ < x₃, не принадлежит прямой y = y₃, поэтому слой f ^–1(y₃) распадается на два непустых непересекающихся замкнутых в f ^–1(y₃)  множества. Это противоречит послойной связности функции  f. Следовательно,  f – монотонна.

Достаточность. Предположим, что функция f не является связной. Следовательно,  f  не является послойно связной (по теореме 2.3). Тогда существует такая точка y¢ Î R, что слой  f ^–1(y¢) – несвязен, т.е.  f ^–1(y¢) = О₁  О₂, где О₁ и О₂ – непустые дизъюнктные замкнутые в f ^–1(y¢) множества (рис. 6). Следовательно, найдутся такие точки x₁ Î О₁, x₂ Î О₂ и  точка х, где x₁ < x < x₂ и x Ï О₁, x Ï О₂, что

              .

Но это противоречит условию монотонности функции f. Значит, функция  f  является связной. ÿ

Данная теорема утверждает, что связные функции, непрерывные на отрезке, – это либо невозрастающие, либо неубывающие функции.

Этот факт обобщается на случай интервала (a; b). Если связная функция f определена на R с конечным числом точек разрыва, то её монотонность в общем виде нарушается, но область определения можно разбить на конечное число промежутков, на каждом из которых функция f  будет монотонной.

2.4. Произведения пространств и проекции

Определение 17. Пусть Х и Y – топологические пространства с топологиями t_Х  и t_Y соответственно. Топологическим произведением этих пространств называется множество X ´ Y с топологией  t_Х ´ Y, образованной семейством всех множеств вида

U ´ V = ,

и их всевозможных объединений, где U Î t_Х,  V Î t_Y  и : X ´ Y ® Х, : X ´ Y ® Y – это проекции, причём (x; y) = x и (x; y) = y. Множества вида U ´ V = называются элементарными (или базисными) открытыми множествами.

Определение 18. Отображение f : X→Y называется открытым, если для каждого открытого множества О Í Х образ f (О) является открытым множеством в Y.

Лемма 2.2. Проекции : X ´ Y ®Х  и  : X ´ Y ® Y являются непрерывными открытыми отображениями.

Доказательство. Возьмём произвольное открытое в Х множество G. Прообраз этого множества  = G ´ Y по определению топологии произведения открыт в X ´ Y. Тогда проекции  и  будут непрерывными отображениями.

 Пусть точка z Î X ´ Y;  Oz – её произвольная окрестность (рис.7). Найдётся базисная окрестность

Лемма 2.3. Пусть пространство Х является компактным. Тогда проекция : X ´ Y ® Y является замкнутым отображением.

Доказательство. Возьмём произвольную точку y Î Y и рассмотрим слой  = {(x; y): x Î X} = X ´ {y}. Он гомеоморфен множеству Х, поэтому является компактным множеством. Пусть О некоторая окрестность слоя . Рассмотрим произвольную точку z = (x; y) слоя  Ì X ´ Y и её элементарную окрестность

G ,

где Ox – окрестность точки x в X, Oy –  окрестность точки y в Y. Так как точка z произвольная, следовательно, такими окрестностями можно покрыть всё множество . Пусть   – это открытое покрытие множества . Тогда можно выделить конечное открытое подпокрытие  , причём  Ì О, которое будем рассматривать как некоторую окрестность слоя . Пусть

U = ,

где О_i j = (G_i j). Тогда

 Í  Ì О,

т.е. проекция  является замкнутым над точкой у, и, следовательно, замкнутым отображением. €

Теорема 2.7. Пусть Х связное топологическое пространство. Тогда проекция  : X ´ Y ® Y является связным отображением.

Доказательство. Пусть х – произвольная фиксированная точка пространства Х. Рассмотрим слой  = = Y ´ {x}. Он гомеоморфен связному пространству Y, поэтому слой также связен. Предположим, что отображение  несвязное над точкой х, т.е. существует такая окресность Ох точки х, что трубка  является несвязной для всякой окрестности U Í Ox точки x. Зафиксируем некоторую такую связную окрестность U. Для неё найдутся непустые открытые в  множества О₁ и О₂, что  О₁ ∩ О₂ = Æ  и  О₁  О₂ = . Слой  связен и , отсюда, по теореме 2.3, содержится либо в О₁, либо в О₂.

Рассмотрим произвольную точку w₁ Î О₁. Образ этой точки  = х₁ Ì U. Слой Ì О₁  О₂ = , и точка w₁ принадлежит множеству О₁ и слою , поэтому Ì О₁ (т.к. О₁ ∩ О₂ = Æ). Поскольку w₁ – произвольная точка множества О₁, то . Аналогично, .

Множества  О₁  и О₂  дизъюнктные открытые в   и    – открытое отображение. Следовательно, (O₁)  и  (O₂) – непустые дизъюнктные открытые в U множества и (O₁)  (O₂) = U. Отсюда окрестность U несвязная, что противоречит выбору окрестности U. Таким образом, отображение  связное над точкой х и точка х произвольная, поэтому проекция  является связным отображением. €

Следствие 2.5. Если пространства Х и Y связные, то и их произведение X ´ Y является связным множеством.

Доказательство. Предположим обратное. Пусть множество X ´ Y несвязное, т.е. X ´ Y = О₁  О₂, где О₁ и О₂ – непустые дизъюнктные открытые в X ´ Y множества.

Возьмём произвольную точку z Î О₁. Образ этой точки (z) = x. Слой  Ì О₁  О₂ связен, и точка х Î О₁, следовательно,  Ì О₁ (так как О₁  О₂ = Æ). В силу того, что точка z –  произвольная, получим . Аналогично, . Множества О₁ и О₂ – непустые дизъюнктные открытые в X ´ Y, и отображение  – открытое, следовательно, множества  и  – непустые дизъюнктные открытые в Y и  = Y. Это противоречит связности Y.

Доказательство можно получить проще. Так как пространство Х связное, то проекция  : X ´ Y ® Y является связным и непрерывным отображением (по теореме 2.7 и лемме 2.2). Пространство Y связное. Тогда, по теореме 2.4,  X ´ Y – связное множество. 

Определение 19. Отображение f : X ® Y называется (замкнуто, открыто) параллельно пространству F, если существует такое топологическое вложение i : X ® Y ´ F пространства Х в топологическое произведение Y ´ F, что (множество i(X) соответственно замкнуто, открыто в Y ´ F и)

f = pr_Y  i,

где pr_Y : Y ´ F® Y – проекция на сомножитель Y.

Теорема 2.8. Пусть отображение f : X ® Y послойно связное и параллельно пространству F. Тогда отображение f  связное.

Доказательство. Отождествим Х с i(X). Тогда f можно отождествить с подотображением проекции pr_Y : Y ´ F® Y. Пусть  y Î Y – фиксированная точка и Oy – её произвольная окрестность. Предположим, что для любой связной окрестности U Í Oy точки у трубка  f ^–1(U) несвязна. Положим  f ^–1(U) = О₁  О₂, где О₁, О₂ – непустые дизъюнктные открытые в f ^–1(U) множества и U Í Oy – некоторая фиксированная связная окрестность точки y.

Пусть х Î f ^–1(y). Тогда х Î О₁ или х Î О₂. Допустим х Î О₁. Найдётся такое открытое в Y ´ F множество G₁, что О₁ =  G₁  X. По определению топологии, в Y ´ F найдутся окрестность V_x Í U точки y и открытое в F множество W такие, что

х Î = V_x ´ W Í G₁.

Так как множество f ^–1(y) – связное по условию, то х Î f ^–1(y) Í О₁.

Пусть х¢ – произвольная точка из (V_x ´ W)  Х. Тогда х¢ Î О₁ и

f ^–1(f (x¢ )) Í О₁.

Следовательно, О₁ содержит всякий слой f ^–1(y¢ ), где y¢ Î V_x (в силу послойной связности f ).

Таким образом, для каждой точки х Î О₁ найдётся окрестность V_x Í U точки f (x), что х Î f ^–1(V_x ) Í О₁. Поэтому

.

Следовательно, множество  является окрестностью точки y и O₁ = f ^–1(V₁). Аналогично устанавливается, что O₂ = f ^–1(V₂), где V₂ непустое открытое в Y множество. Откуда, U = V₁  V₂, что противоречит связности U. Значит, отображение f  связное над точкой y. €

Пример. Если отображение f : X ® Y связное над точкой y, то слой   f ^–1(y) необязательно является связным множеством. Например, пусть f = pr_Y : X ´ Y ® Y – проекция на Y, где Х = Y = [0; 1] (рис. 8). Рассмотрим точку y =  Î Y и слой f ^–1(y) над точкой y. Пусть точка z = (x; y) Î X ´ Y, где х = , y = . Тогда слой                f ^–1(y) \ {z} – несвязное множество. Отображение f = pr_Y при этом останется связным, поскольку для любой связной окрестности U точки y трубка f ^–1(U) – линейно связна, следовательно, трубка f ^–1(U)  – связна.

2.5. Послойное произведение отображений

Определение 20. Пусть f : X ® Y и g : Z ® Y – непрерывные отображения. Послойным произведением f ´ g этих отображений называется отображение h : Т ® Y, где

и

.

Из данного определения вытекает смысл названия такого определения:

для любой точки y Î Y.

Таким образом, в силу следствия 2.5, становится очевидной следующая теорема:

Теорема 2.9. Пусть отображения f : X ® Y  и  g : Z ® Y послойно связные. Тогда произведение h = f ´ g также является послойно связным отображением.

Лемма 2.4. Пусть f, g : X ® Y непрерывные отображения в хаусдорфово пространство Y. Тогда множество Т = {x Î X : f (x) = g(x)} является замкнутым в Х.

Доказательство. Докажем, что множество Х \ Т открытое, т.е. для любой точки x Î X найдётся такая окрестность Ох точки х, что Ох Ì Х \ Т.

Возьмём произвольную точку x Î X \ Т. Тогда f (x) = y₁ Î Y,  g(x) = y₂ Î Y. Так как пространство Y хаусдорфово, то существуют окрестности Оy₁ точки y₁ и Оy₂ точки y₂ такие, что

Оy₁  Оy₂ = Æ.              {*}

Отображения f и g – непрерывные, поэтому множества  f ^–1(Oy₁),  g^–1(Oy₂) – открытые в Y  и  x Î f ^–1(Oy₁),  x Î g^–1(Oy₂). Рассмотрим окрестность Ох = f ^–1(Oy₁)  g^–1(Oy₂) точки х. Предположим, что  Ох  Т ≠ Æ, т.е. существует такая точка х₁ Î Ох, что f (x₁) = g (x₁) = y. Но точка y должна принадлежать как окрестности Oy₁, так и окрестности Oy₂, что противоречит условию {*}. ÿ

Лемма 2.5. Если пространства Х и Y компактные, то и их произведение X ´ Y является компактным множеством.

Доказательство. Пусть х – произвольная фиксированная точка пространства Х, и пусть Ω =  – открытое покрытие пространства X ´ Y. Рассмотрим слой

 = Y ´ {x}.

Он гомеоморфен связному пространству Y, поэтому  – компактное множество. Тогда из открытого покрытия

Ω(х) =  Í Ω,

(где U_a(x) множество, содержащее некоторые точки слоя над точкой x) слоя  можно выбрать конечное открытое подпокрытие ω(х) = . Объединение

U(x) = (x)                               (**)

есть открытое множество, содержащее слой , и pr_X – замкнутое отображение (в силу компактности пространства Y и леммы 2.3). Следовательно, существует такая окрестность Ох точки х, что  Í U(x). Семейство {Оx: x Î X} образует открытое покрытие пространства X. В силу компактности X, найдется конечное подпокрытие {Ox_i : i = 1,.., k}. Тогда семейство ω =  образует конечное подпокрытие пространства  X ´ Y. ÿ

Теорема 2.10. Пусть  f : X ® Y  и  g : Z ® Y – связные отображения компактных пространств X  и  Z в хаусдорфово пространство  Y. Тогда произведение h = f ´ g также является связным отображением компактного пространства Т.

Доказательство. По определению послойного произведения,  (,  – непрерывные отображения в хаусдорфово пространство Y ) и . Тогда, по лемме 2.4, множество Т является замкнутым в пространстве Х ´ Z, которое, по лемме 2.5, является компактным. Следовательно, множество Т компактно (по теореме 1.7), и его образ h(T)  при непрерывном отображении  h замкнут в Y (в силу теорем 1.9 и 1.8). Отсюда, отображение h является замкнутым.

Таким образом, в силу теорем 2.9 и 2.3, отображение h = f ´ g является связным. €

Следующая теорема указывает, в каком случае отображения могут быть параллельными пространству Х. Для её доказательства понадобится

Лемма 2.6. Если пространства Х и Y хаусдорфовы, то и их произведение X ´ Y является хаусдорфовым множеством.

Доказательство. Пусть z₁ и z₂ – произвольные фиксированные точки пространства X ´ Y.  Рассмотрим точки x₁ = pr_X (z₁), x₂ = pr_X (z₂) и y₁ = pr_Y (z₁), y₂ = pr_Y (z₂) пространств X и Y соответственно. Точки z₁ и z₂ различны, следовательно, x₁ ¹ x₂ или y₁ ¹ y₂. Пусть y₁ ¹ y₂. Тогда, по определению хаусдорфова пространства, в Y существуют такие окрестности Oy₁ и Oy₂ точек y₁ и y₂ соответственно, что Oy₁  Oy₂ = Æ. Проекция pr_Y является непрерывным отображением, поэтому множества  и  – открытые в X ´ Y и непересекающиеся. Причём, z₁ Î  и z₂ Î . Следовательно, пространство X ´ Y – хаусдорфово по определению. 

Теорема 2.11. Непрерывное отображение f : X ® Y компактного хаусдорфова пространства Х в хаусдорфово пространство Y является замкнуто параллельным пространству Х.

Доказательство. Рассмотрим послойное произведение h = = f ´ i : T ® Y  отображений  f : X ® Y  и  i : Y ® Y, где i – тождественное отображение и множество Т = {(x; y): fpr_X = ipr_Y = pr_Y}. По лемме 2.4, множество Т замкнуто в X ´ Y. Пусть (x₁; y₁) Î T – произвольная фиксированная точка. Тогда pr_Y (x₁; y₁) = y₁ = fpr_X (x₁; y₁). Отсюда, для точек (x₁; y₁), (x₂; y₂) Î Т выполняется неравенство  pr_X (x₁; y₁) ¹ pr_X (x₂; y₂) при х₁ ¹ х₂. Следовательно, непрерывное отображение  pr_X : Т ® Х биективно. Но пространство T компактно как замкнутое подможество компактного пространства X ´ f (X) Í X ´ Y (в силу теорем 1.7, 1.9 и леммы 2.5). Поэтому отображение g = pr_X : T ® X по следствию 2.1 является гомеоморфизмом, т.е. Т  Х, и  f = pr_Y. Тогда в качестве топологического вложения можно рассматривать гомеоморфизм d = g^–1: X ® T. Таким образом, множество d(Х) = Т замкнуто в  X ´ Y, и f = pr_Yd. Отождествим множества Т и Х с помощью d.. Тогда отображение f замкнуто параллельно пространству Х по определению. 

Литература.

1.  Александров П.С. Введение в теорию множеств и общую топологию. – М.: «Наука»,1977.

2.  Александров П.С. Геометрия.

3.  Вернер А.Л., Кантор Б.Е. Элементы топологии и дифференциальной геометрии. – М.: «Просвещение», 1985.

4.  Мусаев Д.К., Пасынков Б.А. О свойствах компактности и полноты топологических пространств и непрерывных отображений. – Ташкент: издательство «Фан» Академии наук республики Узбекистан, 1994.

5.  Рубанов И.С. Элементы теоретико-множественной топологии для студентов пединститута. – Киров, 1990.