Курсовая работа: Уравнение и функция Бесселя

Содержание

Задание на курсовую работу ....................................................................... 2

Замечания руководителя .............................................................................. 3

1. Бесселевы функции с любым индексом ................................................... 5

2. Формулы приведения для бесселевых функций ..................................... 10

3. Бесселевы функции с полуцелым индексом ............................................. 13

4. Интегральное представление бесселевых функций с целым индексом .. 15

5. Ряды Фурье-Бесселя ................................................................................. 18

6. Асимптотическое представление бесселевых функций с целым индексом для больших значений аргумента ...................................................................................... 23

Список литературы ...................................................................................... 30

1. Бесселевы функции с любым индексом

Уравнение Лапласа в цилиндрических координатах

Чтобы объяснить происхождение бесселевых функций, рассмотрим уравнение Лапласа в пространстве:

.                                                                                  (1)

Если перейти к цилиндрическим координатам по формулам:

,   ,   ,

то уравнение (1) примет следующий вид:

.                                                                  (2)

Поставим задачу: найти все такие решения уравнения, которые могут быть представлены в виде произведения трех функций, каждая из которых зависит только от одного аргумента, то есть найти все решения вида:

,

где , ,  предполагаются дважды непрерывно дифференцируемыми.

Пусть  есть решение упомянутого вида. Подставляя его в (2), получим:

,

откуда (после деления на )

.

Записав это в виде:

,

найдем, что левая часть не зависит от , правая не зависит от , ; следовательно, общая величина этих выражений есть некоторая постоянная . Отсюда:

;     ;

;  ;

.

В последнем равенстве левая часть не зависит от , правая не зависит от ; следовательно, общая величина этих выражений есть некоторая постоянная . Отсюда:

,    ;

,    .

Таким образом, , ,  должны удовлетворять линейным дифференциальным уравнениям второго порядка:

,

(3)

,     ,

из которых второе и третье есть простейшие линейные уравнения с постоянными коэффициентами, а первое является линейным уравнением с переменными коэффициентами нового вида.

Обратно, если , ,  удовлетворяют уравнениям (3), то  есть решение уравнения (2). В самом деле, подставляя  в левую часть (2) и деля затем на , получим:

.

Таким образом, общий вид всех трех решений уравнения (2), которые являются произведением трех функций, каждая из которых зависит от одного аргумента, есть , где , ,   – любые решения уравнений (3) при любом выборе чисел , .

Первое из уравнений (3) в случае ,  называется уравнением Бесселя. Полагая в этом случае , обозначая независимую переменную буквой  (вместо ), а неизвестную функцию – буквой  (вместо ), найдем, что уравнение Бесселя имеет вид:

.                                                                    (4)

Это линейное дифференциальное уравнение второго порядка с переменными коэффициентами играет большую роль в приложениях математики. Функции, ему удовлетворяющие, называются бесселевыми, или цилиндрическими, функциями.

Бесселевы функции первого рода

Будем искать решение уравнения Бесселя (4) в виде ряда:

.

Тогда

,

,

,

.

Следовательно, приходим к требованию

или к бесконечной системе уравнений

           ,

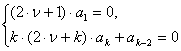
которая распадается на две системы:

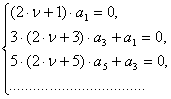
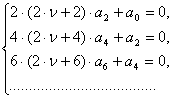
Первая из них удовлетворится, если взять … Во второй системе  можно взять произвольно; тогда … однозначно определяются (если  не является целым отрицательным числом). Взяв

 ,

найдем последовательно:

,

,

,

и в качестве решения уравнения (4) получим ряд:

Этот ряд, формально удовлетворяющий уравнению (4), сходится для всех положительных значений  и, следовательно, является решением уравнения (4) в области  (в случае целого  в области ).

Функция

                                                                         (5)

называется бесселевой функцией первого рода с индексом . Она является одним из решений уравнения Бесселя (4). В случае целого неотрицательного индекса  получим:

,                                                                        (5`)

и, в частности,

.                                                                         (5``)

Общее решение уравнения Бесселя

В случае нецелого индекса  функции  и  являются решениями уравнения (4). Эти решения линейно независимы, так как начальные члены рядов, изображающих эти функции, имеют коэффициенты, отличные от нуля, и содержат разные степени . Таким образом, в случае нецелого индекса общее решение уравнения Бесселя есть:

.                                                                           (6)

Если  (целое отрицательное число), то функция, определяемая формулой (5) (учитывая, что  равно нулю для …), принимает вид:

                                 (5```)

или, после замены индекса суммирования  на ,

,                                             (7)

откуда видно, что  удовлетворяет вместе с  уравнению Бесселя

.

Но формула (6) в случае целого  уже не дает общего решения уравнения (4).

Полагая

             ( – не целое)                               (8)

и дополняя это определение для  (целое число) формулой:

,                                                                                      (8`)

получим функцию , удовлетворяющую уравнению Бесселя (4) и во всех случаях линейно независимую от  (в случае , где  – целое). Функция  называется бесселевой функцией второго рода с индексом . Общее решение уравнения Бесселя (4) можно записать во всех случаях в виде:

.                                                                            (9)

2. Формулы приведения для бесселевых функций

Имеем:

;          ;

,                 ;

.

Следовательно,

.                                                                             (10)

Таким образом, операция  (состоящая в дифференцировании с последующим умножением на ), примененная к , повышает в этом выражении индекс  на единицу и меняет знак. Применяя эту операцию  раз, где  – любое натуральное число, получаем:

.                                                               (10`)

Имеем:

;

Следовательно,

.                                                                  (11)

Таким образом, операция , примененная к , понижает в этом выражении индекс  на единицу. Применяя эту операцию  раз, получаем:

.                                                           (11`)

Из выведенных формул можно получить некоторые следствия. Используя (10), получим:

;      ;       .

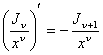Отсюда, в частности, следует, что . Используя (11), получим:

;   ;     .

Почленное сложение и вычитание полученных равенств дает:

,                                                                                    (12)

.                                                                                (13)

Формула (13) позволяет выразить все бесселевы функции с целыми индексами через , . Действительно, из (13) находим (полагая ):

,                                                                          (13`)

откуда последовательно получаем:

,

, …………………

3. Бесселевы функции с полуцелым индексом

Бесселевы функции, вообще говоря, являются новыми трансцендентными функциями, не выражающимися через элементарные функции. Исключение составляют бесселевы функции с индексом , где  – целое. Эти функции могут быть выражены через элементарные функции.

Имеем:

 ,

,

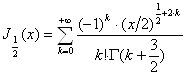следовательно,

.

Но , значит:

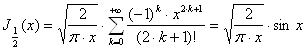.                                               (14)

Далее

,

,

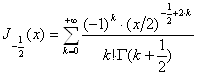следовательно,

.

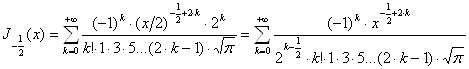Но , поэтому

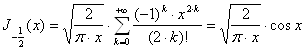.                                               (15)

С помощью (10`) находим:

,

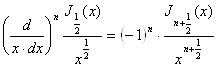а учитывая (14)

,

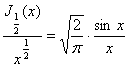следовательно, при целом положительном

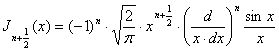.                                                   (14`)

С помощью (11`) находим:

,

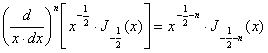но в силу (15)

,

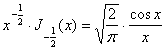и, следовательно, при целом положительном

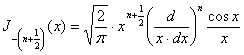.                                                          (15`)

4. Интегральное представление бесселевых функций с целым индексом

Производящая функция системы функций

Рассмотрим систему  функций  (с любой общей областью определения), пронумерованных с помощью всех целых чисел:

Составим ряд

,

где  – комплексная переменная. Предположим, что при каждом  (принадлежащем области определения рассматриваемых функций) этот ряд имеет кольцо сходимости, содержащее внутри себя единичную окружность . В частности, это кольцо может представлять собой полную плоскость комплексной переменной без точек 0 и ∞.

Функция

                                                                                     (16)

(где x лежит в области определения функций системы ,  – внутри кольца сходимости, соответствующего рассматриваемому значению ) называется производящей функцией системы .

Обратно, пусть задана функция , где  пробегает некоторое множество,  находится внутри некоторого кольца, зависящего от , с центром 0 и содержащего внутри себя единичную окружность. Тогда, если   при каждом  аналитична относительно  внутри соответствующего кольца, то  есть производящая функция некоторой системы  функций. В самом деле, разложив при каждом  функцию  в ряд Лорана по степеням :

,

найдем, что система коэффициентов  этого ряда будет искомой системой .

Формулы для коэффициентов ряда Лорана позволяют выразить функции  рассматриваемой системы через производящую функцию. Применяя эти формулы и преобразовывая затем интеграл вдоль единичной окружности  в простой интеграл, получим:

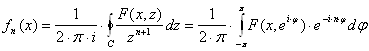.                                  (17)

Производящая функция системы бесселевых функций с целыми индексами

Покажем, что для системы бесселевых функций первого рода с целыми индексами  (…) производящая функция есть:

.

Имеем:

,        ,

откуда после почленного перемножения этих равенств найдем:

(так как в предпоследней внутренней сумме  и  были связаны зависимостью , то мы могли положить , получив суммирование по одному индексу ). В последней внутренней сумме суммирование производится по всем целым , для которых , следовательно, при  это будет ; при  это будет . Таким образом, во всех случаях внутренняя сумма есть  в силу формул (5`) и (5```). Итак,

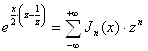,                                                                              (18)

но это и доказывает, что  есть производящая функция для системы .

Выведем некоторые следствия из формулы (18). Полагая в ней , получим:

,

откуда после разделения действительной и мнимой части (учитывая, что )

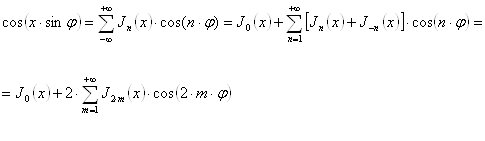           (18`)

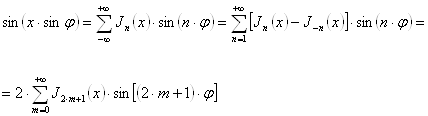                      (18``)

Заменяя в (18`) и (18``)  на , найдем:

,                               (18```)

.                                 (18````)

Интегральное представление J_n(x)

Так как, по доказанному, при  имеем , то по формуле (17) получаем (используя в преобразованиях формулы Эйлера):

где принято во внимание, что  есть четная функция от  есть нечетная функция от . Итак, доказано, что для любого целого числа

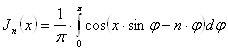.                                                              (19)

Формула (19) дает представление бесселевых функций с целым индексом в виде определенного интеграла, зависящего от параметра . Эта формула называется интегральным представлением Бесселя для , правая часть формулы называется интегралом Бесселя. В частности, при  найдем:

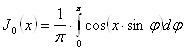.                                                                      (19`)

5. Ряды Фурье-Бесселя

Рассмотрим на каком-либо интервале  (конечном или бесконечном) два дифференциальных уравнения

,                           ,                                      (20)

где  и  – непрерывные функции на . Пусть  и  – ненулевые решения этих уравнений. Умножение на  и на  и последующее вычитание дают

.

Пусть  и  принадлежат  и , тогда после интегрирования в пределах от  до  получим

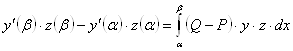.                                                 (21)

Если  и  – соседние нули решения , то между  и   сохраняет постоянный знак, пусть, например,  на (, ) (в противном случае следует заменить  на ), тогда ,  (равенство нулю исключено, так как  – ненулевое решение дифференциального уравнения второго порядка). Если на  , то  должна, по крайней мере, раз обращаться в нуль между  и , так как иначе  сохранит постоянный знак на (,). Пусть, например,  на (,) (в противном случае заменяем  на ), и тогда из (21) получим противоречие, ибо левая часть ≤0, а правая >0. Таким образом доказана теорема сравнения Штурма: если P(x)<Q(x) на рассматриваемом интервале I и если y и z – ненулевые решения уравнений (20), то между каждыми двумя соседними нулями y(x) находится по крайней мере один нуль z(x).

Из теоремы сравнения Штурма вытекают нижеследующие следствия. Если  на , то каждое ненулевое решение уравнения  может иметь на  не более одного нуля (это легко видеть, если положить   и взять ). Если  на  (где ), то для всяких двух соседних нулей  и  () каждого ненулевого решения уравнения  имеем  (это легко видеть, если положить , взять  и заметить, что нулями  будут только числа вида ,  целое). Если  на  (где ), то для всяких двух соседних нулей каждого ненулевого решения уравнения  имеем  (это легко видеть, если положить  и взять ). Из сказанного следует, что если  на , то для всяких двух соседних нулей  и  () каждого ненулевого решения уравнения  имеем .

Изложенное показывает, что если  непрерывна на  и превышает некоторое положительное число вблизи +∞, то каждое ненулевое решение  уравнения имеет на  бесконечно много нулей. Если еще  вблизи  не обращается в нуль, то эти нули образуют бесконечную возрастающую последовательность , имеющую пределом +∞, а если, кроме того, , где , то .

Рассмотрим уравнение Бесселя

на интервале . Подстановка  приводит к уравнению

.

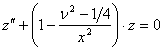Очевидно,  и  имеют одни и те же нули. Так как , где  – целая функция, то  не имеет нулей на  при достаточно малом , и так как  при , то при каждом  нули  на  образуют бесконечную возрастающую последовательность

причем .

Если , то  удовлетворит уравнению

на интервале (0, +∞). Подстановка  приводит к уравнению

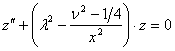
и, следовательно,  удовлетворяет этому уравнению. Таким образом, при любых положительных  и  имеем

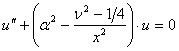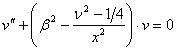, где  ,

, где ,

откуда

,

следовательно,

, где .                                        (22)

Пусть теперь . Разложение  по степеням  начинается с члена, содержащего , разложение  по степеням  начинается с члена, содержащего , так как коэффициент при  равен нулю, что легко видеть, исходя из формулы (5). Следовательно, из (22) при  получим

,

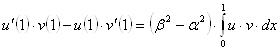то есть

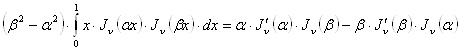,                (23)

откуда видно, что если  и  являются разными нулями функции , то

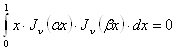.                                                                        (23`)

Этим доказано, что при  система функций

на интервале  является ортогональной относительно веса .

Переходя к пределу при  в соотношении

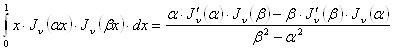
и используя правило Лопиталя, получим при всяком

,                       (24)

следовательно, если  является нулем функции , то

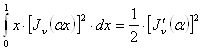.                                                                   (24`)

Таким образом, при каждом  всякой непрерывной функции  на , удовлетворяющей требованию

,

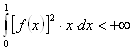поставлен в соответствие ряд Фурье-Бесселя

,                                                                              (25)

коэффициенты которого определяются формулами

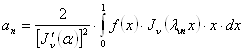.                                                          (25`)

Можно доказать, что система функций  на , ортогональная относительно веса , замкнутая. В частности, если ряд Фурье-Бесселя (25) равномерно сходится к порождающей его непрерывной функции .

Можно показать, что если  и  непрерывная на  и кусочно-гладкая на  функция, то ряд Фурье-Бесселя этой функции сходится к ней при .

6. Асимптотическое представление бесселевых функций с целым индексом для больших значений аргумента

Пусть  - положительная функция и  - какая-нибудь (вообще комплекснозначная) функция, определенные для достаточно больших значений . Запись

        при

означает, что найдутся такие числа  и M, что при  имеем .

Подобная запись употребляется и в других аналогичных случаях. Например, если  - положительная функция и  - какая-нибудь функция, определенные для достаточно малых положительных значений , то запись

        при   

означает, что найдутся такие числа  и , что  на .

Вспомогательная лемма

Если  дважды непрерывно дифференцируема на , то для функции

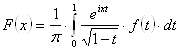
имеет место асимптотическое представление

   при .

Докажем эту лемму. Заменяя на , получим:

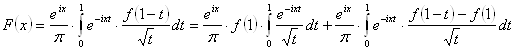.     (26)

Рассмотрим интеграл, фигурирующий в первом слагаемом правой части формулы (20). Заменяя  на , найдем:

,

но, заменив на , получим:

.

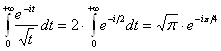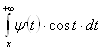Если  положительна, убывает и стремиться к нулю при , то  и 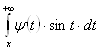, а следовательно, и  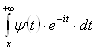есть  при , поэтому

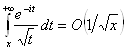      при ,

откуда

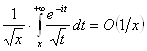    при .

Итак, получаем асимптотическое представление:

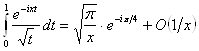    при .                                              (27)

Рассмотрим теперь интеграл, фигурирующий во втором слагаемом правой части формулы (20). Имеем:

,

.

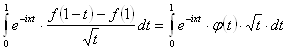Очевидно,  дважды непрерывно дифференцируема на , но существуют  и , поэтому  становится непрерывно дифференцируема на . Интегрирование по частям дает:

,

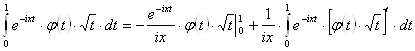где первое слагаемое правой части  есть  при , а интеграл во втором слагаемом несобственный при нижнем пределе мажорируется интегралом

,

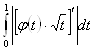который сходится, так как

     при ;

следовательно, второе слагаемое есть тоже  при .

Итак, имеем:

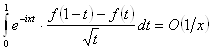    при .                                           (28)

Из (26), (27), (28) получаем искомое асимптотическое представление:

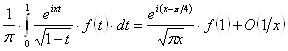    при .                            (29)

Из этой формулы, переходя к сопряженным величинам, найдем еще:

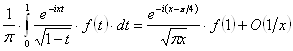   при .                           (29`)

Формулы (29) и (29`) верны и для комплекснозначных функций .

Вывод асимптотической формулы для J_n(x)

Заменяя  на , получим:

(учитывая, что  есть четная функция от , а  есть нечетная функция от ). Подстановка  дает:

,

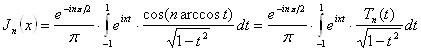где  есть, очевидно, полином n-й степени (полином Чебышева), так как из формулы Муавра видно, что  есть полином n-й степени относительно . Но

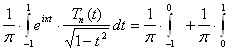
и, заменяя в первом из этих интегралов  на , получим:

Так как  и  на  имеют производные всех порядков, то к двум последним интегралам применимы формулы (29) и (29`), и мы получаем:

;

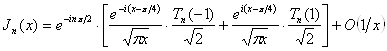но ; , следовательно,

.

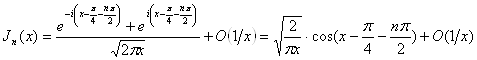Итак, имеем искомое асимптотическое представление бесселевой функции первого рода с целым индексом для больших значений аргумента:

   при .                              (30)

Эта формула показывает, что  с точностью до слагаемого порядка  является затухающей гармоникой с волной постоянной длины и амплитудой, убывающей обратно пропорционально квадратному корню из абсциссы.

В частности,

   при ;                                        (30`)

    при .                                    (30``)

Графики этих функций изображены ни рисунках 1 и 2.

Рассмотрим несколько примеров решения уравнения Бесселя.

1. Найти решение уравнения Бесселя при

,

удовлетворяющее начальным условиям при ,  и .

Решение.

На основании формулы (5`) находим одно частное решение:

.

2. Найти одно из решений уравнения:

,         .

Решение.

Сделаем замену

.

При  получим:

.

При  будем искать решение в виде обобщенного степенного ряда:

.

Уравнение на  имеет вид ;

,  ,  ,  , поэтому

,

,   .

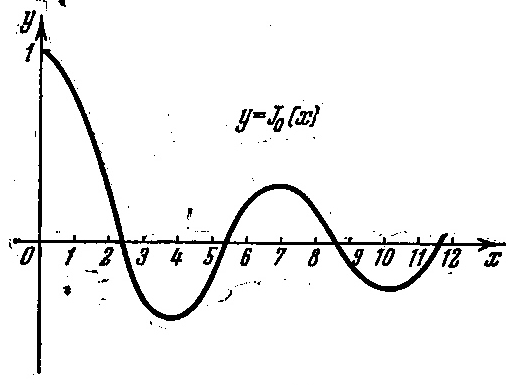
Рисунок 1 – График функции y=J₀(x)

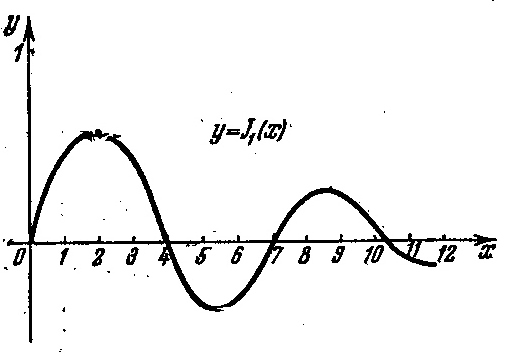
Рисунок 2 – График функции y=J₁(x)

Список литературы

1. Пискунов Н. С. «Дифференциальное и интегральное исчисления», учебное пособие для втузов, М: Наука, 1985г., 560 стр.

2. Романовский П. И. «Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа», учебное пособие для втузов, М: Наука, 1983г., 336 стр.