Курсовая работа: Уравнения и неравенства с модулем на централизованном тестировании
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
Математический факультет
Кафедра алгебры и геометрии
Допущена к защите
Зав. кафедрой Шеметков Л.А.
« » 2008 г.
Курсовая работа
Уравнения и неравенства с модулем на централизованном тестировании
Исполнитель:
студент группы М-51 С.М. Горский
Научный руководитель:
к.ф.- м.н., старший преподаватель В.Г. Сафонов
Гомель 2008
Оглавление
Введение
Абсолютная величина и её свойства
Простейшие уравнения и неравенства с модулем
Графическое решение уравнений и неравенств с модулем
Иные способы решения уравнений и неравенств с модулем
Метод раскрытия модулей
Использование тождества, при решении уравнений
Решение уравнений содержащих модули неотрицательных выражений
Решение уравнений с использованием геометрической интерпретации
Решение уравнений с использованием тождества
Применение теоремы о знаках при решении уравнений
Решение уравнений переходом к следствию
Решение уравнений методом интервалов
Решение уравнений домножением на положительный множитель
Типовые тестовые задачи, содержащие переменную под знаком модуля
Заключение
Список использованных источников
Введение
Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел.
Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы, на ЦТ и на ЕГЭ.
Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. Данный пробел и пытается восполнить настоящий диплом.
Дипломная работа состоит из 5 разделов.
В первом разделе приведены равносильные определения модуля, его геометрическая интерпретация, свойства абсолютной величины. На примере показано, как используя модуль, любую систему уравнений и неравенств с одной и тоже областью определения можно представить в виде одного равносильного сравнения. Так же показано на примере, как линейный сплайн, предствавить в виде одного уравнения с модулями. Приведены примеры заданий, в которых используются либо свойства модуля, либо уравнения и неравенства, содержащие знак абсолютной величины, возникают в процессе решения.
Во втором разделе представлены методы решения простейших уравнений и неравенств с модулями, решение которых не требует использование трудоемкого процесса раскрытия модулей.
В
третьем разделе представлено графическое решение уравнений и неравенств,
содержащих знак абсолютной величины. Графическое решение уравнений и неравенств
с модулем в некоторых случаях гораздо более простое, чем аналитическое. В этом
разделе рассмотрены построение графиков функций ![]() ,
,
![]() и
и ![]() . Много внимания уделено
построению графиков функций, представляющих собой сумму линейных выражений под
знаком абсолютной величины. Так же приведены примеры построения графиков
функций с ``вложенными'' модулями. Приведены теоремы об экстремумах функций,
содержащих сумму линейных выражений под знаками абсолютных величин, позволяющие
эффективно решать задачи как на нахождение экстремумов подобных функции, так и
решать задачи с параметрами.
. Много внимания уделено
построению графиков функций, представляющих собой сумму линейных выражений под
знаком абсолютной величины. Так же приведены примеры построения графиков
функций с ``вложенными'' модулями. Приведены теоремы об экстремумах функций,
содержащих сумму линейных выражений под знаками абсолютных величин, позволяющие
эффективно решать задачи как на нахождение экстремумов подобных функции, так и
решать задачи с параметрами.
В
четвертом разделе представлены дополнительные методы решения уравнений и
неравенств, содержащих знак абсолютной величины. В первую очередь описан
трудоемкий и не всегда рациональный, а в некоторых случаях и неприменимый метод
раскрытия модулей, иногда называемый метод интервалов, с помощью которого можно
решить любое уравнение и неревенство с модулем. Описан метод использования
тождества ![]() ; рассмотрены метод
геометрической интерпретации, использование тождества
; рассмотрены метод
геометрической интерпретации, использование тождества ![]() , применение теоремы о
знаках, метод перехода к следствию, метод интервалов, метод домножения на
положительный множитель.
, применение теоремы о
знаках, метод перехода к следствию, метод интервалов, метод домножения на
положительный множитель.
В пятом разделе приведены примеры решения типовых тестовых задач связанных с понятием абсолютная величина. Приведены решения как ``стандартных'' задач, в решении которых необходимо получить какую-либо комбинацию решений, так и заданий с параметрами. Для некоторых задач приведено несколько способов решения, иногда указаны типичные ошибки возникающие в процессе решения. Для всех заданий приведено наиболее эффективное, по быстроте, решение.
Абсолютная величина и её свойства
Модуль. Свойства модуля
Определение.
Модуль числа ![]() или абсолютная
величина числа
или абсолютная
величина числа ![]() равна
равна ![]() , если
, если ![]() больше или равно нулю и
равна
больше или равно нулю и
равна ![]() , если
, если ![]() меньше нуля:
меньше нуля:
![]()
Из
определения следует, что для любого действительного числа ![]() ,
, ![]() .
.
Теорема
Абсолютная
величина действительного числа ![]() равна
большему из двух чисел
равна
большему из двух чисел ![]() или
или ![]() .
.
1.
Если число ![]() положительно, то
положительно, то ![]() отрицательно, т. е.
отрицательно, т. е. ![]() . Отсюда следует, что
. Отсюда следует, что ![]() .
.
В
этом случае ![]() , т. е.
, т. е. ![]() совпадает с большим из
двух чисел
совпадает с большим из
двух чисел ![]() и
и ![]() .
.
2.
Если ![]() отрицательно, тогда
отрицательно, тогда ![]() положительно и
положительно и ![]() , т. е. большим числом
является
, т. е. большим числом
является ![]() . По определению, в этом
случае,
. По определению, в этом
случае, ![]() --- снова, равно большему
из двух чисел
--- снова, равно большему
из двух чисел ![]() и
и ![]() .
.
Следствие
Из
теоремы следует, что ![]() .
.
В
самом деле, как ![]() , так и
, так и ![]() равны большему из чисел
равны большему из чисел ![]() и
и ![]() , а значит, равны между
собой.
, а значит, равны между
собой.
Следствие
Для
любого действительного числа ![]() справедливы
неравенства
справедливы
неравенства ![]() ,
, ![]() .
.
Умножая
второе равенство ![]() на
на ![]() (при этом знак неравенства
изменится на противоположный), мы получим следующие неравенства:
(при этом знак неравенства
изменится на противоположный), мы получим следующие неравенства: ![]() ,
, ![]() справедливые для любого
действительного числа
справедливые для любого
действительного числа ![]() . Объединяя
последние два неравенства в одно, получаем:
. Объединяя
последние два неравенства в одно, получаем: ![]() .
.
Теорема
Абсолютная
величина любого действительного числа ![]() равна
арифметическому квадратному корню из
равна
арифметическому квадратному корню из ![]() :
: ![]() .
.
В
самом деле, если ![]() , то, по
определению модуля числа, будем иметь
, то, по
определению модуля числа, будем иметь ![]() .
С другой стороны, при
.
С другой стороны, при ![]() ,
, ![]() , значит
, значит ![]() .
.
Если
![]() , тогда
, тогда ![]() и
и ![]() и в этом случае
и в этом случае ![]() .
.
Эта
теорема дает возможность при решении некоторых задач заменять ![]() на
на ![]() .
.
Геометрически
![]() означает расстояние на
координатной прямой от точки, изображающей число
означает расстояние на
координатной прямой от точки, изображающей число ![]() ,
до начала отсчета.
,
до начала отсчета.
Если
![]() , то на координатной прямой
существует две точки
, то на координатной прямой
существует две точки ![]() и
и ![]() , равноудаленной от нуля,
модули которых равны.
, равноудаленной от нуля,
модули которых равны.
Если
![]() , то на координатной прямой
, то на координатной прямой
![]() изображается точкой
изображается точкой ![]() .
.
Свойства модуля
![]()
Из
этого свойства следует, что ![]() ;
; ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Равносильные переходы между уравнениями с модулями
Тема ``Абсолютная величина'' (или ``Модуль числа'') является наиболее эксплуатируемой в практике вступительных экзаменов. Вероятно, это объясняется ощущением простоты понятия абсолютной величины числа и тем обстоятельством, что, используя модуль, любую систему и совокупность уравнений и неравенств с одной и той же областью определения можно представить в виде одного равносильного сравнения.
Посмотрим, на примере, как система одного неравенства и совокупность двух неравенств преобразуется к одному равносильному уравнению.
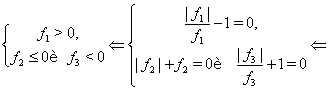
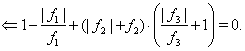
В основе указанных преобразований лежат следующие легко доказываемые утверждения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вариант приведения одного отношения к равносильному ему отношению другого типа
| < |
|
|
|
> | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейные сплайны
Пусть
заданы ![]() --- точки смены формул.
Функция
--- точки смены формул.
Функция ![]() , определенная при всех
, определенная при всех ![]() , называется кусочно-линейной,
если она линейная на каждом интервале
, называется кусочно-линейной,
если она линейная на каждом интервале ![]() ,
,
![]() ,
, ![]() , ...,
, ...,![]() , т. е.
, т. е.
![]()
где
обозначено ![]() ,
, ![]() .
.
Если к тому же выполнены условия согласования
![]()
то рассматриваемая кусочно-линейная функция непрерывна. Непрерывная кусочно-линейная функция называется также линейным сплайном.
Подобный график изображен на рисунке (??):
pics/ex1.eps
Функцию
с графиком, показанным на этом рисунке, можно задать и одной и тремя формулами:
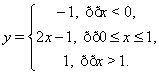
Однако
нетрудно заметить, что эту же функцию можно задать и одной формулой, используя
модули: ![]() . Оказывается, что и любую
непрерывную кусочно-линейную функцию вида (1) можно задать некоторой формулой
вида
. Оказывается, что и любую
непрерывную кусочно-линейную функцию вида (1) можно задать некоторой формулой
вида
![]() (??)
(??)
где
числа ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() легко найти по графику
данной функции.
легко найти по графику
данной функции.
Заметим,
что две ломанные с бесконечными крайними звеньями и одинаковыми абсциссами
вершин ![]() ,
, ![]() , ...,
, ..., ![]() совпадают, если у них
равны угловые коэффициенты всех ``одноименных'' звеньев и имеется общая точка.
Иными словами, знание угловых коэффициентов всех звеньев и координат одной
точки такой ломаной на основе указанной информации, при котором данная точка
совпадают, если у них
равны угловые коэффициенты всех ``одноименных'' звеньев и имеется общая точка.
Иными словами, знание угловых коэффициентов всех звеньев и координат одной
точки такой ломаной на основе указанной информации, при котором данная точка ![]() берется за исходную, см.
рисунок (??).
берется за исходную, см.
рисунок (??).
pics/ex2.eps
Отмеченный
факт мы и положим в основу получения формулы для непрерывной кусочно-линейной
функции, заданной своим графиком. Напомним, что ![]() равняется
равняется
![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() . Поэтому на каждом из
промежутков
. Поэтому на каждом из
промежутков ![]() ,
, ![]() , ...,
, ..., ![]() , на которые числовая
прямая разбивается точками, функция, определяемая формулой ((??)), будет
линейная (как сумма линейных функций), и для нахождения углового коэффициента
соответствующего звена ломанной достаточно найти коэффициент при
, на которые числовая
прямая разбивается точками, функция, определяемая формулой ((??)), будет
линейная (как сумма линейных функций), и для нахождения углового коэффициента
соответствующего звена ломанной достаточно найти коэффициент при ![]() после раскрытия всех
модулей в выражении ((??)) на соответствующих этим звеньям промежутках,
находим:
после раскрытия всех
модулей в выражении ((??)) на соответствующих этим звеньям промежутках,
находим:
Вычитая
из второго равенства первое, получаем ![]() вычитая
из третьего второе, получаем
вычитая
из третьего второе, получаем ![]() и т. д.
Мы приходим в итоге к соотношениям
и т. д.
Мы приходим в итоге к соотношениям
![]()
Складывая
первое равенство с последним, получаем ![]() откуда
откуда
Обратно, нетрудно проверить, что из равенств (3) и ((??)) вытекают соотношения ((??)).
Итак,
если коэффициенты ![]() определяются
формулами (3) и ((??)), то угловые коэффициенты всех звеньев графика функции ((??))
совпадают с соответствующими угловыми коэффициентами заданного графика и,
значит, остается обеспечить всего одну общую точку этих ломанных для их
совпадения.
определяются
формулами (3) и ((??)), то угловые коэффициенты всех звеньев графика функции ((??))
совпадают с соответствующими угловыми коэффициентами заданного графика и,
значит, остается обеспечить всего одну общую точку этих ломанных для их
совпадения.
Этого
всегда можно добиться выбором подходящего значения оставшегося пока не
определенным коэффициента ![]() . С этой
целью достаточно подставить в формулу ((??)), коэффициенты которой уже
вычислены из соотношений (3) и ((??)), координаты какой-либо одной точки данной
ломаной и найти
. С этой
целью достаточно подставить в формулу ((??)), коэффициенты которой уже
вычислены из соотношений (3) и ((??)), координаты какой-либо одной точки данной
ломаной и найти ![]() из полученного
равенства.
из полученного
равенства.
Пример Найдем уравнение ломаной, изображенной на рисунке (??) (треугольный импульс).
pics/ex3.eps
Решение.
Угловые
коэффициенты звеньев таковы: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Поэтому
. Поэтому ![]() .
.
Значит, уравнение данной ломаной имеет вид
![]()
Найдем
значение коэффициента ![]() из условия
из условия ![]() , подставляя координаты
вершины (0; 1) нашей ломаной в уравнение, получим
, подставляя координаты
вершины (0; 1) нашей ломаной в уравнение, получим ![]() , откуда находим,
, откуда находим, ![]() , и уравнение окончательно
запишем в виде
, и уравнение окончательно
запишем в виде
![]()
Примеры решения задач, использующих свойства модуля
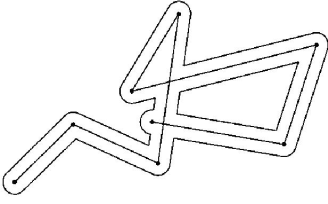
Пример В некотором лесу расстояние между любыми двумя деревьями не превосходит разности их высот. Все деревья имеют высоту меньше 100 м. Докажите, что этот лес можно огородить забором длиной 200 м.
Решение.
Пусть
деревья высотой ![]() растут в точках
растут в точках ![]() . Тогда по условию
. Тогда по условию ![]() . Следовательно, длина
ломаной
. Следовательно, длина
ломаной ![]() не превосходит
не превосходит ![]() м. Эту ломаную можно
огородить забором, длина которого не превосходит 200 м (см. рис. (??)).
м. Эту ломаную можно
огородить забором, длина которого не превосходит 200 м (см. рис. (??)).
Пример
На
отрезке ![]() числовой оси расположены
четыре точки:
числовой оси расположены
четыре точки: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Докажите, что найдётcя
точка
. Докажите, что найдётcя
точка ![]() , принадлежащая
, принадлежащая ![]() , такая, что
, такая, что ![]() .
.
Решение.
Точки
![]() ,
, ![]() ,
, ![]() ,
, ![]() делят отрезок
делят отрезок ![]() не более чем на пять
частей; хотя бы одна из этих частей является интервалом длины не меньше
не более чем на пять
частей; хотя бы одна из этих частей является интервалом длины не меньше ![]() . Возьмём за
. Возьмём за ![]() центр этого интервала.
Расстояние от
центр этого интервала.
Расстояние от ![]() до концов этого
интервала не меньше
до концов этого
интервала не меньше ![]() , а до других
точек из числа
, а до других
точек из числа ![]() ,
, ![]() ,
, ![]() ,
, ![]() --- больше
--- больше ![]() . Поэтому два из чисел
. Поэтому два из чисел ![]() ,
, ![]() ,
, ![]() ,
, ![]() не меньше
не меньше ![]() , а остальные два строго
больше
, а остальные два строго
больше ![]() . Так что все обратные
величины не больше 10, а две из них строго меньше 10. Тогда сумма обратных
величин меньше 40, что и требуется.
. Так что все обратные
величины не больше 10, а две из них строго меньше 10. Тогда сумма обратных
величин меньше 40, что и требуется.
Пример
Два
тела начинают одновременно двигаться равномерно по прямым ![]() и
и ![]() , пересекающимися под
прямым углом. Первое тело движется со скоростью 3 км/ч по прямой
, пересекающимися под
прямым углом. Первое тело движется со скоростью 3 км/ч по прямой ![]() от точки
от точки ![]() к точке
к точке ![]() , находящейся на расстоянии
2 км от точки
, находящейся на расстоянии
2 км от точки ![]() . Второе тело
движется со скоростью 4 км/ч по прямой
. Второе тело
движется со скоростью 4 км/ч по прямой ![]() от
точки
от
точки ![]() к точке
к точке ![]() , находящейся на расстоянии
3 км от точки
, находящейся на расстоянии
3 км от точки ![]() . Найти
наименьшее расстояние (в км) между этими телами во время движения.
. Найти
наименьшее расстояние (в км) между этими телами во время движения.
Решение.
Через
![]() часов первое тело будет
находится от точки
часов первое тело будет
находится от точки ![]() на расстоянии
на расстоянии ![]() км, а второе --- на
расстоянии
км, а второе --- на
расстоянии ![]() км. По теореме Пифагора
расстояние между телами составит
км. По теореме Пифагора
расстояние между телами составит ![]() .
. ![]() км.
км.
Ответ.
![]() км.
км.
Пример
Пункты
![]() и
и ![]() расположены на
прямолинейной магистрали в 9 км друг от друга. Из пункта
расположены на
прямолинейной магистрали в 9 км друг от друга. Из пункта ![]() в направлении пункта
в направлении пункта ![]() выходит автомашина,
двигающаяся равномерно со скоростью 40 км/ч. Одновременно из пункта
выходит автомашина,
двигающаяся равномерно со скоростью 40 км/ч. Одновременно из пункта ![]() в том же направлении с
постоянным ускорением 32 км/ч
в том же направлении с
постоянным ускорением 32 км/ч ![]() выходит
мотоцикл. Найти наибольшее расстояние между машиной и мотоциклом в течении
первых двух часов движения.
выходит
мотоцикл. Найти наибольшее расстояние между машиной и мотоциклом в течении
первых двух часов движения.
Решение.
Расстояние
между автомобилем и мотоциклом через ![]() часов
составит
часов
составит ![]() .
. ![]() .
.
Ответ. 16 км.
Пример
Из
пункта ![]() в пункт
в пункт ![]() вышел пешеход. Не позже
чем через 40 мин вслед за ним вышел второй. Известно, что в пункт
вышел пешеход. Не позже
чем через 40 мин вслед за ним вышел второй. Известно, что в пункт ![]() один из них пришел раньше
другого не менее, чем на 1 час. Если бы пешеходы вышли одновременно, то они бы
пришли в пункт
один из них пришел раньше
другого не менее, чем на 1 час. Если бы пешеходы вышли одновременно, то они бы
пришли в пункт ![]() с интервалом не
более чем в 20 мин. Определить, сколько времени требуется каждому пешеходу на
путь от
с интервалом не
более чем в 20 мин. Определить, сколько времени требуется каждому пешеходу на
путь от ![]() до
до ![]() , если скорость одного из
них в 1,5 раза больше скорости другого.
, если скорость одного из
них в 1,5 раза больше скорости другого.
Решение.
Пусть
![]() и
и ![]() (мин) --- время,
затраченное соответственно первым и вторым пешеходом на путь из
(мин) --- время,
затраченное соответственно первым и вторым пешеходом на путь из ![]() в
в ![]() , и пусть второй пешеход
вышел позже первого на
, и пусть второй пешеход
вышел позже первого на ![]() минут. Рассмотри
2 возможности 1)
минут. Рассмотри
2 возможности 1) ![]() и 2)
и 2) ![]() . В случае
. В случае ![]() имеем равенство
имеем равенство ![]() и систему
и систему
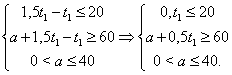
Из
первого и третьего неравенства получим ![]() ,
учитывая второе условие получим, что
,
учитывая второе условие получим, что ![]() , и это
в свою очередь дает равенства
, и это
в свою очередь дает равенства ![]() и
и ![]() . Т.о.
. Т.о. ![]() ,
, ![]() ,
, ![]() .
.
В
случае ![]() имеем
имеем ![]() и сиcтему
и сиcтему
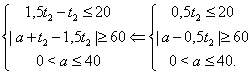
Но
так как ![]() , то система не совместна,
и, следовательно, случай 2 не может иметь места.
, то система не совместна,
и, следовательно, случай 2 не может иметь места.
Ответ.
![]() ,
, ![]() ,
, ![]() .
.
Пример
По
расписанию автобус должен проходить путь ![]() ,
состоящий из отрезков
,
состоящий из отрезков ![]() ,
, ![]() ,
, ![]() длиной 5, 1, 4 км
соответственно, за 1 час. При этом выезжая из пункта
длиной 5, 1, 4 км
соответственно, за 1 час. При этом выезжая из пункта ![]() в 10 ч, он проходит пункт
в 10 ч, он проходит пункт ![]() в 10 ч 10 мин, пункт
в 10 ч 10 мин, пункт ![]() в 10ч 34 мин. С какой
скоростью
в 10ч 34 мин. С какой
скоростью ![]() должен ехать автобус,
чтобы время за которое автобус проходит половину пути от
должен ехать автобус,
чтобы время за которое автобус проходит половину пути от ![]() до
до ![]() (со скоростью
(со скоростью ![]() ), сложенное с суммой
абсолютных величинотклонения от расписания при прохождении пунктов
), сложенное с суммой
абсолютных величинотклонения от расписания при прохождении пунктов ![]() и
и ![]() , превышало абсолютную
величину отклонения от расписания при прохождении пункта
, превышало абсолютную
величину отклонения от расписания при прохождении пункта ![]() не более, чем на 28 мин.
не более, чем на 28 мин.
Решение. Условие задачи приводит к системе
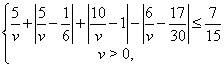
которая
имеет единственное решение ![]() .
.
Ответ. 30 км/ч.
Пример
Согласно
расписанию катер проходит по реке, скорость течения которой 5 км/ч, путь из ![]() в
в ![]() длиной 15 км за 1 час. При
этом выходя из пункта
длиной 15 км за 1 час. При
этом выходя из пункта ![]() в 12ч, он
прибывает в пункты
в 12ч, он
прибывает в пункты ![]() и
и ![]() , отстоящие от
, отстоящие от ![]() на растояние 11 км и 13 км
соответственно, в 12 ч 20 мин и в 12 ч 40 мин. Известно, что если бы катер
двигался из
на растояние 11 км и 13 км
соответственно, в 12 ч 20 мин и в 12 ч 40 мин. Известно, что если бы катер
двигался из ![]() в
в ![]() без остановок с постоянной
скоростью
без остановок с постоянной
скоростью ![]() (относительно воды), то
сумма абсолютных величин отклонений от расписания прибытия в пункты
(относительно воды), то
сумма абсолютных величин отклонений от расписания прибытия в пункты ![]() ,
, ![]() ,
, ![]() не превышало бы
уменьшенного на полчаса времени, необходимого катеру для прохождения 5 км со
скоростью
не превышало бы
уменьшенного на полчаса времени, необходимого катеру для прохождения 5 км со
скоростью ![]() в стоячей воде. Какой из
пунктов находится выше по течению:
в стоячей воде. Какой из
пунктов находится выше по течению: ![]() или
или ![]() ?
?
Решение.
Рассмотрим
2 случая 1) пункт ![]() находится выше
по течению 2) пункт
находится выше
по течению 2) пункт ![]() находится ниже
по течению.
находится ниже
по течению.
В первом случае получаем систему
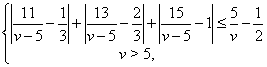
которая не имеет решения. Тогда выполняется второй случай.
Ответ.
![]() .
.
Пример
Даны
три квадратных трехчлена: ![]() ,
, ![]() и
и ![]() . Докажите, что уравнение
. Докажите, что уравнение ![]() имеет не более восьми
корней.
имеет не более восьми
корней.
Решение.
Каждый
корень данного уравнения является корнем одного из квадратных трехчленов ![]() ,
, ![]() ,
, ![]() с некоторым набором
знаков. Таких наборов 8, и все они дают действительно квадратные трехчлены, так
как коэффициент при
с некоторым набором
знаков. Таких наборов 8, и все они дают действительно квадратные трехчлены, так
как коэффициент при ![]() имеет вид
имеет вид ![]() , т.е. отличен от нуля.
Однако двум противоположным наборам знаков соответствуют квадратные уравнения,
имеющие одни и те же корни. Значит, все решения уравнения
, т.е. отличен от нуля.
Однако двум противоположным наборам знаков соответствуют квадратные уравнения,
имеющие одни и те же корни. Значит, все решения уравнения ![]() содержатся среди корней
четырех квадратных уравнений. Следовательно, их не более восьми.
содержатся среди корней
четырех квадратных уравнений. Следовательно, их не более восьми.
Пример
Шабат Г.Б. Бесконечная последовательность чисел
![]() определяется условиями:
определяется условиями: ![]() , причем
, причем ![]() . Докажите, что
последовательность, начиная с некоторого места, периодическая в том случае,
если
. Докажите, что
последовательность, начиная с некоторого места, периодическая в том случае,
если ![]() рационально.
рационально.
Решение.
Если
![]() , то
, то ![]() . Действительно,
. Действительно, ![]() . Если
. Если ![]() рациональное, то
рациональное, то ![]() рациональное, причем со
знаменателем не большим чем у
рациональное, причем со
знаменателем не большим чем у ![]() .
Действительно, пусть
.
Действительно, пусть ![]() --- несократимая
дробь. Тогда
--- несократимая
дробь. Тогда
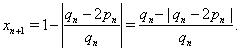
Если
эта дробь несократима, то ее знаменатель такой же, как и у ![]() , если она сократима, то
после сокращения знаменатель уменьшится.
, если она сократима, то
после сокращения знаменатель уменьшится.
Итак,
все члены последовательности --- рациональные числа, заключенные между 0 и 1,
т. е. правильные дроби. Но правильных дробей со знаменателями, не большими
заданной величины ![]() , --- конечное
число. Поэтому какие-то члены последовательности повторятся, и с этого момента
последовательность будет периодической.
, --- конечное
число. Поэтому какие-то члены последовательности повторятся, и с этого момента
последовательность будет периодической.
К
простейшим (не обязательно простым) уравнениям мы будем относить уравнения,
решаемые одним из нижеприведенных равносильных переходов: 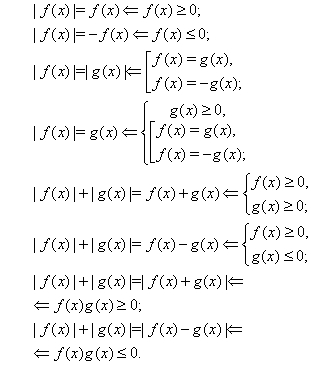 (??) (??) (??) (??)
(??) (??) (??) (??)
Примеры решения простейших уравнений.
Пример
Решим
уравнение 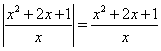 .
.
Решение.
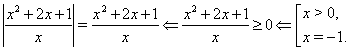
Ответ.
![]() .
.
Пример
Решим
уравнение ![]() .
.
Решение.
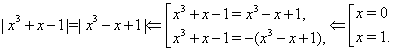
Ответ.
![]() .
.
Пример
Решим
уравнение ![]() .
.
Решение.
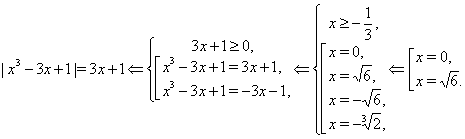
Ответ.
![]() .
.
Остановимся подробнее на уравнениях, в которых встречается сумма модулей [??] (формулы (??)--(??)).
Теорема Сумма модулей равна алгебраической сумме подмодульнх величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму.
Пример Решить уравнение
![]()
Решение.
Так
как ![]() , то мы имеем равенство
вида
, то мы имеем равенство
вида ![]() , где
, где ![]() ,
, ![]() . Поэтому исходное
уравнение равносильно системе:
. Поэтому исходное
уравнение равносильно системе:
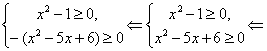
![]()
Ответ.
![]() .
.
Теорема Сумма модулей равна модулю алгебраической суммы подмодульных величин тогда и только тогда, когда все величины имеют тот знак, с которым они входят в алгебраическую сумму, либо все величины имеют противоположный знак одновременно.
Пример Решить уравнение
![]()
Решение. ``Загоняем'' коэффициенты 2 и 5 под знак модуля и ``изолируем'' сумму модулей:
![]()
По
константам получаем ![]() . Действительно,
. Действительно, ![]() , то есть уравнение имеет
вид
, то есть уравнение имеет
вид ![]() . Следовательно, уравнение
равносильно совокупности двух систем:
. Следовательно, уравнение
равносильно совокупности двух систем:
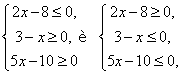
то
есть ![]() .
.
Ответ.
![]() .
.
К простейшим (не обязательно простым) неравенствам мы будем относить неравенства, решаемые одним из нижеприведенных равносильных переходов:
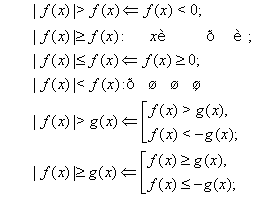 (??)
(??)
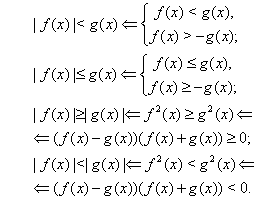 (??)
(??)
Примеры решения простейших неравенств.
Пример
Решим
неравенство ![]() .
.
Решение.
![]() .
.
Ответ.
![]() .
.
Пример
Решим
неравенство ![]() .
.
Решение.
![]()
Ответ.
![]() .
.
Как
ни странно, но ![]() достаточно,
чтобы избавиться от знака модуля в любых неравенствах.
достаточно,
чтобы избавиться от знака модуля в любых неравенствах.
Пример Решить неравенство
![]()
Решение.
![]()

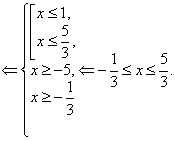
Ответ.
![]() .
.
Пример Решить неравенство
![]()
Решение.
Относительно
любого модуля данное неравенство имеет вид ![]() .
Поэтому перебрав все комбинации знаков двух подмодульных выражений, имеем
.
Поэтому перебрав все комбинации знаков двух подмодульных выражений, имеем
![]()
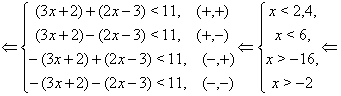
Ответ.
![]() .
.
Пример
При
каких значениях параметра ![]() неравенство
неравенство
![]()
выполняется
при всех значениях ![]() ?
?
Решение. Исходное уравнение равносильно системе:
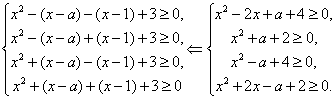
Выполнение
для всех ![]() исходного неравенства
равносильно выполнению для
исходного неравенства
равносильно выполнению для ![]() всех
неравенств последней системы. А это равносильно тому, что дискриминанты всех
четырёх квадратных трёхчленов неположительны:
всех
неравенств последней системы. А это равносильно тому, что дискриминанты всех
четырёх квадратных трёхчленов неположительны: 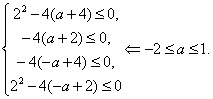
Ответ.
![]() .
.
Пример
Найти
все значения параметра ![]() , при каждом из
которых число целочисленных решений неравенства
, при каждом из
которых число целочисленных решений неравенства
![]()
максимально.
Решение.
Так
как ![]() то исходное уравнение
равносильно системе:
то исходное уравнение
равносильно системе:
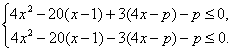
Поскольку
оба неравенства в системе линейны относительно ![]() .
Решим систему относительно
.
Решим систему относительно ![]() :
:
Условия
существования параметра ![]() равносильно
требованию
равносильно
требованию
![]()
![]()
Неравенство
(??) объявляет все значения ![]() ,
которые могут быть решением исходного неравенства хотя бы при одном значении
параметра. Следовательно, целочисленными решениями исходного неравенства могут
быть только целые числа из промежутка
,
которые могут быть решением исходного неравенства хотя бы при одном значении
параметра. Следовательно, целочисленными решениями исходного неравенства могут
быть только целые числа из промежутка ![]() ,
то есть
,
то есть
Естественно,
что для любого целого числа из набора (??) надо выяснить, при каких значениях
параметра ![]() это число будет решением
исходного неравенства.
это число будет решением
исходного неравенства.
Поскольку исходное неравенство равносильно (??), то поочерёдно подставляя числа из набора (??) в неравенства (??), мы сразу и найдём все соответствующие значения параметра. Имеем

Чтобы выявить значения параметра, при которых исходное неравенство имеет максимальное число целочисленных решений, воспользуемся ``разверткой'', полученной информации вдоль от параметра (см. рис. (??)):
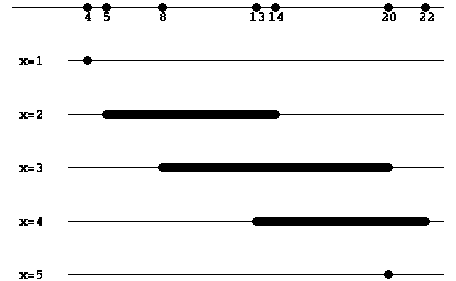
Очевидно,
что максимальное количество целочисленных решений равно трём, и это
достигается, когда ![]() или
или ![]() .
.
Ответ.
![]() .
.
Графическое решение уравнений и неравенств с модулем
Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры).
Построение
графиков вида ![]() ,
, ![]() и
и ![]()
Отметим
правило построения графика функции ![]() .
.
1)
Строим сначала график функции ![]() .
.
2)
Там, где график функции ![]() лежит
выше оси
лежит
выше оси ![]() или на ней, оставляем его
без изменения; точки графика, которые лежат ниже оси
или на ней, оставляем его
без изменения; точки графика, которые лежат ниже оси ![]() , заменяем симметричными им
относительно оси
, заменяем симметричными им
относительно оси ![]() точками.
точками.
Для
примера, на рисунке (??) изображен график функции ![]() .
.
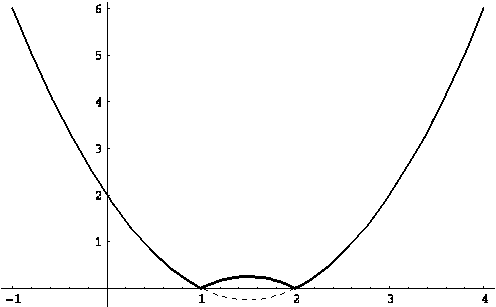
Для
построения графика функции ![]() cтроим
график функции
cтроим
график функции ![]() для
для ![]() и отображаем симметрично
относительно оси
и отображаем симметрично
относительно оси ![]() .
.
Для
примера, на рисунке (??) изображен график функции ![]() .
.
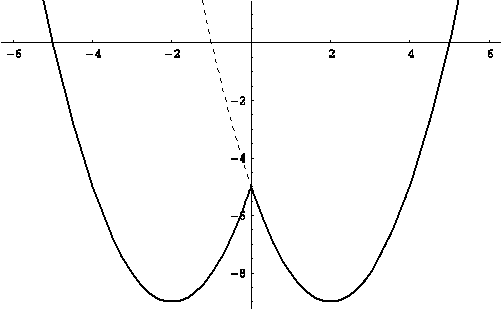
Для
построения графика функции ![]() строим
график функции
строим
график функции ![]() для
для ![]() и симметрично отображаем
относительно оси
и симметрично отображаем
относительно оси ![]() .
.
Для
примера, на рисунке (??) изображен график функции ![]() .
.
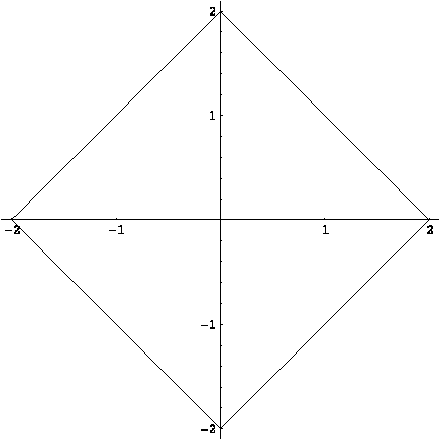
Пример
Построить
график функции ![]() .
.
Решение. Воспользуемся правилами преобразования графиков.
1.
График функции ![]() --- биссектриса
первого и третьего координатных углов.
--- биссектриса
первого и третьего координатных углов.
2.
График функции ![]() получается из
графика функции
получается из
графика функции ![]() отображением его
части, расположенной ниже оси абсцисс (при
отображением его
части, расположенной ниже оси абсцисс (при ![]() )
симметрично относительно оси абсцисс.
)
симметрично относительно оси абсцисс.
3.
График функции ![]() получается из
предыдущего сдвигом влево по оси абсцисс на две единицы.
получается из
предыдущего сдвигом влево по оси абсцисс на две единицы.
4.
Полученный график сдвигаем по оси ординат на 3 единицы вниз. Получаем график
функции ![]() .
.
5. Часть его, расположенную ниже оси абсцисс, отображаем симметрично относительно этой оси. Итак, получаем график данной функции (см. рис (??)).
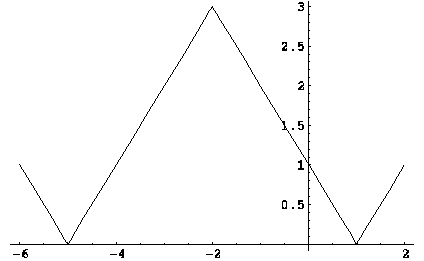
Исследуемая
функция допускает другую форму записи 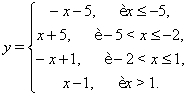
Пример
В
зависимости от параметра ![]() , найти
количество решений уравнения
, найти
количество решений уравнения
![]()
Решение.
Построим
график функции ![]() (см. рис. (??)).
(см. рис. (??)).
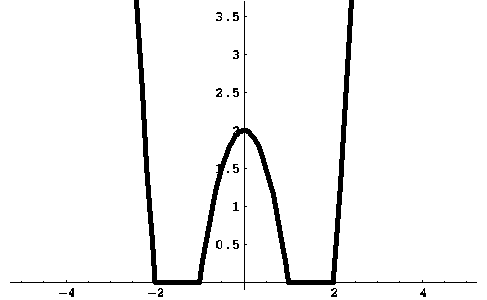
В
зависимости от положения прямой ![]() ,
получаем следующее: при
,
получаем следующее: при ![]() нет
корней, при
нет
корней, при ![]() --- бесконечно много
корней, при
--- бесконечно много
корней, при ![]() --- четыре корня, при
--- четыре корня, при ![]() --- три корня, при
--- три корня, при ![]() --- два корня.
--- два корня.
Пример
Докажите,
что на графике функции ![]() можно отметить
такую точку
можно отметить
такую точку ![]() , а на графике функции
, а на графике функции ![]() --- такую точку
--- такую точку ![]() , что расстояние
, что расстояние ![]() не превышает
не превышает ![]() .
.
Решение.
Положим
![]() . Точка
. Точка ![]() с координатами
с координатами ![]() , где
, где ![]() , очевидно, лежит на
графике функции
, очевидно, лежит на
графике функции ![]() .
.
Рассмотрим
положительное число ![]() . Тогда
. Тогда ![]() , следовательно, точка
, следовательно, точка ![]() с координатами
с координатами ![]() лежит на графике функции
лежит на графике функции ![]() .
.
Расстояние
между точками ![]() и
и ![]() равно
равно ![]() . Но из равенства
. Но из равенства ![]() следует, что
следует, что ![]() ,
, ![]() ,
, ![]() .
.
Пример
На
координатной плоскости изобразите все точки, координаты которых являются
решениями уравнения: ![]() .
.
Решение.
![]() или
или ![]() .
.
Ответ. см. рисунок (??)
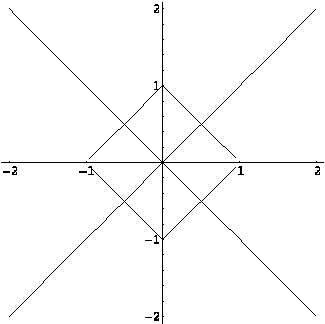
Пример
Дана
функция ![]() . Сколько решений имеет
уравнение
. Сколько решений имеет
уравнение ![]() ?
?
Решение.
Пусть
![]() --- решение уравнения
--- решение уравнения ![]() , а
, а ![]() . Тогда и
. Тогда и ![]() , а потому точка с
координатами
, а потому точка с
координатами ![]() лежит на каждом из
графиков
лежит на каждом из
графиков ![]() и
и ![]() . Наоборот, если точка
. Наоборот, если точка ![]() лежит на пересечении этих
графиков, то
лежит на пересечении этих
графиков, то ![]() и
и ![]() , откуда
, откуда ![]() . Тем самым показано, что
число решений уравнения
. Тем самым показано, что
число решений уравнения ![]() совпадает
с числом точек пересечения графиков
совпадает
с числом точек пересечения графиков ![]() и
и ![]() , а их 16 (см. рис. (??)).
, а их 16 (см. рис. (??)).
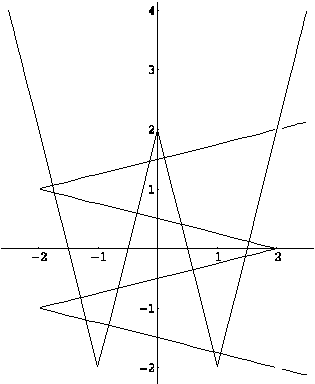 Ответ. 16.
Ответ. 16.
Графики функций, содержащих линейные выражения под знаком абсолютной величины
Сформулируем утверждение, позволяющее строить график алгебраической суммы модулей, не раскрывая модули (это особенно удобно, когда модулей много).
Теорема
Алгебраическая
сумма модулей ![]() линейных
выражений представляет собой кусочно-линейную, график которой состоит из
линейных
выражений представляет собой кусочно-линейную, график которой состоит из ![]() прямолинейного участка.
Поэтому график может быть построен по
прямолинейного участка.
Поэтому график может быть построен по ![]() точкам,
точкам,
![]() из которых представляют
собой корни внутримодульных выражений, ещё одна --- произвольная точка, с
абсциссой меньше наименьшего из этих корней, и последняя --- с абсциссой,
большей наибольшего из этих корней.
из которых представляют
собой корни внутримодульных выражений, ещё одна --- произвольная точка, с
абсциссой меньше наименьшего из этих корней, и последняя --- с абсциссой,
большей наибольшего из этих корней.
Замечание.
Аналогично можно строить графики вида ![]() .
.
Примеры построения графиков
1.
![]() . Вычисляем значения
функции в точках 1, 0 и 2, получаем график, состоящий из двух лучей (см. рис. (??)).
. Вычисляем значения
функции в точках 1, 0 и 2, получаем график, состоящий из двух лучей (см. рис. (??)).
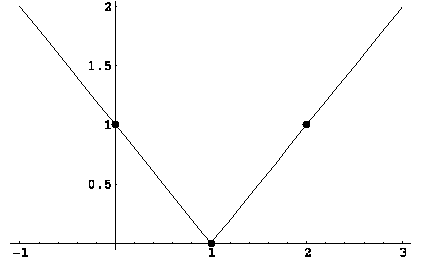
2.
![]() . Вычисляя значение функции
в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из отрезка и двух
лучей (см. рис. (??)).
. Вычисляя значение функции
в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из отрезка и двух
лучей (см. рис. (??)).
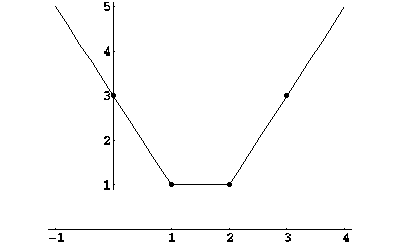
3.
![]() . Для построения графика
``по отрезкам'' вычислим значение функции в точках 1, 2, 3, 0, 4 (см. рис. (??)).
. Для построения графика
``по отрезкам'' вычислим значение функции в точках 1, 2, 3, 0, 4 (см. рис. (??)).
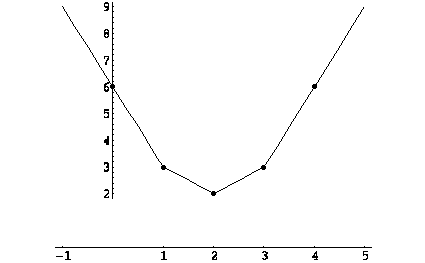
4.
![]() . График разности модулей
строиться аналогично (см. рис. (??)).
. График разности модулей
строиться аналогично (см. рис. (??)).
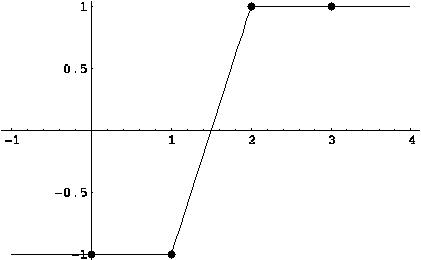
Анализируя
вид графиков 1, 2 и 3, можно предположить, а затем и доказать, что сумма
модулей линейных выражений вида ![]() достигает
своего наименьшего значения либо в единственной точке, если число модулей
нечетно, либо во всех точках некоторого отрезка, если число модулей чётно.
График суммы нечетного числа модулей линейных выражений имеет форму клина, а
график суммы чётного числа модулей имеет участок параллельный оси абсцисс. Более
точно:
достигает
своего наименьшего значения либо в единственной точке, если число модулей
нечетно, либо во всех точках некоторого отрезка, если число модулей чётно.
График суммы нечетного числа модулей линейных выражений имеет форму клина, а
график суммы чётного числа модулей имеет участок параллельный оси абсцисс. Более
точно:
Теорема
Пусть
корни подмодульных выражений упорядочены по возрастанию ![]() . Тогда если число
слагаемых
. Тогда если число
слагаемых ![]() нечётно и
нечётно и ![]() , то наименьшее значение
функции
, то наименьшее значение
функции ![]() достигается в точке
достигается в точке ![]() , а если число слагаемых
, а если число слагаемых ![]() чётно и
чётно и ![]() , то наименьшее значение
функции достигается во всех точках отрезка
, то наименьшее значение
функции достигается во всех точках отрезка ![]() .
.
Используем утверждение для решения задачи, предлагавшейся на одной из олимпиад Санкт-Петербургского государственного университета.
Пример
В
зависимости от значения параметра ![]() , найти
количество корней уравнения
, найти
количество корней уравнения
![]()
Решение.
Решим
задачу графически. Пусть ![]() ,
определим количество точек пересечения графика функции
,
определим количество точек пересечения графика функции ![]() и прямой
и прямой ![]() в зависимости от
в зависимости от ![]() . Исходя из
сформулированного выше утверждения, график функции
. Исходя из
сформулированного выше утверждения, график функции ![]() будет
иметь участок, параллельный оси абсцисс. Заметим, что абсциссы точек этого
участка составляют отрезок
будет
иметь участок, параллельный оси абсцисс. Заметим, что абсциссы точек этого
участка составляют отрезок ![]() , и во
всех его точках функция достигает наименьшего значения, равного, например,
, и во
всех его точках функция достигает наименьшего значения, равного, например, ![]() , причем
, причем
![]()
Поскольку указанная сумма представляет собой удвоенную арифметическую прогрессию с первым членом 1, последним членом 999, сложенную с числом 1000, то она равна
![]()
Тогда
при ![]() уравнение не будет иметь
решений, при
уравнение не будет иметь
решений, при ![]() их будет бесконечно много,
а при
их будет бесконечно много,
а при ![]() уравнение будет иметь два
решения.
уравнение будет иметь два
решения.
Метод раскрытия модулей
Метод раскрытия модулей рассмотрим на примере:
Пример Решить уравнение
![]()
Решение. Это уравнение содержит более одного модуля.
Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем.
1.
Найти значения переменной, при которых каждый из модулей обращается в нуль: ![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
2. Отметить эти точки на числовой прямой.
3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями.
1)
При ![]() или
или ![]() . Чтобы определить знак
каждого из выражений под модулем на этом промежутке, достаточно взять любое
значение
. Чтобы определить знак
каждого из выражений под модулем на этом промежутке, достаточно взять любое
значение ![]() из этого промежутка и
подставить в выражение. Если полученное значение отрицательно, значит, при всех
из этого промежутка и
подставить в выражение. Если полученное значение отрицательно, значит, при всех
![]() из этого промежутка
выражение будет отрицательным; если полученное числовое значение положительно,
значит, при всех значениях
из этого промежутка
выражение будет отрицательным; если полученное числовое значение положительно,
значит, при всех значениях ![]() из
этого промежутка выражение будет положительным.
из
этого промежутка выражение будет положительным.
Возьмем
значение ![]() из промежутка
из промежутка ![]() и подставим его значение в
выражение
и подставим его значение в
выражение ![]() , получаем
, получаем ![]() , значит на этом промежутке
, значит на этом промежутке
![]() отрицательно, а
следовательно ``выйдет'' из под модуля со знаком ``минус'', получим:
отрицательно, а
следовательно ``выйдет'' из под модуля со знаком ``минус'', получим: ![]() .
.
При
этом значении ![]() , выражение
, выражение ![]() получит значение
получит значение ![]() , значит, оно на промежутке
, значит, оно на промежутке
![]() также принимает
отрицательные значения и ``выйдет'' из модуля со знаком ``минус'', получим:
также принимает
отрицательные значения и ``выйдет'' из модуля со знаком ``минус'', получим: ![]() .
.
Выражение
![]() получит значение
получит значение ![]() и ``выйдет'' из под модуля
со знаком ``минус'':
и ``выйдет'' из под модуля
со знаком ``минус'': ![]() .
.
Уравнение
на этом промежутке получится таким: ![]() , решая
его, находим:
, решая
его, находим: ![]() .
.
Выясняем,
входит ли это значение в промежуток ![]() .
Оказывается входит, значит
.
Оказывается входит, значит ![]() является
корнем уравнения.
является
корнем уравнения.
2)
При ![]() . Выбираем любое значение
. Выбираем любое значение ![]() из этого промежутка. Пусть
из этого промежутка. Пусть
![]() . Определяем знак каждого
из выражений под модулем при этом значении
. Определяем знак каждого
из выражений под модулем при этом значении ![]() .
Оказывается, что выражение
.
Оказывается, что выражение ![]() положительно,
а два других отрицательны.
положительно,
а два других отрицательны.
Уравнение
на этом промежутке примет вид: ![]() . Решая
его, находим
. Решая
его, находим ![]() . Это значение не входит в
промежуток
. Это значение не входит в
промежуток ![]() , а значит, не является
корнем уравнения.
, а значит, не является
корнем уравнения.
3)
При ![]() . Выбираем произвольное
значение
. Выбираем произвольное
значение ![]() из этого промежутка,
скажем,
из этого промежутка,
скажем, ![]() и подставляем в каждое из
выражений. Находим, что выражения
и подставляем в каждое из
выражений. Находим, что выражения ![]() и
и ![]() положительны, а
положительны, а ![]() --- отрицательно. Получим
следующее уравнение:
--- отрицательно. Получим
следующее уравнение: ![]() .
.
После
преобразования, получим: ![]() , а
значит, уравнение не имеет корней на этом промежутке.
, а
значит, уравнение не имеет корней на этом промежутке.
4)
При ![]() . Нетрудно установить, что
все выражения на этом промежутке положительны, а значит получим уравнение:
. Нетрудно установить, что
все выражения на этом промежутке положительны, а значит получим уравнение: ![]() ,
, ![]() ,
, ![]() которое входит в
промежуток и является корнем уравнения.
которое входит в
промежуток и является корнем уравнения.
Ответ.
![]() ,
, ![]() .
.
Пример Решить уравнение
![]()
Решение.
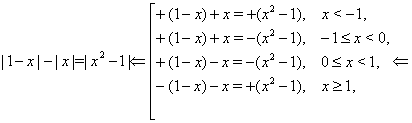
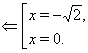
Ответ.
![]() ,
, ![]() .
.
Использование тождества
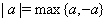 , при решении уравнений
, при решении уравнений
Из сформулированного свойства модуля можно вывести два полезных следствия:
![]()
![]()
Проиллюстрируем применение первого из них для решения задачи вступительного экзамена в Санкт-Петербургский государственный университет.
Пример Изобразить график функции
![]()
Решение. Перепишем задающую функцию выражение, используя первое следствие:
![]() .
.
Осталось
только построить графики функций ![]() ,
, ![]() в одной системе координат
и определить участки, на которых один из них выше другого (см. рис. (??)).
в одной системе координат
и определить участки, на которых один из них выше другого (см. рис. (??)).

Использование
второго тождества удобно для построения графика функции ![]() .
.
Решение.
В
силу второго тождества, выражение задающее функцию, записывается в виде: ![]() .
.
Искомый график изображен на рисунке (см. рис. (??)).

Пример Найдите масимальное значение выражения
![]()
где
![]() ,
, ![]() , ...,
, ..., ![]() --- различные натуральные
числа от 1 до 1990.
--- различные натуральные
числа от 1 до 1990.
Решение.
Заметим,
что модуль разности двух неотрицательных чисел не больше их максимума. Поэтому ![]() не больше, чем
не больше, чем ![]() ,
, ![]() не больше, чем
не больше, чем ![]() ,
, ![]() не больше, чем
не больше, чем ![]() . Далее, данное выражение
не может равняться 1990, поскольку четность этого выражения совпадает с четностью
суммы
. Далее, данное выражение
не может равняться 1990, поскольку четность этого выражения совпадает с четностью
суммы ![]() . Наконец приведем пример,
показывающий, что значение выражения может равняться 1989:
. Наконец приведем пример,
показывающий, что значение выражения может равняться 1989:
![]()
Ответ. 1989.
Решение уравнений содержащих модули неотрицательных выражений
Пример Чему равна сумма корней уравнения (корень, если он один) уравнения
![]()
Решение. Рассмотрим выражение
![]()
и преобразуем его к виду
![]()
Очевидно,
что числитель дроби при любых значениях переменной является положительным
числом. Значит дробное выражение положительно, если ![]() (т.к.
(т.к.
![]() ). Преобразуем полученное
выражение, при условии
). Преобразуем полученное
выражение, при условии ![]() . Получим
уравнение, равносильное исходному:
. Получим
уравнение, равносильное исходному:
![]()
![]()
Ответ.
![]() .
.
Пример Решить уравнение
![]()
Решение.
Поскольку
левая часть уравнения неотрицательна, при всех допустимых значениях переменной,
на множестве корней уравнения правая его часть тоже должна быть неотрицательной,
отсюда условие ![]() , на этом
промежутке знаменатели обеих дробей равны, и остается решить уравнение
, на этом
промежутке знаменатели обеих дробей равны, и остается решить уравнение ![]() . Решая его и учитывая
ограничение
. Решая его и учитывая
ограничение ![]() , получаем
, получаем
Ответ.
![]() .
.
Пример Решить уравнение:
![]()
Решение. Нетрудно догадаться, что все выражения, стоящие под знаками второго, третьего и т.д. модулей, положительны. И поскольку модуль положительного выражения равен самому этому выражению, получим
![]()
![]()
Ответ.
![]() .
.
Решение уравнений с использованием геометрической интерпретации
Геометрический
смысл выражения ![]() --- длина
отрезка координатной оси, соединяющего точки с абсциссами
--- длина
отрезка координатной оси, соединяющего точки с абсциссами ![]() и
и ![]() . Перевод алгебраической
задачи на геометрический язык часто позволяет избежать громоздких выкладок.
. Перевод алгебраической
задачи на геометрический язык часто позволяет избежать громоздких выкладок.
Пример
Решим
уравнение ![]() .
.
Решение.
Будем
рассуждать следующим образом: исходя из геометрической интерпретации модуля,
левая часть уравнения представляет собой сумму расстояний от некоторой точки с
абсциссой ![]() до двух фиксированных
точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка
до двух фиксированных
точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка ![]() обладают требуемым
свойством, а точки, расположенные вне этого отрезка,--- нет.
обладают требуемым
свойством, а точки, расположенные вне этого отрезка,--- нет.
Ответ.
![]() .
.
Пример
Решим
уравнение ![]() .
.
Решение. Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2.
Ответ.
![]() .
.
Пример
Решить
неравенство ![]() .
.
Решение.
Изобразим
на координатной прямой точки, сумма расстояний от которых до точек ![]() и
и ![]() в точности равна
в точности равна ![]() . Это все точки отрезка
. Это все точки отрезка ![]() . Для всех чисел вне
данного отрезка сумма расстояний будет больше двух.
. Для всех чисел вне
данного отрезка сумма расстояний будет больше двух.
Ответ.
![]() .
.
Замечание. Обобщением решения вышеприведенных уравнений являются следующие равносильные переходы:
![]()
Пример
Решите
неравенство: ![]() .
.
Решение.
Решим
неравенство, используя координатную прямую. Данное неравенство выполняется для
всех точек c координатой ![]() ,
которые находятся ближе к точке с координатой
,
которые находятся ближе к точке с координатой ![]() ,
чем к точке с координатой
,
чем к точке с координатой ![]() . Так
как
. Так
как ![]() , то искомыми являются все
точки, расположенные левее точки с координатой
, то искомыми являются все
точки, расположенные левее точки с координатой ![]() .
.
Ответ.
![]() .
.
Пример
Решите
уравнение ![]() .
.
Решение.
Рассмотрим
на числовой прямой точку с координатой ![]() .
Сумма
.
Сумма ![]() равна сумме расстояний от
точки
равна сумме расстояний от
точки ![]() до точек с координатами 2,
1, 0, -1, -2. Заметим, что сумма расстояний от любой точки до точек
до точек с координатами 2,
1, 0, -1, -2. Заметим, что сумма расстояний от любой точки до точек ![]() и
и ![]() не меньше длины отрезка
не меньше длины отрезка ![]() (и равенство достигается
тогда и только тогда, когда точка расположена на отрезке
(и равенство достигается
тогда и только тогда, когда точка расположена на отрезке ![]() ). Отсюда получаем, что
). Отсюда получаем, что ![]() не меньше 4, а
не меньше 4, а ![]() не меньше 2 при любом
не меньше 2 при любом ![]() . Поэтому для того, чтобы
сумма
. Поэтому для того, чтобы
сумма ![]() была равна
была равна ![]() , необходимо, чтобы
, необходимо, чтобы ![]() . Итак,
. Итак, ![]() необходимо равен
необходимо равен ![]() . Легко проверить, что
значение
. Легко проверить, что
значение ![]() действительно является
решением данного уравнения.
действительно является
решением данного уравнения.
Ответ.
![]() .
.
Пример
Гальперин Г.А. Положительные числа ![]() ,
, ![]() ,
, ![]() и
и ![]() таковы, что система
уравнений
таковы, что система
уравнений
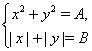
имеет
![]() решений, а система
уравнений
решений, а система
уравнений
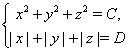
имеет
![]() решений. Известно, что
решений. Известно, что ![]() . Найдите
. Найдите ![]() и
и ![]() .
.
Решение.
Первое
уравнение есть уравнение окружности, второму удовлетворяют точки квадрата с
центром в начале координат и с диагоналями, принадлежащими осям координат.
Система из двух первых уравнений в зависимости от ![]() и
и
![]() либо не имеет решений,
либо имеет четыре решения, либо восемь. Итак,
либо не имеет решений,
либо имеет четыре решения, либо восемь. Итак, ![]() может
равняться либо 0, либо 4, либо 8. Первое уравнение второй системы есть
уравнение сферы. Второму удовлетворяют точки октаэдра с центром в начале
координат и с вершинами, лежащими на осях координат на равных расстояниях от
центра. Эта система в зависимости от
может
равняться либо 0, либо 4, либо 8. Первое уравнение второй системы есть
уравнение сферы. Второму удовлетворяют точки октаэдра с центром в начале
координат и с вершинами, лежащими на осях координат на равных расстояниях от
центра. Эта система в зависимости от ![]() и
и ![]() либо не имеет решений,
либо имеет 6 решений (вершины октаэдра лежат на сфере), либо имеет 8 решений
(сфера касается граней октаэдра), либо имеет бесконечное число решений (сфера
пересекает грани октаэдра по окружностям или нескольким дугам окружностей).
Итак,
либо не имеет решений,
либо имеет 6 решений (вершины октаэдра лежат на сфере), либо имеет 8 решений
(сфера касается граней октаэдра), либо имеет бесконечное число решений (сфера
пересекает грани октаэдра по окружностям или нескольким дугам окружностей).
Итак, ![]() может равняться либо 0,
либо 6, либо 8, либо
может равняться либо 0,
либо 6, либо 8, либо ![]() . Условию
. Условию ![]() удовлетворяет только
вариант
удовлетворяет только
вариант ![]() ,
, ![]() .
.
Ответ.
![]() ,
, ![]() .
.
Перевод алгебраической задачи на геометрический язык --- удобный и мощный метод решения задач. В качестве еще одного примера разберем блок задач олимпиады математико-механического факультета СПбГУ:
Пример
Дана
функция: ![]() .
.
а)
Решите уравнение ![]() ;
;
б)
Решите неравенство ![]() ;
;
в)
Найдите количество решений уравнения ![]() в
зависимости от значений параметра
в
зависимости от значений параметра ![]() .
.
Решение.
Построим
график функции ![]() . Для этого
заметим, что
. Для этого
заметим, что ![]() , а тогда мы
можем сначала построить график функции
, а тогда мы
можем сначала построить график функции ![]() ,
и затем отразить его относительно оси ординат. Преобразуем выражение, задающее
функцию
,
и затем отразить его относительно оси ординат. Преобразуем выражение, задающее
функцию ![]() :
:
![]()
Поскольку данная система определяет верхнюю полуокружность радиуса 2 с центром в точке (2; 0), график исходной функции представляет собой объединение двух полуокружностей (см. рис. (??)).
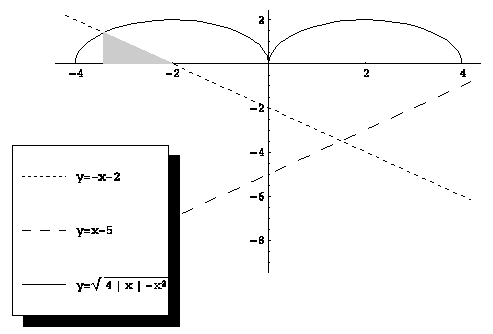
Теперь решение задач не представляет труда:
а)
Корень уравнения есть абсцисса точки пересечения прямой ![]() с графиком функции
с графиком функции ![]() . Найдем ее геометрически:
заштрихованный на рисунке прямоугольный треугольник является равнобедренным
(угловой коэффициент прямой равен
. Найдем ее геометрически:
заштрихованный на рисунке прямоугольный треугольник является равнобедренным
(угловой коэффициент прямой равен ![]() ), его
гипотенуза есть радиус окружности, ее длина 2. Тогда длина катета, лежащего на
оси абсцисс, есть
), его
гипотенуза есть радиус окружности, ее длина 2. Тогда длина катета, лежащего на
оси абсцисс, есть ![]() , а искомая
абсцисса равна
, а искомая
абсцисса равна ![]() .
.
б)
Неравенство ![]() выполнено при всех
выполнено при всех ![]() из отрезка
из отрезка ![]() .
.
в)
При ![]() ,
, ![]() решений нет, при
решений нет, при ![]() уравнение
уравнение ![]() имеет три решения, при
имеет три решения, при ![]() --- четыре решения, при
--- четыре решения, при ![]() --- два решения.
--- два решения.
Решение уравнений с
использованием тождества 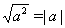
Пример Решить уравнение
![]()
Решение.
Дважды
применяя тождество ![]() , получим
уравнение
, получим
уравнение
![]()
решением
которого является интервал ![]() .
.
Ответ.
![]() .
.
Пример Решить уравнение
![]()
Решение.
![]() .
.
Ответ.
![]() .
.
Применение теоремы о знаках при решении уравнений
Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей:
Теорема Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений.
Пример Решить неравенство
![]()
Решение. Воспользуемся теоремой:
![]()
Используя формулу разности квадратов, разложим числитель и знаменатель на множители и решим полученное рациональное неравенство.
![]()
Ответ.
![]()
Решение уравнений переходом к следствию
Все уравнения с модулями могут быть решены следующим образом: рассмотрим весь набор уравнений, который может получится при раскрытии модулей, но не будем выписывать соответствующие промежутки. Решая каждое из полученных уравнений, получим следствия исходного уравнения. Остается только проверить не приобрели ли мы посторонних корней прямой их подстановкой в исходное уравнение.
Пример Решим уравнение
![]()
Решение. Последовательно переходя к следствиям, получаем:
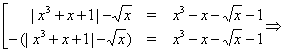
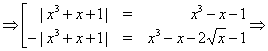
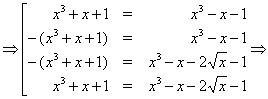
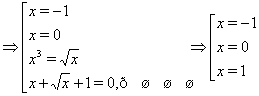
Нетрудно убедится, что найденные числа не являются корнями исходного уравнения.
Ответ. нет решения.
В случае вложенных знаков модуля тоже можно рассмотреть весь набор получающихся при раскрытии модуля уравнений среди решений которых содержатся решения исходного уравнения, а потом отобрать из всех полученных решений подходящие хотя бы с помощью проверки.
Пример Решите уравнение
![]()
Решение. Все корни исходного уравнения содержатся среди корней двух уравнений
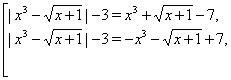
которые можно переписать в виде
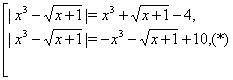
Аналогично, каждое из этих уравнений распадается на два:
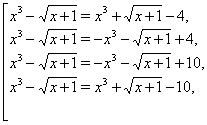
что приводит к четырём уравнениям:
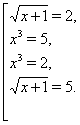
Отсюда
получаем 4 решения: ![]() ,
, ![]() ,
, ![]() ,
, ![]() среди которых содержатся
корни исходного уравнения. 1-й корень, очевидно, удовлетворяет уравнению. Это
проверяется легко. 2-й и 3-й не походят, так как правая часть исходного
уравнения при этих значениях отрицательна. 4-й корень тоже является лишним, так
как этот корень должен удовлетворять уравнению (*), а при этом значении его
правая часть отрицательна.
среди которых содержатся
корни исходного уравнения. 1-й корень, очевидно, удовлетворяет уравнению. Это
проверяется легко. 2-й и 3-й не походят, так как правая часть исходного
уравнения при этих значениях отрицательна. 4-й корень тоже является лишним, так
как этот корень должен удовлетворять уравнению (*), а при этом значении его
правая часть отрицательна.
Ответ. 3.
Решение уравнений методом интервалов
Применение метода интервалов основано на следующей
Теорема Функция, непрерывная на промежутке и необращающаяся на нем в нуль, сохраняет на этом промежутке свой знак.
Это означает, что нули функции и границы промежутков ее непрерывности разделяют область определения функции на участки, где она сохраняет постоянный знак. Применение метода поясним на примере.
Пример Решим неравенство
![]()
Пусть
![]() . Областью определения
данной функции есть
. Областью определения
данной функции есть ![]() . Решая уравнение
(см. (??)), получим, что функция
. Решая уравнение
(см. (??)), получим, что функция ![]() не
обращается в нуль ни при каком значении переменной. Это означает, что на всей
области определения функция является знакопостоянной. Вычисляя, например,
не
обращается в нуль ни при каком значении переменной. Это означает, что на всей
области определения функция является знакопостоянной. Вычисляя, например, ![]() , получаем, что функция
принимает только положительные значения.
, получаем, что функция
принимает только положительные значения.
Ответ.
![]() .
.
Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток).
Решение уравнений домножением на положительный множитель
Пример Решить неравенство
![]()
Решение. ``Ловушка'' заключается в том, что в задаче имеется несколько модулей, раскрывать которые -- значит получить, громоздкое решение. Умножим дробь на некоторое выражение, принимающее лишь положительные значения и такое, чтобы упростить исходное неравенство:
![]()
![]()
![]()
Ответ.
![]() .
.
Пример
Найти
корни уравнения ![]() .
.
Решение.
Так
как ![]() , то из уравнения следует,
что
, то из уравнения следует,
что ![]() ,
, ![]() . Тогда исходное уравнение
примет вид:
. Тогда исходное уравнение
примет вид: ![]() ,
, ![]() . Корни этого уравнения
. Корни этого уравнения ![]() ,
, ![]() . Корень
. Корень ![]() , поэтому он не является
решением, а
, поэтому он не является
решением, а ![]() .
.
Ответ.
![]() .
.
Пример
Найти
произведение корней уранения ![]() .
.
Решение.
Обозначим
![]() ,
, ![]() . Тогда исходное уравнение
примет вид:
. Тогда исходное уравнение
примет вид: ![]() . Корни этого уравнения
. Корни этого уравнения ![]() ,
, ![]() . Так как
. Так как ![]() , то
, то ![]() . Отсюда
. Отсюда ![]() ,
, ![]() . Произведение корней равно
. Произведение корней равно
![]() .
.
Ответ.
![]() .
.
Пример
Найти
разность между наибольшими и наименьшим корнями уравнения ![]() .
.
Решение.
Обозначим
![]() ,
, ![]() . Тогда исходное уравнение
примет вид:
. Тогда исходное уравнение
примет вид: ![]() . Решим его. Корни этого
уравнения
. Решим его. Корни этого
уравнения ![]() ,
, ![]() . Так как
. Так как ![]() , то значение
, то значение ![]() не подходит. Поэтому
не подходит. Поэтому ![]() . Разность между наибольшим
и наименьшим корнями уравнения равна
. Разность между наибольшим
и наименьшим корнями уравнения равна ![]() .
.
Ответ.
![]() .
.
Пример
Найти
сумму корней уравнения ![]() .
.
Решение.
Используем
правило: ![]() . Исходное уравнение
запишем в виде совокупности уравнений:
. Исходное уравнение
запишем в виде совокупности уравнений: ![]() Таким образом сумма корней
исходного уравнения равна
Таким образом сумма корней
исходного уравнения равна ![]() .
.
Другой
путь. Поскольку обе части уравнения неотрицательны,
возведем уравнение в квадрат. Получим: ![]() ,
,
![]() . Так как дискриминант
уравнения положительный, то по теореме Виета сумма корней равна
. Так как дискриминант
уравнения положительный, то по теореме Виета сумма корней равна ![]()
Ответ.
![]() .
.
Пример
Сколько
целых корней на отрезке ![]() имеет
уравнение
имеет
уравнение
![]()
Решение.
Рассмотрим
квадратный трехчлен ![]() . Так как
. Так как ![]() , то
, то ![]() , поэтому исходное
уравнение запишется как
, поэтому исходное
уравнение запишется как
![]()
![]()
Последнее
уравнение эквивалентно неравенству ![]() ,
решение которого
,
решение которого ![]() . Таким образом,
уравнение имеет 6 корней на отрезке
. Таким образом,
уравнение имеет 6 корней на отрезке ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Ответ. 6.
Пример Какое наибольшее конечное число корней может иметь уравнение
![]()
где
![]() ,
, ![]() ,...,
,..., ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() --- различные числа?
--- различные числа?
Решение.
Положим
![]() и перепишем исходное
уравнение в виде
и перепишем исходное
уравнение в виде ![]() .
.
Пусть
![]() --- все числа из множества
--- все числа из множества
![]() , упорядоченные по
возрастанию. На каждом из 101 промежутка
, упорядоченные по
возрастанию. На каждом из 101 промежутка ![]() ,
,
![]() ,...,
,..., ![]() ,
, ![]() , функция
, функция ![]() линейна. Заметим, что на
первом и последнем из этих промежутков
линейна. Заметим, что на
первом и последнем из этих промежутков ![]() и
и
![]() соответственно, при этом
соответственно, при этом ![]() , так как количество корней
конечно.
, так как количество корней
конечно.
Пойдем по числовой оси слева направо.
Вначале
угловой коэффициент функции ![]() равен
0. Всякий раз, когда мы проходим одну из точек
равен
0. Всякий раз, когда мы проходим одну из точек ![]() ,
он за счет смены знака при раскрытии соответствующего модуля изменяется на
,
он за счет смены знака при раскрытии соответствующего модуля изменяется на ![]() .
.
Таким образом, он всегда равен четному целому числу и не может поменять знак, не обратившись перед этим в 0.
Значит,
угловые коэффициенты на любых двух соседних промежутках либо оба
неотрицательны, либо оба неположительны, т.е. функция ![]() на объединении этих
промежутков либо неубывающая, либо невозрастающая.
на объединении этих
промежутков либо неубывающая, либо невозрастающая.
Стало
быть, если число ее корней конечно, то на каждом из 50 промежутков ![]() ,...,
,..., ![]() ,
, ![]() она имеет не более одного
корня. Кроме того, на крайних интервалах значения имеют разные знаки, и в
каждом корне знак функции меняется. Следовательно, количество корней нечетно и
не превышает 49.
она имеет не более одного
корня. Кроме того, на крайних интервалах значения имеют разные знаки, и в
каждом корне знак функции меняется. Следовательно, количество корней нечетно и
не превышает 49.
Нетрудно
проверить, что если роль ![]() будут
играть числа 1, 4, 5, 8, 97, 100, а роль
будут
играть числа 1, 4, 5, 8, 97, 100, а роль ![]() ---
числа 2, 3, 6, 7, 94, 95, 98,
---
числа 2, 3, 6, 7, 94, 95, 98, ![]() , то
уравнение
, то
уравнение ![]() будет иметь ровно 49
корней.
будет иметь ровно 49
корней.
Ответ. 49.
Пример Решите систему неравенств
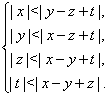
Решение.
Предположим,
что данная система неравенств имеет решение ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Тогда, в частности,
. Тогда, в частности, ![]() , т. е.
, т. е.
![]()
Аналогично получаем
![]()
![]()
![]()
Перемножим все полученные неравенства. С одной стороны, произведение четырёх положительных чисел положительно. С другой стороны, это произведение равно ---
![]()
Приходим к противоречию.
Ответ. Система не имеет решений.
Пример
Существуют
ли действительные числа ![]() ,
, ![]() и
и ![]() такие, что при всех
действительных
такие, что при всех
действительных ![]() и
и ![]() выполняется неравенство
выполняется неравенство
![]()
Решение.
Предположим,
что такие числа ![]() ,
, ![]() и
и ![]() существуют. Выберем
существуют. Выберем ![]() и
и ![]() такие, что
такие, что ![]() ,
, ![]() ,
, ![]() . Тогда разность между
левой и правой частями равна
. Тогда разность между
левой и правой частями равна ![]() . А если
взять
. А если
взять ![]() и
и ![]() такие, что
такие, что ![]() ,
, ![]() ,
, ![]() , то эта разность будет
равна
, то эта разность будет
равна ![]() . Таким образом, с одной
стороны,
. Таким образом, с одной
стороны, ![]() , с другой
, с другой ![]() . Противоречие.
. Противоречие.
Ответ. Нет.
Пример
Сколько
различных целочисленных решений имеет неравенство ![]() ?
?
Решение.
При
натуральном ![]() уравнение
уравнение ![]() имеет ровно
имеет ровно ![]() целочисленных решений, а
при
целочисленных решений, а
при ![]() решение единственно. Таким
образом, количество решений исходного неравенства равно
решение единственно. Таким
образом, количество решений исходного неравенства равно ![]() .
.
Ответ. 19801.
Пример
Найдите
все значения параметра ![]() , при каждом из
которых уравнение имеет три различных корня; найдите эти корни:
, при каждом из
которых уравнение имеет три различных корня; найдите эти корни: ![]() .
.
Решение.
Возведем
обе части уравнения в квадрат: ![]() .
.
Если
![]() , тогда получим уравнение:
, тогда получим уравнение:
![]()
Дискриминант этого уравнения равен:
![]() .
.
Уравнение
(1) будет иметь один корень, при ![]() и
и ![]() . Два корня, при
. Два корня, при ![]() и
и ![]() .
.
Если
![]() , тогда получим уравнение:
, тогда получим уравнение:
![]()
Дискриминант этого уравнения равен:
![]() .
.
Уравнение
(2) будет иметь один корень при ![]() и
и ![]() . Два корня --- при
. Два корня --- при ![]() и
и ![]() .
.
Делаем
вывод, что при ![]() уравнение (1)
имеет один корень, а уравнение (2) --- два корня. При
уравнение (1)
имеет один корень, а уравнение (2) --- два корня. При ![]() , уравнение (1) имеет два
корня, а уравнение (2) --- один.
, уравнение (1) имеет два
корня, а уравнение (2) --- один.
Таким
образом, при ![]() и
и ![]() данное уравнение имеет три
корня.
данное уравнение имеет три
корня.
Найдем
эти корни. При ![]() , первое
уравнение примет вид:
, первое
уравнение примет вид: ![]() . Оно имеет один
корень:
. Оно имеет один
корень: ![]()
Уравнение
(2) примет вид: ![]() которое имеет
два корня:
которое имеет
два корня: ![]() ,
, ![]() .
.
При
![]() , уравнение (2) примет вид:
, уравнение (2) примет вид:
![]() . Оно имеет один корень:
. Оно имеет один корень: ![]() .
.
Уравнение
(1) при этом станет: ![]() , которое будет
иметь корни:
, которое будет
иметь корни: ![]() ,
, ![]() .
.
Ответ.
При
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
При
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пример
Для
каждого значения параметра ![]() определите
число решений уравнения
определите
число решений уравнения ![]() .
.
Решение.
1.
Если ![]() , тогда уравнение не имеет
решений, модуль любого вещественного числа неотрицателен.
, тогда уравнение не имеет
решений, модуль любого вещественного числа неотрицателен.
2.
Если ![]() , тогда получим уравнение
, тогда получим уравнение ![]() . Это уравнение имеет два
корня, так как
. Это уравнение имеет два
корня, так как ![]() .
.
3.
Если ![]() , тогда получаем
совокупность двух уравнений:
, тогда получаем
совокупность двух уравнений:
![]()
![]()
Первое
уравнение имеет дискриминант: ![]() . Оно
не будет иметь корней при
. Оно
не будет иметь корней при ![]() ,
, ![]() , но это невозможно, так
как
, но это невозможно, так
как ![]() . Также оно не может иметь
один корень (тогда
. Также оно не может иметь
один корень (тогда ![]() , что также
невозможно). Таким образом, при
, что также
невозможно). Таким образом, при ![]() уравнение
(1) имеет два корня.
уравнение
(1) имеет два корня.
Второе уравнение имеет дискриминант:
![]() . Оно не будет
иметь корней, если
. Оно не будет
иметь корней, если ![]() ,
, ![]() ,
, ![]() . Будет иметь один корень,
если
. Будет иметь один корень,
если ![]() . Будет иметь два корня,
если
. Будет иметь два корня,
если ![]() .
.
Окончательно получаем.
Ответ.
Если
![]() , тогда уравнение не имеет
корней.
, тогда уравнение не имеет
корней.
Если
![]() и
и ![]() , тогда уравнение имеет два
корня.
, тогда уравнение имеет два
корня.
Если
![]() , тогда уравнение имеет три
корня.
, тогда уравнение имеет три
корня.
Если
![]() , тогда уравнение имеет
четыре корня.
, тогда уравнение имеет
четыре корня.
Пример
Найдите
все значения параметра ![]() из промежутка
из промежутка ![]() , при каждом из которых
больший из корней уравнения
, при каждом из которых
больший из корней уравнения ![]() принимает
наибольшее значение.
принимает
наибольшее значение.
Решение.
Преобразуем
уравнение к виду ![]() .
.
Значит,
если ![]() ,
, ![]() , тогда
, тогда ![]() . Найдем наибольшее
значение
. Найдем наибольшее
значение ![]() , при котором
, при котором ![]() , т. е. наибольшее решение
неравенства
, т. е. наибольшее решение
неравенства ![]() .
.
Преобразуем
это неравенство: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Последнее
неравенство решим методом интервалов, помня, что ![]() .
.
Решение
неравенства будет множество: ![]() .
.
Ясно,
что дробь ![]() принимает наибольшее
значение при
принимает наибольшее
значение при ![]() , тогда значение
, тогда значение ![]() будет равно:
будет равно: ![]() .
.
Ответ.
При
![]() .
.
Пример
Найти
все значения параметра ![]() , при каждом из
которых уравнение
, при каждом из
которых уравнение ![]() имеет
единственное решение.
имеет
единственное решение.
Решение.
Найдем
решения для каждого значения ![]() , а
затем отберем те, которые удовлетворяют условию задачи, т. е. при которых
уравнение имеет единственное решение.
, а
затем отберем те, которые удовлетворяют условию задачи, т. е. при которых
уравнение имеет единственное решение.
Для
каждого фиксированного ![]() будем искать
решения данного уравнения сначала на промежутке
будем искать
решения данного уравнения сначала на промежутке ![]() ,
а потом на промежутке
,
а потом на промежутке ![]() , поскольку
модуль обращается в нуль при
, поскольку
модуль обращается в нуль при ![]() :
:
1)
Пусть ![]() . На этом промежутке
. На этом промежутке ![]() и поэтому данное уравнение
примет вид
и поэтому данное уравнение
примет вид ![]() .
.
Найдем дискриминант полученного приведенного квадратного уравнения
![]() , значит, при
любом действительном значении
, значит, при
любом действительном значении ![]() уравнение
имеет два idth="339" height="24" src="images/4757206.png">, значит, при
любом действительном значении
уравнение
имеет два idth="339" height="24" src="images/4757206.png">, значит, при
любом действительном значении ![]() уравнение
имеет два различных действительных корня:
уравнение
имеет два различных действительных корня: ![]() и
и
![]() .
.
Выясним,
входят ли они в промежуток ![]() . Корень
. Корень
![]() лежит в этой области
только тогда, когда выполняется неравенство:
лежит в этой области
только тогда, когда выполняется неравенство: ![]() или
или
![]() .
.
Последнее неравенство равносильно системе неравенств:
![]()
Последняя
система неравенств не имеет решений, значит, ни при каком значении параметра a
число ![]() не лежит в области
не лежит в области ![]() .
.
Корень
![]() лежит в рассматриваемой
области тогда, когда выполнено неравенство:
лежит в рассматриваемой
области тогда, когда выполнено неравенство: ![]() или
или
![]() .
.
Решим
последнее неравенство. Ясно, что этому неравенству удовлетворяют все значения ![]() из промежутка
из промежутка ![]() .
.
При
![]() получим неравенство
получим неравенство ![]() . Отсюда находим:
. Отсюда находим: ![]() .
.
Таким
образом, при ![]() уравнение имеет
единственное решение
уравнение имеет
единственное решение ![]() .
.
2)
Пусть ![]() . На этом промежутке
. На этом промежутке ![]() и поэтому исходное
уравнение можно переписать в виде
и поэтому исходное
уравнение можно переписать в виде ![]() .
Найдем дискриминант этого уравнения:
.
Найдем дискриминант этого уравнения: ![]() .
.
Уравнение
не имеет решений, если ![]() , т. е. если
, т. е. если ![]() .
.
Значит,
уравнение не имеет корней для ![]() из
промежутка
из
промежутка ![]() .
.
Если
![]() не принадлежат этому
промежутку, то квадратное уравнение имеет корни
не принадлежат этому
промежутку, то квадратное уравнение имеет корни ![]() ,
,
![]() , причем
, причем ![]() при
при ![]() и
и ![]() . Выясним теперь, при каких
значениях параметра
. Выясним теперь, при каких
значениях параметра ![]() найденные корни
лежат в области
найденные корни
лежат в области ![]() .
.
Для
этого нужно решить неравенства ![]() и
и ![]() .
.
Неравенство
![]() равносильно неравенству
равносильно неравенству ![]() или совокупности двух
систем неравенств:
или совокупности двух
систем неравенств:
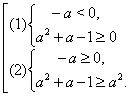
Множество
решений первой системы имеет вид ![]() , вторая
система не имеет решений. Значит, только при значении
, вторая
система не имеет решений. Значит, только при значении ![]() корень уравнения
корень уравнения ![]() лежит в области
лежит в области ![]()
Неравенство
![]() равносильно неравенству
равносильно неравенству ![]() или системе неравенств
или системе неравенств
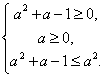
Множество
решений полученной системы неравенств есть отрезок ![]() .
.
Только
при этих значениях параметра ![]() , корень
, корень
![]() принадлежит области:
принадлежит области: ![]() . Таким образом, при
. Таким образом, при ![]() данное уравнение в области
данное уравнение в области
![]() решений не имеет.
решений не имеет.
Если
![]() , то уравнение в
рассматриваемой области имеет единственное решение
, то уравнение в
рассматриваемой области имеет единственное решение ![]() .
.
При
значениях ![]() , лежащих в области
, лежащих в области ![]() исходное уравнение имеет
два различных корня
исходное уравнение имеет
два различных корня ![]() и
и ![]() . Если же
. Если же ![]() , то исходное уравнение
имеет единственный корень
, то исходное уравнение
имеет единственный корень ![]() .
Полученные результаты удобно свести в таблицу:
.
Полученные результаты удобно свести в таблицу:
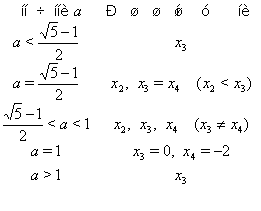
Таким
образом, искомые значения ![]() образуют
два промежутка:
образуют
два промежутка: ![]() и
и ![]() .
.
Ответ.
![]() ,
, ![]() .
.
Пример
Найти
все корни уравнения ![]() , удовлетворяющее
неравенству
, удовлетворяющее
неравенству ![]() .
.
Решение.
Строим
графики функций ![]() и
и ![]() . Получим две точки
пересечения, абсцисса только одной из них меньше
. Получим две точки
пересечения, абсцисса только одной из них меньше ![]() ,
т. е. удовлетворяет условию задачи (см. рис. (??)).
,
т. е. удовлетворяет условию задачи (см. рис. (??)).
pics/ex14.eps
Абсциссу
точки можно получить решив уравнение ![]() .
.
Ответ.
![]() .
.
Пример Решить аналитически и графически уравнение
![]()
Аналитическое решение
Преобразуем уравнение, умножив обе его части на 2, будучи положительным числом, его можно вносить под знак модуля, поэтому получим:
![]()
У каждого из трехчленов положительные дискриминанты. Это дает возможность разложить каждый из них на линейные множители.
Уравнение
примет вид: ![]() .
.
На числовой прямой отложим точки, в которых каждый из множителей обращается в нуль. В результате получим пять промежутков, на каждом из которых определим знаки трехчленов под модулем и решим полученные уравнения.
Однако такой способ не будет рациональным. Целесообразнее изобразить промежутки знакопостоянства каждого из трехчленов на числовых осях. Тогда определение их знаков будет упрощено и сделается более наглядным (см. рис. (??)).
pics/ex9.eps
При таком схематическом изображении понятно, что:
1)
при ![]() оба трехчлена положительны
и уравнение примет вид:
оба трехчлена положительны
и уравнение примет вид:
![]()
Решая
его, находим ![]() ,
, ![]() . Оба корня не входят в
промежуток
. Оба корня не входят в
промежуток ![]() и являются посторонними;
и являются посторонними;
2)
при ![]() первый трехчлен
отрицателен, а второй положителен, получим уравнение:
первый трехчлен
отрицателен, а второй положителен, получим уравнение: ![]() откуда находим корень
откуда находим корень ![]() , который входит в
промежуток
, который входит в
промежуток ![]() и является решением
уравнения;
и является решением
уравнения;
3)
при ![]() оба трехчлена
отрицательны, получаем:
оба трехчлена
отрицательны, получаем:
![]() , откуда
, откуда ![]() , который входит в
промежуток
, который входит в
промежуток ![]() и является решением
уравнения;
и является решением
уравнения;
4)
при ![]() первый трехчлен
положителен, второй --- отрицателен, получаем уравнение:
первый трехчлен
положителен, второй --- отрицателен, получаем уравнение:
![]() , отсюда
, отсюда ![]() , который входит в
промежуток
, который входит в
промежуток ![]() и является решением
уравнения;
и является решением
уравнения;
5)
при ![]() оба трехчлена
положительны, получается такая же ситуация, как и в первом случае. И здесь, оба
корня
оба трехчлена
положительны, получается такая же ситуация, как и в первом случае. И здесь, оба
корня ![]() ,
, ![]() не входят в промежуток и
являются посторонними.
не входят в промежуток и
являются посторонними.
Ответ.
![]() ,
, ![]() ,
, ![]() .
.
Графическое решение
Для графического решения преобразуем уравнение:
![]()
![]()
Построим
графики функций ![]() и
и ![]()
График
функции ![]() будем строить в несколько
этапов:
будем строить в несколько
этапов:
а)
строим график функции ![]() ;
;
б)
строим график функции ![]() ,
``зеркально'' отразив нижнюю часть кривой
,
``зеркально'' отразив нижнюю часть кривой ![]() в оси
в оси ![]() ;
;
в)
строим график функции ![]() для
этого достаточно график функции
для
этого достаточно график функции ![]() ``опустить''
вниз (осуществить параллельный перенос вдоль оси
``опустить''
вниз (осуществить параллельный перенос вдоль оси ![]() )
на
)
на ![]() ;
;
г)
полученный график полностью симметрично отразим в оси ![]() , ``перевернем'' вокруг оси
, ``перевернем'' вокруг оси
![]() на
на ![]() .
.
В
результате получим график функции ![]() .
.
График
функции ![]() построим уже известным
способом: строим параболу
построим уже известным
способом: строим параболу ![]() и
зеркально отражаем в оси
и
зеркально отражаем в оси ![]() только
часть параболы, находящуюся ниже оси
только
часть параболы, находящуюся ниже оси ![]() .
.
Находим абсциссы точек пересечения графиков, которые и будут являться решениями уравнения (см. рис. (??)).
pics/ex10.eps
Абсциссы точек пересечения следующие: 1,75; 2,5 и 3,25. Они и будут решениями уравнения.
Пример
Решите
уравнение ![]() .
.
Решение.
Решать
будем это уравнение последовательно ``раскрывая'' модули, начиная с
``внешнего'' и ``приближаясь'' к переменной ![]() .
.
После раскрытия первого модуля, получим совокупность двух уравнений:
(1)
![]() или (2)
или (2) ![]() .
.
Решая уравнение (1), в свою очередь, получаем два уравнения:
![]() ,
,
(3)
![]() или (4)
или (4) ![]() .
.
Из
уравнения (3) находим: ![]() ,
, ![]() из уравнения (4) находим:
из уравнения (4) находим: ![]() ,
, ![]()
Решая
уравнение (2), также получим: ![]() ,
которое распадается два уравнения:
,
которое распадается два уравнения:
(![]() )
) ![]() или (
или (![]() )
) ![]() .
.
Из
(![]() ) получаем:
) получаем: ![]() ,
, ![]() ,
, ![]() Из (
Из (![]() )
) ![]() , которое не имеет решений.
, которое не имеет решений.
Ответ.
![]()
Пример Решить уравнение:
![]()
Решение. ОДЗ данного уравнения:
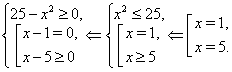
Простой
проверкой нетрудно убедиться, что ![]() и
и ![]() --- решения данного
уравнения.
--- решения данного
уравнения.
Ответ.
![]() .
.
Если решать уравнение путем возведения в квадраты обеих его частей, то получится уравнение
![]()
У
этого уравнения добавится ``лишний'' корень ![]() ,
не принадлежащий ОДЗ.
,
не принадлежащий ОДЗ.
Преобразование
![]() , не равносильное, т.к.
, не равносильное, т.к. ![]() входит в ОДЗ исходного
выражения, но не входит в ОДЗ преобразованного.
входит в ОДЗ исходного
выражения, но не входит в ОДЗ преобразованного.
Нюанс
состоит в том, что при ![]() функция
функция ![]() существует и при
существует и при ![]() , т.к. на что ноль ни
умножай --- будет ноль.
, т.к. на что ноль ни
умножай --- будет ноль.
Пример
Решить
уравнение ![]() .
.
Решение. Начнем раскрывать внутренний модуль (раскрытие внешнего модуля займет гораздо больше времени):
1.
При ![]() имеем
имеем ![]() .
.
Теперь рассмотрим два случая:
а)
![]() , т.е.
, т.е. ![]() ;
;
б)
![]() и
и ![]()
Т.к.
функция, стоящая в первой части исходного уравнения, --- четная, то решением
так же будет ![]() и
и ![]() .
.
Ответ.
![]() .
.
Пример Чему равна сумма корней уравнения (корень, если он один) уравнения
![]()
Решение. Рассмотрим выражение
![]()
и преобразуем его к виду
![]()
Очевидно,
что числитель дроби при любых значениях переменной является положительным
числом. Значит дробное выражение положительно, если ![]() (т.к.
(т.к.
![]() ). Преобразуем полученное
выражение, при условии
). Преобразуем полученное
выражение, при условии ![]() . Получим
уравнение, равносильное исходному:
. Получим
уравнение, равносильное исходному:
![]()
![]()
Ответ.
![]() .
.
Пример
Все
значения квадратного трёхчлена ![]() на
отрезке
на
отрезке ![]() по модулю не превосходят
1. Какое наибольшее значение при этом может иметь величина
по модулю не превосходят
1. Какое наибольшее значение при этом может иметь величина ![]() ?
?
Ответ.
Максимальное
значение величины ![]() равно 17.
равно 17.
Докажем
это. Сначала докажем, что эта величина не может быть больше 17. Так как
значения трёхчлена ![]() на отрезке
на отрезке ![]() по модулю не превосходят
единицы, то
по модулю не превосходят
единицы, то ![]() ,
, ![]() ,
, ![]() , то есть
, то есть ![]() ,
, ![]() ,
, ![]() . Так как модуль суммы не
превосходит суммы модулей, то
. Так как модуль суммы не
превосходит суммы модулей, то
![]()
![]()
Следовательно,
![]() . Осталось заметить, что
квадратный трёхчлен
. Осталось заметить, что
квадратный трёхчлен ![]() удовлетворяет
условию задачи и для него величина
удовлетворяет
условию задачи и для него величина ![]() равна
17.
равна
17.
Пример
Найдите наибольшее целое значение параметра ![]() ,
при котором уравнение
,
при котором уравнение ![]() не имеет
решений.
не имеет
решений.
Решение. Исходное уравнение равносильно уравнению
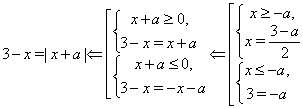
Вторая
система имеет решение только при ![]() (при
этом ее решениями будут все
(при
этом ее решениями будут все ![]() ).
Первая система не имеет решений, если
).
Первая система не имеет решений, если ![]() При этом наибольшее целое
При этом наибольшее целое ![]() , очевидно, равно
, очевидно, равно ![]() .
.
Ответ.
![]() .
.
Заключение
Материал данной дипломной работы адресован учителям математики, преподавателям подготовительных курсов, школьникам и абитуриентам. Рассмотрены свойства абсолютных величин, приведены теоремы о равносильных преобразованиях уравнений и неравенств, содержащих знак модуля. Сформулированы малоизвестные утверждения, существенно упрощающие традиционные алгоритмические способы решения школьных, конкурсных и олимпиадных задач. Теоретический материал проиллюстрирован значительным количеством заданий (более 80) из вступительных экзаменов, математических олимпиад и заданий централизованного тестирования.
Список использованных источников
[1] Веременок В. В., Практикум по математикеке, подготовка к тестированию и экзамену/Веременок В. В., Кожушко В. В. --- Мн.: Тетра-Системз, 2006.
[2] Д. Гущин, Мощное решение. Уравнения и неравенства с модулями //Учительская газета №39.
[3] В.Голубев, Школа решения нестандартных задач. Занятие 3. Нестандартная техника решения неравенств с модулем // Математика №5, 2005 с. 24--31.
[4] В.Голубев, Школа решения нестандартных задач. Занятие 5. Сумма модулей// Математика № 12, 2005 с.41--48.
[5] Тишин В. И., Математика для учителей и учащихся: рациональные алгебраические уравнения/ Тишин В. И. --- п. Комаричи, 2002. --- 167с.
[6] О. Игудисман, Математика на устном экзамене/ О. Игудисман --- М.: Айрис Пресс, Рольф, 2001---254с.
[7] Математика: готовимся к централизованному тестированию: Анализ ошибок 2007 года. Комментарии к ответам. Тренировочные тесты/ Респ. ин-т контроля знаний М-ва образования Респ. Беларусь.--- Мн.: Аверсэв, 2008. --- 64 с.
[8] Азаров А.И., Математика: задачи-<<ловушки>> на централизованном тестировании и экзамене/ А.И. Азаров, С.А. Барвенов, В.С. Романчик. --- 2-е изд., перераб.,--- Мн.: Аверсэв, 2006. --- 176с.
[9] Куланин Е.Д., 3000 конкурсных задач по математике/Куланин Е.Д., Норин В.П., Федин С.Н., Шевченко Ю.А. --- 10-е изд. --- М.: Айрис-пресс, 2007. --- 624с.
[10] Веременюк В. В., Математика: учимся быстро решать тесты: пособие для подгот. к тестированию и экзамену/ В. В. Веременюк, Е. А. Крушевский, И. Д. Беганская. --- 4-е изд. --- Минск: ТетраСистемс, 2006. --- 176с.
[11] Азаров А. И., Математика для старшеклассников: Методы решения алгебраических уравнений, неравенств и систем: Пособие для учащихся учреждений, обеспечивающих получение общего среднего образования/А. И. Азаров, С. А. Барвенов. --- Мн.: Аверсэв, 2004. --- 448с.