Учебное пособие: Численные методы для решения нелинейных уравнений
Министерство общего и профессионального образования Российской Федерации
Саратовский государственный технический университет
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Методические указания
к самостоятельной работе по курсу «Высшая математика»
для студентов всех специальностей
под контролем преподавателя
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов 2008
Введение
Данная работа ориентирована на изучение некоторых численных методов приближенного решения систем нелинейных уравнений с любым числом уравнений, составление на базе этих методов вычислительных схем алгоритмов и программ на алгоритмическом языке ФОРТРАН – IV.
Методические указания могут быть использованы как в процессе выполнения курсовой работы, так и для решения практических задач.
Задача настоящих указаний состоит в том, чтобы научить студентов решать системы нелинейных уравнений с помощью ЭВМ и затем полученные навыки использовать в курсовом и дипломном проектировании.
Предполагается, что студенты прослушали лекционный курс по основам алгоритмического языка ФОРТРАН – IV.
В качестве справочного пособия по языкам программирования может быть использована литература. [5]
Численные методы для решения нелинейных уравнений
Цель работы: изучение численных методов приближенного решения нелинейных систем уравнений, составление на базе вычислительных схем алгоритмов; программ на алгоритмическом языке ФОРТРАН – IV, приобретение практических навыков отладки и решения задач с помощью ЭВМ.
1. Определения и условные обозначения
![]() – конечномерное
линейное пространство, элементами (точками, векторами) являются группы из
– конечномерное
линейное пространство, элементами (точками, векторами) являются группы из ![]() упорядоченных действительных чисел,
например:
упорядоченных действительных чисел,
например:
![]()
где ![]() – действительные числа,
– действительные числа, ![]() .
.
В ![]() введена операция
сложения элементов, т. е.
введена операция
сложения элементов, т. е. ![]() определено
отображение
определено
отображение ![]() ,
,
где ![]()
Оно обладает следующими свойствами:
1.
![]() ,
,
2.
![]() ,
,
3.
![]() , что
, что ![]() (элемент
(элемент
![]() называется нулевым),
называется нулевым),
4.
![]() , что
, что ![]() (элемент
(элемент
![]() называется противоположным
элементу
называется противоположным
элементу ![]() ).
).
В ![]() введена операция
умножения элементов на действительные числа, т.е.
введена операция
умножения элементов на действительные числа, т.е. ![]() определено
отображение
определено
отображение ![]() ,
,
где ![]()
Оно обладает следующими свойствами:
1.
![]() ,
,
2.
![]()
Операции сложения элементов и умножения их на числа удовлетворяют законам дистрибутивности:
1.
![]() ,
,
2.
![]() .
.
Каждой паре элементов ![]() поставлено в соответствие
действительное число, обозначаемое символом
поставлено в соответствие
действительное число, обозначаемое символом ![]() и
называемое скалярным произведением, где
и
называемое скалярным произведением, где
![]()
и выполнены следующие условия:
1.
![]() ,
,
2.
![]() ,
,
3.
![]() ,
,
4.
![]() , причем
, причем ![]() –
нулевой элемент.
–
нулевой элемент.
Матрица ![]() вида
вида
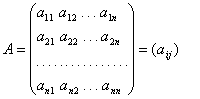
![]() , (1)
, (1)
где ![]() – действительные числа (
– действительные числа (![]() ,
,![]() ) определяет линейный
оператор, отображающий линейное пространство
) определяет линейный
оператор, отображающий линейное пространство ![]() в себя, а именно, для
в себя, а именно, для ![]()
![]() ,
,
где ![]() .
.
Над линейными
операторами, действующими в линейном пространстве ![]() ,
вводятся следующие операции:
,
вводятся следующие операции:
1.
сложение
операторов ![]() , при этом, если
, при этом, если ![]() , то
, то ![]() ,
,
2.
умножение
операторов на числа: ![]() при этом, если
при этом, если ![]() , то
, то ![]() ,
,
3.
умножение
операторов: ![]() , при этом, если
, при этом, если ![]() , то
, то ![]() .
.
Обратным к оператору ![]() называется оператор
называется оператор ![]() такой, что
такой, что ![]() , где
, где ![]() – единичный оператор,
реализующий тождественное отображение, а именно,
– единичный оператор,
реализующий тождественное отображение, а именно,
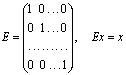 .
.
Пусть число ![]() и элемент
и элемент ![]() , таковы, что
, таковы, что ![]() .
.
Тогда число ![]() называется собственным
числом линейного оператора
называется собственным
числом линейного оператора ![]() , а
элемент
, а
элемент ![]() – собственным вектором
этого оператора, соответствующим собственному числу
– собственным вектором
этого оператора, соответствующим собственному числу ![]() .
.
Линейный оператор ![]() называется сопряженным к
оператору
называется сопряженным к
оператору ![]() , если для любых элементов
, если для любых элементов ![]() выполняется равенство
выполняется равенство ![]() .
.
Для всякого оператора ![]() сопряженный оператор
сопряженный оператор ![]() существует, единствен;
если
существует, единствен;
если ![]() , то
, то ![]() .
.
Справедливы равенства:
1.
![]() ,
,
2.
![]() ,
,
3.
![]() ,
,
4.
![]() , если
, если ![]() существует.
существует.
Каждому элементу ![]() ставится в соответствие
действительное положительное число, обозначаемое символом
ставится в соответствие
действительное положительное число, обозначаемое символом ![]() и называемое нормой
элемента
и называемое нормой
элемента ![]() .
.
Введем в рассмотрение три
нормы для ![]() :
:
![]() ,
,
![]() ,
,
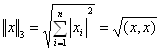 .
.
При этом выполняются следующие неравенства:
![]() .
.
Норма элемента удовлетворяет следующим условиям (аксиомам нормы):
1.
![]() , причем
, причем ![]() ,
лишь если
,
лишь если ![]() ,
,
2.
![]() ,
,
3.
![]() .
.
Говорят, что последовательность
элементов ![]() сходится к элементу
сходится к элементу ![]() ,
,
а именно, ![]() ,
,
или ![]() ,
,
если ![]() .
.
Определенная таким
образом сходимость в конечномерном линейном пространстве ![]() называется сходимостью по
норме.
называется сходимостью по
норме.
Множество элементов ![]() , удовлетворяющих
неравенству
, удовлетворяющих
неравенству ![]() называется замкнутым
(открытым) шаром в пространстве
называется замкнутым
(открытым) шаром в пространстве ![]() с
центром в точке
с
центром в точке ![]() и обозначается
и обозначается ![]() .
.
Каждому линейному
оператору, определяемому квадратной матрицей (1), ставится в
соответствие действительное неотрицательное число, обозначаемое символом ![]() и называемое нормой
линейного оператора
и называемое нормой
линейного оператора ![]() .
.
Норма линейного оператора удовлетворяет следующим условиям аксиомам норм:
4.4
![]() , причем
, причем ![]() ,
лишь если
,
лишь если ![]() – нулевая матрица,
– нулевая матрица,
4.4
![]() ,
,
4.4
![]() .
.
Введем в рассмотрение три
нормы для А отображающего ![]() в
в ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() i-ое собственное значение матрицы
i-ое собственное значение матрицы ![]() .
.
Эти нормы линейного
оператора А согласованы с соответствующими нормами элемента (вектора) ![]() в смысле условия
в смысле условия ![]() .
.
2.
Основные сведения о системах нелинейных уравнений в ![]()
Общая форма систем
нелинейных уравнений в ![]() имеет вид:
имеет вид:
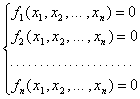 (2)
(2)
или F(x) = 0,
где ![]() – заданные функции n переменных,
– заданные функции n переменных,
![]() – неизвестные.
– неизвестные.
Функция ![]() при действительных значениях
аргументов принимают действительные значения, т.е. являются
действительнозначными. Вычислять будем только действительные решения.
при действительных значениях
аргументов принимают действительные значения, т.е. являются
действительнозначными. Вычислять будем только действительные решения.
Решением системы
нелинейных уравнений (2) называется совокупность (группа) чисел ![]() , которые, будучи
подставлены на место неизвестных
, которые, будучи
подставлены на место неизвестных ![]() ,
обращают каждое уравнение системы в тождество.
,
обращают каждое уравнение системы в тождество.
Частным случаем системы (2) является система линейных уравнений:
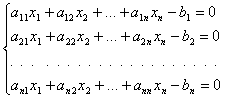
или ![]() ,
,
где А – матрица
вида (1), порождающая линейный оператор, отображающий ![]() в
в ![]()
![]()
Система линейных
уравнений (2) поставим в соответствие линеаризованное уравнение (первые
два члена из разложения в ряд Тейлора (2)) в точке ![]() вида
вида
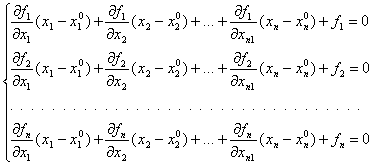 (2
(2![]() )
)
или ![]() ,
,
где ![]() – квадратная матрица
Якоби, составленная из частных производных первого порядка функций, а именно
– квадратная матрица
Якоби, составленная из частных производных первого порядка функций, а именно ![]() , вычисленных точке
, вычисленных точке ![]() .
.
Для
дальнейшего нам потребуется еще одна форма записи системы нелинейных уравнений
в ![]() , а именно:
, а именно:
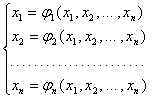 (3)
(3)
или ![]() ,
,
где ![]() .
.
Операции, с помощью которых осуществляется преобразование системы (2) к системе (3), могут быть любыми, необходимо только, чтобы искомое решение системы (3) удовлетворяло системе (2).
Функции ![]() удовлетворяют тем же
условиям, что и функции
удовлетворяют тем же
условиям, что и функции ![]() .
.
3. Отделение решений
Задача отделения решений систем нелинейных уравнений состоит в определении достаточно малой окрестности (шара малого радиуса, центром которого является решение) около какого-нибудь одного решения и в выборе в этой окрестности начального приближения к решению. Начальное приближение должно попасть при этом в область сходимости метода.
Задача отделения решений не имеет достаточно эффективных методов общего характера. При решении уравнения предполагается знание начальных приближений к изолированному решению из постановки конкретной задачи. Если же таких данных нет, то можно дать лишь некоторые рекомендации для конкретных видов уравнений.
Так, если дано скалярное
уравнение ![]() , то его решение с
геометрической точки зрения можно рассматривать как абсциссы точек пересечения
графика функции с осью абсцисс. Построив график функции y=f (x), приближенно определяем окрестности изолированных точек
пересечения графика с горизонтальной осью. Сами точки пересечения берем за
начальные приближения к точным решениям.
, то его решение с
геометрической точки зрения можно рассматривать как абсциссы точек пересечения
графика функции с осью абсцисс. Построив график функции y=f (x), приближенно определяем окрестности изолированных точек
пересечения графика с горизонтальной осью. Сами точки пересечения берем за
начальные приближения к точным решениям.
Безусловно, графические построения имеют большие погрешности, и выбранные начальные приближения могут не попасть в область сходимости применяемого метода.
Тогда нужно провести пробные решения на ЭВМ выбранным методом с исследованием сходимости.
Если приближения сходятся, то начальные приближения выбраны в области сходимости метода и можно получить приближенное решение с заданной точностью.
Если приближения расходятся, следует провести более точные графические построения и выбрать начальное приближение в области сходимости.
Аналогично отделяются решения для системы двух нелинейных уравнений
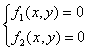 ,
, ![]() .
.
В этом случае на
плоскости x,y строятся линии уровня функции двух переменных ![]() и
и ![]() . Координаты точек
пересечения графиков этих функций дают начальные приближения изолированных
решений.
. Координаты точек
пересечения графиков этих функций дают начальные приближения изолированных
решений.
4. Методы решения нелинейных уравнений
4.1 Метод простой итерации
Метод простой итерации (см. [1]) применяется для решения систем нелинейных уравнений с любым числом уравнений. Его можно применять как для уточнения найденного решения, так и для первоначального нахождения решения. В последнем случае, однако, метод может не дать результата.
Для применения метода простой итерации система уравнений (2) приводится к виду (3).
Затем, взяв начальное
приближение ![]() , которое предполагается
либо известным, либо произвольным, строим последовательность
, которое предполагается
либо известным, либо произвольным, строим последовательность
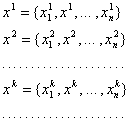 (4)
(4)
по следующим формулам
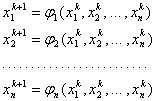 (5)
(5)
Замечание. Для приведения системы уравнений (2) к виду (3) можно использовать прием:
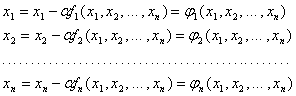
где ![]() – релаксационный параметр,
определяется методом Зейделя.
– релаксационный параметр,
определяется методом Зейделя.
4.2 Метод Зейделя
Метод Зейделя отличается от метода простой итерации тем, что вычисления ведутся по формулам:
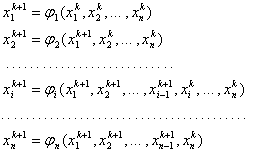 (6)
(6)
Иными словами, при
вычислении ![]() используются не
используются не ![]() , как в методе простой
итерации, а
, как в методе простой
итерации, а ![]() .
.
4.3 Метод Ньютона
Этот метод (см.[1], [4]) предложен И.Ньютоном в 1669 году, однако наиболее полное обоснование было сделано советским математиком Л.В.Канторовичем в 1949 году (см.[4]), поэтому в литературе этот метод часто называют методом Ньютона-Канторовича.
Метод Ньютона является одним из итерационных методов, получаемых линеаризацией линейного оператора
![]() ,
,
где ![]() из уравнения (2).
из уравнения (2).
Так, для к-го приближения ![]() к точному решению
к точному решению ![]() уравнения (2)
ставится в соответствие линеаризованное уравнение вида (2
уравнения (2)
ставится в соответствие линеаризованное уравнение вида (2![]() ), а именно:
), а именно:
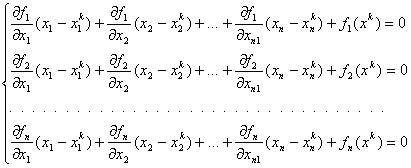
или ![]() ,
,
где ![]() –
квадратная матрица Якоби, составленная из частных производных первого порядка
функций,
–
квадратная матрица Якоби, составленная из частных производных первого порядка
функций, ![]() т.е.
т.е. ![]() , вычисленных в точке
, вычисленных в точке ![]() .
.
Таким образом, последовательность (4) строится по следующим правилам:
![]() (),
(),
где ![]() –
обратный оператор к линейному оператору
–
обратный оператор к линейному оператору ![]() ,
определяемому квадратной матрицей
,
определяемому квадратной матрицей
![]()
Трудности построения алгоритма метода
Ньютона, связанные с обращением производной ![]() (построение
(построение
![]() ), обычно преодолеваются
тем, что вместо методов обращения матрицы
), обычно преодолеваются
тем, что вместо методов обращения матрицы ![]() решают
алгебраическую систему уравнений (7) относительно неизвестных
решают
алгебраическую систему уравнений (7) относительно неизвестных ![]() . Алгоритмы решения системы
линейных алгебраических уравнений хорошо отработаны, для них имеются
стандартные программы для ЭВМ и, кроме того, в результате решения системы
одновременно с обращением матрицы получается умножение обратной матрицы на
вектор
. Алгоритмы решения системы
линейных алгебраических уравнений хорошо отработаны, для них имеются
стандартные программы для ЭВМ и, кроме того, в результате решения системы
одновременно с обращением матрицы получается умножение обратной матрицы на
вектор ![]() .
.
Итерационная формула метода Ньютона при таком подходе будет иметь вид:
![]() (7)
(7)
![]() . (8)
. (8)
4.4 Модифицированный метод Ньютона
Эта разновидность метода Ньютона строится путем определения производной только в одной точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам:
![]() , (9)
, (9)
где ![]() –
начальное приближение к точному решению
–
начальное приближение к точному решению ![]() .
.
4.5 Метод Зейделя на основе линеаризованного уравнения
Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид:

4.6 Метод наискорейшего спуска
Методы спуска (см. [2]) сводят
решение системы (2) к задаче нахождения минимума специально построенного
функционала (функционал – отображение ![]() в
R), а именно:
в
R), а именно:
![]() ,
,
где ![]() .
.
Функционал в конечном пространстве Rn можно рассматривать как функцию
многих переменных ![]() .
.
Для нахождения точки ![]() , в которой функционал f принимает минимальное нулевое значение, выбирают точку
, в которой функционал f принимает минимальное нулевое значение, выбирают точку
![]() , находят
, находят ![]() и строят итерационную
формулу:
и строят итерационную
формулу: ![]() с начальным приближением
с начальным приближением ![]() .
.
В итерационной формуле параметр hk пока не определен, выберем его таким
образом, чтобы выполнилось условие: ![]() ,
начиная с x0, в предположении, что f – монотонный функционал.
,
начиная с x0, в предположении, что f – монотонный функционал.
Для выбора hk построим функционал, зависящий от
параметра, который изменяется непрерывно: ![]() .
.
При h=0 имеем, что f (0) – линия уровня функционала, проходящая через точку xk . Для нахождения следующей линии уровня, более близкой к минимуму, будем выбирать h таким образом, чтобы для данного xk
![]()
Это условие минимума по h будем рассматривать как уравнение для получения hk.
Решим его приближенно, т.к. ошибка в
несколько процентов обычно не влияет на скорость сходимости. Отметим кстати,
что число hk всегда должно быть
положительным. Для этого разложим функцию ![]() в
ряд Тейлора по h в точке h=0 и возьмем только линейную часть
этого разложения
в
ряд Тейлора по h в точке h=0 и возьмем только линейную часть
этого разложения
![]() .
.
Подстановка линейной части в условие ![]() , дает уравнение для
приближенного определения
, дает уравнение для
приближенного определения
![]() .
.
Решая построенное уравнение относительно h, получим:
![]() или
или 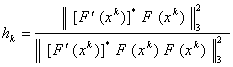 .
.
Таким образом, итерационная формула метода наискорейшего спуска имеет вид:
![]() или
или ![]() , где производные
, где производные ![]() вычислены в точке
вычислены в точке ![]() .
.
Метод наискорейшего спуска требует большего количества вычислений, чем другие методы первого порядка. Однако он обладает по сравнению с другими методами важным преимуществом, заключающемся в неизбежной сходимости процесса. При этом нужно помнить, что метод наискорейшего спуска может привести не к решению системы уравнений (2), а к значениям аргумента, дающим относительный экстремум функции
![]() , т.е.
, т.е. ![]() .
.
5. Сходимость методов решения нелинейных уравнений
Если метод сходится, то
есть ![]() , где
, где
![]() – точное решение
– точное решение
![]() – k-тое приближение к точному решению, то итерационный процесс
следовало бы закончить по достижению заданной погрешности
– k-тое приближение к точному решению, то итерационный процесс
следовало бы закончить по достижению заданной погрешности ![]() , где e – заданная точность (погрешность).
, где e – заданная точность (погрешность).
Однако практически это
условие выполнить нельзя, так как ![]() неизвестно,
тогда для окончания итерационного процесса можно воспользоваться неравенствами
неизвестно,
тогда для окончания итерационного процесса можно воспользоваться неравенствами ![]() , или
, или ![]() , где
, где ![]() и
и ![]() – заданные величины.
– заданные величины.
При таком окончании
итераций погрешность может возрасти по сравнению с ![]() и,
поэтому, чтобы не увеличивалась, величины
и,
поэтому, чтобы не увеличивалась, величины ![]() и
и
![]() соответственно уменьшают
или увеличивают число итераций.
соответственно уменьшают
или увеличивают число итераций.
Методы простой итерации,
Зейделя, модифицированный метод Ньютона, метод наискорейшего спуска (см. [1],
[2], [3], [4]) являются методами первого порядка – это
значит, что имеет место неравенство ![]() , k=1, 2, . . . , где
, k=1, 2, . . . , где ![]() – константа, своя у
каждого метода, зависящая от выбора начального приближения
– константа, своя у
каждого метода, зависящая от выбора начального приближения ![]() , функции fi , i = 1, 2, . . . , n, и их частных производных первого и второго порядков
– точнее их оценок в некоторой окрестности искомого решения, которой
принадлежит начальное приближение.
, функции fi , i = 1, 2, . . . , n, и их частных производных первого и второго порядков
– точнее их оценок в некоторой окрестности искомого решения, которой
принадлежит начальное приближение.
Метод Ньютона является
методом второго порядка, то есть для него имеет место неравенство ![]() , k=1, 2, . . . , где
, k=1, 2, . . . , где ![]() – константа, зависящая от
тех же величин, что и константа
– константа, зависящая от
тех же величин, что и константа ![]() .
.
А теперь рассмотрим достаточные условия сходимости метода простой итерации и метода Ньютона.
Сходимость процесса
простой итерации зависит от двух условий. Первое условие состоит в том, что
какая-нибудь точка ![]() должна оказаться
близкой к исходному решению
должна оказаться
близкой к исходному решению ![]() .
Степень необходимой близости зависит от функций j1, j2, . . . , jn . Это требование не относится к
системам линейных уравнений, для которых сходимость процесса простой итерации
зависит только от второго условия.
.
Степень необходимой близости зависит от функций j1, j2, . . . , jn . Это требование не относится к
системам линейных уравнений, для которых сходимость процесса простой итерации
зависит только от второго условия.
Второе условие связано с матрицей, составленной из частных производных первого порядка функций j1, j2, . . . , jn – матрицей Якоби
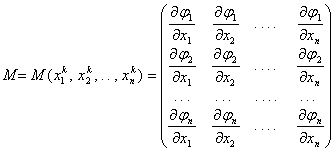 ,
,
вычисленных в точке ![]() .
.
В случае, когда
рассматривается система линейных алгебраических уравнений, матрица M состоит из постоянных чисел – коэффициентов,
стоящих при неизвестных в правой части уравнения (3). В случае
нелинейных уравнений элементы ![]() матрицы
M зависят, вообще говоря, от
матрицы
M зависят, вообще говоря, от ![]() . Для сходимости процесса
простой итерации достаточно, чтобы выполнялось неравенство:
. Для сходимости процесса
простой итерации достаточно, чтобы выполнялось неравенство: ![]() для
для ![]() из некоторой окрестности
точного решения
из некоторой окрестности
точного решения ![]() , которой должно
принадлежать начальное приближение
, которой должно
принадлежать начальное приближение ![]() .
.
Приведем также
достаточные условия сходимости метода Ньютона для системы уравнений вида (2)
по норме ![]() .
.
Предположим, что имеется
начальное приближение ![]() к искомому решению
системы (2)
к искомому решению
системы (2) ![]() , функции
, функции ![]() непрерывны и имеют
непрерывные частные производные до второго порядка в шаре
непрерывны и имеют
непрерывные частные производные до второго порядка в шаре ![]() , тогда, если выполнены условия:
, тогда, если выполнены условия:
1)
Матрица Якоби ![]() системы (2) на
начальном приближении имеет обратную
системы (2) на
начальном приближении имеет обратную ![]() и
известна оценка нормы обратной матрицы
и
известна оценка нормы обратной матрицы ![]() ,
,
2)
Для всех точек
шара ![]() выполнено неравенство
выполнено неравенство
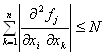 при i, j = 1, 2, . . . , n ,
при i, j = 1, 2, . . . , n ,
3) Выполнено неравенство
![]() ,
,
где L – постоянная 0 £ L £ 1,
4)
Числа b, N, r
подчинены условию a = nbNr < 0,4, тогда система уравнений (2)
в шаре ![]() имеет единственное
решение, к которому сходятся последовательные приближения (8) или (7’), (9’).
имеет единственное
решение, к которому сходятся последовательные приближения (8) или (7’), (9’).
Для других методов условия сходимости имеют сложный вид, и мы отсылаем читателя к специальной литературе [1], [2], [3], [4].
6. Примерный перечень возможных исследований
1) Сравнение различных методов на экономичность при решении конкретной задачи:
· по числу операций на одной итерации;
· по числу итераций, необходимых для достижения заданной точности;
2) Зависимость числа итераций для достижения заданной точности:
· от выбора вида нормы;
·
от выбора
критерия окончания итерационного процесса по ![]() или
по невязке
или
по невязке ![]() ;
;
· от выбора начального приближения;
· от погрешности задания коэффициентов в уравнении.
7. Контрольные вопросы
1) Понятие о нелинейных системах уравнений в Rn.
2) Понятие приближенного и точного решения нелинейной системы уравнений.
3) Сущность графического метода отделения решения для системы двух нелинейных уравнений, каковы его преимущества и недостатки?
4) Сущность метода простой итерации и метода Зейделя. Каковы условия применимости метода простой итерации?
5) Сущность метода Ньютона и его модификации. Какова скорость сходимости метода Ньютона?
6) Сущность метода наискорейшего спуска. Как выбирается параметр спуска?
8. Порядок выполнения курсовой работы
1) Получить вариант задания, индивидуальный для каждого студента, у преподавателя, а именно:
Найти решение системы нелинейных уравнений в первой координатной четверти с номером – N1 (см. варианты заданий п.10), применив для первого этапа уточнения метод с номером – N2, а для второго этапа уточнения метод с номером – N3 , точность вычислений на первом этапе – EPS1Î[0.1 – 0.01], на втором этапе – EPS2 Î [0.1 - 0.0001], N4 – номер нормы, I – номер параметра a, J – номер параметра b, начальное приближение выбрать произвольно или графически, aÎ(0,1).
2) Разработать обязательные для выполнения задания разделы данных методических указаний.
| Анализ методов определения минимального, максимального значения ... | |
|
Федеральное агентство по образованию Московский государственный открытый университет Чебоксарский политехнический институт Курсовой проект по ... На каждой итерации величина шага ak выбирается из условия минимума функции f(x) в направлении спуска, т.е. Поэтому естественно искать решение x* как первые m координат стационарной точки функции Лагранжа, например, методом Ньютона, мы приходим к методу Ньютона решения задач с ... |
Раздел: Рефераты по информатике, программированию Тип: курсовая работа |
|
Кафедра: ИТ МЕТОДЫ ОПТИМИЗАЦИИ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Екатеринбург 2007 Оглавление Введение Лабораторная работа № 1. 1. Методы безусловной ... Выбор точки x0 (-2,-2) в качестве начальной для реализации метода Ньютона оказался неудачным, так как матрица Гессе в ней не является положительно определенной. Введем формулы, соответствующие системе (рис.2), и начальное приближение для решения системы уравнений (рис.3). |
Раздел: Рефераты по математике Тип: лабораторная работа |
| Вычислительная математика | |
|
... методами. Основные понятия 1.1 Погрешность 1.2 Корректность 1.3 Вычислительные методы Тема 2. Решение нелинейных уравнений 2.1 Постановка ... Сходимость метода Ньютона зависит от того, насколько близко к корню выбрано начальное приближение. 5. Решение нелинейных уравнений методом простых итераций и методом Ньютона. |
Раздел: Рефераты по математике Тип: учебное пособие |
| Классификации гиперболических дифференциальных уравнений в частных ... | |
|
Содержание Введение 1. Гиперболические уравнения как подкласс дифференциальных уравнений в частных производных. Классификация уравнений в частных ... Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Широкое распространение получили методы приближённого решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений. |
Раздел: Рефераты по математике Тип: контрольная работа |
| Численные методы решения систем линейных уравнений | |
|
Курсовая работа по информатике на тему: "Численные методы решения систем линейных уравнений" Выполнил: студент 06-ИСТ, Фадеева Т.В. Проверил: Ловыгина ... Среди задач линейной алгебры наибольшее значение имеют две: решение системы линейных алгебраических уравнений определение собственных значений и собственных векторов матрицы. Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы, подобно тому, как это делается для одного уравнения. |
Раздел: Рефераты по информатике, программированию Тип: курсовая работа |