Реферат: Степенные ряды
ВЫСШАЯ МАТЕМАТИКА
Степенные ряды
Содержание
1. Определение степенного ряда. Теорема Абеля
2. Свойства степенных рядов
3. Ряды Тейлора, Маклорена для функций
4. Разложение некоторых элементарных функций в ряд Маклорена
5. Приложения степенных рядов
1. Определение степенного ряда. Теорема Абеля
Степенные ряды являются частным случаем функциональных рядов.
Определение 1.1. Степенным рядом называется
функциональный ряд вида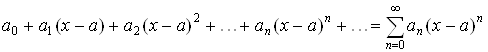 
.(1.1)
Здесь 
–
постоянные вещественные числа, называемые коэффициентами степенного ряда;
а – некоторое постоянное число, х – переменная, принимающая
значения из множества действительных чисел.
При 
степенной
ряд (1.1) принимает вид
. (1.2)
Степенной ряд (1.1) называют рядом
по степеням разности 
, ряд
(1.2) – рядом по степеням х.
Если переменной х придать какое-либо значение, то степенной ряд (1.1) (или (1.2)) превращается в числовой ряд, который может сходиться или расходиться.
Определение 1.2. Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится.
Ряд (1.1) с помощью подстановки 
приводится к более простому
виду (1.2), поэтому вначале будем рассматривать степенные ряды вида (1.2).
Для нахождения области сходимости степенного ряда важную роль играет следующая теорема.
Теорема 1.1 (Теорема Абеля):
если степенной ряд (1.2) сходится при
, то он абсолютно сходится
при всех значениях х, удовлетворяющих неравенству 
;
если же ряд (1.2) расходится при , то он
расходится при всех значениях х, удовлетворяющих неравенству 
.
Теорема Абеля дает ясное представление о структуре области сходимости степенного ряда.
Теорема 1.2:
область сходимости степенного ряда (1.2) совпадает с одним из следующих интервалов:
1) 
;
2) 
; 3) 
; 4) 
,
где R – некоторое неотрицательное
действительное число или 
.
Число R называется радиусом сходимости,
интервал – интервалом
сходимости степенного ряда (1.2).
Если 
,
то интервал сходимости представляет собой всю числовую ось 
.
Если 
,
то интервал сходимости вырождается в точку 
.
Замечание: если –
интервал сходимости для степенного ряда (1.2), то 
–
интервал сходимости для степенного ряда (1.1).
Из теоремы 1.2 следует, что для
практического нахождения области сходимости степенного ряда (1.2) достаточно
найти его радиус сходимости R
и выяснить вопрос о сходимости этого ряда на концах интервала сходимости , т. е. при 
и 
.
Радиус сходимости R степенного ряда можно найти по одной из следующих формул:
формула Даламбера:
;(1.3)
формула Коши:
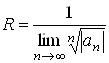.(1.4)
Если в формуле Коши 
, то полагают , если 
, то полагают .
Пример 1.1. Найти радиус сходимости, интервал
сходимости и область сходимости степенного ряда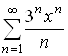 
.
Решение
Найдем радиус сходимости данного ряда по формуле
В нашем случае
, 
.
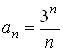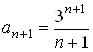Тогда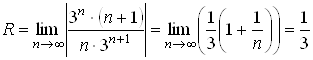 
.
Следовательно, интервал сходимости
данного ряда имеет вид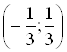 
.
Исследуем сходимость ряда на концах интервала сходимости.
При 
степенной
ряд превращается в числовой ряд
.
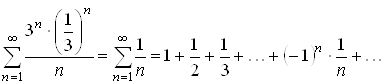который расходится как гармонический ряд.
При 
степенной
ряд превращается в числовой ряд
.
Это – знакочередующийся ряд, члены
которого убывают по абсолютной величине и 
. Следовательно, по признаку
Лейбница этот числовой ряд сходится.
Таким образом, промежуток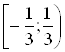 
– область сходимости
данного степенного ряда.
2. Свойства степенных рядов
Степенной ряд (1.2) представляет
собой функцию 
, определенную в
интервале сходимости , т. е.
.
Приведем несколько свойств функции .
Свойство 1. Функция является непрерывной на
любом отрезке 
, принадлежащем
интервалу сходимости .
Свойство 2. Функция дифференцируема на
интервале , и ее производная 
может быть найдена
почленным дифференцированием ряда (1.2), т. е.
,
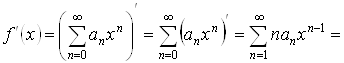
для всех 
.
Свойство 3. Неопределенный интеграл от
функции для всех может быть получен
почленным интегрированием ряда (1.2), т. е.
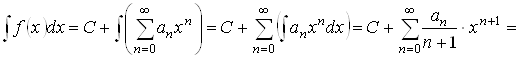
для всех .
Следует отметить, что при почленном
дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость
на концах интервала может
измениться.
Приведенные свойства справедливы также и для степенных рядов (1.1).
Пример 2.1. Рассмотрим степенной ряд
.
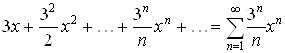Область сходимости этого ряда, как
показано в примере 1.1, есть промежуток .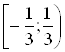
Почленно продифференцируем этот ряд:
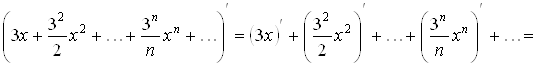
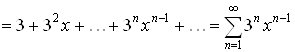.(2.1)
По свойству 2 интервал сходимости
полученного степенного ряда (2.1) есть интервал .
Исследуем поведение этого ряда на
концах интервала сходимости, т. е. при и
при .
При степенной
ряд (2.1) превращается в числовой ряд
.
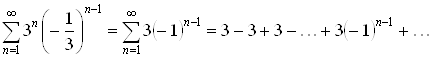Этот числовой ряд расходится, так как
не выполняется необходимый признак сходимости 
:
, который не существует.
При степенной
ряд (2.1) превращается в числовой ряд
,
который также расходится, так как не выполняется необходимый признак сходимости.
Следовательно, область сходимости
степенного ряда, полученного при почленном дифференцировании исходного
степенного ряда, изменилась и совпадает с интервалом .
3. Ряды Тейлора, Маклорена для функций
Пусть –
дифференцируемая бесконечное число раз функция в окрестности точки 
, т. е. имеет производные
любых порядков.
Определение 3.1. Рядом Тейлора
функции в точке называется степенной ряд
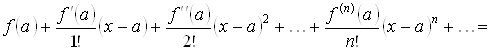
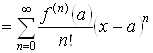. (3.1)
В частном случае при ряд (3.1) называется рядом
Маклорена:
. (3.2)
Возникает вопрос: в каких случаях ряд
Тейлора для дифференцированной бесконечное число раз функции в окрестности точки совпадает с функцией ?
Возможны случаи, когда ряд Тейлора
функции сходится, однако его
сумма не равна .
Приведем достаточное условие
сходимости ряда Тейлора функции к
этой функции.
Теорема 3.1:
если в интервале функция имеет производные любого
порядка и все они по абсолютной величине ограничены одним и тем же числом, т.
е. 
, то ряд Тейлора этой
функции сходится к для любого х из
этого интервала , т. е. имеет
место равенство
.
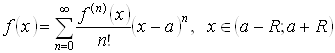Для выяснения выполнения этого равенства на концах интервала сходимости требуются отдельные исследования.
Следует отметить, что если функция разлагается в степенной ряд, то этот ряд является рядом Тейлора (Маклорена) этой функции, причем это разложение единственно.
4. Разложение некоторых элементарных функций в ряд Маклорена
1. 
.
Для этой функции 
, 
.
По формуле (3.2) составим ряд Маклорена данной функции:
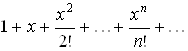. (3.3)
Найдем радиус сходимости ряда (3.3) по формуле (1.3):
.
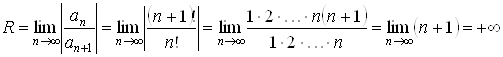Следовательно, ряд (3.3) сходится при
любом значении 
.
Все производные функции 
на любом отрезке 
ограничены, т. е.
.
Поэтому, согласно теореме 3.1, имеет место разложение
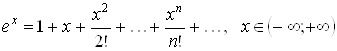. (3.4)
2. 
.
Для этой функции 
, 
, 
.
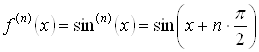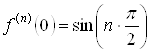Отсюда следует, что при производные четного
порядка равны нулю, а производные нечетного порядка чередуют знак с плюса на
минус.
По формуле (3.2) составим ряд Маклорена:
.
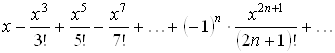При любом фиксированном значении этот ряд сходится как знакочередующийся по признаку Лейбница. При этом
.
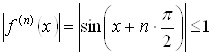
Поэтому, согласно теореме 3.1, имеет место разложение
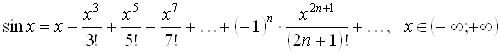. (3.5)
3. 
.
Воспользуемся разложением (3.5) в ряд Маклорена функции 
и свойством 2 о
дифференцировании степенного ряда. Имеем
|
|
(3.6) |
.Поскольку при почленном
дифференцировании интервал сходимости степенного ряда не изменяется, то
разложение (3.6) имеет место при любом .
Приведем без доказательства разложения других элементарных функций в ряды Маклорена.
4. 
– биномиальный ряд (
– любое действительное
число).
Если 
–
положительное целое число, то получаем бином Ньютона:
.
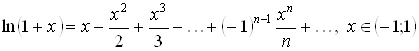– логарифмический ряд.
.
5. Приложения степенных рядов
Степенные ряды находят применение в таких задачах, как приближенное вычисление функций с заданной степенью точности, определенных интегралов, решение дифференциальных уравнений и др.
Приближенное значение функции вычисляют, заменяя ряд Маклорена этой функции конечным числом его членов.
Приведем приближенные формулы для вычисления некоторых наиболее часто встречающихся функций при достаточно малых значениях х:
; 
; 
; 
;
; 
.
Литература
1. Высшая математика: Общий курс: Учебник – 2-е изд., перераб. / А.И. Яблонский, А.В. Кузнецов, Е.И. Шилкина и др.; Под общ. ред. С.А. Самаля. – Мн.: Выш. шк., 2000.– 351 с.
2. Марков Л.Н., Размыслович Г.П.
Высшая математика. Ч. 2. Основы математического анализа и элементы
дифференциальных уравнений. – Мн.: Амалфея, 2003. – 352 с.
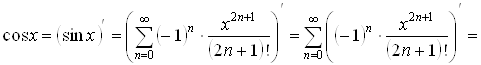
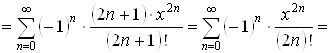
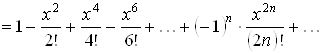