Курсовая работа: Представления конечных групп

Курсовая работа

"Представления конечных групп"

Содержание

Основные обозначения

Введение

1. Представления конечных групп

1.1 Представления групп

Заключение

Список использованных источников

Основные обозначения

Введение

В данной работе приведены доказательства следующих теорем:

Теорема. Непустое подмножество  группы  будет подгруппой тогда и только тогда, когда  и  для всех .

Группой называется непустое множество  с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием:

1) операция определена на , т.е.  для всех ;

2) операция ассоциативна, т.е.  для любых ;

3) в  существует единичный элемент, т.е. такой элемент , что  для всех , что  для всех ;

4) каждый элемент обладает обратным, т.е. для любого  существует такой элемент , что .

Более кратко: полугруппа с единицей, в которой каждый элемент обладает обратным, называется группой.

Группу с коммутативной операцией называют коммутативной или абелевой. Если  – конечное множество, являющиеся группой, то  называют конечной группой, а число  элементов в  – порядком группы .

Подмножество  группы  называется подгруппой, если  – группа относительно той же операции, которая определена на . Запись  означает, что – подгруппа группы , а  – что – собственная подгруппа группы , т.е.  и .

Централизатор. Пусть  – непустое подмножество группы . Совокупность всех элементов группы , перестановочных с каждым элементом множества , называется централизатором множества  в группе  и обозначается через .

Лемма

1. Если  – подмножество группы , то централизатор  является подгруппой.

2. Если  и  – подмножество группы  и , то

3. Если  – подмножество группы  и , то

Центр группы. Центром группы  называется совокупность всех элементов из , перестановочных с каждым элементом группы. Центр обозначается через . Ясно, что , т.е. центр группы  совпадает с централизатором подмножества  в группе . Кроме того, .

Зафиксируем в группе  элемент . Пересечение всех подгрупп группы , содержащих элемент , назовем циклической подгруппой, порожденной элементом , и обозначим через .

Теорема. Циклическая подгрупппа , порожденная элементом , состоит из всевозможных целых степеней элемента , т.е.

Следствие. Циклическая подгруппа абелева.

Порядок элемента. Пусть  – элемент группы . Если все степени элемента  различны, т.е.  для всех целых , то говорят, что элемента  имеет бесконечный порядок.

Нормализатор. Если  – непустое подмножество группы  и  то  и  Элемент  называется перестановочным с подмножеством , если . Равенство  означает, что для любого элемента  существует такой элемент , что . Если элемент  перестановочен с подмножеством , то  и . Совокупность всех элементов группы , перестановочных с подмножеством , называется нормализатором подмножества  в группе  и обозначается через . Итак,

Лемма. Пусть  – непустое подмножество группы ,  – произвольный элемент группы . Тогда:

1) ;

2) ;

3) ;

4) ;

5) если  – подгруппа группы , то

Подгруппа  называется нормальной подгруппой группы , если  для всех . Запись  читается: » – нормальная подгруппа группы «. Равенство  означает, что для любого элемента  существует элемент  такой, что .

Теорема. Для подгруппы  группы  следующие утверждения эквивалентны:

1) – нормальная подгруппа;

2) подгруппа  вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е.  для всех ;

3) подгруппа  совпадает с каждой своей сопряженной подгруппой, т.е.  для всех .

Лемма. Пусть  – подгруппа группы . Тогда:

1) ;

2) если  и , то ;

3)  – наибольшая подгруппа группы , в которой  нормальна;

4) если , то . Обратно, если , то ;

5)  для любого непустого подмножества  группы .

Простая группа. В каждой группе  тривиальные подгруппы (единичная подгруппа  и сама группа ) являются нормальными подгруппами. Если в неединичной группе  нет других нормальных подгрупп, то группа  называется простой. Единичную группу  считают непростой.

Представления конечных групп

Пусть  – группа всех невырожденных матриц порядка  над полем  комплексных чисел. Если  – произвольная группа, то ее (матричным) представлением называется любой ее гомоморфизм в

G,

такой, что

,

 (единичная матрица),

. Число n называется степенью этого представления. Если гомоморфизм A иньективен, то представление называется точным.

Пример 1.1 Отображение, переводящее каждый элемент группы  в , является представлением степени . Оно называется тождественным представлением группы  и обозначается через .

Пример 1.2 Если  – некоторое представление группы , то для каждой невырожденной матрицы  отображение  также является представлением этой группы.

Пусть  и  – два представления группы . Если существует невырожденная матрица , такая, что что

,

то представления  и  называются эквивалентными. Тот факт, что представления  и  эквивалентны, мы будем обозначать так: . Отношение  определяет классы эквивалентных представлений группы .

Пример 1.3. Пусть  – симметрическая группа степени . Для элемента

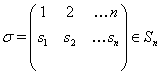
через  обозначим матрицу,  строка которой имеет вид , где 1 стоит на  месте. Другими словами,

где

Такое отображение  является точным представлением группы .

1.4. Пусть –конечная группа, состоящая из элементов  и пусть – симметрическая группа на . Отображение, которое ставит в соответствие элементу  подстановку

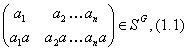
является инъективным гомоморфизмом группы  в . С такой подстановкой  мы свяжем матрицу

где, как и в примере ,

Тогда отображение  является точным представлением группы . Оно называется правым регулярным представлением этой группы. Определим  следующим образом:

Тогда

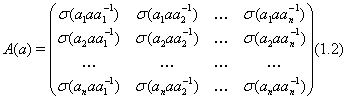
и, если , то каждый диагональный элемент равен нулю.

регулярное представление группы  определяется аналогично с использованием гомоморфизма

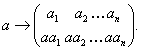
Другими словами,

Пусть  – некоторый гомоморфизм из  в , т.е. подстановочное представление группы . Представив подстановку  в виде матрицы , как это сделано в примере 1.3, мы получим представление

Пусть  – представление степени . Говорят, что  приводимо, если существует такая невырожденная матрица , что

где  и  – квадратные матрицы порядка  и  соответственно, причем  Отметим, что представления

эквивалентны, поскольку для матрицы

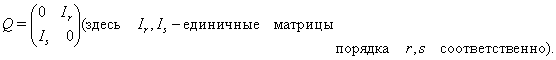
Скажем, что представление  неприводимо, если оно не является приводимым. Отметим, что в (1.3) отображения  и  являются представлении степеней  и  соответственно.

Для заданных представлений  и  группы  степеней  и  соответственно отображение

является представление степени  этой группы. Такое, представление называется прямой суммой представлений  и  и обозначается через .

Представление  группы  называется вполне приводимым, если оно эквивалентно прямой сумме некоторых неприводимых представлений, т.е. если найдется невырожденная матрица , такая, что

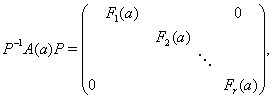
где каждое  является неприводимым представлением группы .

Представление  группы  называется унитарным, если для всех  матрица  является унитарной, т.е. . Здесь  обозначает матрицу, транспонированную к , где , а  – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.

Матрица  называется эрмитовой, если , и положительно определенной, если  для каждого ненулевого столбца . Следующая лемма тривиальна.

Лемма 2.1. Пусть  – произвольная невырожденная матрица. Тогда – положительно определенная эрмитова матрица. Кроме того, сумма положительно определенных эрмитовых матриц также является положительно определенной эрмитовой матрицей.

Лемма 2.2. Для любой положительно определенной эрмитовой матрицы  найдется невырожденная верхнетреугольная матрица , такая, что .

Доказательство. Пусть . Тогда  и . Пусть

.

Положим

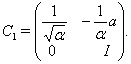
Тогда

и  – положительно определенная эрмитова матрица. Для завершения доказательства достаточно воспользоваться индукцией по порядку матрицы .

Теорема 2.3. Пусть  – конечная группа. Для каждого представления  группы  найдется невырожденная верхнетреугольная матрица , такая, что  является унитарной матрицей для всех .

Доказательство. Положим

Тогда в силу леммы 2.1  является положительно определенной эрмитовой матрицей. Таким образом, найдется невырожденная верхнетреугольная матрица , такая, что  и поэтому . Так как

то , т.е. ; поэтому – унитарная матрица.

Теорема 2.4. Каждое представление конечной группы вполне приводимо.

Доказательство. Пусть – приводимое представление конечной группы , и пусть  разлагается следующим образом:

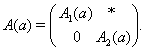
В силу предыдущей теоремы существует невырожденная матрица , такая, что  – унитарная матрица. Так как  верхнетреугольная, то  имеет вид

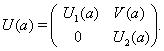
Поскольку , мы получаем

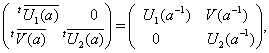
откуда следует, что .

Лемма 3.1. (Лемма Шура.) Пусть  и  – неприводимые представления группы  степеней  и  соответсвенно. Пусть  – такая  – матрица, что

Тогда либо

,

либо

 и  невырожденная.

Доказательство. Допустим, что . Покажем, что тогда имеет место . Предположим, что либо , либо  и  вырожденна. Тогда существуют матрицы  и , такие, что

где . Так как , то

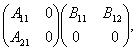
где

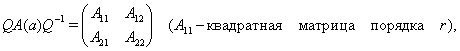
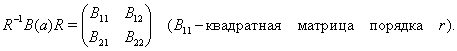
Таким образом, , если , и , если . В любом случае  или  приводимо, что противоречит условию.

Теорема 3.2. Пусть  – неприводимое представление группы . Пусть  – такая матрица, что  для всех . Тогда , где .

Доказательство. Пусть  – некоторое собственное значение матрицы . Тогда , а, кроме того,

откуда в силу леммы Шура следует, что

Теорема 3.3. Пусть  – абелева группа. Тогда каждое ее неприводимое представление имеет степень 1.

Доказательство. Пусть  – неприводимое представление группы . Поскольку  коммутирует с каждой матрицей , из предыдущей теоремы следует, что , где . Поскольку  неприводимо, отсюда вытекает, что его степень равна 1.

Ниже везде предполагается, что рассматриваемые группы конечны.

Характеры. Для квадратной матрицы  порядка  обозначим через  ее след, т.е.

Путем прямых вычислений доказывается следующая

Лемма 4.1.

 для произвольной квадратной матрицы .

Для представления  группы  положим  Тогда  – функция, принимающая значения в множестве  и называемая характером представления . Очевидно, что  равно степени представления . Характеры неприводимых представлений называются неприводимыми характерами. Из леммы 4.1 (2) вытекает следующая

Лемма 4.2. Эквивалентные представления имеют один и тот же характер.

Поскольку , имеет место равенство . Таким образом,  принимает одно и то же значение на всем классе сопряженных элементов группы . Такие функции называются функциями классов.

Первое соотношение ортогональности для характеров. Пусть  – группа порядка , а  и  – ее неприводимые представления степеней  и  соответственно. Для произвольной  – матрицы  пусть

Тогда, положив , получаем

Поскольку , как и , пробегает группу , то

Предположим, что  и  неэквивалентны. Тогда в силу леммы Шура . Отсюда для -го элемента матрицы  получаем

В частности, если взять  для некоторой пары  и  в остальных случаях, то

Пусть теперь . Тогда в силу теоремы 3.2  для некоторого . При этом -ый элемент матрицы  равен

где  и  для . Вычислив след матрицы

мы получаем  (здесь  – степень представления ), откуда

Пусть  для некоторой пары  и , если  или . Тогда

Тем самым мы получаем следующее утверждение.

Теорема 4.3. Пусть – группа порядка g.

(1) Пусть  – неприводимое представление группы  степени . Тогда

(2) Пусть  – неприводимое представление, не эквивалентное представлению . Тогда

Пусть  – характеры представлений  и . Положив в предыдущей теореме  и просуммировав по , мы получаем теорему.

Теорема 4.4. (Первое соотношение ортогональности для характеров.) Пусть  – группа порядка g.

(1) Если  – неприводимый характер группы , то

(2) Если  – характеры неэквивалентных неприводимых представлений группы , то

Отметим, что  для всех , поскольку теорема 2.3 утверждает, что  эквивалентно некоторому унитарному представлению  и потому

Пусть  – представители классов эквивалентности неприводимых представлений группы  и  – характеры представлений . Обозначим через  классы сопряженных элементов группы , причем , и пусть  – представители этих классов. Поскольку характеры – это функции классов, теорема 4.4 может быть переписана в следующем виде.

Теорема .

Для функций , определенных на группе  порядка  и принимающих значения в поле , определим скалярное произведение  по следующему правилу:

В случаях, когда ясно, о какой группе идет речь, мы иногда вместо  будем писать . Очевидно, что скалярное произведение является симметричной билинейной формой:

В этих обозначениях первое соотношение ортогональности для характеров можно сформулировать так:

Теорема . Пусть  – характеры попарно неэквалентных неприводимых представлений группы . Тогда

Кратности неприводимых представлений. Пусть  – некоторое представление группы . Поскольку оно вполне приводимо в силу теоремы 2.3, оно эквивалентно представлению

где  – неэквивалентные неприводимые представления. Число  называется кратностью представления  в , и мы записываем

Пусть  – характер представления  и  – характер представления . Тогда

Если , то  и  называют неприводимыми компонентами представления  и характера  соответственно.

Теорема 4.5. Пусть  – группа и  – характер некоторого ее представления. Пусть  – кратность неприводимого характера  в . Тогда

Доказательство. Пусть разложение  в сумму неприводимых характеров имеет вид , где  – кратность . Тогда

Теорема 4.6. Пусть  – представления группы , а  – их характеры. Тогда  и  эквивалентны в том и только том случае, когда .

Доказательство. В силу предыдущей теоремы кратности компоненты  в  и  определяются характерами последних. Поскольку каждое представление группы  вполне приводимо, представления  и  эквивалентны тогда и только тогда, когда каждое неприводимое представление  имеет в  и  одну ту же кратность. Таким образом,  тогда и только тогда, когда .

Пусть  – характер правого регулярного представления группы  порядка . Отметим, что

Для характера  произвольного неприводимого представления  выполняется соотношение

 равно степени представления ). Следовательно, справедлива следующая

Теорема 4.7. Пусть  – характер правого регулярного представления группы . Тогда каждое неприводимое представления  этой группы входит в  с кратностью , где  – степень представления . Таким образом,

где суммирование ведется по всем неприводимым характерам  группы .

Заметим, что правое и левое регулярные представления эквивалентны, поскольку характер  левого регулярного представления также удовлетворяет равенству (4.8). Поэтому .

Теорема 4.7 утверждает, что каждый неприводимый характер входит в  в качестве компоненты, и поэтому  имеет лишь конечное число неприводимых характеров. Ниже мы покажем, что число неприводимых характеров группы  совпадает с числом ее классов сопряженных элементов.

Теорема 4.8. Пусть  – полный набор различных неприводимых характеров группы . Пусть  – степень , а  – порядок группы . Тогда

и

для .

Для доказательства достаточно вычислить  на элементе , используя (4.8).

Второе соотношение ортогональности для характеров. Пусть  – группа, а  – ее классы сопряженных элементов. Образуем формальную сумму элементов из класса :

Определим произведение  и  по правилу

где , а суммирование ведется по . Для элемента  обозначим через  число пар , таких, что . Тогда для  имеется в точности  пар , таких, что , поскольку  тогда и только тогда, когда  для . Поэтому каждый элемент из  появляется в правой части равенства (4.9) одно и то же число раз, т.е.

Совокупность всех элементов  для  также образует класс сопряженных элементов. Обозначим этот класс через .

Тогда

Пусть  – неприводимое представление группы  и  – степень . Определим  по правилу

Тогда

поскольку  пробегает , как и . Значит,  коммутируют с  и в силу теоремы 3.2

Взяв след от обеих частей равенства (4.12), мы получим

где  – характер представления  и . В силу (4.10)

Подставив в это равенство (4.13), мы придем к равенству

или

Пусть  – все различные неприводимые характеры группы  и  – степень . Равенство (4.14) имеет место для каждого . Просуммировав (4.14) по , получим

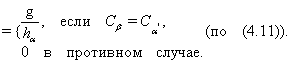
Отсюда

Величина  равна порядку централизатора  элемента  в группе . Поскольку в силу (4.5) , мы получаем следующее утверждение.

Теорема 4.9. (Второе соотношение ортогональности для характеров.) Пусть  – множество всех различных неприводимых характеров группы , и пусть  – полный набор представителей классов сопряженных элементов группы . Тогда

где  – порядок  и суммирование ведется по всем неприводимым характерам  группы .

Теорема 4.10. Число различных неприводимых характеров группы  равно числу ее классов сопряженных элементов.

Доказательство. Мы воспользуемся следующим простым фактом, касающимся матриц. Пусть  есть  – матрица, а  есть  – матрица. Если определитель квадратной матрицы , имеющий порядок , отличен от нуля, то .

Пусть  – все различные неприводимые характеры группы , а  – полный набор представителей классов сопряженных элементов этой группы. Тогда по теореме

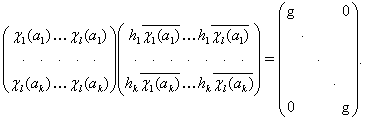
Поэтому . В силу теоремы 4.9

Отсюда следует, что  и потому .

Пусть  – группа и  – ее подгруппа. Обозначим через  и  порядки групп  и  соответственно. Если  – некоторая функция на , то через  обозначим ее ограничение на . В случае когда  – функция классов на ,  также является функцией классов на . Если  – характер некоторого представления  группы , то  представляет собой характер ограничения  представления  на .

По функции , заданной на , определим функцию  на  правилом

полагая  для , не принадлежащих . Отметим, что  является функцией классов на , даже еслм  не является функцией классов на . Если  не сопряжен ни с каким элементом из , то .

Лемма 5.1. Пусть  – функция классов на группе , а  – функция классов на подгруппе  группы . Тогда

Доказательство. Имеем

Вклад в сумму дают лишь такие пары , что . Поэтому, суммируя по тем парам , для которых  при некотором , получаем

Если  – характер некоторого представления группы , то назовем  индуцированным характером группы  и скажем, что  индуцирован с . Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы .

Пусть  – множество представителей левых смежных классов группы  по :

Для представления  подгруппы  определим матрицу  так:

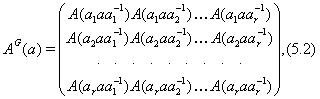
где для , не содержащихся в , полагаем . Это обобщение правого регулярного представления группы . Мы покажем, что

– представление группы  степени , где , а  – степень . При фиксированных  и  множество  содержит по одному представителю из каждого левого смежного класса по , поэтому среди матриц , лишь одна ненулевая. Аналогично, множество  содержит по одному представителю из каждого правого смежного класса по  и среди матриц , также лишь одна ненулевая. Обозначим -й блок матрицы  через . Тогда

Покажем, что . Имеется единственное число , такое, что , и единственное число , такое, что . Если , то . Если же , то  и , поскольку . В любом случае  и следовательно, . Поскольку , матрица  невырожденна. Таким образом  является представлением группы .

Пусть  – характер , а  – характер . Тогда

Тем самым мы получим . Назовем  индуцированным представлением группы  и будем говорить, что  индуцировано с . Сказанное суммирует следующая

Теорема 5.2. Пусть  – группа и  – ее подгруппа. Пусть  – представление  степени , а  – его характер. Тогда индуцированное представление  имеет степень , где , и характер

Теорема 5.3. (Закон взаимности Фробениуса.) Пусть  – подгруппа в . Пусть  – полный набор неприводимых характеров группы , а  – полный набор неприводимых характеров группы . Тогда

в том и только том случае, когда

Другими словами, если  – неприводимое представление группы , а  – неприводимое представление , то  является неприводимой компонентой в  кратности  тогда и только тогда, когда  является неприводимой компонентой в  кратности .

Доказательство. Пусть  и . В силу леммы 5.1

Пусть  – квадратные матрицы порядков  и  соответственно, и пусть . Определим кронекерово, или тензорное, произведение  матриц  и  следующим образом:

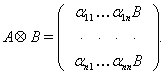
Значит,  представляет собой квадратную матрицу порядка . Непосредственными вычислениями устанавливается следующая

Лемма 6.1.

(1) ,

(2) если  имеют степень , a  – степень , то

Пусть  и  – представления группы . Тогда в силу леммы 6.1 (2) отображение

также является представлением этой группы. Такое представление называют произведением представлений  и обозначают через . Пусть  – характеры представлений  соответственно. По лемме 6.1 (1)

Пусть  – полный набор неприводимых представлений группы , а  – характер . Отображение  также является неприводимым, и его характер – это , где . Пусть .

Теорема 6.2. Равенство

имеет место тогда и только тогда, когда

Доказательство.

Таким образом, кратность вхождения  в  равна кратности вхождения  в

Теорема 6.3. Пусть  – точное представление группы  и  – его характер. Пусть  – число различных значений, которые принимает  на . Тогда каждое неприводимое представление группы  входит в

для некоторого , где .

Доказательство. Предположим, что неприводимое представление  не входит в . Пусть  – характеры  и  соответственно. Тогда

для . Пусть  принимает на  значение . Положим  и . В силу (6.1)

для  Рассмотрим (6.2) как систему линейных уравнений для . Поскольку , эта система имеет решение .

Пусть  – степень представления , т.е. . Мы можем считать, что . Покажем, что . Пусть , т.е. . Обозначим через  циклическую группу, порожденную элементом . По теореме 3.3  эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы

Пусть  – порядок элемента . Тогда . Взяв след в равенстве (6.3), получаем . Это означает, что , т.е. . Плскольку  точно, . Поэтому  и . Полученное противоречие доказывает теорему.

Таблицы характеров. Пусть  – группа и  – классы сопряженных элементов в . Пусть  – нерпиводимые характеры группы , а  – представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения  таким образом, чтобы получить таблицу характеров группы , в которой строки помечены различными неприводимыми характерами, начиная с , а столбцы – классами сопряженности группы , начиная с класса .

Различные строки таблицы характеров ортогональны между собой в смысле теоремы , а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.

Заключение

Таким образом, в данной работе мы показали, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.

Путем прямых вычислений доказали лемму:

 для произвольной квадратной матрицы  и теорему: Пусть  – группа и  – ее подгруппа. Пусть  – представление  степени , а  – его характер. Тогда индуцированное представление  имеет степень , где , и характер

Непосредственными вычислениями была устанавлена следующая лемма: ,

(2) если  имеют степень , a  – степень , то

Список использованных источников

[1] Сыскин С.А. Абстрактные свойства простых спорадических групп. – Усп. мат. наук, 1980, т. 35, №5, (215), с. 181–212.

[2] Монахов В.С. О трижды факторизуемых группах. – Изв. АН БССР. Сер. физ.-мат. наук, 1981, №6, с. 18–23.

[3] Монахов В.С. Произведение разрешимой и циклической групп // Сб. VI всес. симпозиум по теории групп.-Киев: Наукова думка, 1980-с. 189–195

[4] Монахов В.С. О произведении двух групп с циклическими подгруппами индекса 2 // Весцi АН Беларусi. сер. фiз.-мат. навук. – 1996, №3-с. 21–24