Курсовая работа: Применение производной при нахождении предела
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им.Ф. СКОРИНЫ
Математический факультет
Кафедра математического анализа
Применение производной при нахождении предела
Курсовая работа
Исполнитель Бурцева Е.А.
студентка группы М-43
Научный руководитель Астапович Г.Е.
ГОМЕЛЬ 2009
Содержание
Введение
1. Бесконечно малые и их сравнения; символы "o малое" и "о большое"
2. Основные теоремы дифференциального исчисления
2.1 Теорема Ферма о нуле производной
2.2 Теорема Ролля о нуле производной
2.3 Теорема Лагранжа о конечных приращениях
2.4 Теорема Коши о конечных приращениях
3. Раскрытие неопределенностей. правило лопиталя
3.1 Раскрытие неопределенностей вида 0/0
3.2 Раскрытие неопределенностей вида ¥/¥
3.3 Использование правила Лопиталя для выделения главных частей и определения порядков бесконечно больших
3.4 Раскрытие неопределенностей вида 0¥, 1¥, 00,¥0,¥ - ¥
4. Формула тейлора. вычисление пределов с помощью формулы тейлора
4.1 Многочлен Тейлора. Формула Тейлора с остаточным членом Rn.
4.2 Остаток в форме Пеано
4.3 Другие формы остатка в формуле Тейлора
4.4 Разложение некоторых элементарных функций по формуле Тейлора
4.5 Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов
4.6 Формула Тейлора для четных и нечетных функций
Заключение
Список использованных источников
Введение
Данная курсовая работа раскрывает применение производной при вычислении пределов. Вычисление пределов важная часть математического анализа, поскольку практически весь курс математического анализа опирается на понятие предела.
Действительно, производная, интеграл, непрерывность функции - все эти понятия используют предел.
Курсовая работа состоит из четырех разделов.
В первом разделе раскрывается понятие скорости роста функции, вводятся символы "О большое" и "о малое", и важное понятие, для вычисления пределов, эквивалентные функции.
Во втором разделе приведены основные теоремы дифференциального исчисления, служащие необходимой основой для правила Лопиталя и формулы Тейлора.
В третьем разделе приведено правило Лопиталя и методы раскрытия всех типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон].
В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов.
1. Бесконечно малые и их сравнения; символы " o малое" и "о большое"
Определение. Бесконечно малой в x0
называется функция f (x) такая, что ![]()
Свойства бесконечно малых функций:
1) Критерий существования конечного предела функции
![]() Û$
б. м. функция a (x) при x®x0:
f (x) =A+a
(x)
Û$
б. м. функция a (x) при x®x0:
f (x) =A+a
(x)
2) a (x),b (x) б. м. Þ a (x) +b (x) б. м.
3) Произведение бесконечно малой функции на ограниченную является бесконечно малой функцией.
4) Произведение бесконечно малых функций является бесконечно малой функцией.
Определение. f (x) определенная в проколотой окрестности x0 называется бесконечно большой в т. x0, если ![]() .
.
5) Если a (x) б. м. при x®x0 и a (x) ¹0, то 1/a (x) является бесконечно большой и наоборот. Символически это записывают в виде 1/¥=0, 1/0=¥.
Сравнение бесконечно малых и бесконечно больших функций. Символы O, o
f,g определенны в некоторой проколотой окрестности x0
Пишут
![]() ,
,
Если
![]() .
.
Аналогично определяется O при x®x0+0, x®x0 - 0, x®±¥, x®¥.
Пример: f (x) =O (1),x®¥ означает локальную ограниченность функции в ¥.
Опр. Если при x®x0, f (x) =O (g) и g (x) =O (f), то f (x), g (x) называются функциями одного порядка.
Пример: Функции x3,x2 являются функциями одного порядка при x®1.
Определение o. Пусть f (x), g (x) определенны в некоторой проколотой окрестности точки x0, пишут f (x) =o (g (x)), x®x0, если
$ ![]() $ б. м. a (x) при x®x0, такая, что"xÎ
$ б. м. a (x) при x®x0, такая, что"xÎ![]() : f
(x) =a (x) g
(x)
: f
(x) =a (x) g
(x)
Аналогично определяется o при x®x0+0, x®x0 - 0, x®±¥, x®¥.
Пример: f (x) =o (1), при x®x0 означает, что f (x) бесконечно малая при x®x0.
Некоторые примеры работы с символами o (подразумевается x®0).
o (xn) ± o (xn) = o (xn)
xm o (xn) = o (xn+m)
c o (xn) = o (xn) (c-константа)
o (xn) ± o (xn+p) = o (xn), здесь p натуральное.
o (xn+p) /xp= o (xn) В частности, o (xp) /xp= o (1).
o (an xn± an+1 xn+1±…± an+p xn+p) = o (xn)
Если a,b б. м. и b=o (a), то говорят, что b бесконечно малая более высокого порядка, чем a.
Определение. Функции f (x), g (x) называются эквивалентными в x0 (говорят так же, в окрестности x0), если выполнено хотя бы одно из двух условий
f (x) =g (x) +o (g (x)), x®x0
g (x) =f (x) +o (f (x)), x®x0.
Условие эквивалентности записывается в виде f~g, при x®x0.
Замечание 1. Если выполнено одно из этих условий, то будет выполнено и второе.
Замечание 2. Эти условия можно записать в другой форме. Например, первое из них: в некоторой проколотой окрестности точки имеет место равенство
f (x)
=h (x) g (x), ![]() =1.
=1.
Замечание 3. Если, например, g (x) ¹0, то первое условие можно записать в виде
![]() .
.
Определение. Если f (x) ~ (x-x0) n при x®x0, то f (x) называется бесконечно малой порядка n при x®x0.
Если f (x) ~ ![]() при x®x0, то f (x) называется бесконечно большой порядка
n при x®x0.
при x®x0, то f (x) называется бесконечно большой порядка
n при x®x0.
Если f (x) бесконечно большая при x®¥ и f (x) эквивалентна xn при x®¥, то f (x) называется бесконечно большой порядка n при x®¥.
Замечание. Если f (x) бесконечно малая порядка n, то 1/f (x) будет бесконечно большой порядка n и наоборот.
Примеры. Определить характер функций
![]() ,
,![]() в 0, 1,+¥.
в 0, 1,+¥.
При вычислении пределов полезна следующая теорема
Теорема 2. Пусть f эквивалентна f1, g эквивалентна g1 при x®x0.
Если существует предел ![]() ,
тогда существует и
,
тогда существует и ![]() .
.
Если существует предел ![]() ,
тогда существует и
,
тогда существует и ![]() .
.
Определение. Если ![]() ,
то g называется главной частью f при x® x0.
,
то g называется главной частью f при x® x0.
2. Основные теоремы дифференциального исчисления
2.1 Теорема Ферма о нуле производной
Теорема. Если f (x) - определена на (a,b) и дифференцируема в точке x0Î (a,b), принимает в точке x0 наибольшее или наименьшее значение, то f¢ (x0) =0.
Доказательство. Для случая наименьшего значения
f¢ (x0+0)
=![]() ³ 0, f¢
(x0-0) =
³ 0, f¢
(x0-0) = ![]() £ 0 Þ f¢ (x0)
=0
£ 0 Þ f¢ (x0)
=0
Геометрическая интерпретация
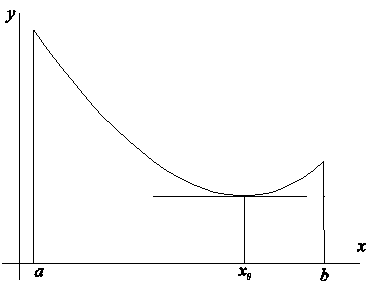
2.2 Теорема Ролля о нуле производной
Теорема. Если f непрерывна на [a,b], дифференцируема на (a,b) и f (a) =f (b). Тогда
$ x0Î (a,b): f¢ (x0) =0.
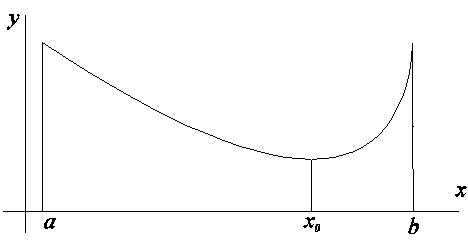
Доказательство. Положим
![]() ,
, ![]() .
.
Хотя бы одна из точек x1, x2 внутренняя и для этой точки утверждение следует из теоремы Ферма.
2.3 Теорема Лагранжа о конечных приращениях
Теорема. Если f непрерывна на [a,b], дифференцируема на (a,b), то
$xÎ (a,b): f (b) - f (a) =f¢ (x) (b-a).
Доказательство. Рассмотрим функцию
![]() .
.
Для этой функции F (a) =F (b) =0, и к ней применима теорема Роля
![]() .
.
Геометрическая интерпретация

Существует точка, касательная в которой, параллельна хорде, соединяющей точки A и B графика.
Следствие 1. Если f непрерывна на [a,b], дифференцируема на (a,b) и f¢ (x) º0 на (a,b), то f (x) ºconst.
Применяя теорему к произвольному отрезку [x0,x], где x0 произвольная фиксированная точка, получим
f (x) - f (x0) =f¢ (x) (x - x0) =0, т.е. f (x) = f (x0).
Следствие 2. Если f непрерывна на [a,b], дифференцируема на (a,b) и f¢ (x) =g¢ (x) на (a,b), то f (x) =g (x) + const.
2.4 Теорема Коши о конечных приращениях
Теорема. Если f, g непрерывны на [a,b], дифференцируемы на (a,b), то существует
xÎ (a,b): g¢ (x) (f (b) - f (a)) = f¢ (x) (g (b) - g (a)).
Доказательство. Рассмотрим вспомогательную функцию
F (x) = g (x) (f (b) - f (a)) - f (x) (g (b) - g (a)).
Для этой функции
F (a) = g (a) (f (b) - f (a)) - f (a) (g (b) - g (a)) = g (a) f (b) - f (a) g (b),
F (b) = g (b) (f (b) - f (a)) - f (b) (g (b) - g (a)) = - f (a) g (b) +g (a) f (b),
таким образом, F (a) =F (b) и к ней применима теорема Ролля: существует точка xÎ (a,b) для которой выполняется равенство
0=F (b) - F (a) =F¢ (x) (b-a) = [g¢ (x) (f (b) - f (a)) - f¢ (x) (g (b) - g (a))] (b-a).
Следствие. Если g¢ (x) ¹0 на (a,b), то
![]() .
.
Доказательство. Если g¢ (x) ¹0, то g (b) - g (a) ¹0. Иначе, в случае g (b) =g (a), по теореме Ролля нашлась бы точка x, где g¢ (x) =0.
3. Раскрытие неопределенностей. правило лопиталя
3.1 Раскрытие неопределенностей вида 0/0
Дано: f (x), g (x) определены на (x0,b) и
1) ![]()
2) f,g дифференцируемы на (x0,b)
3) g¢ (x) ¹0 на (x0,b).
Тогда
![]() ,
,
если существует конечный или бесконечный предел
![]() .
.
Доказательство. Доопределим f, g в точке x0
по непрерывности нулем f (x0) =g (x0) =0. По
тереме Коши, примененной к отрезку [x0,x], будет существовать
x (x) Î (x0,x): x0<x (x) < x и ![]() , из условия x0<x (x) <x следует, что
, из условия x0<x (x) <x следует, что ![]() , причем x (x) ¹x0,
если x¹x0.
По теореме о существовании предела суперпозиции
, причем x (x) ¹x0,
если x¹x0.
По теореме о существовании предела суперпозиции
![]() =
=![]() ч. т.д.
ч. т.д.
Замечание. Аналогично это утверждение доказывается для левой окрестности. Откуда получаем утверждение для x® x0.
Следствие 1. Если
1) Существуют f (k),g (k), k=1,2,…,n на (x0,b)
2) ![]() ,
k=0,1,…,n-1
,
k=0,1,…,n-1
3) Существуeт g (n) (x) ¹0 на (x0,b), то
![]() ,
,
если
![]()
существует, конечный или бесконечный.
Следствие 2. Если f, g дифференцируемы для x>a,
![]() , то
, то
![]() ,
,
если последний существует, конечный или бесконечный.
Доказательство. Сделаем замену
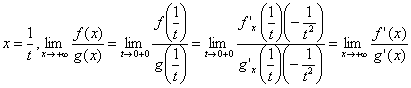
Замечание. Аналогичные утверждения имеют место для x® - ¥.
3.2 Раскрытие неопределенностей вида ¥/¥
f,g определены на (x0,b) и
1) ![]()
2) f,g дифференцируемы на (x0,b)
3) g¢ (x) ¹0 на (x0,b)
Тогда
![]() ,
,
если последний существует конечный или бесконечный.
Замечание. Аналогичные утверждения имеют место для x® x0 - 0, x® x0, x® +¥, x® - ¥.
3.3 Использование правила Лопиталя для выделения главных частей и определения порядков бесконечно больших
В некоторых случаях порядок бесконечно малой или бесконечно большой можно определить, последовательно вычисляя производные. Предположим, что f (x) - бесконечно малая при x® x0 и в точке x0 обращаются в ноль все производные до (n-1) - го порядка включительно f (x0) =0, f¢ (x0) =0,…, f (n-1) (x0) =0 и f (n) (x0) ¹0. В этом случае порядок этой бесконечно малой будет равен n. При этом главная часть будет равна
![]() .
.
Это утверждение следует из равенства
![]() ,
,
в котором в качестве функции g (x) берется (x-x0) n.
![]() .
.
Похожее утверждение можно сформулировать и для бесконечно больших функции.
Пример: f (x) = 3sh x - 3sin x - x3 при x® 0
f¢ (x) =![]() =0,f¢¢ (x) =
=0,f¢¢ (x) =![]() =0,f¢¢¢ (x)
=
=0,f¢¢¢ (x)
=![]() =0,f (4) (x) =
=0,f (4) (x) =![]() =0,f (5) (x) =
=0,f (5) (x) =![]() =0,f (6) (x) =
=0,f (6) (x) =![]() =0,f (7) (x) =
=0,f (7) (x) =![]() =6¹0.
=6¹0.
Таким образом, порядок этой бесконечно малой равен 7 и
f (x) ~![]() x7, x®0.
x7, x®0.
3.4 Раскрытие неопределенностей вида 0 ¥, 1¥, 00,¥0,¥ - ¥
Неопределенности вида 0¥ сводятся к уже рассмотренным.
Примеры.
1) ![]()
2) ![]()
3) ![]()
4) ¥ - ¥
![]()
Можно, например, так
![]()
5) Неопределенности вида 1¥,00,¥0 сводятся к уже рассмотренным логарифмированием
y=uv=ev ln u
Пример 1.
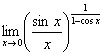 .
.
Вычисление.
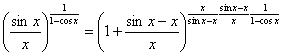 .
.
Этот предел рассматриваем, как
![]() ,
,
где
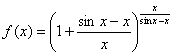 , а
, а ![]() .
.
Из теоремы о существовании предела суперпозиции двух функций
следует, что ![]() . Далее
. Далее
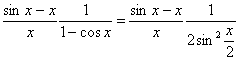 ,
,
заменяя знаменатель на эквивалентную бесконечно малую получим
![]()
![]() =
=![]() .
.
Таким образом,
![]() .
.
Пример 2.
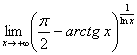 .
.
Представим функцию в следующем виде.
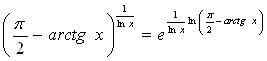
и вычислим предел
![]()
![]()
Пример 3. Вычислить предел:
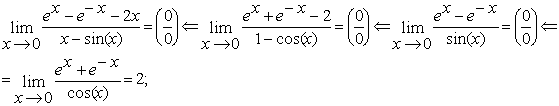
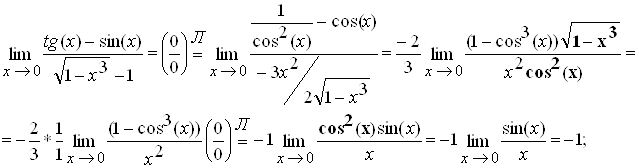
Пример
4. 
Пример 5.
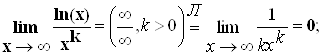

При х®¥

при ![]() ex возрастает быстрее любой
степенной функции хк, k>0
ex возрастает быстрее любой
степенной функции хк, k>0
ln (x) возрастает медленнее любой степенной функции хк
4. Формула тейлора. вычисление пределов с помощью формулы тейлора
4.1 Многочлен Тейлора. Формула Тейлора с остаточным членом Rn.
Пусть f (n-1) - раз дифференцируема в окрестности U= (x0-a,x0+a) точки x0 и существует f (n) (x0). Многочленом Тейлора в точке x0 называется многочлен вида
![]() .
.
Свойства многочлена Тейлора
![]() (1)
(1)
Из (1) следует
![]() =
=![]() (2)
(2)
Из (1) следует
Pn (x0) =f (x0), ![]() (3)
(3)
В частности,
![]() ,
k=0,1,…,n.
,
k=0,1,…,n.
Обозначим Rn (x) =f (x) - Pn (x), тогда
![]() (4)
(4)
(4) - формула Тейлора функции f в окрестности точки x0 с остаточным членом Rn. Основная задача будет состоять в представлении остатка в удобной для оценок формах.
4.2 Остаток в форме Пеано
Теорема 1. Если функция f (x) (n-1) - раз дифференцируема в окрестности U= (x0-a,x0+a) точки x0 и существует f (n) (x0), то имеет место равенство
![]() .
.
Другими словами
![]()
![]() (5)
(5)
Доказательство. Для краткости будем обозначать R (x) =Rn (x)
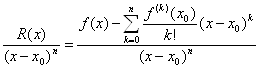 (10)
(10)
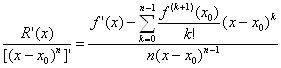 (11)
(11)
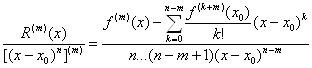 (1m)
(1m)
…
![]() (1n-1)
(1n-1)
f (n-1) (x) дифференцируема в точке x0, поэтому
![]()
Откуда
![]()
По правилу Лопиталя
![]()
Теорема 2. (Единственность представления функции по формуле Тейлора) Если f имеет n-ю производную в точке x0 и
![]() ,
,
то ![]()
Лемма. Если
![]() , (2)
, (2)
то bk=0, k=0,1,…,n
Доказательство. в (2) перейдем к пределу при x® x0, получим
b0 = 0,![]() ,
,
делим полученное выражение на (x-x0) и переходим к пределу при x® x0 и т.д.
Доказательство теоремы.
![]()
откуда и следует утверждение.
4.3 Другие формы остатка в формуле Тейлора
Пусть функция f (x) (n+1) -раз дифференцируема в
окрестности Ua (x0) = (x0-a,x0+a)
и y (x) дифференцируема в ![]() , y¢¹0 в
, y¢¹0 в ![]() ,
y (x) непрерывна в
,
y (x) непрерывна в ![]() .
.
Возьмем xÎ (x0-a,x0+a), x¹x0 и фиксируем. Для определенности будем считать x0<x и рассмотрим на [x0,x] функцию
![]() .
.
Отметим следующие свойства этой функции
j (x) =0
j (x0) =Rn (x)
j (z) непрерывна на [x0,x], дифференцируема на (x0,x).
![]()
Не очевидным является только четвертое свойство
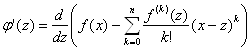 =
=![]() =
=![]() =
=![]() .
.
К функциям j и y применим теорему Коши о конечных приращениях на отрезке [x0,x]
![]() . Откуда
. Откуда ![]() и, далее,
и, далее,
![]() (1)
(1)
Следствие 1. Если функция f (n+1) - раз дифференцируема на (x0-a, x0+a), то
![]() ,
,
где xÎ (x0,x) (или (x,x0)),p>0. Остаток Шлемильха-Роша.
Для доказательства этой формулы следует в качестве функции y (z) взять
y (z) = (x-z) p.
Следствие 2. (Формула Тейлора с остатком в форме Лагранжа) Если f (n+1) -раз дифференцируема на (x0-a, x0+a), то
![]()
![]() .
.
Получено из общей формулы при p=n+1.
Замечание. Формулу с остатком Лагранжа можно представить в виде.
![]() .
.
Следствие 3. Если f (n+1) -раз дифференцируема на (x0-a, x0+a), то справедлива формула Тейлора с остатком в форме Коши
![]()
Получено из общей формулы при p=1.
4.4 Разложение некоторых элементарных функций по формуле Тейлора
ex, x0=0
![]() ,xÎ
(0,x),
,xÎ
(0,x),
если x>0 или xÎ (x,0) в случае x <0.
Например, при |x|<1, |Rn (x) |£![]()
sin x, x0=0
Вспомогательная формула:
![]()
![]()
sin x =![]() =
=![]() , x®0,
, x®0,
выберем m=2n+2, тогда
sin x=![]() , x®0,
, x®0,
откуда, с учетом равенства f (2n+2) (0) =0, получаем разложение для синуса
sin x=![]() , x®0
, x®0
В формуле Тейлора с остатком Лагранжа
sin x =![]() , xÎ
(0,x) (или xÎ (x,0)).
, xÎ
(0,x) (или xÎ (x,0)).
Действительно,
sin x =
![]() =
=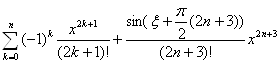 =
=![]() =
=![]() .
.
Откуда следует, что
![]()
cos x, x0=0
Вспомогательная формула:
![]()
![]()
![]() =
=![]() , x®0,
, x®0,
выберем m=2n+1, тогда
cos x=![]() , x®0,
, x®0,
откуда, с учетом равенства f (2n+1) (0) =0, получаем разложение для косинуса
cos x=![]() , x®0
, x®0
В формуле Тейлора с остатком Лагранжа
cos x =![]() , xÎ
(0,x) (или xÎ (x,0)).
, xÎ
(0,x) (или xÎ (x,0)).
Действительно,
cos x =
![]() =
=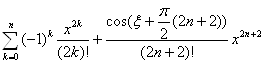 =
=![]() =
=![]() .
.
Откуда следует, что
![]()
ln (1+x), x0=0
![]()
![]() , x®0
, x®0
(1+x) a, x0=0,
интерес представляет случай, когда a не является натуральным числом.
f¢=a (1+x) a-1,…,f (k) =a (a - 1) … (a - k+1) (1+x) a - k
![]() , x®0
, x®0
Важный частный случай
![]() =
=![]() =
=![]() .
.
4.5 Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов
Из формул Тейлора следуют известные "равносильности при
![]() "; например,
"; например,
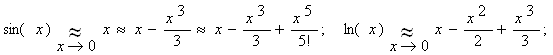

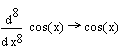
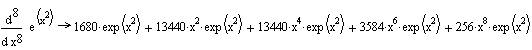
Пример 1.
![]()
Пример 2.
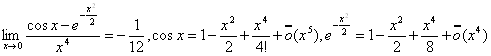 .
.
Пример 3. Разложить функцию f (x) =![]() по формуле Тейлора с
остатком Пиано по степеням x до x5 включительно.
по формуле Тейлора с
остатком Пиано по степеням x до x5 включительно.
![]() . Для решения
задачи возьмем разложения функции
. Для решения
задачи возьмем разложения функции
e2x = 1+2x+![]() +
+![]() +
+![]() +
+![]() +o (x5),
+o (x5),
![]()
![]() = (1+2x+
= (1+2x+![]() +
+![]() +
+![]() +
+![]() +o (x5)) (
+o (x5)) (![]() ) =
) =
1+2x+![]() x2+
x2+![]() x3+
x3+![]() x4+
x4+![]() x5+o (x5)
=
x5+o (x5)
=
1+2x+x2![]() x3
x3![]() x4
x4![]() x5+o (x5).
x5+o (x5).
Пример 4. Разложить функцию f (x) =1/cos x по формуле Тейлора с остатком Пиано по степеням x до x5 включительно. Представим функцию в виде
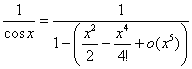 =1+u+u2+u3+o
(u3), где u =
=1+u+u2+u3+o
(u3), где u =![]() .
.
Тогда
![]() =1+u+u2+u3+o
(u3) =1+
=1+u+u2+u3+o
(u3) =1+![]() +
+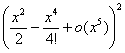 +
+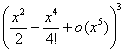 +
+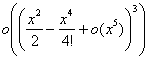 .
.
При вычислении степеней
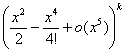
нас интересуют только слагаемые степеней не выше x5, более высокие степени войдут в o (x5). Таким образом,
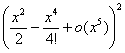 =
=![]() ,
,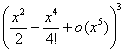 =
=![]() ,
, 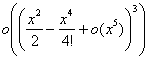 =
=![]() .
.
Выражение
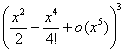 =
=![]()
показывает, что в разложении
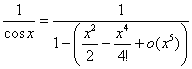 =1+u+u2+u3+o
(u3)
=1+u+u2+u3+o
(u3)
можно, с самого начала, ограничится второй степенью
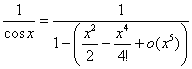 =1+u+u2+o
(x5).
=1+u+u2+o
(x5).
Подставляя нужные выражения в это равенство получим
![]() =1+
=1+![]() +
+![]() +
+![]() =1+
=1+![]() +
+![]() +
+![]() .
.
Пример 5. Используя разложение из предыдущего примера, разложить функцию f (x) =tg x по формуле Тейлора с остатком Пиано по степеням x до x6 включительно.
tg x=![]() =
=
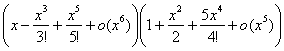 =
=
x+x2 (0) +x3![]() +x4 (0) +x5
+x4 (0) +x5![]() +x6 (0) =
+x6 (0) =
=![]()
Пример 6. Разложить функцию f (x) = (1+x) a - (1 - x) a по формуле Тейлора с остатком Пиано.
![]()
![]()
k = 2l+1,![]()
Таким образом,
![]()
Следствие. ![]()
Пример 7. Используя следствие из предыдущего примера, найти предел (1401)
![]() .
.
Имеем:
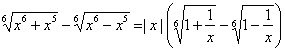 =|x|
=|x|![]() =
= ![]() sign x +o (
sign x +o (![]() ).
).
Пример 8. Разложить функцию
f (x) =![]()
по формуле Тейлора с остатком Пиано по степеням x до x4 включительно.
Сначала выпишем разложение функции ![]() по степеням x
до x3 включительно.
по степеням x
до x3 включительно.
Положим u=x - x2, тогда
![]() =
=![]() =1+u+u2+u3+o (u3) =1+ x - x2+ (x - x2)
2+ (x - x2) 3+o
(x3) =1+x - x3 +o (x3).
=1+u+u2+u3+o (u3) =1+ x - x2+ (x - x2)
2+ (x - x2) 3+o
(x3) =1+x - x3 +o (x3).
Далее,
![]() =
=![]() =1+2x (1+x -
x3 +o
(x3)) =1+2x+2x2-2x4+o (x4).
=1+2x (1+x -
x3 +o
(x3)) =1+2x+2x2-2x4+o (x4).
Второй способ. Так как
![]() ,
,
то на первом шаге выделяем единицу:
![]() =
=![]() .
.
Второе слагаемое представляем в виде Cxng2
(x) так, чтобы ![]() , после чего
следует представить функцию g2 (x) в виде g2 (x)
= 1+g3 (x) и т.д. В нашем случае:
, после чего
следует представить функцию g2 (x) в виде g2 (x)
= 1+g3 (x) и т.д. В нашем случае:
![]() =
=![]() =
=![]() =
=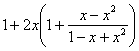 =
=
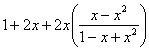 =
=![]() =1+2x+
=1+2x+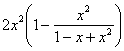 =
=
1+2x+2x2![]() =1+2x+2x2-2x4+o
(x4).
=1+2x+2x2-2x4+o
(x4).
4.6 Формула Тейлора для четных и нечетных функций
Теорема 1. Если функция f (x) четна и существует f (2n+1) (0), то имеет место следующее разложение этой функции
![]() .
.
Если функция f (x) нечетна и существует f (2n+2) (0), то имеет место следующее разложение этой функции
![]() .
.
Теорема 2. Если функция f (x) четна и существует f (2n+2) (x) в некоторой окрестности U (0), то для xÎU (0) справедливо равенство
![]() ,
,
где xÎ (0,x) или xÎ (x,0).
Если функция f (x) нечетна и существует f (2n+3) (x) в некоторой окрестности U (0), то для xÎU (0) справедливо равенство
![]() ,
,
где xÎ (0,x) или xÎ (x,0).
Доказательство. Как уже отмечалось ранее, у четной функции все производные нечетного порядка являются нечетными функциями и, поэтому, они равны нулю с точке ноль
f (2k+1) (0) = 0, если f (x) четна.
Отсюда и получаются указанные формулы, если использовать многочлен Тейлора до порядка 2n+1 включительно. У нечетной функции все производные четного порядка будут нечетными функциями и
f (2k) (0) = 0, если f (x) нечетна.
В этом случае необходимо использовать многочлен Тейлора до порядка 2n+2 включительно.
Заключение
В данной курсовой работе были рассмотрены методы вычисления пределов использующие понятие производной, а именно: правило Лопиталя и формула Тейлора.
Для каждого метода рассмотрены примеры вычисления пределов. Так же было рассмотрено такое важное понятие, как скорость роста функции, играющее большую роль при вычислении пределов.
Список использованных источников
1. Дадаян А.А., Математический анализ: учебное пособие / Дадаян А.А., Дударенко В.А., - Минск, Вышэйшая школа, 1990. - 428с.
2. Марон И.А., Дифференциальное и интегральное исчисление в примерах и задачах (функции одной переменной) / Марон И.А., - М., Наука, 1970. - 400с.