Учебное пособие: Эконометрика
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
Тихоокеанский государственный университет
Программа дисциплины
по кафедре Экономическая кибернетика
Эконометрика
Утверждена научно-методическим советом университета для направлений подготовки (специальностей) в области экономики и управления
Специальности: 080116.65 «Математические методы в экономике»
080103.65 «Национальная экономика»
Хабаровск 2007 г.
Программа разработана в соответствии с требованиями государственного образовательного стандарта, предъявляемыми к минимуму содержания дисциплины и в соответствии с примерной программой дисциплины, утвержденной департаментом образовательных программ и стандартов профессионального образования с учетом особенностей региона и условий организации учебного процесса Тихоокеанского государственного технического университета.
Программу составил (и)
| Порошина Л.А. | Старший преподаватель, кафедра «Экономическая кибернетика» | ||||
| Ф.И.О. автора (ов) |
Ученая степень, звание, кафедра |
||||
|
Программа рассмотрена и утверждена на заседании кафедры протокол № ______ от «____»__________________ 2007 г. |
|||||
| Зав. кафедрой_________«__»______ 200_г | ________________ | ||||
| Подпись дата | Ф.И.О. | ||||
|
Программа рассмотрена и утверждена на заседании УМК и рекомендована к изданию протокол № ______ от «____»_____________ 200_г |
|||||
| Председатель УМК _______«__»_______ 200_г |
_____Корнилов А.М. |
||||
| Подпись дата | Ф.И.О. | ||||
| Директор института _______«__»_______ 200_г |
Зубарев А.Е. _ |
|
|||
| (декан факультета) Подпись дата | Ф.И.О. |
|
|||
| Директор института _______«__»_______ 200_г |
____Лысак С.Г. _ |
|
|||
| (декан факультета) Подпись дата | Ф.И.О. |
|
|||
| Директор института _______«__»_______ 200_г |
_______Вайнер Л.Г. |
|
|||
| (декан факультета) Подпись дата | Ф.И.О. |
|
|||
1. Цели и задача дисциплины
Эконометрика – это совокупность методов анализа связей между различными экономическими показателями на основании реальных статистических данных, с использованием аппарата теории вероятностей и математической статистики. При помощи этих методов выявляют новые, ранее неизвестные связи, уточняют или отвергают гипотезы о существовании определенных связей между экономическими показателями, предлагаемые экономической теорией. Это - вводный курс эконометрики для студентов, специализирующихся в области экономики.
Акцент в курсе делается на содержательном смысле фактов, методов и подходов эконометрического анализа. Выводы и доказательства даются для ряда базовых формул и моделей, что позволяет студентам понять принципы построения эконометрической теории. Главный акцент делается на экономической интерпретации и приложениях рассматриваемых эконометрических моделей.
Эконометрика объединяет совокупность методов и моделей, позволяющих на базе экономической теории, экономической статистики и математико-статистического инструментария исследовать количественные выражения качественных зависимостей. При изучении дисциплины «Эконометрика» предполагается, что студент владеет основами теории вероятностей, математической статистики и матричной алгебры в объеме курса высшей математики для экономических специальностей.
Студенты должны получить базовые знания и навыки эконометрического анализа. Они должны уметь применять их в исследовании экономических процессов, а также понимать эконометрические методы, идеи, результаты и выводы, встречаемые в большинстве экономических книг и статей. В данном курсе студенты должны освоить традиционные эконометрические методы, предназначенные в основном для работы с данными перекрестных выборок.
В то же время, студенты должны понимать содержательные различия данных перекрестных выборок и временных рядов и те специфические эконометрические проблемы, которые возникают при работе с данными этих типов. Студенты должны приобрести навыки построения и развития моделей парной и множественной линейной регрессии, познакомиться с некоторыми видами нелинейных моделей и специальными методами эконометрического анализа и оценивания, понимая область и границы их применения в экономике. Рассматриваемые методы и модели должны быть освоены на практике с использованием реальных массивов экономических данных и современного эконометрического программного обеспечения.
Конечной целью изучения дисциплины является:
- ознакомление студентов с проблемами, возникающими при практическом применении различных количественных моделей экономической теории, таких как модели спроса, производства, совокупного потребления, инвестиций;
- формирование у будущих специалистов теоретических знаний и практических навыков по применению статистических методов для исследования и обобщения эмпирических зависимостей экономических переменных, а также построения надежных прогнозов в банковском деле, финансах, различных сферах предпринимательской деятельности с целью обоснования принимаемых решений.
Основные задачи курса:
- освоение методов эконометрического анализа статистических данных;
- освоение методов построения адекватных статистическим данным моделей, имеющих соответствующую экономическую интерпретацию;
- освоение методов статистического анализа стационарных и нестационарных временных рядов;
- овладение навыками применения пакетов компьютерных программ эконометрического анализа статистических данных.
2. Требования к уровню освоения содержания дисциплины
Студент должен знать:
- место, роль и возможности эконометрики в современной экономической науке и практике;
- особенности эконометрического метода;
- собирать и проводить статистическую обработку экономической информации с целью выявления основных характеристик числовой совокупности;
- особенности измерений в экономике;
- основные понятия и методы эконометрического моделирования;
- основные понятия, связанные с регрессионными моделями, временными рядами и системами одновременных уравнений;
- методы и особенности эконометрического прогнозирования социально-экономических процессов.
Студент должен уметь:
- осуществлять спецификацию эконометрической модели;
- обоснованно применять метод наименьших квадратов и его модификации;
- оценивать параметры эконометрической модели;
- оценивать значимость уравнений и параметров эконометрических моделей;
- использовать основные приемы и правила моделирования временных рядов;
- применять основные методы эконометрического прогнозирования.
3. Объем дисциплины и виды учебной работы
Таблица 1. Объем дисциплины и виды учебной работы
| Наименование | По учебным планам (УП) | ||
| с максимальной трудоёмкостью | с минимальной трудоёмкостью | ||
|
Общая трудоёмкость дисциплины по ГОС по УП |
120 170 |
||
| Изучается в семестрах | 4,5 | ||
|
Вид итогового контроля по семестрам зачёт экзамен курсовой проект (КП) курсовая работа (КР) расчётно-графическая работа (РГР) реферат (РФ) домашние задания (ДЗ) |
4 5 |
||
|
Аудиторные занятия по семестрам Всего лекции (Л) лабораторные занятия (ЛР) практические занятия (ПЗ) |
4 | 5 | |
| 102 | |||
|
34 - 17 |
34 - 17 |
||
|
Самостоятельная работа Общий объем часов (С2) В т.ч. на подготовку к лекциям на подготовку к лабораторным занятиям на подготовку к практическим занятиям на выполнение КР на выполнение РГР на написание РФ на выполнение ДЗ |
4 | 5 | |
| 68 | |||
|
17 - 17 |
17 - 17 |
4. Содержание дисциплины
4.1 Разделы дисциплины и виды занятий и работ
Таблица 2. Разделы дисциплины и виды занятий и работ
| № | Раздел дисциплины |
Л |
ПЗ |
С2 |
| 1 | Методологические основы курса | 2 | 1 | |
| 2 | Парная регрессия и корреляция | 13 | 5 | 15 |
| 3 | Множественная регрессия и корреляция | 8 | 5 | 13 |
| 4 | Метод наименьших квадратов | 4 | 3 | 4 |
| 5 | Системы экономических уравнений | 7 | 4 | 7 |
| 6 | Моделирование одномерных временных рядов | 20 | 10 | 15 |
| 7 | Динамические эконометрические модели | 14 | 7 | 13 |
4.2 Содержание разделов дисциплин
4.2.1 Методологические основы курса
Предмет эконометрики. Место эконометрики в ряду экономических и математико-статистических дисциплин. Примеры применения методов анализа данных. Основные математические предпосылки эконометрического моделирования.
4.2.2 Парная регрессия и корреляция
Содержание корреляционного анализа. Понятия функциональной, статистической и корреляционной зависимости. Типы связи экономических переменных: линейные и нелинейные связи. Статистическая зависимость (независимость) случайных переменных. Анализ линейной статистической связи экономических данных, корреляция. Нелинейная статистическая связь. Меры тесноты линейной связи переменных: парный, частный и множественный коэффициент корреляции. Проверка статистических гипотез для оценки значимости корреляции. Свойства основных корреляционных коэффициентов. Корреляционное отношение как оценка нелинейной связи. Оценка тесноты связи между ординальными (порядковыми) переменными - коэффициент ранговой корреляции Спирмена.
Задачи регрессионного анализа. Понятия регрессионного анализа: результирующая (зависимая, эндогенная) переменная у и объясняющие (прели кг орные, экзогенные) переменные X, функция регрессии у по X, возмущения. Регрессионные модели. Дисперсионный анализ в регрессии
Основные предпосылки регрессионного анализа. Уравнение регрессионной связи между у и X. Геометрическая интерпретация регрессии.
Метод наименьших квадратов для оценки параметров регрессионной модели, Статистические свойства оценок параметров. Стандартизованные коэффициенты регрессии и коэффициенты эластичности.
Построение точечных и интервальных прогнозов, основанных на моделях линейной регрессии. Построение и интерпретация доверительных интервалов. Общее качество регрессии: коэффициент детерминации R2. F-статистика и F-тест. Связь R2 с коэффициентами корреляции. Модель парной ЛР без свободного члена.
Статистическая значимость оценок коэффициентов парной ЛР: проверка гипотез с помощью t-статистик.
Нелинейные модели регрессии и линеаризующие преобразования.
Анализ вариации результирующего показателя и выборочный коэффициент детерминации. Проверка значимости уравнения регрессии и коэффициентов уравнения регрессии. Оценка качества регрессионной зависимости.
Линеаризация нелинейных зависимостей и их оценивание с помощью МНК. Спецификация случайного члена. Интерпретация линейных, логарифмических и линейно-логарифмических зависимостей.
4.2.3 Множественная регрессия и корреляция
Классическая линейная модель множественной регрессии.
Описание и интерпретация модели с
двумя и m объясняющими переменными. Примеры:
функции спроса, функции заработка, производственные функции. Оценивание по МНК
модели с двумя объясняющими переменными. Свойства коэффициентов модели.
Мультиколлинеарность. Коэффициент детерминации ![]() . Скорректированный
. Скорректированный ![]() . Проверка гипотез с
помощью t-статистик и F-статистик.
. Проверка гипотез с
помощью t-статистик и F-статистик.
МНК-оценки модели с m объясняющими переменными в векторно-матричной форме. Свойства коэффициентов. F-тест для групп переменных. Оценивание производственных функций в объемной и темповой записи как моделей множественной регрессии.
Понятие мультиколлинеарности. Признаки и причины мультиколинеарности. Методы устранения мультиколлинеарности. Отбор наиболее существенных переменных в классической линейной модели множественной регрессии. Скорректированный коэффициент детерминации.
Линейные регрессионные модели с переменной структурой. Фиктивные переменные в моделях линейной регрессии. Типы фиктивных переменных. Тест Чоу.
4.2.4 Метод наименьших квадратов
Предпосылки использования МНК.
Понятие, последствия, обнаружение гетероскедастичности. Гетероскедастичность и автокоррелированность как нарушения условий теоремы Гаусса-Маркова. Причины и последствия гетероскедастичности. Диагностика гетероскедастичности: тесты ранговой корреляции Спирмена, Голдфелда-Квандта, Уайта. Средства при гетероскедастичности. Природа, виды автокорреляции, ее последствия. Обнаружение автокорреляции. Тест Дарбина-Уотсона и его практическое использование. Взвешенный метод наименьших квадратов. Причины и примеры гетероскедастичности в экономических моделях.
4.2.5 Системы экономических уравнений
Понятие системы одновременных уравнений. Смещение и несостоятельность оценок при непосредственном оценивании. Структурная и приведенная формы эконометрической модели, построенной на базе систем одновременных уравнений.
Условия идентифицируемости уравнений системы. Рекурсивная модель как частный случай модели и структурной форме. Идентификация систем одновременных уравнений (статистическое оценивание неизвестных значений параметров системы): идентификации рекурсивных систем, косвенный метод наименьших квадратов, двухшаговый МНК оценивания структурных параметров отдельного уравнения, трехшаговый МНК одновременного оценивания всех параметров системы. Оценивание параметров системы внешне не связанных уравнений.
4.2.6 Моделирование одномерных временных рядов
Понятие временного ряда и его отличия от случайной выборки. Составляющие временного ряда. Проверка гипотезы о неизменности среднего значения временного ряда как процедура проверки наличия тренда. Процедуры аналитического выравнивания (сглаживания) временного ряда. Подбор порядка аппроксимирующего полинома с помощью метода последовательных разностей.
Стационарные временные ряды и их характеристики. Понятия автокорреляции, автокорреляционной функции, временного лага, коэффициента автокорреляции, коррелограммы. Интерпретация коррелограмм.
Гетероскедастичкостъ пространственной выборки. Искажение характеристик точности МНК-оненок, обусловленное игнорированием автокоррелированности остатков. Проверка гипотезы о наличии/отсутствии aвтокоррелированности регрессионных остатков. Положительная и отрицательная автокорреляция.
Использование авторегрессионных моделей: модель авторсгрессии порядка р, определение порядка авторегрессионной модели. Методы исключения из временных рядов основной тенденции с целью устранения автокорреляции: метод последовательных или конечных разностей и метод коррелирования отклонений уровней ряда от основной тенденции.
Способы построения множественной регрессионной модели по временным рядам. Модели рядов, содержащих сезонную компоненту.
4.2.7 Динамические эконометрические модели
Распределенные лаги: геометрический лаг, полиномиальный лаг. Преобразование Койка и непосредственное нелинейное оценивание параметров геометрического лага. Частичная корректировка. Адаптивные ожидания. Проблемы оценивания и анализа.
5. Практические занятия
Таблица 3. Практические занятия
| № | № раздела дисциплины | Наименование тем |
| 1 | 1 | Измерения в экономике |
| 2 | 2 | Линейная регрессия и корреляция |
| 3 | 2 | Дисперсионный анализ |
| 4 | 2 | Построение интервального прогноза по линейному уравнению регрессии |
| 5 | 2 | Нелинейная регрессия |
| 6 | 2 | Корреляция для нелинейной регрессии |
| 7 | 3 | Множественные уравнения регрессии |
| 8 | 3 | Уравнения регрессии с фиктивными переменными |
| 9 | 4 | Исследование случайной составляющей e: (предпосылки МНК) |
| 10 | 5 | Структурные модели |
| 11 | 6 | Аддитивная модель. Мультипликативная модель. |
| 12 | 6 | Автокорреляция |
| 13 | 6 | Авторегрессия |
| 14 | 7 | Модели с распределенным лагом |
Краткие характеристики практических занятий.
Парная регрессия и корреляция.
Задание. Эконометрический анализ парной регрессии и корреляции.
Исполнение. Решение задач по теме «Парная регрессия и корреляция».
Оценка. Формирует необходимые представления о применимости того или иного статистического инструментария к заданному классу задач.
Время выполнения заданий: 5 часов.
Множественная регрессия и корреляция.
Задание. Эконометрический анализ множественной регрессии и корреляции.
Исполнение. Решение задач по теме «Множественная регрессия и корреляция».
Оценка. Формирует типологию множественной регрессии, способы оценки значимости модели и возможность использования моделей для моделирования экономических процессов.
Время выполнения задания: 5 часов.
Метод наименьших квадратов.
Задание. Проведение анализа предпосылок МНК.
Исполнение: решение задачи. Использование математико-статистического инструментария подготовки исходных данных и метода решения. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования МНК.
Время выполнения заданий: 3 часа.
Системы экономических уравнений.
Задание. Проведение идентификации системы. Нахождение параметров уравнений системы.
Исполнение: решение задачи. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования систем эконометрических уравнений в экономическом анализе.
Время выполнения заданий: 4 часа.
Моделирование одномерных временных рядов.
Задание. Анализ рядов динамики. Построение трендовых моделей, аддитивных и мультипликативных моделей. Анализ автокорреляции уровней и остатков временных рядов.
Исполнение: решение задачи. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования трендовых моделей в экономическом анализе.
Время выполнения заданий: 10 часов.
Динамические эконометрические модели.
Задание. Анализ временных рядов. Построение моделей авторегрессии, моделей с распределенным лагом.
Исполнение: решение задачи. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования динамических эконометрических моделей в экономическом анализе.
Время выполнения заданий: 7 часов.
6. Контроль самостоятельной работы студентов-заочников
В четвертом семестре для студентов заочников предусмотрено выполнение контрольной работы по дисциплине. Целью контрольной работы является формирование и контроль знаний по основным разделам дисциплины. Студенту рекомендуется, руководствуясь предлагаемой программой и используя литературу, самостоятельно изучить ряд вопросов и примеров. Затем следует выполнить задание. Контрольная работа разработана и имеется в электронном виде на кафедре.
Содержание задания контрольной работы:
- построение парной регрессии; оценка надёжности модели по основным статистическим показателям; определение силы связи между показателями; расчет прогноза по модели;
- построение уравнение множественной регрессии; отбор факторов в модель; оценка надёжности модели;
- идентификация эконометрических систем;
- анализ рядов динамики; подбор трендовой модели; оценка автокорреляции уровней временного ряда; оценка качества модели.
В пятом семестре для студентов заочников предусмотрено тестирование по дисциплине. Целью тестирования является закрепление пройденного материала и возможность практического использования полученных навыков. Необходимо в результате решить простейшие практические задания, например:
· Определите, сколько наблюдений потребуется для построения парной линейной регрессии.
· Объясните, какое стандартное распределение нужно для сравнения двух дисперсий.
· Объясните, какое стандартное распределение нужно при изучении среднего значения.
·
Постройте
доверительный интервал и проверьте значимость коэффициента регрессии: ![]() , a=3, n=50, p=95%.
, a=3, n=50, p=95%.
· Составьте список из 7 существенных и 7 несущественных признаков для модели рентабельности предприятия.
· Приведите примеры уравнений и графиков степенной и показательной функций.
· Проведите спецификацию модели:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
· Проведите спецификацию модели:
![]() ;
; ![]() ;
; ![]() ;
; ![]()
·
Найдите
эластичность функции: ![]()
· Выведите систему нормальных уравнений для модели:
![]()
· Проведите интерпретацию уравнения:
Цена (тыс.руб.) = 40 – 8·Предложение (шт.) + 16·Спрос (шт.)
·
Проведите
интерпретацию уравнения: ![]() .
.
· Найдите коэффициент детерминации двумя способами:
![]() ;
; ![]() ;
; ![]() .
.
· Постройте 68% доверительный интервал для линейного прогноза и нанесите его на график:
![]()
·
Проведите
линеаризацию функции: ![]() .
.
· Составьте уравнение регрессии с фиктивными переменными для учета сезонности по 4 кварталам года.
·
К какому виду
относится система уравнений: ![]() .
.
·
Постройте
приведенную форму для модели: 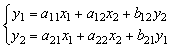 .
.
· Проведите простое экспоненциальное сглаживание временного ряда: yt = [10 20 10 30 20 35], = 0,8
7. Контроль знаний студента
7.1 Входной контроль
Входной контроль осуществляется в форме контрольного задания по разделам дисциплины базового курса «Теория вероятностей и математическая статистика».
7.2 Тематика текущего контроля
Текущий контроль знаний осуществляется в процессе выполнения практических заданий путём индивидуального и группового опроса, собеседования и тестового контроля. Результаты текущего контроля знаний учитываются при промежуточной аттестации и на зачёте.
7.3 Выходной контроль
Выходной контроль осуществляется в форме зачёта и экзамена по дисциплине.
В программу зачёта по дисциплине включены следующие вопросы:
ü Основные этапы прикладного эконометрического исследования.
ü Свойства оценок параметров при выполнении исходных предположений классической нормальной модели линейной множественной регрессии.
ü Доверительные интервалы для параметров при выполнении исходных предположений классической нормальной модели линейной множественной регрессии.
ü Интервальные прогнозы при выполнении исходных предположений классической нормальной модели линейной множественной регрессии.
ü Проверка гипотез о значениях коэффициентов при выполнении исходных предположений классической нормальной модели линейной множественной регрессии.
ü Основные типы нарушений исходных предположений классической нормальной модели линейной множественной регрессии.
ü Последствия различных нарушений исходных предположений классической нормальной модели линейной множественной регрессии.
ü Методы обнаружения гетероскедастичности.
ü Методы обнаружения автокоррелированности.
ü Обнаружение ненормальности распределения ошибок.
ü Выявление неправильного выбора объясняющих переменных (критерий RESET).
ü Выявление непостоянства коэффициентов на периоде наблюдения (критерии Чоу, рекурсивные остатки).
ü Методы коррекции статистических выводов при неоднородности дисперсий ошибок.
ü Методы коррекции статистических выводов при автокоррелированности ошибок.
ü Коррекция статистических выводов при непостоянстве параметров модели на периоде наблюдений. Учет сезонности. Фиктивные переменные.
ü Модели с распределенными запаздываниями объясняющих переменных.
Итоговый контроль знаний – экзамен.
Примерный набор тестов на экзамен:
Вариант 1
1. Парный линейный коэффициент корреляции характеризует наличие тесной обратной связи. Он может принимать следующие значения:
А) 1,2; б) –0,82; В) 0,23; Г) 0,92; Д) –0,24.
2. Коэффициент уравнения парной регрессии показывает:
а) тесноту связи между зависимой и независимой переменными;
б) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на единицу;
в) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%;
г) на сколько ед. изменится зависимая переменная, если независимая переменная изменится на 1 ед.
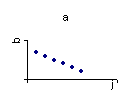
3. Если лаговые воздействия фактора не имеют тенденцию к убыванию во времени, то графическое представление структуры лага примет вид:
|
|
|
|
|
4. Величину, характеризующую влияние лаговых переменных на результат, называют:
А) медиана; Б) мода; В) лаг; Г) мультипликатор; Д) регрессор.
5. Наличие гомоскедастичности можно определить используя:
А) критерий Стьюдента; Б) критерий Фишера; В) критерий Чоу; Г) критерий Энгеля-Грангера;
Д) критерий Уайта; Е) критерий Дарбина-Уотсона.
6. Оценить значимость парного линейного коэффициента корреляции можно при помощи:
А) критерия Фишера;
Б) коэффициента автокорреляции;
В) критерия Стьюдента;
Г) критерия Энгеля-Грангера;
Д) критерия Дарбина-Уотсона.
7. Автокорреляция уровней может быть вызвана следующими причинами:
А) ошибка измерения результативного признака;
Б) ошибка в спецификации модели;
В) ошибка в вычислениях;
Д) нет правильного ответа.
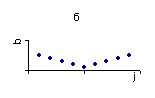
8. В ситуациях, когда остатки содержат циклические колебания, график примет вид:
|
|
|
|
9. Изложите алгоритм использования критерия Энгеля-Грангера.
10. Степень влияния неучтенных факторов в рассматриваемой модели можно определить на основе:
А) парного линейного коэффициента корреляции;
Б) частного коэффициента корреляции;
В) индекса корреляции;
Г) коэффициента детерминации;
Д) коэффициента регрессии.
11. Частный критерий Фишера вычисляется по формуле:
А) 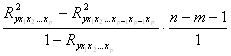 ; Б)
; Б)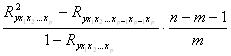 ;
;
В) 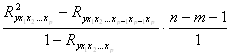 ; Г)
; Г) 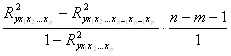 .
.
12. Факторная дисперсия вычисляется по формуле:
А) ![]() ; б)
; б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]() ; е)
; е) ![]() ; Ж)
; Ж) ![]() .
.
13. Что характеризует ![]() -коэффициент в уравнениях
множественной регрессии?
-коэффициент в уравнениях
множественной регрессии?
14. Уравнение множественной регрессии в стандартизованном
виде имеет вид: ![]() . Сила влияния какого фактора выше
на результативный признак?
. Сила влияния какого фактора выше
на результативный признак?
А) x1<x2; Б) x1>x2; B) x1=x2.
15. Для двух видов продукции А и В модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
уА=85+0,5х,
уВ=20х0,3.
Определите, каким должен быть объем выпускаемой продукции, чтобы коэффициенты эластичности для продукции А и В были равны.
А) 73; Б) 0,02; В) 0,3; Г) 85; Д) 20.
Вариант 2
1. Автокорреляция остатков уравнения регрессии означает:
а) наличие ошибки в спецификации уравнения регрессии;
б) незначимость уравнения регрессии;
в) отсутствие зависимости между переменными;
г) их случайность.
2. h-критерий Фишера используется для оценки:
А) Наличия коинтеграции временных рядов.
Б) Наличия коинтеграции рядов распределения.
В) Автокорреляции остатков.
Г) Автокорреляции уровней рядов динамики.
Д) Автокорреляции уровней рядов распределения.
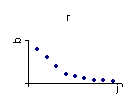
3. Если лаговые воздействия фактора имеют тенденцию к убыванию во времени, то графическое представление структуры лага примет вид:
|
|
|
|
|
4. Коэффициент детерминации показывает:
а) на сколько единиц изменится зависимая переменная, если независимая переменная изменится на 1 единицу;
б) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%;
в) на сколько процентов изменение зависимой переменной зависит от изменения независимой переменной;
г) долю вариации независимой переменной, обусловленную вариацией независимой переменной.
5. Наличие гетероскедастичности можно определить используя:
А) критерий Стьюдента; Б) критерий Фишера; В) критерий Чоу; Г) критерий Энгеля-Грангера;
Д) критерий Спирмена; Е) критерий Дарбина-Уотсона.
6. Оценить значимость коэффициентов регрессии в множественной линейной модели можно при помощи:
А) коэффициента корреляции;
Б) коэффициента автокорреляции;
В) критерия Стьюдента;
Г) критерия Энгеля-Грангера;
Д) критерия Дарбина-Уотсона.
7. Парный линейный коэффициент корреляции определяется по формуле:
А)  ;
;
Б) 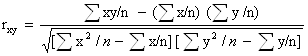 ;
;
В)  .
.
8. В ситуациях, когда остатки содержат циклические колебания, график примет вид:
|
|
|
|
9. Изложите алгоритм использования критерия Спирмена.
10. Степень усредненного влияния неучтенных факторов в рассматриваемой модели можно определить на основе:
А) парного линейного коэффициента корреляции;
Б) частного коэффициента корреляции;
В) индекса корреляции;
Г) коэффициента детерминации;
Д) коэффициента регрессии;
Е) свободного члена уравнения регрессии.
11 . Как вычисляется коэффициент эластичности для модели у=а+b lnx?
12. Критерий Пирсона используется:
А) для оценки автокорреляции уровней;
Б) для оценки автокорреляции остатков;
В) для оценки мультиколлиниарности факторов;
Г) для оценки коинтеграциии.
13. Что характеризует t-критерий Стьюдента?
14. Уравнение множественной регрессии в стандартизованном
виде имеет вид: ![]() . Сила влияния какого фактора выше
на результативный признак?
. Сила влияния какого фактора выше
на результативный признак?
А) x1<x2; Б) x1>x2; B) x1=x2.
15. Модель имеет вид:
Y1 = a1+b11X1+ b12X2+C12Y2+e1,
Y2 = a2+b22X2+ C21Y1 +e2,
Y3 = a3+b31X1 + b33X3+e3.
А) модель идентифицируема;
Б) модель сверхидентифицируема;
В) модель неидентифицируема.
Вариант 3
1. Модель авторегрессии с распределенным лагом имеет вид:
а) ![]() , где
, где ![]() - эмпирически ненаблюдаемая
переменная результативного признака, хt – фактическое значение факторного
признака; et – ошибка модели;
- эмпирически ненаблюдаемая
переменная результативного признака, хt – фактическое значение факторного
признака; et – ошибка модели;
б) ![]() , где
, где ![]() - фактическое значение
результативного признака,
- фактическое значение
результативного признака, ![]() –ожидаемое значение факторного
признака; et – ошибка модели;
–ожидаемое значение факторного
признака; et – ошибка модели;
в) ![]() , где
, где ![]() - эмпирически ненаблюдаемая
переменная результативного признака,
- эмпирически ненаблюдаемая
переменная результативного признака, ![]() – ожидаемое значение факторного
признака; et – ошибка модели;
– ожидаемое значение факторного
признака; et – ошибка модели;
г) ![]() , где
, где ![]() - фактическое значение результативного
признака, хt –
фактическое значение факторного признака; et – ошибка модели;
- фактическое значение результативного
признака, хt –
фактическое значение факторного признака; et – ошибка модели;
д) нет правильного ответа.
2. Модель Койка является:
А) моделью авторегрессии с бесконечной структурой лага;
Б) моделью авторегрессии с конечной структурой лага;
В) моделью авторегрессии.
3. Графическая модель параболы имеет вид:
|
|
|
|
|
4. Дисперсионный анализ уравнения парной регрессии проверяет:
а) значимость коэффициента корреляции;
б) значимость уравнения регрессии;
в) значимость коэффициента регрессии;
г) значимость свободного члена уравнения регрессии.
5. Наличие гетероскедастичности можно определить используя:
А) критерий Стьюдента; Б) критерий Фишера; В) критерий Чоу; Г) критерий Энгеля-Грангера;
Д) критерий Спирмена; Е) критерий Дарбина-Уотсона.
6. Коэффициент множественной детерминации показывает
а) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%;
б) долю вариации зависимой переменной, обусловленную вариацией независимых переменных;
в) на какую часть своего стандартного отклонения изменится зависимая переменная, если независимая переменная изменится на величину своего стандартного отклонения;
г) насколько изменится зависимая переменная, если независимая переменная изменится на единицу.
7. Критерий Дарбина-Уотсона определяется:
А)  ; Б)
; Б)  ; В)
; В)  ;
;
Г) ; Е)
; Е)  .
.
8. Изложите алгоритм использования критерия Энгеля-Грангера.
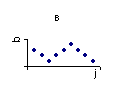
9. В ситуациях, когда остатки не содержат циклические колебания, график примет вид:
|
|
|
|
10.Лаговые переменные в системах одновременных уравнений обычно рассматриваются как
а) независимые.
б) зависимые.
в) эндогенные.
г) экзогенные.
11 . Как вычисляется коэффициент эластичности для параболы II порядка?
12. Прямая неопределенности используется при определении:
А) Наличия коинтеграции временных рядов.
Б) Наличия коинтеграции рядов распределения.
В) Автокорреляции остатков.
Г) Автокорреляции уровней рядов динамики.
Д) Автокорреляции уровней рядов распределения.
13. Что характеризует ![]() -коэффициент?
-коэффициент?
14. Уравнение множественной регрессии в стандартизованном
виде имеет вид: ![]() . Сила влияния какого фактора выше
на результативный признак?
. Сила влияния какого фактора выше
на результативный признак?
А) x1<x2; Б) x1>x2; B) x1=x2.
15. Модель имеет вид:
Y1 = a1+b11X1+ b13X3+C12Y2+e1,
Y2 = a2+b22X2+ C21Y1 +e2,
Y3 = a3+b32X2 + b33X3+e3.
А) модель идентифицируема;
Б) модель сверхидентифицируема;
В) модель неидентифицируема.
8. Учебно-методическое обеспечение дисциплины
8.1 Основная литература
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. -М: ЮНИТИ, 1998, - 102 с.
2. Бородич С.А. Эконометрика. – М.: Новое знание, 2001.
3. Грицан В.Н. Эконометрика. – М.: Издательско-торговая корпорация “Дашков и К”, 2002.
4. Доугерти Кристофер. Введение в эконометрику. Пер. с англ. – М.: ИНФРА-М.-XIV, 1997, - 402 с.
5. Дуброва Т.А. Статистические методы прогнозирования в экономике: Учебное пособие. – М.: МЭСИ, 2002. – 52 с.
6. Замков О.О. Эконометрические методы в макроэкономическом анализе. – М.: ГУ ВШЭ, 2001.
7. Катышев П.К., Магнус Я.Р., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. – М.: Дело, 2002.
8. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2003. – 311 с.
9. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. 3-е изд. - М.: Дело, 1997, - 400 с.
10. Мардас А.Н. Эконометрика. – СПб.: Питер, 2001.
11. Носко В.П. Эконометрика для начинающих: основные понятия, элементарные методы, границы применимости, интерпретация результатов. М., ИЭПП, 2000. - 252 с.
12. Орлов А.И. Эконометрика: Учеб. пособ.. – М.: Из-во «Экзамен»,2002.
13. Практикум по эконометрике: Учеб. Пособие/ под. ред И.И. Елисеевой. – М.: Финансы и статистика, 2001.
14. Четыркин Е.М. Статистические методы прогнозирования. – М.:Статистика, 1977.
15. Эконометрика: Учебник/Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2002. – 344 с.
8.2 Дополнительная литература
1. Практикум по эконометрике/ Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2002.
2. Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2-х кн. М.: Финансы и статистика, 1986-1987.
3. Клейнер Г. Производственные функции. М.: Финансы и статистика, 1986.
4. Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование. М.: Финансы и статистика, 2001.
5. Джонстон Дж. Эконометрические методы. М.: Статистика, 1980.
6. Образцова О.Н., Назарова О.В., Канторович Г.Г. Экономическая статистика. Эконометрика. Методические материалы. – М.: ГУ – ВШЭ, 2000.
7. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 543 с.
8.3 Интернет-ресурсы
http://econline.h1.ru/theor.php Economics Online. Экономическая теория - англоязычные и русскоязычные ресурсы.
http://www.xplore-stat.de/ebooks/ebooks.php Учебники по прикладной статистике и эконометрике.
http://www.qmw.ac.uk/~ugte133/book/protsdbk.php Pollock. Time Series, Analysis Signal Processing and Dynamics.
http://tumania.econ.msu.ru/study.php Сайт экономического факультета МГУ.
http://www.nsu.ru/ef/tsy/ecmr/index.php Эконометрическая страничка Цыплакова А.
http://molchanov.narod.ru/ Персональный сайт Молчанова И.Н.
http://u-pereslavl.botik.ru/UP/ECON/econometrics/index0.koi8.php Кульбака Н.Э. Основы эконометрики. Слайды лекций.
http://www.oup.com/uk/best.textbooks/economics/dougherty2e Персональный сайт Доугерти.
9. Материально-техническое обеспечение дисциплины
Для освоения данной дисциплины необходим определенный объем информации. Это информация об основных экономических показателях, рассматриваемых на микро- и макроуровнях.
10. Методические рекомендации по организации изучения дисциплины
На основании программы разрабатываются рабочие учебные программы дисциплины с учетом фактического количества часов, отведенных на ее изучение. Исходя из этого, в рабочей программе отдельные разделы программы могут быть либо усилены, либо сокращены, либо опущены.
Знания и навыки, полученные при изучении данного курса, широко применяются студентами в дипломном проектировании.
Программа составлена в соответствии с государственными образовательными стандартами высшего профессионального образования.
11. Словарь терминов
Автокорреляция. Автокорреляция имеет место, когда значения последовательных наблюдений, следующих друг за другом во времени, связаны между собой.
Аппроксимация – приближенное выражение математических объектов через более простые объекты, например, сведение задачи выпуклого программирования к кусочно-линейной задаче путем аппроксимации целевой функции и ограничений кусочно-линейными функциями.
Автокорреляция – корреляция между величиной и ее запаздыванием на один и более периодов времени.
Биноминальное распределение – это распределение дискретной случайной величины, значения которой равны Х успехам в n испытаниях результата биноминального эксперимента.
Временной ряд – это ряд, состоящий из данных, зафиксированных или наблюдаемых в течение последовательных промежутков времени.
Выборочное распределение – это ряд всех возможных значений выборочной статистики, который может быть получен из генеральной совокупности для выборки данного объёма.
Интервальная оценка – это числовой интервал, в котором, вероятно, находится некоторый параметр генеральной совокупности.
Корреляционный анализ изучает взаимосвязи, между переменными.
Коррелограмма – это график коэффициентов автокорреляции для различных значений временного лага.
Кросс-секционные данные – это наблюдения, произведенные в один тот же момент времени.
Коэффициент детерминации – измеряет процент изменчивости У, которая может быть объяснена информацией об изменчивости независимой переменной Х.
Коэффициент корреляции определяет тесноту связи.
Коэффициент регрессии измеряет среднее изменение зависимой переменной при единичном изменении соответствующей независимой переменной, если остальные независимые переменные постоянны.
Метод наименьших квадратов. Этот метод используется для получения уравнения регрессии, минимизирующей сумму квадратов отклонений фактических значений результативного признака от теоретических.
Методология Бокса-Дженкинса опирается на ряд процедур идентификации, корректировки и проверки моделей ARIMA с целью анализа данных временных рядов. Прогноз вытекает непосредственно из подобранной модели.
Многомерная регрессия использует более чем одну независимую переменную для прогноза значений зависимой переменной.
Модель авторегрессии. Это модель, в которой значение прогноза находится как функция от предыдущих значений временных рядов.
Мультиколлинеарность – это ситуация, при которой независимые переменные в многомерном уравнении регрессии сильно коррелируют между собой.
Нормальное распределение. Диаграмма нормального распределения имеет форму колокола и определяется математическим ожиданием и среднеквадратичеким отклонением.
Ошибка прогноза. Представляет собой разность между действительно наблюдаемым значением и его прогнозом.
Пошаговая регрессия – это процедура выбора «лучшей» функции регрессии посредством добавления или удаления отдельных независимых переменных на разных этапах анализа.
Простое среднее. Вычисляется как среднее значение для всего набора участвующих в расчетах данных, которое затем принимается для построения прогноза на следующий период.
Регрессионный анализ обеспечивает подбор уравнения по серии исходных данных.
Сезонная компонента. Это модель изменения данных, повторяющаяся из года в год.
Скользящее среднее. Вычисляется как среднее значение для определенного количества элементов данных, которое затем применяется для построения прогноза на следующий период или для сглаживания ряда динамики.
Среднеквадратическое отклонение характеризует разброс значений случайной величины.
Стандартная ошибка оценивания. Измеряет величину, на которую
имеющиеся значения У отличаются от их оценок ![]() . Она равна оценке стандартного
отклонения слагаемого ошибки
. Она равна оценке стандартного
отклонения слагаемого ошибки ![]() в модели простой линейной
регрессии.
в модели простой линейной
регрессии.
Стационарный ряд – это временной ряд данных, основные статистические характеристики которого, такие как среднее значение и дисперсия, остаются постоянными во времени.
Степени свободы. Степени свободы для набора данных определяют количество единиц данных, независимых друг от друга, т.е. таких, которые могут являться носителями отдельных единиц информации.
Точечная оценка. Это единичная оценка параметра генеральной совокупности.
Тренд – это долгосрочная компонента, представляющая возрастание или убывание значений временного ряда в течение продолжительного промежутка времени.
Фиктивные переменные – переменные, используемые для определения взаимосвязи между качественными независимыми переменными и зависимой переменной.
Циклическая компоненита – это волнообразная флуктуация значений данных вокруг линии тренда.
Эконометрия – наука, изучающая конкретные количественные закономерности и взаимосвязи экономических объектов и процессов с помощью математических методов и моделей.
Экспоненциальное сглаживание - это процедура для постоянного пересмотра прогнозов в свете наиболее свежих поступающих данных.
Экстраполяция тенденций – прогнозирование временных рядов.
| Эконометрические методы в сельском хозяйстве | |
|
Содержание Введение 1. Теоретические аспекты эконометрического изучения и анализа производственных затрат и себестоимости зерна 2. Многофакторный ... Линейная модель парной регрессии и корреляции Линейная регрессия находит широкое применение в эконометрике ввиду четкой эконометрической интерпретации ее параметров. |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Анализ экономических данных в странах третьего мира | |
|
Задание для выполнения практической работы по дисциплине эконометрика корреляция регрессия гетероскедастичность Работа включает в себя анализ реальных ... Определите значимость переменных, найдите среднюю ошибку аппроксимации (вручную в экселе), коэффициент детерминации, линейные коэффициенты корреляции между всеми членами регрессии ... Для парной регрессии Множественный R равен коэффициенту корреляции (rxу). |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Статистика | |
|
Университет экономики и управления Горячих М.В. СТАТИСТИКА Учебно-методическое пособие для самостоятельного изучения дисциплины г. Симферополь 2003 ... С точки зрения взаимодействующих факторов связь бывает парной - если характеризуется связь двух признаков, и множественной - если изучаются более, чем две переменные. ... в экономике, равномерно увеличивается число зарегистрированных преступлений (), то оценку зависимости проводим с помощью линейного уравнения регрессии, а оценку тесноты связи ... |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Парная регрессия | |
|
Смысл регрессионного анализа - построение функциональных зависимостей между двумя группами переменных величин Х1, Х2, Хр и Y. При этом речь идет о ... Парная регрессия - уравнение связи двух переменных у и x: Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии |
Раздел: Рефераты по экономико-математическому моделированию Тип: контрольная работа |
| Теория экономического анализа | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Красноярский государственный ... При этом если показатель зависит от одного фактора, то речь идет о парной корреляции, если он зависит от множества факторов, то о множественной корреляции. Коэффициент корреляции (парный коэффициент корреляции, линейный коэффициент корреляции) между фактором х и результативным показателем Y определяется следующим образом: |
Раздел: Рефераты по экономике Тип: учебное пособие |