Контрольная работа: Эконометрический анализ основных числовых характеристик
Эконометрический анализ основных числовых характеристик
Введем обозначения: Х1 – удельный вес пашни в с/х угодьях, %;
Х2 – удельный вес лугов и пастбищ, %
У – уровень убыточности продукции животноводства, %
Найдем основные числовые характеристики:
1. Объем выборки – суммарное количество наблюдений: n = 15.
2. Минимальное значение х1 – min х1 = 68,1%
максимальное значение х1 – max х1 = 94,7%
Значит, удельный вес пашни в с/х угодьях изменяется от 68,1% до 94,7%.
3. min х2 = 9,2%, max х2 = 28,7%.
Значит, удельный вес лугов и пастбищ изменяется от 9,2%, до 28,7%.
4. min у = 15%, max у = 45,6%.
Значит, уровень убыточности продукции животноводства изменяется от 15%% до 45,6%.
5. Среднее значение вычисляется по формуле
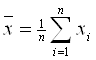
Среднее значение удельного веса пашни в с/х угодьях и составляет x1=80,98%
Среднее значение удельного веса лугов и пастбищ составляет х2 = 17,02%
Среднее значение уровня убыточности продукции животноводства составляет у = 28,2%.
6. Дисперсия вычисляется по формуле
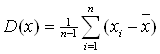
Дисперсия по х1: D(х1) = 58,83;
по х2: D(х2) = 42,45;
по у: D(у) = 92,96.
7. Среднеквадратичное отклонение вычисляется по формуле:
σх1= 7,67 – значит, среднее отклонение удельного веса пашни в с/х угодьях от среднего значения составляет 7,67%
σх2= 6,52 – значит, среднее отклонение удельного веса лугов и пастбищ от среднего значения составляет 6,52%
σу= 9,642 – значит, среднее отклонение уровня убыточности продукции животноводства от среднего значения составляет 9,642%.
Эконометрический анализ
По таблице строим корреляционное поле (диаграмму рассеивания). Нанесем точки хi, уi на координатную плоскость.
Точка с координатами (х; у) = (80,98; 17,15) называется центром рассеивания.
По виду корреляционного поля можно предположить, что зависимость между х и у линейная.
Для определения линейной связи найдем коэффициент корреляции.
r =0,776111538
Т.к. в данном случае коэффициент корреляции 0,6 ≤| r | ≤ 0,9, то линейная связь между х и у достаточная.
Попытаемся описать связь между х и у зависимостью у = b0 + b1x
Параметры b0 и b1 находим по методу наименьших квадратов.
b1 = rху σу/ σх =-0,6520, b0 = у – b1x = 69,9498
Т.к. b1<0, то зависимость между х и у обратная. Т.е. с ростом удельного веса пашни в с/х угодьях, уровень убыточности продукции животноводства уменьшается.
Проверим значимость коэффициентов bi. Значимость может быть проверена с помощью критерия Стьюдента.
Для коэффициента b0:
=5,854852846
Значимость t наблюдаемого: α·tнабл = 0,0001, т.е. 0,01%<5%, значит, коэффициент b0 статистически значим.
Для коэффициента b1:
= -4,437566168
Значимость t наблюдаемого: α·tнабл = 0,0010, т.е. 0,1%<5%,
Значит, коэффициент b1 статистически значим.
Получим модель зависимости уровня убыточности продукции животноводства от удельного веса пашни в с/х угодьях и удельного веса лугов и пастбищ.
у = -0,652х + 69,9498.
После того, как была построена модель, проверяем её на адекватность.
Разброс данных, объясняемый регрессией:
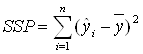SSP = 350,083702
Остатки необъясняемые – разброс:
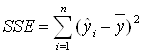SSЕ = 231,1136313
Общий разброс данных:
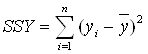SSY = 581,1973333
Для анализа общего качества модели найдем коэффициент детерминации.
R2 = SSR/ SSY = 0,57176059
Разброс данных объясняется: линейной моделью на 57,26% и на 42,74% случайными ошибками ((1 – R2)·100%).
Качество модели плохое.
Проверим с помощью критерия Фишера. Для проверки найдем величины:
MSR = SSR / R1 = 350,083702 и MSЕ = SSЕ / R2 = 17,77797164.
Вычисляем k1 = 1 и k2 = 14.
Находим наблюдаемое значение критерия Фишера.
Fнабл = MSR / MSE = 19,6919935.
Значимость этого значения: α = 0,000669742, т.е. процент ошибки равен ≈0,067% < 5%.
Следовательно, модель у = -0,652х + 69,9498 считается адекватной с гарантией более 95%.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза.
x 
[xmin,
xmax]; хпр = 88
Рассчитываем прогнозируемые значения по модели для всех точек выборки и для точки прогноза.
у(х=88) = у = -0,652х + 69,9498= 12,577
Найдем полуширину доверительного интервала в каждой точке и в точке прогноза.
,
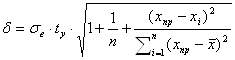где σе – среднеквадратическое отклонение выборочных точек от линии регрессии
= 4,216393
tγ – критическая точка распределения Стьюдента для надежности
γ =0,95 R = 13;
n = 15 – объем выборки;
сумма знаменателя – 
,
где D(x) – дисперсия выборки,
хпр – точка прогноза.
Прогнозируемый доверительный интервал для любой точки х:
, где δ для точки прогноза – δ (х=88) = 9,668, т.е.
доверительный интервал для хпр составляет от 2,909 до 22,244 с
гарантией 95%.
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область.
Т.е. при удельном весе пашни в с/х угодьях 1,458%. уровень убыточности продукции животноводства составит от 2,909% до 22,244%.
Найдем эластичность. Для линейной модели эластичность Ех вычисляется по формуле:
Коэффициент эластичности показывает, что при изменении удельного веса пашни в с/х угодьях на 1% уровень убыточности продукции животноводства уменьшится на 4,593%.
Эконометрический анализ
По таблице строим корреляционное поле (диаграмму рассеивания). Нанесем точки хi, уi на координатную плоскость.
Точка с координатами (х; у) = (17,02; 28,2) называется центром рассеивания.
По виду корреляционного поля можно предположить, что зависимость между х и у нелинейная.
Попытаемся описать связь между х и у зависимостью:
y = a ln x + b.
Перейдем к линейной модели. Делаем линеаризующую подстановку:
U= ln x; V = y.
Для этих данных строим линейную модель:
V = b0 + b1U.
Для определения линейной связи найдем коэффициент корреляции.
r =0,864
Т.к. в данном случае коэффициент корреляции | r | > 0,9, то линейная связь между U и V сильная.
Попытаемся описать связь между U и V зависимостью
V = b0 + b1U.
Параметры b0 и b1 находим по методу наименьших квадратов.
b1 = r U V σ V / σ U = 370.76, b0 = V – b1 U = 3.53.
Т.к. b1 > 0, то зависимость между U и V прямая. Т.е. с ростом удельного веса лугов и пастбищ, уровень убыточности продукции животноводства повышается.
Проверим значимость коэффициентов bi. Значимость может быть проверена с помощью критерия Стьюдента.
Для коэффициента b0:
=0,845
Значимость t наблюдаемого: α·tнабл = 0,413221639, т.е. 41%>5%,
Значит, коэффициент b0 статистически не значим.
Для коэффициента b1:
=6,2
Значимость t наблюдаемого: α·tнабл = 3,23039E‑05, т.е. ≈0%<5%,
Значит, коэффициент b1 статистически значим.
Получим модель зависимости уровня убыточности продукции животноводства от удельного веса лугов и пастбищ.
V = 370,76U +3,53.
После того, как была построена модель, проверяем её на адекватность.
Разброс данных, объясняемый регрессией:
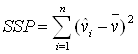SSP = 972,42
Остатки необъясняемые – разброс:
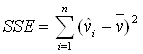SSЕ = 329,1
Общий разброс данных:
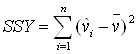SSY = 1301,51
Для анализа общего качества модели найдем коэффициент детерминации.
R2 = SSR/ SSY = 0.747
Разброс данных объясняется: линейной моделью на 74,7% и на 25,3% случайными ошибками ((1 – R2)·100%).
Качество модели хорошее.
Проверим с помощью критерия Фишера. Для проверки найдем величины: MSR = SSR / R1 = 972,42 и MSЕ = SSЕ / R2 = 25,3.
Вычисляем k1 = 1 и k2 = 13.
Находим наблюдаемое значение критерия Фишера.
Fнабл = MSR / MSE = 38.41.
Значимость этого значения: α = 3,23Е‑05, т.е. процент ошибки равен ≈0% < 5%.
Следовательно, модель V = 370,76U +3,53. считается адекватной с гарантией более 95%.
Т.к. линейная модель адекватна, то и соответствующая нелинейная модель то же адекватна. Находим параметры исходной нелинейной модели a и b. Вид нелинейной функции:
y = 370,76/x +3,53.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза.
x [xmin,
xmax];
хпр = 17,02, соответственно Uпр= 1/17,02 = 0,06
Рассчитываем прогнозируемые значения по модели для всех точек выборки и для точки прогноза.
V(х=17,02) = 370,76U +3,53. = 25,32,
у(х=17,02) = 370,76/x +3,53 = 25,32.
Т.к. y(x) = V(U), то полуширина доверительного интервала и доверительный интервал будет равен как для y так и для V.
Найдем полуширину доверительного интервала в каждой точке и в точке прогноза.
,
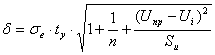Прогнозируемый доверительный интервал для любой точки х:
, где δ для точки прогноза – δ (х=17,02) = 11,27 т.е.
доверительный интервал для хпр составляет от 8,50 до 12,87 с
гарантией 95%.
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область.
Т.е. при удельном весе лугов и пастбищ 17,02% уровень убыточности продукции животноводства составит от 14,05% до 36,59%.
Найдем эластичность. Для линейной модели эластичность Ех вычисляется по формуле:
Коэффициент эластичности показывает, что при изменении удельного веса лугов и пастбищ на 1% уровень убыточности продукции животноводства изменяется на 0,86%.
Эконометрический анализ
Прежде, чем строить модель, проверим факторы на коллинеарность. По исходным данным строим корреляционную матрицу. Коэффициент корреляции между х1 и х2 равен:
rх1х2 =-0,79 < 0,95, следовательно х1 и х2 неколлинеарны.
Определим связаны ли х1, х2 и у между собой. Для определения тесноты линейной связи найдем коэффициент корреляции.
r = 0,92
Попытаемся описать связь между х1, х2 и у зависимостью
у = b0 + b1∙х1 + b2 ∙х2
Параметры b0, b1 и b2 находим по методу наименьших квадратов.
b0 = -19.995, b1 = 0.72, b2 = -0.6
Проверим значимость коэффициентов bi. Значимость может быть проверена с помощью критерия Стьюдента.
Для коэффициента b0:
= -0,87
Значимость t наблюдаемого: α·tнабл = 0,40, т.е. 40% > 5%,
Значит, коэффициент b0 статистически не значим.
Для коэффициента b1:
= 3,04
Значимость t наблюдаемого: α·tнабл = 0,01, т.е. 1% < 5%,
Значит, коэффициент b1 статистически значим.
Для коэффициента b2:
= -2,11
Значимость t наблюдаемого: α·tнабл = 0,06, т.е. 6% > 5%,
Значит, коэффициент b2 статистически не значим.
Получим модель зависимости уровня убыточности продукции животноводства от удельного веса пашни в с/х угодьях и и удельного веса лугов и пастбищ.
у = -19,995 + 0,72∙х1 – 0,6∙х2
После того, как была построена модель, проверяем её на адекватность.
Разброс данных, объясняемый регрессией:
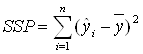SSP = 1090,3
Остатки необъясняемые – разброс:
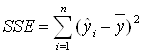SSЕ = 211,17
Общий разброс данных:
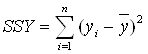SSY = 1301,5
Для анализа общего качества модели найдем коэффициент детерминации.
R2 = SSR/ SSY = 0.84
Разброс данных объясняется: линейной моделью на 84% и на 16% случайными ошибками ((1 – R2)·100%).
Качество модели хорошее.
Проверим с помощью критерия Фишера. Для проверки найдем величины: MSR = SSR / R1 = 545,17 и MSЕ = SSЕ / R2 = 17,6.
Вычисляем k1 = 2 и k2 = 12.
Находим наблюдаемое значение критерия Фишера.
Fнабл = MSR / MSE = 30.98.
Значимость этого значения: α = 1,82E‑05, т.е. процент ошибки равен ≈0% < 5%.
Следовательно, модель
у = -19,995 + 0,72∙х1 – 0,6 ∙х2 – считается адекватной с гарантией более 95%.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза.
X1,2 [xmin, xmax]; хпр = (80,98; 17,02)
Рассчитываем прогнозируемые значения по модели для всех точек выборки и для точки прогноза.
У(80,98;17,02) = у = -19,995 + 0,72∙80,98 – 0,6 ∙17,02=28,17
Найдем коэффициенты частичной эластичности Ех1, Ех2.
Для линейной модели эластичность Ех вычисляется по формуле:
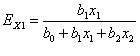
Коэффициент эластичности показывает, что при увеличении удельного веса пашни в с/х угодьях на 1% и удельного веса лугов и пастбищ на 80,98% уровень убыточности продукции животноводства увеличится на 2,064%
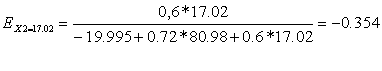
Коэффициент эластичности показывает, что при увеличении производительности труда на 1% и удельного веса пашни в с/х угодьях на 17,02% уровень убыточности продукции животноводства уменьшится на 0,354%.