Реферат: Элементы теории вероятности

Содержание

ВВЕДЕНИЕ………………………………………………………………………3

Анализ различных подходов к определению вероятности.. 4

Примеры стохастических зависимостей в экономике. 6

Проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты как один из этапов эконометрического исследования.. 9

Заключение. 14

Список использованной литературы.. 16

Введение

Сегодня деятельность в любой области экономики (управлении, учете, финансово- кредитной сфере, маркетинге, аудите) требует от специалиста применения современных методов работы, знания достижений мировой экономической мысли, понимания научного языка. Большинство современных методов основано на эконометрических моделях, концепциях, приемах. Без глубоких знаний эконометрики научиться их использовать невозможно. На практике далеко не все экономические явления и процессы можно свести к функциональным зависимостям, когда величине факторного показателя соответствует единственная величина результативного показателя.

Чаще в экономических исследованиях встречаются стохастические зависимости, которые отличаются приблизительностью, неопределенностью. Они проявляются только в среднем по значительному количеству объектов (наблюдений). Здесь каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции). Например, увеличение фондовооруженности труда рабочих дает разный прирост производительности труда на разных предприятиях даже при очень выровненных прочих условиях. Это объясняется тем, что все факторы, от которых зависит производительность труда, действуют в комплексе, взаимосвязано. В зависимости от того, насколько оптимально сочетаются разные факторы, будет неодинаковой степень воздействия каждого из них на величину результативного показателя.

 Целью настоящей работы является  изучение эконометрических методов и использование стохастических зависимостей в эконометрике.

Для достижения данной цели поставлены следующие задачи:

·  проанализировать различных подходов к определению вероятности: априор­ный подход, апостсриорно-частотный подход, апостериорно - модельный подход.

·  рассмотреть примеры стохастических зависимостей в экономике, их особен­ности и теоретико-вероятностные способы их изучения.

·  рассмотреть ряд гипотез о свойствах распределения вероятностей для случайной компоненты как один из этапов эконометрического исследования.

Объектом исследования данной работы являются эконометрические методы и стохастических зависимости, которые используются в эконометрике.

Предметом исследования работы является методы эконометрического исследования.

В данной работе использованы следующие методы исследования: графический, статистический, абстрактно-логический, эконометрический, сравнительного анализа.

Анализ различных подходов к определению вероятности

Вероятность любого собы­тия А определяется как сумма вероятностей всех элементарных событий, составляющих событие А, т.е. если использовать символику Р{А} для обозначения вероятности события А, то

       (1)                   

Отсюда следует, что всегда 0<Р{А}<1, причем вероятность достоверного события равна единице, а вероятность невозможного события равна нулю..

Таким образом, для исчерпывающего описания механизма исследуе­мого случайного эксперимента (в дискретном случае) необходимо задать конечное или счетное множество всех возможных элементарных исходов   и каждому элементарному исходу  поставить в соответствие некото­рую неотрицательную (не превосходящую единицы) числовую характери­стику p, интерпретируемую как вероятность появления исхода  (будем обозначать эту вероятность символами P{w_i}).

Вероятностное пространство является понятием, форма­лизующим описание механизма случайного эксперимента. Задать вероятностное пространство - это значит задать пространство элемен­тарных событии   и определить в нем вышеуказанное соответствие типа:

  (2)

Очевидно, соответствие типа (2) может быть задано различными способами: с помощью таблиц, графиков, аналитических формул, наконец, алгоритмически.

Чтобы определить из конкретных условий решаемой задачи вероятности P{w_i} отдельных элементарных событий используется один из следующих трех подходов.

Априорный подход к вычислению вероятностей P{w_i} заключается в теоретическом, умозрительном анализе специфических условий данного конкретного случайного эксперимента (до проведения самого эксперимен­та). В ряде ситуаций этот предопытный анализ позволяет теоретически обосновать способ определения искомых вероятностей. Например, возмо­жен случай, когда пространство всех возможных элементарных исходов состоит из конечного числа N элементов, причем условия производства исследуемого случайного эксперимента таковы, что вероятности осуще­ствления каждого из этих N элементарных исходов нам представляют­ся равными (именно в такой ситуации мы находимся при подбрасывании симметричной монеты, бросании правильной игральной кости, случайном извлечении игральной карты из хорошо перемешанной колоды и т.п.). В силу аксиомы, вероятность каждого элементарного события равна в этом случае 1/N. Это позволяет получить простой рецепт и для подсчета вероятности любого события: если событие А содержит N_A элементарных событий, то в соответствии с определением (3)

Смысл формулы (3) состоит в том, что вероятность события в данном классе ситуаций может быть определена как отношение числа благопри­ятных исходов (т. е. элементарных исходов, входящих в это событие) к числу всех возможных исходов (так называемое классическое определение вероятности). В современной трактовке формула (3) не является опре­делением вероятности: она применима лишь в том частном случае, когда все элементарные исходы равновероятны.

Апостериорно-частотный подход к вычислению вероятностей Р{w_i} отталкивается, по существу, от определения вероятности, принятого так называемой частотной концепцией вероятности. В соответствии с этой концепцией вероятность Р{w_i} определяется как предел относительной частоты появления исхода   в процессе неограниченного увеличения об­щего числа случайных экспериментов n, т.е. (4)

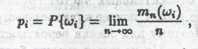
где m_n(w_i) - число случайных экспериментов (из общего числа n про­изведенных случайных экспериментов), в которых зарегистрировано по­явление элементарного события w_i. Соответственно для практического (приближенного) определения вероятностей p_i предлагается брать отно­сительные частоты появления события   в достаточно длинном ряду слу­чайных экспериментов.

Апостериорно-модельный подход к заданию вероятностей Р{w_i}, от­вечающему конкретно исследуемому реальному комплексу условий, явля­ется в настоящее время, пожалуй, наиболее распространенным и наиболее практически удобным. Логика этого подхода следующая. С одной сторо­ны, в рамках априорного подхода, т. е. в рамках теоретического, умозри­тельного анализа возможных вариантов специфики гипотетичных реаль­ных комплексов условий разработан и исследован набор модельных веро­ятностных пространств (биномиальное, пуассоновское, нормальное, пока­зательное и т.п.). С другой стороны, исследователь располагает результатами ограниченного ряда случайных экспериментов. Далее с помощью специальных математико-статистических приемов исследователь как бы прила­живает гипотетичные модели вероятностных пространств к имеющимся у него результатам наблюдения (отражающим специфику изучаемой реаль­ной действительности) и оставляет для дальнейшего использования лишь ту модель или те модели, которые не противоречат этим результатам и в некотором смысле наилучшим образом им соответствуют.

Первая принципиальная идея, с которой встречается каждый изучающий экономист – идея о взаимосвязи между экономическими переменными. Формирующийся на рынке спрос на некоторый товар рассматривается как функция его цены; затраты, связанные с изгото­влением какого-либо продукта, предполагаются зависящими от объема производства; потребительские расходы могут быть функцией дохода ит.д. Все это примеры связей между двумя переменными, одна из кото­рых (спрос на товар, производственные затраты, потребительские расхо­ды) играет роль объясняемой переменной (или результирующего пока­зателя), а другие интерпретируются как объясняющие переменные (или факторы-аргументы). Однако для большей реалистичности в каждое та­кое соотношение приходится вводить несколько объясняющих перемен­ных и остаточную случайную составляющую, отражающую влияние на результирующий показатель всех неучтенных факторов. Спрос на товар можно рассматривать как функцию его цены, потребительского дохода и цен на конкурирующие и дополняющие товары; производственные за­траты будут зависеть от объема производства, от его динамики и от цен на основные производственные ресурсы; потребительские расходы мож­но определить как функцию дохода, ликвидных активов и предыдущего уровня потребления. При этом участвующая в каждом из этих соотноше­ний случайная составляющая, отражающая влияние на анализируемый результирующий показатель всех неучтенных факторов, обусловливает стохастический характер зависимости, а именно: даже зафиксировав на определенных уровнях значения объясняющих переменных, скажем, це­ны на сам товар и на конкурирующие с ним или дополняющие товары, а также потребительский доход, мы не можем ожидать, что тем самым однозначно определяете спрос на этот товар. Другими словами, переходя в своих наблюдениях спроса от одного временного или пространственного такта к другому, мы обнаружим случайное варьирование величины спроса около некоторого уровня даже при сохранении значений всех объясняю­щих переменных неизменными.

В прикладном статистическом анализе анализируются различные ва­рианты формализации понятия стохастической зависимости между результирующим показателем у и объясняющими переменными х⁽¹⁾_,х ⁽²⁾_,…,х ^(р).

Наиболее распространенной в эконометрических приложениях формой представления стохастической зависимости является аддитивная линей­ная форма, которая и будет главным предметом исследования в нашем изложении:

 (5)

Здесь y_t - значение результирующей (объясняемой) переменной, измерен­ное в t-u временном (или пространственном) такте, х _t⁽¹⁾_,х _t ⁽²⁾_…х _t ^(р) - значения участвующих в соотношении объясняющих переменных, полу­ченные в том же t-м измерении, θ₁, θ₂,..., θ _t - некоторые параметры (как правило, не известные до проведения соответствующего статистическо­го анализа), δ _t - случайная составляющая, характеризующая разницу между модельный и наблюденным значениями анализируемой результи­рующей переменной, зафиксированную в t-м измерении. Под модельный значением результирующей переменной ỹ_t здесь и в дальнейшем мы бу­дем понимать ее значение, восстановленное по заданным величинам объ­ясняющих переменных при условии, что коэффициенты θ ₁, θ ₂,..., θ _p нам известны, т.е.

 (6)

При такой интерпретации модельного значения результирующей пе­ременной случайную составляющую   можно интерпретировать как слу­чайную ошибку прогноза у по заданным значениям  х ⁽¹⁾_,х ⁽²⁾_,х ^(р), причем, чтобы исключить систематическую ошибку в оценке y_t по ỹ_t, обычно полагают, что среднее значение случайной составляю­щей _t при всех значениях t равно нулю (т.е. Еδ _t =0). Очевидно, чем больше информации заключено в значениях объясняющих переменных х _t⁽¹⁾_,х _t ⁽²⁾_,…,х _t ^(р)  относительно величины у, тем надежнее будет прогноз и тем меньше будет ошибка прогноза δ. Малость случайной величины - это значит, что ее значения сосредоточены в окрестности нуля с малой дисперсией.

Следующий шаг в развитии экономических теорий состоит в группи­ровке отдельных соотношений в модель. Всякая математическая модель является лишь упрощенным формализованным представлением реально­го объекта (явления, процесса), и искусство ее построения состоит в том, чтобы совместить как можно большую лаконичность параметризации мо­дели с достаточной адекватностью описания именно тех сторон моделиру­емой реальности, которые интересуют исследователя. Количество связей, включаемых в экономическую модель, зависит от условий, при которых эта модель конструируется, и от подробности объяснения, к которой мы стремимся. Например, традиционная модель спроса и предложения долж­на объяснять соотношения между ценой и объемом выпуска, характерные для некоторого определенного рынка. Она содержит три уравнения, а именно: уравнение спроса, уравнение предложения и уравнение реакции рынка. В эти уравнения, помимо интересующих нас объема выпуска и цены, будут входить и другие переменные; так, например, в уравнение спроса войдет потребительский доход, а в уравнение предложения - цена. Объяснение, достигнутое с помощью такой модели, обусловлено значени­ями некоторых «внешних» по отношению к модели переменных и в этом смысле модель является неполной, или условной. Более претенциозные модели содержат гораздо больше уравнений и с их помощью пытаются отразить поведение существенно большего числа переменных; однако и они остаются условными, поскольку тоже содержат переменные, не опре­деляемые или не объясняемые моделью.

Все экономические модели, независимо от того, относятся они ко все­му хозяйству или к его элементам (т. е. к макроэкономике, отрасли, фирме или рынку), имеют некоторые общие особенности. Во-первых, они осно­ваны на предположении, что поведение экономических переменных опре­деляется с помощью совместных и одновременных операций с некоторым числом экономических соотношений. Во-вторых, принимается гипотеза, в силу которой модель, допуская упрощение сложной действительности, тем не менее улавливает главные характеристики изучаемого объекта. В-третьих, создатель модели полагает, что на основе достигнутого с ее помощью понимания реальной системы удастся предсказать ее будущее движение и, возможно, управлять им в целях улучшения экономического благосостояния.

Чтобы проиллюстрировать сказанное и наметить пути для выяснения специфической роли эконометрики, рассмотрим пример весьма общей и приближенной макромодели.

Пример1:

Предположим, что экономист-теоретик сформули­ровал следующие положения:

• потребление есть возрастающая функция от имеющегося в наличии дохода, но возрастающая, видимо, медленнее, чем рост дохода;

• объем инвестиций есть возрастающая функция национального дохода и убывающая функция характеристики государственного регулирова­ния (например, нормы процента);

• национальный доход есть сумма потребительских, инвестиционных и государственных закупок товаров и услуг.

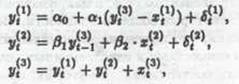Наша первая задача - перевести эти положения на математический язык. И тут мы немедленно сталкиваемся с многообразием открываю­щихся перед нами возможных способов удовлетворения сформулирован­ным априорным требованиям теоретика. Какие соотношения выбрать между переменными - линейные или нелинейные? Если остановиться на нелинейных, то какими они должны быть - логарифмическими, поли­номиальными или какими-либо еще? Даже определив форму конкретного соотношения, мы оставляем еще нерешенной проблему выбора для раз­личных уравнений запаздываний по времени. Будут ли, например, ин­вестиции текущего периода реагировать только на национальный доход, произведенный в последнем периоде, или же на них скажется динамика не скольких предыдущих периодов? Обычный выход из этих трудностей со­стоит в выборе при первоначальном анализе наиболее простой из возмож­ных форм этих соотношений. Тогда появляется возможность записать на основе указанных выше положений следующую линейную относительно анализируемых переменных и аддитивную относительно случайных со­ставляющих модель:

где априорные ограничения выражены неравенствами

Эти три соотношения вместе с ограничениями образуют модель. В ней у_t⁽¹⁾ обозначает потребление, у _t⁽²⁾_,- инвестиции, у _t⁽³⁾ - национальный до­ход, х _t⁽¹⁾ -  подоходный налог, х _t⁽²⁾ - норму процента как инструмент государственного регулирования, х_t⁽³⁾  - государственные закупки това­ров и услуг, измеренные в «момент времени»   t.

Присутствие в уравнениях (6а) и (6б) «остаточных» случайных составляющих  δ_t⁽¹⁾ и  δ_t⁽²⁾ обусловлено необходимостью учесть влияние со­ответственно на у _t⁽¹⁾  и у _t⁽²⁾ ряда неучтенных факторов. Действительно, нереалистично ожидать, что величина потребления у_t⁽¹⁾ будет однозначно определяться уровнями национального дохода (у _t⁽³⁾ ) и подоходного налога (х_t⁽¹⁾); аналогично величина инвестиций у _t⁽²⁾  зависит, очевидно, не только от достигнутого в предыдущий год уровня национального дохода (у _t-1⁽³⁾) и от величины нормы процента (х _t⁽²⁾), но и от ряда не учтенных в уравнении ( 6б ) факторов. Полученная модель содержит два уравнения, объясняющие поведение потребителей и инвесторов, и одно тождество. Модель сформулирована для дискретных периодов времени и имеет запаздывание (лаг) в один период для отражения воздействия национального дохода на инвестиции.

Этот пример объясняет общие черты од­ного из важнейших этапов эконометрического моделирования, в процессе которого исследователь математически формализует отдельные положе­ния экономической теории и объединяет их в систему. В дальнейшем мы используем этот пример для пояснения ряда основных понятий экономе­трического моделирования.

По своему назначению и характеру решаемых задач статистические критерии чрезвычайно разнообразны. Однако их объединяет общность логической схемы, по которой они строятся. Коротко эту логическую схему можно описать так.

1.Выдвигается гипотеза Н₀.

Задаются величиной так называемого уровня значимости критерия
ά. Дело в том, что всякое статистическое решение, т. е. решение, прини­маемое на основании ограниченного ряда наблюдений, неизбежно сопрово­ждается некоторой, хотя, возможно, может и очень малой, вероятностью ошибочного заключения как в ту, так и в другую сторону. Скажем, в какой-то небольшой доле случаев а гипотеза Н₀ может оказаться отверг­нутой, в то время как на самом деле она является справедливой, или, наоборот, в какой-то небольшой доле случаев β мы можем принять нашу гипотезу, в то время как на самом деле она ошибочна, а справедливым оказывается некоторое конкурирующее с ней предположение - альтер­нативная гипотеза Н_1.  При фиксированном объеме выборочных данных величину вероятности одной из этих ошибок мы можем выбирать по сво­ему усмотрению. Если же объем выборки можно как угодно увеличивать, то имеется принципиальная возможность добиваться как угодно малых вероятностей обеих ошибок ά и β при любом фиксированном конкуриру­ющем предположительном утверждении Н_1.  В частности, при фиксиро­ванном объеме выборки обычно задаются величиной а вероятности оши­бочного отвержения проверяемой гипотезы Н₀, которую часто называют «основной»    или «нулевой».   Эту вероятность ошибочного отклонения «нулевой»   гипотезы принято называть уровнем значимости или разме­ром критерия.  Выбор величины уровня значимости а зависит от сопо­ставления потерь, которые мы понесем в случае ошибочных заключений в ту или иную сторону: чем весомее для нас потери от ошибочного отвержения высказанной гипотезы Н₀, тем меньшей выбирается величина ά.

3. Задаются некоторой функцией от результатов наблюдения (крити­ческой статистикой) γ⁽ⁿ⁾= γ (х_1,  х_2,…, х_3).  Эта критическая стати­стика γ⁽ⁿ⁾, как и всякая функция от результатов наблюдения, сама явля­ется случайной величиной и в предположении справедливости гипотезы Н₀ подчинена некоторому хорошо изученному (затабулированному) закону распределения с плотностью f γ⁽ⁿ⁾(u).

4.Из таблиц распределения f γ⁽ⁿ⁾(u) находятся 100(1 - ά/2)%-ная точка γ^min_ά/2  и 100 ά/2%-ная точка γ^max_ά/2, разделяющие всю область мыслимых зна­чений случайной величины γ⁽ⁿ⁾ на три части: область неправдоподобно малых (I), неправдоподобно больших (III) и естественных или правдопо­добных (в условиях справедливости гипотезы Н₀) значений (II) (рис.1). В тех случаях, когда основную опасность для нашего утверждения пред­ставляют только односторонние отклонения, т.е.  только «слишком ма­ленькие»   или только «слишком большие»  значения критической стати­стики  γ⁽ⁿ⁾ находят лишь одну процентную точку: либо 100(1 -ά) %- ную точку γ^min_ά, которая будет разделять весь диапазон значений γ⁽ⁿ⁾  на две части:   область неправдоподобно малых и область правдоподобных зна­чений; либо 100 ά %-ную точку γ^(max)_ά, она будет разделять весь диапазон значений γ⁽ⁿ⁾ на область неправдоподобно больших и область правдопо­добных значений.

5. В функцию γ⁽ⁿ⁾ подставляют имеющиеся конкретные выборочные данные х_1,...,х₂ и подсчитывают численную величину γ⁽ⁿ⁾. Если окажется, что вычисленное значение принадлежит области правдо­подобных значении γ⁽ⁿ⁾  то гипотеза Н₀ считается не противоречащей вы­борочным данным. В противном случае, т. е. если γ⁽ⁿ⁾  слишком мала или слишком велика, делается вывод, что γ⁽ⁿ⁾  на самом деле не подчиняется закону f γ⁽ⁿ⁾(u), и это несоответствие мы вынуждены объяснить ошибочностью высказанного нами предположения Н₀ и, следовательно, отказаться от него.

На разных стадиях статистического исследования и моделирования возникает необходимость в формулировке и экспериментальной провер­ке некоторых предположительных утверждений (гипотез) относительно природы или величины неизвестных параметров анализируемой стохасти­ческой системы. Например, исследователь высказывает предположение: «исследуемые наблюдения извлечены из нормальной генеральной совокуп­ности» или «среднее значение анализируемой генеральной совокупности равно нулю».

Процедура обоснованного сопоставления высказанной гипотезы с име­ющимися в нашем распоряжении выборочными данными х_1,х_2…х_n, со­провождаемая количественной оценкой степени достоверности получаемо­го вывода, осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотез.

Результат подобного сопоставления может быть либо отрицатель­ным (данные наблюдения противоречат высказанной гипотезе, а потому от этой гипотезы следует отказаться), либо неотрицательным (данные наблюдения не противоречат высказанной гипотезе), а потому ее можно принять в качестве одного из естественных и допустимых решений. При этом неотрицательный результат статистической проверки ги­потезы не означает, что высказанное нами предположительное утвер­ждение является наилучшим, единственно подходящим: просто она не противоречит имеющимся у нас выборочным данным, однако таким же свойством могут наряду с H обладать и другие гипотезы.

По своему прикладному содержанию высказываемые в ходе статистической обработки данных гипотезы можно подразделить на несколько основных  типов.

При обработке ряда наблюдений     х_1,х_2…х_{n ,}        (5) 

  исследуемой случайной величины ξ очень важно понять механизм форми­рования выборочных значений х_i, т.е. подобрать и обосновать некоторую модельную функцию распределения Fмод(x), с помощью которой можно адекватно описать исследуемую функцию распределения Fξ(x). На определенной стадии исследования это приводит к необходимости проверки гипотез типа: (6)

где гипотетичная модельная функция может быть как заданной однознач­но (тогда Fξ(x) = F₀(x), где F₀(x) - полностью известная функция), так и заданной с точностью до принадлежности к некоторому параметри­ческому семейству (тогда F_мод(x) = F(х;θ), где θ - некоторый, вообще говоря, к-мерный параметр, значения которого неизвестны, но могут быть оценены по выборке (5).

Проверка гипотез типа (6) осуществляется с помощью так назы­ваемых критериев согласия и опирается на ту или иную меру различия между анализируемой эмпирической функцией распределения Fξ⁽ⁿ⁾(x) и гипотетическим модельным законом Fмод(x).

Наиболее типичные задачи такого рода характеризуются следующей обшей ситуацией. Пусть мы имеем несколько «порций» выборочных дан­ных типа(5):

 (7)

Эти порции могли образоваться, например, естественным образом - в ходе проведения выборочного обследования (скажем, за счет разделенности условий их регистрации во времени или пространстве). Обозначая функцию распределения, описывающую вероятностный закон, которому подчиняются наблюдения j-й выборки, с помощью Fj(x) и снабжая тем же индексом все интересующие нас эмпирические и теоретические харак­теристики этого закона (средние значения âj  и аj; дисперсии σ²j  и σ²j  ).

В случае неотрицательного результата проверки этих гипотез го­ворят, что соответствующие выборочные характеристики (например, а₁, а₂,..,а_i) различаются статистически незначимо.

Пусть, например, ряд наблюдений (5) дает нам значения некоторого параметра изделий, измеренные на n изделиях, случайно отобранных из массовой продукции определенного станка автоматической линии, и пусть а₀ заданное номинальное значение этого параметра. Каждое отдельное значение х_i - может, естественно, как-то отклоняться от заданного номина­ла. Очевидно, для того чтобы проверить правильность настройки этого станка, надо убедиться в том, что среднее значение параметра у произво­димых на нем изделий будет соответствовать номиналу, т. е. проверить гипотезу типа

           (11)

В общем случае гипотезы подобного типа имеют вид:

                 (12)

где θ - некоторый параметр (многомерный), от которо­го зависит исследуемое распределение, а Δ₀ - область его конкретных гипотетических значений, которая может состоять всего из одной точки.

Статистическая проверка гипотез о числовых значениях параметров играет важную роль в эконометрическом моделировании, регрессионном анализе, в широком спектре задач статистического исследования зависи­мостей, существующих между анализируемыми показателями. В частности, принятие решения о включении или исключении той или иной переменной в анализируемую регрессионную (эконометрическую) модель, о наличии-отсутствии статистической связи между наблюдаемыми при­знаками существенно опирается обычно на проверку гипотез типа (12) при   Δ₀= 0.

Заключение

На основании проделанной работы можно сделать следующие выводы.

Вероятность любого собы­тия А определяется как сумма вероятностей всех элементарных событий, составляющих событие.

Априорный подход к вычислению вероятностей P{w_i} заключается в теоретическом, умозрительном анализе специфических условий данного конкретного случайного эксперимента. Вероятность события в данном классе ситуаций может быть определена как отношение числа благопри­ятных исходов (т. е. элементарных исходов, входящих в это событие) к числу всех возможных исходов (так называемое классическое определение вероятности).

В соответствии с апостериорно-частотным подходом, вероятность Р{w_i} определяется как предел относительной частоты появления исхода   в процессе неограниченного увеличения об­щего числа случайных экспериментов n.

Апостериорно-модельный подход заключается в следующем: в рамках априорного подхода разработан и использован набор модельных вероятностных пространств. Исследователь располагает результатами ограниченного ряда случайных экспериментов, согласно которому он выбирает ту или иную вероятностную модель или модели, которые соответствуют этим результатам наилучшим способом.

Стохастические зависимости проявляются только в массовых процессах и при большом числе единиц совокупности. При стохастической зависимости для заданного значения объясняющей переменной можно указать ряд значений зависимой переменной, случайным образом рассеянных в интервале, то есть каждому фиксированному значению аргумента соответствует определенное статистиче5ское распределение значений функции. Это объясняется тем, что зависимая переменная кроме выделенной переменной подвержена влиянию ряда не контролируемых факторов, а также тем, измерения переменных неизбежно сопровождаются случайными ошибками. Наиболее распространенной в эконометрических приложениях формой представления стохастической зависимости является аддитивная линей­ная форма.

Процедура обоснованного сопоставления высказанного исследовате­лем предположительного утверждения (гипотезы) относительно природы или величины неизвестных параметров рассматриваемой стохастической системы с имеющимися в его распоряжении результатами наблюдения, сопровождаемая количественной оценкой степени достоверности получае­мого вывода, осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотез.

По своему прикладному содержанию гипотезы, высказываемые в ходе статистического анализа и моделирования, подразделяют на следую­щие типы: об общем виде закона распределения исследуемой случайной величин; об однородности двух или нескольких обрабатываемых выборок; о числовых значениях параметров исследуемой генеральной совокуп­ности; об общем виде зависимости, существующей между компонентами ис­следуемого многомерного признака; о независимости и стационарности ряда наблюдений.

Все статистические критерии строятся по общей логической схе­ме. Построить статистический критерий - это значит: а) определить тип проверяемой гипотезы; б) предложить и обосновать конкретный вид функции от результатов наблюдения (критической статистики  на основании значений которой принимается окончательное решение; в) указать такой способ выделения из области возможных значений критической статистики   области   отклонения проверяемой гипотезы Н_о, чтобы было соблюдено требование к величине вероятности ошибочного отклоне­ния гипотезы Но (т.е. к уровню значимости критерия а).

1.  Айвазян С.А., Мхитарян B.C. Прикладная статистика и основы
эконометрики. - М.: ЮНИТИ, 1998.

2.  Вентцель Е.С. Теория вероятностей. - М.: Высшая школа, 1998.

3.  Эконометрика. /Под ред. Елисеевой И.И. - М.: Финансы и стати­стика, 2001.