Курсовая работа: Синтез системы угловой стабилизации дозвукового транспортного самолета по заданному курсу
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Тульский государственный университет
Кафедра «Приборы управления»
КУРСОВАЯ РАБОТА
по дисциплине
«Системы автоматического управления летательными аппаратами»
на тему:
«Синтез системы угловой стабилизации
дозвукового транспортного самолета по заданному курсу»
Выполнил: студент группы 130461 Ефимов Д.А.
Проверил: д.т.н., профессор Малютин Д.М.
Тула 2010
Содержание
Задание на курсовую работу
Введение
1 Уравнение движения рыскания
2 Датчики сигналов о параметрах движения летательных аппаратов
3 Основные законы управления автопилотов
4 Рулевой привод с жесткой обратной связью
5 Синтез системы
Вывод
Список использованной литературы
Задание на курсовую работу
по курсу
«Системы автоматического управления летательными аппаратами»
Исходные данные для проектирования:
- объект статически устойчивый;
- схема расположения рулей нормальная;
- тип закона управления: по углу;
- тип обратной связи: жесткая обратная связь;
- числовые значения параметров, соответствующие дозвуковому транспортному самолету:
Тн1=1/3 с;
Тн=0,5 с;
![]() ;
;
Тр.м.=0,02 с;
Кн=1;
Кнf=0,5,
где Тн1, Тн, ![]() - параметры
передаточной функции ЛА, Трм - постоянная времени рулевого привода.
- параметры
передаточной функции ЛА, Трм - постоянная времени рулевого привода.
В процессе выполнения работы необходимо:
Составить схему сил и моментов, действующих на объект, составить систему уравнений «система угловой стабилизации - транспортный самолет», линеаризовать эту систему, составить структурную схему и получить передаточные функции разомкнутой и замкнутой системы.
Методом ЛАФЧХ исследовать устойчивость объекта, определить значение общего коэффициента усиления по контуру при котором система имеет необходимые запасы устойчивости по амплитуде и фазе. Построить ЛАФЧХ разомкнутой системы.
Рассмотреть возможность применения корректирующего звена для улучшения динамических свойств системы, построить ЛАФЧХ скорректированной системы.
Построить ЛАФЧХ замкнутой системы по отношению к внешнему возмущающему моменту.
Построить ЛАФЧХ замкнутой системы по отношению к управляющему моменту.
Построить графики переходных процессов, как реакции на единичное управляющее и возмущающее воздействие.
Проанализировать полученные результаты.
Введение
В результате непрерывного развития техники к настоящему времени созданы разнообразные по конструктивному исполнению и решаемым задачам летательные аппараты (ЛА) – от простейших воздушных шаров, дирижаблей, дельтапланов до сверхзвуковых реактивных самолетов, управляемых ракет и автоматических межпланетных кораблей.
Основным назначением любого ЛА является осуществление полета по требуемой траектории. При этом движение ЛА можно рассматривать состоящим из движения центра масс и углового движения вокруг центра масс. Необходимость управления угловым движением вызывается тем, что ЛА должен занимать вполне определенное положение по отношению к вектору скорости центра масс. В частности, для самолетов и ракет продольная ось ЛА должна совпадать или быть близкой к направлению вектора скорости.
При движении ЛА в пределах атмосферы на него действуют сила тяги, аэродинамические силы, зависящие от режима полета и состояния атмосферы, сила тяжести. Под действием указанных сил движение ЛА непрерывно возмущается, а параметры полета отклоняются от расчетных.
Для устранения возникающих отклонений от заданного режима полета производятся изменение режима работы двигателя и отклонение соответствующих рулей управления ЛА.
На пилотируемых ЛА рули отклоняются пилотом с помощью системы ручного управления. Для обнаружения отклонений ЛА от заданного режима пилоту необходимо вести непрерывное наблюдение, как за видимыми ориентирами, так и за показаниями многочисленных приборов. Для устранения непрерывно возникающих отклонений ЛА, т. е. для удержания его в заданном режиме полета, пилоту приходится непрерывно воздействовать на органы управления. Все это приводит к быстрой утомляемости пилота и в результате к снижению точности выдерживания заданного режима полета, к увеличению времени для решения задач, возникающих в полете. Поэтому почти одновременно с появлением первых ЛА возникло стремление к автоматизации управления полетом.
Автоматические устройства управления полетом выполняют на ЛА следующие основные функции:
- управляют движением центра масс ( высотой полета, боковым отклонением, скоростью полета и т.д.);
- управляют угловым движением (поддерживают неизменными или изменяют в соответствии с сигналами команды углы тангажа, рыскания и крена);
- улучшают динамические характеристики ЛА (обеспечивают демпфирование, устойчивость, управляемость).
При автоматическом управлении движением ЛА должны быть достигнуты: заданное качество переходного процесса, требуемая точность исполнения команд, слабая реакция на внешние возмущения, безопасность полета.
1 Уравнение движения рыскания
Допустим, что ЛА совершает горизонтальный полет с постоянной скоростью и управляется автопилотом. Для получения уравнений движения рыскания приравняем проекции внешних и инерционных сил на нормаль (ось Oz) к траектории, а также внешний и инерционный моменты относительно нормальной оси ЛА (оси Oyc):

где Z – боковая аэродинамическая сила;
Y - угол поворота траектории;
Iy – момент инерции ЛА относительно связанной оси Oyc;
wy – скорость рыскания (угловая скорость ЛА относительно оси Oyc);
My – аэродинамический момент рыскания.
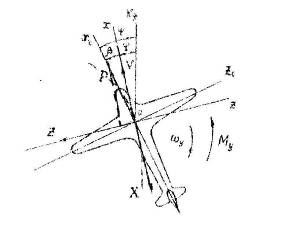
Рис.1. Схема сил и моментов действующих на объект
Линейные дифференциальные уравнения движения рыскания имеют вид:
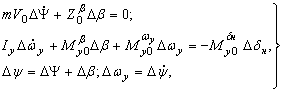 ,
,
где для постоянных коэффициентов введены следующие обозначения:
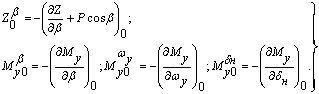
Нулевой индекс у скобок обозначает, что производная и параметры взяты для выбранного невозмущенного движения.
В некоторых случаях уравнения движения рыскания еще более упрощают. Дальнейшее упрощение этих уравнений основывается на том, что в большинстве режимов полета руль направления устраняет скольжение и можно положить, что Db=0. Тогда движение рыскания будет описываться одним уравнением:
![]()
Это же
уравнение описывает движение ЛА, нейтрального в путевом отношении, т.е. ЛА, у
которого коэффициент момента путевой устойчивости равен нулю: ![]() .
.
Если пренебречь движением центра масс под действием боковых сил и рассматривать лишь колебания продольной оси ЛА относительно вектора скорости, т.е. положить Db=Dy, то уравнение движения примет вид:
![]()
2 Датчики сигналов о параметрах движения ЛА
Характеристиками датчиков являются передаточные функции и статические погрешности. Статические погрешности датчиков должны быть меньше допустимых погрешностей процессов управления. Динамические погрешности датчиков, определяемые по передаточным функциям, в полосе пропускания контура ЛА-АП должны быть малы.
Для измерения углов тангажа, рыскания и крена ЛА применяются свободные гироскопы (на беспилотных ЛА с малым временем полета), корректируемые трехстепенные гироскопы и гироскопические системы типа гировертикалей, гироскопов направления, курсовертикалей, пространственных гиростабилизированных платформ. Иногда (для беспилотных ЛА) для измерения угла применяются двухстепенные интегрирующие гироскопы.
При исследовании системы стабилизации ЛА-АП датчики углов будем считать безынерционными звеньями, полагая, что
![]()
где ![]() - напряжение,
снимаемое с гироскопического датчика угла;
- напряжение,
снимаемое с гироскопического датчика угла;
kГ – коэффициент передачи гироскопа;
![]() - угол,
измеряемый гироскопом.
- угол,
измеряемый гироскопом.
Измерение угловых скоростей ЛА осуществляется двухстепенными или трехстепенными гиротахометрами (ГТ). В последние годы для этих целей начали применять ГТ, построенные на базе лазерных и вибрационных гироскопов. ГТ на базе обычного и вибрационного гироскопа можно рассматривать как колебательное звено. Однако, если собственная частота ГТ выбрана порядка 10-50 Гц, то такой прибор будет иметь малые динамические погрешности при измерении угловых колебаний ЛА по тангажу, рысканию и крену, происходящих с частотой, обычно не превышающей несколько герц. Уравнение датчика угловой скорости, частота собственных колебаний которого во много раз превышает частоту изменения измеряемой угловой скорости, при исследовании системы ЛА-АП будем записывать в виде:
![]()
где UГГ – напряжение, снимаемое с ГТ;
kГТ – коэффициент передачи с ГТ;
![]() - измеряемая
угловая скорость.
- измеряемая
угловая скорость.
Сигнал, пропорциональный угловому ускорению ЛА, получают либо дифференцируя сигнал ГТ, либо путем применения трехстепенных гиротахоакселерометров. Для датчика углового ускорения, имеющего частоту собственного колебания, во много раз превышающую частоту изменения измеряемого углового ускорения, положим:
где UДУУ - сигнал, снимаемый с датчика углового ускорения;
kДУУ – коэффициент передачи;
![]() - измеряемое
угловое ускорение.
- измеряемое
угловое ускорение.
Сигналы, пропорциональные угловой скорости и угловому ускорению ЛА, можно получить и дифференцированием сигнала датчика угла с помощью RC-цепочки. Однако в этом случае в сигналах по угловой скорости и угловому ускорению будут значительные динамические погрешности, обусловленные RC-цепочкой.
3 Основные законы управления автопилотов
Законом управления или регулирования АП обычно называют простейшее уравнение, отображающее наиболее существенные связи и преобразования, реализуемые автопилотом.
В реальном АП закон управления не может быть точно обеспечен из-за инерционности элементов и нелинейности их характеристик. Поэтому закон управления можно рассматривать еще как уравнение идеального автопилота.
По виду закона управления автопилоты классифицируются на статические и астатические. Статическими называют АП, у которых в установившемся состоянии отклонение руля пропорционально изменению регулируемого параметра (углу отклонения ЛА по соответствующему каналу), а при постоянном внешнем возмущении, действующем на ЛА, имеет место статическая ошибка: установившееся отклонение регулируемого параметра от исходного положения на величину, пропорциональную внешнему возмущению. У астатических автопилотов при наличии постоянного возмущающего воздействия на ЛА статическая ошибка отсутствует (отклонение регулируемого параметра сводится к нулю). В таких АП каждому значению регулируемого параметра соответствует пропорциональная этому отклонению скорость отклонения руля.
Законы управления можно классифицировать по составу суммарного сигнала управления с датчиков: по углу; по углу и угловой скорости; по углу, угловой скорости и угловому ускорению; по углу, угловой скорости и интегралу от угла; и по типу обратной связи в рулевом приводе АП: жесткая обратная связь; скоростная обратная связь; изодромная обратная связь.
В данной работе в автопилоте используется жесткая обратная связь с датчиками по углу, закон управления которого имеет вид:
![]()
4 Рулевой привод с жесткой обратной связью
Жесткая
обратная связь ![]() обеспечивает пропорциональность
угла отклонения руля величине управляющего сигнала и слабую зависимость этого
отклонения от шарнирного момента. Сигнал, пропорциональный углу отклонения
руля, при помощи обратной связи сравнивается с управляющим сигналом. В качестве
элемента обратной связи может быть использован потенциометрический датчик,
измеряющий угол отклонения руля. На рис.2 показана структурная схема рулевого
привода с жесткой обратной связью.
обеспечивает пропорциональность
угла отклонения руля величине управляющего сигнала и слабую зависимость этого
отклонения от шарнирного момента. Сигнал, пропорциональный углу отклонения
руля, при помощи обратной связи сравнивается с управляющим сигналом. В качестве
элемента обратной связи может быть использован потенциометрический датчик,
измеряющий угол отклонения руля. На рис.2 показана структурная схема рулевого
привода с жесткой обратной связью.
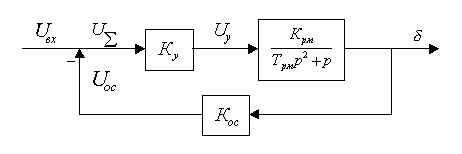
Рис.2. Структурная схема рулевого привода с жесткой обратной связью
Передаточная функция рулевого привода:
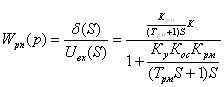
или
![]()
где ![]() - постоянная
времени рулевого привода,
- постоянная
времени рулевого привода, 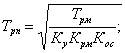
![]() - степень
затухания колебаний рулевого привода,
- степень
затухания колебаний рулевого привода,
![]()
![]() -коэффициент
передачи рулевого привода,
-коэффициент
передачи рулевого привода, ![]()
Введение
жесткой обратной связи, кроме обеспечения пропорциональности угла отклонения
руля величине управляющего сигнала, снижает постоянную времени рулевого
привода, т. е. увеличивает его быстродействие. Частота собственных колебаний
рулевого привода 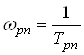 должна быть примерно на порядок
выше частоты угловых колебаний ЛА.
должна быть примерно на порядок
выше частоты угловых колебаний ЛА.
5 Синтез системы
Составим структурную схему разомкнутой системы рулевого привода с жесткой обратной связью и определим значения коэффициентов.
Структурная схема разомкнутой системы рулевого привода показана на рис 1:
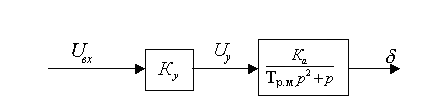
Рис. 1. Структурная схема разомкнутой системы рулевого привода
Для определения коэффициента Ку смоделируем структурную схему разомкнутой системы рулевого привода с жесткой обратной связью в программной среде MathLab 6.5.
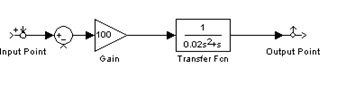
Рис. 2. Структурная схема разомкнутой системы рулевого привода в среде MathLab 6.5
Приведем ЛАФЧХ разомкнутой системы рулевого привода с жесткой обратной связью при значении коэффициента Ку=100
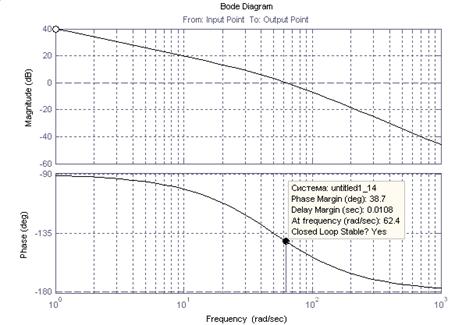
Рис . 3. ЛАФЧХ рулевого привода разомкнутой системы
Из графика видно, что при значении коэффициента Ку=100 запас по фазе составляет φ=38,7˚. Из этого следует, что данная система устойчива.
Составим структурную схему замкнутой системы рулевого привода с жесткой обратной связью и определим значение коэффициента Кос.
Структурная схема замкнутой системы рулевого привода с жесткой обратной связью имеет вид показана на рис. _

Рис. 4. Структурная схема замкнутой системы рулевого привода с жесткой ОС
Для определения коэффициента Кос смоделируем структурную схему замкнутой системы рулевого привода с жесткой обратной связью в программной среде MathLab 6.5.
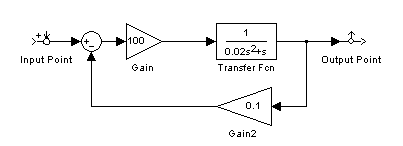
Рис. 5. Структурная схема замкнутой системы рулевого привода с жесткой ОС в среде MathLab 6.5
Приведем ЛАФЧХ замкнутой системы рулевого привода с жесткой обратной связью при значении коэффициента Кос=0.1 (рис. 6):
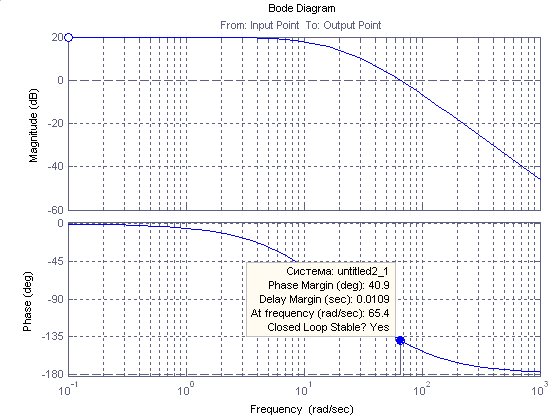
Рис . 6. ЛАФЧХ рулевого привода замкнутой системы
Из графика видно, что при значении коэффициента Кос=0.1 запас по фазе составляет φ=40.9˚. Из этого следует, что данная система устойчива.
График переходного процесса в замкнутом рулевом приводе с жесткой обратной связью имеет вид при значении коэффициентов Ку=100 и Кос=0.1:
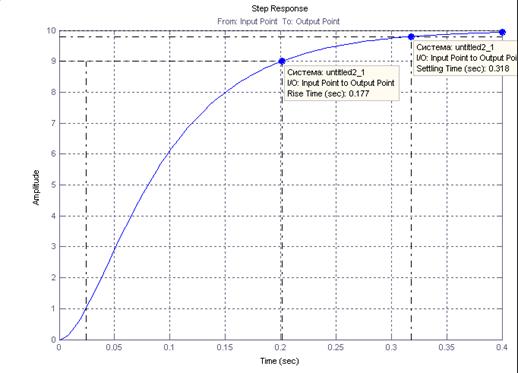
Рис. 7. Переходный процесс в рулевом приводе
Из графика рис. 7 видно, что время переходный процес в замкнутом рулевом приводе с жесткой обратной связью при значении коэффициентов Ку=1, Кос=0.1 имеет следующие параметры:
Время переходного процесса – 0.318 сек.
Время нарастания – 0.177 сек.
Установившееся величина – 10 град.
Составим структурную схему разомкнутой системы управления автопилотом и определим значение коэффициентов Кп, К1 .
Структурная схема разомкнутой системы управления автопилотом имеет вид:
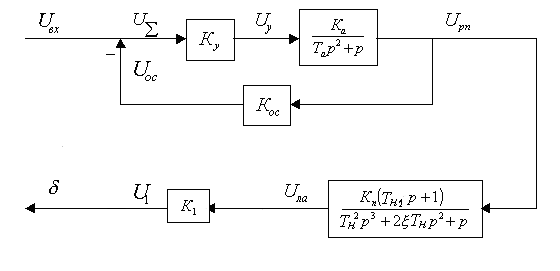
Рис. 8. Структурная схема разомкнутой системы управления автопилотом
Для определения коэффициентов Кп, К1 смоделируем структурную схему разомкнутой системы управления автопилотом в программной среде MathLab 6.5 (рис 9).
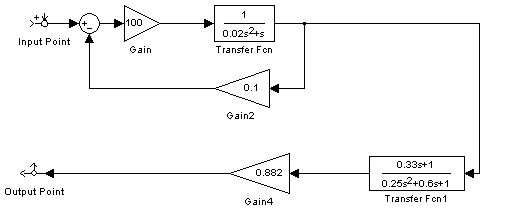
Рис. 9. Структурная схема разомкнутой системы управления автопилотом в среде MathLab 6.5
Приведем ЛАФЧХ разомкнутой системы управления автопилотом:
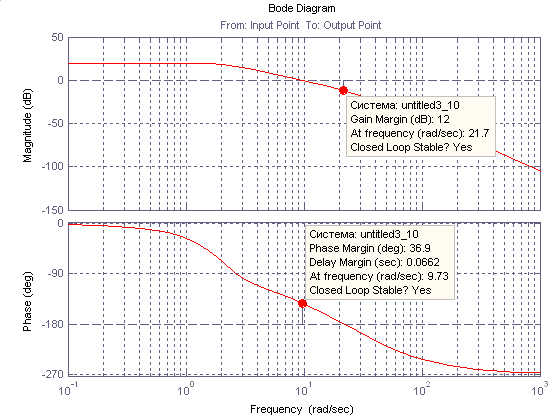
Рис. 10. ЛАФЧХ разомкнутой системы управления автопилотом
Приняв Кп=1 и построив графики ЛАФЧХ разомкнутой системы управления автопилотом (рис. 10), можно сказать, что при значении коэффициента, К1=0.882, запас по фазе составляет Δφ=36,9˚, а запас по амплитуде ΔL =12Дб. Из этого следует, что данная система устойчива.
Составим структурную схему замкнутой системы по отношению к внешнему управляющему моменту и построим ЛАФЧХ и график переходного процесса этой системы.
Структурная схема замкнутой системы по отношению к внешнему управляющему моменту показана на рис 11.
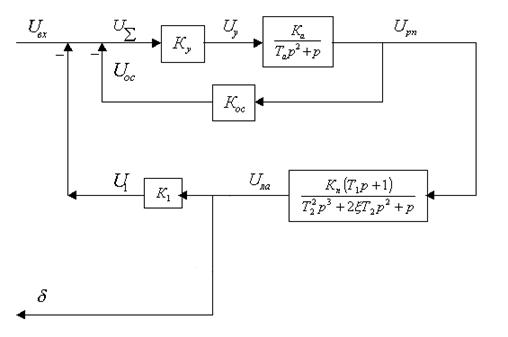
Рис. 11. Структурная схема замкнутой системы управления автопилотом по отношению к внешнему управляющему моменту
Согласно техническому заданию коэффициент по управляющему моменту равен 1. С учетом этого построим ЛАФЧХ и график переходного процесса этой системы. Смоделируем структурную схему замкнутой системы по отношению к внешнему управляющему моменту в программной среде MathLab 6.5 (рис. 12).
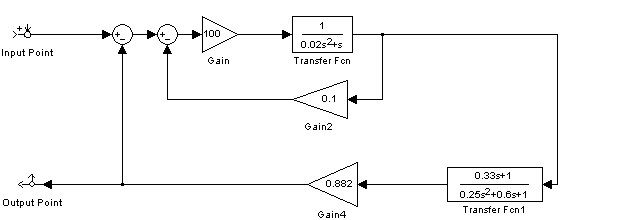
Рис. 12. Структурная схема замкнутой системы управления автопилотом по отношению к внешнему управляющему моменту ОС в среде MathLab 6.5
На рис. 13 показана ЛАФЧХ замкнутой системы по отношению к внешнему управляющему моменту.
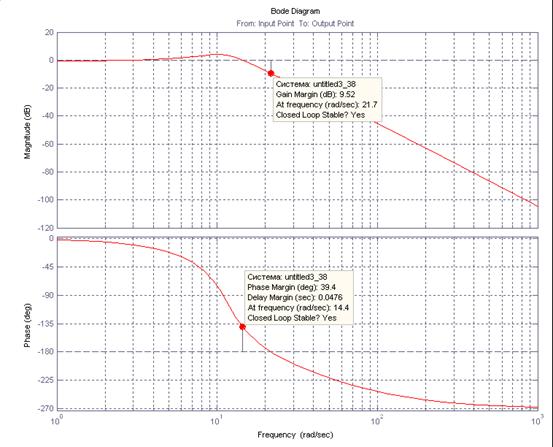
Рис. 13. замкнутой системы по отношению к внешнему управляющему моменту
График переходного процесса замкнутой системы как реакции на единичное управляющее воздействие показан на рис. 14.
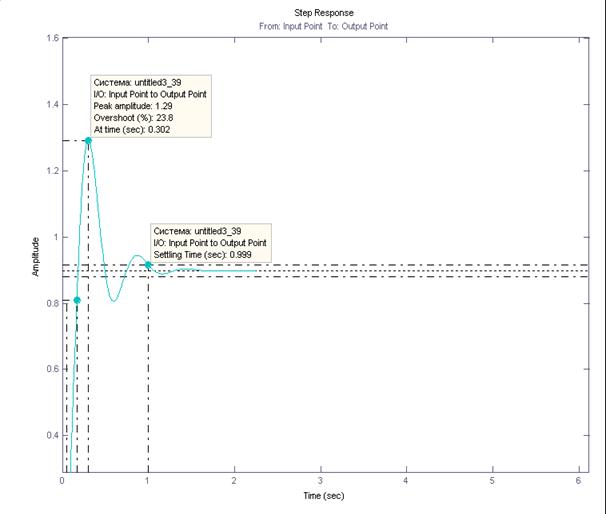
Рис. 14. Переходный процес замкнутой системы на единичное управляющее воздействие
Из графика видно, что время переходного процесса как реакции на единичное управляющее воздействие при соответствующих коэффициентах составляет примерно 1с, Перерегулирование составляет 23,8%. Время нарастания 1 сек. Максимальная величина равна 1,29 град.
Составим структурную схему замкнутой системы по отношению к внешнему возмущающему моменту и построим ЛАФЧХ и график переходного процесса этой системы.
Структурная схема замкнутой системы по отношению к внешнему возмущающему моменту показана на рис 15.
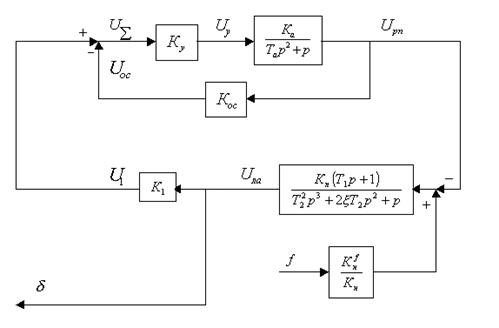
Рис. 15. Структурная схема замкнутой системы по отношению к внешнему возмущающему моменту
Для построения ЛАФЧХ и графика переходного процесса этой системы смоделируем структурную схему замкнутой по отношению к внешнему возмущающему моменту в программной среде MathLab 6.5 (рис. 16).
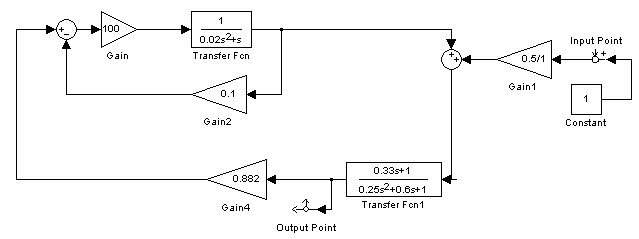
Рис. 16. Замкнутая схема ЛА-АП по отношению к внешнему возмущающему моменту в программной среде MathLab 6.5
Приведем ЛАФЧХ замкнутой системы по отношению к внешнему возмущающему моменту:
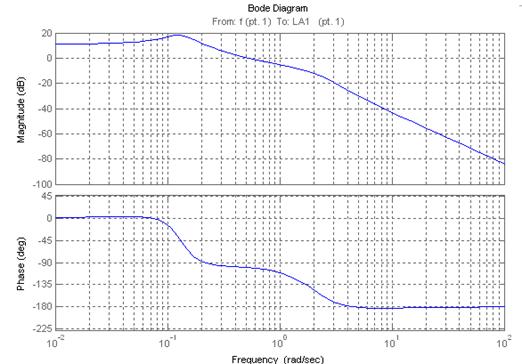
Рис. 17. ЛАФЧХ замкнутой системы ЛА-АП по отношению к внешнему возмущающему моменту
График переходного процесса замкнутой системы как реакции на единичное возмущающее воздействие имеет вид:
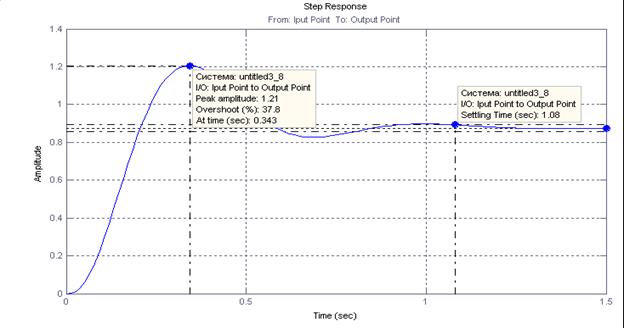
Рис. 18. Переходный процесса замкнутой системы ЛА-АП на единичное возмущающее воздействие
Из графика видно, что переходный процесс замкнутой системы ЛА-АП по возмущающему воздействию при соответствующих выбранных коэффициентах имеет следующие параметры:
Время переходного процесса – 1,08 сек.
Время нарастания – 0,343 сек.
Установившееся величина – 0,875 град.
Вывод
В процессе выполнения работы по синтезу системы угловой стабилизации дозвукового транспортного самолета по заданному курсу была составлена схема сил и моментов, действующих на объект, составлена система уравнений «система угловой стабилизации - транспортный самолет», линеаризована эта система, составлены структурные схемы и получены передаточные функции разомкнутой и замкнутой системы. Методом ЛАФЧХ исследована устойчивость объекта, определено значение общего коэффициента усиления по контуру при котором система имеет необходимые запасы устойчивости по амплитуде и фазе. Построена ЛАФЧХ разомкнутой системы. Построена ЛАФЧХ замкнутой системы по отношению к внешнему возмущающему моменту. Построена ЛАФЧХ замкнутой системы по отношению к управляющему моменту. Построены графики переходных процессов, как реакции на единичное управляющее и возмущающее воздействие.
На основе полученных результатов и анализа построенных ЛАФЧХ и графиков переходных процессов системы угловой стабилизации дозвукового транспортного самолета по заданному курсу можно сказать, что при подобранных значениях коэффициентов система устойчива, имеет хороший запас по фазе и небольшое время переходных процессов.
Список использованной литературы
1. Боднер В.А. Системы управления летательными аппаратами. – М.: Машиностроение, 1973. 504с.
2. Кузовков Н.Т. Системы стабилизации летательных аппаратов.-М.:Высшая школа,1976.304с.
3. Павлов В.А., Понырко Е.А., Хованский Ю.М. Стабилизация летательных аппаратов и автопилоты.-М.: Высш.шк., 1964.483 с.
4. Савельев В.В. Основные элементы системы стабилизации самолет – автопилот.Законы управления автопилотов.- Тул. политехн. ин-т. Тула, 1990. 64с.