Дипломная работа: Компьютерная модель СГ в координатах d, q, 0 в режиме ХХ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ХАРЬКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ»

Кафедра “Электрические станции”

Расчетное задание

по курсу

«Моделирование в энергетике»

Выполнили: студенты гр. Э – 52Б

Мовчан А.Е.

Жирма О.В.

Семенюк Н.

Принял: доцент Пискурев М.Ф.

Харьков – 2006

СОДЕРЖАНИЕ

Задание

1.  Простейшая компьютерная модель турбоагрегата. Исследование динамической устойчивости

1.1  Исследование динамической устойчивости при отключении ЛЭП

а) При отклонении угла  меньше

б) При отклонении угла  больше

в) При выпадении из синхронизма

2.2  Исследование динамической устойчивости при КЗ

1.3.  Исследование динамической устойчивости при КЗ с учетом АПВ

2.  Компьютерная модель СГ в координатах d, q, 0 в режиме ХХ

ЗАДАНИЕ

1.Создать простейшую компьютерную модель турбоагрегата и исследовать на ней динамическую устойчивость при:

1.1. отключении ЛЭП

1.2. КЗ

1.3. КЗ с учетом АПВ

Примечание:

В п. 1.1 получить осциллограммы мощности и угла  при отклонении угла  меньше , больше , при выпадении из синхронизма.

В п. 1.2 и 1.3 получить осциллограммы мощности турбины, синхронной мощности, асинхронной мощности и угла .

2.Создать компьютерную модель СГ в координатах d, q, 0 и получить осциллограммы токов в обмотках статора и ротора и напряжения в обмотках статора в режиме ХХ.

1. Простейшая компьютерная модель турбоагрегата. Исследование динамической устойчивости

Простейшая компьютерная модель турбоагрегата была получена путем реализации системы уравнения (1):

(1)    

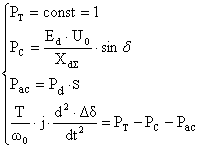
         где  - мощность турбины;

 - синхронная мощность;

 - асинхронная мощность;

 - суммарное сопротивление;

 - потери мощности на демпфирование;

 - скольжение.

Рисунок 1 - Математическая модель турбоагрегата с учетом демпферного момента

Блок 3 моделирует рост суммарного сопротивления ЛЭП при ее отключении, влияя, таким образом, на величину отклонения угла .

I Блоки 1,2,3,8 позволяю получить максимальную электрическую мощность турбоагрегата.

II Блоки 5,7,9,10,12,13,15,16,17,18,19,21,25 моделируют изменение угла  ( угол отклонения величины электрической мощности от мощности турбины).

Блоки группы I, II совместно с блоком 11 моделируют синхронную мощность турбоагрегата (электрическую мощность).

А блоки 22,23 с частью бл. I, II - асинхронную мощность турбоагрегата.

С помощью блока 14 задается постоянная величина мощности турбины.

1.1 Исследуем динамическую устойчивость при отключении ЛЭП:

а) При отклонении угла  меньше

Рисунок 2 – Осциллограммы мощности и угла , при отклонении угла  меньше

Видим, что в нормальном режиме =, угол . При отключении ЛЭП в момент времени 0,2 с суммарное сопротивление увеличивается на 20%. Этот момент соответствует провалу в характеристике мощности турбины.

Затем мощность турбины плавно возрастает до момента, соответствующего максимальному отклонению угла  от величины . Отклонение угла  = 57^о.

При заданных условиях модель динамически устойчива. При t = 5 с система возвращается к нормальному режиму работы.

б) При отклонении угла  больше

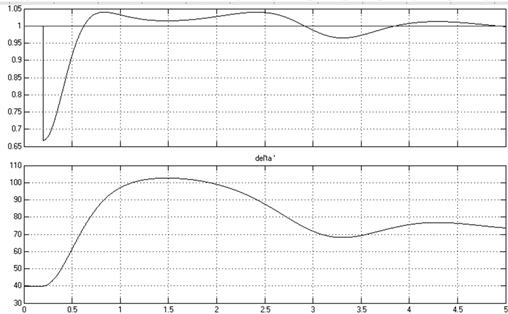
Рисунок 3 – Осциллограммы мощности и угла , при отклонении угла  больше

В нормальном режиме =, угол . При отключении ЛЭП в момент времени 0,2 с суммарное сопротивление увеличивается на 50%. Этот момент соответствует провалу в характеристике мощности турбины.

Затем мощность турбины плавно возрастает до момента, соответствующего углу  = . Максимальное отклонение угла  = 104^о.

При заданных условиях модель еще динамически устойчива. При t = 5 с система возвращается к нормальному режиму работы.

в) При выпадении из синхронизма

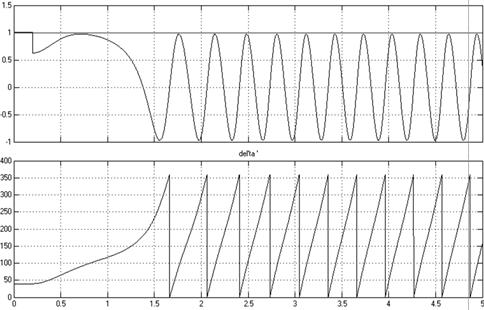
Рисунок 4 – Осциллограммы мощности и угла , при выпадении из синхронизма

В нормальном режиме =, угол . При отключении ЛЭП в момент времени 0,2 с суммарное сопротивление увеличивается на 60%. Этот момент соответствует провалу в характеристике мощности турбины.

Затем мощность турбины плавно возрастает до момента, соответствующего углу  = . Максимальное отклонение угла  = 360^о.

При заданных условиях модель динамически не устойчива.

1.2 Исследование динамической устойчивости при КЗ

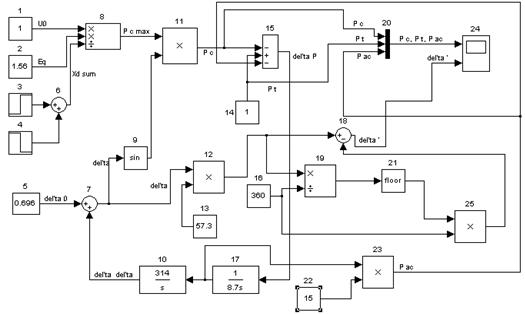
Рисунок 5 - Математическая модель турбоагрегата при КЗ

Блок 3 моделирует увеличение сопротивления ЛЭП при КЗ.

Блок 4 позволяет получить снижение суммарного сопротивления в послеаварийном режиме, вызванное отключением РЗ поврежденного участка.

Блоки 3,4,6 моделируют изменение суммарного сопротивления ЛЭП при КЗ.

Остальные блоки выполняют прежние функции.

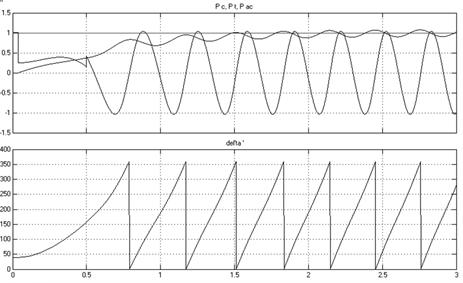
Рисунок 6 – Осциллограммы мощности турбины, синхронной мощности, асинхронной мощности и угла  при КЗ

В нормальном режиме =, , угол . При КЗ в момент времени 0,04 с суммарное сопротивление увеличивается на 400%. Этот момент соответствует провалу в характеристике синхронной мощности турбины. Асинхронная мощность начинает возрастать.

Затем синхронная мощность турбины плавно возрастает до момента, соответствующего углу  = . Максимальное отклонение угла  = 360^о.

В момент времени 0,5 с срабатывает РЗ, отключая поврежденный участок.

Однако в послеаварийном режиме система динамически не устойчива.

1.3 Исследование динамической устойчивости при КЗ с учетом АПВ

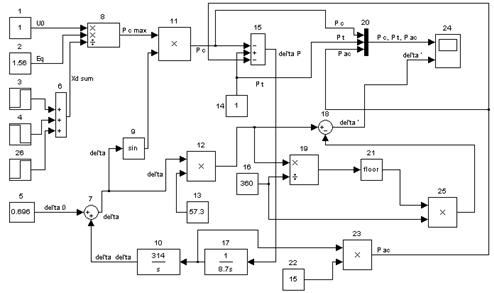
Рисунок 7 - Математическая модель турбоагрегата при КЗ с учетом АПВ

         Блок 3 моделирует увеличение сопротивления ЛЭП при КЗ.

Блок 4 позволяет получить снижение суммарного сопротивления в послеаварийном режиме, вызванное отключением РЗ поврежденного участка.

Блок 26 характеризует снижение суммарного сопротивления, вызванное срабатыванием АПВ.

   Блоки 3,4,6,26 моделируют изменение суммарного сопротивления ЛЭП при КЗ с учетом АПВ.

Остальные блоки выполняют прежние функции.

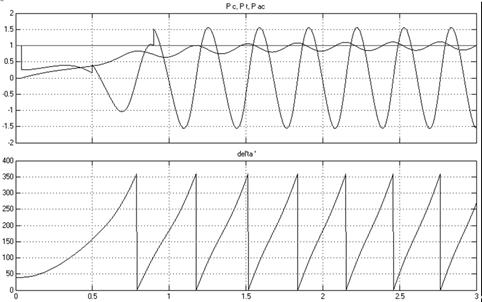
Рисунок 8 – Осциллограммы мощности турбины, синхронной мощности, асинхронной мощности и угла  при КЗ с учетом АПВ

В нормальном режиме =, , угол . При КЗ в момент времени 0,04 с суммарное сопротивление увеличивается на 400%. Этот момент соответствует провалу в характеристике синхронной мощности турбины. Асинхронная мощность начинает возрастать.

Затем синхронная мощность турбины плавно возрастает до момента, соответствующего углу  = . Максимальное отклонение угла  = 360^о.

В момент времени 0,5 с срабатывает РЗ, отключая поврежденный участок.

В момент времени 0,9 с срабатывает АПВ. Но модель остается динамически неустойчивой.

2. Компьютерная модель СГ в координатах d, q, 0

а) Режим ХХ

Компьютерная модель СГ в координатах d, q, 0 была получена путем реализации системы уравнений (2), (3), (4).

(2)    

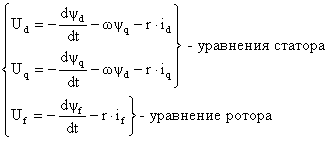
Так как ОВ расположена перпендикулярно относительно обмотки статора по оси q, то никаких потоков в этой обмотке ток, протекающий в ОВ не создает. Следовательно:

(3)    

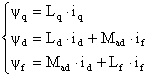
В системе уравнений (3) все коэффициенты постоянные величины: , , , .

Учитывая, что в относительных единицах собственные и взаимные индуктивности равны индуктивным сопротивлениям, то:

,   ,   ,   

Тогда систему уравнений (3) можно записать в таком виде:

(4)    

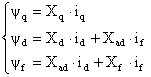
Системы уравнений (2), (3), (4) представляют собой основу математической модели СГ – суперблок Generator.

Реализация суперблока – Generator:

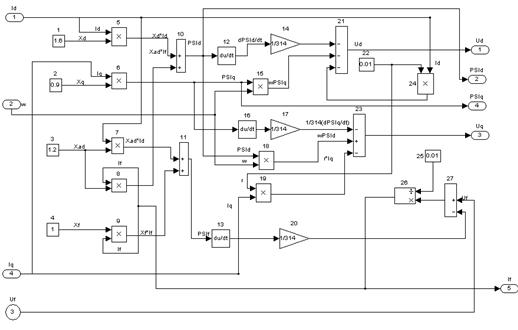
Рисунок 9 – Математическая модель суперблока Generator

I Блоки 1,2,3,4 моделируют сопротивления обмоток статора и ротора.

II Часть бл. I группы совместно с бл.5,8,10 создают потокосцепление обмотки d статора.

III Блоки 2,6 - потокосцепление обмотки q статора.

Часть бл. I группы совместно с бл.7,9,11 – потокосцепление ОВ.

Часть бл. II, III групп совместно с бл.12,14,15,21,22,24 моделируют напряжение обмотки d статора.

Часть бл. II, III групп совместно с бл.16,17,18,19,22,23 моделируют напряжение обмотки q статора.

Часть бл. III группы совместно с бл.13,20,25,26,27 моделируют ток ОВ.

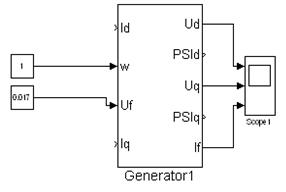
Рисунок 10 – Математическая модель СГ в режиме ХХ

В режиме ХХ токи в обмотках d, q статора равны 0. Напряжение в ОВ зададим равным 0,017 о.е.

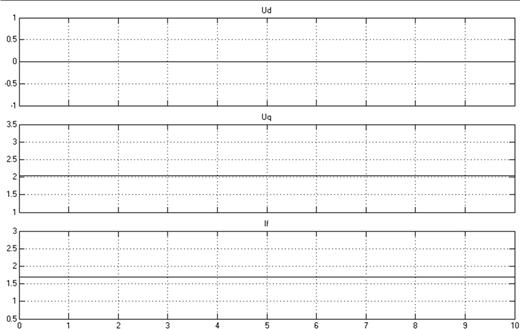
Рисунок 11 – Осциллограммы токов в обмотках статора и ротора и напряжения в обмотках статора в режиме ХХ

         Таким образом, в режиме ХХ напряжение в обмотке d статора отсутствует. А напряжение в обмотке q статора и ток в ОВ постоянны по величине.