Курсовая работа: Проектирование и исследование механизмов поршневого насоса
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Сарапульский политехнический институт (филиал)
Ижевского государственного технического университета
Кафедра ТММСиИ
Дисциплина "Теория механизмов и машин"
Пояснительная записка к курсовому проекту
на тему "Проектирование и исследование механизмов поршневого насоса"
Выполнил: студент группы 512
Коробейников С.Н.
Проверил: Урбанович В.С.
Сарапул 2010 г.
Содержание
Введение
1. Техническое задание
1.1 Краткое описание работы механизма
1.2 Исходные данные
2. Исследование рычажных механизмов
2.1 Метрический синтез механизма
2.2 Структурный анализ механизма
2.3 Кинематическое исследование механизма
3. Проектирование кулачкового механизма
3.1 Построение диаграмм движения толкателя
3.2 Определение минимального радиуса кулачка
3.3 Профилирование кулачка
4. Проектирование зубчатой передачи
4.1 Расчет привода машины
4.2 Расчет внешнего неравносмещенного зацепления с прямыми зубьями
4.3 Качественные показатели зацепления
5. Силовой расчет механизма
6. Расчет маховика
Список литературы
Введение
Развитие современной науки и техники неразрывно связано с созданием новых машин, имеющих целью повышение производительности и облегчение труда людей, а также обеспечение средств исследования законов природы и жизни человека.
Целью создания машины являются увеличение производительности и облегчение физического труда человека путем замены человека машиной. Созданные человеком машины могут управлять производственными и другими процессами по определенным, заранее составленным программам и в некоторых случаях автоматически обеспечивать процесс с оптимальными результатами. [1]
Основной целью курсового проектирования является подготовка к комплексному проектированию определенной машины или механизма. Выполняя курсовой проект, студенты знакомятся с общими принципами исследований кинематических и динамических свойств механизмов методами проектирования их. При курсовом проектировании начинается профессиональное становление будущего инженера – приобретение опыта самостоятельного решения задач, связанных с производственной деятельностью. [2]
1. Техническое задание
1.1 Краткое описание работы механизма
Поршневой насос принадлежит к насосам объемного типа и характеризуется наличием одной или нескольких камер, в которых возвратно-поступательно двигаются поршни, сообщая перекачиваемой жидкости или газу избыточное давление. Изоляция камеры от полостей всасывания и нагнетания в процессе работы осуществляется с помощью впускного и нагнетающего клапанов. Особенностью поршневых насосов является периодический, пульсирующий характер подачи, обуславливающий неравномерность давлений и подачи по времени.
Для поршневых насосов наряду с кривошипно-ползунными механизмами для увеличения производительности применяются кулисные механизмы. В задании поршневой насос состоит из кулисного О2АО3 и шатунного ОВС механизмов (рис. 1а). На ведущий вал О2 крутящий момент передается от вала электродвигателя через привод насоса (рис. 1б). Рабочим ходом является процесс нагнетания. Нагнетание происходит медленнее, чем всасывание рабочего тела, соответственно этому необходимо выбирать направление вращения кривошипа О2А.
Кулачковые механизмы служат для открывания всасывающего и нагнетающего клапанов. В задании необходимо спроектировать кулачковый механизм, показанный на рис. 1в, который служит для нагнетания рабочего тела. Кулачки получают вращение от вала кривошипа через ременную передачу с передаточным отношением 1 (на рис. не показана). Диаграммы ускорений толкателя даются на рис. 1г. [3]
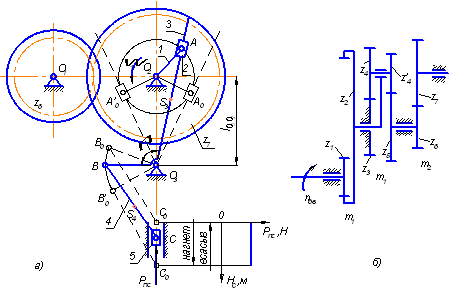
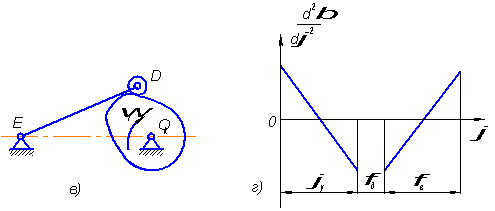
Рис. 1
1.2 Исходные данные
Расстояние между стойками
![]()
ход ползуна H = 0,11 м;
отношения 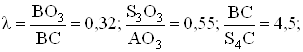
конструктивный угол III звена ν = 80°;
коэффициент изменения скорости хода К = 2;
длина толкателя ℓED = 0,22 м;
полный угол размаха толкателя βmax = 19°;
минимальный угол передачи движения γmin = 45°;
числа зубьев колес Z1 = 21, Z2 = 47, Z6 = 12, Z7 = 18;
модули m1 = 5 мм; m2 = 5,5 мм;
коэффициент неравномерности хода δ = 1/3;
погонный вес q = 120 H/м;
межосевое расстояние ![]()
частота вращения двигателя nдв = 1530 об/мин;
передаточное отношение u1-5 = 15,85;
зацепления Z6 – Z7 неравносмещенное;
сила полезного сопротивления Рпс = 158 Н;
коэффициент смещения Х выбирать из условия обеспечения заданного межосевого расстояния.
Примечания:
1. Фазовые углы кулачкового механизма для нагнетающего клапана φу = 0,5 φрх, φд = 0,2 φрх, φв = 0,6 φхх.
2. Веса звеньев G3 = q∙ℓ3, G4 = q∙ℓ4, G5 = λ∙G4.
3. Моменты инерции
вычисляются по формуле 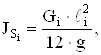 где g – ускорение свободного падения.
где g – ускорение свободного падения.
4. Приведенный момент сил движущих – величина постоянная.
2. Исследование рычажных механизмов
2.1 Метрический синтез механизма
Задачей метрического синтеза является определение размеров механизма, удовлетворяющих некоторым заданным условиям. В нашем случае задан коэффициент изменения скорости хода К.
![]() ,
,
где θ – острый угол между крайними положениями кривошипа.
Отсюда получаем
![]() ;
;
![]() .
.
Определяем недостающие
длины звеньев. Решение задачи проводим аналитически. Рассмотрим два крайних положения
механизма (рис. 2а), для которых ![]() .
.
Прямоугольные треугольники ∆О2А0О3 и ∆О2А'0О3 равны по двум катетам и гипотенузе (катеты О2А0 = О2А'0 = О2А, гипотенуза О2О3 – общая).
![]() ;
;
![]() ;
;
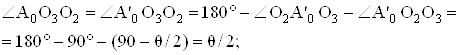
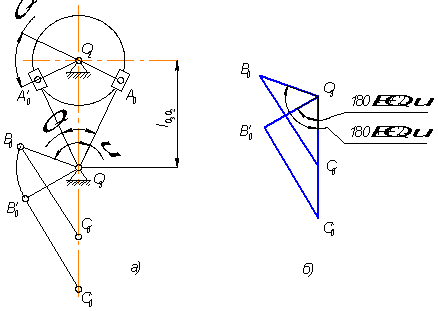
Рис. 2
В нашем случае получаем
![]()
![]()
Определяем длину кривошипа О2А
![]()
Длины звеньев ВО3 и ВС определяем из геометрических соображений по схеме, изображенной на рис. 2б.
![]()
![]()
C0C'0 = H = 0,11 м.
Пусть ВС = х, С0О3 = у; тогда ВО3 = λ·х = 0,32х, С'0О3 = у + 0,11.
Используя теорему косинусов получаем систему уравнений
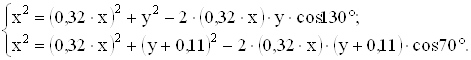
Решая систему, получаем х = 0,367 м, у = 0,280 м.
Отсюда ВС = 0,367 м, ВО3 = 0,32·0,367 = 0,117 м.
Таким образом, определены длины всех звеньев механизма
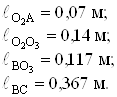
2.2 Структурный анализ механизма
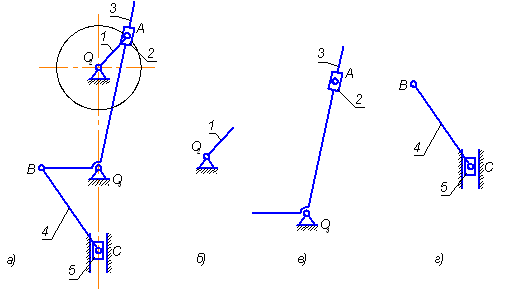
Рис. 3
Количество подвижных звеньев механизма, изображенного на рис. 3а, равно n = 5. Звенья соединяются между собой при помощи пяти вращательных пар (0-1, 1-2, 0-3, 3-4, 4-5) и двух поступательных пар (2-3 и 5-0). Все пары являются парами V класса. Степень подвижности механизма вычисляем по формуле Чебышева
W = 3n – 2p5 – p4 = 3∙5 – 2∙7 = 1.
Ведущее звено – кривошип О2А (рис. 3б). Ведомая часть состоит из двух двухповодковых групп Ассура: звенья 2 и 3 образуют группу II класса, 2-го порядка, 3-го вида (рис. 3в), а звенья 4 и 5 группу II класса, 2-го порядка, 2-го вида (рис. 3г).
Формула построения механизма может быть записана в следующем виде:
![]()
2.3 Кинематическое исследование механизма
Выбираем масштаб μℓ
= 0,00125 ![]() и вычерчиваем
кинематические схемы механизма в 12-ти положениях. Для всех положений механизма
строим планы скоростей и ускорений. Масштаб планов скоростей выбираем μv = 0,01
и вычерчиваем
кинематические схемы механизма в 12-ти положениях. Для всех положений механизма
строим планы скоростей и ускорений. Масштаб планов скоростей выбираем μv = 0,01 ![]() ,
планов ускорений – μа = 0,05
,
планов ускорений – μа = 0,05 ![]() .
Рассмотрим построение плана скоростей на примере 1-го положения механизма (рис
4а).
.
Рассмотрим построение плана скоростей на примере 1-го положения механизма (рис
4а).
Рассчитываем скорость точки А1 кривошипа О2А
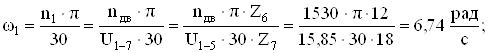
![]()
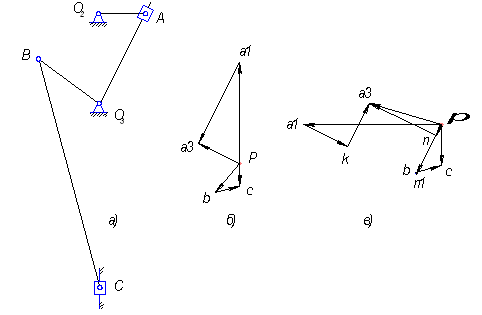
Рис. 4
Из произвольно выбранной
точки Р (рис. 4б), принимаемой за полюс, откладываем отрезок 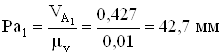 перпендикулярно О2А,
изображающий скорость точки А1 кривошипа. Скорость точки А3
можно рассматривать как геометрическую сумму переносной вращательной скорости
точки А1 кривошипа и относительной поступательной скорости точки
вдоль кулисы:
перпендикулярно О2А,
изображающий скорость точки А1 кривошипа. Скорость точки А3
можно рассматривать как геометрическую сумму переносной вращательной скорости
точки А1 кривошипа и относительной поступательной скорости точки
вдоль кулисы:
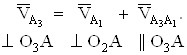
Из точки а1 плана скоростей проводим прямую параллельно О3А, а из полюса Р – прямую, перпендикулярную О3А, и в точке их пересечения ставим букву а3. Отрезок Ра3 изображает в масштабе μv скорость точки А3 кулисы, а отрезок а1а3 – относительную скорость точки А, вдоль кулисы
![]()
![]()
Отрезок Pb на плане скоростей, соответствующий скорости точки В, находится из пропорции
 или
или 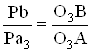
и проводится так, что ![]() .
.
Скорость точки С определяется построением геометрического равенства
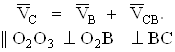
Отрезок Рс изображает в масштабе μv скорость точки С поршня, а отрезок bc – относительную скорость точки С, вокруг точки В
![]()
![]()
Построим для того же положения механизма план ускорений (рис. 4в).
Рассчитываем ускорение точки А1 кривошипа О2А (нормальное ускорение)
![]()
Из произвольно выбранной
точки π, принимаемой за полюс плана ускорений, откладываем отрезок 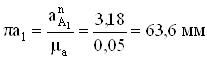 параллельно О2А,
который будет изображать нормальное ускорение кривошипа. Так как точка А3
кулисы участвует в переносном движении вместе с кривошипом и относительном
вдоль кулисы, то абсолютное ускорение тоски А3 будет состоять из
переносного, относительного и кориолисова ускорений
параллельно О2А,
который будет изображать нормальное ускорение кривошипа. Так как точка А3
кулисы участвует в переносном движении вместе с кривошипом и относительном
вдоль кулисы, то абсолютное ускорение тоски А3 будет состоять из
переносного, относительного и кориолисова ускорений
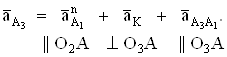
Истинное значение кориолисова ускорения равно
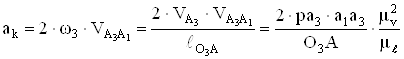 ,
,
а величина отрезка,
изображающего его на плане ускорений 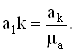
Чтобы определить
направление кориолисова ускорения, нужно вектор относительной скорости ![]() повернуть на 90° в сторону
вращения кулисы, в нашем случае – по часовой стрелке.
повернуть на 90° в сторону
вращения кулисы, в нашем случае – по часовой стрелке.
С другой стороны ускорение точки А3 можно определить из равенства
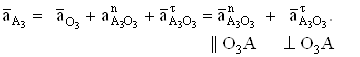
Истинное значение ![]() определяем по формуле
определяем по формуле
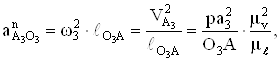
а величину отрезка,
изображающего его на плане ускорений 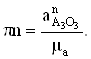
Таким образом, остаются
неизвестными величины двух ускорений ![]() и
и ![]() , которые определяем из
построения плана ускорений. Из точки k плана ускорений проводим прямую параллельно О3А, а из точки n – прямую, перпендикулярную О3А,
и в точке их пересечения ставим букву а3. Отрезок πа3
изображает в масштабе μа ускорение точки А3 кулисы, отрезок
nа3 – ускорение
, которые определяем из
построения плана ускорений. Из точки k плана ускорений проводим прямую параллельно О3А, а из точки n – прямую, перпендикулярную О3А,
и в точке их пересечения ставим букву а3. Отрезок πа3
изображает в масштабе μа ускорение точки А3 кулисы, отрезок
nа3 – ускорение ![]() , а отрезок kа3 – ускорение
, а отрезок kа3 – ускорение ![]()
![]()
![]()
![]()
Отрезок πb на плане скоростей, соответствующий скорости точки В, находится из пропорции
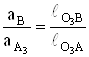 или
или 
и проводится так, что ![]() .
.
Величина ускорения точки С определяется графическим решением векторного уравнения
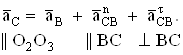
Истинное значение
ускорения ![]() определяем по формуле
определяем по формуле
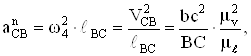
а величину отрезка,
изображающего его на плане ускорений 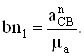
Тангенциальная составляющая
![]() известна только по
направлению (перпендикулярно ВС), а абсолютное ускорение точки С направлено по
вертикали. Величины этих векторов определяются построением
известна только по
направлению (перпендикулярно ВС), а абсолютное ускорение точки С направлено по
вертикали. Величины этих векторов определяются построением
![]()
![]()
Аналогично строим планы скоростей и ускорений для остальных положений механизма. Результаты всех замеров и расчетов с планов скоростей занесены в таблицу 1, с планов ускорений – в таблицу 2.
Таблица 1.
| № |
Замер О3А, мм |
Замер ра3, мм |
Замер а1а3, мм |
Расч. pb, мм |
Замер bc, мм |
Замер pc, мм |
Расч. Vc, м/с |
| 0 | 97,0 | 0,0 | 47,2 | 0,00 | 0,0 | 0 | 0,000 |
| 1 | 125,2 | 21,1 | 42,2 | 15,78 | 11,7 | 10,51 | 0,105 |
| 2 | 148,2 | 35,7 | 30,9 | 22,54 | 11,4 | 16,51 | 0,165 |
| 3 | 162,9 | 44,3 | 16,2 | 25,46 | 9,1 | 21,22 | 0,212 |
| 4 | 168,0 | 47,2 | 0,0 | 26,30 | 4,8 | 24,39 | 0,244 |
| 5 | 162,9 | 44,3 | 16,2 | 25,46 | 0,1 | 25,44 | 0,254 |
| 6 | 148,2 | 35,7 | 30,9 | 22,54 | 3,8 | 23,44 | 0,234 |
| 7 | 125,2 | 21,1 | 42,2 | 15,78 | 4,7 | 16,57 | 0,166 |
| 8 | 97,0 | 0,0 | 47,2 | 0,00 | 0,0 | 0 | 0,000 |
| 9 | 69,4 | 27,9 | 38,1 | 37,60 | 10,3 | 43,11 | 0,431 |
| 10 | 56,0 | 47,2 | 0,0 | 78,89 | 14,4 | 73,16 | 0,732 |
| 11 | 69,4 | 27,9 | 38,1 | 37,60 | 21,7 | 25,5 | 0,255 |
Таблица 2
| № |
Расч. аk, м/с2 |
Расч. a1k, мм |
Расч. м/с2 |
Расч. πn, мм |
Замер πa3, мм |
Расч. πb, мм |
Расч aCB, м/с2 |
Расч bn1, мм |
Замер πc, мм |
Расч. aC, м/с2 |
| 0 | 0,000 | 0,00 | 0,000 | 0,00 | 63,6 | 61,38 | 0,000 | 0,00 | 37,1 | 1,854 |
| 1 | 1,139 | 22,78 | 0,285 | 5,69 | 34,6 | 25,85 | 0,038 | 0,76 | 19,1 | 0,956 |
| 2 | 1,191 | 23,81 | 0,687 | 13,75 | 22,5 | 14,22 | 0,036 | 0,72 | 13,9 | 0,697 |
| 3 | 0,706 | 14,12 | 0,965 | 19,29 | 20,8 | 11,94 | 0,023 | 0,45 | 10,3 | 0,514 |
| 4 | 0,000 | 0,00 | 1,061 | 21,22 | 21,2 | 11,82 | 0,006 | 0,13 | 5,8 | 0,288 |
| 5 | 0,706 | 14,12 | 0,965 | 19,29 | 20,8 | 11,94 | 0,000 | 0,00 | 0,7 | 0,035 |
| 6 | 1,191 | 23,81 | 0,687 | 13,75 | 22,5 | 14,22 | 0,004 | 0,08 | 10,3 | 0,516 |
| 7 | 1,139 | 22,78 | 0,285 | 5,69 | 34,6 | 25,85 | 0,006 | 0,12 | 26,8 | 1,340 |
| 8 | 0,000 | 0,00 | 0,000 | 0,00 | 63,6 | 61,38 | 0,000 | 0,00 | 64,3 | 3,214 |
| 9 | 2,448 | 48,97 | 0,896 | 17,92 | 101,9 | 137,41 | 0,029 | 0,58 | 140,6 | 7,030 |
| 10 | 0,000 | 0,00 | 3,183 | 63,65 | 63,7 | 106,39 | 0,057 | 1,15 | 51,9 | 2,596 |
| 11 | 2,448 | 48,97 | 0,896 | 17,92 | 101,9 | 137,41 | 0,129 | 2,59 | 108,0 | 5,401 |
Замеряем ход поршня во всех положениях механизма, результаты заносим в таблицу 3.
Табл. 3
| № | 0 | 1 | 2 | 3 | 4 | 5 |
|
С0Сi, мм |
0,0 | 3,5 | 11,9 | 23,7 | 38,0 | 53,6 |
|
hc, м |
0,000 | 0,004 | 0,015 | 0,030 | 0,047 | 0,067 |
| № | 6 | 7 | 8 | 9 | 10 | 11 |
|
С0Сi, мм |
68,9 | 81,7 | 87,6 | 77,0 | 38,0 | 6,5 |
|
hc, м |
0,086 | 0,102 | 0,109 | 0,096 | 0,047 | 0,008 |
Строим диаграмму
изменения хода поршня С в масштабах ![]() и
и ![]() . Методом графического
дифференцирования строим диаграммы скорости и ускорения поршня С. Для
дифференцирования берем полюсные расстояния Н1 = 25 мм и Н2 = 16 мм. Рассчитываем масштабы диаграмм скорости и ускорения
. Методом графического
дифференцирования строим диаграммы скорости и ускорения поршня С. Для
дифференцирования берем полюсные расстояния Н1 = 25 мм и Н2 = 16 мм. Рассчитываем масштабы диаграмм скорости и ускорения
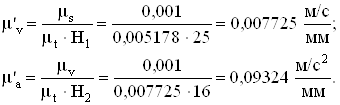
Замеряем значения скоростей и ускорений поршня С по диаграммам и производим сравнение с их величинами, измеренными по планам скоростей и ускорений. Результаты замеров и сравнения приведены в таблице 4.
Табл. 4
| № |
i-i'', мм |
VC (диаг.), м/с |
VC (план), м/с |
Разница VC,% |
i-i''', мм |
aC (диаг.), м/с2 |
aC (план), м/с2 |
Разница aC ,% |
| 0 | 0,00 | 0,000 | 0,000 | 0,0 | 19,29 | 1,799 | 1,854 | 3,0 |
| 1 | 13,28 | 0,103 | 0,105 | 2,3 | 11,12 | 1,037 | 0,956 | 8,5 |
| 2 | 21,88 | 0,169 | 0,165 | 2,4 | 6,85 | 0,639 | 0,697 | 8,3 |
| 3 | 27,84 | 0,215 | 0,212 | 1,4 | 6,01 | 0,560 | 0,514 | 9,0 |
| 4 | 31,93 | 0,247 | 0,244 | 1,1 | 2,90 | 0,270 | 0,288 | 6,1 |
| 5 | 33,27 | 0,257 | 0,254 | 1,2 | 0,00 | 0,000 | 0,000 | 0,0 |
| 6 | 31,13 | 0,240 | 0,234 | 2,8 | 5,21 | 0,486 | 0,516 | 5,9 |
| 7 | 22,37 | 0,173 | 0,166 | 4,1 | 15,63 | 1,457 | 1,340 | 8,8 |
| 8 | 0,00 | 0,000 | 0,000 | 0,0 | 34,82 | 3,247 | 3,214 | 1,0 |
| 9 | 59,56 | 0,460 | 0,431 | 6,8 | 76,20 | 7,105 | 7,030 | 1,1 |
| 10 | 100,62 | 0,777 | 0,732 | 6,2 | 25,89 | 2,414 | 2,596 | 7,0 |
| 11 | 33,17 | 0,256 | 0,255 | 0,5 | 57,98 | 5,406 | 5,401 | 0,1 |
Построение планов скоростей и ускорений и диаграмм характеристик движения рабочего органа машины построены с достаточной точностью, так как отклонения между значениями величин с планов и с диаграмм не превосходят 10%.
3. Проектирование кулачкового механизма
3.1 Построение диаграмм движения толкателя
Дано:
длина толкателя ℓED = 0,22 м;
полный угол размаха толкателя βmax = 19°;
минимальный угол передачи движения γmin = 45°;
вид диаграммы ускорения толкателя – см. рис. 1в.
Определяем фазовые углы кулачкового механизма по рекомендациям из технического задания, учитывая, что
φрх = 240° и φхх = 120°
φу = 0,5 φрх = 0,5∙240 = 120°,
φд = 0,2 φрх = 0,2∙240 =48°,
φв = 0,6 φхх = 0,6∙120 =72°.
Строим график углового ускорения ведомого звена кулачкового механизма (коромысла) в произвольном масштабе με и масштабе
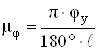 ,
,
где φу – угол удаления, в °;
ℓ – отрезок оси абсцисс, изображающий угол φу, в мм.
![]() .
.
Учитываем то, что отношение ординат, соответствующих максимальным значениям ускорений при удалении и возвращении, связано зависимостью
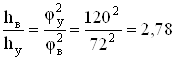 .
.
Методом графического интегрирования строим диаграммы угловой скорости и углового перемещения толкателя. Для интегрирования выбираем полюсные расстояния Н1 = 10 мм и Н2 = 20 мм. Получаем максимальное значение ординаты диаграммы перемещения толкателя равно Smax = 108,3 мм.
Определяем масштабы диаграмм, начиная с масштаба μs.
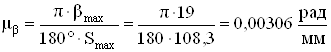 ,
,
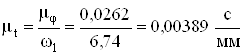 ,
,
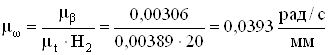 ,
,
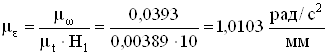 ,
,
![]() ,
,
![]() ,
,
![]() .
.
Замеряем значения β и V с диаграмм, результаты заносим в таблицу 5.
Табл. 5
| № |
ℓβ, мм |
β, градус |
ℓv, мм |
V, м/с | V/ω, м |
ℓV/ω, мм |
γ, градус | |
| 0 | 0,00 | 0,00 | 0,00 | 0,000 | 0,000 | 0,00 | 75,94 | |
| 1 | 8,24 | 1,45 | 22,22 | 0,192 | 0,029 | 14,25 | 50,03 | |
| 2 | 28,23 | 4,95 | 35,56 | 0,307 | 0,046 | 22,81 | 45,00 | |
| 3 | 54,13 | 9,50 | 40,00 | 0,346 | 0,051 | 25,66 | 46,87 | |
| 4 | 80,03 | 14,04 | 35,56 | 0,307 | 0,046 | 22,81 | 51,69 | |
| 5 | 100,00 | 17,54 | 22,22 | 0,192 | 0,029 | 14,25 | 59,22 | |
| 6 | 108,3 | 19,00 | 0,00 | 0,000 | 0,000 | 0,00 | 71,62 | |
| 7 | 108,3 | 19,00 | 0,00 | 0,000 | 0,000 | 0,00 | 71,62 | |
| 8 | 100,00 | 17,54 | 37,07 | 0,321 | 0,048 | 23,78 | 82,26 | |
| 9 | 80,03 | 14,04 | 59,31 | 0,513 | 0,076 | 38,04 | 62,24 | |
| 10 | 54,13 | 9,50 | 66,72 | 0,577 | 0,086 | 42,79 | 49,84 | |
| 11 | 28,23 | 4,95 | 59,31 | 0,513 | 0,076 | 38,04 | 45,00 | |
| 12 | 8,24 | 1,45 | 37,07 | 0,321 | 0,048 | 23,78 | 53,53 | |
| 13 | 0,00 | 0,00 | 0,00 | 0,000 | 0,000 | 0,00 | 0,00 | 75,94 |
3.2 Определение минимального радиуса кулачка
Для проектирования кулачкового
механизма очень важно правильно выбрать минимальный радиус кулачка ![]() . Определение
. Определение ![]() является одной из задач динамического
синтеза кулачковых механизмов. Проще всего эта задача решается графическим
способом. Изображаем коромысло ED в
двух крайних положениях в масштабе
является одной из задач динамического
синтеза кулачковых механизмов. Проще всего эта задача решается графическим
способом. Изображаем коромысло ED в
двух крайних положениях в масштабе ![]() .
Траекторию движения точки D
коромысла делим в соответствии с диаграммой углового перемещения, получаем
точки D0 – D13, соединив которые с точкой Е,
получаем мгновенные положения толкателя. В каждом положении коромысла
откладываем отрезок ℓV/ω (табл. 5) –
получаем точки 1 – 13. Из получившихся точек под углом γmin = 45° к данному положению коромысла
проводим прямые – получаем точку центра вращения кулачка. Расстояние ОD0 будет равно
.
Траекторию движения точки D
коромысла делим в соответствии с диаграммой углового перемещения, получаем
точки D0 – D13, соединив которые с точкой Е,
получаем мгновенные положения толкателя. В каждом положении коромысла
откладываем отрезок ℓV/ω (табл. 5) –
получаем точки 1 – 13. Из получившихся точек под углом γmin = 45° к данному положению коромысла
проводим прямые – получаем точку центра вращения кулачка. Расстояние ОD0 будет равно ![]() .
.
![]() .
.
Точку центра кулачка
соединяем отрезком с каждой из точек 1 – 13 и измеряем углы, образуемые этими
отрезками и соответствующими положениями коромысла – получаем значения угла
передачи движения в определенных положениях кулачкового механизма (табл. 5).
Строим график изменения угла передачи движения в масштабах μγ
= 1°/мм и ![]() .
.
3.3 Профилирование кулачка
Из центра О проводим
окружность радиусом ![]() . На дуге,
описанной из центра Е радиусом ℓED, проводим разметку пути точки D согласно графику
. На дуге,
описанной из центра Е радиусом ℓED, проводим разметку пути точки D согласно графику
β = β(t).
Обращаем движение. Из центра О радиусом ОЕ описываем дугу и в направлении обратном вращению кулачка откладываем от радиуса ОЕ углы φу, φд, φв, которые делим затем на равные части соответственно промежуткам графика β = β(t); обозначаем полученные точки деления 1' – 13'.
Из этих точек проводим дуги радиусом ℓED, а из центра О засекаем их радиусами ОD1 – OD13. Соединяя точки пересечения построенных дуг плавной кривой, получаем теоретический профиль кулачка.
Радиус ролика выбираем из следующих соображений:
rp ≤ 0,4∙![]() или rp ≤ 0,8∙ρmin,
или rp ≤ 0,8∙ρmin,
где ρmin – минимальный радиус кривизны профиля кулачка.
Определяем графически ρmin = 6,64 мм.
0,4∙![]() = 0,4∙44,28 = 17,71 мм,
= 0,4∙44,28 = 17,71 мм,
0,8∙ρmin = 0,8∙6,64 = 5,32 мм.
Из двух значений
принимаем наименьшее, тогда rp = 5,32 мм (в масштабе чертежа μℓ получаем ![]() мм).
Внутренняя огибающая окружностей, описанных радиусом ролика, центр которого
перемещается по теоретическому профилю, образует искомый рабочий профиль
кулачка.
мм).
Внутренняя огибающая окружностей, описанных радиусом ролика, центр которого
перемещается по теоретическому профилю, образует искомый рабочий профиль
кулачка.
4. Проектирование зубчатой передачи
4.1 Расчет привода машины
Дано:
числа зубьев колес Z1 = 21, Z2 = 47, Z6 = 12, Z7 = 18;
модули m1 = 5 мм; m2 = 5,5 мм;
передаточное отношение U1-5 = 15,85;
частота вращения двигателя nдв = 1530 об/мин;
межосевое расстояние ![]()
зацепления Z6 – Z7 неравносмещенное, коэффициент смещения Х выбирать из условия обеспечения заданного межосевого расстояния;
кинематическая схема привода представлена на рис. 5.
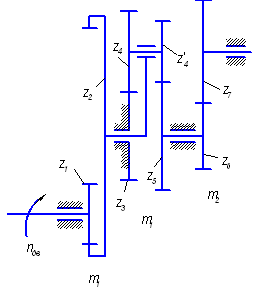
Рис. 5
Привод машины состоит из
двух пар зубчатых колес с неподвижными осями и планетарной передачи. Определим
передаточное отношение планетарной передачи 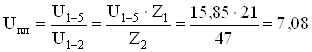 .
.
Передаточное отношение от водила к 5-му колесу определяется по формуле
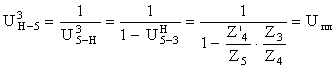 ,
,
![]() .
.
Методом подбора разбиваем передаточное число следующим образом
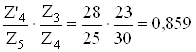 , Z3 = 23, Z4 = 30, Z'4
= 23, Z5 = 25.
, Z3 = 23, Z4 = 30, Z'4
= 23, Z5 = 25.
4.2 Расчет внешнего неравносмещенного зацепления с прямыми зубьями
Заданы следующие величины:
модуль зацепления m = 5,5 мм.
угол исходного профиля рейки α = 20º;
коэффициент высоты
головки зуба исходного профиля ![]() ;
;
коэффициент радиального
зазора ![]() ;
;
число зубьев шестерни Z6 = 12;
число зубьев колеса Z7 = 18;
межосевое расстояние aw = 85 мм.
Порядок проведения расчета. Делительные диаметры
![]() ;
;
![]() .
.
Основные диаметры
![]() ;
;
![]() .
.
Окружные делительный и основной шаги
![]() ;
;
![]() .
.
Угол зацепления
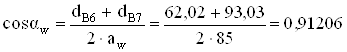 ;
;
αw = arccos 0,91206 = 24,208° = 24° 12' 30".
Суммарный коэффициент смещения
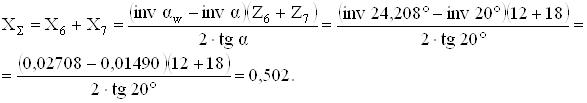
По блокирующему контуру [4, фиг. 32] разбиваем ХΣ на слагаемые и определяем Х6 = 0,383 и Х7 = 0,12.
Начальные диаметры
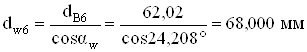 ;
;
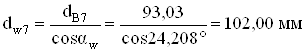 .
.
Диаметры впадин зубьев
![]() ;
;
![]() .
.
Диаметры вершин зубьев
![]() ;
;
![]() .
.
Окружные толщины зубьев (о делительной окружности)
![]() ;
;
![]() .
.
Проверка на заострение
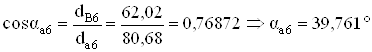 ;
;
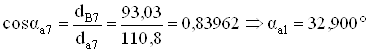 ;
;
![]() ;
;
![]() ;
;
Sa = 0,2 ∙ 5,5 = 1,1 мм, выполняется условие Sa6, Sa7 ≥ Sa, значит, заострения зубьев нет. По данным проведенных расчетов вычерчиваем зубчатое зацепление в масштабе μ'ℓ = 0,00025 м/мм.
4.3 Качественные показатели зацепления
1. Коэффициент перекрытия
![]() ;
;
![]() ;
;
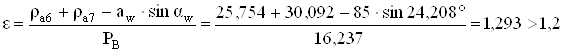 .
.
2. Коэффициент удельного скольжения
![]() ;
;
![]() ;
;
![]() ,
, ![]() ;
;
![]() ;
; ![]() .
.
3. Коэффициент удельного давления в полюсе
![]() ;
;
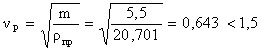 .
.
Все показатели находятся в допускаемых пределах.
5. Силовой расчет механизма
Данные для расчета:
отношения 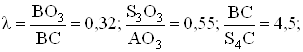
погонный вес q = 120 H/м;
сила полезного сопротивления Рпс = 158 Н;
Требуется определить давление в кинематических парах, уравновешивающую силу (момент).
Выбираем положение во
время рабочего хода машины, в котором имеет место наибольшее ускорение рабочего
органа – 7-е положение. Строим планы положения механизма в масштабе μℓ
= 0,00175 ![]() , скоростей – μv = 0,01
, скоростей – μv = 0,01 ![]() ,
ускорений – μа = 0,05
,
ускорений – μа = 0,05 ![]() .
.
Определяем положение центров тяжестей звеньев на планах
а) механизма
![]() ;
;
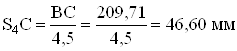 ;
;
б) скоростей
![]() ;
;
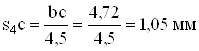 ;
;
в) ускорений
![]() ;
;
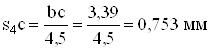 .
.
Определяем веса звеньев
G3 = q∙ℓ3 = 120∙0,157 = 18,84 H;
G4 = q∙ℓ4 = 120∙0,367 = 44,04 H;
G5 = λ∙G4 = 0,32∙44,04 = 14,09 H.
Определяем силы инерции
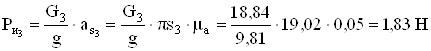 ;
;
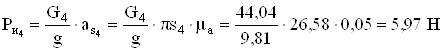 ;
;
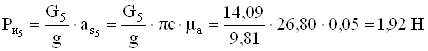 .
.
Определяем моменты инерции звеньев
 ;
;
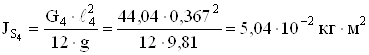 ;
;
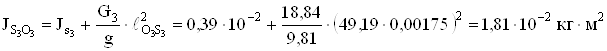 .
.
Определяем угловые ускорения и моменты сил инерции звеньев
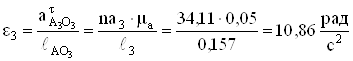 ;
;
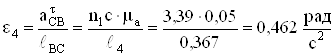 ;
;
![]() ;
;
![]() .
.
Определяем плечи сил инерции
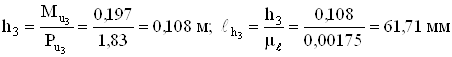 ;
;
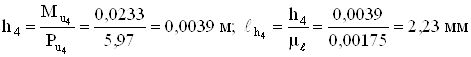 .
.
Силовой расчет механизма
начинаем с последней присоединенной группы Ассура – ![]() .
На эту группу действует сила полезного сопротивления Рпс, сила
тяжести поршня G5, сила инерции поршня Ри5,
реакция стойки R05, вес шатуна G4, сила инерции шатуна Ри4, реакция отброшенного
звена R34 (
.
На эту группу действует сила полезного сопротивления Рпс, сила
тяжести поршня G5, сила инерции поршня Ри5,
реакция стойки R05, вес шатуна G4, сила инерции шатуна Ри4, реакция отброшенного
звена R34 (![]() и
и
![]() ).
).
Уравнение равновесия группы под действием этих сил имеет следующий вид
![]() .
.
Величину и направление
силы ![]() можно найти из уравнения
моментов всех сил, действующих на звено 4, относительно точки С
можно найти из уравнения
моментов всех сил, действующих на звено 4, относительно точки С
![]() ;
;
![]()
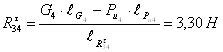 .
.
Строим план сил в
масштабе μР = 1 Н/мм и замеряем недостающие силы R05 = 33,15 Н; ![]() = 97,73 Н;
= 97,73 Н; ![]() = 97,67 Н.
= 97,67 Н.
Переходим к следующей
группе Ассура ![]() . На нее
действуют сила реакции предыдущей группы R43, сила инерции коромысла Ри3, вес коромысла G3, реакция стойки R03, реакция отброшенного звена R12.
. На нее
действуют сила реакции предыдущей группы R43, сила инерции коромысла Ри3, вес коромысла G3, реакция стойки R03, реакция отброшенного звена R12.
Уравнение равновесия группы под действием этих сил имеет следующий вид
![]() .
.
Величину и направление
силы ![]() можно найти из уравнения
моментов всех сил, действующих на звено 3, относительно точки О3
можно найти из уравнения
моментов всех сил, действующих на звено 3, относительно точки О3
![]() ;
;
![]() .
.
 .
.
Строим план сил и замеряем недостающие силы R03 = 103,27 Н.
Рассмотрим ведущее звено – кривошип. На него действует сила реакции предыдущей группы R21, реакция стойки R01, уравновешивающая сила Рур.
Уравнение равновесия группы под действием этих сил имеет следующий вид
![]() .
.
Величину и направление силы Рур можно найти из уравнения моментов всех сил, действующих на звено 1, относительно точки О2
![]() ;
;
![]() .
.
 .
.
Строим план сил и определяем недостающие силы R01 = 59,29 Н.
Определим уравновешивающую силу с помощью рычага Жуковского.
Строим план скоростей и в соответствующих точках прикладываем внешние силы и силы инерции, поворачивая их на 90° по часовой стрелке. Составляем уравнение равновесия рычага
![]() ;
;
![]() 0.
0.
Отсюда получаем
![]()
6. Расчет маховика
Для каждого положения механизма определяем приведенный к главному валу момент сил сопротивления, определяемый из условия равенства мощности приведенного момента и мощности силы полезного сопротивления
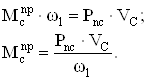
Для каждого положения механизма определяем приведенный к главному валу момент инерции, определяемый из условия равенства кинетических энергий
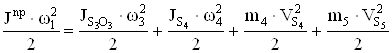 ;
;
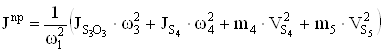 .
.
Результаты всех расчетов и замеров сведены в таблицу 6.
Табл. 6
| № |
Mпр, Н∙м |
Jпр, кг∙м2 |
ℓΔЕ, мм |
|
JMX + Jnp, кг∙м2 |
ω1, рад |
| 0 | 0,00 | 0,0000 | 0,00 | 6,55 | 0,2214 | 7,69 |
| 1 | 2,46 | 0,0025 | 6,83 | 6,91 | 0,2239 | 7,86 |
| 2 | 3,87 | 0,0064 | 4,75 | 6,80 | 0,2278 | 7,73 |
| 3 | 4,97 | 0,0104 | -3,52 | 6,37 | 0,2318 | 7,41 |
| 4 | 5,72 | 0,0128 | -16,47 | 5,69 | 0,2342 | 6,97 |
| 5 | 5,96 | 0,0126 | -31,96 | 4,87 | 0,2340 | 6,45 |
| 6 | 5,49 | 0,0095 | -47,00 | 4,08 | 0,2309 | 5,95 |
| 7 | 3,88 | 0,0042 | -57,42 | 3,54 | 0,2256 | 5,60 |
| 8 | 0,00 | 0,0000 | -56,23 | 3,60 | 0,2214 | 5,70 |
| 9 | 0,0245 | -42,17 | 4,34 | 0,2459 | 5,94 | |
| 10 | 0,0732 | -28,11 | 5,08 | 0,2946 | 5,87 | |
| 11 | 0,0104 | -14,06 | 5,81 | 0,2318 | 7,08 |
Строим графики Мпр и Jпр в масштабах μφ = 0,0175 рад/мм, μМ = 0,1 Н∙м/мм и μJ = 0,0008 кг∙м2/мм. Графическим интегрированием графика моментов получаем график приведенных работ (полюсное расстояние H = 30). Далее получаем график ΔЕпр(φ), его масштаб будет равен
![]() .
.
Определяем минимальную и максимальную угловую скорость кривошипа
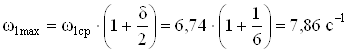 ;
;
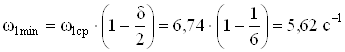 .
.
Находим углы касательных к диаграмме
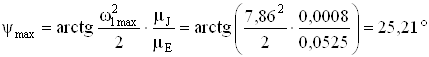 ;
;
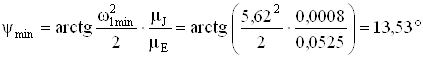 .
.
Графически исключаем параметр φ и строим график ΔЕпр(J). Проводим к нему касательные под углами ψmax и ψmin. Точка пересечения касательных – новое начало координат графика.
Замеряем
JMX = 276,75∙0,0008 = 0,2214 кг∙м2;
Епр0 = 124,79∙0б0525 = 6,552 Дж.
Принимаем диаметр маховика dMX = 0,5 м, тогда вес обода будет
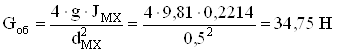 ;
;
вес маховика с ободом и спицами равен GMX = 1,3∙Gоб = 1,3∙34,75 = 45,18 Н.
Угловую скорость
кривошипа в каждом положении механизма находим по формуле 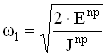 , результаты расчета
занесены в таблицу 6. График изменения угловой скорости строим в масштабе 0,1
(рад/с)/мм.
, результаты расчета
занесены в таблицу 6. График изменения угловой скорости строим в масштабе 0,1
(рад/с)/мм.
Определяем мощность двигателя по формуле
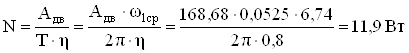 .
.
Список литературы
1. Артоболевский И.И. Теория механизмов. – М., Издательство "Наука", 1965. – 776 с., ил.
2. Аллилуева Л.А., Езерская С.В., Кунивер А.С., Янченко Т.А. Методические указания к выполнению курсового проекта по теории механизмов и машин. 3-е изд., стереотипное. – Ижевск, Издательство ИжГТУ, 2004. – 72 с., ил.
3. Газизова З.С., Русаева В.А., Янченко Т.А. Задания для курсового проекта по теории механизмов и машин. Насосы и двигатели внутреннего сгорания. – Ижевск, Издательство ИжГТУ, 1980. – 32 с., ил.
4. Болотовская Т.П., Болотовский И.А., Смирнов В.Э. Справочник по корригированию зубчатых колес. – М.: Машгиз, 1962. – 216 с., ил.
5. Кореняко А.С. и др. Курсовое проектировании по теории механизмов и машин. – Киев, Издательство "Вища школа", 1970. – 332 с., ил.