Курсовая работа: Рішення лінійних рівнянь першого порядку

Курсова робота: Рішення лінійних рівнянь першого порядку

Зміст

1. Введення

2. Постановка задачі

3. Знаходження власних чисел і побудова ФСР

4. Побудова фундаментальної матриці рішень методом Ейлера

5. Знаходження наближеного рішення у вигляді матричного ряду

6. Побудова загального рішення матричним методом

7. Задача Коші для матричного методу

8. Рішення неоднорідної системи

Графіки

Висновок

Література

Розглянемо систему лінійних рівнянь першого порядку, записану в нормальній формі:

 (1)

де коефіцієнти а_ij, i=1,2,….,n, до=1,2,.,n, є постійними величинами;

y_i=y_i (t), i=1,2,…,n-невідомі функції змінної t.

Якщо всі b_i (t) (i=1,2,…,n) покласти рівним нулю (b_i (t) =0), те вийде однорідна система, що відповідає неоднорідній системі (1).

Позначаючи матрицю системи через А (х), а вектор  через  тоді систему (1) можемо переписати в матричній формі

 (1а)

Якщо , то одержуємо відповідну систему однорідних рівнянь

. (2)

Усяка сукупність n функцій

певних і безупинно в інтервалі (a; b), називається рішенням системи (1) у цьому інтервалі, якщо вона обертає всі рівняння системи (1) у тотожності:

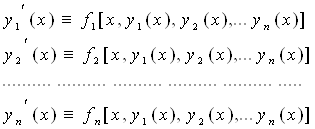
справедливі при всіх значеннях x з інтервалу (a, b). Загальне рішення неоднорідної системи являє собою суму загального рішення відповідної однорідної системи й приватного рішення неоднорідної.

Ціль роботи: дослідження методів рішення системи диференціальних рівнянь із постійною матрицею:

; ;

Завдання.

1.  Знайти власні числа й побудувати фундаментальну систему рішень (ФСР).

2.  Побудувати фундаментальну матрицю методом Ейлера.

3.  Знайти наближене рішення у вигляді матричного ряду.

4.  Побудувати загальне рішення матричним методом. Досліджувати залежність Жорданової форми матриці А від її власних чисел.

5.  Вирішити задачу Коші.

Початкові умови:

Вектор початкових умов: [1, 2, 3, 4]

t = 0

Однорідною лінійною системою диференціальних рівнянь називається система рівнянь виду:

 (3)

Якщо в матриці системи  всі =const, то дана система називається системою з постійними коефіцієнтами або з постійною матрицею.

Фундаментальною системою рішень однорідної лінійної системи рівнянь називається базис лінійного простору рішень (, тобто n лінійно незалежних рішень цієї системи.

Для побудови фундаментальної системи рішень диференціального рівняння необхідно знайти власні числа характеристичного полінома, тому що залежно від їхнього виду (характеристичні числа можуть бути дійсними різними, кратними, комплексними) будується фундаментальна система рішень. Для того щоб ця система n лінійних однорідних рівнянь із n невідомими мала нетривіальне рішення, необхідно й досить, щоб визначник системи (вронскиан) дорівнює нулю:

 (4)

Із цього рівняння ступеня n визначається значення k, при яких система має нетривіальні рішення. Рівняння (4) називається характеристичним.

Запишемо характеристичний поліном, для цього скористаємося функцією CHARPOLY

Для знаходження власних чисел скористаємося функцією SOLVE (U, (), що повертає характеристичні числа матриці А в вектор (. Одержимо:

Вийшло два дійсно корені  й два комплексно-комплексно-сполучених корені . Отже, вектора, що утворять фундаментальну матрицю, для даного типу корінь будуть перебувати окремо для  й окремо для . Запишемо ФСР для даних для отриманих характеристичних чисел:

Матрицю y (x (, стовпцями якої є рішення, що утворять фундаментальну систему, називають фундаментальною матрицею.

І загальне рішення системи буде виглядати в такий спосіб:

Знайдемо рішення даної системи за допомогою методу Ейлера.

Метод Ейлера полягає в наступному.

Рішення системи (1) перебуває у вигляді:

 (5)

Функція (5) є рішенням системи (1), якщо  - власне значення матриці А, а а - власний вектор цієї матриці, що відповідає числу .

Якщо власні значення ₁, ₂, …,_n матриці А попарно різні й a₁, a₂, …, a_n відповідні власні вектори цієї матриці, то загальне рішення системи рівнянь (1) визначається формулою:

де З₁, З₂, …, С_n - довільні числа.

Для випадку кратних корінь рішення системи приймає вид

 (6)

де Pi (x) - поліноми ступеня не вище, ніж (до-1), що мають у сукупності до довільних коефіцієнтів. Так що серед коефіцієнтів цих поліномів до коефіцієнтів є довільними, а залишилися до·n-k выражаются через них. Якщо для кратного власного значення  матриці А є стільки лінійно незалежних власних векторів , яка його кратність, то йому відповідає k незалежних рішень вихідної системи:

Якщо для власного значення  кратності k є тільки m (m<k) лінійно незалежних власних векторів, то рішення, що відповідають , можна шукати у вигляді добутку векторного багаточлена ступеня k - m на , тобто у вигляді:

Щоб знайти вектори , треба підставити вираження (4) у систему (3). Дорівнявши коефіцієнти подібних членів у лівій і правій частинах системи, одержимо рівняння для знаходження векторів .

Для даного завдання минулого знайдені наступні власні значення:

.

Побудували фундаментальну систему рішень:

Знайдемо 1 рядок фундаментальної матриці рішень для характеристичного числа . Запишемо третій рядок рішень у загальному виді:

Де аij знайдемо по вираженню:

 або

Отримана матриця:

Вирішуємо систему:

Отриманих корінь:

Тоді перший рядок буде мати вигляд:

Аналогічно знайдемо другий рядок фундаментальної матриці рішень для першого характеристичного числа - 1. Отримані значення:

Тоді другий рядок буде мати вигляд:

Знайдемо третю й четверту рядки фундаментальної матриці рішень для першого характеристичного числа . Сполучений корінь не породжує нових речовинних лінійно незалежних приватних рішень.

Отримані значення:

Відокремлюючи в ньому речовинні й мнимі частини, одержимо два речовинних рішення, які й становлять першу й другу рядки фундаментальної матриці рішень

Аналогічно інші 3:

Запишемо знайдену фундаментальну матрицю рішень:

Помножимо транспоновану фундаментальну матрицю рішень на вектор вільних коефіцієнтів і одержимо вектор загального рішення вихідної системи:

Зробимо перевірку знайденого рішення в такий спосіб:

Одержуємо нульову матрицю-стовпець:

що показує, що загальне рішення знайдене вірно.

Дамо визначення матричному ряду й експонентній функції матриці.

Матричні ряди. Розглянемо нескінченну послідовність матриць , ,. Будемо говорити, що послідовність матриць сходиться до матриці А: , якщо  при . З визначення норми треба, що збіжність матриць еквівалентна заелементної збіжності. Матричним рядом називається символ , причому говорять, що цей ряд сходиться до суми , якщо до f сходиться послідовність часткових сум S_k, де

Нехай , тоді можна визначити ступінь матриці А звичайним образом:  (k раз). Розглянемо ряд, називаний статечним:

, , ,

де по визначенню покладемо A₀ = E_n.

Експонентна функція матриці. Як приклад розглянемо статечної ряд, рівний:

.

Тому що радіус збіжності відповідного числового ряду

Дорівнює нескінченності, то ряд сходиться при всіх А. Сума ряду називається експонентною функцією (експонентою) і позначається через е^А, якщо ехр{А}.

Приблизно вектор рішень можна знайти як добуток матричного ряду:

і вектора початкових умов y₀= [y₁,y₂, ….y_k].

Формула є матричною задачею Коші в наближеному виді.

Експонентою  матриці А називається сума ряду

де Е - одинична матриця. Матриця є рішенням матричної задачі Коші:  є фундаментальною матрицею системи. Знайдемо розкладання матричного ряду послідовно по сімох, вісьмох і десяти перших членах.

Для одержання розкладання по 7 перших членах (аналогічно по 8,10 і 10). Результатом буде матриця 4*4. Отримані матриці множимо на вектор початкових умов S= [1,2,3,4] і одержуємо наближене рішення у вигляді матричного ряду.

При збільшенні членів розкладання ряду вектор наближених рішень буде прагнути до вектора точних рішень. Цей факт можна спостерігати, графічно порівнюючи зображення точного й наближеного рішень (див. додаток).

Помножимо на відповідний вектор початкових умов і одержимо наближене рішення у вигляді матричного ряду, запишемо отримане рішення для n=7.

[s1 ≔ 1, s2 ≔ 2, s3 ≔ 3, s4 ≔ 4]

Матричний метод рішення системи рівнянь (1) заснований на безпосереднім відшуканні фундаментальної матриці цієї системи.

де Е - одинична матриця.

Властивість матричної експоненти: а) якщо АВ=ВА, те е^А+В=е^А*е^В= е^В *е^А; б) якщо А=S^-1*B*S, те е^А=S^-1*e^B*S, де матриця S - це матриця перетворення змінних із власного базису в базис вихідних змінних. в) матриця y (t) =e^At є рішенням матричної задачі Коші: т.е. є фундаментальною матрицею системи (1).

Із властивості в) треба, що рішення y (t) системи (1) задовольняючій умові y (0) =y₀, визначається вираженням y (t) =e^At*y₀. Таким чином, задача знаходження рішень системи рівнянь (1) еквівалентна задачі відшукання матриці e^At по матриці А.

Для обчислення матриці e^At зручно представити матрицю А в виді:

,

де матриця S - це матриця перетворення змінних із власного базису в базис вихідних змінних, а B_А - жорданова форма матриці А, тому що e^At = S^-1*e^Bt*S.

Жорданова форма матриці залежить від виду характеристичних чисел.

1.  Нехай характеристичні числа дійсні кратні, тоді Жорданова форма матриці розмірності nxn має вигляд:

де  - дійсний корінь кратності n.

2. Якщо серед корінь характеристичного полінома є, як дійсні різні, так і дійсних кратних корінь, то матриця В має вигляд:

де  - дійсних різних корінь, а  - дійсний корінь кратності 2.

3.  При наявності серед корінь характеристичного полінома корінь комплексно-комплексно-сполучених Жорданова клітка виглядає в такий спосіб:

де а  комплексно сполучений корінь характеристичного полінома.

Тому що в нашім випадку серед характеристичних чисел присутні, як комплексно-комплексно-сполучені корінь л = 2 - ?? л = 2 +?, так і дійсний різних корінь л = - 1? л = 1, те жорданова матриця виглядає в такий спосіб:

З рівняння A_*S = S_*В, де S - матриця, одержуємо систему 16-го порядку, з якої знаходимо елементи матриці S. Отримана матриця S буде виглядати в такий спосіб:

Вирішуємо систему 16-го порядку з рівняння A_*S = S_*В

Знаходимо деякі елементи й одержуємо наступну матрицю S:

Зробимо перевірку A_*S - S_*В=0:

Значить матриця переходу знайдена вірно.

Для знаходження вектора рішень y необхідно помножити матрицю S на , де  - це вектор, елементи якого залежать від корінь характеристичного багаточлена:

Для комплексних чисел  має такий вигляд:

Для випадку корінь дійсних різних:

У нашім випадку  виходить рівної:

 =

Звідси знайдемо загальне рішення в=S*, одержимо:

При підстановці рішення у вихідну систему виходить вірна рівність, із цього треба, що рішення знайдене вірно:

Необхідно із всіх рішень системи рівнянь знайти таке рішення, у якому y ^{(i) (}t) приймає задане числове значення y_0i у заданій крапці, тобто знайти значення с_i для наступних заданих значень: x=0, y= [1, 2, 3,4].

У вектор рішень y (t) підставляємо задані умови й вирішуємо отриману систему відносно c1, c2, c3, c4:

У результаті одержуємо:

При підстановці c1, c2, c3, c4 у загальне рішення одержимо рішення у формі Коші:

Зробимо перевірку, підставивши загальне рішення у вихідну систему

:

Вийшов нульовий вектор . Отже, знайдена матриця є рішенням вихідної системи.

Дослідження залежності жордановой форми матриці А від властивостей матриці системи.

Нехай J - жорданова клітка матриці А. Для випадку дійсних різних корінь жорданова клітка буде виглядати в такий спосіб:

Нехай серед дійсних власних чисел матриці А є кратні. Жорданова клітка буде перебувати по наступній формулі:

Наприклад, якщо кратність k=2, те жорданову клітку матриці ми можемо записати так:

Якщо кратність k=3, то жорданову клітку матриці ми можемо записати так:

Якщо ж серед трьох власних чисел  є коріннями кратності 2, то жорданова форма буде виглядати в такий спосіб:

Якщо два власних числа матриці А є комплексними сполученими, то запис жордановой клітки буде виглядати так:

де  - дійсна,  - мнима частина власного числа .

Права частина:

Загальне рішення неоднорідної системи можна знайти по формулі:

Де  - фср, З - матриця , F (t) - вектор праві частини.

 - загальне рішення однорідної системи

 - приватне рішення неоднорідної системи

Отримане приватне рішення неоднорідної системи:

Загальне рішення однорідної системи

Тоді їхня сума буде шуканим загальним рішенням неоднорідної системи:

Перевіримо

Знайдене рішення вірно.

Зобразимо графічно точне приватне рішення однорідної лінійної системи диференціальних рівнянь із постійними коефіцієнтами для початкових умов: t₀ = 0, y₀ = [1, 2, 3, 4].

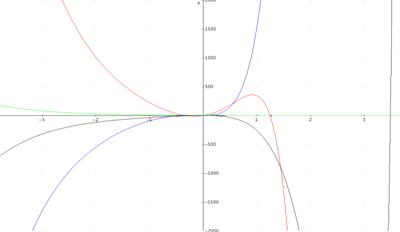
Зрівняємо графік однієї функції вектора точного рішення й однієї функції вектора наближеного рішення з 3-мя, 5-ю й 7-ю членами ряду:

Де 1 - графік наближеного рішення для трьох членів ряду; 2 - графік наближеного рішення для шести членів ряду; 3 - графік наближеного рішення для дев'яти членів ряду; 4 - графік точного рішення.

Можна зробити висновок:

Зі збільшенням числа членів ряду, число збігу членів ряду з точним рішенням буде збільшуватися, область збігу буде рости.

У ході проробленої роботи було вивчено 3 методи знаходження загального рішення однорідної системи лінійних диференціальних рівнянь: метод Ейлера, рішення у вигляді матричного ряду й матричний метод. У порівнянні з методом Ейлера й матричним методом, метод розкладання в матричний ряд простий у реалізації, але дає наближене рішення. Також була вивчена задача Коші, що була використана для знаходження приватного рішення однорідної системи лінійних диференціальних рівнянь для даного виду початкових умов.

Для встановлення правильності проведених обчислень була проведена перевірка за допомогою підстановки отриманих рішень у вихідну систему рівнянь.

Для реалізації цієї роботи в DERIVE були використані наступні функції пакета:

1.  EIGENVALUES (A, ) - обчислення власних чисел матриці A з наступним записом у вектор .

2.  SOLVE (Pm=0, ) - рішення рівняння Pm=0, де Pm - поліном ступеня m: Pm=p0* ^m p1* ^m-1+…+pm-1*+pm, а  - змінна, щодо якої вирішується дане рівняння.

3.  EXACT_VECTOR (A, ) - обчислення точного власного вектора матриці А и розміщення цих значень в.

4.  DIF (A,x,n) - диференціювання A по x n раз.

5.  SUM (M,n,f,g) - обчислення суми M по n змінюється з f до g.

6.  VECTOR (u,k,n) - завдання (обчислення) вектора значень при k змінюється від 1 до n.

А також функції меню:

1.  SOLVE/SYSTEM - рішення системи з наступним завданням у діалоговому вікні кількості рівнянь, самих рівнянь і змінних, щодо яких вирішується дане рівняння.

2.  Simplify > Expand - розкриття виражень.

Команда Expand використовується для розкриття математичних виражень.

Expand expression: #n: де n - номер рядка вираження (операнда).

Expand Variable: #n.

У цьому варіанті команди необхідно вказати ім'я змінної, по якій буде проведене перетворення. Якщо по всім - <Enter>.

3. Для побудови графіків використовували функцію 2D-plot.

1.  Лобоцка Н.Л. Основи вищої математики. - К., 2003

2.  Минорський В.П. Збірник задач по вищої математики. - К., 2004

3.  Кудрявцев В.О., Демидович Б.П. Курс вищої математики. - К., 2004

4.  Гмурман В.О. Теорія ймовірностей і математична статистика. - К., 2000

5.  Гмурман В.О. Посібник з рішення задач по теорії ймовірностей і математичній статистиці. - К., 2005