Курсовая работа: Рішення систем диференціальних рівнянь за допомогою неявної схеми Адамса 3-го порядку
Курсова робота
"Рішення систем диференціальних рівнянь за допомогою неявної схеми Адамса 3-го порядку"
Введення
Бурхливий розвиток в останнє десятиліття інформаційних технологій і комп'ютерної техніки сприяє виникненню усе більше складних математичних задач, для рішення яких без застосування чисельних методів потрібне значний час. Дуже часто перед фахівцем виникають задачі, що не вимагають абсолютно точного рішення; як правило, потрібно знайти наближене рішення із заданою погрішністю. Поряд з удосконалюванням комп'ютерної техніки відбувається процес удосконалювання й чисельних методів програмування, що дозволяють за мінімальний відрізок часу одержати рішення поставленої задачі із заданим ступенем точності.
Однієї з таких задач є рішення систем диференціальних рівнянь. Звичайними диференціальними рівняннями можна описати поводження матеріальних крапок у силовому полі, закони хімічної кінетики, рівняння електричних кіл і т.д. Ряд фізичних задач може бути зведені до рішення диференціальних рівнянь або системи диференціальних рівнянь. Задача рішення системи диференціальних рівнянь має важливе прикладне значення при рішенні наукових і технічних проблем. Крім того, вона є допоміжною задачею при реалізації багатьох алгоритмів обчислювальної математики, математичної фізики, обробки результатів експериментальних досліджень. Тому для інженерів надто важливо грамотно знаходити рішення цієї задачі.
1. Постановка задачі
Необхідно вирішити із заданим ступенем точності задачу Коші для системи диференціальних рівнянь на заданому інтервалі [a, b]. Домогтися погрішності на другому кінці не більше 0,0001. Результат одержати у вигляді таблиці значень наближеного й точного рішень у крапках заданого інтервалу. Побудувати графіки отриманих рішень і зрівняти їх з точним рішенням.
Вихідні дані:
– система диференціальних рівнянь виду:
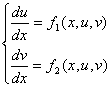
– інтервал, на якому шукається рішення: [a, b]
– погрішність, з якої шукається рішення: е
–
формулювання задачі Коші в початковій крапці заданого інтервалу: ![]() u(a)=u, v(a)=v
u(a)=u, v(a)=v
Вихідні дані:
– таблиця значень наближеного й точного рішень у вузлах заданої сітки;
– графіки отриманих і точних рішень.
2. Опис математичних методів рішення задачі
Конкретна прикладна задача може привести до диференціального рівняння будь-якого порядку або до системи таких рівнянь. Довільну систему диференціальних рівнянь будь-якого порядку можна привести до деякої еквівалентної системи диференціальних рівнянь першого порядку. Серед таких систем виділяють клас систем, дозволених відносно похідній невідомих функцій:
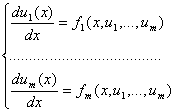 (2.1)
(2.1)
Диференціальне рівняння або система диференціальних рівнянь має нескінченну множину рішень. Єдині рішення виділяють за допомогою додаткових умов, яким повинні задовольняти шукані рішення. Залежно від виду таких умов розглядають три типи задач, для яких доведене існування й одиничність рішень.
Перший тип – це задачі Коші, або задачі з початковими умовами. Для таких задач крім вихідного рівняння в деякій крапці a повинні бути задані початкові умови, тобто значення функції u1 (a),…, um(a):
u1 (a)=![]() ,…, um(a)=
,…, um(a)=![]() (2…2)
(2…2)
До другого типу задач ставляться так звані граничні, або крайові задачі, у яких додаткові умови задаються у вигляді функціональних співвідношень між шуканими рішеннями. Кількість умов повинне збігатися з порядком n рівняння або системи. Якщо рішення задачі визначається в інтервалі x([a, b], то такі умови можуть бути задані як на границях, так і усередині інтервалу.
Третій тип задач для систем диференціальних рівнянь – це задачі на власні значення. Такі задачі відрізняються тим, що крім шуканих функцій u1 (x),…, um(x) у рівняння входять додатково n невідомих параметрів l1, l2,…, ln, які називаються власними значеннями. Для одиничності рішення на інтервалі [a, b] необхідно задати n + m граничних умов.
Розглянемо докладніше задачу Коші. Скористаємося компактним записом задачі (2.1), (2.2) у векторній формі:
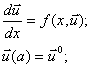 (2.3)
(2.3)
Потрібно
знайти ![]() на інтервалі [a, b].
на інтервалі [a, b].
Задачу Коші зручніше за все вирішувати методом сіток. Метод сіток полягає в наступному:
1) Вибираємо в області інтегрування впорядковану систему крапок a=x1<x2<…<xn<b, називану сіткою. Крапки xi називають вузлами різницевої сітки, різниця між сусідніми вузлами h=xi-xi-1 – крок сітки. Формула для обчислення кроку рівномірної сітки, заданої на інтервалі [a, b]:
![]() , (2.4)
, (2.4)
де nx – кількість вузлів заданої сітки.
2)
Рішення ![]() шукається у вигляді
таблиці значень у вузлах обраної сітки, для чого диференціювання заміняється
системою алгебраїчних рівнянь, що зв'язують між собою значення шуканої функції
в сусідніх вузлах. Таку систему рівнянь прийнято називати кінцево-різницевою
схемою.
шукається у вигляді
таблиці значень у вузлах обраної сітки, для чого диференціювання заміняється
системою алгебраїчних рівнянь, що зв'язують між собою значення шуканої функції
в сусідніх вузлах. Таку систему рівнянь прийнято називати кінцево-різницевою
схемою.
Для одержання кінцево-різницевої схеми зручно використовувати метод, відповідно до якого необхідно інтегрувати рівняння (2.3) на кожному інтервалі [xk, xk+1] і розділити отримане вираження на довжину цього інтервалу:
 (2.5)
(2.5)
Далі
апроксимуємо інтеграл у правій частині однієї із квадратурних формул і
одержуємо систему рівнянь щодо наближених невідомих значень шуканих функцій,
які на відміну від точних позначимо ![]() . При
цьому виникає погрішність?, обумовлена неточністю апроксимації:
. При
цьому виникає погрішність?, обумовлена неточністю апроксимації:
ε(h)=||
![]() || (2.6)
|| (2.6)
Відповідно до основної теореми теорії методу сіток (теорема Лакса), для стійкої кінцево-різницевої схеми при прагненні кроку h до нуля погрішність рішення прагне до нуля з тим же порядком, що й погрішність апроксимації:
![]() , (2.7)
, (2.7)
де З0 – константа стійкості, p – порядок апроксимації.
Тому для збільшення точності рішення необхідно зменшити крок сітки h.
На практиці застосовується множина видів кінцево-різницевих схем, які підрозділяються на одно крокові, багатокрокові схеми й схеми із дробовим кроком.
Одно крокові схеми – Метод Ейлера
Заміняємо інтеграл у правій частині рівняння (2.5) по формулі лівих прямокутників:
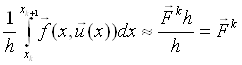 (2.8)
(2.8)
Одержимо:
![]() , (2.9)
, (2.9)
де k=0,1,2,…, n.
Схема
явна стійка. У силу того, що формула для лівих прямокутників має погрішність
другого порядку, точність ε(h) першого порядку. ![]()
– Неявна схема 1-го порядку
Використовуючи формулу правих прямокутників, одержимо:
![]() (2.10)
(2.10)
Ця
схема нерозв'язна в явному виді відносно ![]() ,
тому проводиться ітераційна процедура:
,
тому проводиться ітераційна процедура:
![]() , (2.11)
, (2.11)
де s=1,2,… – номер ітерації. Звичайно схема сходиться дуже швидко – 2–3 ітерації. Неявна схема першого порядку ефективніше явної, тому що константа стійкості З0 у неї значно менше.
– Метод Ейлера-Коші
Обчислення проводяться у два етапи: етап прогнозу й етап корекції.
На етапі прогнозу визначається наближене рішення на правому кінці інтервалу по методу Ейлера:
![]() (2.12)
(2.12)
На етапі корекції, використовуючи формулу трапецій, уточнюємо значення рішення на правому кінці:
![]() (2.13)
(2.13)
Тому що формула трапецій має третій порядок точності, то порядок погрішності апроксимації – дорівнює двом.
– Неявна схема 2-го порядки (метод Ейлера-Коші)
Використовуючи в (2.5) формулу трапецій, одержимо:
![]() (2.14)
(2.14)
Схема не дозволена в явному виді, тому потрібна ітераційна процедура:
![]() , (2.15)
, (2.15)
де s=1,2,… – номер ітерації. Звичайно схема сходиться за 3–4 ітерації.
Тому що формула трапецій має третій порядок точності, то погрішність апроксимації – другий.
Схеми із дробовим кроком
– Схема предиктор-коректор (Рунге-Кутта) 2-го порядки
Використовуючи в (2.5) формулу середніх, одержимо:
![]() , (2.16)
, (2.16)
де ![]() – рішення системи на
середині інтервалу [xk, xk+1]. Рівняння явно дозволене відносно
– рішення системи на
середині інтервалу [xk, xk+1]. Рівняння явно дозволене відносно ![]() , однак у правій частині
присутня невідоме значення
, однак у правій частині
присутня невідоме значення ![]() . Тому
спочатку рахують
. Тому
спочатку рахують ![]() (предиктор):
(предиктор):
![]() . (2.17)
. (2.17)
Потім
![]() (коректор) по формулі
(2.16). Схема має перший порядок погрішності.
(коректор) по формулі
(2.16). Схема має перший порядок погрішності.
– Схема Рунге-Кутта 4-го порядку
Використовуючи в (2.5) формулу Симпсона, одержимо:
![]() (2.18)
(2.18)
Найбільше
часто розраховують неявне по ![]() рівняння
за наступною схемою:
рівняння
за наступною схемою:
Спочатку розраховують предиктор виду:
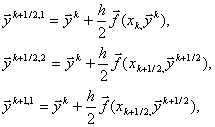 (2.19)
(2.19)
потім коректор по формулі:
![]() (2.20)
(2.20)
Оскільки формула Симпсона має п'ятий порядок погрішності, то точність? (h) – четвертого порядку.
Багатокрокові схеми
Багатокрокові методи рішення задачі Коші характеризуються тим, що рішення в поточному вузлі залежить від даних не в одному попередньому або наступному вузлі сітки, як це має місце в одно крокових методах, а залежить від даних у декількох сусідніх вузлах.
Ідея
методів Адамса полягає в тім, щоб для підвищення точності використовувати
обчислені вже на попередніх кроках значення ![]()
Якщо
замінимо в (2.5) вираження інтерполяційним багаточленом Ньютона, побудованого
по вузлах ![]() , то після інтегрування на
інтервалі
, то після інтегрування на
інтервалі ![]() одержимо явну схему
Адамса. Якщо замінимо в (2.5) вираження на багаточлен Ньютона, побудованого по
вузлах
одержимо явну схему
Адамса. Якщо замінимо в (2.5) вираження на багаточлен Ньютона, побудованого по
вузлах ![]() , то одержимо неявну
інтерполяційну схему Адамса.
, то одержимо неявну
інтерполяційну схему Адамса.
– Явна екстраполяційна схема Адамса 2-го порядки
![]()
![]() (2.21)
(2.21)
Схема
двох крокова, тому необхідно для розрахунків знайти за схемою Рунге-Кутта 2-го
порядку ![]() , після чого
, після чого ![]() ,
, ![]() , … обчислюють по формулі
(2.21)
, … обчислюють по формулі
(2.21)
– Явна екстраполяційна схема Адамса 3-го порядки
![]() (2.22)
(2.22)
Схема
двох крокова, тому необхідно спершу знайти ![]() й
й
![]() за схемою
предиктор-коректор 4-го порядку, після чого
за схемою
предиктор-коректор 4-го порядку, після чого ![]() ,
,
![]() , … обчислюють по формулі
(2.22).
, … обчислюють по формулі
(2.22).
3. Опис використовуваного методу
Для рішення системи диференціальних рівнянь обрана неявна схема Адамса 3-го порядки, як одна з найбільш точних схем для рішення задачі Коші. Щоб прийти до неявної схеми Адамса, замінимо вираження в рівнянні:
 (3.1)
(3.1)
інтерполяційним багаточленом Ньютона 2-го порядки, виду:
![]() (3.2)
(3.2)
Після
інтегрування отриманого вираження на інтервалі ![]() ,
приходимо до рівняння неявної схеми Адамса 3-го порядки:
,
приходимо до рівняння неявної схеми Адамса 3-го порядки:
![]() . (3.3)
. (3.3)
Дана
схема не дозволена явно відносно ![]() , тому
спочатку необхідно обчислити
, тому
спочатку необхідно обчислити ![]() будь-яким
підходящим методом, наприклад методом Рунге-Кутта четвертого порядку. Потім для
знаходження
будь-яким
підходящим методом, наприклад методом Рунге-Кутта четвертого порядку. Потім для
знаходження ![]() потрібно використовувати
метод простої ітерації:
потрібно використовувати
метод простої ітерації:
![]() , (3.4)
, (3.4)
де s=1,2,3,… – номер ітерації. Умова виходу із циклу ітераційної процедури:
![]() , (3.5)
, (3.5)
де? – задана погрішність.
Початкове наближення задається формулою для явної схеми Адамса 2-го порядки:
![]() . (3.6)
. (3.6)
Схема стійка, сходиться швидко. Найчастіше досить однієї ітерації. Порядок погрішності? (h) неявної схеми Адамса третього порядку дорівнює чотирьом.
4. Опис блок-схеми алгоритму
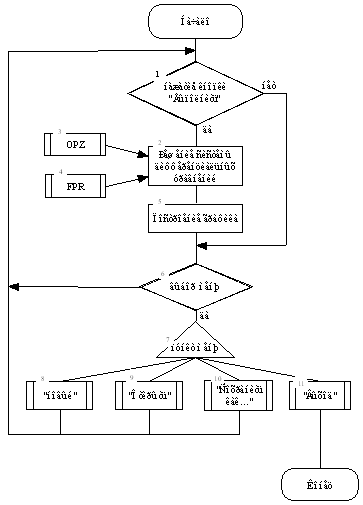
При розробці програми були побудовані блок-схеми алгоритму програми, що спрощують процес проектування й полегшують розуміння вихідного коду готової програми (див. Додаток 1).
Блок-схема алгоритму умовно розбита на 11 блоків.
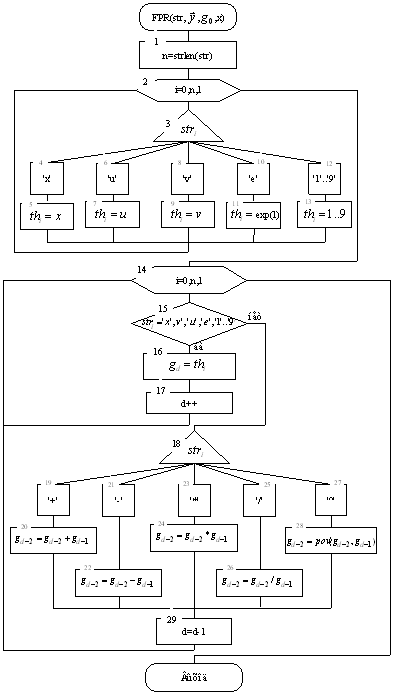
Головна функція програми відповідає за обробку події створення форми, взаємодія зі стандартним компонентом Tсhart, а також за реалізацію рішення системи диференціальних рівнянь неявною схемою Адамса 3-го порядки. Блок-схема алгоритму рішення задачі Коші розбитий умовно на 35 блоків:
1-й блок відповідає за ручне уведення інтервалу [a, b], на якому шукається рішення системи; кількості кроків сітки nx; крок висновку результатів на екран np; рядків u1 і v1, що відповідають рівнянням системи; значення шуканих функцій на початку заданого інтервалу; припустима погрішність e.
У другому блоці відбувається обчислення кроку h і установка поточного вузла на x=a. Блок 3 – функція перетворення вихідних записів рівнянь системи в рівносильні їм рядка з формою записом математичних операцій (див. далі «алгоритм зворотного польського запису»). Як аргументи функції виступають уведені раніше рядка u1 і v1.
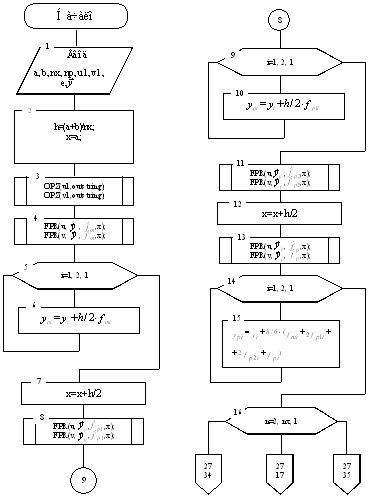
Блоки
4–15 – розрахунок перших 2-х крапок заданої сітки методом Рунге-Кутта 4-го
порядку. У даних блоках і далі використовується користувальницька функція FPR,
що розраховує значення рівнянь, що вводяться користувачем, у вузлах заданої
сітки. Як аргументи функції виступають: уже перетворені у зворотний польський
запис рядка, що задають рівняння системи; поточне значення x; значення шуканих
функцій на попередньому кроці (умовно позначаємо ![]() ).
).
У
блоках 16–34 у циклі (16) розраховуються значення шуканих рішень у вузлах 2-nx
заданої сітки неявною схемою Адамса 3-го порядки. Цикл 21–29 здійснює
ітераційну процедуру неявної схеми. Умова виходу із цього циклу – виконання
нерівності de<e, де de – найбільший з модулів ![]() ,
e – задана точність. Оскільки на екран виводяться значення шуканих функцій не у
всіх вузлах, а тільки у вузлах з номером, кратним кроку висновку nx, що
вводиться із клавіатури, то блоки 33–34 здійснюють вибір цих вузлів.
,
e – задана точність. Оскільки на екран виводяться значення шуканих функцій не у
всіх вузлах, а тільки у вузлах з номером, кратним кроку висновку nx, що
вводиться із клавіатури, то блоки 33–34 здійснюють вибір цих вузлів.
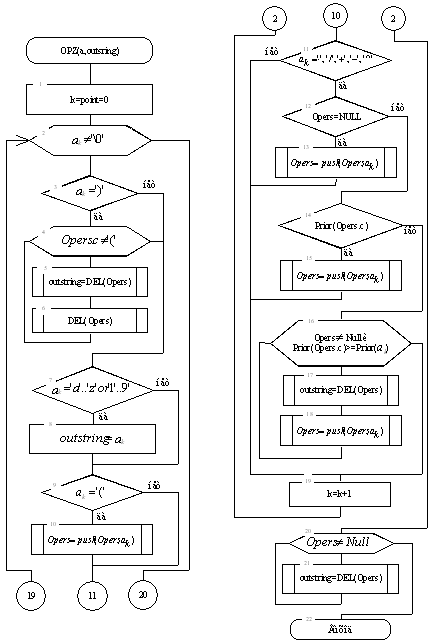
Перетворення у зворотний польський запис відбувається за наступними правилами:
Розглядаємо по черзі кожний символ:
1. Якщо цей символ – число (або змінна), то просто поміщаємо його у вихідний рядок.
2. Якщо символ – знак операції (+, -, *, /,^), то перевіряємо пріоритет даної операції. Операція піднесення в ступінь має найвищий пріоритет (дорівнює 4). Операції додавання й вирахування мають менший пріоритет (дорівнює 2). Найменший пріоритет (дорівнює 1) має відкриваюча дужка.
Одержавши один із цих символів, ми повинні перевірити стек:
а) Якщо стік усе ще порожній, або символи, що перебувають у ньому (а перебуває в ньому можуть тільки знаки операцій і відкриваюча дужка) мають менший пріоритет, чим пріоритет поточного символу, те поміщаємо поточний символ у стек.
б) Якщо символ, що перебуває на вершині стека має пріоритет, більший або дорівнює пріоритету поточного символу, те витягаємо символи зі стека у вихідний рядок доти, поки виконується ця умова; потім переходимо до пункту а).
3. Якщо поточний символ – відкриваюча дужка, то поміщаємо її в стек.
4. Якщо поточний символ – закриваюча дужка, то витягаємо символи зі стека у вихідний рядок доти, поки не зустрінемо в стеці відкриваючу дужку (тобто символ із пріоритетом, рівним 1), яку варто просто знищити. Закриваюча дужка також знищується.
Якщо весь вхідний рядок розібраний, а в стеці ще залишаються знаки операцій, витягаємо їх зі стека у вихідний рядок.
Згідно із цими правилами створений модуль «Unit3.cpp», що містить функцію перетворення рядка у зворотний польський запис OPZ (блок 3 у блок-схемі алгоритму), алгоритм якої наведений у додатку. У даному модулі використані також допоміжні функції PUSH, PRIOR, DEL. Функція PUSH записує в стек, на вершину якого вказує HEAD, символ a. Повертає покажчик на нову вершину стека. Функція PRIOR обчислює пріоритет поточного символу, природно, лише в тому випадку, якщо поточний символ – математична операція. Функція DEL видаляє символ.
Для роботи з отриманим зворотним польським записом створена функція (блок 4), організована у вигляді модуля, що підключається, «Unit5.cpp». Блок-схема даної функції наведена в додатку. На початковому етапі (блоки 1–13) у циклі аналізується рядок, що містить зворотний польський запис. Якщо символ раніше задекларований ('x', 'u', 'v', 'e', '1'..'9'), те його значення заноситься в поточний елемент масиву th. На наступному етапі (блоки 14–29) здійснюється «зворотний хід» польської нотації: аналізується кожний символ рядка, і якщо цей символ раніше задекларований, те його значення міститься в стек (блоки 15–17). У випадку, якщо поточний символ – знак математичної операції, то зі стека витягають останні два елементи й з ними проводиться зазначена операція. Результат заноситься на вершину стека. Стік у функції реалізований у вигляді односпрямованого масиву типу double. Функція повертає перший елемент стека.
5. Опис програми
Після проведеного огляду програмних засобів для розробки даного програмного продукту, було обране середовище Borland C++ Builder. Мова С++ добре зарекомендував себе ефективністю, лаконічністю запису алгоритмів, логічною стрункістю програми. Програми, написані мовою С++, порівнянні по швидкості із програмами, написаними мовою асемблера; при цьому вони більше наочні й прості в супроводі. Середовище Borland C++ Builder є засобом швидкої розробки windows-додатків, що дозволяє створювати додатка мовою С++, використовуючи середовище розробки й бібліотеку компонентів Delphi.
Готова програма являє собою файл, що виконується, з ім'ям «Adams3.exe», реалізований у вигляді Widows-Додатка в середовищі Borland C++ Builder. Після запуску програми на робочому вікні з'являється робоче вікно із заголовком «Рішення систем диференціальних рівнянь». В активному вікні можна виділити наступні області:
1) Область уведення вихідних даних.
2) Вікно висновку результатів.
3) Поле відображення графіків отриманих функцій, що є
рішенням заданої системи, і графіків щирого рішення.
4) Основне меню.
1) Область вихідних даних містить поля, у які потрібно ввести початкові дані: систему диференціальних рівнянь; інтервал, на якому потрібно знайти рішення заданої системи; припустиму погрішність; умови Коші в початковій крапці заданого інтервалу; кількість кроків «сітки» і крок висновку отриманих значень шуканих функцій у вузлах сітки.
У поля «du/dx= «і «dv/dx= «уводяться диференціальні рівняння, що містять символи, 'u', 'v' 'x', 'e', '1'..'9', '+', '-', '*', '/', '^', ' (', ')'. Тут: символи 'u' і 'v' являють собою шукані функції, символ 'e' є підставою натурального логарифма, символ '^' позначає операцію піднесення в ступінь. Використання інших символів небажано, тому що вони будуть зігноровані програмою.
Поля із заголовком «інтервал [a; b]» містять початкову й кінцеву крапку проміжку, на якому буде знайдене рішення заданої системи.
У поле «кількість кроків сітки» потрібно ввести ціле число, рівне кількості крапок по осі OX на заданому інтервалі, у яких шукаємо значення функцій u(x) і v(x).
Поле «крок висновку» містить ціле число, що визначає частоту висновку на екран результатів із множини результатів у всіх вузлах заданої сітки.
Поля під загальною назвою «початкові умови» містять умови Коші – значення шуканих функцій на початку заданого інтервалу [a, b].
Для коректної роботи програми всі поля повинні бути заповнені. При запуску програми всі перераховані вище поля вже містять стандартну інформацію для тесту програми, яку можна змінювати.
Користувачеві надається можливість вибору режиму програми. При запуску програми мітка біля напису «Не використовувати метод сіток, що згущаються,» відсутній, і програма, використовуючи метод сіток, що частішають, підбере після першого натискання кнопки «виконає» оптимальне значення кількості кроків для досягнення заданої точності. Після повторного натискання кнопки «виконати» будуть зроблені обчислення вже для значення кроку, що рекомендується, сітки. Якщо мітка поставлена, то після натискання кнопки «виконати» буде вирішена задача Коші для заданого інтервалу, але задана точність не буде досягнута. Даний режим дозволяє вводити різні системи диференціальних рівнянь, відмінних від стандартних тестових, рішенням яких є функції u(x)=2*x, v(x)=exp(x).
2) Всі результати, отримані в ході роботи програми, відображаються в окремому вікні (мал. 2). При бажанні, всю інформацію із цього вікна можна зберегти в окремий файл.
3) Отримане рішення у вигляді графіків шуканих функцій виводиться в окреме поле (мал. 2). Тут відображаються також графіки функцій f(x)=2*x і f(x)=exp(x), що є точним рішенням для тестових систем диференціальних рівнянь. Поле відображення графіків надобіддя.
4) Основне меню містить наступні пункти: «Файл» і «Про програму» (мал. 3). У свою чергу пункт меню «Файл» містить наступні підпункти: «новий», «відкрити», «зберегти як…» і «вихід».
При виборі пункту «новий» всі поля й вікна будуть очищені. Поле відображення графіків буде також очищено.
Вибравши пункт «зберегти як…», вся інформація з вікна результатів буде збережена в обраний користувачем файл (за замовчуванням txt).
Вибір пункту «відкрити» приводить до завантаження із уже збереженого раніше файлу системи диференціальних рівнянь.
Програма працює стабільно, не приводить до помилок.
6. Аналіз результатів
Результатом роботи програми «Adams3.exe» є таблиця значень отриманого рішення у вузлах заданої сітки, значень точного рішення й різниця між точним і отриманим рішеннями. Дану таблицю можна зберегти в текстовий файл із можливістю подальшого перегляду й редагування.
Як
тестова задача була вирішена задача Коші за допомогою неявної схеми Адамса 3-го
порядки на інтервалі [2,4] з початковими умовами ![]()
![]() :
:
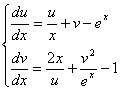 .
.
Точним рішенням даної системи є функції:
![]()
Було потрібно домогтися рішення системи диференціальних рівнянь із точністю до 0.0001.
Результат рішення (вихідний файл):
Вхідні дані:
du/dx= u/x+v-e^x;
dv/dx= 2*x/u+v^2/e^x-1;
Інтервал: [2; 4]
Припустима погрішність: е=0,0001
Початкові умови:
u=4
v=7,389056098930650230
Кількість кроків сітки: 320
Крок висновку: 32
Результати:
x | u(x) | точне | різн. | v(x) | точне | різн. |
2,000 4,0000 4,0000 0,0000 7,3891 7,3891 0,0000
2,200 4,4000 4,4000 0,0000 9,0250 9,0250 0,0000
2,400 4,8000 4,8000 0,0000 11,0232 11,0232 0,0000
2,600 5,2000 5,2000 0,0000 13,4637 13,4637 0,0000
2,800 5,6000 5,6000 0,0000 16,4446 16,4446 0,0000
3,000 6,0000 6,0000 0,0000 20,0855 20,0855 0,0000
3,200 6,4000 6,4000 0,0000 24,5325 24,5325 0,0000
3,400 6,8000 6,8000 0,0000 29,9641 29,9641 0,0000
3,600 7,2000 7,2000 0,0000 36,5982 36,5982 0,0000
3,800 7,6000 7,6000 0,0000 44,7012 44,7012 0,0000
4,000 8,0000 8,0000 0,0000 54,5981 54,5982 0,0000
Час виконання: 0,015з
Як видно з отриманого результату, точність в 0.0001 досягається вже при кількості кроків, рівному 320. Час. Витрачене на розрахунок таблиці значень на заданому інтервалі становить усього 0.015 секунд, що практично не відчутно. Збільшення кроку сітки приведе до підвищення точності рішення, однак це збільшить і час роботи обчислювального процесу.
Задана точність досягається за мінімальну кількість ітерацій (1–3 ітерації).
Нижче наведений графік функцій отриманого й точного рішень:
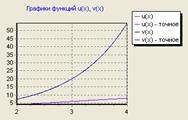
Рис. 5.1 Графік отриманого й точного рішення
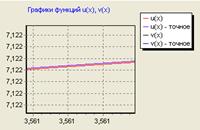
Рис. 5.2 Графік отриманого й точного рішення
Як видно з малюнків 5.1, 5.2, розбіжність кривих спостерігається тільки при досить великому збільшенні графіка.
Запропонована задача Коші була також вирішена в математичному пакеті «Mathcad 11» двома методами: методом Рунге-Кутта 5-го порядку й методом Рунге-Кутта з непостійним кроком. Реалізація рішення системи диференціальних рівнянь в «Mathcad 11» і таблиці результатів наведені нижче:
Реалізація рішення задачі Коші методом Рунге-Кутта 5-го порядку:

Таблиця 5.1 – Результати рішення задачі Коші методом Рунге-Кутта 5-го порядку.
| x | u(x) | v(x) | x | u(x) | v(x) | |
| 2 | 4 | 7,3890561 | 3,1 | 6,2 | 22,19795 | |
| 2,02 | 4,04 | 7,5383249 | 3,12 | 6,24 | 22,64638 | |
| 2,04 | 4,08 | 7,6906092 | 3,14 | 6,28 | 23,10387 | |
| 2,06 | 4,12 | 7,8459698 | 3,16 | 6,32 | 23,5706 | |
| 2,08 | 4,16 | 8,0044689 | 3,18 | 6,36 | 24,04675 | |
| 2,1 | 4,2 | 8,1661699 | 3,2 | 6,4 | 24,53253 | |
| 2,12 | 4,24 | 8,3311375 | 3,22 | 6,44 | 25,02812 | |
| 2,14 | 4,28 | 8,4994376 | 3,24 | 6,48 | 25,53372 | |
| 2,16 | 4,32 | 8,6711376 | 3,26 | 6,52 | 26,04954 | |
| 2,18 | 4,36 | 8,8463062 | 3,28 | 6,56 | 26,57577 | |
| 2,2 | 4,4 | 9,0250135 | 3,3 | 6,6 | 27,11264 | |
| 2,22 | 4,44 | 9,2073308 | 3,32 | 6,64 | 27,66035 | |
| 2,24 | 4,48 | 9,3933313 | 3,34 | 6,68 | 28,21913 | |
| 2,26 | 4,52 | 9,5830891 | 3,36 | 6,72 | 28,78919 | |
| 2,28 | 4,56 | 9,7766804 | 3,38 | 6,76 | 29,37077 | |
| 2,3 | 4,6 | 9,9741824 | 3,4 | 6,8 | 29,9641 | |
| 2,32 | 4,64 | 10,175674 | 3,42 | 6,84 | 30,56941 | |
| 2,34 | 4,68 | 10,381237 | 3,44 | 6,879999 | 31,18696 | |
| 2,36 | 4,72 | 10,590951 | 3,46 | 6,919999 | 31,81698 | |
| 2,38 | 4,76 | 10,804903 | 3,48 | 6,959999 | 32,45972 | |
| 2,4 | 4,8 | 11,023176 | 3,5 | 6,999999 | 33,11545 | |
| 2,42 | 4,84 | 11,245859 | 3,52 | 7,039999 | 33,78443 | |
| 2,44 | 4,88 | 11,473041 | 3,54 | 7,079999 | 34,46692 | |
| 2,46 | 4,92 | 11,704811 | 3,56 | 7,119999 | 35,1632 | |
| 2,48 | 4,96 | 11,941264 | 3,58 | 7,159999 | 35,87354 | |
| 2,5 | 4,9999999 | 12,182494 | 3,6 | 7,199999 | 36,59823 | |
| 2,52 | 5,0399999 | 12,428597 | 3,62 | 7,239999 | 37,33757 | |
| 2,54 | 5,0799999 | 12,679671 | 3,64 | 7,279999 | 38,09184 | |
| 2,56 | 5,1199999 | 12,935817 | 3,66 | 7,319999 | 38,86134 | |
| 2,58 | 5,1599999 | 13,197138 | 3,68 | 7,359999 | 39,64639 | |
| 2,6 | 5,1999999 | 13,463738 | 3,7 | 7,399999 | 40,4473 | |
| 2,62 | 5,2399999 | 13,735723 | 3,72 | 7,439999 | 41,26439 | |
| 2,64 | 5,2799999 | 14,013204 | 3,74 | 7,479999 | 42,09799 | |
| 2,66 | 5,3199999 | 14,296289 | 3,76 | 7,519999 | 42,94842 | |
| 2,68 | 5,3599999 | 14,585093 | 3,78 | 7,559999 | 43,81604 | |
| 2,7 | 5,3999999 | 14,879732 | 3,8 | 7,599999 | 44,70118 | |
| 2,72 | 5,4399999 | 15,180322 | 3,82 | 7,639999 | 45,60421 | |
| 2,74 | 5,4799999 | 15,486985 | 3,84 | 7,679999 | 46,52547 | |
| 2,76 | 5,5199999 | 15,799843 | 3,86 | 7,719999 | 47,46535 | |
| 2,78 | 5,5599999 | 16,119021 | 3,88 | 7,759999 | 48,42421 | |
| 2,8 | 5,5999999 | 16,444647 | 3,9 | 7,799999 | 49,40245 | |
| 2,82 | 5,6399999 | 16,776851 | 3,92 | 7,839999 | 50,40044 | |
| 2,84 | 5,6799999 | 17,115765 | 3,94 | 7,879999 | 51,4186 | |
| 2,86 | 5,7199999 | 17,461527 | 3,96 | 7,919999 | 52,45732 | |
| 2,88 | 5,7599999 | 17,814273 | 3,98 | 7,959998 | 53,51703 | |
| 2,9 | 5,7999998 | 18,174145 | 4 | 7,999998 | 54,59815 | |
| 2,92 | 5,8399998 | 18,541287 | ||||
| 2,94 | 5,8799998 | 18,915846 | ||||
| 2,96 | 5,9199998 | 19,297972 | ||||
| 2,98 | 5,9599998 | 19,687816 | ||||
| 3 | 5,9999998 | 20,085537 | ||||
| 3,02 | 6,0399998 | 20,491291 | ||||
| 3,04 | 6,0799998 | 20,905243 | ||||
| 3,06 | 6,1199998 | 21,327557 | ||||
| 3,08 | 6,1599998 | 21,758402 |
Реалізація рішення задачі Коші методом Рунге-Кутта з непостійним кроком:

Таблиця 5.2 – Результати рішення задачі Коші методом Рунге-Кутта з непостійним кроком.
| X | u(x) | v(x) |
| 2 | 4 | 7,389056099 |
| 2,2 | 4,4 | 9,025013486 |
| 2,4 | 4,8 | 11,02317634 |
| 2,6 | 5,2 | 13,46373796 |
| 2,8 | 5,6 | 16,44464663 |
| 3 | 6 | 20,08553669 |
| 3,2 | 6,4 | 24,53252981 |
| 3,4 | 6,8 | 29,96409944 |
| 3,6 | 7,2 | 36,59823348 |
| 3,8 | 7,6 | 44,701183 |
| 4 | 8 | 54,59814775 |
Як видно з отриманих таблиць результатів, точність рішення в 0.0001 при рішенні методом Рунге-Кутта з непостійним кроком досягається всього за 10 кроків, у той час, коли для досягнення цієї ж точності при рішенні методом Рунге-Кутта 5-го порядку з постійним кроком потрібно близько 100 кроків.
Порівнюючи отримані результати з результатами роботи програми «Adams3.exe», доходимо висновку, що неявна схема Адамса третього порядку досить ефективна при чисельному рішенні задачі Коші (швидкість, висока точність рішення), однак по своїх характеристиках вона уступає більше зробленим методам, що застосовуються в різних математичних пакетах.
Висновок
Результатом виконання курсового проекту є готовий програмний продукт, що дозволяє вирішувати задачу Коші для системи диференціальних рівнянь за допомогою неявної схеми Адамса 3-го порядки, що демонструє можливості чисельного рішення поставленої задачі із заданим ступенем точності.
Готовий програмний продукт може знайти широке застосування при рішенні багатьох прикладних технічних програм, а зокрема, ефективне використання застосованої схеми Адамса 3-го порядки для рішення так званих «твердих» систем диференціальних рівнянь, для яких існує лише чисельне рішення.
Дана програма вирішує задану користувачем систему диференціальних рівнянь із зазначеною точністю за мінімальний проміжок часу. При цьому користувачеві надається можливість візуально оцінити неточність рішення, порівнюючи графіків отриманого й точного рішень.
До достоїнств програми можна віднести також зручний користувальницький інтерфейс, можливість уведення користувальницьких систем диференціальних рівнянь, а також висока стабільність роботи. Однак є й деякі недоліки. До недоліків програми можна віднести: відсутність обробки виняткових подій. Це, природно, обмежує можливості програми.
Література
1. Архангельський О.Я. Програмування в С++ Builder 6. – К., 2004
2. Каліткин М.М. Чисельні методи. – К., 2003
3. Самарський А.А., Гулін А.В. Чисельні методи. – К., 2003
4. Синіцин О.К., Навроцкий А.А. Алгоритми обчислювальної математики. – К., 2003
5. Синіцин О.К. Програмування алгоритмів у середовищі Builder C++. – К., 2003
6. Страуструп Бьерн. Язык программирования C++. – М., 2002
7. Шилд Г. Программирование на Borland C++ для профессионалов – М., 1999.
Додаток 1
1. Блок-схема алгоритму
2. Блок-схема рішення задачі Коші неявною схемою Адамса 3-го порядки
3. Блок-схема алгоритму перетворення рядка у зворотний польський запис
4. Блок-схема обчислення функцій