Лабораторная работа: Контроль і діагностика програмних систем
Міністерство освіти і науки
Відкритий міжнародний університет розвитку людини ”Україна”
Лабораторна робота №1
З предмету:
Контроль і діагностика програмних систем
На тему:
Перевірка коду на парність
Виконала
студентка групи ПА-41
Руденко О.М.
Перевірив викладач
Капшук О.О.
Київ – 2010
Лабораторна робота №1
Теоретична частина
Припустимо, що ми передаємо інформацію, використовуючи деякий канал зв’язку (наприклад, телефонну лінію). В процесі передачі інформація може спотворюватися, тому виникає задача розроблення прийомів, які дали б змогу або зробити такі спотворення неможливими або звести можливі спотворення до мінімуму. Суть таких прийомів полягає в тому, що перед відсиланням інформації до каналу зв’язку розкодовують.
Найпростіший код з перевіркою на парність полягає в тому, що ми дописуємо до послідовності з нулів та одиниць, яку збираємося пропустити через канал зв’язку, ще один символ (0 або 1) так, щоб загальна кількість одиниць стала парною. Наприклад до слова 00101 дописуємо 0, а до слова10101 дописуємо 1. одержуємо довші слова 001010 та 101011, які передаємо. На виході з каналу зв’язку спочатку підраховують парність кількості входжень одиниць в одержаному слові. Якщо ця кількість парна, то роблять висновок, що помилки при передачі не з’явилося, а процес декодування полягає просто у закресленні останнього символу в одержаному слові. Якщо ж кількість одиниць в одержаному слові виявилась непарною, то можна лише зробити висновок, що при передачі з’явились помилки, але не можна відновити передане слово. Кажуть, що такий код виявляє помилки, тоді як розглянутий вище код з повтореннями не лише їх виявляє, а й виправляє.
Розглянутий код дуже елементарний, тому має серйозні недоліки. Предмет теорії кодування полягає у створенні досконаліших кодів, які б об’єднували переваги і не мали недоліків щойно розглянутих кодів.
Практична частина
1 Запишемо усі інформаційні розряди в комірки B11 : I11.
2. У комірку J11 запишемо формулу для підрахунку парності або непарності одиниць в інформаційних розрядах - =ОСТАТ(СУММ($B11:$I11)+1;2) .
![]()

Формула записує 1 в розряд контролю, якщо кількість одиниць в інформаційних полях парна або 0 - якщо непарна.
3 Аналогічно заповнюємо комірки B19 : J19

4. Почергово вносимо однократну, двократну та трьохкратну помилки.
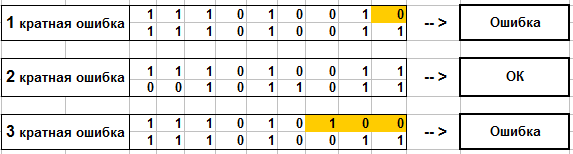
5. З наведених результатів видно програма в змозі знаходити непарну кількість помилок, але не здатна знаходити парну кількість
Висновок
Під час виконання роботи я засвоїла основні методи контролю помилок.
Міністерство освіти і науки
Відкритий міжнародний університет розвитку людини ”Україна”
Лабораторна робота №2
З предмету:
Контроль і діагностика програмних систем
На тему:
Построение груповых кодов и их применение для обнаружения и исправления ошибок
Виконав студент групи ПА-41
Руденко О.
Перевірив викладач
Капшук О.О.
Київ – 2010
Лабораторна робота №2
Теоретична частина
Лінійним блоковим (n,k) кодом – називається безліч N послідовностей довжини n над GF(q), званих кодовими словами, які характеризується тим, що сума двох кодових слів є кодовим словом, а твір будь-якого кодового слова на елемент поля також є кодовим словом.
Зазвичай N=qk, де до - деяке ціле число. Якщо q=2, лінійні коди називаються груповими, оскільки кодові слова утворюють математичну структуру, звану групою. При формування цієї коди лінійною операцією є підсумовування по mod2.
Способи завдання лінійних кодів
1. Перерахуванням кодових слів, тобто складанні списку всіх кодових слів коди.
Приклад. У таблиці 1 представлені всі кодові слова (5,3) - коди (ai - інформаційні, а bi - перевірочні символи).
Таблиця 1 |
|||||
|
№ |
a1 | a2 | a3 | b1 | b2 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 | 1 |
| 3 | 0 | 1 | 1 | 0 | 1 |
| 4 | 1 | 0 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 1 | 1 |
| 6 | 1 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 |
2. Системою перевірочних рівнянь, що визначають правила формування перевірочних символів по відомих інформаційних:
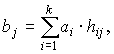
де
j - номер перевірочного символу;
i - номер інформаційного символу;
hij - коефіцієнти, що приймають значення 0 або 1 відповідно до правил формування конкретних групових код.
Приклад. Для коди (5,3) перевірочні рівняння мають вигляд:
b1= a2 + a3;
b2= a1 + a2.
3. Матричне, засноване на побудові матриць, що породжують і перевірочної.
Векторний простір Vn над GF(2) включає 2n векторів (n-последовательностей), а підпростором його є множина з 2k кодових слів довжини n, яке однозначно визначається його базисом, що складається з до лінійно незалежних векторів. Тому лінійний (n,k) - код повністю визначається набором з до кодових слів, що належать цьому коду. Набір з до кодових слів, відповідних базису, зазвичай представляється у вигляді матриці, яка називається такою, що породжує.
Приклад. (5,3) - код, який був представлений в таблиці 1, може бути заданий матрицею
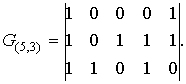
Решта кодових слів виходить складанням рядків матриць в різних поєднаннях.
Загальна кількість різних варіантів що породжують матрицю визначається виразом
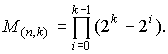
Для виключення неоднозначності в записі G(n,k) вводять поняття про канонічну або систематичну форму матриці, яка має вигляд
![]()
де
Ik - одинична матриця, що містить інформаційні символи;
Rk,r - прямокутна матриця, складена з перевірочних символів.
Приклад. Матриця, що породжує, в систематичному вигляді для (5,3) - коди
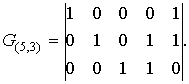
Матриця G(n,k), що породжує, в систематичному вигляді може бути отримана з будь-якої іншої матриці за допомогою елементарних операцій над рядками (перестановкою двох довільних рядків, заміною довільного рядка на суму її самій і ряду інших) і подальшою перестановкою стовпців.
Перевірочна матриця в систематичному вигляді має вигляд
![]()
де Ir - одинична матриця;![]() - прямокутна матриця в
транспонованому виді матриці Rk,r з
матриці, що породжує.
- прямокутна матриця в
транспонованому виді матриці Rk,r з
матриці, що породжує.
Приклад. Перевірочна матриця (5,3) - коди
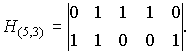
Практична частина
1. Запишемо генеруючу матрицю.
|
кол строк = длине инфор = 4 |
1 | 0 | 0 | 0 | 1 | 0 | 1 | |
|
G 7,4 = |
0 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
информационая часть = 10 => 1 0 1 0
|
X = |
1 | 0 | 1 | 0 | 1 | 1 | 0 |
2. На основі неї створимо перевірочну.
|
кол строк = |
1 | 1 | 0 | 1 | 1 | 0 | 0 | |
|
H = |
0 | 1 | 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
3. Запишемо наші інформаційні поля та згенеруємо перевірочні поля.
| Х= | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
|
исползуя соотношение H * X^T = S |
| если S = 0 то ош в код комб нет |
| в прот случ с имеет вид |
| s1 | 1 | результат декодиров | ||
|
S = |
s2 | 0 |
|
|
| s3 | 0 | error |
4. Внесемо помилку.
|
X = |
1 | 0 | 1 | 0 |
0 |
1 | 0 |
5. Ми отримали скореговане значення.
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
|
|||||||
|
s1 | 0 | результат декодиров | |||||||||||
|
S = |
s2 | 0 | |||||||||||
|
s3 | 0 | знач верно | |||||||||||
Висновок
Під час виконання роботи я написала програму що виявляє та виправляє однократну помилку в повідомленні, а також знаходить багатократні помилки.
Міністерство освіти і науки
Відкритий міжнародний університет розвитку людини ”Україна”
Лабораторна робота №3
З предмету:
Контроль і діагностика програмних систем
На тему:
Коди Хемминга
Виконала студентка групи ПА-41
Руденко О.
Перевірив викладач
Капшук О.О.
Київ – 2010

Теоретична частина

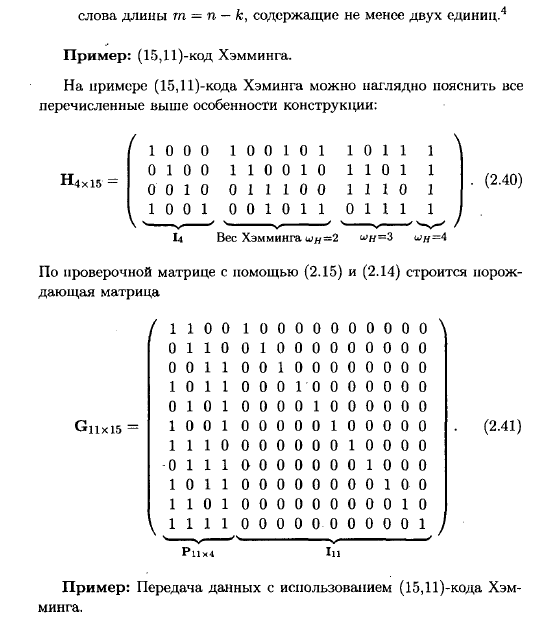

Практична частина
Проверочная матрица для кода Хемминга
|
кол строк = |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
|
H 15,4 = |
0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ||
перепишем ее, переставив столбцы с одной единицей в конец
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | b1 | b2 | b3 | b4 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
на ее основе создадим генерирующюю матрицу
информационая часть = 10 => 1 0 1 0
| кол строк = длине инфор. = 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | ||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | ||
|
G 15,4 |
0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | ||
Кодер
информационая часть = 10 => 1 0 1 0
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
X отпр = |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
Декодер
|
Х получ |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
|
исползуя соотношение H * X^T = S |
|
| если S = 0 то ош в код комб нет | |
| в прот случ с имеет вид |
| результат декодиров | ||
|
знач верно |
| s1 | 0 | |
|
S = |
s2 | 0 |
| s3 | 0 | |
| s4 | 0 |
Скоректированое значение
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |