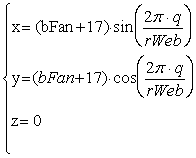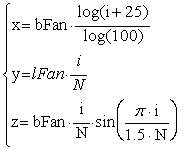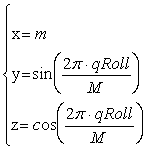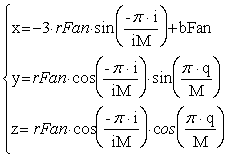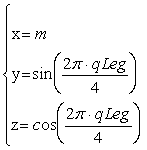Курсовая работа: Модель трехмерной сцены и библиотека OpenGL
Министерство образования и науки Российской Федерации
ФГАОУ ВПО «Уральский федеральный университет
им. первого Президента России Б.Н.Ельцина»
Теплоэнергетический факультет
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
Курсовая работа
по дисциплине «Компьютерная графика»
Модель трехмерной сцены и библиотека OpenGL
Студент: Котовский В.В.
Екатеринбург,
2010
Формулировка задачи
Средствами графической библиотеки OpenGL построить динамическую трехмерную сцену, включающую заданные тело и поверхность вида z=f(x,y). Заданные графические объекты должны быть представлены в следующих видах:
· в виде каркасной модели, позволяющей видеть контуры примитивов, из которых составлены объекты;
· в виде реалистических изображений, построенных с учетом параметров источника освещения и параметров отражающих свойств материала;
· в виде объектов с наложенной на них текстурой.
Заданное тело: вентилятор.
Заданная
поверхность: ![]() ,
,
где а, b – параметры.
Описание представления тела
Каркасные модели и поверхности могут быть представлены с помощью примитивов OpenGL, таких как:
× GL_LINES
× GL_LINE_STRIP
× GL_LINE_LOOP
× GL_TRIANGLES
× GL_TRIANGLE_STRIP
× GL_TRIANGLE_FAN
× GL_QUADS
× GL_QUAD_STRIP
× GL_POLYGON
×
Примитивы LINE могут быть использованы только для создание, например, сетки, поскольку нормали к ним не пропишешь и освещение на них не будет правильно отображаться.
Примитивы TRIANGLE и QUAD применимы для создания, пожалуй, всех поверхностей и тел – куб, пирамида, параллелепипед, сфера, цилиндр и т.д. С использованием TRIANGLE поверхности и тела получаются верно сглаженными при меньшем разбиении, нежели с QUAD.
Примитив POLYGON применим для получения круга.
В данной работе используются примитивы: GL_QUADS, GL_LINES, GL_POLYGON для построение каркасной модели тела, а для построения поверхности используется GL_QUADS.
Составные части модели вентилятора
Сетка
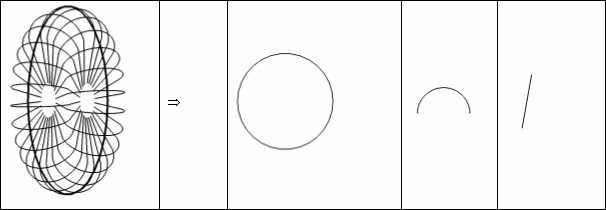
Сетка вентилятора составлена из трех основных частей
- Круговая составляющая сетки
|
|
|
| где bFan+17 – радиус окружности, rWeb – разбиение окружности |
Фрагмент кода программы круговой составляющей сетки
q=0;
while(q<rWeb)
{
glBegin(GL_LINES);
glVertex3f(0,(bFan+17)*sin(q*2*M_PI/rWeb),(bFan+17)*cos(q*2*M_PI/rWeb));
glVertex3f(0,(bFan+17)*sin((q+1)*2*M_PI/rWeb),(bFan+17)*cos((q+1)*2*M_PI/
rWeb));
glEnd();
q++;
}
- Дуговая составляющая сетки
|
|
|
| где bFan+2 – радиус полуокружности, rWeb – разбиение окружности |
Фрагмент кода программы дуговой составляющей сетки
int iWeb=0;
while(iWeb<rWeb)
{
glBegin(GL_LINES);
glVertex3f((bFan+2)*cos(iWeb*M_PI/rWeb),(bFan+2)*sin(iWeb*M_PI/rWeb)+15,0);
glVertex3f((bFan+2)*cos((iWeb+1)*M_PI/rWeb),(bFan+2)*sin((iWeb+1)*M_PI/rWeb)+15,0);
glEnd();
iWeb++;
}
- Косой прут сетки
|
|
| где a, b – параметры отрезка |
Фрагмент кода программы косого прута сетки
glBegin(GL_LINES);
glVertex3f(bFan+2,15,0);
glVertex3f(bFan,rFan,0);
glEnd();
1. Винт
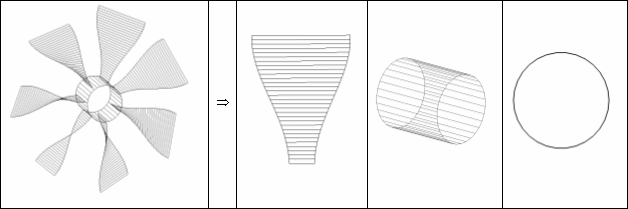
Винт вентилятора составлен из трех основных частей
- Лопасть вентилятора
|
|
|
| где bFan – половина ширины лопасти в основании, lFan – длина лопасти, N – разбиение лопасти |
Фрагмент кода программы лопасти вентилятора
double bFan=5;
double lFan=15;
glBindTexture(GL_TEXTURE_2D,texture4);
float N=30;
float NNN=100;
int i=0;
while(i<N)
{
glBegin(GL_QUADS);
glTexCoord2d(i/N,0);
glNormal3f(-2*lFan*bFan*i/(N*N)*sin(i*M_PI/(1.5*N)), 2*bFan*bFan/(N*log(NNN))*(log(i+26)*i*sin(i*M_PI/(1.5*N))-log(i+25)*(i+1)*sin((i+1)*M_PI/(1.5*N))), 2*bFan*lFan*log(i+25)/(N*log(NNN)));
glVertex3f(-bFan*log(i+25)/log(NNN),lFan*i/N,-bFan*(i)/N*sin(i*M_PI/(N*1.5)));
glTexCoord2d(i/N,1);
glNormal3f(-2*lFan*bFan*i/(N*N)*sin(i*M_PI/(1.5*N)), 2*bFan*bFan/(N*log(NNN))*(log(i+26)*i*sin(i*M_PI/(1.5*N))-log(i+25)*(i+1)*sin((i+1)*M_PI/(1.5*N))),2*bFan*lFan*log(i+25)/(N*log(NNN)));
glVertex3f(bFan*log(i+25)/log(NNN),lFan*i/N,bFan*(i)/N*sin(i*M_PI/(N*1.5)));
glTexCoord2d((i+1.0)/N,1);
glNormal3f(-2*lFan*bFan*i/(N*N)*sin(i*M_PI/(1.5*N)), 2*bFan*bFan/(N*log(NNN))*(log(i+26)*i*sin(i*M_PI/(1.5*N))-log(i+25)*(i+1)*sin((i+1)*M_PI/(1.5*N))),2*bFan*lFan*log(i+25)/(N*log(NNN)));
glVertex3f(bFan*log((i+26))/log(NNN),lFan*(i+1)/N,bFan*(i+1)/N*sin((i+1)*M_PI/(N*1.5)));
glTexCoord2d((i+1.0)/N,0);
glNormal3f(-2*lFan*bFan*i/(N*N)*sin(i*M_PI/(1.5*N)), 2*bFan*bFan/(N*log(NNN))*(log(i+26)*i*sin(i*M_PI/(1.5*N))-log(i+25)*(i+1)*sin((i+1)*M_PI/(1.5*N))),2*bFan*lFan*log(i+25)/(N*log(NNN)));
glVertex3f(-bFan*log((i+26))/log(NNN),lFan*(i+1)/N,
![]() *(i+1)/N*sin((i+1)*M_PI/(N*1.5)));
*(i+1)/N*sin((i+1)*M_PI/(N*1.5)));
glEnd();
i++;
}
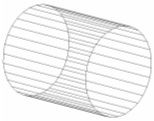
- Цилиндр, объединяющий лопасти вентилятора в винт
|
|
|
| где M – разбиение цилиндра |
Фрагмент кода программы цилиндра, объединяющего лопасти вентилятора в винт
M=30;
int qRoll=0;
glBindTexture(GL_TEXTURE_2D,texture2);
while (qRoll<M)
{
glBegin(GL_QUADS);
glTexCoord2d(0,qRoll/M);
glNormal3f(0,sin((2*M_PI*qRoll)/M),cos((2*M_PI*qRoll)/M));
glVertex3f(-1,sin((2*M_PI*qRoll)/M),cos((2*M_PI*qRoll)/M));
glTexCoord2d(0,(qRoll+1.0)/M);
glNormal3f(0,sin((2*M_PI*(qRoll+1))/M),cos((2*M_PI*(qRoll+1))/M));
glVertex3f(-1,sin((2*M_PI*(qRoll+1))/M),cos((2*M_PI*(qRoll+1))/M));
glTexCoord2d(1,(qRoll+1.0)/M);
glNormal3f(0,sin((2*M_PI*(qRoll+1))/M),cos((2*M_PI*(qRoll+1))/M));
glVertex3f(1,sin((2*M_PI*(qRoll+1))/M),cos((2*M_PI*(qRoll+1))/M));
glTexCoord2d(1,qRoll/M);
glNormal3f(0,sin((2*M_PI*qRoll)/M),cos((2*M_PI*qRoll)/M));
glVertex3f(1,sin((2*M_PI*qRoll)/M),cos((2*M_PI*qRoll)/M));
glEnd();
qRoll++;
}
- Крышка на цилиндр
|
|
|
| где M – разбиение круга |
Фрагмент кода программы цилиндра, объединяющего лопасти вентилятора в винт
int M=30;
int qFan=0;
glBegin(GL_POLYGON);
while (qFan<M)
{
glNormal3f(1,0,0);
if(qFan<M/4)
{
glTexCoord2d(0,1-qFan*4/M);
}
if((qFan>=M/4)&&(qFan<M/2))
{
glTexCoord2d((qFan-M/4)*4/M,0);
}
if((qFan>=M/2)&&(qFan<3*M/4))
{
glTexCoord2d(1,(qFan-M/2)*4/M);
}
if(qFan>=3*M/4)
{
glTexCoord2d(1-(qFan-3*M/4)*4/M,1);
}
glVertex3f(1,sin((2*M_PI*qFan)/M),cos((2*M_PI*qFan)/M));
qFan++;
}
glEnd();
2. Стойка
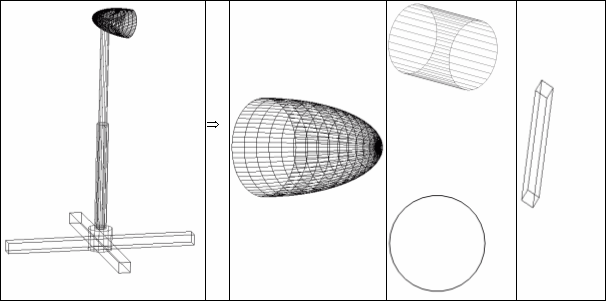
Стойка вентилятора составлена из трех основных частей
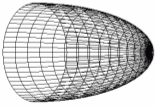
- Верхняя часть корпуса (полусфера)
|
|
|
| где rFan – наибольший радиус в фигуре, iM, M – разбиения полусферы |
Фрагмент кода программы верхней части корпуса (полусферы)
M=30;
int iM=30;
double phi, psi;
q=0;
int i=0;
while (q<M)
{
while (i<iM)
{
glBindTexture(GL_TEXTURE_2D, texture2);
glBegin(GL_QUADS);
phi=(-(M_PI*(i))/iM); psi=((M_PI*(q))/M);
glNormal3f(-3*rFan*sin(phi),rFan*cos(phi)*sin(psi),rFan*cos(phi)*cos(psi));
glTexCoord2d((sin(phi)+1)/2,(cos(psi)+1)/2);
glVertex3d(![]() *rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
*rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
phi=(-(M_PI*(i+1))/iM); psi=((M_PI*(q))/M);
glNormal3f(-3*rFan*sin(phi),rFan*cos(phi)*sin(psi),rFan*cos(phi)*cos(psi));
glTexCoord2d((sin(phi)+1)/2,(cos(psi)+1)/2);
glVertex3d(![]() *rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
*rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
phi=(-(M_PI*(i+1))/iM); psi=((M_PI*(q+1))/M);
glNormal3f(-3*rFan*sin(phi),rFan*cos(phi)*sin(psi),rFan*cos(phi)*cos(psi));
glTexCoord2d((sin(phi)+1)/2,(cos(psi)+1)/2);
glVertex3d(![]() *rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
*rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
phi=(-(M_PI*(i))/iM); psi=((M_PI*(q+1))/M);
glNormal3f(-3*rFan*sin(phi),rFan*cos(phi)*sin(psi),rFan*cos(phi)*cos(psi));
glTexCoord2d((sin(phi)+1)/2,(cos(psi)+1)/2);
glVertex3d(![]() *rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
*rFan*sin(phi)+bFan,rFan*cos(phi)*sin(psi),
rFan*cos(phi)*cos(psi));
glEnd();
i++;
}
i=0;
q++;
}
- Цилиндрический элемент стойки
|
|
Этот элемент стойки вентилятора состоит из цилиндров и кругов (крышки для цилиндров). Все они вызываются с помощью функции OpenGL – glCallList. Большая часть кода элементов вентилятора считывается программой лишь однажды, в СallLists, а вызов уже происходит неоднократно, по мере необходимости, в функции RenderGLScene(). Этот способ наиболее эффективен как для скорости работы программы, так и для редактирования готового кода программы, благодаря чему одинаковые примитивы (цилиндр, круг, квадрат, линии и т.д.) было легко использовать вызовом CallList и, применяя элементарные преобразования – поворот, перемещение, масштабирование объектов, видоизменять необходимым образом для получения данных элементов тела. Элементы цилиндр и круг были описаны выше, поэтому не будем повторяться. |
- Ножка стойки
|
|
Этот элемент тела строится через функцию CallList, в которой задан квадрат, вызываемый 4 раза и масштабированный по разным координатам по разному. |
Фрагмент кода программы ножек стойки вентилятора
//--- Квадрат
square=basis_leg+1;
glNewList(square,GL_COMPILE);
glBindTexture(GL_TEXTURE_2D,texture1);
glBegin(GL_QUADS);
glNormal3f(1,0,0);
glTexCoord2d(0,0);
glVertex3f(1,-1,-1);
glTexCoord2d(1,0);
glVertex3f(1,1,-1);
glTexCoord2d(1,1);
glVertex3f(1,1,1);
glTexCoord2d(0,1);
glVertex3f(1,-1,1);
glEnd();
glEndList();
//--- Ножка вентилятора
leg=square+1;
glNewList(leg,GL_COMPILE);
glCallList(square);
glRotatef(90,0,0,1);
glCallList(square);
glRotatef(90,0,0,1);
glCallList(square);
glRotatef(90,0,0,1);
glCallList(square);
glEndList();
3. Пульт управления
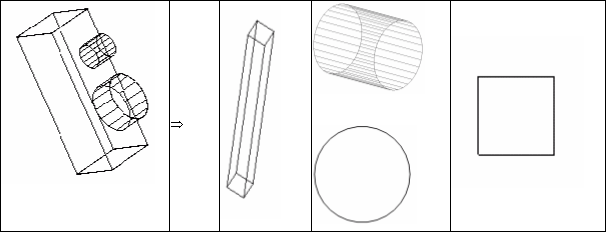
Пульт управления вентилятором составлен из четырех основных частей
- Основание пульта
|
|
Элемент строится из цилиндра с разбиением уменьшенным до 4х. |
Фрагмент кода программы основания пульта
M=4;
float qLeg=0;
glBindTexture(GL_TEXTURE_2D,texture5);
while (qLeg<M)
{
glBegin(GL_QUADS);
glNormal3f(0,sin(M_PI/4+qLeg*M_PI/2),cos(M_PI/4+qLeg*M_PI/2));
glTexCoord2d(0,qLeg/M);
glVertex3f(-1,sin((2*M_PI*qLeg)/M),cos((2*M_PI*qLeg)/M));
glTexCoord2d(0,(qLeg+1.0)/M);
glVertex3f(-1,sin((2*M_PI*(qLeg+1))/M),cos((2*M_PI*(qLeg+1))/M));
glTexCoord2d(1,(qLeg+1.0)/M);
glVertex3f(1,sin((2*M_PI*(qLeg+1))/M),cos((2*M_PI*(qLeg+1))/M));
glTexCoord2d(1,qLeg/M);
glVertex3f(1,sin((2*M_PI*qLeg)/M),cos((2*M_PI*qLeg)/M));
glEnd();
qLeg=qLeg+1.0;
}
- Крышки для пульта
|
|
Элемент состоит из квадрата, фрагмент кода которого содержался еще в описании ножки стойки вентилятора. |
- Кнопки на пульте
|
|
Элемент состоит из цилиндра и круга, примитивов описанных ранее. |
Описание освещения фигуры
Освещение тела происходит в OpenGL благодаря включению функции SetupLighting() с необходимыми параметрами и условиями, а также за счет правильной расстановки нормалей к примитивам, из которого состоит тело. Чтобы задаваемые нормали нормировались автоматически необходимо включить функцию – glEnable(GL_NORMALIZE);
Подробней остановимся на нахождении нормалей к отдельным элементам тела.
Всего нормали были найдены и прописаны в код программы для 6 примитивов, элементов тела.
1. Лопасть
Для определения нормалей лопасти, поскольку она представляет собой некую поверхность, была использована аналитическая формула для нахождения уравнения поверхности по трём точкам и формула для нахождения нормали к поверхности, что находится через частные производные уравнения поверхности.
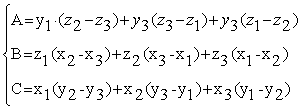
![]()
- уравнение поверхности, D не считаем, поскольку оно не влияет на выбор нормали.
Тогда координаты для нормали функции glNormal3f(a1,a2,a3) ,будет высчитываться по следующим формулам:
![]()
![]()
![]()
Исходя из записи уравнения поверхности и формулам, выписанные для коэффициентов в этой формуле получим:
![]()
![]()
![]()
Проведя расчет по данным формулам, получим что:
![]()
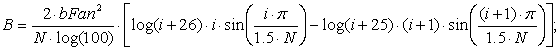
![]()
Для одинаково верного отображения освещения лопасти вентилятора как с одной, так и с другой стороны пришлось прибегнуть к подключению двустороннего освещения с помощью функции glLightModelf(GL_LIGHT_MODEL_TWO_SIDE, k), где к =1 для включения и к =0 для её вылючения.
2. Цилиндр
Чтобы определить нормаль для цилиндра нужно координату, что изменяется линейно оставить нулевой, а две другие координаты будут совпадать с соответствующими координатами цилиндра ввиду того, что в основании цилиндра лежит окружность.
В итоге получим координаты нормали:
(0,sin((2*M_PI*qRoll)/M),cos((2*M_PI*qRoll)/M));
3. Круг
Нормаль для круга определяется как перпендикуляр к этой поверхности.
4. Квадрат
Нормаль для квадрата определяется аналогичным образом как и для круга.
5. Параллелепипед
У параллелепипеда нормаль определяется перпендикуляром к каждой грани и значит для всей грани нормаль будет одна и направлена наружу.
6. Полусфера
Нормаль для полусферы определяется координатами самой фигуры, поэтому просто переписаны координаты из glVertex3f в glNormal3f.
Графическое представление тела с освещением

Описание наложения текстуры на тело
Для наложения текстур на тела, поверхности применяется функция SetupTextures(); В своей работе я использовал 4 вида текстуры, различных размеров. Текстура накладывается на цилиндр, параллелепипед, лопасть, квадрат. Способ наложения примитивно прост. По порядку разберёмся с каждой из фигур.
- Цилиндр.
Для того, чтобы наложить текстуру на фигуру необходимо было абстрактно раскрутить цилиндр в ровную поверхность, прямоугольник и сопоставить координаты полученного прямоугольника с координатами текстуры, как показанно на рисунках.
|
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


- Параллелепипед.
По аналогии с цилиндром абстрактно раскучиваем параллелепипед и наложим текстуру.
- Лопасть.
На лопасть текстура накладывается также исходя из особенности посторения. Поскольку лопасть получается путем видоизменения прямоугольника, т.е. строится из прямоугольником накладывающихся сторонами друг на друга и поворачивающихся по мере наложения на некий угол, то на лопасть текстура накладывается по аналогии с прямоугольником, как это было показано на цилиндре.
- Квадрат.
Текстура на квадрат накладывается один к одному с существующими координатами.
Графическое представление тела с текстурой

Описание представления поверхности
Поверхность ![]() строится перебором
координат x и y в пределах от -N до N и вычислением для каждой пары (x,y)
значения z.
строится перебором
координат x и y в пределах от -N до N и вычислением для каждой пары (x,y)
значения z.

![]()
Нормаль к поверхности в
точке ![]() находятся через честные
производные функции
находятся через честные
производные функции ![]() по x, y, z
по x, y, z
![]()

Примечание: Поскольку при обходе циклов по i и j они оба обращаются в ноль, то для того, чтобы избежать выход из области действительных значений координат в выражения для вектора нормали по х и по у вписаны незначительные для конечного результата добавки.
Текстура на поверхность
накладывается целиком и растягивается по размерам поверхности. Наложение
происходит соотношением координат поверхности и координат текстуры так, что
каждому QUAD, из которого строится поверхность,
соотносится часть растрового изображения, разбивая его, свои образом, на сетку.
Координаты текстуры для точки ![]() :
:
![]()
Графическое представление поверхности
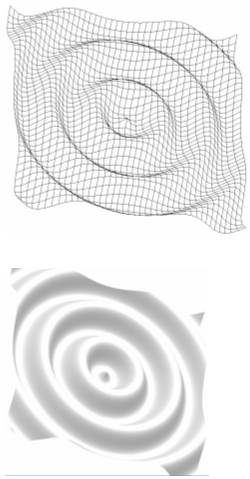

Список используемой литературы
1. А.В. Боресков. Графика Трехмерной Компьютерной Игры на Основе OpenGL. М.: «Диалог-МИФИ»,2004
2. Ю.М. Боянковский, А.В. Игнатенко, А.И. Фролов. Графическая библиотека OpenGL. уч.-мет.пособие. Москва,2003
3. NeHe Tutorials