Статья: Методика оценки живучести сложных систем военного назначения
Подполковник Р.А.Сафонов,
научный сотрудник Научно-исследовательского института Вооруженных Сил Республики Беларусь
Методика оценки живучести сложных систем военного назначения
УДК 519.876
В статье предложена разработанная методика оценки живучести сложных систем военного назначения, позволяющая получать комплексную оценку живучести системы с точки зрения ее структурной уязвимости и функциональности. Выработан математический аппарат для моделирования распространения внешних воздействий по структуре системы.
Деятельность современных сложных систем военного назначения неразрывно связана с функционированием их организационной и технической составляющих.
Поиск путей обеспечения живучести сложных систем требует постановки ряда научно-технических задач связанных с оценкой их живучести и синтезом живучих систем в дальнейшем.
Определения
В контексте данной статьи под теорией живучести систем будем понимать комплекс научных знаний о закономерностях сохранения системой определенного качества при повреждениях ее элементов и о способах обеспечения данного качества. Под повреждением принято понимать событие, заключающееся в нарушении исправности элемента или его составляющих вследствие влияния внешних воздействий (повреждающих факторов), превышающих установленные уровни. Совокупность внешних воздействий, составляющих нормальные (расчетные) условия эксплуатации не попадает под определение повреждающего фактора [1].
Живучесть – свойство войск (сил), оружия, военной техники, тыловых объектов, систем управления сохранять или восстанавливать в установленные сроки боевую способность в условиях воздействия противника [2, 3].
Боевая способность (боеспособность) – состояние войск (сил), позволяющее им успешно вести боевые действия в соответствии с предназначением в любых условиях обстановки и реализовать свои боевые возможности [3].
Боевые возможности – количественные и качественные показатели, характеризующие возможности воинских формирований по выполнению возложенных на них определенных боевых задач за установленное время в конкретной обстановке [3].
Следовательно, такое свойство систем, как живучесть во многом зависит от состояния системы, ее боевой способности, которое характеризуется ее боевыми возможностями, представляющими собой количественные и качественные показатели, позволяющие решать стоящие перед ней боевые задачи в интересах достижения основной цели ее функционирования [1, 2, 3].
Система – это совокупность (множество) элементов и связей (отношения, взаимодействия) между ними, обладающая определенной целостностью. Таким образом, под системой понимается не любая совокупность, а упорядоченная [4, 5].
Исследуемая система – реальная, физическая (модель будет являться виртуальной), сложная (структурно и функционально), искусственная, непрерывная (модель будет представлять собой дискретную систему), открытая система с управлением.
Состояние вопроса
Понятие живучести условно следует разделять на структурную и функциональную составляющие. Если исследование структурной составляющей живучести в основном сводится к выявлению уязвимых мест в топологии системы и определению степени их влияния на целостность системы (в большей степени присуще исследованию технических систем), то исследование функциональной составляющей живучести сводится к определению способности системы решать стоящие перед ней задачи при изменяющихся возможностях ее элементов (в основном относится к системам, обладающих поведенческим характером, зависящий от множества внешних и внутренних факторов).
Непредсказуемость изменения большинства факторов, влияющих на свойства систем и их топологию, придает особое значение оценке функциональной составляющей живучести с учетом состояния элементов системы и действующих между ними взаимосвязей.
Исследования, проведенные в работах [1, 6, 7, 8], подробно рассматривают подходы к оценке и управлению свойством живучести систем, основанные на построении логико-вероятностных моделей живучести с использованием вероятностных и детерминированных показателей.
В большинстве работ особое значение уделяется оценке живучести систем с точки зрения структуры ее построения и позволяет достаточно достоверно определять ее показатели.
Автором [1] разработано несколько методик, применимых для ассоциативных, ассоциативно-структурных и структурных систем, в которых учитывается их связность. Однако весомости действующих в системе взаимосвязей должного значения не придается.
В работе [7] этот недостаток устранен, но в предлагаемой методике не предусматривается оценка степени способности системы в целом функционировать после повреждающих воздействий на ее элементы.
Методика, предложенная в [8], направлена на оценку живучести систем с точки зрения ее функциональности с учетом иерархических взаимосвязей. Недостатком является то, что структурный аспект живучести представлен только одним видом взаимосвязей к тому же без учета их значимости.
Таким образом, можно считать, что на настоящий момент в теории живучести систем не обозначен устоявшийся методологический подход, позволяющий решать задачу комплексной оценки живучести сложной системы с точки зрения ее структурной уязвимости и функциональности с учетом значимости существующих в системе взаимосвязей.
Выбор показателей
Поскольку выбор показателей живучести должен удовлетворять требованиям соответствия его смыслового содержания определению живучести, обеспечения системности исследований, доступности моделирования и расчетов, чувствительности к манипуляциям на уровне характеристик, то их выбор предлагается осуществить следующим образом.
Проявление свойства живучести системы в целом предполагает рассмотрение структуры показателя успешности функционирования системы по назначению, как состоящего из множества параметров, характеризующих (определяющих) [1]:
условия, в которых осуществляется применение системы;
физическую природу внешних воздействий;
готовность системы к решению предстоящих задач;
решаемые системой задачи в условиях внешних воздействий;
необходимые для реализации задачи с вероятностью не ниже заданной.
Необходимость обеспечения сопоставимости оценок свойства живучести различных систем диктует требования к стандартизации первых двух групп параметров. Приняв допущение о том, что исследование живучести имеет смысл только в отношении систем, находящихся в состоянии готовности (третья группа параметров), можно прийти к выводу, что в ходе исследований соответствующий показатель живучести системы будет зависеть от двух последних групп параметров, удовлетворение которых определенным критериям будет говорить о сохранении системой состояния боеспособности.
Таким образом, свойство живучести систем с достаточно высоким уровнем доступности моделирования, расчетов и системности исследований может быть охарактеризовано вероятностью сохранения системой состояния боеспособности после внешнего воздействия на ее элементы.
Этим требованиям соответствует предлагаемая система общих и частных показателей:
общие
показатели (коэффициенты боеспособности элементов системы ![]() , коэффициент
живучести системы
, коэффициент
живучести системы ![]() );
);
частные
показатели (коэффициенты значимости существующих в системе взаимосвязей ![]() , вершинная
и реберная связность графа системы, структурная уязвимость ее элементов
, вершинная
и реберная связность графа системы, структурная уязвимость ее элементов ![]() ,
показатели проникновения внешнего воздействия
,
показатели проникновения внешнего воздействия ![]() и
времени его распространения
и
времени его распространения ![]() ).
).
Поскольку пути получения частных показателей подробно рассматривались в [12, 13, 14], то в рамках данной статьи будут рассматриваться только общие показатели.
Критерии оценки
Критериями для формализации коэффициента живучести могут служить результаты проведенных ранее исследований или собственные исследования, осуществленные, к примеру, одним из методов экспертной оценки.
При рассмотрении одной из систем, представляющей собой вид оперативного (боевого) обеспечения военных (боевых) действий, автором [8] выработаны критерии, характеризующие свойство живучести системы, которые применительно к формулировкам и определениям, используемым в предлагаемой методике, представляют собой следующие соотношения:
![]() ≥ 0,7
– система боеспособна;
≥ 0,7
– система боеспособна;
![]() при
обязательном решении наиболее значимой (весомой) задачи – система ограничено
боеспособна;
при
обязательном решении наиболее значимой (весомой) задачи – система ограничено
боеспособна;
![]() или
отсутствует возможность решения наиболее значимой (весомой) задачи – система не
боеспособна.
или
отсутствует возможность решения наиболее значимой (весомой) задачи – система не
боеспособна.
В этой же работе выработаны критерии для определения уровня боеспособности элементов системы в отдельности.
Специалистами в области управления, авторами [9], так же предложены критерии для оценки боеспособности элементов, относящихся к системе управления, и подходы к определению времени восстановления нарушенного управления.
Содержание методики
Предлагаемая ниже методика базируется на комплексном использовании метода анализа иерархии и теоретико-графового подхода, которые позволяют решить задачу оценки живучести системы военного назначения с учетом уязвимости топологии ее построения и влияния структурной уязвимости на достижимость основной цели функционирования системы.
Методика подразделяется на несколько этапов:
определение содержания боевой способности элементов системы и декомпозиция целей и задач функционирования системы;
схематизация существующих взаимосвязей между элементами;
построение взвешенного орграфа системы;
моделирование распространения внешних воздействий на структуру системы;
структурно-функциональный анализ живучести системы.
Определение боевой способности элементов системы предлагается осуществлять путем декомпозиции основной цели функционирования элемента в дерево стоящих перед элементом задач, частных задач и т.д. [10]. Назовем такое дерево – орграфом боеспособности элемента.
К примеру, рассматривая в самом общем случае систему, состоящую из 5 элементов (рисунок 1), в которой: элемент С – орган военного управления стратегического уровня, элемент О – орган военного управления оперативного уровня, элементы В1 и В2 – воинские части оперативного подчинения, В3 – воинская часть центрального подчинения.
Предположим,
что осуществлена декомпозиция цели и задач функционирования элемента С. В результате,
построен взвешенный орграф боеспособности элемента с весовыми коэффициентами ![]() ,
, ![]() дуг
орграфа боеспособности элемента С, который представлен на рисунке 2.
дуг
орграфа боеспособности элемента С, который представлен на рисунке 2.
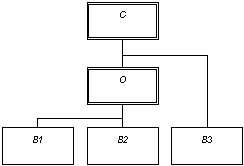
Рисунок 1 – Организационная структура системы
Взвешенные орграфы боеспособности элементов О и В исследуемой системы будут иметь вид, подобный представленному на рисунке 2.
При этом следует заметить, что в целях упрощения рассматриваемого примера, декомпозиции целей и задач функционирования элементов В1, В2 и В3 рассматриваются как идентичные, а их взвешенные орграфы боеспособности изоморфные.

Рисунок 2 – Взвешенный орграф боеспособности элемента С
Будем
считать, что определенные экспертами, к примеру, методом парных сравнений весовые
коэффициенты ![]() ,
, ![]() дуг орграфов боеспособности элемента О
имеют следующие значения:
дуг орграфов боеспособности элемента О
имеют следующие значения: ![]() . Для элементов В весовые коэффициенты
. Для элементов В весовые коэффициенты ![]() ,
, ![]() дуг орграфов боеспособности примут
значения:
дуг орграфов боеспособности примут
значения: ![]() . Приведенные значения будут в дальнейшем
использованы при вычислениях показателей живучести с использованием
рассматриваемого примера.
. Приведенные значения будут в дальнейшем
использованы при вычислениях показателей живучести с использованием
рассматриваемого примера.
В общем
случае вершина ![]() орграфа будет соответствовать основной
цели функционирования k-го элемента. Значение
орграфа будет соответствовать основной
цели функционирования k-го элемента. Значение ![]() назовем коэффициентом боеспособности
структурного элемента системы, который будет являться ее численной
характеристикой.
назовем коэффициентом боеспособности
структурного элемента системы, который будет являться ее численной
характеристикой.
Теоретическая
база метода определения весовых коэффициентов ![]() ,
, ![]() дуг орграфа боеспособности подробно изложена в [10] и практически
реализована при решении многих задач, например в [11].
дуг орграфа боеспособности подробно изложена в [10] и практически
реализована при решении многих задач, например в [11].
Построенные взвешенные орграфы боеспособности элементов в дальнейшем будут использованы для построения орграфа взаимосвязи системы и определения значимости действующих в ней взаимосвязей. Полученная информация может быть использована при декомпозиции целей и задач функционирования системы и определении исходных состояний ее элементов в ходе моделирования влияния внешних воздействий на систему.
Декомпозиции целей и задач функционирования системы является основой для реализации структурно-функционального анализа живучести исследуемой системы. Подходы к решению подобных задач рассматривалось выше, при построении орграфов боеспособности элементов системы [10, 11]. Особенностью можно считать лишь то, что декомпозиция осуществляется не для элементов в отдельности, а для системы в целом. При этом возможно использование информации, полученной в ходе построения орграфов боеспособности, при условии соответствия требуемой степени необходимой и достаточной детализации.
Построенную иерархию можно называть единый граф целей и задач. Для определения значимости элементов в системе и их вклада в решение каких-либо задач можно использовать метод анализа иерархий [10] или просто маркировать (цветом, цифрой, буквой) принадлежность составляющих граф вершин к какому-либо элементу системы.
В общем
случае, вершина ![]() единого орграфа целей и задач будет
соответствовать основной цели функционирования системы, степень реализации
которой характеризует ее живучесть и боеспособность. Показатель
единого орграфа целей и задач будет
соответствовать основной цели функционирования системы, степень реализации
которой характеризует ее живучесть и боеспособность. Показатель ![]() можно назвать коэффициентом живучести
системы, числовое значение которого будет отражать боевые возможности системы. Чем в большей степени
сохранились боевые возможности системы после внешнего воздействия на нее, тем в
более лучшем состоянии боеспособности она находится, а, значит, обладает наилучшим
свойством живучести.
можно назвать коэффициентом живучести
системы, числовое значение которого будет отражать боевые возможности системы. Чем в большей степени
сохранились боевые возможности системы после внешнего воздействия на нее, тем в
более лучшем состоянии боеспособности она находится, а, значит, обладает наилучшим
свойством живучести.
Реализуя
предлагаемую методику на примере системы (рисунок 1), строится декомпозиция
целей и задач ее функционирования, структура которой аналогична изображенной на
рисунке 2. Нижний уровень функциональной декомпозиции маркирован буквенными
символами, соответствующими элементам, задействованным в решении
соответствующих задач (элемент С – подзадачи ![]() ; О
–
; О
– ![]() ; В
–
; В
– ![]() ;
совместно С и О –
;
совместно С и О – ![]() ; О,
В –
; О,
В – ![]() ; С,
В –
; С,
В – ![]() ).
).
Будем
считать, что определенные экспертами весовые коэффициенты ![]() ,
, ![]() ,
, ![]() дуг
единого орграфа целей и задач имеют следующие значения:
дуг
единого орграфа целей и задач имеют следующие значения: 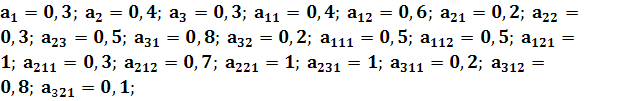
![]() .
.
Вероятность
достижения исследуемой системой основной цели ее функционирования в
установленные сроки характеризуется коэффициентом ![]() .
.
Проделав процедуру декомпозиции основной цели, представляется возможность получить единый n уровневый граф целей и задач с логикой «И». С его помощью можно определить степень влияния частных целей, задач на достижение основной цели функционирования системы, выражающееся в изменении значения коэффициента живучести.
Зная принадлежность вершин единого графа целей и задач к структурным элементам системы, можно установить элементы, наиболее значимые для живучести системы, а так же определить, как изменится значение коэффициента живучести в результате изменения боеспособности ее элементов. Коэффициент живучести, полученный после некоторого количества внешних воздействий на структуру системы, будет отражать способность системы функционировать в соответствии с предназначением с учетом структурной уязвимости ее элементов.
Схематизацию существующих взаимосвязей между элементами системы предлагается осуществлять на основе детального изучения и глубокого анализа их взаимодействия, путем построения орграфа взаимосвязи.
Построенные ранее орграфы боеспособности элементов системы будем рассматривать как связные компоненты орграфа взаимосвязи. Изоморфные орграфы боеспособности однотипных элементов можно отображать одной компонентой, если существующие взаимосвязи с другими элементами системы так же будут идентичными.
В дальнейшем, соединяя дугами вершины различных связных компонент орграфа взаимосвязи таким образом, чтобы дуга была направлена только от вершины одной компоненты к вершине другой, и эти вершины принадлежали низшему из рассматриваемых уровней иерархии, можно получить орграф взаимосвязи, характеризующий, в общем случае, связность системы и значимость существующих в ней взаимосвязей.
Наличие дуги и ее направление отражает существование реальной взаимосвязи между элементами (компонентами) системы (орграфа), выражающееся в конкретных действиях, мероприятиях, материальном или информационном обмене между элементами в ходе решения конкретных задач (соединяемых вершин орграфов боеспособности).
Степень детализации, используемой при построении орграфа взаимосвязи, необходимо выбирать исходя из размерности возникающей задачи. Если размерность возникающей задачи затрудняет ее решение, следует отказаться от низшего уровня иерархии (ослабление условий) и использовать для построения орграфа взаимосвязи уровень иерархии, предшествующий низшему уровню [5].
На примере рассматриваемой системы (рисунок 1) построение орграфа взаимосвязи осуществляется путем установления взаимосвязей между вершинами нижних уровней взвешенных орграфов боеспособности элементов системы (рисунок 3).
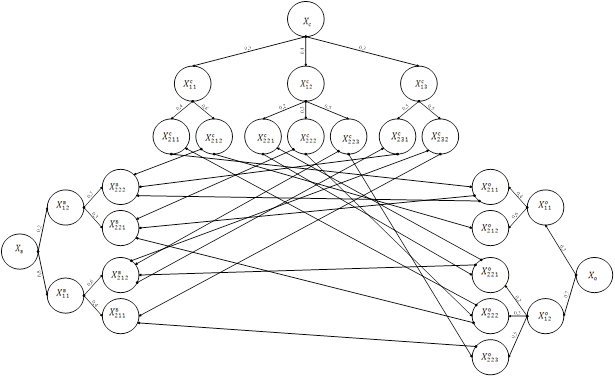
Рисунок 3 – Орграф взаимосвязи исследуемой системы
При необходимости детального анализа динамически сложных систем каждой дуге в орграфе взаимосвязи можно придавать определенный тип (цвет), в зависимости от того, какого типа возмущение она способна передавать (информационное, энергетическое и т.п.). Подобное усложнение позволит детализировать анализ, хотя, по сути, не повлияет на адекватность модели. Поэтому, в дальнейшем, при рассмотрении примера, будем считать дуги орграфа однотипными.
Помимо достижения основной цели, построение орграфа взаимосвязи позволит путем выявления на нем висячих и тупиковых вершин выявить неопределенности в распределении задач между элементами системы, уточнить корректность их формулировок при декомпозиции. Орграф взаимосвязи будет являться основой для вычисления коэффициентов значимости существующих взаимосвязей между структурными элементами системы и построении взвешенного орграфа системы.
Построение взвешенного орграфа системы и моделирование внешних воздействий на систему с использованием предлагаемой методики позволяют учитывать при оценке живучести системы влияние изменения возможностей элементов выполнять стоящие перед ними задачи на показатели качественного состояния других элементов, не подвергнувшихся воздействию непосредственно, и способность системы достигать основной цели ее функционирования.
Определение
значимости взаимосвязи между элементами системы (связными компонентами орграфа)
возможно осуществить исходя из значений весовых коэффициентов дуг ![]() ,
, ![]() ,
, ![]() орграфов
боеспособности элементов, используемых при построении орграфа взаимосвязи. При
этом, предлагается вычисление коэффициента значимости
орграфов
боеспособности элементов, используемых при построении орграфа взаимосвязи. При
этом, предлагается вычисление коэффициента значимости ![]() взаимосвязи
элементов
взаимосвязи
элементов ![]() и
и ![]() производить
по формуле
производить
по формуле
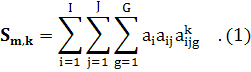
Значимой
для k-го элемента считается взаимосвязь с элементом ![]() ,
если из подмножества вершин k-й компоненты орграфа взаимосвязи, принадлежащих низшему уровню иерархии
графа боеспособности элемента, выходят n дуг к подмножеству вершин низшего
уровня иерархии k-й компоненты орграфа взаимосвязи. Вычисление весового
коэффициента значимости, взаимосвязи k-го элемента с m-м элементом осуществляется по формуле (1) для тех вершин k-й компоненты, которые являются
окончанием n дуг. При этом
,
если из подмножества вершин k-й компоненты орграфа взаимосвязи, принадлежащих низшему уровню иерархии
графа боеспособности элемента, выходят n дуг к подмножеству вершин низшего
уровня иерархии k-й компоненты орграфа взаимосвязи. Вычисление весового
коэффициента значимости, взаимосвязи k-го элемента с m-м элементом осуществляется по формуле (1) для тех вершин k-й компоненты, которые являются
окончанием n дуг. При этом
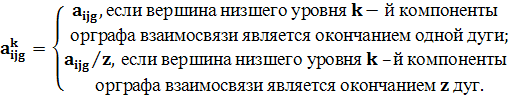
Подобный
подход к определению значимости существующих в системе взаимосвязей позволит определить
их численное выражение. Из (1) очевидно, что ![]() , т.е.
так как в (1) используются весовые коэффициенты орграфа боеспособности
структурного элемента системы, являющегося окончанием дуг взаимосвязи двух
элементов, то сумма
, т.е.
так как в (1) используются весовые коэффициенты орграфа боеспособности
структурного элемента системы, являющегося окончанием дуг взаимосвязи двух
элементов, то сумма ![]() всех
взаимосвязей k-го элемента не превысит 1. При этом значение 1 для суммы
всех
взаимосвязей k-го элемента не превысит 1. При этом значение 1 для суммы ![]() всех
взаимосвязей k-го элемента означает, что его боеспособность целиком зависит от
наличия действующих между элементами системы взаимосвязей и качественного состояния
взаимосвязанных элементов. Значение 0 – говорит об автономности элемента при
решении стоящих перед ним задач или, что одно и то же, об отсутствии
взаимосвязи между элементами. В случае, отличном от рассмотренных выше,
значение суммы
всех
взаимосвязей k-го элемента означает, что его боеспособность целиком зависит от
наличия действующих между элементами системы взаимосвязей и качественного состояния
взаимосвязанных элементов. Значение 0 – говорит об автономности элемента при
решении стоящих перед ним задач или, что одно и то же, об отсутствии
взаимосвязи между элементами. В случае, отличном от рассмотренных выше,
значение суммы ![]() всех
взаимосвязей k-го элемента примет вид:
всех
взаимосвязей k-го элемента примет вид:
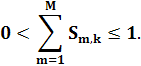
Таким образом, взаимосвязи структурных элементов системы могут быть формализованы при помощи дуг орграфа взаимосвязи, а их значимость определена по правилу (1).
В результате реализации предложенного подхода предоставляется возможность преобразовать орграф взаимосвязи во взвешенный орграф системы. При этом следует считать тождественными понятия: граф (орграф) системы и структура системы, вершина графа и элемент системы, ребро (дуга) графа и связь меду элементами системы, вес вершины и боеспособность элемента.
Для этого связные компоненты орграфа взаимосвязи необходимо стянуть в вершины. Их численность должна соответствовать количеству действующих структурных элементов системы, даже если какой-то из них в орграфе взаимосвязи представлял несколько изоморфных орграфов боеспособности.
Для всякого
конечного графа примем обозначение ![]() ,
где
,
где ![]() –
множество вершин, а
–
множество вершин, а ![]() –
множество его ребер. Орграф моделируемой системы не должен иметь петель.
–
множество его ребер. Орграф моделируемой системы не должен иметь петель.
Построение взвешенного орграфа системы (рисунок 4), рассматриваемой на примере, следует осуществлять с учетом организационной структуры системы (рисунок 1), построенного орграфа взаимосвязи (рисунок 3) и полученных экспертным путем весовых коэффициентов на всех предыдущих этапах реализации методики. Боеспособность всех элементов в начальный момент времени будем считать идеальной, т.е. равной 1.
В общем случае, воздействие, распространяясь по системе, «теряет свою силу» в той степени, насколько менее значима существующая между элементами взаимосвязь.
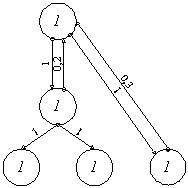
Рисунок 4 – Взвешенный орграф системы
Таким
образом, на орграфе системы ![]() для
вершины
для
вершины ![]()
![]() ,
соответствующей k-му элементу системы, весовой коэффициент
,
соответствующей k-му элементу системы, весовой коэффициент ![]() является
величиной, характеризующей боеспособность k-го элемента. А весом
является
величиной, характеризующей боеспособность k-го элемента. А весом ![]() ,
, ![]() ,
, ![]() дуги
дуги
![]() является
число
является
число ![]() , соответствующее
значимости действующей между элементами взаимосвязи, которое будет
характеризовать сохранившуюся долю передаваемого внешнего воздействия при
переходе от вершины
, соответствующее
значимости действующей между элементами взаимосвязи, которое будет
характеризовать сохранившуюся долю передаваемого внешнего воздействия при
переходе от вершины ![]() к
вершине
к
вершине ![]() .
.
Процесс
изменения значений коэффициентов боеспособности элементов системы можно
отразить следующим правилом внешнего воздействия. Внешнее воздействие ![]() определяется
в дискретном времени
определяется
в дискретном времени ![]() ,
которое задается выражением
,
которое задается выражением
![]()
при ![]() .
.
Тогда для ![]() для
k-й вершины
графа G результатом внешнего воздействия будет
для
k-й вершины
графа G результатом внешнего воздействия будет
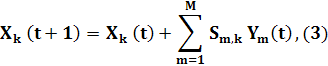
полагая при этом, что M – число вершин, смежных k-й, которые являются началом ![]() дуг.
дуг.
Формулы (2) и (3) задают
изменения весов вершин графа ![]() ,
определяя динамику распространения внешних воздействий по структуре системы.
,
определяя динамику распространения внешних воздействий по структуре системы.
При этом, в соответствии с
(2), внешние воздействие ![]() будет
иметь отрицательный знак, если оно влечет снижение боеспособности элемента, и
знак «+» – если направлено на восстановление его боеспособности.
будет
иметь отрицательный знак, если оно влечет снижение боеспособности элемента, и
знак «+» – если направлено на восстановление его боеспособности.
Внешнее воздействие на
взвешенном орграфе G предлагается определять по правилу (2) с вектором начальных
значений ![]() и
вектором внешний воздействий
и
вектором внешний воздействий ![]() ,
задающим внешнее воздействие
,
задающим внешнее воздействие ![]() в
каждой k-й вершине в момент времени
в
каждой k-й вершине в момент времени ![]() . Внешнее
воздействие в паре с вектором начальных значений описывает состояние системы в
начальный момент времени, когда под влияние внешних воздействий попадают все
или часть элементов системы.
. Внешнее
воздействие в паре с вектором начальных значений описывает состояние системы в
начальный момент времени, когда под влияние внешних воздействий попадают все
или часть элементов системы.
Внешнее воздействие, в
котором вектор ![]() ,
, ![]() имеет
только k-ю, отличную от 0 компоненту, можно считать простым воздействием с
начальной вершиной
имеет
только k-ю, отличную от 0 компоненту, можно считать простым воздействием с
начальной вершиной ![]() .
.
К примеру, смоделируем простое внешнее воздействие на систему (рисунок 4) с начальной вершиной В3, при котором одноименный элемент системы в определенной степени утратит часть имеющихся ранее боевых возможностей, что повлечет снижение его боеспособности, т.е. вероятности достижения цели его функционирования до 0,7. Исходя из этого, с учетом (2) начальные условия будут иметь вид:
![]()
![]()
Рассматривая на первом этапе однократное распространение внешнего воздействия по всем действующим в системе взаимосвязям, с помощью (2), (3) установим снижение боеспособности элементов системы до уровня:
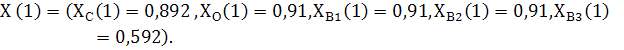
Представление исследуемой системы в виде взвешенного орграфа G и формализация внешнего влияния на систему внешнего воздействия (2), (3) определяют модель распространения воздействий по системе. Построение этой модели позволяет выяснить, как внешнее воздействие распространяется по структуре системы и влияет на качественное состояние ее элементов.
Оценку живучести сложной системы предлагается производить на едином графе целей и задач, построенном в результате декомпозиции целей и задач функционирования системы, путем определения значения коэффициента живучести. Значение коэффициента живучести приобретает структурный аспект в результате коррекции коэффициентов качества решения задач на едином графе целей и задач по результатам моделирования распространения внешнего воздействия по взвешенному орграфу системы и изменения коэффициентов боеспособности ее элементов.
Возвращаясь к рассматриваемому примеру, при анализе декомпозиции целей и задач функционирования системы установлено, что наиболее значимым в функционировании системы является элемент С. Суммарная значимость задач и их более мелких составляющих, решаемых с его помощью, превышает в 1,4 раза аналогичный показатель элемента О и в более чем в 2,4 раза любой из элементов В в отдельности. Соотношение суммарной значимости задач, решаемых элементами О и любым из В, составляет 1,73.
Подставив в
единый граф целей и задач системы полученные значения боеспособности элементов ![]() ,
характеризующие их боевые возможности по качественному и своевременному решению
стоящих перед ними задач, представляется возможность с использованием
математического аппарата [10, 11] определить значение коэффициента живучести
,
характеризующие их боевые возможности по качественному и своевременному решению
стоящих перед ними задач, представляется возможность с использованием
математического аппарата [10, 11] определить значение коэффициента живучести ![]() системы,
полученного в результате первого этапа распространения внешнего воздействия по
структуре системы
системы,
полученного в результате первого этапа распространения внешнего воздействия по
структуре системы
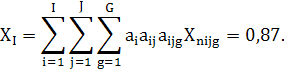
При этом,
значения качественных показателей совместного решения задач ![]() несколькими
элементами вычислялись с учетом определенной выше суммарной значимости
соответствующих элементов при их решении.
несколькими
элементами вычислялись с учетом определенной выше суммарной значимости
соответствующих элементов при их решении.
Однако имеющиеся во взвешенном орграфе системы циклы при распространении внешнего воздействия вызовут дальнейшее изменение показателей качественного состояния ее элементов, хотя и с эффектом «затухания».
В
результате этого, второй этап распространения внешнего воздействия по структуре
системы, характеризующийся его повторным распространением по всем действующим
взаимосвязям, вызовет изменение показателей боеспособности элементов системы на
значения, не превышающее 0,04, а коэффициента живучести ![]() – до
уровня
– до
уровня ![]() .
.
Завершение
третьего этапа будет характеризоваться значением коэффициента живучести ![]() и
т.д.
и
т.д.
Следует заметить, что предложенное в методике правило распространения внешнего воздействия по структуре системы (2), (3) позволяет осуществлять формирование внешних воздействий положительного характера, т.е. моделировать мероприятия по восстановлению боеспособности системы в интересах повышения ее живучести.
Анализ
состояния системы и оценку ее живучести следует производить, моделируя внешние
воздействия на несколько или на все элементы системы, прикладывая поочередно к
различным вершинам графа системы внешние воздействия типа ![]() .
Это позволит выявить в структуре системы «окна уязвимости», представляющие
собой структурные элементы системы, воздействие на которые в течении
незначительного промежутка времени, повлечет потерю боеспособности более
90 % системы, а так же определить глубину распространения внешнего воздействия
по структуре системы [7].
.
Это позволит выявить в структуре системы «окна уязвимости», представляющие
собой структурные элементы системы, воздействие на которые в течении
незначительного промежутка времени, повлечет потерю боеспособности более
90 % системы, а так же определить глубину распространения внешнего воздействия
по структуре системы [7].
Существенной особенностью предложенного подхода к исследованию живучести сложных систем является возможность предусмотреть потерю боеспособности элементом с наиболее значительным в первоначальный момент времени потенциалом его качественного состояния. Этот подтверждает зависимость динамики показателя функциональной составляющей живучести системы от расположения ее элементов в структуре.
Проведенные в ходе рассмотрения примера вычисления позволили подчеркнуть особенность, позволяющую проводить достаточно быструю, хотя и приблизительную оценку состояния живучести системы. Она состоит в том, что изменение боевой способности наиболее значимого элемента (элемент С) во многом отражало изменение коэффициента живучести системы, полученного на едином графе целей и задач. Иными словами, достаточно характерным для оценки живучести системы в целом является показатель достижения определенного состояния наиболее значимым ее элементом. К примеру, можно считать, что система находится в не боеспособном состоянии, если показатель качественного состояния хотя бы одного из наиболее значимых ее элементов ниже некоторого допустимого уровня.
В рассматриваемом примере боеспособность элемента С по результатам моделирования третьего этапа распространения внешнего воздействия по системе не опустилась ниже 0,84. Используя критерии, предложенные для элементов системы управления в [9], можно установить, что элемент и система в целом находятся в боеспособном состоянии.
Таким образом, предлагаемая методика дает возможность:
определить значимость действующих в системе взаимосвязей;
моделировать распространения внешних воздействий по структуре системы;
получить комплексную оценку живучести исследуемых систем с точки зрения их функциональности и структурной уязвимости.
ЛИТЕРАТУРА
1. Стекольников Ю.И. Живучесть систем. – СПб.: Политехника, 2002.
2. Сборник основных военных терминов и понятий/ ГУ «НИИ ВС РБ»; редкол.: Турбан Н.Н. [и др.]. – Минск: Изд-во ГШ ВС РБ. – 2009.
3. Военный энциклопедический словарь/редкол.: Н.В.Огарков. – М.: Воениздат, 1984.
4. Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении. – М.: Финансы и статистика, 2002.
5. Романов В.Н. Системный анализ для инженеров. – СПб.: СЗГЗТУ, 2006.
6. Черкесов Г.Н. Методы и модели оценки живучести сложных систем. – М.: Знание, 1987.
7. Кочкаров А.А., Малинецкий Г.Г. Обеспечение стойкости сложных систем. Структурные аспекты. М.: ИПМ им. М.В.Келдыша РАН, 2005.
8. Казаков В. И., Основы теории топогеодезического обеспечения боевых действий войск. Раздел 1. – М.: ВИА, 1977.
9. Глод И.В., Синявский В.К. Решение проблемы восстановления нарушенного управления войсками (силами) в современных условиях// Наука и военная безопасность. – 2009. – № 3.
10. Т. Саати, К. Кернс. Аналитическое планирование. Организация систем. – М.: Радио и связь, 1991.
11. Разработка методического аппарата оценки эффективности системы вооружения Вооруженных Сил и предложений по совершенствованию существующей системы вооружения Вооруженных Сил Республики Беларусь (шифр «Почин-1М»): отчет о НИР (промежут.)/ ГУ «НИИ ВС РБ»; рук. темы А.А.Петьков. – Минск, 2003. – инв. № 16.
12. Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс. – СПб.: Издательство «Лань», 2004.
13. Емеличев В.А. Мельников О.И. Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: Наука, 1990.
14. Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки бесконтурных графов. – Новосибирск: Наука, 1998.