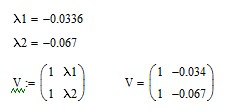Курсовая работа: Дослідження властивостей технологічного агрегата як многомірної системи
Розрахунково-пояснювальна записка
До курсової роботи з основ теорії систем та системного аналізу:
Дослідження властивостей технологічного агрегата як многомірної системи
Одеса - 2010
1. Еквівалентні та апроксимаційні перетворення моделі
1.1 Нелінійна модель агрегату
На прикладі розглянемо конкретну технічну систему - змішувальний бак:
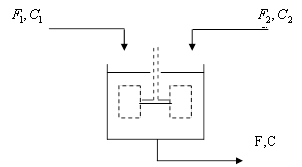
Рисунок 1. Модель бака.
F1,F2,F - витрати рідини на притоці і витоці системи, м3/с;
C1,C2,C - концентрація на витоці і притоці системи, кмоль/м3;
h - рівень рідини в бакові, м; S - площа бака, м2;
V - об'єм рідини в бакові, м3;
Запишемо рівняння системи в стаціонарному (встановленому) стані, коли притік дорівнює витоку (рівняння матеріального балансу):
F10+F20-F0=0;
C1![]() ,
,
де індекс 0 означає встановлений стан.
Записавши умови балансу кінетичної і потенціальної енергії на виході із бака
![]() ,
,
де
p - густина рідини, кг/м3;
w - швидкість витоку, м/с;
q - прискорення вільного падіння,q=9.81 м/с2;
і припускаючи, що
d - діаметр вихідного трубопроводу, м.
Одержимо:
![]() чи, відповідно,
чи, відповідно,
![]() , де
, де
k - коефіцієнт.
При зміні витрат у системі відбувається накопичення речовини і перехід до нового встановленого стану. Цей перехідний процес описується диференціальними рівняннями
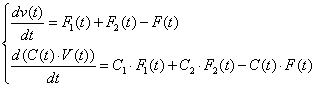
де dv/dt - приріст об'єму рідини, ![]() - приріст маси рідини.
- приріст маси рідини.
Наведемо цю систему у стандартному вигляді:
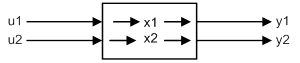
Позначимо:
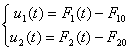
![]() − зміна у часі відхилення витрати від номінального щодо першого
каналу
− зміна у часі відхилення витрати від номінального щодо першого
каналу
![]() − теж щодо другого каналу
− теж щодо другого каналу
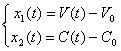
![]() − зміна у часі відхилення об'єму від номінального у бакові;
− зміна у часі відхилення об'єму від номінального у бакові;
![]() − відхилення концентрації від номінальної;
− відхилення концентрації від номінальної;
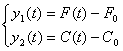
![]() - зміна втрати на виході;
- зміна втрати на виході;
![]() - зміна концентрації на виході.
- зміна концентрації на виході.
1.2 Нелінійна модель в стандартній формі
Розглянемо поповнення бака від 0 до номінального значення витрати з урахуванням приросту поданого лінеаризованій моделі. Таким чином, розглянемо стрибок u1=0,03; u2=0.
Позначивши ![]() ,
рівняння бака запишемо у вигляді системи:
,
рівняння бака запишемо у вигляді системи:
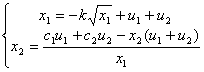
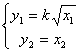
![]()
Перше рівняння є нелінійним зі змінними що розділяються
![]()
З урахуванням того, що ![]() запишемо:
запишемо:
![]() ,
,
чи підставляючи
![]()
Виразимо ![]()
Підставляємо ![]() та
та
![]()
Таблиця 1.
| y1 | 0.141 | 0.142 | 0.143 | 0.144 | 0.145 | 0.146 | 0.147 | 0.148 | 0.149 | 0.150 | 0.151 |
| t, с | 0 | 1.5 | 3.188 | 5.116 | 7.357 | 10.026 | 13.315 | 17.585 | 23.643 | 34.072 | 68.958 |
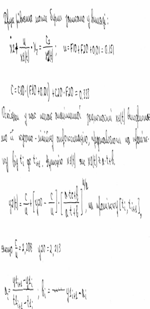

1.3 Отримання квадратичної моделі
Рівняння квадратичної моделі має вигляд:
![]()
Матриці з підстановкою номінального режиму:


1.4 Запис білінійної моделі
![]()
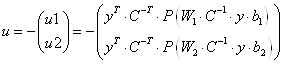
![]()
![]()
![]()
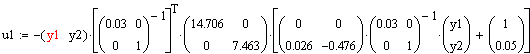
![]()
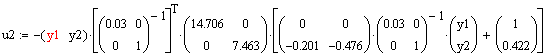
![]()
1.5 Лінеаризована модель
Лінеаризуємо залежність ![]() , розклавши її на ряд
Тейлора.
, розклавши її на ряд
Тейлора.
![]()
![]()
![]()
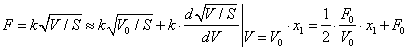
З урахуванням раніше викладеного запишемо:
![]()
![]() ; (т.к
; (т.к ![]() ), где
), где ![]() ;
;
![]()
Припустивши у випадку остатку ![]() . Тоді підставивши похідну
. Тоді підставивши похідну ![]() , отримаємо
, отримаємо
![]() ;
;
![]()
![]()
В результаті маємо
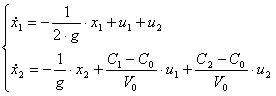
Представивши цю систему в матричній формі:
![]()
Тоді матриці А і В запишуться в вигляді
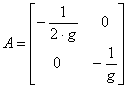 ,
, 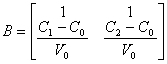
Для визначення матриці С необхідно встановити
зв'язок між векторами x и y. Оскільки ![]() ,
,
![]() , то
, то
![]() ;
; ![]()
![]() , то
, то ![]()
Тоді
![]()
Система буде мати вигляд
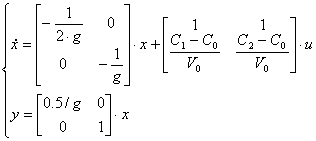
Коефіцієнти моделі системи:
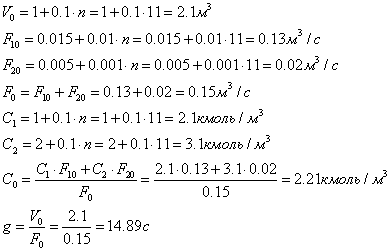
![]()
![]()
![]()
1.6 Модель в дискретному часі
система в дискретному часі має вид:
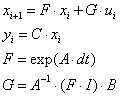
dt=14,89 c.
![]()
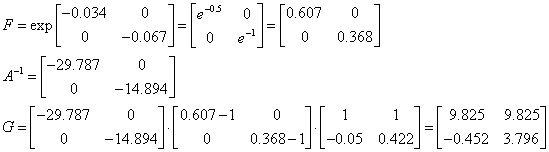
Таким чином
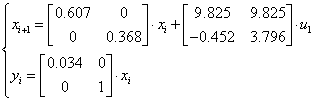
Задавшись ![]() ,
,
![]() , тоді
, тоді
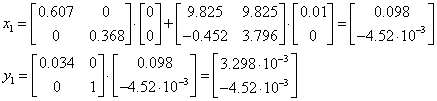
Результати подальших ітерацій представлено в таблиці:
Таблиця 3.
| Збурення | Реакція виходу системи y (t) |
|
|||||||
|
u1=0 u2=0,01 |
y1 y2 |
0 0 |
0,003298 0,00452 |
0,005299 0,00469 |
0,00773 0,006183 |
0,006512 0,006795 |
0,00725 0,00702 |
0,00769 0,00713 |
|
| час t, с | 0 | 14,894 | 29,787 | 44,681 | 59,574 | 74,468 | 89,362 | ||
1.7 Перетворення моделі у форму Ассео
![]()
![]()
![]()
![]()
![]()
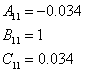
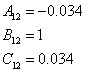
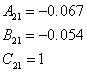
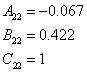
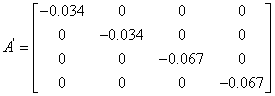
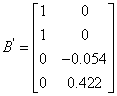
![]()
1.8 Обчислення МПФ системи
![]()
![]() ;
; ![]() ;
; ![]() ; n=2; i=1;
; n=2; i=1; ![]()
![]()
![]()
![]()
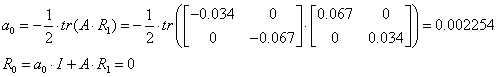
Таким чином
![]()
![]()
![]()
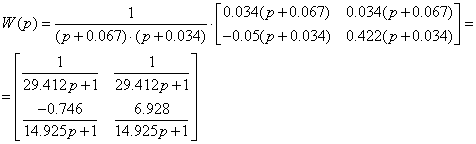
1.9 Структурні схеми системи в початковій формі, формі Ассео, ЗЗП
![]()
![]()
![]()
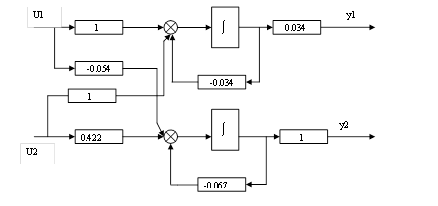
Рисунок 2. Структурна схема системи в початковій формі.
![]()
![]()
![]()
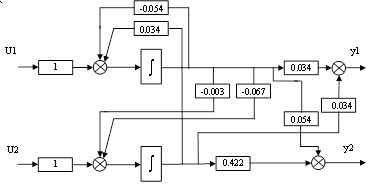
Рисунок 3. Структурна схема системи в формі Ассео.
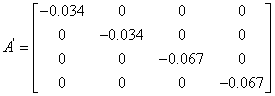
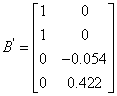
![]()
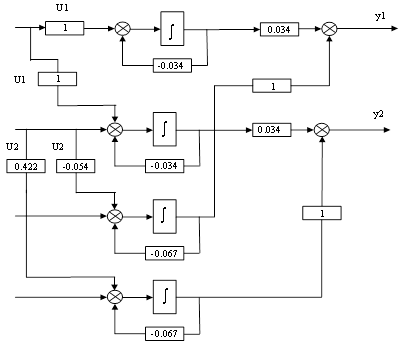
Рисунок 4. Структурна схема системи у зовнішньозв'язанному поданні.
1.10 Лінеаризована модель в непереривному і дискретному часі з датчиками і ВМ
a) в непереривному часі
![]()
![]()
![]()
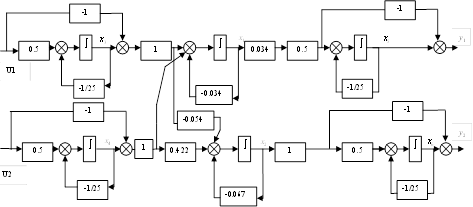
Рисунок 5. Структурна схема системи в неперервному часі з датчиками і ВМ.


![]()
б) в дискретному часі
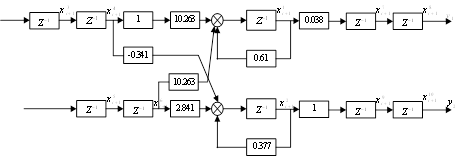
Рисунок 6. Структурна схема системи в дискретному часі з датчиками і ВМ.
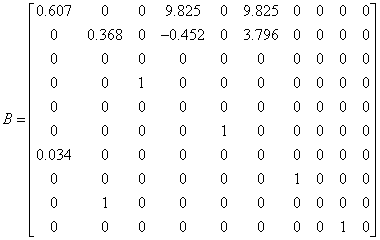
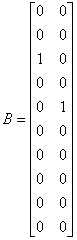
![]()
![]()
1.11 Умова правомірності децентралізації
Система в формі Ассео:
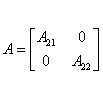
![]()
![]() ,
, ![]() ,
,![]() ,
,
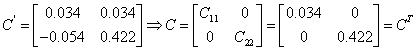
![]()
![]()
Спектральна норма матриці ![]() , тобто максимальне
сингулярне число матриці:
, тобто максимальне
сингулярне число матриці:
![]() ,
, ![]() .
.
Спектральна норма матриці F:
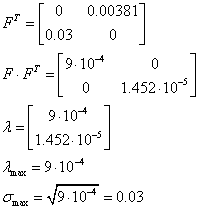
Тоді:
![]()
![]()
Похибка складає:
![]()
Можна допустити, що децентралізація є допустимою.
2. Аналіз якісних властивостей системи
А) ![]()
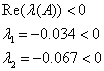
Матриця являється гурвіцевою.
Б) ![]()
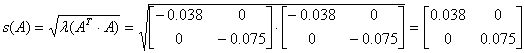
max s1 (A) =||A||2=0.067<1
Відповідно, матриця А є нільпотентною.
Перевірити, чи є система (А, В, С) сталою, керованою, спостережною, ідентифікованою з вектором-стовпцем х = (1; 1.25), параметрично інваріантною, мінімально фазовою, розчеплюваною, мінімально.
А) сталість:
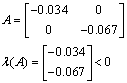
Відповідно система являється сталою.
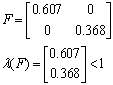
Відповідно система являється сталою.
Б) керованість:
![]()
![]() ;
; ![]()
![]()
По першому входу:
![]()
![]()
Система керована по першому входу.
По другому входу:
![]()
![]()
Система керована по другому входу.
В) спостережність:
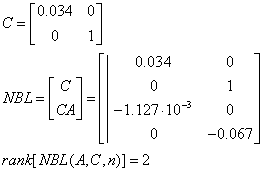
Система спостережна.
Г) ідентифікованість:
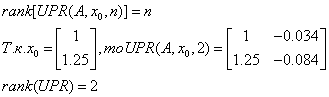
Система є ідентифікована.
Д) параметрична інваріантність:
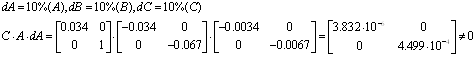
Система не інваріантна відносно відхилення dA.
![]()
Система не інваріантна відносно відхилення dB.
![]()
Система не інваріантна відносно відхилення dС.
Е) мінімальнофазовість і астатичність:
![]()
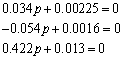
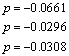
![]()
![]() система являється мінімально фазовою і статичною.
система являється мінімально фазовою і статичною.
Ж) розчеплюваність:
![]()
![]()
![]()
![]() det=0.016
det=0.016
Система є розчеплюваною.
3. Дослідження процесів в системі і аналіз кількісних властивостей системи
3.1 Побудова графіків розгінних кривих непереривної системи
Побудова графіку розв'язання у (t) для системыи {А, В, С}, якщо
![]() и
и ![]()
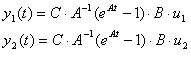
![]()
![]()
![]()
Таблиця 4.
| Збурення | Реакція виходу системи y (t) | |||||||
|
u1=0,01 u2=0 |
y1 y2 |
0 0 |
0,00435 0,00445 |
0,00681 0,00609 |
0,00820 0,0067 |
0,00898 0,00692 |
0,00942 0,00700 |
0,00967 0,00703 |
|
u1=0 u2=0,01 |
y1 y2 |
0 0 |
0,00435 0,037 |
0,00681 0,051 |
0,00820 0,056 |
0,00898 0,058 |
0,00942 0,059 |
0,00967 0,059 |
| час t, с | 0 | 14,3 | 28,6 | 42,9 | 57,2 | 71,5 | 85,8 |
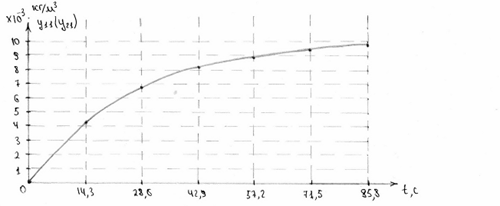
Рисунок 7. Розгінна крива витрати рідини для неперервної системи при збуренні 0 і 0,01.
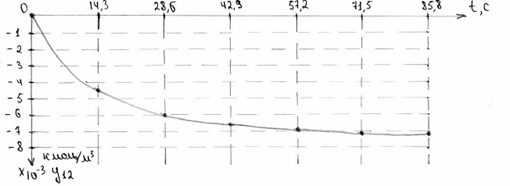
Рисунок 8. Розгінна крива концентрації для неперервної системи при збуренні 0.
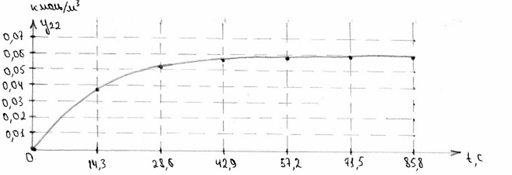
Рисунок 9. Розгінна крива концентрації для неперервної системи при збуренні 0,01.
3.2 Побудова графіків кривих разгону дискретної системи
Система в дискретному часі має вид:
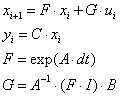
dt=14,89 c.
![]()
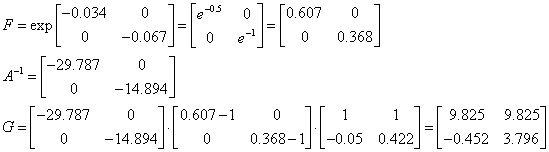
Таким чином
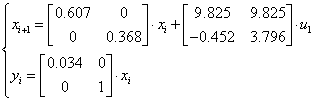
Задавшись ![]() ,
,
![]() , тоді
, тоді
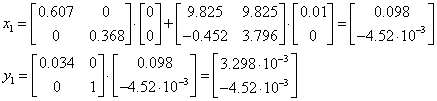
Результати подальших ітерацій представлено в таблиці:
Таблиця 5.
| Збурення | Реакція виходу системи y (t) |
|
|||||||
|
u1=0 u2=0,01 |
y1 y2 |
0 0 |
0,003298 0,00452 |
0,005299 0,00469 |
0,00773 0,006183 |
0,006512 0,006795 |
0,00725 0,00702 |
0,00769 0,00713 |
|
| час t, с | 0 | 14,894 | 29,787 | 44,681 | 59,574 | 74,468 | 89,362 | ||
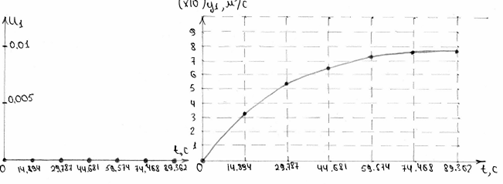
Рисунок 10. Характеристика витрати рідини в дискретному часі.
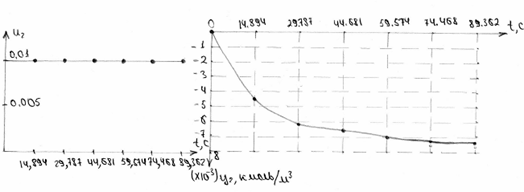
Рисунок 11. Характеристика концентрації в дискретному часі.
3.3 Побудова графіків кривих разгону нелінійної системи
Розглянемо поповнення бака від 0 до номінального значення витрати з урахуванням приросту поданого лінеаризованій моделі. Таким чином, розглянемо стрибок u1=0,03; u2=0.
Позначивши ![]() ,рівняння
бака запишемо у вигляді системи:
,рівняння
бака запишемо у вигляді системи:
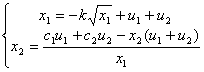
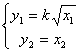
![]()
Перше рівняння є нелінійним зі змінними що розділяються
![]()
З урахуванням того, що ![]() запишемо:
запишемо:
![]() , чи підставляючи
, чи підставляючи
![]()
Виразимо ![]()
Підставляємо ![]() та
та
![]()
Таблиця 6.
| y1 | 0.141 | 0.142 | 0.143 | 0.144 | 0.145 | 0.146 | 0.147 | 0.148 | 0.149 | 0.150 | 0.151 |
| t, с | 0 | 1.5 | 3.188 | 5.116 | 7.357 | 10.026 | 13.315 | 17.585 | 23.643 | 34.072 | 68.958 |
По отриманим даним побудуємо графік:

Рисунок 12. Лінійна та нелінійна характеристика витрати води.
Так як немає аналітичної залежності ![]() , використаємо її кус очно-лінійну
апроксимацію, представляючи на проміжкові від
, використаємо її кус очно-лінійну
апроксимацію, представляючи на проміжкові від ![]() до
до
![]() функцію
функцію ![]() как
как ![]() . Тоді,
. Тоді,
![]() ;
; ![]()
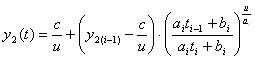
Отримані дані занесемо в таблицю:
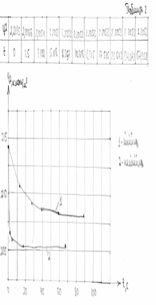
Рисунок 13. Лінійна та нелінійна характеристика концентрації.
3.4 Сталий стан системи
Вичислимо постійне значення системи при умовах
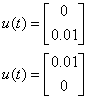
І порівняємо його з результатом розрахунку.
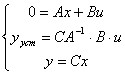
![]()
4. Ідентифікація багатомірної математичної моделі по даним експеремента
4.1 Активна ідентифікація
Для дискретної форми системи (F, G, C) провести реалізацію системи.
Запишемо систему у вигляді:
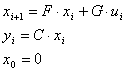
![]()
![]()
![]()
Подавши імпульс по першому входу, розрахуємо:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Із власних векторів від (![]() ) і (
) і (![]() ) побудуємо:
) побудуємо:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При ![]()
![]()
![]()
Знайдемо передаточну функцію системи:
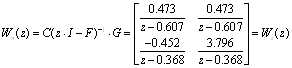 .
.
4.2 Пасивна ідентифікація
Для дискретної форми системи (F, G, C) провести пасивну ідентифікацію системи:
Таблиця 7.
| Такт, n | 0 | 1 | 2 | 3 | 4 | 5 |
| U (n) | 0.01 | 0 | 0 | 0.04 | 0 | 0 |
| 0 | 0.01 | 0.02 | 0 | 0.03 | 0 |
![]()
![]()
![]()
Використовуючи матриці системи в дискретній формі для заданих значень вектора входу, розрахуємо значення вектора виходу
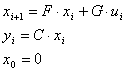
Результати розрахунку занесемо до таблиці:
Таблиця 8.
| Такт, n | 1 | 2 | 3 | 4 | 5 | 6 |
| y (n) | 0.117 | 0.188 | 0,349 | 0.68 | 0.765 | 0.464 |
| -0.00509 | 0.03787 | 0.09342 | 0.01402 | 0.12438 | 0.04577 |
Тогда
![]()


Следовательно, ![]()
![]()
![]()
5. Конструювання багатомірних регуляторів, оптимізуючи динамічні властивості агрегату
5.1 Конструювання П-регулятора, оптимізую чого систему по інтегральному квадратичному критерію
Регулятор стану який оптимізує систему по критерію:
![]()
![]()
Визначається по співвідношенню: P=LR1 (A,B,Q,R);
![]()
![]()
![]()
Притом Q=R=I
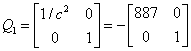
Так як матриця С є інвертованою, для створення регулятора виходу немає
![]()
Необхідно конструювати спостерігач стану -недосяжний
стан вичислюється по формулі ![]() . Відповідно
регулятор виходу має вид
. Відповідно
регулятор виходу має вид ![]()
![]()
Позначивши через z задане значення виходу у і
припускаючи, що ![]() , отримаємо
, отримаємо
![]()
![]()
5.2 Конструювання компенсаторів завдань і вимірюваних збурень
Прийнявши до уваги, що А=В

Якщо при компенсації збурень і завдань зчитувати "вартість" управління, записавши критерій в виді
![]() ,
,
то компенсатори визначаються залежностями
![]()
Значення виходу при дії збурення f в системі без компенсаторів при z=0
![]()
З оптимальною компенсацією
![]() f
f
![]()
5.3 Конструювання регулятора з компенсатором взаємозв'язків
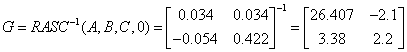
![]()
![]()
![]()
Следовательно,
![]()
Перевіримо чи регулятор дійсно розчіплює систему, тобто матриця передаточних функцій являється діагональною
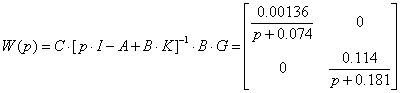
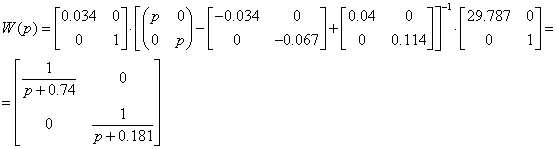
![]() ,
, ![]() , де
, де ![]() ,
, ![]() .
.
Знайдемо
1. ![]()
![]()
2. ![]()
![]() .
.
5.4 Конструювання аперіодичного
Аперіодичний регулятор для дискретної системи
може бути отриманий із умови ![]() . Запишем
. Запишем
![]()
![]()
![]()
5.5 Конструювання децентралізованого регулятора
Використовуючи форму Ассео, запишем:
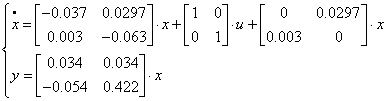
![]()
![]()
Відповідно, отримаємо ![]()
![]() ,
, ![]()
Розв'яжим рівняння Ляпунова.
![]() T=B
T=B
![]()
![]()
5.6 Конструювання надійного регулятора
Якщо матриця G моделяє відмови каналів
вимірювання, то регулятор знаходиться в виді ![]()
![]()
нехай s=0.041
![]()
![]()
![]()
Відповідно, система являеться постійною при любих відхиленнях.
5.7 Конструювання блочно-ієрархічного регулятора
Використаємо регулятор стану і перевіримо чи можна створити послідовність регуляторів стану.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
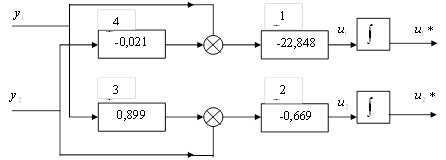
Рисунок 14. Схема блочно-ієрархічного регулятора.
5.8 Конструювання регулятора для білінійної моделі
![]()
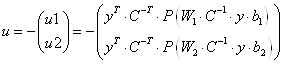
![]()
![]()
![]()
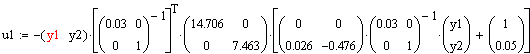
![]()
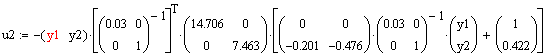
![]()
5.9 Конструювання регулятора для нелінійної системи
Сконструювати нелінійний регулятор, використовуючи початкову не спрощену модель бака.
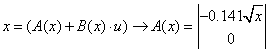 ,
, 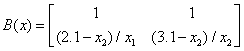
Розрахункове співвідношення для регулятора - ![]() , де
, де ![]()
При s=4, W=1 запишемо
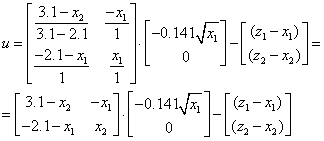
Підставивши ![]() запишемо
запишемо

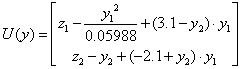
5.10 Конструювання програмного регулятора
Використовуючи лінеаризовану модель в
дискретному часі, запишемо програму переходу системи із стану ![]() в стан
в стан
![]() .
.
![]()
При ![]() ;
; ![]()
Отримаємо
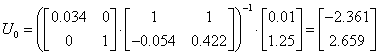
6. Аналіз властивостей зконструйованої системи з оптимальним П-регулятором
6.1 Побудова процесу в системі з П-регулятором
Стале значення виходу при дії збурення f у системі без компенсаторів при z=0
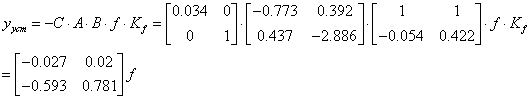
З оптимальною компенсацією
![]() f
f
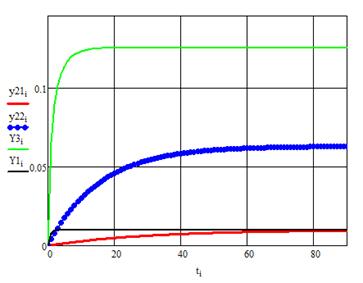
Рисунок 15. Графіки перехідних процесів та кривих розгону по першому та другому виходах з оптимальним П-регулятором з компенсатором і без.
6.2 Обчислення критерію оптимальності в системі
Величина критерію оптимальності обчислюється
за залежністю![]() . Для обчислення величини
критерію з довільним регулятором слід використовувати формулу
. Для обчислення величини
критерію з довільним регулятором слід використовувати формулу
![]() , де
, де ![]() .
.
розв'язавши рівняння Ляпунова отримаємо
![]()
![]()
![]()
розв'язавши рівняння Ляпунова отримаємо
![]()
![]()
При 10% та 5%
![]() ,
,![]()
![]() ,
,![]()
![]() ,
, ![]()
Розв'яжемо ![]() для
всіх матриць при нових значеннях
для
всіх матриць при нових значеннях
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
При 10% та 5%
![]() ,
, ![]()
![]() ,
,![]()
![]() ,
, ![]() .
.
6.3 Обчислити чуйність системи
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6.4 Проаналізувати робастність системи
![]()

6.5 Розв'язати зворотну задачу конструювання
Знайти за яким критерієм є оптимальний регулятор з компенсаторів взаємозв'язків.
![]()
![]()
де W - довільна матриця яка задовольняє умові S>0
![]()
розв'язавши отримаємо
![]()
![]()
![]()
Висновок
Таким чином, в ході виконання курсової роботи на прикладі моделі змішувального бака була розгляне на технологічна послідовність конструювання систем: побудова та перетворення моделей системи, аналіз властивостей початкової системи, конструювання регуляторів, аналіз властивостей і порівняння сконструйованих систем. Також при виконанні були отримані ряд кривих розгону та перехідних процесів для моделі бака, були побудовані структурні схеми моделі в початковій формі, Ассео, зовнішньо зв’язаній формі. Отримали навики конструювання систем з використанням регулятора з компенсатором взаємозв”язків, аперіодичного, децентралізованого, надійного, блочно-ієерархічного регуляторів, програмного регулятора, регулятора для нелінійної моделі, регулятора для білінійної моделі.
Література
1. Методические указания к практическим занятиям по курсу "Основы системного анализа и теория систем", А.А. Стопакевич
2. "Сложные системы: анализ, синтез, управление", А.А. Стопакевич
Додаток
Розв'язання рівняння Рікарті
Розв'язання рівняння Рікарті ![]() визначення матриці Р.
визначення матриці Р.
Сформуємо матрицю
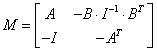
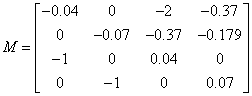
Для обчислення власних значень розкриємо
визначник ![]()
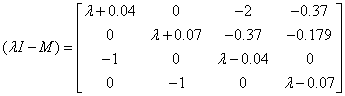
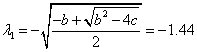
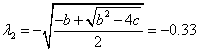
![]()
![]()
![]() .
.
Розв'язання рівняння Ляпунова ![]()
![]()
![]()
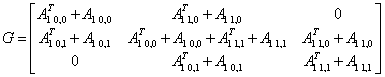
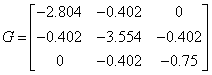
![]() .
.
Обчислення матричної експоненти
![]()
![]()
![]() ,
,![]()
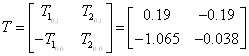
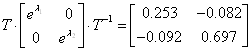 .
.
Фробеніусові матриці
![]()
![]()
![]()
![]()
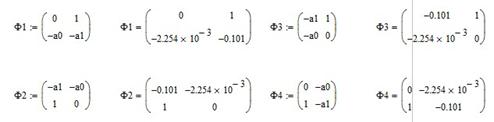
Вандермордова матриця