Контрольная работа: Цифровые устройства и микропроцессоры
Министерство общего и профессионального образования
Самарский государственный технический университет
Кафедра: Робототехнические системы
Контрольная работа
Цифровые устройства и микропроцессоры
Самара, 2001
1. Используя одноразрядные полные сумматоры построить функциональную схему трехразрядного накапливающего сумматора с параллельным переносом.
РЕШЕНИЕ:
Одноразрядный сумматор рис.1 имеет три входа (два слагаемых и перенос из предыдущего разряда) и два выхода (суммы и переноса в следующий разряд).
|
|
||||||
|
ai |
bi |
ci-1 |
Si |
Ci |
||
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 1 | 0 | ||
| 0 | 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 0 | 1 | ||
| 1 | 0 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 0 | 1 | ||
|
|
1 | 0 | 0 | 1 | ||
| 1 | 1 | 1 | 1 | 1 |
Сумматоры для параллельных операндов с параллельным переносом разработаны для получения максимального быстродействия.
Для построения сумматора с параллельным переносом введем две вспомогательные функции.
Функция генерации – принимает единичное значение если перенос на выходе данного разряда появляется независимо от наличия или отсутствия входного переноса.
![]()
Функция прозрачности – принимает единичное значение, если перенос на выходе данного разряда появляется только при наличии входного переноса.
![]()
Сформируем перенос на выходе младшего разряда:
![]()
На выходе следующего разряда:
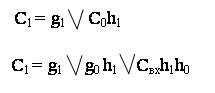
В базисе И-НЕ:
Накапливающий сумматор представляет собой сочетание сумматора и регистра. Регистр выполним на D-триггерах (рис. 2).
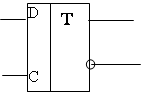 |
|||||
|
|||||
|
2.
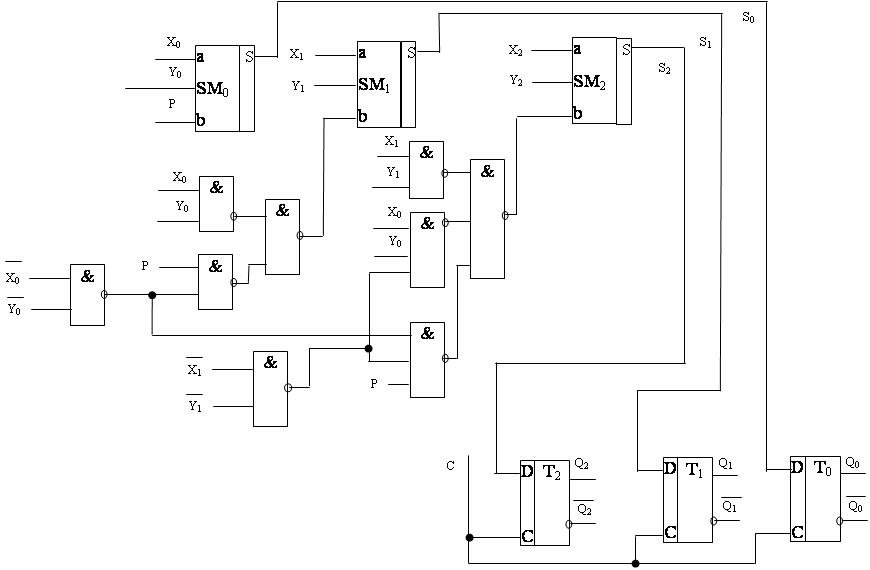
3. Построить схему электрическую принципиальную управляющего автомата Мили для следующей микропрограммы:

РЕШЕНИЕ:
1. Построение графа функционирования:
Управляющее устройство является логическим устройством последовательностного типа. Микрокоманда выдаваемая в следующем тактовом периоде, зависит от состояния в котором находится устройство. Для определения состояний устройства произведем разметку схемы алгоритма, представленной в микрокомандах (Рис. 1).
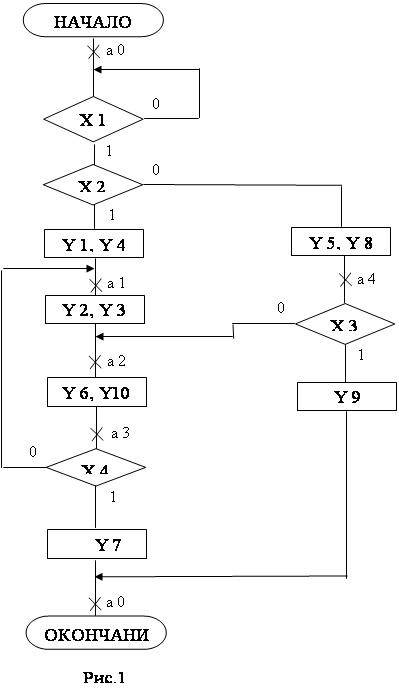
Полученные отметки а0, а1, а2, а3, а4 соответствуют состояниям устройства.
Устройство имеет пять состояний. Построим граф функционирования.
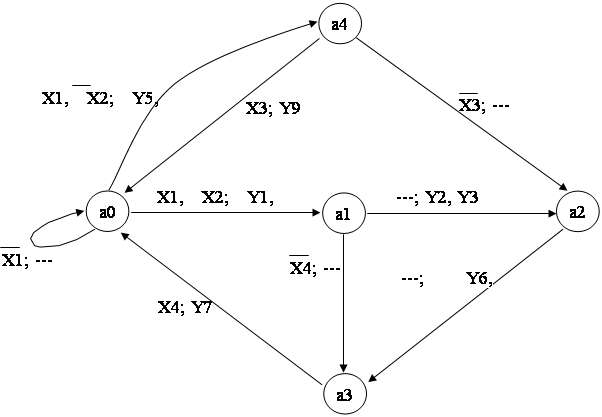
Кодирование состояний устройства.
|
В рассматриваемом устройстве М = 5 k = 3. |
Таблица 1 | ||
| Состояние | Кодовые комбинации | ||
|
Q3 |
Q2 |
Q1 |
|
| а0 | 0 | 0 | 0 |
| а1 | 0 | 0 | 1 |
| а2 | 0 | 1 | 0 |
| а3 | 0 | 1 | 1 |
| а4 | 1 | 0 | 0 |
Соответствие между состояниями устройства и кодовыми комбинациями зададим в таблице 1.
2. Структурная схема управляющего устройства.
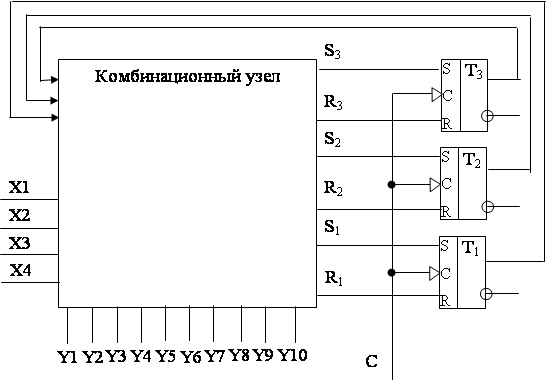
3. Построение таблицы функционирования.
| Текущее состояние | Следующее состояние | Условия перехода | Входные сигналы | |||||||
| обозначение | Кодовая комбинация | обозначение | Кодовая комбинация | Сигналы установки триггеров | Управляющие микрокоманды | |||||
|
Q3 |
Q2 |
Q1 |
Q3 |
Q2 |
Q1 |
|||||
| а0 | 0 | 0 | 0 | а1 | 0 | 0 | 1 | Х1; Х2 |
S1 |
Y1; Y4 |
|
|
0 | 0 | 0 | а0 | 0 | 0 | 0 | Х1 | --- | --- |
|
|
0 | 0 | 0 | а4 | 1 | 0 | 0 | Х1; Х2 |
S3 |
Y5; Y8 |
| а1 | 0 | 0 | 1 | а2 | 0 | 1 | 0 | --- |
S2; R1 |
Y2;Y3 |
| а2 | 0 | 1 | 0 | а3 | 0 | 1 | 1 | --- |
S1 |
Y6;Y10 |
| а3 | 0 | 1 | 1 | а0 | 0 | 0 | 0 | Х4 |
R2; R1 |
Y7 |
|
|
0 | 1 | 1 | а1 | 0 | 0 | 1 | Х4 |
R2 |
--- |
| а4 | 1 | 0 | 0 | а0 | 0 | 0 | 0 | Х3 |
R3 |
Y9 |
|
|
1 | 0 | 0 | а2 | 0 | 1 | 0 | Х3 |
R3; S2 |
--- |
Таблица перехода RS триггера.
| Вид перехода триггера | Сигналы на входах триггера | |
| S | R | |
|
|
0 | - |
|
|
1 | 0 |
|
|
0 | 1 |
|
|
- | 0 |
4. Запишем логические выражения для выходных значений комбинационного узла.
|
S1 Y1 Y4 = a0 |
|
|
|
S2 R1 Y2 Y3 = a1 |
|
S1 Y6 Y10 = a2 |
|
R2 R1 Y7 = X4 a3 |
|
|
|
R3 Y9 = X3 a4 |
|
|
Определим логическое выражение для каждой выходной величины.
|
|
|
|
|
S1 = a0 Ú a1 |
|
|
|
|
|
R1 = a1 Ú X4 a3 |
| Y1 Y4 = a0 |
|
|
| Y2 Y3 = a1 |
| Y6 Y10 = a2 |
| Y7 = X4a3 |
| Y9 = X3a4 |
5. Построение логической схемы комбинационного узла.
Входящие в выражения значения a0, a1, a2, a3, a4, определяемые комбинацией значений Q3, Q2, Q1 могут быть получены с помощью дешифратора.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
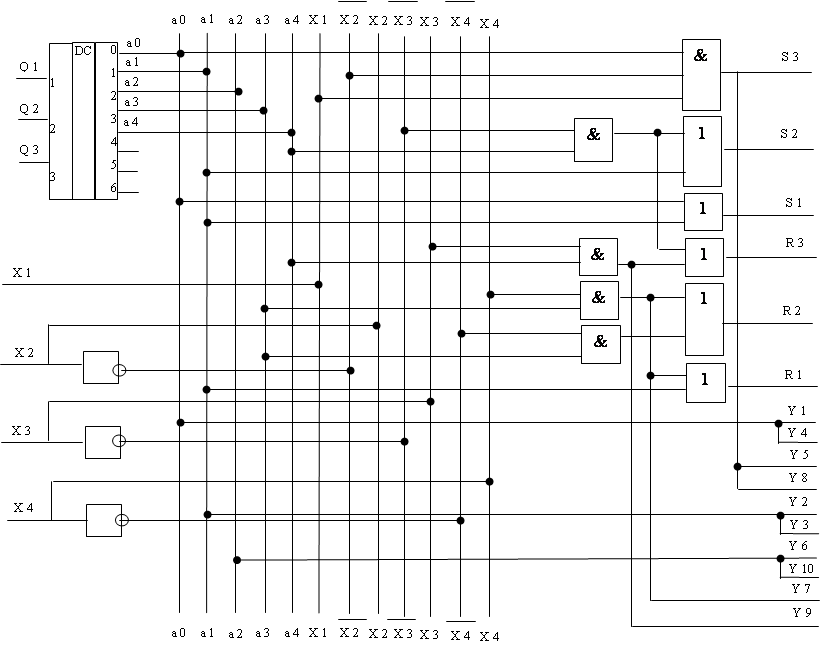
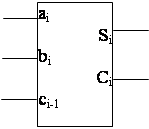 Таблица истинности одноразрядного сумматора.
Таблица истинности одноразрядного сумматора.